Against better knowledge: The magical force of amodal volume completion

Abstract

In a popular magic routine known as “multiplying billiard balls”, magicians fool their audience by using an empty shell that the audience believes to be a complete ball. Here, we present some observations suggesting that the spectators do not merely entertain the intellectual belief that the balls are all solid, but rather automatically and immediately perceive them as such. Our observations demonstrate the surprising potency and genuinely perceptual origin of amodal volume completion.

In the popular and powerful conjuring routine known as “multiplying billiard balls” or “Chicago ball trick”, magicians start by showing a single ball held between the thumb and the index finger (Figure 1[a]). Then, after a small flick of the wrist, a second ball magically appears between the index finger and the middle finger. After repositioning the second ball one step up, such that it is held between the middle finger and the ring finger, a third ball “magically” appears between the index finger and the middle finger – and so on (see http://www.youtube.com/watch?v=seaO1c5awYw).

Figure 1.

In the multiplying billiard balls routine, the magician first presents a single ball (a). Then, after a quick flick of the wrist, a second ball suddenly appears (b).

This stunning trick basically relies on two simple principles. The first one, which is of primary interest here, is that the first ball is actually an empty semi-spherical shell already containing the second ball, which, using the middle finger, is quickly rolled out of the shell during the swift flick of the wrist. The second principle, which shall not concern us further here, is that while the magician relocates the second ball using the other hand, he uses this opportunity to secretly load a new ball into the empty shell. Thus, on the face of it, this magical effect may be said to rest on the simple facts (a) that a semi-spherical shell looks indistinguishable from a full sphere (be it solid or hollow) when it is viewed from the right direction and (b) that the spectators erroneously believe that the semi-spherical shell is a full sphere. At first thought, this simple explanation may seem quite satisfactory. It is, however, incomplete in two regards. First, it fails to specify why the spectators adopt the belief that they are seeing solid full balls rather than empty shells. Second, it fails to explain the curious strength of this conviction, which is evidenced by the fact that spectators have a hard time figuring out how the trick works: In an investigation of problem solving using 34 different magical routines as test material, Faber (2012) found that only five of the tricks investigated were more difficult to debunk than this one. Even after repeated exposure, only 29% of the subjects were able to figure out how it works.

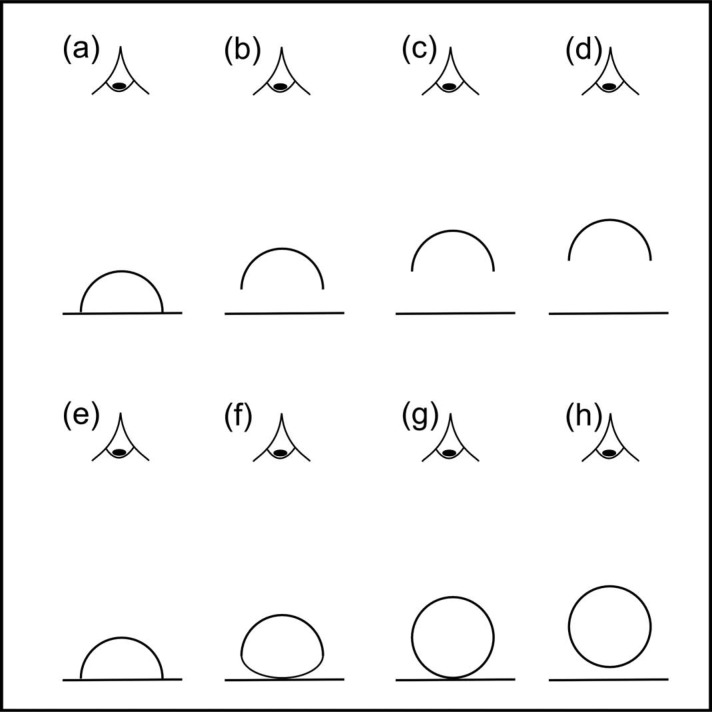
We believe that the key to understanding the impressive powerfulness and robustness of this magical routine is this: Amodal volume completion (Tse, 1999; van Lier, 1999; van Lier & Wagemans, 1999) must be understood as a genuinely perceptual phenomenon (Gerbino & Zabai, 2003; Kanizsa, 1970, 1985; Kanizsa & Gerbino, 1982; Michotte, Thinès, & Crabbé, 1964) in the sense that it is automatic and cognitively impenetrable (Pylyshyn, 1999). Viewed from this perspective, the spectators do not merely entertain the intellectual belief that the semi-spherical shell is a solid ball, but rather automatically and immediately perceive it as such because that is what their visual systems tell them to be the case. Here, we describe how a simple and intriguing observation supporting this explanation can be made. Put a semi-spherical shell on a table and view it directly from above, as illustrated in Figure 2. In this situation, the shell is perceived as a semi-sphere. If you hold it slightly above the table, however, it looks like a full sphere. These observations can be made with the same result irrespective of whether the semi-spherical shell is viewed monocularly or binocularly. Note, however, that if the semi-spherical shell is photographed rather than viewed directly, it looks like a full sphere in both cases. Together, these observations suggest (1) that the visual system prefers the full sphere interpretation by default and (2) that this default can be overridden by cues signalling (a) that the semi-spherical shell is so close to the plane of the table that there is not enough free space to accommodate a full sphere and (b) that the surface of the table is indeed completely planar.

Figure 2.

Schematic illustration of the basic effect. A semi-spherical shell is put on the table and viewed directly from above. As the shell is lifted up from the table towards the eye of the observer (a)–(d), it is perceived to morph gradually into a complete ball (e)–(h).

Although the latter may seem self-evident and unproblematic, the visual stimulus is in fact compatible with an infinite number of different completions of the visible parts of the semi-spherical shell and the table (Gerbino & Zabai, 2003). For instance, it is also compatible with a full sphere resting in a semi-spherical indentation in the table. Based on the findings of Gerbino and Zabai (2003), one would actually expect the latter interpretation to be perceived. In a systematic investigation of the factors determining how the visual ambiguities associated with joined objects are resolved, they found that two factors were particularly effective. First, the smaller of the two objects tends to be perceived as penetrating the other. Second, the same tendency was found for the object that is above the other. In our case, both of these tendencies should favour the percept of a full sphere partially penetrating the table, but what we actually perceive is a semi-sphere on a completely planar surface. So, what are the differences between our situation (Figure 3[a]) and the stimuli investigated by Gerbino and Zabai (2003) that may potentially explain this discrepancy? First, most of their stimuli were uniformly coloured, while the table surface in our Figure 3(a) is textured. Thus, amodal completion of the texture elements (the small dots on the table cloth) may be a factor that favours the perception of an unbroken planar surface. Second, the object intersections studied by Gerbino and Zabai (2003) all had the property that if one of the two objects was completed in the most simple way, the other one would necessarily have a concave indentation. In our case, however, the percept actually observed involves two non-concave objects, namely a flat surface and a semi-sphere, while the converse solution would involve a cavity in the table surface. Thus, the discrepancy between our observation and the results of Gerbino and Zabai (2003) may be taken to suggest that (a) the visual system has a tendency to avoid concave completions, and (b) that this tendency may override those documented in Gerbino and Zabai's (2003) study. Although this issue is not the main point of the present note, it appears interesting and important enough to warrant further research.

Figure 3.

Two views of the same semi-spherical shell. When it is lying on the table (a) it is perceived as a semi-sphere. When it is tilted off the table towards the observer (b), however, it looks like a complete ball.

When observing the actual scene (but not the photographic reproduction), both binocular cues and dynamic accommodation cues (Held, Cooper, O'Brien, & Banks, 2010), which are absent in a photographic reproduction, may contribute to signalling that the semi-spherical shell is so close to the table that a full sphere and an unindented table would intersect. It is, however, worth noting that the latter appear to be sufficient in themselves, since the semi-spherical shell located directly on the table is perceived as semi-spherical also when it is viewed monocularly.

Importantly, the ostensive knowledge that one is in fact viewing a semi-spherical shell, and the fact that it looks like a semi-sphere when it is placed directly on the table, does not prevent one from immediately experiencing it as a full sphere once it is lifted sufficiently far away from the plane of the table. In fact, lifting the semi-spherical shell slowly upwards from the table gives rise to the very compelling impression that a semi-sphere is dynamically transforming into a full sphere, whereby the amount of “growth” seems to accord with the space available between the semi-sphere and the plane of the table. Putting the semi-spherical shell down again produces a corresponding shrinking experience.

Naïvely, one may be tempted to say that the percept of a full sphere evoked when the semi-spherical shell is lifted up from the table is “illusory”, while the percept evoked when it is located on the table is “veridical”. It should be pointed out, though, that also the latter case involves an interesting case of perceptual volume completion: The hollow semi-spherical shell actually looks more like a solid semi-sphere. Moreover, it is worth pointing out that the perception of a completely planar table extending behind the semi-spherical shell, albeit corresponding to the reality of the particular scene used to generate the stimulus, is also not trivial, and constitutes an interesting case of amodal volume completion in itself. As already mentioned, other scenes (e.g. an indented table and a full sphere) could in principle produce the same visual stimulus (Gerbino & Zabai, 2003).

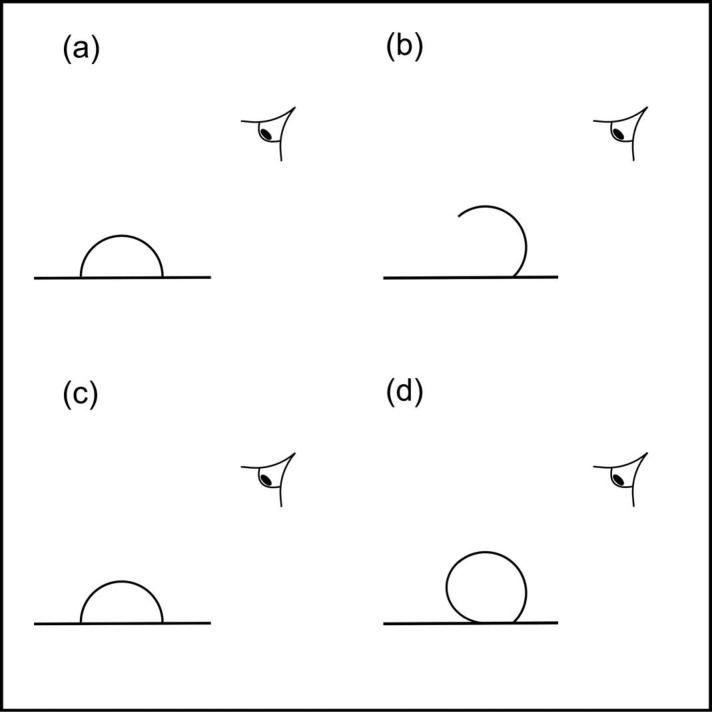
A slight modification of this demonstration produces much the same result, but has the advantage that some notion of the effect can be conveyed by a photograph (Figure 3). As schematically illustrated in Figure 4, the semi-spherical shell lying on the table is now viewed from an oblique angle rather than directly from above, and rather than lifting it vertically up from the table, you lift it by tilting it towards your eye. Also here, a dynamic morphing into a full sphere can be observed (Supplementary Movie 1). The main important difference between these two manners of presentation is that now, the projection of the semi-spherical shell lying on the table onto the film plane of the camera (or the eye) is no longer compatible with a full sphere, which makes it clear that it is a semi-sphere also in the photographic reproduction.

Figure 4.

Schematic illustration of the effect demonstrated in Figure 3 and Supplementary Movie 1. A semi-spherical shell is observed from an oblique angle, while lying on a table (a) or tilted towards the observer (b). In the former case, it is perceived as a semi-sphere (c). When it is tilted away from the table towards the observer, though, it seems to morph into a complete ball (d).

Our demonstration reiterates a point previously made by Metzger (1941, p. 32): A spoon may easily look like an “egg” when viewed from the convex side, but an egg will never look like a spoon.

Perhaps the most intriguing aspect of our demonstration is the compelling visual quality of the dynamic shape changes, which seems to defy the fact that the parts of the visual object that are perceived as changing are, of course, always hidden from direct view. A strange percept indeed: compellingly visual, yet at the same time experienced as pertaining to a hidden portion of the visual object. If you have not seen it yourself, you probably would not believe it. Seeing is believing.