A Method to Predict Blood-Brain Barrier Permeability of Drug-Like Compounds Using Molecular Dynamics Simulations

Abstract

The blood-brain barrier (BBB) is formed by specialized tight junctions between endothelial cells that line brain capillaries to create a highly selective barrier between the brain and the rest of the body. A major problem to overcome in drug design is the ability of the compound in question to cross the BBB. Neuroactive drugs are required to cross the BBB to function. Conversely, drugs that target other parts of the body ideally should not cross the BBB to avoid possible psychotropic side effects. Thus, the task of predicting the BBB permeability of new compounds is of great importance. Two gold-standard experimental measures of BBB permeability are logBB (the concentration of drug in the brain divided by concentration in the blood) and logPS (permeability surface-area product). Both methods are time-consuming and expensive, and although logPS is considered the more informative measure, it is lower throughput and more resource intensive. With continual increases in computer power and improvements in molecular simulations, in silico methods may provide viable alternatives. Computational predictions of these two parameters for a sample of 12 small molecule compounds were performed. The potential of mean force for each compound through a 1,2-dioleoyl-sn-glycero-3-phosphocholine bilayer is determined by molecular dynamics simulations. This system setup is often used as a simple BBB mimetic. Additionally, one-dimensional position-dependent diffusion coefficients are calculated from the molecular dynamics trajectories. The diffusion coefficient is combined with the free energy landscape to calculate the effective permeability (P_eff) for each sample compound. The relative values of these permeabilities are compared to experimentally determined logBB and logPS values. Our computational predictions correlate remarkably well with both logBB (R² = 0.94) and logPS (R² = 0.90). Thus, we have demonstrated that this approach may have the potential to provide reliable, quantitatively predictive BBB permeability, using a relatively quick, inexpensive method.

Introduction

Most drugs need to pass through at least one cellular membrane to reach their intended target. Although tight binding of a drug molecule to its intended target is important for potency, poor membrane permeability will likely result in a lack of efficacy in vivo. Thus, a detailed understanding of the partitioning of the solute in the membrane is vitally important for pharmacokinetics and rational drug design. Two possible transport modes are available for a molecule to pass through a membrane: active and passive (1). Active transport involves a transport protein that uses energy, e.g., ATP hydrolysis, to shuttle a molecule across a membrane. Passive transport, however, is the most common mode of drug passage through membranes and involves diffusion with no outside assistance or energy consumption. The rate of passive diffusion across a membrane is proportional to the partition coefficient of the compound between the membrane and the external medium, the diffusion coefficient of the compound through the membrane, and the compound’s concentration gradient across the membrane (2). Important chemical properties of small molecules for the process of membrane binding and diffusion are lipophilicity, molecular weight, and measures of molecular polarity (3).

Drugs that specifically target the central nervous system (CNS) must first pass the blood-brain barrier (BBB). Consisting of endothelial cells that form the brain capillaries (4), the BBB restricts the penetration of molecules, because of tight junctions formed by lateral transmembrane proteins, lack of fenestrations, the negative surface polarity, and the high level of efflux transporters, especially P-glycoprotein (P-gp) (5). The tight junctions significantly reduce permeation of ions and other small hydrophilic solutes through the intercellular cleft (paracellular pathway), thus forming the physical barrier. Essential molecular fluxes must use predominantly transcellular pathways. Passive diffusion of small compounds is assumed to be the most important permeability process through the BBB, although active transport of compounds may be more significant than originally thought (6). Although the BBB is protective in nature, the inability for drug molecules to permeate the BBB is a significant impediment for CNS drug candidates and should be addressed early in the drug discovery process (7). Additionally, drugs targeting peripheral organs need to be investigated for BBB permeability to avoid possible CNS side effects.

Based upon the large assumption that a compound’s activity is equivalent to its BBB permeability, compounds are often classified by the terms CNS+ or CNS−. (8–10) CNS+ refers to compounds that show a desired in vivo effect in the CNS, whereas CNS− refers to compounds that do not show an expected in vivo CNS effect. However, this descriptor is phenotypic and does not properly describe those compounds that have low BBB permeability but high potency. Thus, this descriptor can be misleading.

Perhaps the most common parameter used to quantify penetration of a compound across the BBB is the ratio of the concentration of compound measured in the brain to the concentration of compound measured in the blood at steady state. This ratio is expressed as logBB (log[brain]/[blood]) and determines the total extent of brain exposure, at a steady state.

A less commonly used descriptor of BBB permeability is the determination of the permeability surface-area product (expressed as logPS). LogPS is perhaps a more appropriate in vivo measurement when considering BBB penetration (11,12) and is more informative than logBB. The logPS measurement is most often performed following the perfusion method that was implemented by Takasato et al. (13). In doing this, the method eliminates the effect of serum binding of the compound in question and provides a direct measure of BBB apparent permeability. However, because of the need for microsurgical expertise, the logPS measurement is resource intensive and relatively low throughput. As a result, significantly less literature data are available. PS can be calculated using the Renkin-Crone (14,15) equation:

$$\mathrm{PS}=-F\ln \left(1-\frac{K_{in}}{F}\right),$$ (1)

where PS (the permeability surface-area product) is measured in (ml/min/g brain), F is the cerebral blood or perfusion flow rate (ml/min/g brain), and K_in is the unidirectional transfer constant. K_in is equal to (Q_br/C_pf)/T, where Q_br is the concentration of compound in the brain (corrected for the vascular volume), C_pf is the concentration of compound in the perfusion fluid, and T is the perfusion time. Note, logBB measures concentrations at equilibrium, whereas logPS is more a measurement of the initial permeability rate. As such, logPS is the pharmacokinetic uptake clearance across the BBB into the brain.

Because of the labor-intensive, expensive, low-throughput, and technically challenging process of obtaining detailed in vivo BBB permeability data, several well-characterized in vitro and in silico permeability prediction methods have been developed. These methods are faster, cheaper, easier to carry out, and are important in the early stages of the drug discovery process.

Two of the most common and relatively simple in vitro BBB permeability prediction methods are the parallel artificial membrane permeability assay (PAMPA) and the immobilized artificial membrane (IAM) technique. The PAMPA in vitro technique was developed in 1998 by Kansy, et al. (16). It was originally developed to rapidly predict passive permeability through the gastrointestinal tract, but has since been adapted for use in BBB studies by Di, et al. (17). PAMPA-BBB has shown good prediction of BBB penetration for CNS classes of drugs (17–22). The technique involves a donor compartment and an acceptor compartment separated by a filter supporting a liquid artificial membrane. The artificial membrane can be composed of a variety of phospholipid mixtures. The compound to be tested is placed in the donor compartment and is allowed to permeate between the donor and the acceptor compartments through the artificial membrane. As the assay can be performed in 96-well plates, high throughput screening is possible. IAMs mimic the phospholipid environment of the BBB by anchoring synthetic lipid analogs to silica particles in monolayer density. These particles are then used as the packing material for a high-performance liquid chromatography column (23–26). The IAM chromatographic retention factors are used to generate predictions of membrane permeability. These systems have shown reasonable results for prediction of permeability, despite the retention time in the column not reflecting actual passage across the membrane (27,28).

An alternate approach is to employ computational methods to compute logBB. Most in silico prediction approaches use quantitative structure-activity relationship (QSAR) models (29–33). In QSAR studies, the biological activity is treated as an outcome of the various interactions that a compound experiences during transport through BBB (whether this be passive or active). These interactions are assumed to be governed by the chemical structure and properties of the compound, also known as descriptors. As such a mathematical model of the biological activity is optimized based on a combination of a variety of descriptors for the small molecule compound. Thus, a change in structure can result in a change in biological response, which in this case is permeability through the BBB.

One of the most powerful (though computer intensive) in silico techniques is molecular dynamics (MD), which allows the simulation of molecular processes, such as diffusion, at the atomic level (34). Coupling MD with free energy techniques provides a powerful tool to study membrane permeability in detail (35). Human membranes are a complicated mixture of small molecules, various lipids, and proteins, but with a judicious choice of lipid a single bilayer may provide similar physicochemical properties to a cellular membrane. Indeed, phosphatidylcholine lipids are the major phospholipid within cellular membranes (36). Previous studies have investigated the permeation of small molecules (such as water and ethanol) and a limited number of drug molecules through homogenous lipid bilayers (37–42). Although these MD simulations could not replicate the same absolute permeability values seen experimentally, they were able to reproduce the relative permeabilities of these compounds.

In this study, we use free-energy simulations to investigate the permeability of 12 diverse small molecule compounds (Fig. 1) through a simple BBB mimic. We compare the computed effective permeabilities (P_eff) of these compounds to experimentally measured values of logBB and logPS and find this approach to be reliable and predictive of compound permeability through the BBB.

Figure 1.

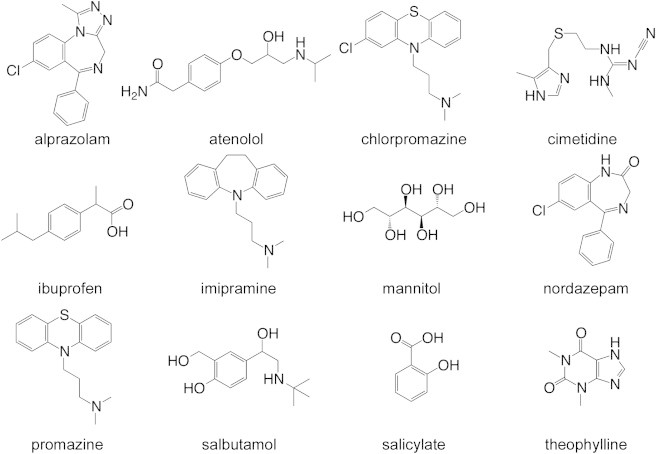
Molecular structure of the 12 small compounds studied.

Methods

For this study, the following small molecule compounds were chosen: alprazolam, atenolol, chlorpromazine, cimetidine, ibuprofen, imipramine, mannitol, nordazepam, promazine, salbutamol, salicylate, and theophylline (Fig. 1). The sample set was selected based upon several criteria, such as their size, charge, general ability to cross the BBB via a passive diffusion mechanism, and most are compounds that have been used in previous BBB permeability studies. Of importance, they cover a wide range of logBB values from ∼1.5 to −2.5 as evenly distributed as possible (Table 1, see Fig. 3 A). Of the 12 compounds, six are identified in the literature (43–46) to cross the BBB, and six are identified to not cross the BBB (Table 1).

Table 1.

List of molecules investigated and their BBB permeability parameters

Compound	logBB	logPS	Calculated logPeff	BBB+/−	aPredicted BBB+/−	bPredicted logBB	References
Mannitol	−2.51	−4.30	−6.62	−	−	−2.30	(46,70,71)
Cimetidine	−1.42	−3.93	−3.94	−	−	−1.34	(20,43,72)
Salicylate	−1.10	−3.40	−5.17	−	−	−1.78	(29,45,73)
Salbutamol	−1.03	c	−1.95	−	−	−1.31	(43,74)
Atenolol	−0.87	c	−1.77	−	−	−0.57	(43,75)
Theophylline	−0.29	−2.80	−0.94	−	−	−0.27	(44,71,73)
Ibuprofen	−0.18	−1.58	−0.63	+	−	−0.16	(45,75,76)
Alprazolam	0.02	c	0.67	+	+	0.30	(43,75)
Nordazepam	0.50	−1.00	2.04	+	+	0.79	(43,77,78)
Imipramine	0.83	−1.43	2.13	+	+	0.82	(43,79,80)
Chlorpromazine	1.06	−1.20	2.68	+	+	1.02	(43,73,81)
Promazine	1.23	c	2.78	+	+	1.05	(43,82)

^aPredicted BBB+ if logP_eff ≥ 0, predicted BBB− if logP_eff < 0.

^bUsing Eq. 7.

^cNo data available.

Figure 3.

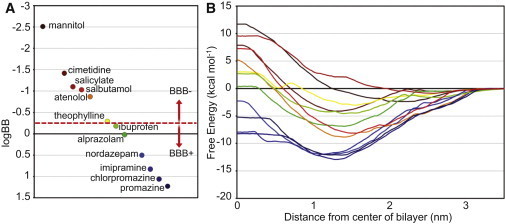
(A) The range of logBBs of the molecules studied. The horizontal axis distances have been introduced only for the purposes of clarity. (B) The PMFs for the molecules studied. For compounds that exist primarily as charged species at physiological pH, PMFs for both the charged and neutral state were calculated (Fig. S2). Their combined PMFs are presented here. BBB+ compounds are colored dark blue to green, whereas BBB− compounds are colored dark red to yellow.

MD setup

All simulations were run using GROMACS 4.5.5 (47). The Berger, et al. force field was used for the 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC) molecules (48), the gromos53a6 force field was used for the small compounds (49), and the SPC model was used to represent the water (50). Each simulation contained a single copy of the compound harmonically restrained at specified locations along the z axis in the solvated DOPC bilayer system. The complete system contained 5124 water molecules, 72 DOPC molecules, and one small compound. A typical system contained a total of ∼19,300 atoms. The system was energy minimized using a combination of steepest descents and conjugate gradients.

The energy-minimized system was used for MD simulations. Simulations were performed at 323 K (well above the gel-liquid phase transition temperature) using the Nosé-Hoover thermostat (51) with τ_T = 0.5 ps. The pressure was maintained at 1 bar using a semi-isotropic Parrinello-Rahman barostat (52) with τ_P = 1 ps and a compressibility of 4.5 × 10⁻⁵ bar⁻¹. Bond lengths were constrained using the LINCS algorithm (53), allowing a 2 fs time step to be used. Nonbonded interactions were truncated at 1.4 nm, and the neighbor list updated every 10 ps. The long-range electrostatic interactions were calculated using the particle mesh Ewald method (54,55).

The topologies for the small molecule compounds were generated using the Automated Topology Builder server [http://compbio.chemistry.uq.edu.au/atb/] (56). The topology-building server combines a knowledge-based approach with quantum mechanical calculations to produce parameters that are compatible with the desired force field. Initially, the molecule is optimized at the HF/STO-3G level of theory, and then reoptimized at the B3LYP/6-31G^∗ level of theory (57–59) in implicit water. The charges are initially estimated by fitting the electrostatic potential using a Kollman-Singh scheme (60). The Hessian matrix is then calculated and used to estimate force constants for bonds and angles. All compounds were modeled in their neutral forms and physiologically relevant charged states. All parameters are freely available from the Automated Topology Builder server.

Free-energy calculations

Umbrella sampling was used to calculate the potential of mean force (PMF) free-energy profiles for the partitioning of compounds. A single harmonic restraint with a force constant of 1000 kJ mol⁻¹ nm⁻² was applied to the distance between the center of mass of the DOPC bilayer and the center of mass of the compound, in the direction of the z axis (the normal to the bilayer). One hundred different umbrella sampling simulations were performed in increments of 0.1 nm along the z axis direction. The center of the bilayer was treated as z = 0, thus the windows spanned z = −5 nm to z = 5 nm. The 10 nm distance completely covers the traversal of the compound from bulk water, through the entire membrane, and out into bulk water again. This set of simulations was carried out for each of the compounds of interest, as well as ethanol (a threonine side-chain analog), which was used as a control for comparison to previously published data (41).

Each simulation window was initially run for ∼45 ns, for a total of ∼100 μs of simulation time for the 20 different drug compounds charged state combinations and one control simulation. The initial ∼20 ns of each simulation was regarded as extensive equilibration time to allow the compound to correctly orient within the system. This equilibration time was tested to see if the PMF curves for each compound had converged (Fig. S1 in the Supporting Material). If needed, simulations were extended or the number of umbrella sampling windows were increased to achieve convergence. All subsequent analyses were carried out only on the final 25 ns of each simulation. The weighted histogram analysis method (61), as implemented within GROMACS, was used to calculate the PMF for each compound based upon the data from the umbrella sampling distributions. The PMF curves are averaged as the distance of the compound from the center of the bilayer (where z = 0) because the lipid bilayer can be treated as symmetrical. All free-energy profiles are normalized to zero in bulk water.

Diffusion and permeability

Membrane permeability of a small molecule can be calculated by combining information from the PMF 1D energy landscape with diffusion coefficients within the membrane. These diffusion rates may vary with position within the membrane.

The position-specific diffusion coefficients were calculated from the MD simulation data using the method of Hummer (62). For each position-restrained simulation, the positions of the compound were sampled at 2 ps intervals, and the variance and autocovariance—at lags from one interval up to 500 intervals—were calculated using 500 points for each variance or covariance calculation. The resulting autocovariance curve decays roughly exponentially with increasing lag time—though experimental noise causes the curve to fluctuate around zero rather than decaying fully to zero with increasing lag. A least-squares fit to the log of the autocovariance data was made to estimate the characteristic time, τ, of the autocovariance decay. The long-run fluctuations around zero were not included in this estimate—points on the curve after it first decays within the standard deviation of the long-run fluctuations were discarded. The diffusion coefficient was calculated as

$$D\left(Z\right)=\frac{\mathrm{var}\left(Z\right)}{{\tau }_Z},$$ (2)

where 〈Z〉 is the average of the reaction coordinate Z in the biased run, and $\mathrm{var}\left(z\right)$ is the variance of the compound position (the auto-covariance at lag zero). The autocovariance curve/diffusion calculation was repeated at 500-sample-point intervals for the duration of the MD simulation, thus providing ∼40 largely independent estimates of the diffusion coefficient for each position-restrained MD simulation. These estimates were averaged to produce the position-specific diffusion coefficient.

The effective membrane permeability, P_eff, can be calculated from the integral for effective resistivity, R_eff, (Marrink and Berendsen (63)),

$$\frac{1}{{\mathrm{P}}_{\mathrm{eff}}}={\mathrm{R}}_{\mathrm{eff}}={\int }_0^{Z}R\left(z\right)dz$$ (3)

where R(z) is the resistivity of each membrane slice,

$$R\left(z\right)=\frac{e^{\beta \left(\Delta G\left(z\right)\right)}}{D\left(z\right)},$$ (4)

where $\beta$ is 1/(k_BT), that is, the inverse of the Boltzmann constant times the temperature, ΔG(z) is the free energy from the PMF calculations, and the integral is over the bounds of the membrane.

In cases where a compound can exist in two protonation states at pH 7.4 (representation of physiological blood (64) and cytoplasmic (65) pH), the position-specific diffusion coefficient calculations are then carried out separately for each form—charged and neutral. In these cases the calculation of the resistivity of each membrane slice takes into account the potential flux of each form, accounting for the free-energy difference between the charged and neutral forms at each position,

$$R\left(z\right)=\frac{R_c\left(z\right)R_n\left(z\right)}{R_c\left(z\right)+R_n\left(z\right)},$$ (5)

where R_c(z) and R_n(z), are the resistivity of the charged and neutral forms, respectively. R_c(z) is calculated as in Eq. 3, with ΔG_c(z), the free energy of the charged form at position z compared to its free energy in bulk water, replacing ΔG(z). R_n(z) is calculated analogously, except that the neutral species PMFs used to calculate ΔG_n(z) have been offset by the free energy required to neutralize the charged species of that compound in bulk water at pH 7.4, according to the method described by MacCallum, Bennett, and Tieleman (41),

$$\Delta G_{\text{neutralize}}=\left(\mathrm{p}{\mathrm{K}}_{\text{a}}-\mathrm{pH}\right)RT\ln 10,$$ (6)

where the pK_a for a compound is obtained from the literature, R is the gas constant, T is the temperature, and the pH is the physiological value of 7.4.

Results

In silico system is consistent with existing published data

Membranes can have complicated phase behavior and care must be taken to simulate the desired phase. To ensure that the DOPC bilayer has the correct fluidity, the partial density profile of the system (Fig. 2 A) was measured to ensure the correct conformation of the bilayer and was compared to previous simulations (41,66–68). The density profile agrees extremely well with the published data, indicating that the system is equilibrated and behaving as anticipated. The membrane thickness (just >4 nm) lies within the limits defined by those previous simulations. The area per lipid is slightly (0.02–0.03 nm²) smaller than previous studies. However, this value is self-consistent (standard deviation of 0.01–0.02 nm²), and is only just outside the experimental range of uncertainty (0.01 nm²). The membrane-solvent interface is at ∼2.5–3.0 nm from the center of the bilayer. Additionally, there is the characteristic dip in the density at the center of the bilayer due to the disorder of the lipid tails.

Figure 2.

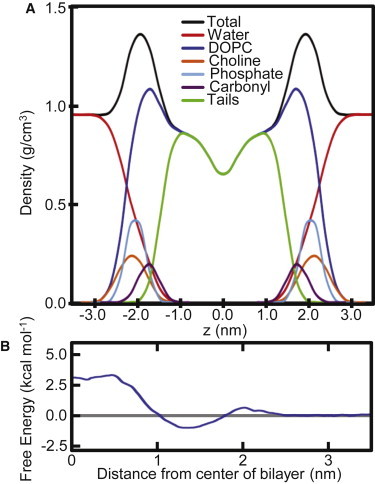
(A) Transverse partial density profile of the various components of the DOPC lipids forming the membrane. (B) PMF free energy for ethanol traversing through the DOPC membrane.

A second validation measure was to carry out a free-energy control simulation on a highly studied molecule (ethanol) to ensure the generated parameters for the drug molecules are compatible with the GROMACS force field. For this simple test, we calculated the PMF profile for ethanol (Fig. 2 B), permeating the DOPC membrane. This small, uncomplicated molecule was previously studied by MacCallum, et al. (41,67), using the same lipid and water models, as the side-chain analog to threonine. The shape of our ethanol PMF curve is almost identical to that calculated by MacCallum, et al. A small maxima occurs at ∼2.0 nm from the bilayer center (hydrophilic portion of the bilayer). There is a single minima at ∼1.3 nm from the bilayer center due to the amphipathic nature of this region. A maximum plateau occurs at ∼0.5 nm from the hydrophobic bilayer center. Indeed, our calculated free energy at the bilayer center (2.9 kcal/mol) is very similar to the reported 3.1 kcal/mol (41), and our calculated free energy at the interface (−0.9 kcal/mol) is also very close to the previously reported value of −1.0 kcal/mol (67). In the study by MacCallum et al., parameters for ethanol were derived from the OPLS force field, which has been shown to be well suited for free-energy calculations. The ethanol parameters generated from the ATB server perform as well as OPLS and should also provide reliable simulation results for the sample set of small molecule compounds.

Despite this excellent agreement with published data, our ethanol simulation was only carried out as a comparative control measure and will not be used for the BBB permeability analysis because ethanol is a notoriously difficult compound to measure (Liu, et al. (29) report an eightfold error in predicting ethanol logPS). Ethanol does not behave in the same way as other small drugs (29), and furthermore may itself alter the integrity of the BBB (69).

Free-energy calculations for compounds crossing the bilayer

PMF profiles for the 12 compounds were calculated (Fig. 3 B). In general, the PMFs for most of these compounds show qualitatively similar overall behavior, but differ quantitatively within the membrane. All the compounds show an initial stabilizing interaction (the range of which varies from ∼0.5–3.0 kcal/mol) when first going from bulk solvent into the headgroup region of the membrane (∼2.5–3.0 nm from the bilayer center). Generally, the most stabilizing region of the membrane is 1.0–1.5 nm from the center of the membrane (with the exceptions of mannitol and salicylate, which are most stabilized at ∼2.0–2.5 nm). This typical stabilization at ∼1.0–1.5 nm from the center of the membrane reflects the amphipathic nature of these compounds because they must be soluble enough to travel in blood yet be hydrophobic enough to penetrate cellular membranes. A relative barrier (compared to the minima) for every compound is at the membrane center.

A general observation can be made about the PMF curves in terms of how they relate to the BBB permeability of the compounds. The PMFs of BBB+ compounds are typically more negative relative to the free energy in bulk solvent, with the free energy at z = 0 also negative (or just slightly above zero). In contrast, the PMFs of BBB− compounds are more positive, with the free energy at z = 0 always positive relative to the free energy in bulk solvent.

The position-dependent diffusion coefficients for these compounds do not vary significantly from one another (Fig. 4). The average diffusion within the region of the bilayer (z < 3.0 nm) for the compounds range from ∼0.7 × 10⁻⁶ cm²/s to ∼1.4 × 10⁻⁶ cm²/s. Throughout the bilayer, the values for each compound reach their minimum plateau at z ≈ 2.5–3.0, tending to be slightly higher at the disordered center. All the compounds show an order of magnitude increase in diffusion in bulk solvent relative to their calculated values within the bilayer. This is consistent with previous constrained MD simulations for small molecule compounds and drugs passing through a lipid bilayer. Our calculated diffusion coefficient for theophylline in bulk solvent (measured when z > 4.0 nm) is 1.4 × 10⁻⁵ cm²/s. This is approximately a factor of two higher than published data (83,84), but is consistent with the calculated self-diffusion of the SPC model of water that is also a factor of two higher than experimental values (85). However, these isolated membrane diffusion coefficients have no correlation with the experimental permeability values (Fig. 4, inset). Thus, in agreement with published data (38,86), the energy landscape of the compound appears to be the largest contribution to its permeability.

Figure 4.

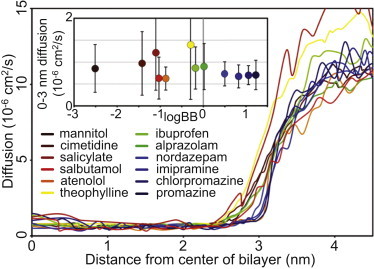
The calculated diffusion profiles for the compounds from bulk water through to the bilayer center. The average diffusion values (for z < 3.0 nm) of the compounds are not significantly different and show no correlation with the logBB for that compound (inset).

Computed P_eff values have high correlation with experimental permeation measurements

Our goal is to assess the ability of our simple BBB mimetic system to reproduce the experimentally determined BBB permeability of these compounds. This assessment is first carried out in a qualitative fashion, to determine if we could correctly identify a compound as either BBB+ (crosses the BBB) or BBB− (does not cross the BBB). Subsequently, we subject our results to a more quantitative comparison, to establish how our relative permeability measurements correlated with experimental data.

Classification schemes reported in the literature use slightly different logBB cutoffs to classify compounds as either BBB+ or BBB−. These values range from −1.00 (87) to +0.63 (9). However, a large number of these classification schemes report the cutoff criteria to be a logBB value of 0.00, with compounds that have a logBB ≥0.00 being BBB+ (43,88–90). Notably, a logBB of zero implies an equal concentration on both sides of the BBB. Ibuprofen is a well-documented example that violates the cut-off rule, albeit by a small amount. Although ibuprofen is a BBB+ compound (45), it actually has a logBB of −0.18 (75), slightly below the cutoff. The equivalent cutoff value for logPS (though not as robustly studied) is about −2.00, with compounds that have a logPS ≥ −2.00 being BBB+ (91). The range of logP_eff values calculated for our sample set of 12 compounds is from ∼2.8 to −6.6, a range of nearly 10 log units (Table 1).

The logP_eff data is plotted against the corresponding logBB and logPS values, and the linear regression line for data is calculated (Fig. 5). The linear regression plots show that when the logBB or logPS values are at their respective cut-off thresholds (0.00 and −2.00), the corresponding logP_eff value is then ∼0.00. This is true for both the logBB and the logPS plots. Thus, logP_eff = 0.00 is chosen as the cut-off for determining BBB+/− in our model. Using this value of logP_eff = 0.00 as the BBB+/− cutoff, our analysis and calculations correctly classifies 11 of the 12 compounds into the appropriate BBB+/− category (Table 1). The only compound incorrectly classified was ibuprofen. Even this incorrect classification was somewhat encouraging, as ibuprofen falls into the blurred region at the interface of BBB+/− classification. Indeed, it was very close (∼0.6) to the cutoff value.

Figure 5.

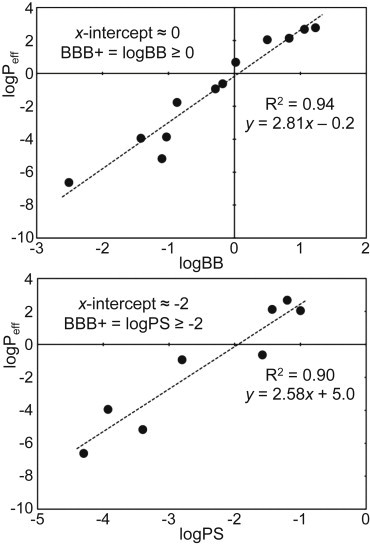
The logP_eff values for the 12 compounds plotted against their corresponding logBB values, and their logPS values (where available). The correlation against both the logBB and logPS values is very high (R² = 0.94 and 0.90, respectively).

As a further qualitative assessment metric, the relative order of the compounds (in terms of their permeability) is also assessed. Of the 12 compounds, 10 are in the correct relative order when comparing our calculated logP_eff values to the experimentally measured logBB values. The only two compounds that are ranked incorrectly are cimetidine and salicylate. The order of these two compounds is switched, with the logP_eff of the two being about one log unit apart.

From a quantitative point of view, the logP_eff values correlate extremely well with the experimentally measured parameters. Comparison of the logP_eff values for the full sample set of 12 compounds against their experimental logBB values gives an excellent correlation coefficient of R² = 0.94. Comparison against the available experimental logPS values also gives an excellent correlation coefficient of R² = 0.90, although only over the subset of eight data points for which logPS data are available.

Thus, by adapting the equation for the linear regression line between logP_eff and logBB (Fig. 5), we propose an equation to predict the logBB of a compound from its calculated logP_eff,

$$\mathrm{logBB}=\frac{\log {\mathrm{P}}_{\mathrm{eff}}-0.1725}{2.808},$$ (7)

The resulting predicted logBB values (Table 1) are, on average, <0.2 log units from their experimental values. This methodology therefore enables a quantitative, accurate predictive technique using MD simulation for compounds for which experimental logBB measurements have not yet been performed.

Discussion

Predictive capability

We have demonstrated that our first proof-of-principle in silico protocol has the potential to accurately predict the passive permeability of 12 small compounds. Our logP_eff predictions are correlated with logBB and logPS with R² values of 0.94 and 0.90, respectively, and are comparable to the commonly used in silico and in vitro prediction methods.

Frequently, the logP (the octanol/water partitioning coefficient—a measure of lipophilicity) of a compound can be used as a quick and simple prediction of its permeability and can be either measured or calculated. Regularly, logP is one of the best single descriptors in QSAR models. For a quick comparison of predictive capabilities, the logP of our 12 small molecules were calculated using a popular on-line logP prediction server (www.molinspiration.com). These calculated logP values correlate extremely well with the experimental logP values (0.95), and have an R² correlation of 0.81 against logBB, and 0.76 against logPS. However, when using the actual experimental logP values, the R² correlations for these experimental logP values against experimental logBB and logPS values are only 0.77 and 0.70. Thus, our methodology offers a marked improvement over this oft-used approximation, as there appears to be certain crucial parameters missing from the logP value that are needed to more accurately predict permeability. The in silico prediction of logP values is extremely accurate, but even if the logP prediction was 100% accurate, the single logP descriptor is not enough to predict BBB permeability with any correlation better than ∼0.75.

Thus, using a single logP descriptor may simply not be enough to predict BBB permeability. To include more descriptors, QSAR models are most frequently used. The equivalent first proof-of-principle in silico protocol for using a QSAR model to predict logBB was constructed in 1988. It consisted of 20 training compounds and had a correlation of R² = 0.69 (92). Since that time, the predictive capabilities of QSAR models have greatly improved. Correlation values of 0.72–0.86 (30–33) against logBB are the typical range of recent QSAR models. Predicting logPS using QSAR models generally correlates slightly better, with typical values of 0.74–0.95 (29,93–95). Recent comparative QSAR studies (33,97) on a test set of 24 compounds produced predicted logBB values that were both an average of 0.46 log units from the experimental values, more than double the 0.20 differential calculated for our 12 compounds. Indeed, even their top 12 closest matching predictions still had an average difference of 0.22 and 0.26 log units. Despite the success of QSAR models, they inherently depend on an adequate training set. In other words, data for similar compounds or compounds that occupy similar regions of the descriptor space are needed to train the initial model. Furthermore, the QSAR modeling approach requires a high quality data set of biological endpoints. Thus, QSAR prediction models depend greatly on the availability of experimental outcomes, and can only be considered accurate when the compound of interest has a common pharmacophore with the compounds in the training set (96). These biological endpoints and experimental outcomes may not be available for a novel compound of interest, especially when screening new lead compounds in drug discovery. The approach we present here is not limited by training sets or available experimental outcomes. Our approach simply needs the chemical structure of the compound to yield predictive results, allowing for any novel compound to be simulated during the drug discovery process, a clear advantage.

Although the protocol presented here is an in silico methodology, this in silico approach appears to yield better correlations than some common in vitro assays. Recently, permeabilities determined in PAMPA assays were compared against in vivo logBB values with correlations in the 0.65–0.75 range (19,22). In addition, R² correlations for IAM results against logBB have also reached as high as 0.75 (98). These methods are resource intensive and slower throughput than most in silico methods. Our approach has the advantage of higher throughput than the traditional in vitro methods, while maintaining comparable (if not better) predictive capabilities.

Due to the highly expensive, time-consuming methods needed to gather accurate in vivo BBB permeability data for new compounds, the method presented here is a reasonable predictive tool to be used in drug design process because it is faster and cheaper and, most importantly, predictive of permeability. Inserting a new tool into the early phase of the drug design process allows better decisions to be made, regarding which candidate compounds merit further investigation and could avoid unwanted side effects in future clinical trials.

Robustness of method

Our in silico approach appears to be robust with respect to possible errors in calculating the PMF near the lipid bilayer center—a phenomena recently suggested by Neale, et al. that can often arise due to inadequate umbrella sampling in this region (99). This inadequate sampling, or hidden sampling barrier, at the center of the bilayer is caused by rare conformational transitions between lipid defects, and can lead to autocorrelation times on the order of 10 μs as the simulation windows get within 0.5 nm of the bilayer center (99).

Thus, the uncertainty of the free-energy value at this central bilayer section is higher, and using a single free-energy point at this region as a metric may contain inherent errors. This may be a potential problem for several recent systematic PMF studies that have made quantitative predictions by taking only a single ΔG free-energy difference between two points on the PMF curve, such as ΔG_{water→lipid tails} (100), or between water and another point near the bilayer center (101).

Similar problems could have occurred in our system if we had adopted the same approach. For example, consider the PMF profiles of two compounds we investigated, theophylline (BBB−) and nordazepam (BBB+) (Fig. 3 B, Fig. 6). If we were to simply take the z = 0 free-energy value as our criterion for determining BBB permeability, these two compounds, which have experimental permeabilities almost an entire log unit apart, would then be separated by only ∼4 kcal/mol. Furthermore, this value is taken from a region of high uncertainty, thus leaving little room for error. However, by implementing our methodology to calculate P_eff (and using it as our measurement criterion), these two compounds are separated by three log units (−0.94 and 2.04 for theophylline and nordazepam, respectively).

Figure 6.

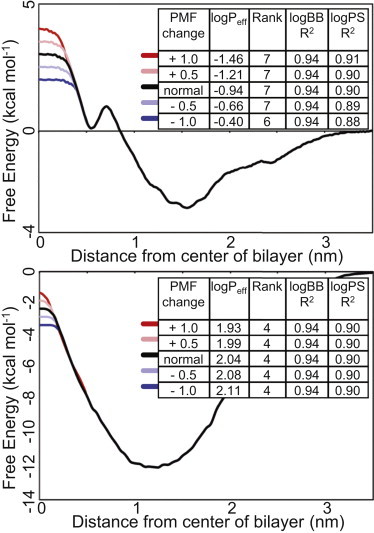
The artificially adjusted PMF profiles for theophylline (top) and nordazepam (bottom) and the resulting changes to the correlations with experimental data (inset).

To further investigate the robustness of our methodology to this potential sampling problem, we generated two artificial PMF profiles. We took the profiles for theophylline (a BBB− compound with a positive free energy at z = 0) and nordazepam (a BBB+ compound with a negative free energy at z = 0) and manipulated the height of the energy barriers at z = 0. The energy barriers were altered by 1.0, 0.5, −0.5, and −1.0 kcal/mol, and these changes in the PMF profile were extended out to almost z = 0.5 (Fig. 6).

The artificial PMFs simulate potential error in the region of the central bilayer. Using these newly generated energy landscapes, various revised logP_eff values can be calculated. After altering the z = 0 energy barriers for each of the nordazepam and theophylline PMF curves, in only one extreme case does the rank order of the compounds (in terms of their P_eff) change (and only by one position). The correlations with the experimental logBB results remain completely unaffected. At most the correlations with logPS are reduced by only 0.02. Even if we take the combination of the extreme values, whereby the nordazepam PMF was increased by 1 kcal/mol and the theophylline PMF was reduced by 1 kcal/mol, the R² correlations with logBB and logPS are still 0.94 and 0.91, respectively. The advantage of our methodology is that it uses the entire PMF energy landscape. Thus, although the free-energy value at the bilayer center is still important, it does not carry the critical weight that it does for single-point measurements.

A further test of the robustness of the methodology is the selection of the cutoff value between what is classified as membrane and bulk solvent. Only within-membrane values of diffusion and PMF free energies are used to calculate the membrane P_eff. Given that the density of the DOPC lipid reaches zero at z = 3.0 nm, and all the PMF curve values are zero (or very close to zero) at z = 3.0 nm, this value was the logical choice for the cutoff limit. However, the possibility remains that the chosen value may be too low or too high, and our model may be sensitive to an unsuitable cutoff. The use of an unsuitable cutoff value could result in inaccurate results due to either information being excluded (cutoff too low) or the inclusion of bulk-water artifacts (cutoff too high). To assess the effect of the cutoff value on our results, the P_eff for each compound was calculated using cutoffs of 2.5 and 3.5 nm, and the data again correlated against experiment. The 2.5 nm cutoff resulted in R² correlations with logBB and logPS of 0.96 and 0.89, although equivalently the 3.5 nm cutoff correlations were 0.93 and 0.92. Thus, the methodology is insensitive to these variations in the membrane width cutoff value.

Limitations

Despite the encouraging success of our system in predicting correlation against experimental values, the model has some limitations that should be noted. As with some simple in vitro methods (such as PAMPA and IAM), our system does not account for nonpassive compound movement of any sort. Thus, the model does not take into consideration the effect on any compounds that are subject to either P-gp-mediated efflux back across the BBB, or active uptake systems. For proof-of-principle testing and calibration, this limitation is less of an issue, as compounds can be selected based upon their purely passive permeability properties. However, for the ultimate goal of BBB permeability prediction of novel compounds this is a more important consideration. We foresee the future possibility of combining our in silico approach with additional in silico methods, such as docking the compounds to efflux/influx protein models, to determine a permeability profile that takes into account the active transportation routes.

Another possible limitation of our system is that for the sake of simplicity we have only included a single type of lipid in our membrane. The use of a mixed-lipid system would require a much longer equilibration time and thus an increased computational burden. Mixed-lipid simulations have a much shallower depth of literature, thus comparison and validation of our results would have proved more difficult.

Furthermore, other PAMPA models actually found better correlation when using a simple Black Lipid Membrane (a pure DOPC bilayer) instead of a bilayer representative of brain endothelial cells, although differences were minimal (19). Additionally, studies using a single type of lipid/detergent have achieved a R² correlation of 0.75 and 0.79 using IAM and MLC (micellar liquid chromatography), respectively (98). Thus, our system agrees with several in vitro models that suggest a simple, single lipid membrane model can be sufficient to predict BBB permeability.

There are also a couple of computational difficulties to consider. We acknowledge that the quality of the force field that is used to carry out the simulations and build high quality all-atom models for each molecule is a limitation. Different MD force fields have different strengths and weaknesses, and using one force field over another may result in slightly varied results (102). Using different methodologies to assign partial charges on compounds can also lead to varied results (68).

Finally, we must consider the computational cost of carrying out the free-energy calculations. Although each compound took an average of 150,000 cpu hours to generate a PMF and permeability value, the resulting values are extremely well correlated to experimental values (>0.90). Calculating logP values is indeed computationally cheap (magnitudes less than PMF calculations). However, the logP values are inherently lacking sufficient information and at best give correlations to experiment of 0.75. Given the expense of late stage failures in drug development, the added computational cost of using PMFs to predict permeability may be well worth the price. Furthermore, with increases in computing power and parallelization, the actual time to complete these measurements will only continue to decrease.

Conclusions

We have demonstrated success of our in silico BBB permeability prediction method using a small but diverse data set. This proof-of-principle study is similar in size to one of the earliest pioneering QSAR models to predict BBB permeability that was built in 1988 (training set of 20 compounds) (92). This early QSAR model only had an R² correlation of 0.69 with experimental data. Our methodology is correct in qualitatively predicting 11 of 12 compounds to be either BBB+ or BBB−, and also establishing 10 of 12 in the exact order in terms of their experimentally measured permeability. Furthermore, we have quantitatively compared our results with the two major in vivo measures of BBB permeability: logBB and logPS. Our results have an R² correlation of 0.94 and 0.90 with logBB and logPS, respectively—values that are comparable to or better than those of other prediction models. On average, our calculated logBB numbers were within 0.2 log units of their experimental values—again, comparable to or better than other prediction models. Thus, we have established the potential of this methodology to be expanded and developed in the future. Perhaps ultimately an in silico method similar to ours may be used in drug discovery as an accurate, relatively fast BBB permeability prediction tool, which does not rely upon (nor is biased by) existing data.