Cross-Talk, Cross-Bridges, and Calcium Activation of Cardiac Contraction

Calcium regulation of striated muscle contraction is complicated, not least because there are multiple components all talking to each other with feedback mechanisms to keep the whole system in balance. Although the reductionist approach has been very effective at defining the individual players and their interrelation, how the system operates in the contracting muscle remains underdetermined. This is most clearly recognized in our long-running struggle to provide a molecular interpretation of the Frank-Starling mechanism in the heart (1), which is a cardiac form of the phenomenon of stretch-activation found in most muscle types. One of its simplest expressions may be the observation that, in skinned muscle fibers, the force pCa curve shifts to lower calcium concentrations as the sarcomere length increases. This implies some type of feedback mechanism between sarcomere length and calcium binding to TnC, but defining how this operates has been difficult because the phenomenon requires an organized muscle fiber to investigate it, and then information on the cross-talk between the different components is much more difficult to define.

By using Förster resonance energy transfer (FRET) between two fluorescent probes on the N-terminal regulatory domain of troponin C (TnC), Lin et al. (2) have succeeded in reporting the effects of calcium, strongly binding myosin cross-bridges, and sarcomere length on the equilibrium between an open and a closed cleft in the TnC regulatory domain. The results show that all three parameters can influence the equilibrium position, thereby providing a mechanism in which increased sarcomere length can modulate calcium binding to TnC via myosin cross-bridges and hence provide a partial explanation for the Frank-Starling mechanism.

Cross-talk between myosin cross-bridges and calcium binding to thin filaments has been known for a long time both in solution and in muscle fibers. Anything that increases myosin binding to the thin filaments (e.g., low-ATP, high-ADP concentrations, or rigor conditions) tends to make the system more sensitive to calcium, and anything that reduces myosin binding (high Pi concentration, myosin inhibitors) reduces calcium sensitivity. Fig. 1 gives simple structural interpretation of the cross-bridge TnC feedback mechanism (for a more detailed review, see Geeves (3) and Gordon et al. (4)). The proteins in the thin filament (actin TnT, TnC, TnI, and Tropomyosin) form an ensemble of two-state allosteric switches. The N-lobe of TnC (TnC-N) can be open (high calcium affinity ∼0.1 μM) or closed (weak calcium binding ∼1 μM). This balanced equilibrium is biased toward the open cleft form by binding either calcium or the switch peptide of TnI, i.e., calcium and switch peptide enhance each other’s binding to TnC. The TnI inhibitory peptide binds to actin, but it cannot bind to actin if the switch peptide is bound to TnC. Essentially, actin and TnC compete for different parts of TnI. Similarly, the TnI inhibitory peptide and myosin compete for the binding site on actin. In the absence of calcium, TnI will out-compete myosin for actin and the muscle is relaxed. If calcium is bound to TnC, TnI will preferentially bind to TnC and the thin filament is activated, allowing myosin (via tropomyosin) access to its binding sites on actin. Thus, any effector that increases the affinity of myosin for its site on actin (or the lifetime of a myosin attachment) can, through TnI, alter the apparent affinity of TnC for calcium. The question asked by Li et al.: how does sarcomere length affect these relationships?

Figure 1.

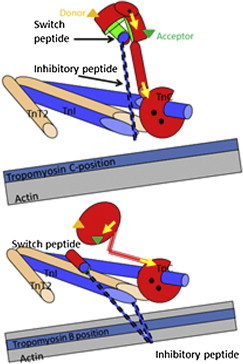
The thin-filament calcium switch. The Tn complex in the thin filament based on crystal structures of skeletal muscle TnC (red) with TnI (blue), and TnT2 (brown). This shows the role of the switch and inhibitory peptides of TnI in transmitting the calcium binding to TnC to the tropomyosin (pale blue strand) position on actin filament (gray strand). (Upper panel) Calcium-bound state. Calcium (black dots) binding to the N-terminal domain causes the regulatory domain to open, allowing the TnI signal peptide to bind in the cleft (the TnC and switch-peptide contact surface is shown in green). This inhibits the peptide from binding to its site on actin. Tm sits in its preferred C- or calcium-induced site on actin. (Lower panel) Calcium-free state with the inhibitory TnI peptide binding to actin and locating Tm in the Blocked position on actin. Note the closed regulatory domain of TnC. Note also that the diagram shows the role of the inhibitory peptide but not the rest of the C-terminus of TnI, which also contributes to the actin binding site. This is based on the crystal structure of skeletal muscle troponin core domain. The crystal structure of the cardiac troponin core domain does not show the central helix straightening as depicted here. This region may therefore be quite mobile. The locations of the fluorescent labels are for illustration only: (green and orange triangles) the FRET probes in the N-domain of TnC; (yellow arrows) the two bifunctional orientation probes in the two TnC domains. The figure is based on an original drawing by M. Vinogradova and R. Fletterick (3). To see this figure in color, go online.

The work by Li et al. brings a new precision to measuring TnC activation in a skinned muscle cell. They have used a pair of fluorescent probes attached to two different sides of the regulatory N-lobe of TnC (see Fig. 1) and use FRET to monitor the distance between the two probes. The labeled TnC has previously been used to explore TnC-N lobe opening in solution (5). Exchange of the labeled TnC into a cardiac muscle fiber allowed similar measurements in the cellular environment (6). The earlier work followed the FRET signal change (intensity) as calcium was titrated into the fiber producing an active contraction (with ATP), in the absence of strongly bound cross-bridges (added Vi and ATP), and in the presence of strongly bound, rigor-like strong cross-bridges (with ADP, no ATP). They confirmed the data from isolated proteins that strongly bound myosin cross-bridges do lead, through the feedback system described above, to an opening of the TnC-N cleft to predispose it for calcium binding. However, such intensity-FRET methods are not suitable for muscle fibers that are moving, because position artifacts can alter the amount of fluorophore observed, and hence, its intensity. To get around this limitation, Li et al. (2) have turned to fluorescence lifetime measurements that are independent of the signal intensity. Put simply, the lifetime of donor fluorescence signal depends upon the distance between the FRET pair; the closer the two fluorophores, the more readily the donor fluorescence is quenched and the shorter the observed lifetime. For the closed cleft, the lifetime data leads to an estimate of the average distance between the probes of ∼25 nm and for the open cleft ∼32 nm. In practice, a distribution of different lifetimes/distances is expected, and these, in principle, can be fitted to one or more Gaussian populations. This is the real potential of this approach: not only is it insensitive to movement artifacts but it can follow the change in distribution from, ideally, a fully closed to a fully open cleft.

The new data collected at sarcomere length of 2.2 μm showed the cleft opening by 7.5 nm on adding calcium to go from relaxed to an active contraction. In the presence of saturating calcium, addition of Vi reduces the number of strongly attached cross-bridges close to zero, and on average closes the cleft by ∼3 nm. That is, in the absence of strongly bound cross-bridges, calcium alone was insufficient to completely open the cleft. This probably means that only 50% of the TnC clefts open on binding calcium. In contrast, going from a relaxed fiber to a low calcium ADP-rigor state with most cross-bridges bound to actin leads to a 1.2-nm opening of the TnC cleft (or ∼17% of the TnC clefts are open), and addition of calcium was required to give the maximal 7-nm opening. Shortening the sarcomere length to 1.8 μm reduced the ability of the cross-bridges to influence the TnC-N domain. A calcium-induced active contraction produces only a smaller 5.2-nm opening of the cleft and addition of vanadate now closed the cleft by 1.4 nm. Thus, the TnC-N cleft is less responsive to the presence of strong cross-bridges at the shorter sarcomere lengths and this could provide part of the explanation for the Frank-Starling mechanism. How the sarcomere length produces this effect is undefined, but the authors speculate that this could be via a mechanical sensor in the thick filament that predisposes the myosin cross-bridges to be available to interact with actin at long sarcomere lengths. A similar conclusion of a mechanical activation of thick filaments was reported by Farman et al. (7), based on x-ray scattering data from rat cardiac fibers, and by Fusi et al. (8), who used a differently fluorescently tagged TnC in skeletal muscle.

The work of Fusi et al. (8) used skeletal muscle TnC with a bifunctional fluorescence probe attached rigidly to helices in either the N-terminal regulatory lobe of TnC or near the C-terminal structural lobe (see Fig. 1). Orientation of the probes, with respect to the filament axis, is then interpreted to report calcium binding to the N-lobe or reorientation of the TnTm complex (probe on C-lobe) as TnI dissociates from actin and Tm moves away from the blocked position. Fusi et al. (8) used a rapid release of calcium and rapid length steps to explore the effects of cross-bridges, calcium, and force on the orientation of the two signals. On a rapid increase of calcium concentration, both helices reorient with a half-time of <1 ms consistent with the expected rate constant of calcium binding. In the absence of cross-bridges, the C-lobe completes 75–80% of the total change observed with this fast rate constant whereas helix E completes 60–67% of the change. Most of the rest of the reorientation occurs at 100–150 s⁻¹, consistent with TnI-inhibitory peptide detachment and Tm movement. When force-generating cross-bridges are also present, the same two phases occur for the probe on the C-lobe. However, in the case of the N-lobe probe, a third phase is additionally seen at 13 s⁻¹, similar to the observed rate constant of tension rise. Fusi et al. (8) point out that the two fast phases are complete before any force is developed or before the formation of any significant population of strong cross-bridges. This leaves no role for strong cross-bridges in the early phases of activation. However, the distribution of amplitudes is altered for the E-helix, with 40–50% in phase 1, 30–38% in phase 2, and 10–15% in phase 3 when force is developed. The questions here: What affects the amplitudes of the fast phases? Is it the weak cross-bridges? It will be interesting to see if this conclusion holds if submaximal calcium is released into the fiber.

The two fluorescent approaches are clearly complimentary and have currently been applied to different classes of muscle fibers—skeletal or cardiac. Of course, we want to know whether the differences between the two sets of data are the result of the fiber type, as in a modification of TnC behavior by the probes or the details of the experimental protocol (Vi versus BTS for eliminating cross-bridges; signals collected during a steady state versus a mechanical transient). At this stage, what unites the two sets of data is as interesting as the differences, but this will change in time as we focus on the discrepancies. As of the time of this writing, the technical achievements required to collect such data are remarkable in themselves.

Both sets of fluorescence probes are limited, in this data, in being unable to distinguish the signal from the overlapping and nonoverlapping regions of the thin filament. The two regions may well show different responses if the cross-bridges’ effects reported here are relatively local. Another limitation of both data sets is that only the behavior of the ensemble average of the probes is reported. It will be of great interest if better data quality or improved modeling would allow the data to be analyzed as populations of FRET distances or orientation parameters. This will help us distinguish whether the signal changes (totaling to 50%) taking place on calcium binding in the steady state or in the fast phase of a transient are the result of the completion of one structural change (e.g., a half-closed cleft) followed by another structural change, or instead are due to only 50% of the N-lobe clefts closing because of a poised equilibrium. Both sets of data are interpreted in terms of a combination of blocked-closed-open, thin-filament conformations modulated by calcium binding (9,10), but we do not yet know exactly how the probe signal matches to the global structural states.

A few words of caution here on the meaning of the terms “global structural states” or “regulatory states” of muscle: these are not always defined well. The data of Li et al. clarify the relationship between the open state of the TnC-N cleft and calcium, and the activity as measured by force. In their schematic figure (see Fig. 4 in Li et al. (2)), they show the probability of TnC-N cleft opening in the various thin-filament states. If one considers force, the blocked and closed states of the thin filament only allow low-force myosin attachments, whereas the open or M-state of the filament (both with or without calcium, M⁻ or M⁺; see Lehrer (11)) allows strong binding and force-holding cross-bridges. This indicates that force/activity and TnC-N cleft opening, whether positive or negative for calcium, are not simply correlated, as was previously shown in a variety of solution studies (reviewed in Lehrer (11)).