Analysis of the Strength of Interfacial Hydrogen Bonds between Tubulin Dimers Using Quantum Theory of Atoms in Molecules

Abstract

Microtubules are key structural elements that, among numerous biological functions, maintain the cytoskeleton of the cell and have a major role in cell division, which makes them important cancer chemotherapy targets. Understanding the energy balance that brings tubulin dimers, the building blocks of microtubules, together to form a microtubule is especially important for revealing the mechanism of their dynamic instability. Several studies have been conducted to estimate various contributions to the free energy of microtubule formation. However, the hydrogen-bond contribution was not studied before as a separate component. In this work, we use concepts such as the quantum theory of atoms in molecules to estimate the per-residue strength of hydrogen bonds contributing to the overall stability that brings subunits together in pair of tubulin heterodimers, across both the longitudinal and lateral interfaces. Our study shows that hydrogen bonding plays a major role in the stability of tubulin systems. Several residues that are crucial to the binding of vinca alkaloids are shown to be strongly involved in longitudinal microtubule stabilization. This indicates a direct relation between the binding of these agents and the effect on the interfacial hydrogen-bonding network, and explains the mechanism of their action. Lateral contacts showed much higher stability than longitudinal ones (–462 ± 70 vs. –392 ± 59 kJ/mol), which suggests a dramatic lateral stabilization effect of the GTP cap in the β-subunit. The role of the M-loop in lateral stability in absence of taxol was shown to be minor. The B-lattice lateral hydrogen bonds are shown to be comparable in strength to the A-lattice ones (−462 ± 70 vs. –472 ± 46 kJ/mol). These findings establish the importance of hydrogen bonds to the stability of tubulin systems.

Introduction

Microtubules are key cellular components that play important roles in several cellular processes. The long filamentous tube-shaped structure of a microtubule is involved in cytoskeletal processes such as maintaining cell morphology, intracellular transport, and formation of the mitotic spindle that segregates chromosomes during cell division. Microtubules have also been implicated in playing direct or indirect roles in signaling, information processing, and consciousness (1–6). Of particular interest is the role of microtubules in cell division, making them important cancer chemotherapy targets (7–10). Generally speaking, the feature that provides microtubules with the ability to carry out their roles in the cells is their delicate dynamic instability, in which microtubules repeatedly and stochastically undergo phases of growth and shrinkage that help them perform their cellular functions (11,12).

As shown in Fig. 1 a, the microtubule structure in mammalian cells is an ∼24-nm-wide hollow cylinder comprising 13 protofilaments (10–15 protofilaments in other types of cells) that associate laterally to form a left-handed three-start helix. Each single protofilament is composed of smaller building blocks, the αβ-tubulin heterodimers (13,14). Because αβ-tubulin dimers attach to each other in a head-to-tail fashion, there is always a plus-end that has β-tubulin exposed and a minus-end that has α-tubulin exposed. The α-subunit is always bound to guanosine triphosphate (GTP), whereas β-subunit is bound to GTP and is prone to hydrolysis to guanosine diphosphate (GDP) shortly after assembly. It is generally accepted, as a result, that a GTP-bound tubulin cap can form on the plus-end of each growing microtubule. If hydrolysis is fast enough to catch up with the GTP-bound cap at the tip of the microtubule plus-end, the molecule becomes unstable and begins rapid depolymerization and shrinkage. Thus, the hydrolysis of GTP crucially affects the energetics of microtubules and their phase (11,12,15,16).

Figure 1.

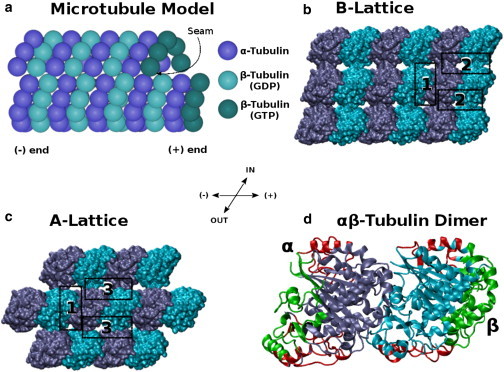
Microtubule lattice and interfaces, with (dark blue) α-subunits and (cyan) β-subunits. (a) A model of a microtubule cylinder. (b) A model of the B-lattice configuration showing only nine tubulin dimers. (c) A model for the A-lattice configuration showing only seven tubulin dimers. In panels b and c, the three different interfaces between tubulin dimers that we studied are highlighted. These are 1), the longitudinal interdimer interfaces, LongAB; 2), the lateral interprotofilament interfaces in B-configuration, LatB; and 3), the lateral interprotofilament interfaces in A-configuration, LatA. (d) A more detailed model of the αβ-tubulin heterodimer showing the domains that make lateral contacts (red) and the domains that make longitudinal contacts (green). To see this figure in color, go online.

As shown in Fig. 1, there are two different geometrical configurations of microtubules, the A-lattice and B-lattice. In the A-lattice configuration, the α-tubulin subunits are lying almost beside the β-subunits in neighboring protofilaments, producing a continuous pattern of alternating α- and β-subunits. In B-lattice, the α-subunits are lying almost beside the α-subunits in neighboring protofilaments (and β beside β). Having 13 protofilaments in a cylinder, the B-lattice would always include a discontinuous seam, one lateral domain where adjacent dimers are in the A-configuration (17,18). There is evidence showing that the B-lattice is the dominant form both in vitro and in vivo (19–23). However, the universality of the B-lattice was revisited because the formation of microtubules in vitro in the presence of End-Binding Protein 1 showed that A-lattice contacts are more favorable under these circumstances (17,24,25). Because End-Binding Protein 1 is present in cells during polymerization of microtubules, the same effect is also expected in vivo (17,24,25). In a 2003 study that considered the contribution of the solvation energy in terms of solvent-accessible surface area energy as well as the Poisson-Boltzmann electrostatic energy, Sept et al. (26) showed computationally that the B-lattice configuration is slightly more stable than the A-lattice one, providing an explanation for the B-lattice predominance. Along the same lines, Drabik et al. (27) calculated the potential of mean force between lateral interfaces of tubulin dimers in a microtubule and arrived at the same conclusion, i.e., that the B-lattice is more stable than the A-lattice configuration. Erickson and Pantaloni (28) also calculated, in 1981, the entropic contribution to the total energy profile.

The motivation for our work stems from noticing that the studies regarding tubulin interfacial energetics have so far not considered the hydrogen-bond energy contribution as a separate component. There is no doubt that hydrogen bonds play a very important role in protein energetics, especially in the stability between subunits in multimeric proteins (29,30). Therefore, studying the effect of hydrogen bonds on the energetics of interfacial interactions between tubulin heterodimers is essential for understanding the proper thermodynamics and kinetics of assembly. As shown in Fig. 1, we studied different interfaces of tubulin-tubulin interactions. Regarding the B-lattice, we studied the lateral interface between two tubulin dimers in two adjacent protofilaments and we called it the “LatB” interface. Regarding the A-lattice, we studied the equivalent lateral interface, calling it the “LatA”. We assumed that the longitudinal interactions between tubulin heterodimers in the same protofilament are identical between the B-lattice and A-lattice cases, as the geometry of the protofilament is not expected to be affected by lateral contacts, at least over the simulation time range. Therefore, we called them both the “LongAB” interface. The three different interfaces were studied and the total as well as per-residue hydrogen-bond energies were calculated. The calculations were performed using molecular dynamics (MD) and quantum mechanics (QM) calculations followed by electron density analysis using Bader’s theory of atoms in molecules (AIM) (31,32) in relation to the hydrogen-bond strength.

Methods

Energy calculation using AIM approach

A hydrogen bond is a bond that involves three atoms: a hydrogen atom (H) attached covalently to an electronegative atom, such as N, O, or F, as one partner and an electronegative atom as another partner. The former electronegative partner is called the hydrogen-bond donor (HD) whereas the latter electronegative partner is called the hydrogen-bond acceptor (HA). The Bader’s AIM theory is a very attractive and successful method of characterizing bond strengths based on properties of critical points (31,32). Several successful studies that characterized hydrogen bonds based on topological properties of electron density at the bond critical points have been reported (33–36). In a previous study, we built a strong linear correlation between the density at the bond critical point (BCP) located between the hydrogen atom and the acceptor atom, ρ_H-A, and the strength of the hydrogen bond obtained from a supermolecular approach (37). The relationship had a coefficient of determination, r², of 0.96. This relationship was true for all kinds of hydrogen bonds that span the range of 0–60 kJ/mol, as reflected by the heterogeneous training set used. Using this relationship, we obtained the parameters necessary for calculating the strength of hydrogen bonds by knowing only the value of the electron density, ρ_H-A, at the BCPs (37). This relationship is given as

$$E_{HB}=m{\rho }_{HA}+b,$$ (1)

where E_HB is the energy calculated from a supermolecular approach, and m and b is the slope and the intercept of the linear correlation obtained, respectively. The parameters m and b were used to calculate the strength of hydrogen bonds in the tubulin interfaces.

MD simulations

Toward calculating the energies of hydrogen bonds in our system using this method, we obtained the Protein Data Bank (PDB) (38) crystal structure of bovine brain tubulin PDB:1JFF (39) and repaired it via basic homology modeling by adding missing residues from PDB:1TUB (40) using the software MODELER 9V6 (41). The repaired PDB:1JFF structure was optimized using energy minimization via a conjugate gradient method over 40,000 time steps in an MD simulation in a neutralized water box using the NAMD program (42). Using this minimized structure, the microtubule A- and B-lattice structures based on the microtubule geometry described in Li et al. (43) and Sept et al. (26) were built using an in-house PYTHON script in the software PYMOL 0.99rc6 (44). Lateral orientation of the B-lattice was verified by overlaying a pair of lateral tubulin heterodimers from our model to the model prepared by Wells and Aksimentiev (45). A root mean-square deviation (RMSD) of only 3.4 Å was reported, which is actually smaller than the resolution of the PDB:1JFF structure itself (3.5 Å).

Subsequently, a pair of interacting αβ-tubulin heterodimers were separated from each lattice to be used to study the hydrogen bonds. Specifically, a pair of longitudinal neighbors from the B-lattice model was separated to study the longitudinal interface (LongAB), a pair of lateral neighbors was separated from the B-lattice model to study the lateral B interface (LatB), and a third pair of lateral neighbors from the A-lattice was separated to study the lateral A interface (LatA). All the interfaces as well as the interacting pairs of αβ-tubulin heterodimers that were separated are shown in Fig. 1. Hence, we investigated three distinct systems, each containing a pair of αβ-tubulin heterodimers. For each αβ-tubulin pair system, we ran an MD simulation to obtain an equilibrated system. In detail, we added the cofactors, GTP and GDP, to their binding sites with the help of SWISS PDBVIEWER 4.1 (46). Taxol, or any other stabilizer, was not added to the system.

As stated earlier, terminal β-subunits that are not capped with GTP are unstable and prone to depolymerization. Therefore, the terminal β-subunits in the three systems were all capped with GTP instead of GDP. The magnesium atom at the α-subunit GTP binding site was also included to stabilize the complex. C-termini were capped with n-methylamide residues. The C-terminal tails were not simulated because they are not available in PDB structures, and they are highly mobile and variable among tubulin isotypes. The C-terminal tail is also far away from lateral and longitudinal interfaces, and hence is not expected to have any direct contribution to lateral interactions. Moreover, the inclusion of this tail would require the usage of a very large water box that would significantly increase the computational load. We parameterized the protein system using the AMBERff12SB force field (47,48). We parameterized the cofactors using the parameter set developed by Meagher et al. (49). Ionization states were assigned using the PROPKA server (50–53). Each system was solvated with a TIP3P water box extending 10 Å in each direction and neutralized by the addition of 72 Na⁺ ions.

Additional ion pairs of Na⁺ and Cl⁻ were added to bring the ion concentration to 100 mM to mimic cellular conditions. Although the initial coordinates were obtained from a 13-protofilament microtubule model, we are effectively simulating a free pair of tubulin heterodimers in each system, given the geometry of the water box used. Then, the AMBER MD package (54) was used to minimize the complex through a series of 2000 steepest-descent and conjugate gradient steps with strong restraints on the protein heavy atoms (500 kcal mol⁻¹ Å⁻²). This was intended to relieve any hydrogen contacts caused by the addition of hydrogens using AMBER residue templates. Another 4500-step minimization was done to bring the whole system to the nearest local energy minimum. Then the system was heated, over 20 ps under constant volume, to a temperature of 310 K by the Langevin thermostat using restraints on the protein (10 kcal mol⁻¹ Å⁻²).

The restraints were then released gradually through a 100-ps run under constant pressure and temperature, and a production phase of 30–45 ns was run under the same conditions to attain RMSD equilibration. This production step was performed using GPU cores on the PharmaMatrix Cluster (University of Alberta) through the AMBER GPU-accelerated code (55). All simulations were performed using periodic boundary conditions where the particle-mesh Ewald method was used for treating long-range electrostatics with a cutoff of 8.0 Å. When considering RMSD equilibration, we gave more attention to the interfacial residues than the residues that are distant from the interface. We clustered the snapshots that correspond to 20 ns extracted from the equilibrated region in the trajectories based on RMSD of the interfacial residues in eight clusters, using the average linkage algorithm (56) through the CPPTRAJ module of AMBER (54).

The centroid of the each cluster was considered to be the most representative structure of the cluster, and was processed further. Therefore, we used eight snapshots for every system. Each snapshot was processed using the CPPTRAJ module of AMBER to detect all hydrogen bonds. This is done by AMBER by listing all possible hydrogen-bond donors (HD) and acceptors (HA) in the system and then analyzing the distances between them as well as the angle made by HA–H–HD atoms. A cutoff of 3.0 Å for distance and 135° for angle are used as default criteria by AMBER for hydrogen bonds. Although these values are reasonable (57), we relaxed the strictness of our criteria to a distance of 3.3 Å and an angle of 120°, and then depended on the AIM method to confirm the presence of each hydrogen bond (a bond is present if there is a nonzero density at the bond critical point).

These relaxed criteria were use to prevent missing any possible hydrogen bonds, i.e., to prevent false-negatives. The hydrogen bonds detected by AMBER were analyzed and all the bonds that are not interfacial in nature, i.e., not binding the two αβ-tubulin heterodimers together, were ignored. Other energetic contributions such as van der Waals and electrostatic interactions were also estimated using the Molecular Mechanics/Generalized Born Surface Area (MM/GBSA) method as implemented in AMBER (58). The program VMD 1.9.1 was used for viewing the MD trajectories (59). After that, every hydrogen-bonding residue pair was analyzed individually using the AIM method.

QM calculations

Each pair of interacting amino-acid residues was characterized in a separate QM single-point calculation. The QM region was specified as the parts of the two residues making the hydrogen-bond contact, and we avoided cutting at polar or saturated bonds. The rest of the αβ-tubulin pair system was treated, together with the solvent, using electronic embedding, which incorporates the partial charges of the embedded region into the quantum-mechanical Hamiltonian. This technique provides a better description of the electrostatic interaction between the QM region and the embedded region (because it is treated at the QM level) and allows the QM wavefunction to be polarized. The QM region was treated using density functional theory with the density functional B3LYP (60–62) and the basis set TZVP (63,64). This functional and basis set were chosen to match the ones that we used to develop the parameters (37).

All the QM calculations were done using the software GAUSSIAN 09 (65). Subsequently, an AIM analysis was carried out using GAUSSIAN 09 and the electron densities at the BCPs were obtained. Difficult cases, i.e., cases that did not converge in Gaussian, were treated using the software suite AIMPAC (http://www.chemistry.mcmaster.ca/aimpac/imagemap/imagemap.htm), which is more stable (66). The hydrogen-bond energy was calculated using the parameters that we had developed in Ayoub et al. (37). This QM calculation was applied to each instance of hydrogen bonding occurring between any pair of residues. Hence, we built several BASH (http://www.gnu.org/software/bash/) scripts to automate all these procedures. As stated earlier, we used eight different representative snapshots for every system, and hence all these calculations were repeated for every snapshot. The total hydrogen-bond energies, as well as the per-residue energies, for each of the three main systems used were then obtained and analyzed.

Results and Discussion

The MD simulation runs were continued until RMSD equilibration of the interfacial residues was attained (interfacial residues are residues that have at least one atom within 8 Å from the neighboring tubulin heterodimer). Other residues distant from the interface were not considered, as they do not contribute to interfacial hydrogen bonding. Fig. S1 in the Supporting Material shows the RMSD equilibration plot of the backbone atoms of interfacial residues relative to the starting structure. The LatB and LongAB systems were equilibrated early in the simulations. For LatA, we pursued the simulations a bit longer to make sure that the system was well equilibrated. The trajectory of the equilibrated region of each system was clustered in eight clusters, as explained before. These eight representative snapshots were analyzed for hydrogen bonds, and each pair of interacting residues was then subjected to a QM calculation and AIM analysis. The results of each system are listed in Tables 1–3. Each table shows the average total hydrogen-bond energies as well as the average per-residue energies over the eight different representative snapshots that were processed.

Table 1.

Energy of hydrogen bonds in the Long-AB interface

TUB 1-α	TUB 2-β	Eaverage	SD
Arg2	Glu71	–40.1	14
Glu434	Arg401	–32.6	17
Tyr262	Arg401	–32.1	17
Arg243	Asp76	–29.9	14
Thr349	Val181	–25.8	12
Asp438	Arg401	–23.9	25
Val260	His406	–22.1	11
Gln133	Gly98	–21.9	8
Thr257	Gly100	–21.4	7
Lys352	Thr180	–18.7	9
Asn249	Gln11	–18.6	11
Asn329	Lys176	–15.3	10
Lys163	Glu411	–14.7	19
Asn258	Val181	–13.9	8
Other bonds		–61.3	—
Total energy		–392	59

The Long-AB interface refers to two αβ-tubulin heterodimers aligned longitudinally (TUB 1 and TUB 2). Average energy and standard deviation (SD) values are taken from eight different representative snapshots. Energies are expressed in kJ/mol.

Table 2.

Energy of hydrogen bonds in the LatB interface

α-α interactions				β-β interactions
TUB 1-α	TUB 2-α	Eaverage	SD	TUB 1-β	TUB 2-β	Eaverage	SD
Arg215	Glu90	–42.7	18	Arg308	Asp116	–44.8	20
Lys338	Asp127	–28.5	8	Glu290	Arg88	–38.9	12
Glu297	Arg121	–24.6	19	Arg308	Asp120	–36.7	14
Glu297	Lys124	–23.6	12	Lys299	Asp90	–32.6	12
Glu284	Ser54	–22.3	14	Asp297	Lys124	–22.3	19
Gln372	Glu55	–18.4	9	Tyr342	Asp120	–18.4	18
Tyr282	Ser48	–11.7	11	Ser280	Arg88	–16.6	16
His283	Phe49	–10.5	8	Lys338	Lys124	–14.8	10
				Lys338	Ser126	–12.0	11
Other bonds		–27.5	—	Other bonds		–14.8	—
Subunit energy		–210	35	Subunit energy		–252	65
Total energy						–462	70

The LatB interface refers to two αβ-tubulin heterodimers (TUB 1 and TUB 2) aligned laterally in the B-configuration. Average energy and standard deviation (SD) values are taken from eight different representative snapshots. Energies are expressed in kJ/mol.

Table 3.

Energy of hydrogen bonds in the LatA interface

α-β interactions				β-α interactions
TUB-α	TUB 2-β	Eaverage	SD	TUB 1-β	TUB 3-α	Eaverage	SD
Asp47	Arg284	–42.2	15	Arg88	Glu279	–35.2	15
Lys124	Asp297	–31.7	9	Lys124	Glu284	–27.0	12
Gln85	Ser280	–23.6	10	Ile86	Tyr282	–23.0	12
Asp46	Arg278	–23.0	13	Asp90	Lys280	–18.6	15
Asp127	Asn334	–22.6	5	Asn54	Glu284	–14.4	13
Asp120	Lys338	–22.4	14	Glu127	Thr334	–13.8	18
Gln128	Gln293	–18.6	12	Asp90	Ala281	–12.9	11
Asp47	Gln282	–16.5	14	Glu127	Thr337	−10.3	14
Glu55	Arg284	–14.8	18
Arg121	Asp297	–13.1	24
Asp47	Arg278	–11.9	13
Other bonds		–58.2	—	Other bonds		–17.8	—
Subunit energy		–299	23	Subunit energy		–173	44
Total energy						–472	46

The LatA interface refers to one αβ-tubulin heterodimer (TUB 1) aligned laterally in the A-configuration with an α-and β-subunit (TUB 2β and TUB 3α). Energies are expressed in kJ/mol.

It should be noted that hydrogen bonds are highly dynamic in nature, which means that they keep forming and breaking over the course of the MD simulation. Therefore, we expect to see large variations in the per-residue hydrogen-bond energies, and this is why the standard deviation (SD) can sometimes be very high. In this case, high SD would represent highly dynamic bonds, whereas low SD would represent bonds that are persistent over the course of the MD trajectory. SD, in this case, does not reflect statistical errors in the calculations; instead, it reflects the transitory nature of each individual bond. However, the total hydrogen-bond energy values are expected to have a relatively smaller SD because bonds that are broken over the course of the trajectory are usually replaced by other bonds that are forming simultaneously.

Hence, we should have more-precise values for the overall hydrogen-bond energies. These variations could, however, be compensated for by other binding interactions, such as electrostatic interactions or van der Waals interactions, which were not included in this study. It is also important to note that the per-residue energies listed in the tables include all hydrogen-bond instances between the residue pairs. Therefore, the energy could be due to more than one hydrogen bond between the interacting pair. The tables only list hydrogen bonds that are stronger than –10 kJ/mol. Other weak bonds are included in the Supporting Material. Residue numbering follows the same scheme as in PDB:1JFF (39).

Longitudinal interactions

The longitudinal (LongAB) interface (see Fig. 1 b) is particularly important as it contributes to the building of a protofilament and happens to accommodate an important class of anticancer agents. This class includes the microtubule destabilizers known as vinca alkaloids (67,68). Understanding the interactions at this interface could give us an insight into the mechanism of action for vinca alkaloids. An all-atom model of the LongAB system with subunit assignment can be found in Fig. S2. Analyzing the results for the LongAB interface listed in Table 1, we find that the total hydrogen-bond energy is –392 ± 59 kJ/mol. The table also shows the per-residue hydrogen-bond energies between the α-subunit of heterodimer 1 and the β-subunit of heterodimer 2. As shown in this table, the strongest bond network is the one between αArg² and βGlu⁷¹ with an average energy of –40.1 kJ/mol. This bond is also persistent along the MD trajectory, as shown by the relatively low SD. αArg² is, in fact, the very first residue in tubulin after the first methionine, and it makes an energetically significant bond. The second partner of this strong bond, βGlu⁷¹, is present in the S2-H2 loop of the β-tubulin, which shows the importance of this loop to longitudinal stability.

Another important residue is βArg⁴⁰¹, which is present in the H11-H11′ loop. This residue alone makes several strong hydrogen-bond networks with αGlu⁴³⁴ (–32.6 kJ/mol), αTyr²⁶² (–32.1 kJ/mol), and αAsp⁴³⁸ (–23.9 kJ/mol), summing up to a total of nearly –90 kJ/mol on average, which is nearly one-fourth of the total binding energy. Thus, residue βArg⁴⁰¹ could be described as the longitudinal glue of microtubules. Two of the partners that bind to this residue, namely αGlu⁴³⁴ and αAsp⁴³⁸, belong to the C-terminal tail of the α-subunit. Residues from 176 to 181 in β-tubulin, which correspond to the S5-H5 loop, make several hydrogen-bond networks with α-residues that belong to helix H10 through loop S9-S10. These bonds collectively make up nearly –90 kJ/mol, which comprises nearly one-fourth of the overall stability, and again reflects the importance of the S5-H5 loop in longitudinal stability.

The bonds involving S5-H5 loop are not only collectively strong, but they are also relatively persistent during the MD simulation, as indicated by their relatively low SD values. In fact, it has been shown that the S5-H5 loop in β-tubulin, particularly residues from 174 to 179, are very important for the vinca alkaloid binding and they comprise part of the vinca-binding site (67,69). Considering that, as shown in this work, the same region contributes significantly to the longitudinal stability indicates that it is very likely that the binding of these anticancer agents destabilizes microtubules simply by disrupting the longitudinal hydrogen-bond networks between adjacent heterodimers along a protofilament. This could be verified by performing another equivalent study in the presence of one of these agents, then comparing the results.

The bonds made by βGly¹⁰⁰ and βGly⁹⁸ on one side and αThr²⁵⁷ and αGln¹³³ on the other side, respectively, are also strong and steady with relatively low SD, suggesting a strong and persistent stabilization due to the S3-H3′ loop of β-tubulin. It is also noticeable that GDP has no contribution to longitudinal stability when hydrogen bonds are considered; it does not appear in our list, although it binds close to the longitudinal interface. It is worth mentioning that residues making hydrogen-bond networks with more than one residue, such as βArg⁴⁰¹, usually have a relatively high SD. This is not surprising because during the MD simulation, such a residue may break its bonds with one residue and soon form other bonds with another residue to maintain the longitudinal stability. This behavior raises the SD calculated over the eight representative snapshots for each bond. All the major hydrogen bonds in the longitudinal interface are shown in Fig. 2. It is obvious that major strong hydrogen bonds are well distributed along the width and the length of the longitudinal interface, which imparts even more stability to the protofilaments because they act as pillars for the protofilament structure. Residue βArg⁴⁰¹ and its strong and persistent hydrogen-bond network is also shown in Fig. 2.

Figure 2.

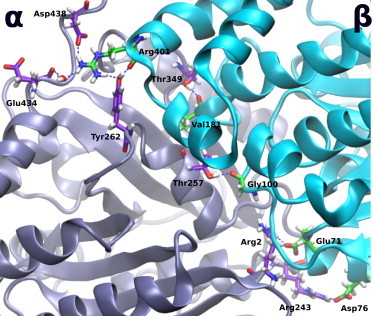
The major hydrogen bonds at the longitudinal interface. It is clear that they are distributed over the entire width and length of the interface to provide stronger support to the protofilament structure. To see this figure in color, go online.

Lateral B interactions

The LatB interface represents the lateral interface between two tubulin dimers in two adjacent protofilaments in the B-configuration (see Fig. 1 b). An all-atom model of the LatB system with subunit assignment can be found in Fig. S3. This interface is especially important not only because it brings protofilaments together to form a microtubule cylinder, but because it is also very close to the taxane-binding site. The taxane-binding site is the binding site for many microtubule-stabilizing antimitotic drugs such as taxol, epothilone, discodermolide, eleutherobin, and sarcodictyin (70–74). Analyzing the lateral interface could give us an insight into the detailed mechanism of action of such agents. The first and most obvious observation in Table 2 is that, in a 95% confidence interval, lateral hydrogen bonds are significantly stronger than longitudinal ones, –462 ± 70 vs. –392 ± 59 kJ/mol.

This is apparently counterintuitive, because we know, a priori, that lateral contacts break before longitudinal ones and this is why depolymerizing microtubules display transient structures that look like ram’s horns (26,75). There could be two justifications for getting such results: the first one is that we only calculated the respective hydrogen-bond energies. Other sources of energies could balance out this energy difference. Particularly, electrostatic interactions and dipole-dipole interactions are expected to be more destabilizing in the lateral orientation than in the longitudinal one. This is because the similarly-charged subunits are packed closer together in the lateral orientation than in the extended longitudinal one. We estimated the van der Waals as well as electrostatic contributions using the MM/GBSA calculation and found that the longitudinal interactions in a protofilament are ∼130 kJ/mol stronger than lateral interactions, which supports our justification. The other possible reason for this difference is that in the LatB simulations we actually modeled GTP-capped tubulin dimers, as explained in Methods.

Terminal tubulin dimers capped with GTP stabilize microtubule structures more strongly than those capped with GDP, which is why depolymerization usually happens after hydrolysis of the terminal GTP (12). Hence, lateral contacts in our case are expected to be enhanced by the presence of GTP, and this could be the reason why they are stronger than longitudinal ones. Preliminary results from other simulations being presently performed support this explanation, because we found out that in the presence of GDP instead of GTP, the two heterodimers are significantly more weakly connected to one another. The data in Table 2 also show that the average contribution of the β-β interactions is comparable to the average contribution of the α-α interactions, namely –252 ± 65 vs. –210 ± 35 kJ/mol at a 95% the confidence interval. However, if the simulations were run in presence of taxol, the relative contributions of the two subunits could have been different.

Examining the β-β subunit interactions, we find out that the strongest hydrogen-bond network is the one between βArg³⁰⁸ (from the H9′ helix) and βAsp¹¹⁶, with a strength of –44.8 kJ/mol and a relatively moderate SD, signifying persistence of the bonds over the MD trajectory. βArg³⁰⁸ still makes another strong and largely persistent bond with βAsp¹²⁰, at a strength of –36.7 kJ/mol. Thus, βArg³⁰⁸ contributes, in total, nearly –80 kJ/mol to lateral stability, which is nearly one-third of the overall β-β stabilization. βGlu²⁹⁰ and βArg⁸⁸ contribute a largely persistent hydrogen-bond network of –38.9 kJ/mol. The H2-S3 loop, which involves βArg⁸⁸ and βAsp⁹⁰, is extensively involved in lateral stabilization, making bonds that sum up to nearly –90 kJ/mol, which is nearly one-third of the overall β-β hydrogen-bond energy. The H3 helix, which involves residues βAsp¹¹⁶, βAsp¹²⁰, βLys¹²⁴, and βSer¹²⁶ and others, is responsible for most of the stabilization occurring between β-subunits. Interactions involving these residues sum up to a total of nearly –165 kJ/mol, which is approximately two-thirds of the overall β-β stabilization.

Thus, H2-S3 is responsible for one-third of β-β hydrogen-bond energy, and the H3 helix is responsible for the remaining two-thirds. On the other hand, the contribution of the M-loop from the opposite β-subunit (TUB 1-β in Table 2) is relatively small compared to the H3 helix contribution from TUB 2-β, amounting to only –16.6 kJ/mol on average, via bonds that involve βSer²⁸⁰ from the M-loop. The H1-S2 loop in TUB 2--β has no contribution to lateral hydrogen-bonding in B-lattice. This is contrary to the conclusions that were drawn by Li et al. (43), who argued that lateral stability is mostly due to interactions between M-loop and H1-S2 loop rather than being due to the H3 helix. However, these authors stated that this result itself is contrary to a previous conclusion they reached, which attributed most of the lateral stability to the H3 helix rather than the H1-S2 loop. This shows some discrepancies that could be attributed to the fact that their conclusions were not based on a study of the energetics of lateral contacts, but only on geometric criteria. It could also be attributed to the fact that we considered hydrogen bonds only, in this study. Other energetic components could still come into play.

However, considering the conditions of our simulations, the difference between the results of Li et al. (43) and our findings may be understood because microtubules stabilized by taxol were used in their experiments but not in ours. It is known that taxol restructures the M-loop in a way that stabilizes lateral contacts (43,76–78). Because our simulations did not include taxol or any other stabilizer, we do not expect our results to match the results of Li et al. (43) with regards to the role of the M-loop in imparting lateral stability. Moreover, Li et al. (43) argued that the role of the H3 helix becomes more pronounced when the number of protofilaments in a microtubule increases, inasmuch as this decreases the angle between laterally adjacent protofilaments and brings the H3 helix closer to the neighboring heterodimer. This could be more similar to our simulated system that included only one pair of heterodimers instead of a complete microtubule, and thus could rearrange during the course of the MD simulations and draw the subunits closer to generate more H3 helix contacts. Fig. 3 shows the LatB system before (orange) and after (cyan) the simulations.

Figure 3.

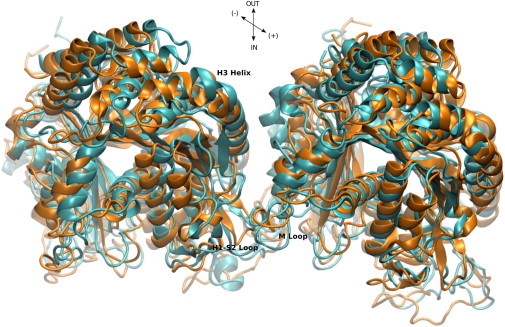
Relative orientation of the two adjacent heterodimers in the LatB system before the simulation (orange) and after 25 ns of the simulation (cyan). To see this figure in color, go online.

It is clear that after the simulations, the two heterodimers have rotated inward, coming closer to each other and creating more interactions with the H3 helix at the expense of breaking interactions between the M-loop and the H1-S2 loop. Comparing the residues on our list to the residues that compose the taxol-binding site, we find that residues βGlu²⁹⁰ and βSer²⁸⁰ are in common. These two residues make hydrogen-bond networks with the neighboring β-tubulin subunit that sum up to –55.5 kJ/mol, most of which comes from the bonds between βGlu²⁹⁰ and βArg⁸⁸, which alone make up –38.9 kJ/mol. Comparing the role of H3 and the M-loop in lateral stability in our study and considering the finding that H3 is much more involved in stabilization than the M-loop, it appears more likely that the binding of taxol may make the M-loop more involved in lateral stability. Addition of taxol could rearrange this domain and favor stronger lateral contacts. (This could be verified by performing another simulation in the presence of taxol and estimating the per-residue contribution of all these residues.) It is worth mentioning that a conformational change of the M-loop into a short helix upon binding of stabilizers was recently confirmed by Prota et al. (79). However, they did not address the energetic effects of this restructuring on lateral contacts. The major hydrogen-bond networks in β-β interactions are shown in Fig. 4 a.

Figure 4.

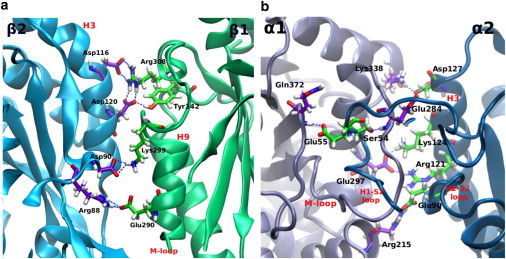
Major hydrogen bonds in the LatB system at the (a) β-β interface and (b) α-α interface. To see this figure in color, go online.

The α-α interactions are similar to the β-β ones in that they extensively involve helix H3, with the H2-S3 loop on one side and the H9-S8 loop on the other side. However, the α-α interactions are different because they also extensively involve interactions between the H1-S2 loop and the M-loop. These interactions involve the bonds between αSer⁵⁴, αSer⁴⁸, and αPhe⁴⁹ on one side and αGlu²⁸⁴, αTyr²⁸², and αHis²⁸³ on the other side. These, and other bonds between the M-loop and the H1-S2 loop shown in Table S2 in the Supporting Material, add up to an average total of nearly –63 kJ/mol. It is also apparent that the hydrogen-bond network between αArg²¹⁵ and αGlu⁹⁰ is the strongest in the system, with an average energy of –42.7 kJ/mol. Fig. 4 b shows the major hydrogen-bond networks that bring α-subunits together in lateral orientation. An interesting phenomenon that is noticed from the figure is the intertwining of the M-loop and the N-terminal H1-S2 loop. This structure was conserved over the entire length of the MD simulation, which reflects its stability. The lateral interface is highly populated with oppositely charged residues as compared to the longitudinal interface; hence, we also expect a stabilizing electrostatic contribution between these charged residues.

Lateral A interactions

This LatA interface represents the lateral interface between protofilaments in an A-lattice configuration, shown in Fig. 1 c. An all-atom model of the LatA system with subunit assignment can be found in Fig. S4. The A-lattice configuration is less significant than the B-lattice because the latter has been empirically observed to be much more predominant. It is worth mentioning that to simulate an A-lattice, three, rather than two, tubulin dimers must be included in the simulation because of the subunit offset. Because this is computationally very demanding, we simulated the relevant subunits only. That is, we used α- and β-subunits from dimer 1, a β-subunit from dimer 2, and an α-subunit from dimer 3, discarding the α-subunit of dimer 2 and the β-subunit of dimer 3. This is acceptable because, as illustrated in Fig. 1 c, the discarded subunits have no contacts with the studied interfaces and are far away from them.

Table 3 lists the hydrogen-bond energies obtained from the simulations. It shows that, in a 95% confidence interval, the average overall hydrogen-bonding in the A-lattice is not significantly different from the B-lattice, with energies of –472 ± 46 vs. –462 ± 70 kJ/mol, respectively. Sept et al. (26) also studied the difference between B-lattice and A-lattice energetics considering solvation energy only, but they found that the B-configuration, corresponding to a subunit rise of 8–9 Å, is more stable than the A-configuration, corresponding to a subunit rise of 52 Å. Drabik et al. (27) also found a similar effect when comparing the potential of mean force in the two configurations. Therefore, in light of our findings, the difference in stability between B-lattice and A-lattice configurations could be attributed to solvation energy and other energetic components rather than to hydrogen bonds. It is worth mentioning that the A-lattice configuration is not exclusive to the A-lattice; it is also a part of the B-lattice that appears only at the seam, as depicted in Fig. 1 a.

In Table 3, we differentiate between α-β interactions and β-α interactions, because, due to differences between α- and β-subunits, they are not identical. In our notation, α-β interactions represent the half of the system in which the N-terminal H1-S2 loop, helix H3, and the H2-S3 loop of the α-subunit interact with the M-loop and other domains of the β-subunit. However, β-α interactions represent the other half of the system in which the opposite is true. An interesting observation is that α-β interactions are much stronger than β-α interactions, as manifested by an energy value of –299 ± 23 vs. –173 ± 44 kJ/mol, respectively. This suggests that the involvement of the M-loop of the β-subunit, rather than the α-subunit, in lateral contacts greatly enhances the stability of the system by interacting with N-terminal H1-S2 loop of the opposite subunit.

In particular, residues βArg²⁸⁴, βArg²⁷⁸, and βGln²⁸² and others make lateral hydrogen bonds with the N-terminal loop of the adjacent α-subunit that add up to nearly –120 kJ/mol. Most of these bonds are absent in the β-α interaction half-system, and the contribution of M-loop H1-S2 loop interactions is nearly –30 kJ/mol. The M-loop of the β-α interaction half-system prefers to bind with H2-S3 loop and H3 helix. This is illustrated in Fig. 5, a and b, which shows the major hydrogen bonds in the two half-systems. Based on this we can also expect taxol, which is hypothesized to induce M-loop lateral interactions, to impart stability to the system via this mechanism. This can even be extrapolated to the B-lattice because Table 2 does not record any major contribution of the β M-loop, especially residue βArg²⁸⁴, to the overall stability. Inclusion of taxol in the simulation could alter this behavior and enhance the role of the M-loop.

Figure 5.

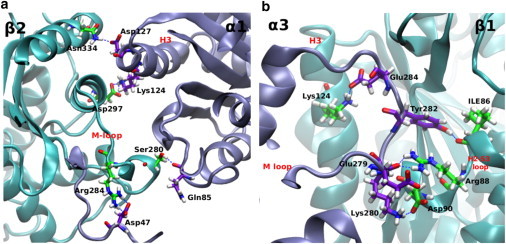
Major hydrogen bonds at the (a) α-β interface and (b) β-α interface of the LatA system. To see this figure in color, go online.

Finally, the comparison of the top-ranking residue pairs in Tables 1–3 to the residues that are conserved throughout different α/β-tubulin isotypes (69,80) showed that there is considerable agreement. In other words, residues important for interfacial stability are highly conserved among different tubulin isotypes.

Conclusions

The concept of the density at the bond critical point obtained from the AIM analysis is very useful in the calculation of hydrogen-bond energies. In this article, we have implemented a seemingly new technique for the application of this method to macromolecules, namely tubulin dimer-dimer systems. The systems were equilibrated by MD simulations and then studied by QM calculations employing density functional theory followed by an AIM analysis. The three different interfaces studied, longitudinal interface as well as lateral interfaces in B- and A-lattice configurations, revealed that hydrogen bonding is an important player in the stability of tubulin systems. One limitation of this study is the fact that we used only eight representative snapshots from the trajectory of every system. Running relatively long simulations, ensuring clustering of the trajectories, and choosing the centroid of each cluster, should alleviate this limitation. Analyzing the overall hydrogen-bond energies in different interfaces showed that lateral contacts are stronger than longitudinal ones, which was attributed to the stabilization imparted by the GTP cap on β-tubulin subunits.

The contribution of the β-β interactions to the overall lateral stability in the B-configuration was shown to be comparable to that of the α-α interactions in a 95% confidence interval. Running the same simulations in the presence of taxol could give different results and offer more insight into this aspect. The study also showed that the stability of the B-lattice configuration is comparable to the A-lattice when hydrogen bonds are concerned. This suggests that other energetic contributions could be responsible for the observed difference in predominance between the two lattice forms. Per-residue hydrogen-bond analysis was found to be in agreement with empirical data regarding residues critical to longitudinal stability and residues involved in the binding of vinca alkaloids. This suggests the mechanism of action of vinca alkaloids could be in the alteration of the conformations of interfacial residues upon binding, which disrupts the interfacial hydrogen-bond network and destabilizes the microtubule.

The β M-loop was shown to have a weak contribution to the stability of the LatB system, contrary to its large contribution to the stability of the LatA system. The weak contribution of the M-loop to the stability of the LatB system was attributed to the absence of taxol or any other microtubule stabilizer in our simulation that causes the M-loop to drift away and be replaced by helix H9 and the H9-S8 loop interacting with helix H3 in lateral contacts. Further elucidation of the role of anticancer agents would require running the simulations in the presence of vinca alkaloids, taxol, and GDP to reach a final conclusion regarding the mechanisms of stabilization or destabilization of microtubules. Most of the residues that contributed significantly to stability of tubulin-tubulin interactions were also found to be highly conserved among different tubulin isotypes.