Identification of Allosteric Disulfides from Prestress Analysis

Abstract

Disulfide bonds serve to form physical cross-links between residues in protein structures, thereby stabilizing the protein fold. Apart from this purely structural role, they can also be chemically active, participating in redox reactions, and they may even potentially act as allosteric switches controlling protein functions. Specific types of disulfide bonds have been identified in static protein structures from their distinctive pattern of dihedral bond angles, and the allosteric function of such bonds is purported to be related to the torsional strain they store. Using all-atom molecular-dynamics simulations for ∼700 disulfide bonded proteins, we analyzed the intramolecular mechanical forces in 20 classes of disulfide bonds. We found that two particular classes, the −RHStaple and the −/+RHHook disulfides, are indeed more stressed than other disulfide bonds, but the stress is carried primarily by stretching of the S-S bond and bending of the neighboring bond angles, rather than by dihedral torsion. This stress corresponds to a tension force of magnitude ∼200 pN, which is balanced by repulsive van der Waals interactions between the cysteine Cα atoms. We confirm stretching of the S-S bond to be a general feature of the −RHStaples and the −/+RHHooks by analyzing ∼20,000 static protein structures. Given that forced stretching of S-S bonds is known to accelerate their cleavage, we propose that prestress of allosteric disulfide bonds has the potential to alter the reactivity of a disulfide, thereby allowing us to readily switch between functional states.

Introduction

Disulfide bonds are essential structural components of many proteins. It has been shown that they play a wide range of active functional roles beyond their contribution to protein stability (1). Because they can be broken and reformed due to the action of redox-catalyzing molecules in the vicinity of the protein, disulfide bonds might in some cases act as switches by which proteins can sense and react to environmental stimuli. Recently, redox reactions involving disulfide bonds have been shown to depend on mechanical force. The mechano-chemical coupling results in altered reaction rates of thiol/disulfide bond exchange, as shown by a number of pioneering force spectroscopy experiments (2–7) and computer simulations (2,8,9), which have demonstrated that force effectively increases or, in some cases, surprisingly decreases the reactivity of a protein disulfide bond. The specific behavior depends on the reducing agent, which might be a small molecule such as DTT (dithiothreitol) or an enzyme such as thioredoxin (2,7,8). Baldus et al. (9) observed that the redox potentials of disulfide bonds increase under mechanical load in quantum and molecular mechanical simulations, suggesting that the destabilization of disulfide bonds by mechanical force is a direct result of stretching, bending, and twisting the sulfur-sulfur bond and other bonds in its immediate neighborhood.

Although it is clear that externally applied forces can modify a disulfide bond’s reactivity, the question arises whether reactivity can be similarly tuned by internal stresses arising from topological constraints in the protein structure. Indeed, based on a survey of static protein structures, three out of 20 classes of disulfide bonds, which are defined by the signs of five χ_i dihedral angles (Fig. 1 A and see Table S1 in the Supporting Material), namely the −RHStaple, −/+RHHook, and −LHHook, were identified as allosteric disulfide bonds. Typically, they were observed to share an unfavorable conformation of the χ_i angles enclosing a disulfide bond (Fig. 1 B and see Fig. S1 in the Supporting Material). The breakage of such bond classes are known to modulate the protein’s function including binding or catalysis (10–14). Thus, such allosteric disulfide bonds can be thought of as functional switches. A dihedral strain energy (DSE), defined in terms of the torsion of the five dihedral angles χ_i comprising the sulfur-sulfur bond, was used as a measure for destabilization, and it was found to be higher for allosteric disulfide bonds than for other types. This correlation implies that mechanical prestress might play an important role in the allosteric function of these bonds. The underlying mechanism can be expected to involve destabilization of the bond by prestress, resulting in an enhanced susceptibility to force-induced chemical reduction, in a way analogous to the effect of an external force on a redox reaction rate.

Figure 1.

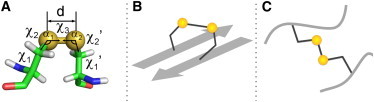
Structure of disulfide bond. (A) Geometry of a disulfide bond. d is the bond length. The values α₁ and α₂ represent the two relevant bending angles of the disulfide, and the five dihedral angles are χ₁, χ₂, χ₃, χ₂′, and χ₁′. (B) The −RHStaple disulfide bond model, which often cross-links antiparallel β-strands (see Fig. S1 in the Supporting Material), supposedly resulting in a prestressed disulfide. The signs of the five χ_i angles in the −RHStaple are −, −, +, −, and −. (C) Other classes of disulfide bonds sample supposedly more relaxed configurations.

In this work, we test the hypothesis that specific classes of disulfides carry mechanical stress in the bond. To this end, we used force distribution analysis (FDA), a technique developed in our group for calculating atom-atom and residue-residue forces from molecular-dynamics (MD) simulations (15–17). Recently, FDA was used to show that globular proteins feature a network of significantly nonzero forces between residues even at equilibrium (18). The balance of preexisting tensile and compressive forces in an equilibrium structure is somewhat reminiscent of the architectural concept of tensegrity (19), which has already been used with some success to describe how cytoskeletons can sense mechanical signals (20–23). We here show that the same concept can also be usefully applied to understand how a protein structure imposes prestress upon allosteric disulfide bonds. We subjected a set of ∼700 disulfide bonded proteins to MD simulations and subsequent FDA. A key finding from our simulations is that the tensile prestress in the bonded interactions between disulfide linked cysteines is significantly larger for the allosteric −RHStaple and −/+RHHook configurations than for other bonds. Interestingly, the majority of the tensile prestress in −RHStaple and −/+RHHook configurations is found to be carried by direct stretching of the sulfur-sulfur bond and the nearby bond angles, rather than by dihedral angle torsions, as assumed by Schmidt et al. (10).

Using extensive MD simulations, we next analyzed the interatomic forces associated with disulfide bonds in two cysteine-rich proteins. The first protein we analyzed was CD4. Its binding to gp120 induces conformational changes in the HIV-1 envelope (24), which primes the virus for entry into the cell. CD4 contains four immunoglobulin domains (D1–D4) expressed on the surface of T cells (25–27). Crystal structures of the D1 and D2 domains show two disulfide bonds (Cys¹⁶-Cys⁸⁴ and Cys¹³⁰-Cys¹⁵⁹) (28). One of these, Cys¹³⁰-Cys¹⁵⁹ in the D2 domain, has been observed to be redox-active (29). The reduced state has a higher affinity for gp120 binding (30), which suggests the cleavage of Cys¹³⁰-Cys¹⁵⁹ has an allosteric effect. Cys¹³⁰-Cys¹⁵⁹ crosslinks antiparallel β-strands (Fig. 1 B and Fig. 3 A, left), as is typical for −RHStaple disulfide bonds.

Figure 3.

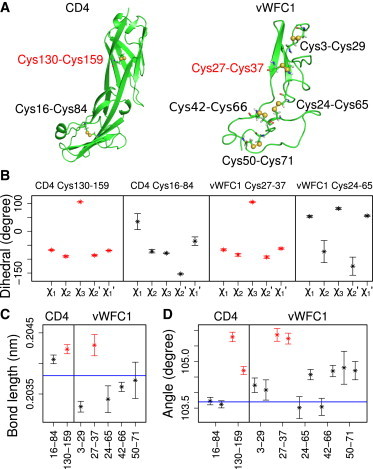
Structural analysis of CD4 and vWFC1. (Red) −RHStaple disulfide bonds both in CD4 and vWFC1; (black) other types of disulfide bonds. (A) Structures of CD4 and vWFC1 with disulfide bonds. Cys¹³⁰-Cys¹⁵⁹ in CD4 and Cys²⁷-Cys³⁷ in vWFC1 are linking antiparallel β-strands. (B) Dihedral angles (compare Fig. 1A) for selected disulfide bonds, with −RHStaple (red) and other disulfides (black). Dihedral angles for the three remaining disulfides in vWFC1 are given in Fig. S5. (C) Disulfide bond length. (D) C-S-S angles. Two neighboring bars stand for two adjacent angles of each disulfide bond. In panels C and D, bars on the left are for CD4, on the right for vWFC1. (Blue horizontal lines) Equilibrium parameters in the OPLS/AA force field.

The second protein, the C1 domain of von Willebrand factor (vWF), was chosen because we wanted to apply FDA to a domain for which an experimental structure is absent, but a homology model can still be generated. In this way, we were able to test whether the detected prestress is robust with regard to the atomic details and accuracy of the structure. vWF is a multidomain blood glycoprotein that plays a major role in blood clotting (31,32). The protein as a whole has a high proportion of cysteine residues (8.3%), with the C1 domain being especially cysteine-rich: 12 of its 74 residues are cysteines. The C1 domain is involved in platelets’ adhesion during hemostasis (33). We prepared a homology model, in which 10 of 12 cysteine residues in the C1 domain pair-up to form five disulfide bonds (Fig. 3 A, right). Of these, Cys²⁷-Cys³⁷ is found to cross-link antiparallel β-strands (Fig. 1, B and 3, A right), and is in the −RHStaple conformation. In these two cases, the prestress amounts to as much as −160 and −195 pN for CD4 and vWFC1, respectively—a force magnitude known to be in the range to significantly alter redox reactivity (4,6,34,35).

We could further confirm the prestress in certain disulfide bond classes by a statistical analysis of ∼20,000 static protein structures. It showed that significant stretching of the S-S bond is evident, on average, for all structurally known −RHStaple and −/+RHHook bonds. Given that mechanical stretching of sulfur-sulfur bonds has been shown to affect their redox potential (9), this strongly suggests that these prestressed bonds are more susceptible to cleavage than other configurations. We propose that mechanically prestressing these bonds, by means of topological constraints, is used by proteins to adjust the breakability of allosteric disulfide bonds and to thereby encode specific functional roles.

Materials and Methods

Homology modeling

A homology model of vWFC1 was created from the crossveinless-2 C domain (Protein Data Bank (PDB) PDB:3BK3 (36)), using the Molecular Operating Environment (MOE) software package (MOE 2008.10, Chemical Computing Group, Quebec, Canada). To this end, a sequence alignment was performed using the software CLUSTALX 2.0 (37) and used to map the vWFC1 sequence to the PDB:3BK3 sequence. The C1 domain consists of residues 2255–2328, as defined in the UNIPROT database. Zhou et al. (38) recently reannotated the domains of vWF and enlarged the definition of the C1 domain to residue 2333. We consider this difference to have a minor influence on the structure and especially on the −RHStaple, which is of our main interest here. Despite only 21% sequence identity, Hogg et al. (39,40) suggested crossveinless-2 to be a good template for the C2 domain (residues 2429–2496, which we refer to here as “domain C3” according to the new annotation by Zhou et al. (38)). Our sequence alignment revealed a high similarity among the domains C1–C5, among which C1 showed a better homology to PDB:3BK3 than C3, which is 23.8%. In addition, the cross-strand disulfide bond of the predicted C3 domain did not remain in the expected −RHStaple configuration, as opposed to the same bond in C1, so that, in this work, we only analyze results for the vWFC1 domain. Zhou et al. (38) predicted four disulfide bonds to cross-link eight out of the 12 cysteine residues in the vWFC1 domain, all of which are included in our model. Additionally, our model contains another disulfide bond, one that, for lack of evidence, was not predicted by Zhou et al. (38). Because the homology model and the disulfide bonds in question are in exact alignment with the bridged cysteines in the template, we expect the disulfide bond to be present, and we included it in our model.

We tested the stability of the model by comparison of the root mean-square deviation (RMSD) from a 50-ns MD simulation to the RMSD of crossveinless-2 (details on MD simulations are given below). For both, we find an RMSD close to 0.5 nm, with high fluctuations primarily restricted to the loops. Instead, the central β-sheet remained intact, with an RMSD <0.5 nm. Also, the −RHStaple was stable over the entire range of the simulation (Fig. 3 B, red) and could also withstand temperatures up to 340 K in a 50-ns simulation.

MD simulations

All simulations were performed with the MD software package GROMACS 4.5.3 (41). CD4 (PDB:1CDY) was inserted into a rhombohedral box of water molecules, allowing a distance of 1.5 nm in all directions. The OPLS all-atom force field (42,43) and the tip4p (44) water model were used. Sodium and chloride ions were added to keep a salt concentration of 150 mM. The system resulted in a dodecahedron box of volume ∼10 × 10 × 10 nm³ with ∼91,000 atoms. Simulations were run in the NpT ensemble. The temperature was kept at 300 K by coupling to a Nosé-Hoover thermostat (45,46) with a coupling time of τ_t = 0.4 ps. The pressure was kept constant at p = 1 bar using isotropic coupling to a Parrinello-Rahman barostat (47) with τ_p = 4.0 ps and a compressibility of 4.5 ×10⁻⁵ bar⁻¹. Lennard-Jones interactions were cut off beyond 1 nm. Electrostatic interactions were calculated explicitly at a distance <1 nm, whereas long-range electrostatic interactions were calculated via particle-mesh Ewald summation (48,49). Bonds including hydrogen atoms were constrained using the LINCS algorithm (50).

We performed an energy-minimization-with-steepest-descent algorithm and a subsequent equilibration of the solvent during an MD simulation of 50 ps with position restraints of 1.66 N/m on all protein heavy atoms. Ten independent MD simulations starting from different starting configurations were performed for equilibrating the protein, each 50 ns in length (2500 frames for each simulation). Simulations with the same parameters were performed on vWFC1, with a box size of 8.25 × 8.25 × 8.25 nm³, comprising ∼52,000 atoms. In addition, for both CD4 and vWFC1, MD simulations were performed with a reduced −RHStaple disulfide bond and with all disulfide bonds being reduced, respectively, with 50 ns simulations for each of these four different cases.

We performed MD simulations and FDA (see below) with the same settings for overall 667 proteins, with 10 ns of simulation time for each protein. These structures were chosen as follows: up to the end of 2012, 86,973 structures were reported in the PDB, with 18,723 structures containing disulfide bonds (see Table S2). We restricted the set of simulated structures to those without metal ions or ligands, with sufficient resolution <2.5 Å and residues numbering <300, resulting in 667 successful simulations containing 2,360 disulfide bonds (Table S2 and the PDB codes in the Supporting Material). To assess the dependence of results on the force field, simulations of a subset of 13 proteins with 54 disulfide bonds were repeated with both the AMBER99SB-ILDN (51) and CHARMM27 (52) force fields.

Force distribution analysis

Force distribution analysis (FDA) (15,16) allows the analysis of internal forces present within a protein structure. Using the FDA implementation in the software GROMACS 4.5.3 (17), for each MD simulation, pairwise residue forces ${\overrightarrow{F}}_{uv}$ between residues u and v were calculated by summing up atomic forces ${\overrightarrow{F}}_{ij}$ between atoms i and j, where atom i is part of residue u and atom j is part of residue v,

$${\overrightarrow{F}}_{uv}=\sum {\overrightarrow{F}}_{ij}.$$ (1)

Atomic forces included both bonded and nonbonded (Lennard Jones and electrostatic) interactions below the 1-nm cutoff, if not otherwise noted. For potentials involving only two atoms (bonds, Coulomb, Lennard-Jones), the pairwise force can be directly calculated from the potential. For potentials involving more than two atoms (angles, proper and improper dihedral angles), the forces need to be decomposed to reflect the interactions between each pair of atoms, as detailed in Costescu and Gräter (17).

An N×N pairwise residue force matrix of the signed scalar forces $\left|{\overrightarrow{F}}_{uv}\right|$ was obtained from averaging over 2500 frames, with N = 178 for CD4 and N = 74 for vWFC1. For the other 667 proteins, to allow an initial equilibration of the systems, pairwise forces of only the last 5 ns over 500 frames were averaged. Attractive (repulsive) forces were signed negative (positive). We note that the sum of forces acting on individual atoms or residues averages to zero over time, whereas the pairwise forces can be nonzero even at equilibrium, as a measure of prestress present for this interaction. We denote forces as prestress in analogy to the engineering prestress, even though no normalization by the area through which the force is acting (which is ill defined for a molecular structure) was carried out. Here, we focused on the forces between disulfide bonded cysteines only.

Disulfide bond lengths and angles of static structures

We calculated the S-S bond length and the C-S-S bond angles for disulfide bonds in protein structures from the PDB (updated as of November 1, 2013) on disulfide bonded proteins listed by Schmidt et al. http://www.med.unsw.edu.au/CRCWeb.nsf/page/Disulfide%20Bond%20Analysis (10). For NMR multiple models, the bond lengths and angles were calculated for each model separately, and then the average values were obtained.

By filtering-out those with sulfur-sulfur distances >5% beyond the disulfide bond equilibrium length of 0.2038 nm, erroneous annotations of disulfide bonds were excluded from the analysis. We obtained structures with 113,094 disulfide bonds in total, out of which 10,735 were classified as −RHStaple, and 6007 as −/+RHHook, according to the dihedral angles involving the sulfur-sulfur bond.

A QQ plot was used to compare the datasets with standard normal distributions (53). It confirmed that the qualities of datasets did improve by filtering (see Fig. S2). However, the datasets did not follow normal distributions, neither before nor after filtering (see Fig. S2), which suggested that the Wilcoxon rank sum and signed rank test (54) should be applied to compare the −RHStaple and −/+RHHook bonds to the other disulfides.

Results

Conformation and prestress of disulfides

We first compared the conformation and intrinsic prestress in several hundred protein structures carrying 20 disulfide bond types. From 10-ns MD simulations of a subset of 667 disulfide bonded structures of the PDB, we calculated the distributions of bond lengths and C-S-S angles of disulfide bonds. After the simulations, the distributions of S-S bond lengths and C-S-S angles show smaller variances than before the MD simulations (see Fig. S3, A and B), suggesting the MD simulations to further refine the atomic positions of the experimental structure at limited resolution. Both S-S bond lengths and C-S-S angles of disulfides in −RHStaple configuration are significantly larger than in other disulfide bonds. Another interesting exception is the −/+RHHook type (Fig. 2 A), which also shows significant enlargement of the S-S bond and the C-S-S angle (Fig. 2, B and C). The difference in bond length is very small (in the 10⁻³ nm range), yet statistically significant, and due to the high stiffness of sulfur-sulfur bonds can entail substantial prestress. Overall, the indicative deviation of the bond lengths and angles in −RHStaples and −/+RHHooks from the equilibrium values as defined by the force field hints toward topological constraints in the protein structures, which prevent the disulfide moiety’s fully relaxing into the state of minimal potential energy.

Figure 2.

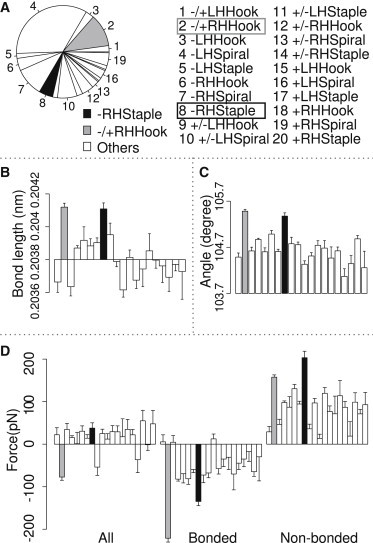
Structural and prestress analysis of 667 proteins. The error bar represents the standard deviation of the mean. (Solid) −RHStaple disulfide bonds; (shaded) −/+RHHook; (open) other types. (A) Pie chart of the sample sizes for each type of disulfide bonds. There are 115 −RHStaple disulfide bonds and 270 −/+RHHook disulfide bonds. All 20 types of disulfide bonds are shown by order of occurrences. (B–D) 20 types of disulfide bonds are shown in the same order as panel A. (B) Mean of S-S bond lengths for each type of disulfide bond. (C) Mean C-S-S angles for each type of disulfide bond. (D) Mean prestress between two adjacent cysteine residues for each type of disulfide bond, including all interactions (left block), only including bonded interactions (middle block), and only including nonbonded interactions (right block).

We next examined the average forces, or prestress, carried by the disulfide bridge in these particular configurations. To this end, we measured pairwise forces between cysteine residues connected by the disulfide bond using FDA. Fig. 2 D shows larger attractive bonded interactions of −RHStaple and −/+RHHook disulfide bonds compared to the others. The mean value of the bonded prestress of −RHStaples and −/+RHHooks are −135 and −221 pN, respectively. This tensile prestress is the value relevant for the disulfide reactivity, as it comprises all force terms involving the sulfur atoms in the disulfide. It is compensated by a repulsive nonbonded force of similar magnitude in both cases, so that the total prestress is largely indistinguishable for the different disulfide geometries. We reproduced the same tendencies with both the AMBER99SB-ILDN and CHARMM27 force fields (see Fig. S4), suggesting the observed prestress to be independent from the details of the underlying potential energy, but instead to primarily stem from the local topology.

Conformation of disulfides in CD4 and vWFC1

We next analyzed in further detail the conformational bias underlying the observed prestress in the −RHStaple disulfide bond for two example proteins, CD4 and vWFC1. We performed a total of 500 ns of MD simulations for each protein, allowing atomic-detailed insight into the structure and dynamics of the disulfide bonds of interest, first, for a well-resolved experimental crystal structure, CD4, and second, for a putative structural model, for which the −RHStaple disulfide bond was only inferred on the basis of homology.

The five dihedral angles involving the sulfur-sulfur bond, χ₁, χ₂, χ₃, χ₂′, and χ₁′ (Fig. 1 A), show algebraic signs of −, −, +, −, and −, respectively, for the −RHStaple in both CD4 (Cys¹³⁰-Cys¹⁵⁹) and vWFC1 (Cys²⁷-Cys³⁷) (Fig. 3, A and B, red). This dihedral conformation lies well within the definition for −RHStaple (Fig. 3 B, red and see Table S3). Other disulfide bonds in CD4 and vWFC1 differ from this specific −RHStaple configuration (Fig. 3 B, black and see Fig. S5). Interestingly, compared with standard disulfide bonds, the dihedrals sampled by the −RHStaple class of disulfide bonds show very small fluctuations, with standard deviations of ≤6°, suggesting the antiparallel β-sheet to strongly restrain and thereby trap this specific disulfide conformation. That none of the dihedrals divert from this configuration in any of the simulations of vWFC1 despite the involved unfavorable stresses supports our structural model of this domain, and suggests prestrain to be primarily the result of the overall topology and not of the atomic detail of the structure.

In accordance with previous observations (10,55), we find the distance between two α-carbons within the prestressed disulfides (∼0.4 nm) to be significantly shorter than within other disulfides (>0.6 nm; see Table S3). The short C_α-C_α′ distance can explain the strong steric repulsion between the involved main-chain atoms, as reflected by the positive Lennard-Jones forces in these cases (see Fig. S6 D). However, the tendency we find in the previously suggested DSE, when averaging over the whole dynamic ensemble of protein conformations, is less clear. From our MD simulations, we obtained an average DSE of 14–17 kcal/mol for the −RHStaple disulfides in vWFC1 and CD4, which lies well within the broad range observed in static crystal and NMR structures previously (56). It does not show any notable difference from the DSE of other disulfide bonds in the two proteins under investigation here (see Table S3). Fig. 3, C and D, shows disulfide bond lengths and the size of the adjacent C-S-S angles, α₁ and α₂ (compare Fig. 1 A).

Disulfide bonds cross-linking antiparallel β-strands feature longer bond lengths (red in Fig. 3 C) as compared to other sulfur-sulfur bonds (black in Fig. 3 C). As for the dihedral angles, these degrees of freedom also show differences between the −RHStaple and other disulfide bonds that are fully recovered in the vWFC1 homology model. Our results support the previous conclusion from the conformational analysis of ∼700 proteins above, that identifying disulfide bonds in unfavorable configurations might be largely aided by considering the S-S bond length and adjacent angles, instead of, or in addition to, the dihedral angles, even if an approximate homology model is under consideration.

Prestress of disulfides in CD4 and vWFC1

We found the bonded interactions between the two disulfide bonded cysteine moieties, more specifically the bonds and angles, to be measurably extended in −RHStaple configurations, presumably carrying characteristic prestress. To quantify the putative prestress in the disulfide bonds of CD4 and vWFC1, we measured pairwise forces between cysteine residues connected by a disulfide bond using FDA. Fig. 4 A displays the average forces between each pair of two cysteine residues in CD4 and vWFC1 averaged over ten 50-ns equilibrium MD simulations. We find total forces between cysteine residues of −RHStaple (Cys¹³⁰-Cys¹⁵⁹ in CD4 and Cys²⁷-Cys³⁷ in vWFC1) to largely fall into the range covered by other disulfides (Fig. 4 A). Interestingly, when decomposing the interresidue force into contributions from bonded (bonds, angles, and dihedrals) and nonbonded interactions (Coulomb, Lennard-Jones, and nonbonded 1–4 interactions, we find −RHStaple disulfides to display strong attractive (negative) bonded forces (Fig. 4 B, red) and even stronger nonbonded repulsive (positive) forces (Fig. 4 C, red). In sharp contrast, common disulfides (disulfides in CD4 except Cys¹³⁰-Cys¹⁵⁹ and disulfides in vWFC1 except Cys²⁷-Cys³⁷) show little prestress in both bonded (Fig. 4 B, black) and nonbonded (Fig. 4 C, black) interactions. The bonded and nonbonded prestress of the disulfide bond Cys^50-71 showed the largest standard deviations (Fig. 4), which is likely caused by its location at the flexible C-terminus (Fig. 3 A).

Figure 4.

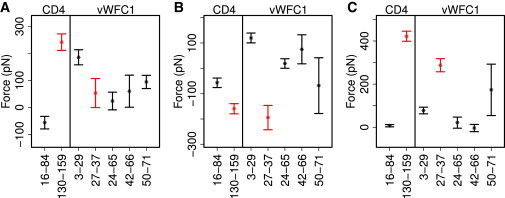
Prestress analysis of disulfides in CD4 and vWFC1. (A) Pairwise residue force between disulfide bonded cysteines in −RHStaple configurations (red) and other configurations (black) including all interactions. (B) Pairwise residue force for bonded interaction including bond stretching, angle bending and dihedral torsion. (C) Pairwise residue force for nonbonded interactions including Lennard-Jones, Coulomb, and nonbonded 1–4. In each subfigure, the x axis shows disulfide bond pairs, and with two bars on the left for CD4, and the five on the right for vWFC1. Averages and standard errors were obtained from 10 independent trajectories, each 50 ns in length.

We further dissected the contributions to these opposing tensile and compressive forces, and found both bonds and angles between the bonded cysteines to carry tensile forces of ∼−100 and −250 pN in bonds and angles, respectively, whereas dihedrals carry a roughly 100-pN compressive force for both −RHStaples in vWFC1 and CD4 (see Fig. S6, A–C). The highly compressive nonbonded forces originate from a van der Waals repulsion (270–390 pN), whereas electrostatic forces of −RHStaples do not differ from those in other disulfide bonds (see Fig. S6, D–E). Thus, in the unfavorable −RHStaple conformation of disulfides bridging two β-strands, bonds and angles are stretched out, giving rise to an overall tensile force between the side chains of the two residues, which contain the only interresidue-bonded interaction. This tension, in turn, is at least partly compensated by a repulsive nonbonded force between the adjacent cysteine residues, which is primarily present between the main chains of the two cysteine residues (we note that nonbonded interactions are excluded for covalently linked atoms in typical force fields, including the one employed here).

Interestingly, the involved tensile and compressive forces in −RHStaples can be as high as several 100 pN, which are of the same order as those forces needed to significantly increase reaction rates such as those of hydroxide-mediated disulfide cleavage (6). They are similar to the force required to dissociate nonbonded interactions (34,35), suggesting the observed prestress to be able to deform the protein locally. Dihedral angles, according to our results, contribute only partly to the overall prestress (see Fig. S6 C), suggesting that a classification of stressed allosteric disulfide bonds based on only their dihedral angles in a crystal structure might be insufficient, and could be improved by also taking bond lengths and angles of the sulfur-sulfur bond into account. We again note that the prestress of the cross-β-strand −RHStaple measured in the homology model (vWFC1) falls into the very same range as the values for this type of bond located in the experimental structure (CD4), hinting toward FDA to be robust with regard to the atomistic details of the model, given that the disulfide configuration is maintained.

Given the significant prestress we measured for the two cross-β-strands disulfide bonds in vWFC1 and CD4, we expected an observable conformational change upon their reduction. To test this, we modeled CD4 and vWFC1 with one or more pairs of reduced cysteines. Our equilibrium MD simulations did not reveal any conformational change for either the entire protein or the β-strands (see Fig. S7, A and B), after we reduced either the −RHStaple or both disulfides in CD4. Similarly, we did not observe a conformational change in vWFC1 upon reduction of the Cys²⁷-Cys³⁷ pair, and the only significant structural deviation was observed with all five vWFC1 disulfides being reduced, although only in the outer loops, while the central β-sheet again remained stable (see Fig. S7, C and D). Thus, redox-dependent allosteric control of these proteins might either involve conformational changes on timescales longer than our nanosecond MD simulations, or do not depend on conformational transitions.

Kinetic estimation

Mechanical force can increase the rate of a redox reaction (3,4,57,58). Baldus and Gräter (9) measured redox potentials of disulfide bonds at different forces by hybrid quantum and molecular mechanical calculation, and it turned out that low mechanical forces (<500 pN) in the range of the bonded prestresses of the −RHStaple bonds we measured here can contribute to the destabilization of the oxidized state of disulfides. We here estimate the expected acceleration of disulfide bond reduction by the internal stress in the disulfide bond using Bell’s model (59), which defines force-dependent reaction rates as

$$r=A\text{exp}\left(\frac{F\text{Δ}{x}_r-E_a}{k_{\text{B}}T}\right),$$ (2)

where r is reaction rate, A is the preexponential factor, F is stretching force, Δx_r is the distance between the reactant and transition state, E_a is the energy barrier, k_B is the Boltzmann constant, and T is the temperature. F includes all bonded terms, i.e., forces in the S-S bond, the C-S-S angles, and the dihedrals involving sulfur atoms, because these have been shown to be the degrees of freedom affecting the energetics of the disulfide (9). We here assume F to persist at least over Δx_r during the reaction. The obtained accelerations should thus be considered as upper boundaries.

With a bonded force between residues 130 and 159 in the CD4 −RHStaple of F_130-159 = −160 pN, a force of F_16-84 = −57 pN in the other CD4 disulfide bond (Fig. 4 B), and a Δx_r of 0.37 Å as measured for thiol/disulfide exchange by either DTT or an hydrosulfide anion (HS⁻) at 298 K (4), we obtain a reduction rate for the prestressed bond, which is a factor of 2–3 larger than the rate for reducing the other nonprestressed disulfide bond in CD4. This relative reactivity is likely to tune the redox sensitivity of CD4, with the −RHStaple configuration being more prone to reduction than the others. The predicted redox reaction rate of Cys²⁷-Cys³⁷ by TCEP (tris-(2-carboxyethyl)-phosphine) in vWFC1 is >30 times faster than for other disulfides (Table 1), because the larger Δx_r of this reaction renders it more sensitive toward prestress.

Table 1.

Bonded prestress and kinetic estimation

Proteins	Disulfide bonds	Bonded prestress (pN) (from FDA calculation)		Reaction ratio
				ΔxDTT/HS− 0.37 ± 0.03 Å (Koti Ainavarapu et al. (4))	ΔxTCEP 0.48 ± 0.02 Å (Koti Ainavarapu et al. (4))
CD4	Cys16-84	−57 ± 19	$\frac{r_{130-159}}{r_{16-84}}$	2.5 ± 0.6	3.3 ± 1.1
	Cys130-159	−160 ± 20
vWFC1	Cys3-29	120 ± 19	$\frac{r_{27-37}}{r_{3-29}}$	16.6 ± 8.6	38.2 ± 23.7
	Cys27-37	−196 ± 48
	Cys24-65	19 ± 19	$\frac{r_{27-37}}{r_{24-65}}$	6.7 ± 3.3	11.9 ± 7.2
	Cys42-66	75 ± 57	$\frac{r_{27-37}}{r_{42-66}}$	11.1 ± 7.7	22.8 ± 19.9
	Cys50-71	−68 ± 110	$\frac{r_{27-37}}{r_{50-71}}$	3.1 ± 3.3	4.3 ± 6.0

The prestress associated with the S-S bond only includes sulfur-sulfur bond, the adjacent bond angles and dihedral angle torsion interactions, which together result in bonded prestress between the adjacent cysteine residues. Standard deviations were obtained over 10 independent simulations. Δx_DTT/HS− and Δx_TCEP are the experimental Δx_r values from Wiita et al. (4).

Structural analysis of static protein structures

According to our equilibrium MD simulations, bond lengths and angles of disulfide bonds linking antiparallel β-strands and the second class −/+RHHook (not significantly abundant in a certain secondary structure element) were observed to be larger than common disulfide bonds. The question arises whether this is a common feature for all disulfide bonds in a −RHStaple or −/+RHHook conformation, and even detectable directly in experimental structures without the need of subsequent MD simulations for relaxation. To address this question, 20,259 NMR and x-ray structures from the PDB of proteins containing all 118,599 disulfide bonds known until November 1, 2013 were analyzed. After excluding disulfide bonds with unresolved sulfur atoms coordinates or with unexpected bond lengths (beyond d₀ ± 0.05, where d₀ = 0.2038 nm), 95.23% structures (19,292) and 95.36% of the disulfide bonds from the sample were considered.

The distribution of bond lengths for the −RHStaples and −/+RHHooks shows a slight shift toward longer disulfide bonds as compared to common disulfide configurations (Fig. 5 A) . The average value of the −RHStaple and −/+RHHook bond length is 0.2040 nm, compared to an average of 0.2038 nm for other disulfides, which is also the equilibrium disulfide bond length in the OPLS/AA force field (0.2038 nm). The observed lengthening of the sulfur-sulfur bond in the −RHStaples and −/+RHHooks was significant (p = 2.2e−16, Wilcoxon rank sum and signed rank test (54)). This tendency was independent of the experimental or refinement method used, be it x-ray crystallography or NMR solved with different NMR software packages (CNS or PLOR), despite differences in the predefined S-S bond length and limited spatial resolution (see Fig. S8). In addition to bond lengthening, the angles of prestressed disulfides were found to be increased by ∼1°, from 104.45° for common disulfides (equilibrium disulfide C-S-S angle is 103.7°) to 105.02° for −RHStaples and −/+RHHooks together (p = 2.2e−16).

Figure 5.

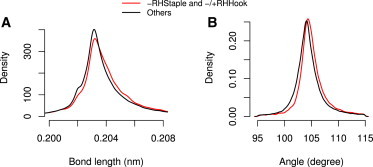
Statistical analysis of disulfide bonds in static protein structures. (Red curve) −RHStaple and −/+RHHook disulfides; (black curve) other disulfides. (A) S-S bond lengths, and (B) angles (both α₁ and α₂ in Fig. 1A) for −RHStaples and −/+RHHooks (red) and other disulfides (black). Distributions for −RHStaple and −/+RHHook bonds in panels A and B differ significantly from those of other bonds (Wilcoxon test).

Thus, our structural analysis of a large set of static NMR and x-ray structures confirms our findings from MD simulations, of a subset of ∼700 structures showing that bonds and angles in disulfide bonds of the −RHStaples and the −/+RHHooks are deformed and tensed. Unsurprisingly, the distributions of bond lengths and angles in protein structures are relatively broad due to the limited resolution (x-ray) or limited set of experimental constraints (NMR). These distributions significantly narrowed in MD simulations (compare to Fig. S3) in a smaller subset. Nevertheless, the significant shift in bond lengths and angles in the −RHStaples and the −/+RHHooks together strongly suggests that the experimental methods successfully reveal topological constraints hampering the C-S-S-C configuration in these disulfides to adopt their model-defined, energetically most favorable parameters.

Discussion

It is increasingly recognized that disulfide/thiol exchange reactions are very dynamic and under strict kinetic—as opposed to thermodynamic—control (60). Disulfide bond reactivity depends on various factors, including their solvent exposure, electrostatic, and hydrophobic environment, the cysteine’s pKa, and structure and stability of the transition state. On the other hand, prestress has been proposed to be a phenomenon involved in regulating protein function and cellular behavior (61). We here focus on the extent of prestress in disulfide bonds as one factor critically influencing the kinetics of disulfide bonds analogously to external forces. We show that the unfavorable geometry of disulfide bonds, when bridging antiparallel β-strands, entails a substantial prestress. The β-strands hosting the disulfide bonds of so-called −RHStaples fix the disulfide bonds in a configuration that imposes a particularly short C_α-C_α distance. The other disulfide configuration, carrying substantial prestress, we could identify in this analysis as the −/+RHHook, which, intriguingly, was suggested as another class of potential allosteric disulfides (11–14).

The resulting prestress manifests itself in tensional forces in the sulfur-sulfur bond and adjacent angles of the covalent sulfur-sulfur bridge, partly compensated by a compression in dihedrals and by a steric repulsion of the involved main-chain in this highly distorted configuration. Other disulfide bonds, in sharp contrast, show prestresses close to zero for the bonded and nonbonded interactions in the disulfide bond. A largely relaxed configuration is taken up because topological constraints are absent or small for these cases, which typically bridge flexible loops or β-strands of separate sheets (Fig. 1 B). The trends, observed for disulfide bonds in hundreds of structures during MD simulations using force distribution analysis, were confirmed by a survey of all disulfide bonds structurally characterized in x-ray and NMR structures to date.

Mechanical stretching forces have been suggested to play an important role in disulfide bond reduction (3–5,9,57). An external force can destabilize a disulfide bond, thereby increasing the rate of reduction by other thiols. Here, we find internal stretching in the 100–250 pN range to be at play for disulfide bonds in specific unfavored configurations. We suggest that, analogously to externally applied stretching forces, internal prestress can destabilize the disulfide, thereby increasing its tendency to be reduced and opened. Along these lines, Cook and Hogg (11) concluded from ab initio simulations that an external force is able to induce a conformational distortion of the S-S-C-C dihedral angles (χ₂ or χ₂′) from the preferred 60 or −60° angle. In accordance, we find the distribution of χ₂ sampled by all disulfide bonds structurally resolved to date to show a maximum at −60°, which shifts toward −90° for −RHStaples (see Fig. S9). This comparison suggests that the magnitude of prestress we detected for −RHStaple disulfide bond might indeed be sufficient to alter redox reactivity analogously to an external stretching force.

An increased reactivity would allow this type of disulfide geometry to play a specific allosteric role in the protein. This hypothesis is supported by the results of Matthias et al. (29,30), who revealed that the −RHStaple disulfide bond in CD4, Cys¹³⁰-Cys¹⁵⁹, is redox-active and its reduction enhances HIV entry. The significant prestress in this disulfide bond can now explain the observed elevated redox activity. We estimate an increase in reduction rate by a factor of 2–3 for the Cys¹³⁰-Cys¹⁵⁹ bond in CD4.

The −RHStaple configuration has been put forward as being characteristic of an allosteric class of disulfide bond, controlling protein function by triggering a conformational change upon switching between the reduced and oxidized states (10). However, our simulations did not reveal any obvious structural changes upon reducing the prestressed disulfide bonds in CD4 or vWFC1. Instead, the antiparallel β-strands remained in their original conformation of the fully oxidized protein. We note that we cannot exclude larger conformational changes that may occur at timescales beyond our nanosecond-scale MD simulations. The possibility that conformational changes involved in a redox switch mechanism could be at play at longer timescales remains to be analyzed by additional experiments or simulations. An alternative scenario for redox-dependent allostery in these cases is that allosteric disulfide bonds such as the prestressed bonds in CD4 and vWFC1 act as redox switches not by undergoing large conformational changes, but instead by virtue of the availability of the free thiols themselves, which in turn can have an impact on protein recognition or subsequent redox reactions.

Conclusion

Our survey of disulfide bonds in the database of currently available protein structures points toward the intriguing scenario that the prestressed disulfide bonds could be a general allosteric mechanism in proteins. A combined prestress and functional analysis of an extended set of dynamic protein ensembles would help to further reveal the underlying principles. Force distribution analysis, in this work, proved useful for identifying prestress in disulfide bonds, and can also be straightforwardly applied to elucidate other potential roles of prestress such as in stressed hydrogen bonds guiding protein allostery (62) or in substrates for efficient enzyme catalysis (63). As far as stressed-bond reactivity is concerned, a quantum mechanical treatment and free energy calculations of the full reaction pathway are required to fully reveal how topological prestress can alter the electronic properties of specific biochemical reaction centers in proteins.