Abstract
Cytoplasmic dynein moves processively along microtubules, but the mechanism of how its heads use the energy from ATP hydrolysis, coupled to a linker swing, to achieve directed motion, is still unclear. In this article, we present a theoretical model based on the winch mechanism in which the principal direction of the linker stroke is toward the microtubule-binding domain. When mechanically coupling two identical heads (each with postulated elastic properties and a minimal ATPase cycle), the model reproduces stepping with 8-nm steps (even though the motor itself is much larger), interhead coordination, and processivity, as reported for mammalian dyneins. Furthermore, when we loosen the elastic connection between the heads, the model still shows processive directional stepping, but it becomes uncoordinated and the stepping pattern shows a greater variability, which reproduces the properties of yeast dyneins. Their slower chemical kinetics allows processive motility and a high stall force without the need for coordination.
Introduction
Dyneins are large motor proteins found in eukaryotic cells (1,2). Axonemal dyneins collectively power the beating of cilia and flagella, whereas cytoplasmic dyneins transport cargoes toward the minus-end of the microtubules (MT). Historically, the first kinetic and motility studies were carried out on axonemal dyneins (3–5). The body of knowledge about cytoplasmic dynein started to grow with the advancement of single-molecule techniques, but due to the complexity of the dynein molecule, it was always lagging behind our understanding of kinesins and myosins. Cytoplasmic dynein is a dimeric molecule and consists of two identical motor domains. Each motor domain contains a ring of six AAA (ATPases associated with diverse cellular activities) domains, four of which can bind ATP (6,7). Protruding from the ring is an ∼15-nm-long stalk, which ends in the microtubule-binding domain (MTBD), and a tail domain responsible for dimerization (8).
Recently, dynein’s crystallographic structure has been determined up to 2.8 Å resolution (9–12). Mammalian cytoplasmic dynein has been shown to walk with speeds up to 800 nm/s and generate a stall force of 1–2 pN (13–15), in some reports up to 5–7 pN (16,17). Based on step-size analysis, Toba et al. (16) reported stepping in a hand-over-hand fashion, and in Dictyostelium dynein the degree of processivity indicated coordination between heads (18). On the other hand, yeast dyneins take less regular steps with speeds of ∼100 nm/s and a stall force of 7 pN (19,20). The observed steps included alternating passing (hand-over-hand), alternating nonpassing (inchworm), and nonalternating modes (21,22).
A unique feature of dynein is the spatial separation between the ATP hydrolysis sites (on the ring) and both the microtubule binding domain (connected to the ring through a coiled-coil stalk) and the tail via the linker (whose docking to the ring acts as a power stroke (23)).
This immediately raises two questions that are central to the walking mechanism of dynein. The first concerns the allosteric interactions between these distant parts. The communication through the stalk is mediated by the relative sliding of the two α-helices forming the coiled-coil (24,25). It is bidirectional: it modulates the microtubule binding affinity, depending on the nucleotide in the primary catalytic site (AAA1) (26), but it also serves gating, such that the ADP release does not occur before binding to the microtubule (27). On the other side, the hydrolysis cycle is coupled to the swing of the linker (8,23). This leads to the second open question: how do the two heads forming a dimer, which are mainly connected through their tails, coordinate their cycles, and how is the tail swing translated into more or less regular stepping with a step size of 8 nm (determined by the periodicity of binding sites on a microtubule)? It is even more surprising that mutants whose rings and tails are rotated by ∼180° maintain the direction of walking on the MT (9). It has been suggested that, in contrast to myosins that achieve their power stroke through a lever arm rotation and kinesins that use neck-linker docking, dynein acts as a winch, which first stretches forward to the next binding site and then effectively contracts to pull the cargo forward (28).
The complexity of the dynein molecule and the lack of structural information have also hampered efforts to build a theoretical model describing its dynamics. So far, only a small part of the molecule (the MTBD) has been accessible to molecular dynamics simulations (29). Other studies performed normal mode analysis on a hypothetical ring structure (30) or the stalk coiled-coil (31). Phenomenological models either concentrated on the kinetics of the molecule without modeling the mechanical properties of the dimer (32–34) or relied on a power-stroke in the stalk domain (35).
In this article, we propose a mechano-chemical model for the dimeric molecule of cytoplasmic dynein, based on the winch mechanism. The model describes each dynein head with a small number of elastic elements and two mechanical states, as known from electron microscopy structures. Their transitions follow a minimal kinetic model with a single ATPase site. We form the dimer by coupling the tails of the two heads and introducing an attractive interaction between the rings.
The purpose of the model is to demonstrate that a power stroke in the tail domain is sufficient to explain processive stepping along a microtubule such that the dominant step size is 8 nm. The direction of motion is determined by the angle at which the stalk is attached to the microtubule, rather than the power-stroke itself. Further, we show that the tail-tail interaction can lead to coordination between the heads and thus improve the processivity and efficiency of the motor.
Model
Elastomechanical model
The fundamental building block of our model is a monomeric dynein head whose description is based on information from electron microscopic (8,23) and crystallographic studies (9–12). We model the ring-shaped head as a rigid disk, 2R = 14 nm in diameter and d = 5 nm thick (Fig. 1 A). We describe the linker as a rigid rod, Ll = 14 nm long, and connected to the head. Depending on the nucleotides bound to the head, it can accommodate two positions: the prestroke, in the following denoted by D∗ (with ADP.Pi or ADP in the primary site); and poststroke position, in the following denoted by D (primary site contains ADP, no nucleotide or ATP in the D.ATP state) (12,36). The third part, the stalk, is considered to be an ideal elastic rod, rigidly connected to the head in the radial direction. The reported values for the length of the stalk vary from 12 to 15 nm (37). However, the part of the stalk close to the head is supported by an additional short coiled-coil, known as a buttress (10) or strut (12), making it stiffer than the remaining part of the stalk. We therefore use the value from the lower end of the range, L = 12 nm. The distal end of the stalk continues into the MTBD. Some authors have considered the possibility that the rotation of the stalk relative to the MT could be the power stroke behind dynein’s motility (38), analogous to the lever-arm swing in myosin. However, electron micrographs of axonemal dyneins show that the stalk angles relative to MT do not change significantly between the ADP.vanadate and no-nucleotide states (39). The averaged angles are found to correspond to θMTBD = 31°–37°. This result is consistent with cryo-EM images of cytoplasmic dynein MTBDs bound to MT (25). We therefore use the same value of this angle for weakly and for strongly bound states. All geometric parameters of the model monomeric dynein molecule are summarized in Table 1.
Figure 1.
Mechanical model for dynein. (A) A monomeric dynein molecule modeled as a rigid disklike head rigidly connected to 1), the flexible rodlike stalk whose end (MTBD) can attach to the MT and 2), the linker that adopts two distinct positions with respect to the nucleotides bound to the head. (B–D) A schematic representation of the interactions between the two monomers. (B) Interaction between dimerized tails is modeled by a harmonic interaction between the ends of the linkers. The interaction between the two rings is a hard-core repulsion between two cylinders with the additional attractive contributions between (C) the ring centers and (D) the ring normals, which favor the parallel stacking of the two rings. To see this figure in color, go online.
Table 1.
Geometric parameters of a dynein motor
| Description | Parameter | Value |
|---|---|---|
| Stalk length | L | 12 nm |
| Stalk angle at MTBD | θMTBD | 34° |
| Head diameter | 2R | 14 nm |
| Head thickness | d | 5 nm |
| Angle head-linker | κ | 30° |
| Linker length | Ll | 14 nm |
| Linker angle poststroke | δpost | 0° |
| Linker angle prestroke | δpre | 40° |
| MT radius | RMT | 12.5 nm |
| Tubulin dimer length | d0 | 8 nm |
| Number of protofilaments | N | 13 |
| MT helical pitch | Δ | 12 nm |
When two monomeric heads are connected to form a dimer, and even more so when an external force is pulling on their tails, they are subject to elastic deformation. We model the stalk, which is the most compliant part of the molecule, as an ideal elastic beam with bending stiffness EI and torsional stiffness C. Instead of EI and C, one can also use the corresponding persistence lengths, λp = EI/kBT and λc = C/kBT, where kBT is the thermal energy. Their values can be estimated from the elasticity of other molecules containing coiled-coils. A suitable molecule is tropomyosin, whose persistence length has long been estimated as ∼100 nm (40,41), but a newer study showed that this value could be an underestimate (42), and we therefore assume λp = λc = 200 nm, also consistent with a theoretical estimate (43).
The two heads of a dimer interact with their dimerized tails and through direct ring-ring interaction (Fig. 1, B–D). We model the connected tails as an elastic cord between the ends of the stiff linkers and assume that its elastic energy is proportional to the square of the elongation,
| (1) |
where rl,i is the end point of the linker of head i, ll is the length of the undeformed cord, and kl its effective stiffness.
It is known that the heads of axonemal two- and three-headed dyneins exhibit parallel stacking (39,44), but in the case of cytoplasmic dynein, crystallographic and position tracking experiments are inconclusive with respect to the head-head stacking, observing either stacked (11,21) or open structures (10,22). We model the ring-ring interaction as hard-core repulsion between two cylinders and an additional attractive interaction that favors parallel stacking of the two rings,
| (2) |
where denote the centers of the facing sides of the two rings, the normals to the facing surfaces, and γi the interaction energies related to the respective interaction. In the following we restrict ourselves to an interaction that favors front-to-back stacking of heads, γ2 > 0. All elastic constants are listed in Table 2.
Table 2.
Parameters of the model
| Description | Parameter | Value |
|---|---|---|
| Persistence length | λp | 200 nm |
| Torsional persistence length | λc | 200 nm |
| Head-head interaction | γ1 | 0.01 kBT/nm2 |
| Head-normals interaction | γ2 | 6.0 kBT |
| Linker-linker interaction | kl | 1.0 kBT/nm2 |
| Linker elastic cord length | ll | 5 nm |
In thermal equilibrium, the most probable structure is the one with minimal energy:
| (3) |
Here Ui values are the energies stored in elastic deformations of the stalk of the ith motor, Uint = Ul + Uh is the interaction between motors, and Fx is the work done against the external load. The force F acts along the MT axis and has a positive sign for resisting loads (pulling toward the MT plus-end). x is the position of the centerpoint between the two linker tips, projected onto the MT axis (positive x indicates the minus-direction on the MT). For a certain configuration of chemical states, binding sites of both MT binding domains, and a given external force, the three-dimensional shape of the dimeric molecule with minimum energy can be calculated numerically with a Monte Carlo method. Some of the calculated shapes are shown in Fig. 2.
Figure 2.
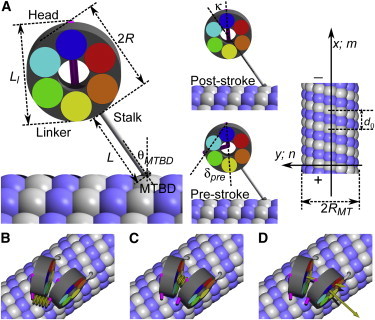
A selection of minimum energy configurations of the tightly coupled dimeric dynein molecule depending on the linker position of the (left/right) heads and for different relative positions m,n of the two MTBDs (right head is attached m tubulin dimers along and n protofilaments to the side with respect to the left one). D denotes the head with the linker in the poststroke position and D∗ in the prestroke position. Below each configuration is the corresponding elastic energy. To see this figure in color, go online.
Kinetic model
We describe the stepping of dynein by a simplified kinetic model based on the ATPase cycle at the primary site (AAA1) and stochastic transitions between the states. We adopt the widely accepted ATPase cycle proposed by Imamula et al. (26) (Fig. 3): Binding of the ATP molecule triggers the release of dynein from the MT. After that, the ATP hydrolysis induces a conformational change, the recovery stroke, which leads to a prestroke configuration. The next step is not yet well established experimentally—whether Pi release occurs before or after rebinding to the MT is somewhat ambiguous. Recent kinetic evidence is consistent with Pi release after MT binding (12).
Figure 3.

The chemical cycle of each dynein head adopted from the model of Imamula et al. (26). Prefix MT denotes states of strong attachment to the MT and D and D∗ correspond to the dynein head with the linker in the post- and prestroke position, respectively.
We therefore propose the following sequence of events after MT binding: Pi is released with the rate k−Pi, followed by the power stroke (rate k+PS) and, finally, ADP release (rate k−ADP). We neglect any transition rates outside this scheme, such as detachment in ADP (k−7) and empty (k−8) states or ATP hydrolysis in the bound state (k′+2). The latter could be possible, but is suppressed kinetically because it competes with the detachment rate k−MT = 500 s−1. Likewise, we neglect the possibility that the motor releases phosphate and undergoes the power stroke in the detached state, because the corresponding rate k+3 ≈ 5 s−1 (24) is much slower than binding to the MT.
The rates used in the above scheme imply that ATP hydrolysis at the primary site increases the MT binding affinity by
This difference needs to be mediated by allosteric coupling through helix sliding in the coiled-coil forming the stalk. Likewise, binding to the microtubule accelerates Pi release by a factor k−Pi/k+3. These values are consistent with the observation that locking the coiled-coil in different registers can influence the ATPase rate (24), as well as MT binding affinity (9) by two orders of magnitude.
The transition rates are also influenced by mechanical strain. For any transition the principle of detailed balance states that , where ΔG is the free energy difference between the final and the initial states. We rewrite this statement as
| (4) |
where values are the unstrained transition rates whose ratio is determined by the free energy difference of the chemical transition. ΔU denotes the change in the elastic energy and the work performed against the external load (Eq. 3). The exact statement in Eq. 4 says nothing about the strain dependence of individual rates and for that, one has to rely on approximations. The approach most widely used when modeling motor proteins involves the Arrhenius theory of reaction rates (45), which assumes that the protein has to reach an activation point somewhere between the initial and the final state by thermal diffusion, but finishes the transition rapidly after that. For transitions that involve binding or unbinding of the motor, one expects the activation point to be much closer to the bound state, therefore k−MT = k0−MT and . In other cases, we will assume that the activation point lies in the middle between the initial and the final state, and thus and .
Another exact relationship between the kinetic rates is obtained by multiplying the detailed balance conditions for an unloaded monomer along a closed cycle that includes the hydrolysis of 1 ATP molecule,
| (5) |
and
is the standard free energy of ATP hydrolysis (46).
The kinetic rates we use are listed in Table 3. Some of them are known from the literature, even though many experiments were carried out on axonemal dyneins and it is not clear to what extent the results are applicable for cytoplasmic dyneins. On the other hand, the observed kinetic behavior of mammalian and yeast cytoplasmic dyneins suggests that some mechanisms are different even within the family of cytoplasmic dyneins. The attachment rate of a head to the MT in a state when the partner head is bound (k′0+MT) is not directly related to the kinetic rates measured in solution. As a rough estimate, we use the diffusion time of an object of 10-nm radius over a distance of 50 nm for the high-affinity state and a correspondingly lower rate for the low affinity state. The ADP release rate k0−ADP is considered to be the rate-limiting process in the dimeric molecule (27,47), and we therefore estimate its value from the velocity at saturating ATP concentration.
Table 3.
Kinetic parameters of the model
| Parameter | Description | Parameter value | Experimental value | Source |
|---|---|---|---|---|
| k0+ATP | ATP binding | 2 × 106 M−1 s−1 | 2.2 × 106 M−1 s−1 | (58) |
| k0−ATP | ATP release | 50 s−1 | 175 s−1a | (58) |
| k0−MT | MT release, D | 500 s−1 | 460 s−1 | (26) |
| k0+MT | MT binding, D | 100 s−1 | ||
| k′0+RS | ATP hydrolysis, linker swing to prestroke | 1000 s−1 | 180 s−1b | (58) |
| k′0−RS | ATP synthesis, linker swing to poststroke | 100 s−1 | 4 s−1; 30 s−1 | (47,58) |
| k′0+MT | MT binding, D∗ | 10,000 s−1 | ||
| k′0−MT | MT release, D∗ | 500 s−1 | ||
| k0−Pi | Pi release | 5000 s−1 | ||
| k0+Pi | Pi binding | 104 M−1 s−1 | 8000 M−1 s−1c | (47) |
| k0+PS | Power stroke | 5000 s−1 | ||
| k0−PS | Reverse stroke | 10 s−1 | ||
| k0−ADP | ADP release | 160 s−1 | ∼1000 s−1 | (27) |
| k0+ADP | ADP binding | 2.7 × 106 M−1 s−1 | 2.7 × 106 M−1 s−1 | (27) |
Calculated from Keq and K+ATP.
Measurement includes the transition between ATP binding and isomerization.
Without MT.
Results and Discussion
Distribution of steps
Although the stepping pattern generally depends on the complete kinetic scheme, its analysis simplifies greatly if one kinetic path dominates and the step always takes place in the same chemical configuration. In this case, the distribution of step sizes can be determined from the probability to bind to a certain site (denoted i), which is proportional to the Boltzmann factor formed from the elastic energy of that state, . Within our model the majority of steps are taken when one head is bound to MT in the post-powerstroke state and the other head is free in the pre-powerstroke state. We will discuss the likelihood of events outside this scheme later.
The model parameters listed in Table 2 describe the tightly coupled dynein dimers, with a strong tendency toward the stacked state, although they can be displaced in a parallel manner when strained (Fig. 2 and see Fig. S1 in the Supporting Material). In general, all processive dimeric motors that walk in a hand-over-hand manner need some asymmetry between consecutive steps (between those when the free head passes the bound one on the left and those where it passes it on the right), but this asymmetry is weak in kinesins (48). Cytoplasmic dynein is different—the ring stacking breaks the symmetry and designates the two heads as left and right, with respect to the direction of walking. In the following, we will always distinguish between the steps of the left and of the right head.
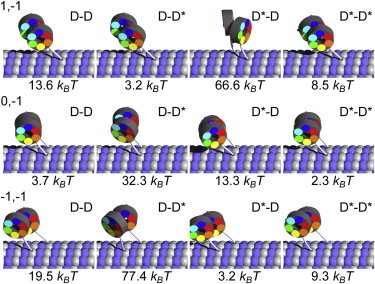
The attachment probabilities to different binding sites are shown in Fig. 4, A and B, for four possible combinations of linker configurations. Two of them, D∗–D and D–D∗, are participating in the regular stepping of the left and the right heads, respectively, whereas the other two (D–D and D∗–D∗) are rare in the absence of load. The stepping of such a molecule is MT-minus-end-directed and characterized by predominantly short ∼8-nm steps, whereas longer steps are infrequent, in agreement with single-molecule experiments on mammalian dynein (16). The two heads of a dimer proceed along separate, adjacent MT protofilaments and keep their track, i.e., the frequency of sideward steps is almost negligible.
Figure 4.
The attachment probabilities to different binding sites. (A and B) Tightly coupled dimers. (A) Binding site distance distributions for the left (red) and right (green) head and for four possible linker configurations; D denotes the post- and D∗ the prestroke state. (B) An illustration of the steps taken by the left or the right head. The cylinders correspond to the probability to make a step to the given position; only the most probable steps are depicted. The head that is to make the step (transparent) is in the prestroke position and the other one is in the poststroke. (C and D) Loosely coupled dimers. Binding site distance distributions (C) and the corresponding illustration of steps (D). (E and F) Binding site distance distributions for steps taken by left/right head of stalk length mutants, l = 19 nm (E) and l = 5 nm (F). To see this figure in color, go online.
Stalk length mutants
Carter et al. (9) investigated mutants with stalk lengths that were seven heptads (half-pitch of the coiled-coil) longer or shorter than wild-type. The lengths were chosen such that the ring orientation relative to the MT was 180° rotated and the linker swing pointed toward the MT plus- instead of minus-end. Surprisingly, the minus-end-directed motility was preserved, albeit with a reduced velocity and processivity. This result suggests that the principal component of the power stroke is along, not perpendicular, to the stalk. Because the stalk has a roughly fixed direction relative to the MT, the direction of the power stroke becomes independent of the ring orientation.
As shown in Fig. 4, E and F, our model calculation shows that binding of the free head in state D∗ is still strongly minus-end-biased both for an elongated and a shortened stalk. Although this has been suggested before at a descriptive level (1,9), our calculations give what we believe to be the first quantitative proof that the winch model is capable of explaining the directionality of stalk mutants.
Head-head coordination
Efficient and processive hand-over-hand stepping requires some degree of coordination between the chemical cycles in both heads. One advantage of coordination is to reduce the likelihood of both heads detaching simultaneously, which leads to the dissociation from the MT and therefore restricts the processivity (however, processive motility is also possible without any coordination if the duty ratio is sufficiently high (49,50)). A second advantage of coordinated stepping is that the trail head detaches before the lead head—otherwise, a futile or backward step occurs. Finally, binding of one head can be inhibited before the other head undergoes the power stroke—this also prevents futile steps. Coordination is most frequently achieved through gating: a certain transition in one head can be inhibited until the partner head reaches some state. Alternatively, a transition in the cycle can also be accelerated. In kinesin (51,52), myosin V (53,54), and myosin VI (50), this gating is purely mechanical, because the heads only interact through the connected tails. The origin of coordination is less clear in cytoplasmic dynein, but its existence is evident from the observation that the duty ratio of a head as part of a walking dimer is higher than in a single-headed construct (18,52).
Without any further interaction between the ATPase sites on both rings, our mechanical model shows the following gating mechanism: when the lead head is in the prestroke state and the trail head is in the poststroke state D, the transition D∗→D in the lead head would increase the elastic energy of the dimer by ∼10 kBT (Fig. 2), which means that transition rate is reduced by a factor of , or 2–3 orders of magnitude. Consequently, the lead head does not release ADP, bind ATP, or detach before the detachment of the trail head. The same kind of coordination also reduces the probability that the heads detach simultaneously. The efficiency of such gating depends further on the relative magnitude of the kinetic rates of the competing transitions.
Unlike in kinesin (51) and myosin V (55), where the binding of a head is mechanically inhibited before the power stroke in the partner head, there is no such effect in dynein. This difference is due to the fact that kinesin’s neck linker is too short to bind with both heads to two parallel sites on adjacent protofilaments (56), and that there is no suitable parallel site on an actin filament. Dynein, on the other hand, can bind to two parallel sites on adjacent protofilaments. Therefore, the attachment of a head to the MT cannot be mechanically gated in dynein.
Stepping kinetics and force generation
The results of a kinetic simulation of the full model are shown in Fig. 5 and the stepping is visualized in Movie S1 in the Supporting Material. The model reproduces the hand-over-hand motility with 8-nm steps at a speed of 800 nm/s at saturating ATP and in the absence of load, as observed with mammalian dynein (16). Yet the stepping is not entirely regular (see Fig. S2). In a small portion of steps the recovery stroke of the free head precedes the power stroke of the attached head and leads to the D∗–D∗ bound state, primarily at the parallel adjacent binding sites (dashed line in Fig. 5 A). This scenario represents the inchworm-like stepping mode in which the cargo moves 4 nm per step. Even more rarely, the step consists of detachment and reattachment of the lead head—such events are generally not detectable in an experiment.
Figure 5.
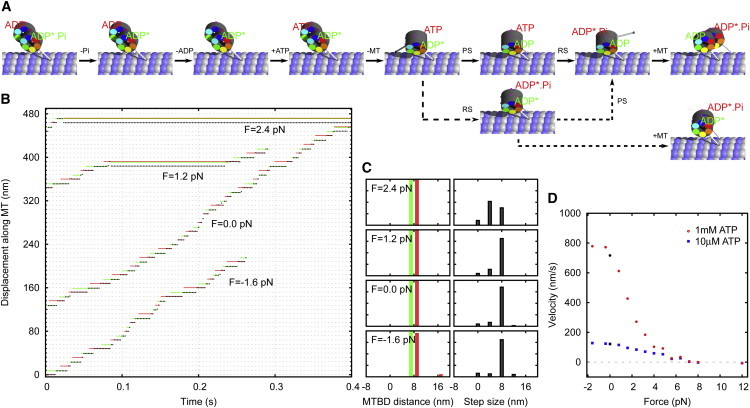
Single-molecule kinetics of tightly coupled dimers. (A) The most probable kinetic pathways for a dimeric dynein molecule. The main path (continuous arrows) leads to an advancing step. If the binding of one head occurs before the power stroke in its partner head, this can lead to a futile step (dashed arrows). (B) A portion of the on-axis stepping trace of a dimeric dynein molecule for different values of the load. Trace of the tail of the dynein (black) and the corresponding x-coordinates of the MTBD of the left (red) and the right (green) head are depicted. (C) Binding site distance and step size (measured at the tail) distributions for the respective loads. (Red and green bars) Steps taken by the left and right heads, respectively. (D) Force velocity diagram for two ATP concentrations, [ATP] = 1 mM and [ATP] = 10 μM. To see this figure in color, go online.
With applied load, the speed and the run length are decreased. There are two factors that contribute toward velocity reduction under load:
-
1.
The power stroke is slowed down, which also slows down the cycle as a whole; and
-
2.
Consequently, the free head is more likely to bind before the power stroke in the bound head, which leads to inch-worming or futile cycles.
With a small assisting force the velocity of the motor slightly increases and longer steps become more probable, but the 8-nm step stays most probable.
The force-velocity relationship, Fig. 5 D, shows a stall force of ∼6 pN. However, the motor reaches a plateau with velocity close to zero and a high termination rate at much lower forces. In a realistic situation, the maximum force achieved by the tightly coupled dimer would be in the range of 1–2 pN. The maximum achievable force is sensitive to model parameters that affect processivity, mainly k−ADP and k−Pi (see Fig. S3). A faster ADP release rate reduces the processivity and thus the maximum force, whereas a faster Pi release increases both. The processivity is also higher at low ATP concentrations.
Under super-stall loads, i.e., for loads higher than 7 pN, the model shows backward stepping without hydrolyzing ATP (see Movie S2). This is reminiscent of the ATP-independent stepping mode observed by Gennerich et al. (20). However, note that we made the assumption that the detachment rate is strain-independent and that it only takes place in D.ATP and .ADP.Pi configurations, which means that we are underestimating the frequency of backward steps.
Loosely coupled dimers
To reproduce the properties of yeast dyneins, we reduced the interaction between the linkers (see Table S1 in the Supporting Material). This leads to a broader step-size distribution, i.e., shorter and longer as well as sideward and backward steps become more probable (Fig. 4, C and D). Another consequence of the weaker interaction is a decreased difference in the elastic energy responsible for mechanical gating, which impairs both the efficiency and the processivity of the motor (see Fig. S4). These findings are also consistent with the reduced processivity observed in Loa mutants that have an alteration in the tail domain responsible for dimerization (57).
Both the richer variety of step sizes and the reduced degree of head-head coordination are in agreement with observations on yeast dyneins (19–22). Interestingly, yeast dyneins achieve run lengths exceeding 1 μm (19) without coordination between the chemical cycles in both heads (22). A plausible explanation is that the lack of coordination is compensated by a slower product release rate, which leads to a higher duty ratio at the cost of a reduced speed (an order-of-magnitude slower than mammalian dyneins (19)). In the simulation of loosely coupled dimers, a value of k−ADP = 15 s−1 leads to run lengths in the micrometer range (Fig. 6 and see Fig. S5 and Movie S3).
Figure 6.
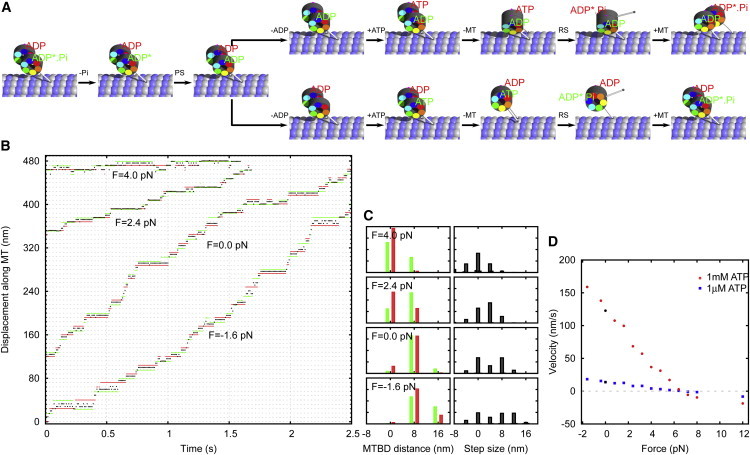
Stepping of loosely coupled dynein dimers. (A) Two common kinetic pathways. The upper branch shows an advancing step. In the lower branch, ADP release from the lead head leads to a futile step. (B) Sample traces of the tail (black), left head (red), and right head (green) under different load forces. (C) Binding site distance and step-size distributions for different loads. (Red bars) Steps taken by the left head; (green bars) steps taken by the right. (D) Force velocity diagram for two ATP concentrations: 1 mM and 1 μM. To see this figure in color, go online.
The force-velocity diagram in Fig. 6 D shows a stall force at ∼6–7 pN. Its higher value as compared to tightly coupled dimers is mainly due to the slower rate-limiting kinetic parameter, k−ADP. Another difference is the absence of the plateau characteristic for the tightly coupled dimers. Loosely coupled dimers move backward as soon as the load exceeds the maximum achievable force.
The simulated runs of loosely coupled dimers show almost no coordination between the heads, which is evident from the fact that alternating and nonalternating steps become equally likely (see Fig. S6 B). However, the results change drastically if we restrict our analysis to steps that are observable experimentally—i.e., we exclude all futile steps where one head detaches and rebinds to the same position (see Fig. S6 C). In that case, the frequency of alternating steps is 3–4 times higher than the frequency of nonalternating steps, which is comparable to the experimental result (21). Almost all alternating steps are passing (hand-over-hand), whereas the majority of the nonalternating steps are nonpassing (futile and inchworm). The ratio between the frequency of passing and nonpassing steps is determined by the relative magnitude of kinetic rates for the recovery stroke of the free head and the power stroke of the bound head.
The model shows a difference between the distributions of steps taken with the left and right heads (Fig. 4, C and D). Namely, the right head is more likely to take longer steps than the left. This is a direct consequence of the helical MT structure. The right head most frequently steps 7 nm ahead of the left head, whereas the predominant step of the left head is 9 nm ahead. For this reason, double steps (7 + 8 nm ahead) are more likely for the right than for the left head (which would need to step 9 + 8 nm ahead). Experiments involving separate tracking of both heads of yeast dynein also show an asymmetry between left and right steps (21,22).
Conclusion
Although it has been suggested before at a descriptive level, we have shown that a model based on the winch mechanism in which the linker displacement pulls the load toward rather than along the microtubule can explain a wide range of experimental results for cytoplasmic dynein. It shows coordinated hand-over-hand stepping and processivity for tightly coupled dimers. If we weaken the connection between the heads the model still shows directional stepping, but the distribution of step sizes is much broader and the head-head coordination is lost—this scenario corresponds to yeast dyneins. With a reduced product release rate, the motor retains a high level of processivity even without any coordination and produces a higher maximal force at the cost of a reduced velocity. This shows that the winch mechanism is in itself robust, but its stepping efficiency can be greatly improved by an attractive interaction that leads to the stacking of the two heads.
When setting up the model we inevitably made several simplifications, mainly due to the lack of experimental information. These include assuming a single ATP hydrolysis site per head, strain-independent detachment rates, and neglecting some transitions outside the main path. Whereas these assumptions are adequate to understand the basic properties of the motor, its dynamics under more extreme conditions (e.g., high loads) will eventually demand a more detailed description.
Acknowledgments
This work was supported by the Human Frontier Science Program (grant No. RGP0009/2008-C), the Slovenian Research Agency (grant No. P1-0099), and the European Union (NAMASTE Center of Excellence).
Supporting Material
References
- 1.Sakakibara H., Oiwa K. Molecular organization and force-generating mechanism of dynein. FEBS J. 2011;278:2964–2979. doi: 10.1111/j.1742-4658.2011.08253.x. [DOI] [PubMed] [Google Scholar]
- 2.Kikkawa M. Big steps toward understanding dynein. J. Cell Biol. 2013;202:15–23. doi: 10.1083/jcb.201304099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Gibbons I.R., Rowe A.J. Dynein: a protein with adenosine triphosphatase activity from cilia. Science. 1965;149:424–426. doi: 10.1126/science.149.3682.424. [DOI] [PubMed] [Google Scholar]
- 4.Johnson K.A. The pathway of ATP hydrolysis by dynein. Kinetics of a presteady state phosphate burst. J. Biol. Chem. 1983;258:13825–13832. [PubMed] [Google Scholar]
- 5.Vale R.D., Toyoshima Y.Y. Rotation and translocation of microtubules in vitro induced by dyneins from Tetrahymena cilia. Cell. 1988;52:459–469. doi: 10.1016/s0092-8674(88)80038-2. [DOI] [PubMed] [Google Scholar]
- 6.Gibbons I.R., Gibbons B.H., Asai D.J. Multiple nucleotide-binding sites in the sequence of dynein β-heavy chain. Nature. 1991;352:640–643. doi: 10.1038/352640a0. [DOI] [PubMed] [Google Scholar]
- 7.Kon T., Nishiura M., Sutoh K. Distinct functions of nucleotide-binding/hydrolysis sites in the four AAA modules of cytoplasmic dynein. Biochemistry. 2004;43:11266–11274. doi: 10.1021/bi048985a. [DOI] [PubMed] [Google Scholar]
- 8.Burgess S.A., Walker M.L., Oiwa K. Dynein structure and power stroke. Nature. 2003;421:715–718. doi: 10.1038/nature01377. [DOI] [PubMed] [Google Scholar]
- 9.Carter A.P., Garbarino J.E., Gibbons I.R. Structure and functional role of dynein’s microtubule-binding domain. Science. 2008;322:1691–1695. doi: 10.1126/science.1164424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Carter A.P., Cho C., Vale R.D. Crystal structure of the dynein motor domain. Science. 2011;331:1159–1165. doi: 10.1126/science.1202393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kon T., Sutoh K., Kurisu G. X-ray structure of a functional full-length dynein motor domain. Nat. Struct. Mol. Biol. 2011;18:638–642. doi: 10.1038/nsmb.2074. [DOI] [PubMed] [Google Scholar]
- 12.Kon T., Oyama T., Kurisu G. The 2.8 Å crystal structure of the dynein motor domain. Nature. 2012;484:345–350. doi: 10.1038/nature10955. [DOI] [PubMed] [Google Scholar]
- 13.Mallik R., Carter B.C., Gross S.P. Cytoplasmic dynein functions as a gear in response to load. Nature. 2004;427:649–652. doi: 10.1038/nature02293. [DOI] [PubMed] [Google Scholar]
- 14.Hendricks A.G., Holzbaur E.L.F., Goldman Y.E. Force measurements on cargoes in living cells reveal collective dynamics of microtubule motors. Proc. Natl. Acad. Sci. USA. 2012;109:18447–18452. doi: 10.1073/pnas.1215462109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Rai A.K., Rai A., Mallik R. Molecular adaptations allow dynein to generate large collective forces inside cells. Cell. 2013;152:172–182. doi: 10.1016/j.cell.2012.11.044. [DOI] [PubMed] [Google Scholar]
- 16.Toba S., Watanabe T.M., Higuchi H. Overlapping hand-over-hand mechanism of single molecular motility of cytoplasmic dynein. Proc. Natl. Acad. Sci. USA. 2006;103:5741–5745. doi: 10.1073/pnas.0508511103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Walter W.J., Koonce M.P., Steffen W. Two independent switches regulate cytoplasmic dynein’s processivity and directionality. Proc. Natl. Acad. Sci. USA. 2012;109:5289–5293. doi: 10.1073/pnas.1116315109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Shima T., Imamula K., Sutoh K. Head-head coordination is required for the processive motion of cytoplasmic dynein, an AAA+ molecular motor. J. Struct. Biol. 2006;156:182–189. doi: 10.1016/j.jsb.2006.03.014. [DOI] [PubMed] [Google Scholar]
- 19.Reck-Peterson S.L., Yildiz A., Vale R.D. Single-molecule analysis of dynein processivity and stepping behavior. Cell. 2006;126:335–348. doi: 10.1016/j.cell.2006.05.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Gennerich A., Carter A.P., Vale R.D. Force-induced bidirectional stepping of cytoplasmic dynein. Cell. 2007;131:952–965. doi: 10.1016/j.cell.2007.10.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Qiu W., Derr N.D., Reck-Peterson S.L. Dynein achieves processive motion using both stochastic and coordinated stepping. Nat. Struct. Mol. Biol. 2012;19:193–200. doi: 10.1038/nsmb.2205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.DeWitt M.A., Chang A.Y., Yildiz A. Cytoplasmic dynein moves through uncoordinated stepping of the AAA+ ring domains. Science. 2012;335:221–225. doi: 10.1126/science.1215804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Roberts A.J., Numata N., Burgess S.A. AAA+ ring and linker swing mechanism in the dynein motor. Cell. 2009;136:485–495. doi: 10.1016/j.cell.2008.11.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kon T., Imamula K., Sutoh K. Helix sliding in the stalk coiled-coil of dynein coupled ATPase and microtubule binding. Nat. Struct. Mol. Biol. 2009;16:325–333. doi: 10.1038/nsmb.1555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Redwine W.B., Hernández-López R., Leschziner A.E. Structural basis for microtubule binding and release by dynein. Science. 2012;337:1532–1536. doi: 10.1126/science.1224151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Imamula K., Kon T., Sutoh K. The coordination of cyclic microtubule association/dissociation and tail swing of cytoplasmic dynein. Proc. Natl. Acad. Sci. USA. 2007;104:16134–16139. doi: 10.1073/pnas.0702370104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Holzbaur E.L.F., Johnson K.A. Microtubules accelerate ADP release by dynein. Biochemistry. 1989;28:7010–7016. doi: 10.1021/bi00443a034. [DOI] [PubMed] [Google Scholar]
- 28.Burgess S.A., Knight P.J. Is the dynein motor a winch? Curr. Opin. Struct. Biol. 2004;14:138–146. doi: 10.1016/j.sbi.2004.03.013. [DOI] [PubMed] [Google Scholar]
- 29.Choi J., Park H., Seok C. How does a registry change in dynein’s coiled-coil stalk drive binding of dynein to microtubules? Biochemistry. 2011;50:7629–7636. doi: 10.1021/bi200834k. [DOI] [PubMed] [Google Scholar]
- 30.Serohijos A.W.R., Chen Y., Dokholyan N.V. A structural model reveals energy transduction in dynein. Proc. Natl. Acad. Sci. USA. 2006;103:18540–18545. doi: 10.1073/pnas.0602867103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Hawkins R.J., McLeish T.C. Dynamic allostery of protein α-helical coiled-coils. J. R. Soc. Interface. 2006;3:125–138. doi: 10.1098/rsif.2005.0068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Singh M.P., Mallik R., Yu C.C. Monte Carlo modeling of single-molecule cytoplasmic dynein. Proc. Natl. Acad. Sci. USA. 2005;102:12059–12064. doi: 10.1073/pnas.0501570102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Gao Y.Q. A simple theoretical model explains dynein’s response to load. Biophys. J. 2006;90:811–821. doi: 10.1529/biophysj.105.073189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Tsygankov D., Serohijos A.W.R., Elston T.C. Kinetic models for the coordinated stepping of cytoplasmic dynein. J. Chem. Phys. 2009;130:025101. doi: 10.1063/1.3050098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Tsygankov D., Serohijos A.W.R., Elston T.C. A physical model reveals the mechanochemistry responsible for dynein’s processive motion. Biophys. J. 2011;101:144–150. doi: 10.1016/j.bpj.2011.05.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Roberts A.J., Malkova B., Burgess S.A. ATP-driven remodeling of the linker domain in the dynein motor. Structure. 2012;20:1670–1680. doi: 10.1016/j.str.2012.07.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Höök P., Yagi T., Vallee R.B. The dynein stalk contains an antiparallel coiled coil with region-specific stability. Biochemistry. 2009;48:2710–2713. doi: 10.1021/bi900223x. [DOI] [PubMed] [Google Scholar]
- 38.Gee M.A., Heuser J.E., Vallee R.B. An extended microtubule-binding structure within the dynein motor domain. Nature. 1997;390:636–639. doi: 10.1038/37663. [DOI] [PubMed] [Google Scholar]
- 39.Ueno H., Yasunaga T., Hirose K. Dynein pulls microtubules without rotating its stalk. Proc. Natl. Acad. Sci. USA. 2008;105:19702–19707. doi: 10.1073/pnas.0808194105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Swenson C.A., Stellwagen N.C. Flexibility of smooth and skeletal tropomyosins. Biopolymers. 1989;28:955–963. doi: 10.1002/bip.360280504. [DOI] [PubMed] [Google Scholar]
- 41.Phillips G.N., Jr., Chacko S. Mechanical properties of tropomyosin and implications for muscle regulation. Biopolymers. 1996;38:89–95. doi: 10.1002/(SICI)1097-0282(199601)38:1%3C89::AID-BIP7%3E3.0.CO;2-S. [DOI] [PubMed] [Google Scholar]
- 42.Li X.E., Holmes K.C., Fischer S. The shape and flexibility of tropomyosin coiled coils: implications for actin filament assembly and regulation. J. Mol. Biol. 2010;395:327–339. doi: 10.1016/j.jmb.2009.10.060. [DOI] [PubMed] [Google Scholar]
- 43.Yogurtcu O.N., Wolgemuth C.W., Sun S.X. Mechanical response and conformational amplification in α-helical coiled coils. Biophys. J. 2010;99:3895–3904. doi: 10.1016/j.bpj.2010.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Nicastro D., Schwartz C., McIntosh J.R. The molecular architecture of axonemes revealed by cryoelectron tomography. Science. 2006;313:944–948. doi: 10.1126/science.1128618. [DOI] [PubMed] [Google Scholar]
- 45.Howard J. Sinauer; Sunderland, MA: 2001. Mechanics of Motor Proteins and the Cytoskeleton. [Google Scholar]
- 46.Alberty R.A., Goldberg R.N. Standard thermodynamic formation properties for the adenosine 5′-triphosphate series. Biochemistry. 1992;31:10610–10615. doi: 10.1021/bi00158a025. [DOI] [PubMed] [Google Scholar]
- 47.Holzbaur E.L.F., Johnson K.A. ADP release is rate limiting in steady-state turnover by the dynein adenosinetriphosphatase. Biochemistry. 1989;28:5577–5585. doi: 10.1021/bi00439a036. [DOI] [PubMed] [Google Scholar]
- 48.Fehr A.N., Gutiérrez-Medina B., Block S.M. On the origin of kinesin limping. Biophys. J. 2009;97:1663–1670. doi: 10.1016/j.bpj.2009.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Baboolal T.G., Sakamoto T., Peckham M. The SAH domain extends the functional length of the myosin lever. Proc. Natl. Acad. Sci. USA. 2009;106:22193–22198. doi: 10.1073/pnas.0909851106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Elting M.W., Bryant Z., Spudich J.A. Detailed tuning of structure and intramolecular communication are dispensable for processive motion of myosin VI. Biophys. J. 2011;100:430–439. doi: 10.1016/j.bpj.2010.11.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Toprak E., Yildiz A., Selvin P.R. Why kinesin is so processive. Proc. Natl. Acad. Sci. USA. 2009;106:12717–12722. doi: 10.1073/pnas.0808396106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Gennerich A., Vale R.D. Walking the walk: how kinesin and dynein coordinate their steps. Curr. Opin. Cell Biol. 2009;21:59–67. doi: 10.1016/j.ceb.2008.12.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Veigel C., Wang F., Molloy J.E. The gated gait of the processive molecular motor, myosin V. Nat. Cell Biol. 2002;4:59–65. doi: 10.1038/ncb732. [DOI] [PubMed] [Google Scholar]
- 54.Vilfan A. Five models for myosin V. Front. Biosci. (Landmark Ed) 2009;14:2269–2284. doi: 10.2741/3378. [DOI] [PubMed] [Google Scholar]
- 55.Vilfan A. Elastic lever-arm model for myosin V. Biophys. J. 2005;88:3792–3805. doi: 10.1529/biophysj.104.046763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Schaap I.A., Carrasco C., Schmidt C.F. Kinesin walks the line: single motors observed by atomic force microscopy. Biophys. J. 2011;100:2450–2456. doi: 10.1016/j.bpj.2011.04.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Ori-McKenney K.M., Xu J., Vallee R.B. A cytoplasmic dynein tail mutation impairs motor processivity. Nat. Cell Biol. 2010;12:1228–1234. doi: 10.1038/ncb2127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Mogami T., Kon T., Sutoh K. Kinetic characterization of tail swing steps in the ATPase cycle of Dictyostelium cytoplasmic dynein. J. Biol. Chem. 2007;282:21639–21644. doi: 10.1074/jbc.M701914200. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


