Abstract
Actin-based cellular protrusions are a ubiquitous feature of cell morphology, e.g., filopodia and microvilli, serving a huge variety of functions. Despite this, there is still no comprehensive model for the mechanisms that determine the geometry of these protrusions. We present here a detailed computational model that addresses a combination of multiple biochemical and physical processes involved in the dynamic regulation of the shape of these protrusions. We specifically explore the role of actin polymerization in determining both the height and width of the protrusions. Furthermore, we show that our generalized model can explain multiple morphological features of these systems, and account for the effects of specific proteins and mutations.
Introduction
Cell morphology is closely related to its functionality and is determined to a large extent by the cell’s actin cytoskeleton. A common morphological feature is that of cellular protrusions, which extend from the cell and are composed of parallel cross-linked actin filaments that polymerize at the protrusion’s tip (1). The shape, size, dynamics, and density of such protrusions change from cell to cell and play a crucial role in a large variety of cellular processes, from cell motility, to specific cell functions (2). Therefore, understanding the mechanisms that control the morphology of cellular protrusions is an important open problem in cell biology.
Previous theoretical works have addressed different aspects of the question of how cells form and maintain such protrusions. Some works focused on the initiation stages (3–6). Others dealt with the internal dynamics of a fully formed steady-state protrusion using either fine-grained molecular-scale simulations of the protein dynamics (7–9) or a coarse-grained continuum description (10,11). Another group of models addresses the growth dynamics (12) and the shape in more details, relating the height to the width and the forces exerted on the actin bundle (13,14). These previous models provide valuable description of certain aspects of the dynamics and shapes of protrusions. Yet, a comprehensive theory for the dynamics of the shape (height and width) of such protrusions is still lacking. In this work, we attempt to provide a theoretical framework for the dynamics and steady-state shape of the protrusions in a way that treats the main forces involved, and explains the phenomena observed in filopodia, microvilli, and stereocilia. Due to the complexity of the problem, we devised a model that combines the biochemistry and physics of the membrane and actin, and takes into account a rather wide range of possibilities for growth mechanisms and their implications.
How might the cell build an actin-filled protrusion? If the support for the actin bundle is rigid, then one could simply imagine the polymerization pushing the membrane outwards until the process stalls or the actin buckles (11). However, if the support for the actin bundle (the cytoplasm) behaves as a viscous medium, the restoring force will act to push the bundle into the cytoplasm. Therefore, to maintain a protrusion, either the restoring force must be eliminated (for example by strong binding between the membrane and the actin bundle), or there must be a protrusive force that balances it. Such a protrusive force is indeed created by the treadmilling actin bundle as it pushes against the underlying viscous cytoplasm. The cytoplasm can be treated as a viscous medium because its reorganization time is measured in seconds compared to the protrusion dynamics, which occurs over minutes (or longer). In this work, we develop the model based on this polymerization-driven protrusive force in order to explain the protrusion’s height. An additional protrusive force due to actin-membrane adhesion is also considered (see the Supporting Material).
The mechanisms that control the width of actin-based protrusions in cells are also not well understood, despite previous experimental (15,16) and theoretical works (17–20), which mostly dealt with the width of the actin-bundle alone. Here we present a model for dynamic width regulation, which allows us to relate observed changes in the width to changes in the protrusion height and rate of actin polymerization (21–23).
The article is organized as follows: we first describe the model for the height of the protrusion (for a given radius), followed by the model for dynamic width regulation. We then combine both parts into a comprehensive model for the protrusion geometry and compare it to the experimental observations. Note that throughout the article we wish to emphasize the generic features, thereby all the numerical calculations plotted in the figures are dimensionless.
Model of the protrusion height
Forces
We begin by listing the main forces that act within the protrusion and affect its height. The dominant protrusive force (Fa) acting on the membrane due to the polymerization of actin is assumed to arise from the friction between the flowing actin rootlet (of surface area Sc) and the cytoplasm below the protrusion (Fig. 1) (13). On the relevant timescales of the actin flow we can treat the cytoplasm as a medium with effective friction coefficient γc. The friction force acting to push the treadmilling actin bundle upwards is therefore proportional to the relative velocity between the actin bundle (va) and the treadmilling velocity of the cytoplasm (vcyto, both velocities are taken as positive for actin flow away from the membrane), as
| (1) |
where vcyto is the treadmilling velocity of the actin cytoskeleton network below the protrusion (due to polymerization and myosin-II contractility), and
is the treadmilling velocity of the actin inside the protrusion, which is simply the difference between the growth velocity of the protrusion height h(t) and the actin polymerization rate A[h(t), t]. Note that the polymerization rate could possibly depend on the radius of the protrusion (13), although we do not include this effect here. We are motivated by observations in stereocilia of different heights and widths (24), suggesting that the rate of actin polymerization is more strongly dependent on the height of the protrusion than on its radius. Note that we describe in Eq. 1 the average force, neglecting stochastic effects that may become important in the limit of small numbers of actin filaments in the bundle (7,25). Below, we shall not include vcyto in our model because it is a simple constant offset.
Figure 1.
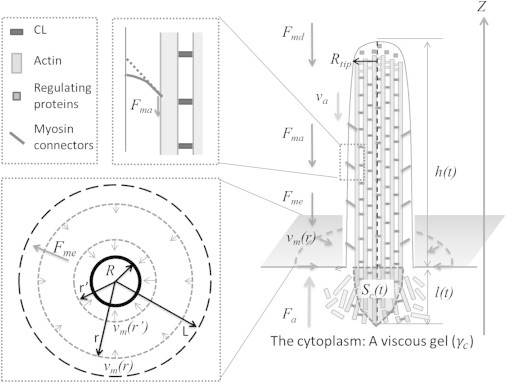
An illustration of the forces acting on the protrusion. The cytoplasm beneath the protrusion is regarded as a gel with an effective viscosity γc, into which the rootlet of length l and surface area Sc penetrates. The downward treadmilling velocity va of the rootlet in the viscous gel generates a pushing force Fa in the opposite direction. The bending and the tension elasticity of the membrane generate a restoring force Fmd. Membrane-bound myosins connect the actin bundle to the membrane and generate an additional restoring force Fma. As the protrusion elongates, the apical membrane of the cell flows toward the protrusion with velocity vm(r), generating a frictional restoring force Fme.
The radius R(z,t) of the protrusion at a coordinate z along its length (Fig. 1)obeys the following equation (10):
| (2) |
Here, β(A, z, t) is the severing rate at the bundle surface (which could, in principle, depend on A, z, t). The first term describes the convection of the bundle downwards at the treadmilling velocity va, while the second term describes the local severing rate. Because the filaments in the bundle are densely packed and cross-linked we assume that the severing proteins can only act on the filaments at the bundle surface. This is motivated by detailed images of the actin bundle, for example in stereocilia (24). Both A and β can depend on the concentration profile of actin regulatory proteins (10).
In addition, protrusions may interact with an external substrate or with a neighboring protrusion, and have adhesion at their tips or along their length, which adds additional forces due to binding energy (26) and friction. For simplicity we will ignore these additional possible contributions, because many protrusions do not bind to external surfaces or to neighboring protrusions, and these terms do not add any qualitatively new behavior. There is an additional protrusive force arising from tip-activated actin-membrane binding proteins (see Eqs. S23–S27 in the Supporting Material for details), which for simplicity we do not include below, but which can be easily added.
Balancing these protrusive forces, there are three restoring forces exerted by the following:
-
1.
The membrane on the actin bundle, which is due to the elastic energy of the deformed membrane (Fmd);
-
2.
The friction between the membrane and the underlying cytoskeleton as the cellular membrane flows toward the growing protrusion (Fme); and
-
3.
A force applied by actin-membrane molecular motors (Fma) (Fig. 1) as the motors walk to the tip and transmit their momentum to the actin bundle.
To simplify the analysis we will neglect here the contribution of the friction force between the growing protrusion and the extracellular viscous medium, because adding this term does not qualitatively change the results.
The membrane elastic restoring force for a protrusion with local radius R(z) can be written as the derivative of the Helfrich Hamiltonian with the usual membrane tension and bending (curvature) terms (27),
| (3) |
where σ is the effective membrane tension, κ is the effective bending modulus, Sm is the protrusion surface area, and H(z) is the mean curvature at location z. For a simple cylindrical protrusion, longer than the initial tentlike shape of height hc, this reduces to a constant value of
| (4) |
where hc is the minimal height above which the membrane adopts a cylindrical shape (27). Note that curved membrane proteins, lipid composition, and passive actin-membrane binding proteins can stabilize membrane tubes by lowering the effective membrane tension and giving the membrane an effective spontaneous curvature, thereby reducing or even canceling the membrane restoring force (2) (see the Supporting Material).
The friction force Fme between the membrane and the underlying actin cytoskeleton around the growing protrusion (Fig. 1) can be written as (28)
| (5) |
where is the effective friction coefficient and L is an upper cutoff length of the order of the free membrane region around the protrusion. This force arises from the flow of the membrane in the flat areas surrounding the protrusion base, toward the protrusion when its height changes. The effective friction depends on the density and strength of the anchoring sites between the surrounding membrane and the underlying cytoskeletal network.
We next describe the effects of actin-membrane connectors on the force balance. Passive connectors will reduce the effective membrane tension σ that contributes to the membrane elastic restoring force, and is therefore included in Fmd (Eq. 4). When the connectors are composed of myosin motors they pull the membrane up the actin core, decreasing the membrane load at the tip (we assume that tip-directed motors, such as myosin-I (29), dominate). Beyond the point where the membrane tension in the protrusion is reduced to zero (σ → 0), the motors end up adding a restoring force that pushes the actin bundle downwards. This active restoring force is linearly increasing with the total number of motors along the surface of the protrusion. For a cylindrical protrusion, we can therefore write the total restoring force acting on the actin bundle due to these motors (in the regime of local σ → 0) as
| (6) |
where α gives the average effective restoring force per motor and 2πRf(h(t)) is the total number of motors along the cylindrical protrusion. The function f(h) is determined by the concentration profile of the motors, and for tip-directed motors (such as myosin-I and myosin-X (30)) is either a constant or a monotonously increasing function of the height (assuming no interactions between the motors).
The role of myosin-I in microvilli was investigated in McConnell and Tyska (29). When the activity of myosin-I was enhanced by exposure to ATP, the rootlets of the protrusions elongated and membrane shedding at the tips was greatly enhanced. This is attributed to myosin-I-induced forces that pull the membrane up along the actin bundle, so that excess membrane accumulates at the tips, where it is released as vesicles. This implies that myosin-I indeed applies a downward force on the actin bundle, contributing to the active restoring force Fma (Eq. 6).
Combining these forces for the regime of low Reynolds number , we extract the equation of motion for the protrusion height:
| (7) |
From this equation, we find that height dynamics is controlled by the rate of polymerization (A), the severing rate profile (β(z)), and the number of actin-membrane motors, all of which are determined by the concentration of regulating proteins in the protrusion and the availability of G-actin. We wish to examine the possible functional dependencies for these parameters on the protrusion height and width. More importantly, we search for the functional dependencies that result in a qualitative change in the solution landscape of the protrusion (i.e., under which conditions the protrusion collapses, or that several steady-state solutions appear).
The polymerization and severing rates depend on the distribution of a variety of actin-binding proteins that get transported within the protrusion. There are four basic types of transportation modes:
-
1.
Free diffusion,
-
2.
Binding to the actin filaments resulting in downward treadmilling velocity,
-
3.
Binding to a myosin that walks toward the tip, or
-
4.
Binding to myosin-VI that walks toward the base.
The resulting concentration profiles for the different transportation mechanisms were investigated in Zhuravlev and Papoian (8) and Naoz et al. (10), and are shown schematically in Fig. 2.
Figure 2.
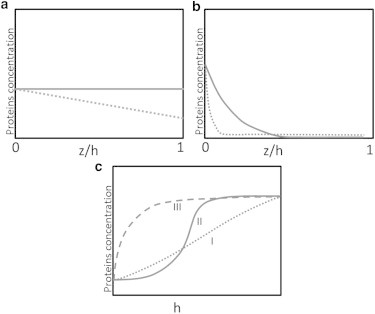
Steady-state protein concentration profiles along the protrusion (a and b) or as a function of the protrusion height h (c). (a) Simple diffusion with a sink at the tip (dotted line) or without it (solid line). (b) Profile of minus-end-directed myosin-VI (solid line) and cargo proteins that are localized to the base by binding to myosin-VI (dotted line). (c) Examples of possible concentrations of tip-directed myosins and their cargoes at the protrusion tip.
Polymerization rate and severing
The polymerization rate A can depend on the tip concentration of two types of proteins that either inhibit (Ci) or promote (Cp) actin polymerization (10),
| (8) |
where Af is the free polymerization rate, Ap is the enhanced polymerization rate due to the promoter, and
with kon being the attachment rate and koff being the detachment rate. Both Af and Ap increase monotonously with the concentration of G-actin at the tip, up to some saturation value.
The polymerization rates Af and Ap in general depend on a variety of factors: the availability of G-actin arriving by diffusion to the tip (7,11), active transportation of G-actin to the tip (12), load applied on the tip by the membrane (11,13), and the influx of ions into the protrusion (9,31), among others (8,10). Here we wish to explore the more general consequences of generic forms of A(h), which in reality may have a complex form due to different interacting proteins that combine to affect the polymerization rate. Below, we will consider two limiting cases where A(h) is either a constant (corresponding to fast diffusion, Fig. 2 a) or a monotonously increasing function of the height (due to tip-directed transport of regulating proteins (10), Fig. 2 c). We consider these two cases because it seems that G-actin availability is not limited due to diffusion along the protrusion length, as demonstrated by the growth of protrusions in a huge variety of heights (up to tens of microns in length) when the amounts of various proteins are varied (32), and by the observed increasing polymerization rate with height in stereocilia (24). These observations strongly suggest that G-actin availability by diffusion is not the limiting factor for actin polymerization in actin-based protrusions, possibly due to active transport (9,12). The case of decreasing A with h due to a reduction in the available G-actin (arriving by diffusion from the cytoplasm) is given in Eqs. S1 and S2 in the Supporting Material. Note that one can add additional mechanisms that affect A(h) in this model.
Let us demonstrate an example of a tip-directed transport of a promoter of actin polymerization (consider for simplicity only one type, and no inhibitors) which results in an exponentially increasing concentration of the promoter at the tip with increasing height h (10) (see calculation given in Fig. S1). From Eq. 8, this results in an increasing function of A(h) with h (see Fig. S1). Depending on the parameters, we find a sigmoidal A(h) with an inflection point (see Fig. S1 and further discussion in the Supporting Material).
The severing rate of the actin filaments β(z) is determined by the local concentration of severing proteins and by the local properties of the actin bundle such as the concentration of cross-linkers, ATP/ADP-actin content, and internal actin twist. We consider two limiting cases for the severing profile β(z):
-
1.
A constant severing rate along the protrusion length β0, which corresponds to uniform distribution of the severing proteins, or
-
2.
Severing that is entirely confined to the actin rootlet below the protrusion base, i.e., no severing at all inside the protrusion, resulting in a cylindrical shape: Rtip = Rbase.
The latter case represents the limit of strong active localization of the severing proteins to the base (Fig. 2 b), which can be achieved (for example) by the active transport of the severing proteins by myosin-VI motors (as was suggested to occur in stereocilia (10,33)). Deviations from a simple cylindrical shape, such as tapering of the protrusion at its base (seen in stereocilia and microvilli), do not qualitatively change the results.
Note that while actin severing always exists inside cells, there are cases where the bundle in the rootlet seems to gradually integrate into the underlying actin network, without any clear severing (34). As long as the effective protrusive forces arise in the region where the filaments spread out from the bundle and merge into the cytoplasmic network, this process can be described as an effective severing that is localized to the rootlet.
We note that the local rate of filament loss (through severing and/or depolymerization (13)) has to depend on the coordinate z along the protrusion (Eq. 2). Otherwise, the only way to maintain a steady-state height would be to perfectly match the polymerization at the tip with the depolymerization in the cytoplasm, which is a highly unstable condition.
Steady-state height of a cylindrical protrusion
We will now focus on the steady-state height and map the different regions of phase space where different behaviors can occur for a cylindrical protrusion. In the Supporting Material we present the case of uniform severing along the protrusion length, which results in a conical actin bundle and the details of the dynamics of the protrusion height.
Assuming that the density of severing proteins is constant and uniform inside the cytoplasm, the rootlet has a conical shape with area Sc (Eq. 2) given by
| (9) |
The protrusive force is now
and therefore has the same behavior as A(h) (Eq. 1), i.e.,
In Fig. 3 we plot the protrusive force for a polymerization rate that increases with the height (23) (as expected for a system where the regulating proteins are carried by tip-directed motors (10)). The membrane restoring force Fmd (Eq. 4) for a cylindrical protrusion is independent of the height. We therefore conclude that the constant restoring force of the membrane cannot, on its own, produce a stable steady-state protrusion (Fig. 3 a, dashed line). The only solution is an unstable one, unless A is decreasing with h or the tension increases with height due to limited membrane area (35), which are both outside our regime of interest (see Eqs. S26 and S27 in the Supporting Material for the special case of the tip-activated actin-membrane binding, which can stabilize the height against a constant restoring force). Note that the constant restoring force of the membrane acts to lower the steady-state height of the protrusion, and, if it is large enough, can prevent protrusions completely (Fig. 3 a). Membrane tension therefore plays an important role in determining the height of protrusions.
Figure 3.
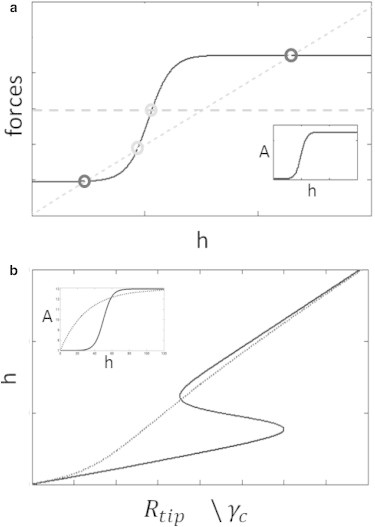
(a) The protrusive force Fa(h) (solid line, and see Eq. 1) in a cylindrical protrusion has the same dependence on height h as the polymerization rate A(h) (inset). (Dotted line) Restoring force due to the myosin motors Fma ∝ h (Eq. 6); (dashed line) constant restoring force of the membrane Fmd (Eq. 4). The stable (unstable) steady-state solutions (solid (shaded) circles). Note that the restoring force of the membrane does not provide a stable solution in this case. (b) The steady-state height of the cylindrical protrusion as a function of the tip complex radius Rtip or the cytoplasm viscosity γc (Eq. 10). The two line types (solid and dashed) correspond to two different functions of A(h), as shown (see inset).
We therefore turn to the active restoring force due to actin-membrane myosins Fma (Eq. 6), which increases with the height. For a uniform concentration, as is observed for the case of myosin-I (36), this force increases linearly with h. We now find that for this case (Fig. 3 a, dotted line) there exist one or two stable steady-state solutions, given by the equation (Eqs. 4, 6, and 7)
| (10) |
Note that when A/β ≫ 1 (weak severing), the height increases quadratically with the polymerization rate (hst ∝ A2), due to both the increase in the flow velocity of the rootlet, and its overall length. Otherwise, when severing is strong (A/β ≪ 1), the relation is linear.
In general, the number of stable steady-state solution depends on the number of zeros of A″(h). In Fig. 3 b we plot the steady-state height as a function of the protrusion radius (Rtip) or the cytoplasmic viscosity γc (Eq. 10), and demonstrate that the system can exhibit a bifurcation where hst jumps discontinuously.
Protrusion width
The protrusion’s radius at the tip (Rtip) was treated above as a free parameter. For certain types of protrusions, such as filopodia, the radius seems to have a wide distribution (33), which may result from random fluctuations in the initiation process and may not be highly regulated. However, there are examples where the width of the protrusion is highly regulated, as in the case of brush-border MV and in stereocilia. In these cases the width is uniform, with only small fluctuations between individual protrusions.
Previous models proposed to account for the radius of the protrusion through the spontaneous curvature of the tip-complex proteins (26), the elastic energy of the actin bundle (17,18), and the nucleation dynamics of the tip complex (20). However, these theories have difficulties explaining the narrow width distribution in microvilli and the observed dependence of the width on the rate of actin polymerization (21).
To account for the observations, we propose a model for the dynamical regulation of the tip-complex size. In this model, the addition and removal of new actin filaments occurs at the rim of the tip complex. Adding a new filament requires an actin nucleator (or processive-capping proteins) attached to the membrane at the tip-complex rim (at a concentration cnuc), a G-actin to start the new filament (at a concentration ρactin(Rtip)), and a free cross-linker (CL) to link the new filament to the bundle (at a concentration ρCL(Rtip)). The nucleators get deactivated at a rate ηnuc, causing a removal of the nucleator and of the entire actin filament. The radius dynamics due to this process is given by
| (11) |
where is the incorporation (and activation) rate of the nucleators at the tip complex and ρf(Rtip) = ρactin(Rtip) ρCL(Rtip). The steady-state radius of the tip complex is therefore given by the solution of
and it is therefore clear that a finite steady-state radius is possible only if the addition and removal of nucleators have different dependencies on Rtip.
Both the CL and the G-actin can reach the tip either through free diffusion or by being carried by myosin along the bundle’s outer surface (7,12) (Fig. 4 a). Once at the tip, they diffuse from the rim of the tip complex into its center, while getting incorporated into the treadmilling bundle (Fig. 4 b). This process of diffusion and incorporation gives rise to a roughly exponential concentration profile for these two components, decaying from the rim inwards (Fig. 4 c). The length-scale that controls the exponential decay is given by
where Dtip is the diffusion coefficient and ktip is the effective incorporation rate (see below). To simplify the analysis, we will assume here that, for G-actin, this length-scale is very large, so that the distribution of G-actin across the tip-complex cross-section can be considered constant (and therefore ρactin(R) is constant), and only the CL have a varying concentration profile, i.e., ρf(Rtip) = ρCL(Rtip) (the result will remain the same if we would instead assume that the G-actin profile is not constant, while the CL are uniformly distributed).
Figure 4.
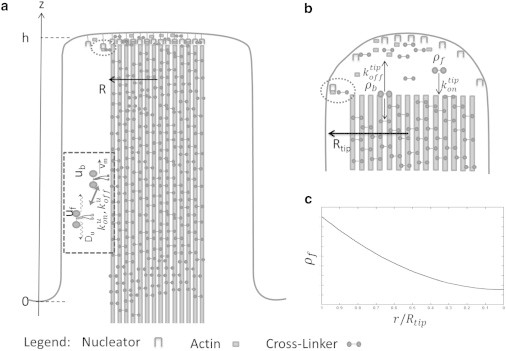
(a) Active transport of CL along the bundle: The myosin bound to the CL can either walk on the actin with a velocity vm, or freely diffuse with diffusion coefficient Du. The rates of switching between these states are kuon and kuoff. Once at the tip, the CL disengages from the myosin and can diffuse along the tip complex, and be integrated into the bundle (b). (c) Resulting steady-state concentration profile of the free CL. The value ρf(r) decays from the rim of the tip complex to the center (Eq. 18).
The following equations describe the CL concentration profile throughout the tip-complex cross-section (as a function of the radius 0 ≤ r ≤ Rtip in cylindrical symmetry):
| (12) |
| (13) |
where ρf(r,t) ρb(r,t) are the freely diffusing and actin-bound surface concentrations of CL, are the binding/unbinding rates of the CL to and from the actin, A is the polymerization velocity of the actin filaments, and a is a molecular length-scale (Fig. 4 b). At steady-state conditions , the solution for these equations is
| (14) |
where J0 is the Bessel function of the first kind. The constant C is determined by the conservation of the total number of CL
| (15) |
where Jin and Jout are the influx and outflux of CL, respectively, at each point along the protrusion (0 ≤ z ≤ h). The last term in Eq. 15 is the total flux of CL that is incorporated into the treadmilling bundle at the tip.
The fluxes Jin and Jout depend on the transportation mechanism of the CL. We will first consider the case where the CLs are carried to the protrusion tip by myosin motors. We shall assume that along the length of the protrusion the CLs are bound to the myosin motors, and can detach only at the tip. At the tip the CL cargo is released, while the myosin motor is deactivated, and is eventually recycled to the cell cytoplasm. A specific example for this scenario can be found in the myosin-III/espin-1 system (37). The motor-cargo complex can either move processively toward the plus-end with a velocity vm = vw – va when actin-bound (where vw is the processive velocity of the motor on the actin filaments), or freely diffuse with a diffusion coefficient Du. We therefore have
The binding and unbinding rates of the motor-cargo to the actin bundle are given by kuon and kuoff (Fig. 4 a). For a cylindrical protrusions we describe this process by the following one-dimensional continuum equations (10) for the concentrations of the freely diffusing and actin-bound processive states (uf(z), ub(z)),
| (16) |
| (17) |
with boundary conditions uf(0) = u0Rbase/Rtip (Rbase might not be equal to Rtip due to tapering near the base, as in stereocilia, u0 is the concentration of free CL+motor complexes in the cytoplasm), and uf(h) = ρf(Rtip).
We assume that the dynamics of the CL transportation is much faster than the dynamics of the protrusion width changes, and therefore can use the steady-state solutions to analytically solve Eqs. 14 and 15, giving
| (18) |
where
We find from Eq. 18 that the concentration of CL at the tip increases with the height h, due to the increasing accumulation of tip-directed motor-cargo (see Fig. S9). For long protrusions, h ≫ z1,|z2|, the outflux due to diffusion at the protrusion base is effectively zero, and the CL inside the protrusion can only exit by being incorporated into the actin bundle at the tip (see Fig. S9). In this limit, ρf(h,Rtip) reaches its maximal asymptotic value, which is independent of h:
| (19) |
For comparison, in the case where the CLs are transported passively by diffusion to the tip, the solution is
| (20) |
and now the CL concentration at the tip decreases with h. Below we will limit the discussion to the active, myosin-driven transport of CL to the protrusion tip, which seems to be ubiquitous (for example, the myosin-III/espin-1 (37) and myosin-X/Eps8 (38) in filopodia and stereocilia).
We wish to study the tip’s radius dependence on h and A(h). For a fixed h, we find from Eqs. 11 and 14 that the radius decreases with increasing polymerization rate (Fig. 5 a), and in the limit of , Rtip ∝ 1/ktip (Eq. 14), meaning that Rtip ∝ 1/A for A/a ≪ koff, and saturates for A/a ≫ koff. This behavior arises due to the increased removal rate of the CLs with increasing polymerization rate, leading to a decrease in the CL concentration at the tip. Note that as A decreases the steady-state Rtip increases, until a critical value of A, where Rtip values can diverge.
Figure 5.
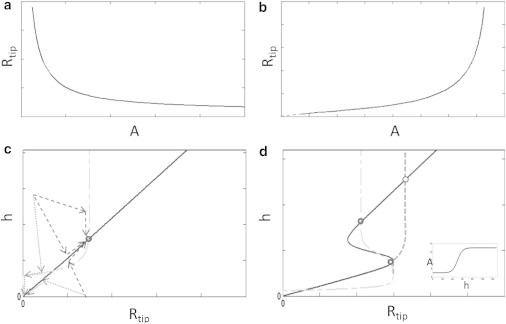
(a) Rtip as a function of the polymerization rate (at a fixed height), when the polymerization rate is independent of the flux of tip complex components. (b) As in panel a, when the tip complex and promoters of actin polymerization have the same transport mechanism (Eq. 21). (c) Steady-state height as a function of radius for a constant A (solid line, Eq. 10), and the steady-state protrusion radius Rtip (gray dashed line). (Dashed arrows) Possible trajectories that can lead to a stable cylindrical protrusion, or to its decay. (d) As in panel c for the case of A(h) given (inset). (Dashed light (dark) shaded line) Conditions of panels a and b, respectively.
For a fixed actin polymerization rate, we find that the outflux of CLs at the protrusion base increases as the height h decreases (Eq. 18), such that there is a critical height below which the steady-state solution of Eq. 11 vanishes (see Fig. S8). For long protrusions there is a constant value of CL concentration (Eq. 19), and the radius is independent of height. This behavior is shown in Fig. 5 c.
When the polymerization rate depends on height, the resulting dependence of the width Rtip on the height is more complicated. Let us consider that there is a promoter of actin polymerization that is carried to the tip by the same myosin motor that also carries the nucleators, or alternatively that the nucleators themselves can also act to promote a higher rate of polymerization. In both of these cases the polymerization rate can be written as
| (21) |
where Knuc and Anuc are the effective affinity and actin polymerization rates due to the nucleator (or the protein that uses the same transport myosin). We shall consider two limiting cases:
-
1.
The polymerization rate A does not depend on cnuc (Anuc = 0), and
-
2.
cnuc is the only promoting protein effecting the polymerization rate (Kp = Ki = 0).
For the first case, we find as before that the radius decreases with increasing polymerization rate (Fig. 5 a), and therefore decreases with the height (dashed light-shaded line in Fig. 5 d). When both the nucleators’ concentration (cnuc) and the polymerization rates increase with the protrusion’s height h, we find that the steady-state radius can also increase with the polymerization rate (Fig. 5 b) and with the height (dashed dark-shaded line in Fig. 5 d).
We conclude that in the general case, the protrusion radius may increase or decrease as a function of the polymerization rate and the height, depending on what determines A(h). This gives the cell a robust and flexible mechanism to control the relation between the protrusion’s radius and height. It can also explain why in some protrusion types, such as the stereocilia, there are multiple proteins that promote actin growth and why the ratio between their concentrations may be different between different cells.
Discussion
We have so far used our model to calculate the steady-state height of a cylindrical protrusion due to the force balance, and proposed a mechanism for the dynamical regulation of the tip radius (which for a cylinder is the radius of the whole protrusion). We now combine both descriptions to arrive at a model that simultaneously gives both the height and the width of cylindrical protrusions. In Fig. 5, c and d, we demonstrate that the mechanisms included in our model can allow the cell to determine the steady-state shape of cylindrical protrusions on its surface.
Note that allowing a protrusion to grow and reach the stable point indicated in Fig. 5 c is not trivial, and depends on the initial conditions: starting with a large tip-complex such that the stable height is reached before it disintegrates, or having a large initial tail such that the height increases fast to a large value (see below regarding filopodia dynamics and in the Supporting Material). We also see in Fig. 5 d that there are systems that allow for two stable solutions. These occur only when A(h) has a sharp inflection point (Figs. 2 c and 3, and see Fig. S1 b), and may be reached by different initial conditions.
We now compare the model we presented above to observations of two main types of actin-driven protrusions, namely filopodia and microvilli. The specialized case of stereocilia, with its unique staircase-type organization, will be treated in a separate article.
Filopodia
We begin with the most unregulated and dynamic form of protrusion, which is observed in many cell types showing a wide distribution in length and width (39,40). These protrusions are observed to grow rapidly and then collapse, sometimes without any significant period of steady-state shape.
For the growth phase, we find that filopodia height often follows a roughly linear growth, occasionally with a pronounced overshoot (41). In our model (Eq. 7) this type of behavior can only arise if there is an initial long rootlet before the formation of the protrusion (see Fig. S2 b). Indeed one mechanism for the formation of filopodia involves the formation of a tight bundle of actin filaments inside the cell, before the emergence of the protrusion, as observed in detailed electron microscopy images of filopodia during their initiation stages (34). Our model relates these two observations to the same mechanism.
The collapse of the filopodia was suggested to be driven by capping events at the tip (8) and active retraction of the cytoplasmic actin network due to myosin-II contractility (42). A recent study has detailed the response of filopodia to attachment of beads at their tips, which results in filopodia retraction (43), due to a reduction in the rate of actin polymerization at the tip. In our model, the cessation of polymerization brings about a rapid collapse (see Fig. S2 d).
As for the overall shape of the filopodia, there are no indications that the severing proteins are actively localized along its length and therefore we may assume that they are evenly distributed along the filopodia. For uniform severing, our model predicts that the steady-state shape of the filopodia should be conical. In Yang et al. (44) there are static high -resolution images of the actin cores of filopodia, which indicate that the filopodia are indeed widest at their tips and shrink in radius toward their base. They are, however, mostly not in the shape of a simple cone—which is not surprising because these are not steady-state shapes, either growing or retracting. Similar noncylindrical shapes of filopodia are reported in Sinnar et al. (45). We further discuss the filopodia shapes in the Supporting Material.
In Zidovska and Sackmann (40) the forces induced by the elongation of filopodia were studied, and their results support some assumptions and conclusions of our model. Applying a pulling force at the filopodia tip was observed not to increase the rate of polymerization, which is in line with our assumption that the pressure of the membrane on the tip-complex is not dominant in controlling the polymerization rate. The filopodia were observed to relax nearly completely to their original lengths after switching off the external force, suggesting the existence of a steady-state length, as our model predicts. Manipulations that are likely to reduce the polymerization rate, such as by Ca2+ chelation or binding a bead to the filopodia tip, result in filopodia shortening, as expected by our model.
Microvilli
The category of protrusions named microvilli (MV) covers a wide range of protrusions ranging from structures that are highly dynamic and have a lifetime of several minutes (46) to structures that are stable and are highly regulated such as those appearing in brush-border cells (47). MV have, in general, a more uniform cylindrical shape than filopodia and contain a different combination of proteins. We wish to focus our discussion on MV that have a highly regulated, well-defined steady-state shape.
The cylindrical shape of the MV suggests that the severing in these systems is confined to the base due to active transport of the severing proteins, which is plausible because myosin-VI is present in these structures (48). Indeed as expected (10), in some cases a small narrowing (tapering) at the MV base is observed. This is also equivalent in our description to the case where the actin filaments spread out from the rootlet and integrate into the cytoplasmic network.
We now compare our model to several observations regarding the steady-state shapes of MV in response to different manipulations of the cell. In Sumigray and Lechler (49), it was observed that MV are distinctly shorter when structural components of the cytoplasmic meshwork, such as keratin filaments, are depleted. Our model rationalizes these observations through a decrease of the effective cytoplasmic viscosity factor γc in Eq. 10.
In Zwaenepoel et al. (21), the activity of two forms of Eps8 was investigated; one form (Eps8L1a) is mainly a capping protein, while the other (Eps8) is a CL. Both proteins are actively transported to the tips of MV by myosin-XV (38). It was observed that overexpression of Eps8L1a resulted in a very large reduction in height (a factor of ∼2–5), accompanied by a small increase in width of ∼10%. The effect of capping proteins at the tip is to decrease the actin polymerization rate, which in our model results in a direct reduction in the height (Eq. 10). The radius in our dynamical regulation model indeed increases with decreasing polymerization rate (Fig. 5 a). The small observed increase may be due to the regime where the radius is weakly dependent on A (A/a ≫ koff). The qualitative changes in both height and width due to changes in the rate of actin polymerization are shown in Fig. 6. When Eps8L1a was depleted, the MV grew to a larger height, while the radius decreased. Again, this fits with our interpretation that the Eps8L1a’s capping activity mainly affects the polymerization rate.
Figure 6.
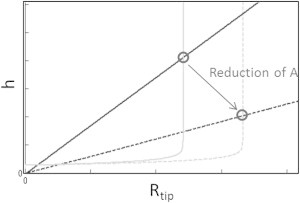
Calculated changes to the steady-state radius (Rtip, shaded line) and height (hst, solid line, Eq. 10) of a cylindrical protrusion due to changes in the overall actin polymerization rate (dashed lines). Reduction of the polymerization rate can result in a proportionately larger decrease in the height compared to the change in radius, similar to what was observed in Zwaenepoel et al. (21).
The role of CL in the MV was investigated in Revenu et al. (50). It was found that the reduction of the overall cellular amount of CL resulted in thinner (by factor of ∼1.4) and shorter (by factor of ∼1.7) MV. From our relation between the height and the radius of cylindrical protrusions we expect a simple linear relation (Eq. 10): h ∝ Rtip (assuming that the polymerization rate is independent of the height). The observed changes in the radius and height are therefore roughly consistent with this linear relation. According to our model for dynamical width regulation, indeed we expect that reducing the concentration of CL will result in a thinner tip complex (u0 in Eqs. 11 and 18). MV with reduced CL also have shorter rootlets, which is what we expect because the rootlet length depends linearly on the radius in our model:
| (22) |
Note that the proteins knocked-out in these experiments (such as villin) have many functions in addition to their cross-linking property, which complicates the comparison to a simple model.
Proteins that connect the actin core to the membrane, such the ERM-family, play a role by inducing an additional protrusive force (see Eq. S23 in the Supporting Material for details). Reduction in the overall concentration of such proteins results in a lower contribution of this protrusive force, and therefore shorter microvilli, as observed in experiments (1,21,51). Because such passive linkers are naturally swept away from the protrusion due to the treadmilling actin, special mechanisms can be used to maintain them along the protrusion length, such as active transport and activation at the tip (52).
In Gorelik et al. (46), the growth phase of MV follows a simple exponential form as arises in our model (see Fig. S2 a), for a simple restoring force that increases linearly with the height and a constant rate of polymerization. In this experiment, the collapse after termination of polymerization using application of a drug seems to be rather linear, in agreement with our model (see Fig. S2 d).
Conclusions
Despite the huge complexity of cellular protrusions, the experimental data point to a direct relation between the resulting shape (height and width) and the rate of actin polymerization and availability of CL. We have presented here a model that unifies biochemical and physical processes involved in the shaping of actin-based cellular protrusions, and which, for the first time to our knowledge, can provide a theoretical framework to explain the different observations.
The model also makes predictions about the underlying processes involved in protrusion formation, which could be used to guide future experiments. For example, our model predicts that actin protrusion lengths should increase with the viscosity of the underlying cytoplasmic network. Our model also predicts that myosin motors that couple the membrane to the actin bundle (e.g., myosin-I) play a crucial role in determining a steady-state height, by inducing a restoring force that balances the protrusive force of actin polymerization.
Our dynamic-width regulation model relates, for the first time to our knowledge, the tip-complex radius to the polymerization rate. This allows us to explain puzzling experimental observations, and provides a mechanism for cellular control over both height and width of protrusions. In addition, our model describes the dynamics of protrusion growth and collapse, including the experimentally observed over-shoot phenomenon.
Our model, as presented here, deals with individual protrusions, but can be extended to include the additional interaction forces between closely-packed protrusions (26), such as in brush-border MV (47) and stereocilia (54). The basic force balance that allows for a single protrusion to exist still needs to prevail as described in our model.
For quantitative testing of this model we would need to have information about the exact components, which does not exist at present. We therefore refrained from attempting to provide an exact quantitative fit to the observations. However, the model provides a framework with which to analyze the roles of different proteins inside such protrusions, which is otherwise difficult to extract from the experimental data.
Acknowledgments
N.S.G. gratefully acknowledges funding from the ISF (grant no. 580/12). This research is made possible in part by the historic generosity of the Harold Perlman Family. G.O. gratefully acknowledges the help of Urska Jelercic in improving the manuscript and the help of Urska Jelercic, Itai Pinkoviezki, and Abhijit Ghosh for their helpful remarks.
Supporting Material
References
- 1.Revenu C., Athman R., Louvard D. The co-workers of actin filaments: from cell structures to signals. Nat. Rev. Mol. Cell Biol. 2004;5:635–646. doi: 10.1038/nrm1437. [DOI] [PubMed] [Google Scholar]
- 2.Mattila P.K., Lappalainen P. Filopodia: molecular architecture and cellular functions. Nat. Rev. Mol. Cell Biol. 2008;9:446–454. doi: 10.1038/nrm2406. [DOI] [PubMed] [Google Scholar]
- 3.Gov N.S., Gopinathan A. Dynamics of membranes driven by actin polymerization. Biophys. J. 2006;90:454–469. doi: 10.1529/biophysj.105.062224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Veksler A., Gov N.S. Phase transitions of the coupled membrane-cytoskeleton modify cellular shape. Biophys. J. 2007;93:3798–3810. doi: 10.1529/biophysj.107.113282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Vaggi F., Disanza A., Ciliberto A. The Eps8/IRSp53/VASP network differentially controls actin capping and bundling in filopodia formation. PLOS Comput. Biol. 2011;7:e1002088. doi: 10.1371/journal.pcbi.1002088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Svitkina T.M. Ultrastructure of protrusive actin filament arrays. Curr. Opin. Cell Biol. 2013;25:574–581. doi: 10.1016/j.ceb.2013.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Lan Y., Papoian G.A. The stochastic dynamics of filopodial growth. Biophys. J. 2008;94:3839–3852. doi: 10.1529/biophysj.107.123778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Zhuravlev P.I., Papoian G.A. Molecular noise of capping protein binding induces macroscopic instability in filopodial dynamics. Proc. Natl. Acad. Sci. USA. 2009;106:11570–11575. doi: 10.1073/pnas.0812746106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Zhuravlev P.I., Lan Y., Papoian G.A. Theory of active transport in filopodia and stereocilia. Proc. Natl. Acad. Sci. USA. 2012;109:10849–10854. doi: 10.1073/pnas.1200160109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Naoz M., Manor U., Gov N.S. Protein localization by actin treadmilling and molecular motors regulates stereocilia shape and treadmilling rate. Biophys. J. 2008;95:5706–5718. doi: 10.1529/biophysj.108.143453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Mogilner A., Rubinstein B. The physics of filopodial protrusion. Biophys. J. 2005;89:782–795. doi: 10.1529/biophysj.104.056515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Zhuravlev P.I., Der B.S., Papoian G.A. Design of active transport must be highly intricate: a possible role of myosin and Ena/VASP for G-actin transport in filopodia. Biophys. J. 2010;98:1439–1448. doi: 10.1016/j.bpj.2009.12.4325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Prost J., Barbetta C., Joanny J.F. Dynamical control of the shape and size of stereocilia and microvilli. Biophys. J. 2007;93:1124–1133. doi: 10.1529/biophysj.106.098038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lenz M., Prost J., Joanny J.F. Actin cross-linkers and the shape of stereocilia. Biophys. J. 2010;99:2423–2433. doi: 10.1016/j.bpj.2010.07.065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Shin H., Purdy Drew K.R., Grason G.M. Cooperativity and frustration in protein-mediated parallel actin bundles. Phys. Rev. Lett. 2009;103:238102. doi: 10.1103/PhysRevLett.103.238102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Claessens M.M., Semmrich C., Bausch A.R. Helical twist controls the thickness of F-actin bundles. Proc. Natl. Acad. Sci. USA. 2008;105:8819–8822. doi: 10.1073/pnas.0711149105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Grason G.M., Bruinsma R.F. Chirality and equilibrium biopolymer bundles. Phys. Rev. Lett. 2007;99:098101. doi: 10.1103/PhysRevLett.99.098101. [DOI] [PubMed] [Google Scholar]
- 18.Gov N.S. Packing defects and the width of biopolymer bundles. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2008;78:011916. doi: 10.1103/PhysRevE.78.011916. [DOI] [PubMed] [Google Scholar]
- 19.Isaac E.B., Manor U., Nir S. Linking actin networks and cell membrane via a reaction-diffusion-elastic description of nonlinear filopodia initiation. Phys. Rev. E. 2013;88:022718. doi: 10.1103/PhysRevE.88.022718. [DOI] [PubMed] [Google Scholar]
- 20.Haviv L., Gov N., Bernheim-Groswasser A. Thickness distribution of actin bundles in vitro. Eur. Biophys. J. 2008;37:447–454. doi: 10.1007/s00249-007-0236-1. [DOI] [PubMed] [Google Scholar]
- 21.Zwaenepoel I., Naba A., Arpin M. Ezrin regulates microvillus morphogenesis by promoting distinct activities of Eps8 proteins. Mol. Biol. Cell. 2012;23:1080–1094. doi: 10.1091/mbc.E11-07-0588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Sekerková G., Richter C.P., Bartles J.R. Roles of the espin actin-bundling proteins in the morphogenesis and stabilization of hair cell stereocilia revealed in CBA/CaJ congenic jerker mice. PLoS Genet. 2011;7:e1002032. doi: 10.1371/journal.pgen.1002032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Rzadzinska A., Schneider M., Kachar B. Balanced levels of Espin are critical for stereociliary growth and length maintenance. Cell Motil. Cytoskeleton. 2005;62:157–165. doi: 10.1002/cm.20094. [DOI] [PubMed] [Google Scholar]
- 24.Rzadzinska A.K., Schneider M.E., Kachar B. An actin molecular treadmill and myosins maintain stereocilia functional architecture and self-renewal. J. Cell Biol. 2004;164:887–897. doi: 10.1083/jcb.200310055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Wolff K., Barrett-Freeman C., Marenduzzo D. Modeling the effect of myosin X motors on filopodia growth. Phys. Biol. 2014;11:016005. doi: 10.1088/1478-3975/11/1/016005. [DOI] [PubMed] [Google Scholar]
- 26.Gov N.S. Dynamics and morphology of microvilli driven by actin polymerization. Phys. Rev. Lett. 2006;97:018101. doi: 10.1103/PhysRevLett.97.018101. [DOI] [PubMed] [Google Scholar]
- 27.Derényi I., Jülicher F., Prost J. Formation and interaction of membrane tubes. Phys. Rev. Lett. 2002;88:238101. doi: 10.1103/PhysRevLett.88.238101. [DOI] [PubMed] [Google Scholar]
- 28.Brochard-Wyart F., Borghi N., Nassoy P. Hydrodynamic narrowing of tubes extruded from cells. Proc. Natl. Acad. Sci. USA. 2006;103:7660–7663. doi: 10.1073/pnas.0602012103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.McConnell R.E., Tyska M.J. Leveraging the membrane - cytoskeleton interface with myosin-1. Trends Cell Biol. 2010;20:418–426. doi: 10.1016/j.tcb.2010.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Sousa A.D., Cheney R.E. Myosin-X: a molecular motor at the cell’s fingertips. Trends Cell Biol. 2005;15:533–539. doi: 10.1016/j.tcb.2005.08.006. [DOI] [PubMed] [Google Scholar]
- 31.Revenu C., Courtois M., Robine S. Villin severing activity enhances actin-based motility in vivo. Mol. Biol. Cell. 2007;18:827–838. doi: 10.1091/mbc.E06-05-0423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Salles F.T., Merritt R.C., Jr., Kachar B. Myosin IIIa boosts elongation of stereocilia by transporting espin 1 to the plus ends of actin filaments. Nat. Cell Biol. 2009;11:443–450. doi: 10.1038/ncb1851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Sakaguchi H., Tokita J., Kachar B. Dynamic compartmentalization of protein tyrosine phosphatase receptor Q at the proximal end of stereocilia: implication of myosin VI-based transport. Cell Motil. Cytoskeleton. 2008;65:528–538. doi: 10.1002/cm.20275. [DOI] [PubMed] [Google Scholar]
- 34.Svitkina T.M., Bulanova E.A., Borisy G.G. Mechanism of filopodia initiation by reorganization of a dendritic network. J. Cell Biol. 2003;160:409–421. doi: 10.1083/jcb.200210174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Sens P., Safran S. Pore formation and area exchange in tense membranes. Europhys. Lett. 1998;43:95. [Google Scholar]
- 36.Schneider M.E., Dosé A.C., Kachar B. A new compartment at stereocilia tips defined by spatial and temporal patterns of myosin IIIa expression. J. Neurosci. 2006;26:10243–10252. doi: 10.1523/JNEUROSCI.2812-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Quintero O.A., Unrath W.C., Yengo C.M. Myosin 3A kinase activity is regulated by phosphorylation of the kinase domain activation loop. J. Biol. Chem. 2013;288:37126–37137. doi: 10.1074/jbc.M113.511014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Manor U., Disanza A., Kachar B. Regulation of stereocilia length by myosin XVa and whirlin depends on the actin-regulatory protein Eps8. Curr. Biol. 2011;21:167–172. doi: 10.1016/j.cub.2010.12.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Lee K.C., Gopinathan A., Schwarz J.M. Modeling the formation of in vitro filopodia. J. Math. Biol. 2011;63:229–261. doi: 10.1007/s00285-010-0371-7. [DOI] [PubMed] [Google Scholar]
- 40.Zidovska A., Sackmann E. On the mechanical stabilization of filopodia. Biophys. J. 2011;100:1428–1437. doi: 10.1016/j.bpj.2011.01.069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Watanabe T.M., Tokuo H., Ikebe M. Myosin-X induces filopodia by multiple elongation mechanism. J. Biol. Chem. 2010;285:19605–19614. doi: 10.1074/jbc.M109.093864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Mallavarapu A., Mitchison T. Regulated actin cytoskeleton assembly at filopodium tips controls their extension and retraction. J. Cell Biol. 1999;146:1097–1106. doi: 10.1083/jcb.146.5.1097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Bornschlgl A.T. Filopodial retraction force is generated by cortical actin dynamics and controlled by reversible tethering at the tip. Proc. Natl. Acad. Sci. USA. 2013;110:18928–18933. doi: 10.1073/pnas.1316572110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Yang C., Czech L., Svitkina T. Novel roles of formin mDia2 in lamellipodia and filopodia formation in motile cells. PLoS Biol. 2007;5:e317. doi: 10.1371/journal.pbio.0050317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Sinnar S.A., Antoku S., Halpain S. Capping protein is essential for cell migration in vivo and for filopodial morphology and dynamics. Mol. Biol. Cell. 2014 doi: 10.1091/mbc.E13-12-0749. 2014 May 14. pii: mbc.E13-12-0749. [Epub ahead of print] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Gorelik J., Shevchuk A.I., Korchev Y.E. Dynamic assembly of surface structures in living cells. Proc. Natl. Acad. Sci. USA. 2003;100:5819–5822. doi: 10.1073/pnas.1030502100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Mooseker M.S. Organization, chemistry, and assembly of the cytoskeletal apparatus of the intestinal brush border. Annu. Rev. Cell Biol. 1985;1:209–241. doi: 10.1146/annurev.cb.01.110185.001233. [DOI] [PubMed] [Google Scholar]
- 48.Hegan P., Giral H., Mooseker M. Myosin VI is required for maintenance of brush border structure, composition, and membrane trafficking functions in the intestinal epithelial cell. Cytoskeleton. 2012 doi: 10.1002/cm.21018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Sumigray K.D., Lechler T. Desmoplakin controls microvilli length but not cell adhesion or keratin organization in the intestinal epithelium. Mol. Biol. Cell. 2012;23:792–799. doi: 10.1091/mbc.E11-11-0923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Revenu C., Ubelmann F., Robine S. A new role for the architecture of microvillar actin bundles in apical retention of membrane proteins. Mol. Biol. Cell. 2012;23:324–336. doi: 10.1091/mbc.E11-09-0765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Yonemura S., Tsukita S., Tsukita S. Direct involvement of ezrin/radixin/moesin (ERM)-binding membrane proteins in the organization of microvilli in collaboration with activated ERM proteins. J. Cell Biol. 1999;145:1497–1509. doi: 10.1083/jcb.145.7.1497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Viswanatha R., Bretscher A., Garbett D. Dynamics of ezrin and EBP50 in regulating microvilli on the apical aspect of epithelial cells. Biochem. Soc. Trans. 2014;42:189–194. doi: 10.1042/BST20130263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Reference deleted in proof.
- 54.Müller U. Cadherins and mechanotransduction by hair cells. Curr. Opin. Cell Biol. 2008;20:557–566. doi: 10.1016/j.ceb.2008.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


