ON THE LIKELIHOOD RATIO TESTS IN BIVARIATE ACDE MODELS

Abstract

The ACE and ADE models have been heavily exploited in twin studies to identify the genetic and environmental components in phenotypes. However, the validity of the likelihood ratio test (LRT) of the existence of a variance component, a key step in the use of such models, has been doubted because the true values of the parameters lie on the boundary of the parameter space of the alternative model for such tests, violating a regularity condition required for a LRT (e.g., Carey in Behav. Genet. 35:653–665, ²⁰⁰⁵; Visscher in Twin Res. Hum. Genet. 9:490–495, ²⁰⁰⁶). Dominicus, Skrondal, Gjessing, Pedersen, and Palmgren (Behav. Genet. 36:331–340, 2006) solve the problem of testing univariate components in ACDE models. Our current work as presented in this paper resolves the issue of LRTs in bivariate ACDE models by exploiting the theoretical frameworks of inequality constrained LRTs based on cone approximations. Our derivation shows that the asymptotic sampling distribution of the test statistic for testing a single bivariate component in an ACE or ADE model is a mixture of χ² distributions of degrees of freedom (dfs) ranging from 0 to 3, and that for testing both the A and C (or D) components is one of dfs ranging from 0 to 6. These correct distributions are stochastically smaller than the χ² distributions in traditional LRTs and therefore LRTs based on these distributions are more powerful than those used naively. Formulas for calculating the weights are derived and the sampling distributions are confirmed by simulation studies. Several invariance properties for normal data (at most) missing by person are also proved. Potential generalizations of this work are also discussed.

1. Introduction

1.1. Testing Variance Components in ACDE Models

The ACE and ADE models (see, e.g., Neale & Cardon, 1992) are widely used in twin studies to estimate variance components in phenotypes due to additive (A) and dominant (D) genetic effects and environmental effects shared between the twins (C) or unique to each of the twin (E). Because the four components usually cannot be estimated simultaneously in a model, either the C or the D component has to be dropped, giving an ACE or an ADE model. A typical p-variate ACE model assumes that the pair of p phenotypic measures on a twin pair follows a 2p-variate normal distribution with mean structures μ_MZ = μ_DZ = (μ′, μ′)′ and covariance structures ${\mathit{\sum }}_{\text{MZ}}=\left(\begin{array}{cc}\mathbf{A}+\mathbf{C}+\mathbf{E}& \mathbf{A}+\mathbf{C}\\ \mathbf{A}+\mathbf{C}& \mathbf{A}+\mathbf{C}+\mathbf{E}\end{array}\right)$ and ${\mathit{\sum }}_{\text{DZ}}=\left(\begin{array}{cc}\mathbf{A}+\mathbf{C}+\mathbf{E}& w_{\text{A}}\mathbf{A}+w_{\text{C}}\mathbf{C}\\ w_{\text{A}}\mathbf{A}+w_{\text{C}}\mathbf{C}& \mathbf{A}+\mathbf{C}+\mathbf{E}\end{array}\right)$ for monozygotic (MZ) and dizygotic (DZ) twin pairs, where μ is the p × 1 vector of the phenotypic means, A, C and E are p × p non-negative definite (n.n.d.) symmetric matrices giving the variance components, and w_C = 1 and w_A = 0.5 are weights. In an ADE model, D replaces C with w_D = 0.25. An important issue of interest in twin studies is whether a particular variance component contributes to phenotypic variation and correlation. In terms of the above ACE model, this corresponds to one of the following three null hypothesis testing problems: ${\text{H}}_0^{\text{A}}:\mathbf{A}=\mathbf{0},{\text{H}}_0^{\text{C}}:\mathbf{C}=\mathbf{0}$ and ${\text{H}}_0^{\text{AC}}:\mathbf{A}=\mathbf{C}=\mathbf{0}$.

The likelihood ratio test (LRT) is usually used to address the above null hypothesis testing problems. Let f(x|θ) be the density function of data x with parameter vector θ in an unbounded parameter space Θ. If the parameter spaces specified by the null and alternative hypotheses are Θ₀ ⊂ Θ₁ ⊆ Θ, under some regularity conditions, the LRT statistic T has an asymptotic null distribution of ${\chi }_{df}^2$, with the degrees of freedom (dfs) df = dimΘ₁ − dimΘ₀. When testing the variance components, a naive user of the LRT would use dfs $p^{\ast }=\frac{1}{2}p(p+1)$ and 2p^* for testing a single component and two components, respectively.

Several critical regularity conditions are needed for the χ² sampling distribution to hold in large samples. They include: (i) that the true parameter value θ₀ be an interior point of both Θ₀ and Θ₁; and (ii) that the Fisher information matrix (FIM) 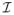(θ₀) have full rank. Unfortunately, for testing variance components, regularity condition (i) does not hold and the test statistic may not have the desired χ² distribution. The validity of the regular LRT for testing those hypotheses has been questioned (e.g., Carey, 2005^; Visscher, 2006). To see this, we note that the alternative hypotheses are directional because the variance components A and C should both be n.n.d. by definition. As a result, under the null hypothesis the true parameter value θ₀ lies on the boundary of Θ₁. It should be noted that the boundary problem cannot be removed by the use of an alternative parametrization of the model. For example, if the Cholesky decomposition is used with A = LL′, where L is lower triangular, the boundary conditions are still present as l_ii ≥ 0. Even worse, the FIM under this parametrization is singular at the true value because the Jacobian of the transformation does not have full rank at L = 0, violating the second regularity condition above.

1.2. LRT with True Parameter on Boundary

The issue of boundary problems in LRT has long been noted in general parametric models (Chernoff, 1954; Self & Liang, 1987; Shapiro, 1987), in psychometric models (Shapiro, 1985, 2007), in variance component models (Stram & Lee, 1994), and in ACDE models (Dominicus et al., 2006). For the general hypothesis testing problem, Chernoff (1954) derived the distribution of test statistic T for a boundary true parameter value using local cone approximations to the parameter spaces of the null and alternative models. Because the sets of n.n.d. matrices are cones, the parameter spaces Θ₀ and Θ₁ are identical to their approximation cones for our problems. The details regarding the cone approximation will not be discussed in this paper. As follows from Chernoff (1954, Theorem 2), the statistic T for testing variance components asymptotically takes the same distribution as it would when testing Θ₀ against Θ₁ with a single observation from N(θ₀, 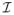(θ₀)⁻¹).

Self and Liang (1987) further explored the problem of boundary LRT and summarized several typical scenarios in which θ₀ lies on the boundary of either the null or the alternative models. They noted that in most cases, the resultant asymptotic distribution of T is a mixture of χ²’s with different dfs, though situations exist in which non-χ² distribution components are present. As will be discussed later, the current problems are more complicated and cannot be reduced to any of the scenarios they discussed.

The mixture of χ²’s, or the χ̄² distribution, was studied in detail by Shapiro (1985^{, 1988, 2007}). Some important conclusions are summarized in Appendix A. In particular, Properties 1 and 2 guarantee that for testing variance components, the LRT statistic T has a χ̄² distribution as long as nuisance parameters are not involved in inequality constraints or constraints involving the variance components.

Dominicus et al. (2006) applied the results of Self and Liang (1987) to the tests in univariate ACDE models. When testing a single (univariate) variance component, the sampling distribution is a 50:50 mixture of ${\chi }_0^2$ (a point mass on 0) and ${\chi }_1^2$. This is equivalent to using half the p-value from ${\chi }_1^2$. When simultaneously testing two (univariate) components, the sampling distribution becomes a mixture of χ²’s with 0, 1 and 2 dfs, with w₁ = 0.5 and w₀ and w₂ depending on the sample size ratio between the twin types.

Beyond univariate analysis, bivariate ACDE models are also widely used to study the genetic and environmental contributions to a pair of correlated phenotypes. In this paper, we discuss the problem of testing a bivariate ACE model in which the variance components are of full rank under the alternative hypothesis and give analytical formulas for the mixing probabilities. The test of a single component is simpler and will be discussed in the next section, while the more complicated test of A = C = 0 will be proved in Appendix D and summarized in Section D.3. We present simulation studies and an example in Sections D.4 and D.5, and conclude the paper in Section D.6.

2. Testing a Single Component A = 0

2.1. Formulation of the Problem

In this section we consider testing a single bivariate variance component $\mathbf{A}=\left(\begin{array}{cc}{a}_1& a_2\\ a_2& a_3\end{array}\right)$. The test for C can be obtained by switching the weights w_A and w_C. We define a = (a₁, a₂, a₃)′ = vechA and define c and e similarly. Let θ be the parameter vector and its FIM be 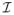(θ). Because E, C and other parameters in the model are not being tested, it follows from Property 2 in Appendix A that the weights in the χ̄² distribution can be determined using Θ₀ = {0₃}, ${\mathrm{\Theta }}_1=\{\mathbf{A}\ge \mathbf{0}\}=\{a_1{a}_3\ge a_2^2,a_1\ge 0,a_3\ge 0\}$ and 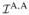, effectively removing nuisance parameters from consideration. We further define 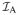= ( 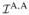)⁻¹ and have

$${\mathcal{I}}_{\text{A}}={\mathcal{I}}_{\text{A},\text{A}}-{\mathcal{I}}_{\text{A},\text{CE}}{{\mathcal{I}}_{\text{CE},\text{CE}}}^{-1}{\mathcal{I}}_{\text{CE},\text{A}}.$$ (1)

Following Chernoff (1954), we consider a ~ N(0₃, 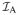(θ₀)⁻¹) and its projection â₁ onto Θ₁. The weights w_k’s are defined as the probability for â₁ to contribute to a ${\chi }_k^2$ component in the sampling distribution of $T={\widehat{\mathit{a}}}_1^{\prime }{\mathcal{I}}_{\text{A}}{\widehat{\mathit{a}}}_1$. Although the nuisance parameters are not directly involved in this formulation, it should still be noted that 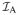is a function of those nuisance parameters, which need to be estimated by fitting the data to the model under the null hypothesis.

To derive the expression of w_k, we first study the geometry of ${\mathrm{\Theta }}_1=\{\mathit{a}\mid a_1{a}_3\ge a_2^2,a_1\ge 0,a_3\ge 0\}$. Note that the quadratic inequality can be written as a′Va ≥ 0 with

$$\mathbf{V}=\left(\begin{array}{ccc}0& 0& \frac{1}{2}\\ 0& -1& 0\\ \frac{1}{2}& 0& 0\end{array}\right).$$ (2)

The eigenvalues of V are $\frac{1}{2},-\frac{1}{2}$, and −1, with corresponding eigenvectors (1, 0, 1)′, (−1, 0, 1)′ and (0, 1, 0)′, so the quadratic form a′Va = 0, along with a₁, a₃ ≥ 0, defines an elliptic cone with axis (1, 0, 1)′. The a₁- and a₃-axes are on this cone. Θ₁ is the part of the space inside this cone. For any a ∈ ℝ³, if a ∈ Θ₁, we have â₁ = a. If a ∉ Θ₁, it is projected onto the boundary of Θ₁. Especially, a part of the space (points in the polar cone ${\mathrm{\Theta }}_1^0$ to be discussed later) will be projected onto 0, the apex of the cone.

It is usually the case that the boundary of the parameter space can be expressed as a union of several planary cones when separate inequalities are imposed on different parameters. Self and Liang (1987) summarize several situations of this type. It should be noted that the geometry of Θ₁ does not fall into this case because n.n.d. is a nonlinear constraint involving all parameters, and Self and Liang’s results do not apply (see correction to Stram & Lee, 1994). Kuriki and Takemura (2000) consider the n.n.d. constraint of a p × p matrix in general, but their results do not apply to the current situation either because they assume the non-duplicated elements in the matrix follow a normal distribution with a special covariance matrix. Below we derive the proportions w_k of the χ̄² distribution.

2.2. Mixture Probabilities

The elliptic cone Θ₁ can be viewed as the limit of a sequence of convex polyhedral cones. Given any convex polyhedral cone, the space ℝ³ can be divided into four types of area, with points in each area projecting onto different parts of the polyhedral cone and giving rise to different mixture components in the sampling distribution of T. The weights in χ̄² distribution are given by the proportions of points from $\text{N}(\mathbf{0},{\mathcal{I}}_{\text{A}}^{-1})$ that lie in the four different types of region. Especially, if is a scalar matrix (scalar multiple of identity matrix), the weights are the proportions of the unit ball, , that lie in the four different types of region. Below we enumerate the four types of region and calculate the corresponding weights assuming is a scalar matrix. See Figure 1 for a visual aid.

Figure 1.

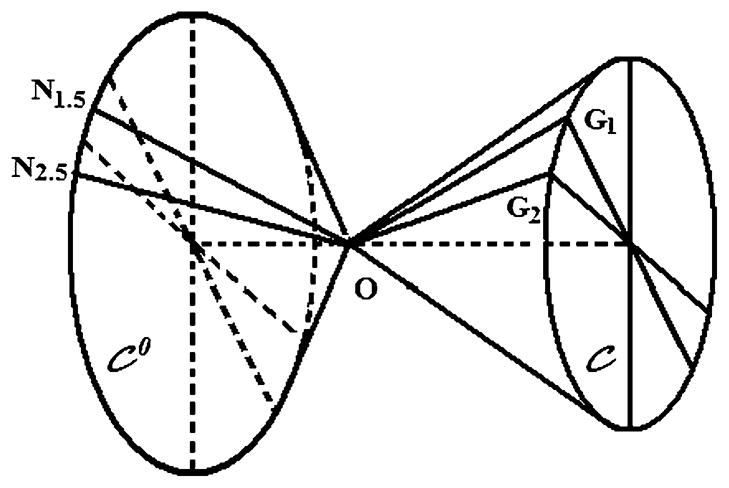
An elliptic cone 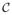and its polar cone 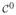. Suppose the cone 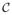is approximated by a polyhedral cone with edges g₁ =OG₁, g₂ =OG₂, etc. If the discretization is fine, the normal vector of the face OG₁G₂ can be approximated by ON_1.5, which is a generatrix on the surface of 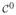with longitude between those of g₁ and g₂. The projections of points inside the pyramid O – N_1.5G₁G₂ to the polyhedral cone lie on the face OG₁G₂; the projections of points inside the pyramid O – G₂N_1.5N_2.5 to the polyhedral cone lie on the edge OG₂.

Points inside this polyhedral cone remain after projection and their squared distances to the origin follow a ${\chi }_3^2$ distribution. If the area of unit sphere in this region (which is also the solid angle) is Ω, we have w₃ = Ω/4π, where 4π is the total area of the unit sphere. Points outside the cone project onto the faces, edges or the apex. For a given face 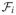between two edges, a normal vector n_i is uniquely determined, and the projections of points between n_i and 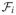lie on this face. The squared distances from those projections to the origin follow a ${\chi }_2^2$ distribution. If the planary angle spanning 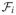is ω_i, the proportion of the unit ball that project onto 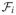is ω_i/4π, so w₂ = ω/4π, where ω = Σ_iω_i is the sum of angles between adjacent edges of the polyhedral cone. For a given edge, two normal vectors are determined by its adjacent faces, and the projections of points between the edge and those two normal vectors lie on this edge, giving rise to a ${\chi }_1^2$ distribution. The collection of all the normal vectors {n_i} determined by the faces { 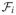} determines another polyhedral cone whose faces lie between those adjacent normal vectors. This is the polar cone of the polyhedral cone. The projections of points inside this polar cone are the origin 0 and they give rise to a point mass on 0 in the sampling distribution of T. Following similar arguments in our derivation of w₃ and w₂, we have w₀ = Ω⁰/4π and w₁ = ω⁰/4π, where Ω⁰ is the area of the unit sphere inside the polar cone, and ω⁰ is the surface angle of the polar cone.

The above result for a polyhedral cone generalizes naturally to an elliptic cone by argument of limit, and the weights are related to the volumes and surface areas of the parts of Θ₁ and ${\mathrm{\Theta }}_1^0$ inside the unit ball. It should be noted that although an elliptic cone does not have edges, the corresponding weight w₁ is still positive and the ${\chi }_1^2$ component still exists.

When 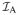is not a scalar matrix, a can be transformed to convert to the case discussed above. Consider any decomposition 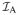= LL′ and then the spectral decomposition L⁻¹VL⁻¹′ = UΛU′. Note the eigenvalues must be of signs (−, −, +) as homogeneous transformations do not change the signs of eigenvalues. Let them be −λ₁, −λ₂ < 0 < λ₃. Define ā = U′L′a and we have ā ~ N(0, n⁻¹I), so the problem is converted to one with a scalar 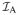. The quadratic form defining the boundary of Θ₁ is given by ā′Λā = 0, or ${\lambda }_1{\overline{a}}_1^2+{\lambda }_2{\overline{a}}_2^2={\lambda }_3{\overline{a}}_3^2$. Using spherical coordinates with latitude φ and longitude ψ, we have λ₁ cos² φ cos² ψ +λ₂ cos² φ sin² ψ = λ₃ sin² φ. If we define function

$$\varsigma (\mathbf{S},\psi )=\sqrt{\frac{{\lambda }_1(\mathbf{S}){cos}^2\psi +{\lambda }_2(\mathbf{S}){sin}^2\psi }{{\lambda }_3(\mathbf{S})+{\lambda }_1(\mathbf{S}){cos}^2\psi +{\lambda }_2(\mathbf{S}){sin}^2\psi }},$$ (3)

where λ₃ is the positive eigenvalue of S and λ₁ and λ₂ are the absolute values of its two negative eigenvalues, we have $\phi =\varsigma ({\mathcal{I}}_{\text{A}}^{-1}\mathbf{V},\psi )$ and the area of the part of the unit sphere inside the elliptic cone can be expressed as

$$\mathrm{\Omega }={\int }_0^{2\pi }{\int }_{\phi (\psi )}^{\frac{\pi }{2}}cos\phi d\phi d\psi =2\pi -{\int }_0^{2\pi }\varsigma ({\mathcal{I}}_{\text{A}}^{-1}\mathbf{V},\psi )d\psi =2\pi -4{\int }_0^{\pi /2}\varsigma ({\mathcal{I}}_{\text{A}}^{-1}\mathbf{V},\psi )d\psi .$$ (4)

So the weight w₃ is given by

$$w_3=\frac{\mathrm{\Omega }}{4\pi }=\frac{1}{2}-\frac{1}{\pi }{\int }_0^{\pi /2}\varsigma ({\mathcal{I}}_A^{-1}\mathbf{V},\psi )d\psi .$$ (5)

The polar cone ${\mathrm{\Theta }}_1^0$ of Θ₁ is defined in Property 4 of Appendix A and can be determined as { $\mathit{a}\mid {\kappa }_2{a}_1^2+{\kappa }_3{a}_2^2={\kappa }_1{a}_3^2$, a₃ ≤ 0}, where the κ’s are the reciprocals of the λ’s. The mixing probability w₀ is therefore given by

$$w_0=\frac{\mathrm{\Omega }}{4\pi }=\frac{1}{2}-\frac{1}{\pi }{\int }_0^{\pi /2}\varsigma ({\mathcal{I}}_{\text{A}}{\mathbf{V}}^{-1},\psi )d\psi .$$ (6)

The remaining two weights w₁ and w₂ are related to the surface areas of the cones. Although they can also be expressed as definite integrals and computed numerically, an easier way is to invoke Property 3 of Appendix A, and we have w₁ = 0.5 − w₃ and w₂ = 0.5 − w₀.

2.3. Complete Normal Data: Invariance Property

From the above discussions we can see that the weights of the χ̄² distribution are entirely determined by λ_i’s, or the sizes of the eigenvalues of ${\mathcal{I}}_{\text{A}}^{-1}\mathbf{V}$. For an ACE model with complete normal data, the FIM 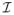has a particular structure (see Appendix B) which can be exploited to establish the following proposition (see Appendix C for proofs of the propositions and corollaries).

Proposition 1

With complete normal data, for arbitrary nonsingular 2×2 matrix X, the sets of true values (C, E) and (C̃, Ẽ) = (X′CX, X′EX) give rise to the same χ̄² distribution.

The above proposition states that the asymptotic sampling distribution is invariant under a particular type of transformation on (C, E) and can be employed to convert a general problem to a simpler situation which shares the same asymptotic distribution, as given by the following corollaries.

Corollary 1

For arbitrary true values C ≥ 0 and E > 0, the χ̄² distribution is the same as for true values C̃ = diag{β₁, β₂} and Ẽ = diag{1 − β₁, 1 − β₂}, where β₁ and β₂ are the two eigenvalues of ${(\mathbf{C}+\mathbf{E})}^{-\frac{1}{2}}\mathbf{C}{(\mathbf{C}+\mathbf{E})}^{-\frac{1}{2}}$. In this case, either λ₁ = λ₃ or λ₂ = λ₃ in Equation (3).

Corollary 2

Especially, if the true values satisfy C = γE for some scalar γ ≥ 0, the weights of the χ̄² distribution are given by $w_0=w_3=\frac{1}{2}-\frac{\sqrt{2}}{4}=0.14645$ and $w_1=w_2=\frac{\sqrt{2}}{4}=0.35355$ and are not dependent on the nuisance parameter E and sample size proportion n_MZ/n_DZ.

Corollary 1 shows that for complete normal data, the class of χ̄² distribution is determined by the ratio between λ₁ and λ₂, or the relative sizes of the radii of the base ellipse of Θ₁, whose height is always equal to one of the radii. Given our discussion of Θ₁ and its polar cone ${\mathrm{\Theta }}_1^0$ above and Property 3 in Appendix A, it can easily be seen that the most conservative (stochastically largest) member in the class of χ̄² has weights w₀ = 0, w₁ = 0.25, w₂ = 0.5 and w₃ = 0.25 (achieved when λ₁ = λ₂ and λ₃ → 0), which is more powerful than the widely used ${\chi }_3^2$. This can be used to obtain an upper bound of p-value given any true values of C and E and sample size proportions.

Corollary 2 gives the weights for the special case when C and E are proportional. We note that the weight for ${\chi }_3^2$, the distribution for a naive user of LRT, is less than 15 %, and most weights are on the χ²’s with one and two dfs. This suggests the naive use of LRT would be too conservative because a χ² distribution with larger df is (stochastically) larger than one with smaller df. In fact, the 95th percentile of ${\chi }_3^2$ distribution (7.815) is much larger than that of the χ̄² distribution (5.485) and corresponds to its 98.4th percentile, so the naive use of LRT at the level of α = 0.05 has an actual asymptotic Type I error rate of 0.016.

2.4. Testing A = 0 when C is Singular

The above discussion of the LRT for A = 0 requires C > 0 and E > 0 in the population. When this requirement is not met, Properties 1 and 2 of Appendix A does not apply and the resulting sampling distribution of T may not be a mixture of χ²’s. Although E cannot be singular (because a singular E implies a singular covariance matrix for the MZ twins), a singular C is possible, indicating that the corresponding latent factor, if present at all, is unidimensional. When this is the case, the χ̄² with four components as derived in Section 2.2 is no longer the correct asymptotic distribution of T and cannot be used in practice.

In practice, a singular C can be detected by a near singular Ĉ under the full ACE model, and its rank can be inferred from the (naive) confidence intervals of the two diagonal elements in the Cholesky decomposition of Ĉ. One option in this case is to incorporate an appropriate restriction on C for both the null and alternative hypotheses. If it is suspected that C = 0, we may consider testing the E model against the AE model, or

$${\text{H}}_0:\mathbf{A}=\mathbf{0},\mathbf{C}=\mathbf{0}\leftrightarrow {\text{H}}_1:\mathbf{A}\ge \mathbf{0},\mathbf{C}=\mathbf{0}.$$ (7)

If it is suspected that C has rank 1, the following test can be performed:

$${\text{H}}_0:\mathbf{A}=\mathbf{0},\text{rank}\mathbf{C}=1\leftrightarrow {\text{H}}_1:\mathbf{A}\ge \mathbf{0},\text{rank}\mathbf{C}=1,$$ (8)

in which the restriction of rank C = 1 can be imposed by the parametrization $\mathit{c}={(c_1^2,c_1{c}_2,c_2^2)}^{\prime }$. The results in Section 2.2 are appropriate for both the two tests above as long as the matrix 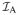is calculated using only the block of the FIM corresponding to the free parameters in the alternative model. Especially, for complete normal data, the test of E model against AE model is independent of the nuisance parameter E, with the weights in the χ̄² distribution given by Corollary 2.

3. Testing Both Components A = C = 0

The joint test of two bivariate variance components is more complicated. We give a brief formulation of the geometry of Θ₁, introduce necessary notations and present the result in this section, but leave the calculation to Appendix D.

3.1. Formulation of the Problem and Notations

Let θ = (a′, c′)′ = (a₁, a₂, a₃, c₁, c₂, c₃)′ be the parameter vector being tested and 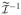be the asymptotic covariance matrix of θ̂, which is a 6 × 6 block of the inverse of the FIM for all parameters in the model. From Property 2 of Appendix A, the weights can be determined using 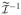, Θ₀ = 0₆ and Θ₁ = Θ_A × Θ_C.

We first consider the decompositions ${\stackrel{\sim }{\mathcal{I}}}_{\text{AA}}={\mathbf{L}}_{\text{A}}{\mathbf{L}}_{\text{A}}^{\prime }$ and ${\stackrel{\sim }{\mathcal{I}}}_{\text{CC}}={\mathbf{L}}_{\text{C}}{\mathbf{L}}_{\text{C}}^{\prime }$ for the two diagonal blocks of 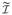and also the spectral decompositions ${\mathbf{L}}_{\text{A}}^{-1}{{\mathbf{VL}}_{\text{A}}^{\prime }}^{-1}={\mathbf{U}}_{\text{A}}{\mathit{\Lambda }}_{\text{A}}{\mathbf{U}}_{\text{A}}^{\prime }$ and ${\mathbf{L}}_{\text{C}}^{-1}{{\mathbf{VL}}_{\text{C}}^{\prime }}^{-1}={\mathbf{U}}_{\text{C}}{\mathit{\Lambda }}_{\text{C}}{\mathbf{U}}_{\text{C}}^{\prime }$. Note that the eigenvalues must be of signs (−, −, +). Now consider the transformation $\mathit{a}={{\mathbf{L}}_{\text{A}}^{\prime }}^{-1}{\mathbf{U}}_{\text{A}}\overline{\mathit{a}}$ and $\mathit{c}={{\mathbf{L}}_{\text{C}}^{\prime }}^{-1}{\mathbf{U}}_{\text{C}}\overline{\mathit{c}}$. In the space of the transformed parameters θ̄ = (ā′, c̄′)′, the metric becomes

$$\stackrel{\sim }{\mathcal{I}}={\left(\begin{array}{cc}{{\mathbf{L}}_{\text{A}}^{\prime }}^{-1}{\mathbf{U}}_{\text{A}}& \mathbf{0}\\ \mathbf{0}& {{\mathbf{L}}_{\text{C}}^{\prime }}^{-1}{\mathbf{U}}_{\text{C}}\end{array}\right)}^{\prime }\stackrel{\sim }{\mathcal{I}}\left(\begin{array}{cc}{{\mathbf{L}}_{\text{A}}^{\prime }}^{-1}{\mathbf{U}}_{\text{A}}& \mathbf{0}\\ \mathbf{0}& {{\mathbf{L}}_{\text{C}}^{\prime }}^{-1}{\mathbf{U}}_{\text{C}}\end{array}\right)=\left(\begin{array}{cc}\mathbf{I}& {\stackrel{\sim }{\mathcal{I}}}_{\text{AC}}\\ {\stackrel{\sim }{\mathcal{I}}}_{\text{CA}}& \mathbf{I}\end{array}\right),$$ (9)

where ${\stackrel{\sim }{\mathcal{I}}}_{\text{AC}}={\mathbf{U}}_{\text{A}}^{\prime }{\mathbf{L}}_{\text{A}}^{-1}{\stackrel{\sim }{\mathcal{I}}}_{\text{AC}}{{\mathbf{L}}_{\text{C}}^{\prime }}^{-1}{\mathbf{U}}_{\text{C}}$. Let ${\mathit{\Lambda }}_{\text{A}}=\text{diag}\{-{\lambda }_1^{\text{A}},-{\lambda }_2^{\text{A}},{\lambda }_3^{\text{A}}\}$ with λ_i > 0 and Λ_C be similarly defined. Also let the orientation of the third eigenvector u₃ be chosen to satisfy (1, 0, 1)L′u₃ > 0 for both cones. If we write ā = (ā₁, ā₂, ā₃)′ and c̄ = (c̄₁, c̄₂, c̄₃)′, the sets Θ_A and Θ_C are represented by ${\lambda }_1^{\text{A}}{\overline{a}}_1^2+{\lambda }_2^{\text{A}}{\overline{a}}_2^2\le {\lambda }_3^{\text{A}}{\overline{a}}_3^2({\overline{a}}_3\ge 0)$ and ${\lambda }_1^{\text{C}}{\overline{c}}_1^2+{\lambda }_2^{\text{C}}{\overline{c}}_2^2\le {\lambda }_3^{\text{C}}{\overline{c}}_3^2({\overline{c}}_3\ge 0)$.

Consider the elliptical coordinates (r_a, ψ_a, φ_a, r_c, ψ_c, φ_c) related to the Cartesian system θ̄ = (ā′, c̄′)′ by

$$\overline{\mathit{a}}=r_a\left(\begin{array}{c}\sqrt{{\kappa }_1^{\text{A}}}cos{\phi }_{a}cos{\psi }_a\\ \sqrt{{\kappa }_2^{\text{A}}}cos{\phi }_{a}sin{\psi }_a\\ \sqrt{{\kappa }_3^{\text{A}}}sin{\phi }_a\end{array}\right)\text{and}\overline{\mathit{c}}=r_c\left(\begin{array}{c}\sqrt{{\kappa }_1^{\text{C}}}cos{\phi }_{c}cos{\psi }_c\\ \sqrt{{\kappa }_2^{\text{C}}}cos{\phi }_{c}sin{\psi }_c\\ \sqrt{{\kappa }_3^{\text{C}}}sin{\phi }_c\end{array}\right),$$

where the κ’s are the reciprocals of the λ’s. Ranges of the new coordinates are r_a, r_c ≥ 0, 0 ≤ ψ_a, ψ_c < 2π and −π/2 ≤ φ_a, φ_c ≤ π/2. We have Θ_A = {π/4 ≤ φ_a ≤ π/2} and Θ_C = {π/4 ≤ φ_c ≤ π/2}. The Jacobian of this transformation is given by J = diag{J_A, J_C}, where J_A = J̄_Adiag{1, r_a, r_a} with J̄_A = (r_a, t_a, r̃_a) defined by

$${\overline{\mathbf{J}}}_{\text{A}}=({\mathit{r}}_a,{\mathit{t}}_a,{\stackrel{\sim }{\mathit{r}}}_a)=\left[\begin{array}{ccc}\sqrt{{\kappa }_1^{\text{A}}}cos{\phi }_{a}cos{\psi }_a& \sqrt{{\kappa }_1^{\text{A}}}sin{\psi }_{a}cos{\phi }_a& -\sqrt{{\kappa }_1^{\text{A}}}sin{\phi }_{a}cos{\psi }_a\\ \sqrt{{\kappa }_2^{\text{A}}}cos{\phi }_{a}sin{\psi }_a& -\sqrt{{\kappa }_2^{\text{A}}}cos{\psi }_{a}cos{\phi }_a& -\sqrt{{\kappa }_2^{\text{A}}}sin{\phi }_{a}sin{\psi }_a\\ \sqrt{{\kappa }_3^{\text{A}}}sin{\phi }_a& 0& \sqrt{{\kappa }_3^{\text{A}}}cos{\phi }_a\end{array}\right].$$

We further define J̃_A = (r_a, t_a), and J_C, J̄_C, r_c, t_c, r̃_c and J̃_C are similarly defined. The following notation will also be used:

$${\alpha }_1={\mathit{r}}_a^{\prime }{\mathit{r}}_a{\alpha }_2={\mathit{r}}_c^{\prime }{\mathit{r}}_c{\alpha }_3={\mathit{r}}_a^{\prime }{\overline{\mathcal{I}}}_{\text{AC}}{\mathit{r}}_c\tau =\frac{{\alpha }_3}{\sqrt{{\alpha }_1{\alpha }_2}}\text{and}t=arccos\tau .$$ (10)

The polar cone of Θ₁ is the part of ℝ⁶ whose projection onto Θ₁ is 0. To express this polar cone, we introduce a new coordinate system ${\overline{\mathit{\theta }}}^{\ast }={({{\overline{\mathit{a}}}^{\ast }}^{\prime },{{\overline{\mathit{c}}}^{\ast }}^{\prime })}^{\prime }={({\overline{a}}_1^{\ast },{\overline{a}}_2^{\ast },{\overline{a}}_3^{\ast },{\overline{c}}_1^{\ast },{\overline{c}}_2^{\ast },{\overline{c}}_3^{\ast })}^{\prime }$, which is related to θ̄ through θ̄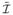^* = θ̄. Appendix D gives a brief proof that the polar cone of Θ₁ is given by ${\mathrm{\Theta }}_1^0={\mathrm{\Theta }}_{\text{A}}^0\cap {\mathrm{\Theta }}_{\text{C}}^0$, where ${\mathrm{\Theta }}_{\text{A}}^0=\{{\overline{\mathit{\theta }}}^{\ast }\mid {\kappa }_1^{\text{A}}{\overline{a}}_1^{\ast 2}+{\kappa }_2^{\text{A}}{\overline{a}}_2^{\ast 2}\le {\kappa }_3^{\text{A}}{\overline{a}}_3^{\ast 2},{\overline{a}}_3^{\ast }\ge 0\}$ and ${\mathrm{\Theta }}_{\text{C}}^0$ is similarly defined. We also define ${\mathcal{I}}_{\text{A}}^{\ast }=\mathbf{I}-{\overline{\mathcal{I}}}_{\text{AC}}{\overline{\mathcal{I}}}_{\text{CA}}={({\overline{\mathcal{I}}}^{\text{AA}})}^{-1}$.

An elliptic coordinate system can also be used for ${\mathrm{\Theta }}_{\text{A}}^0$ and ${\mathrm{\Theta }}_{\text{C}}^0$. If we express

$${\overline{\mathit{a}}}^{\ast }=r_a^{\ast }\left[\begin{array}{c}\sqrt{{\lambda }_1^{\text{A}}}cos{\phi }_a^{\ast }cos{\psi }_a^{\ast }\\ \sqrt{{\lambda }_2^{\text{A}}}cos{\phi }_a^{\ast }sin{\psi }_a^{\ast }\\ -\sqrt{{\lambda }_3^{\text{A}}}sin{\phi }_a^{\ast }\end{array}\right]\text{and}{\overline{\mathit{c}}}^{\ast }=r_c^{\ast }\left[\begin{array}{c}\sqrt{{\lambda }_1^{\text{C}}}cos{\phi }_c^{\ast }cos{\psi }_c^{\ast }\\ \sqrt{{\lambda }_2^{\text{C}}}cos{\phi }_c^{\ast }sin{\psi }_c^{\ast }\\ -\sqrt{{\lambda }_3^{\text{C}}}sin{\phi }_c^{\ast }\end{array}\right],$$

we have ${\mathrm{\Theta }}_{\text{A}}^0=\{\pi /4\le {\phi }_a^{\ast }\le \pi /2\}$ and $Q_{\text{C}}^0=\{\pi /4\le {\phi }_c^{\ast }\le \pi /2\}$. The Jacobian matrix J^* can be calculated similarly to J with notations J̄^*, J̃^*, r^*, t^*, r̃^* similarly defined for both A and C. We also use ${\alpha }_1^{\ast }={\mathit{r}}_a^{\ast \prime }{\overline{\mathcal{I}}}^{\text{AA}}{\mathit{r}}_a^{\ast },{\alpha }_2^{\ast }={\mathit{r}}_c^{\ast \prime }{\overline{\mathcal{I}}}^{\text{CC}}{\mathit{r}}_c^{\ast },{\alpha }_3^{\ast }={\mathit{r}}_a^{\ast \prime }{\overline{\mathcal{I}}}^{\text{AC}}{\mathit{r}}_c^{\ast }$, and t^* and τ^* as defined similarly to t and τ.

Following Chernoff (1954, Theorem 2), the LRT statistic T has asymptotically the same distribution as $T={\overline{\mathit{\theta }}}_1^{\prime }\overline{\mathcal{I}}{\overline{\mathit{\theta }}}_1$, where θ̄₁ ∈ Θ₁ minimizes the quadratic form (θ̄₁ − θ̄)′ 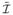(θ̄₁ − θ̄) with θ̄ ~ N(0, 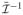). Note the matrix 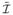serves as the metric tensor of the 6-dimensional space and θ̄₁ is the projection of θ̄ onto Θ₁ (with respect to ).

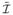3.2. Mixture Probabilities

If both the elliptic cones that define the boundaries of Θ_A and Θ_C are approximated by polyhedral cones, the projection of θ̄ on Θ₁, θ̄₁, may be located in the interior (3-face), on a face (2-face), on an edge (1-face), or at the apex (0-face) of either of the two polyhedral cones, leading to a partition of 16 different regions in ℝ⁶ with probabilities w_ij (i, j = 0, 1, 2, 3). T has a mixture of χ² distributions with mixture weights w_ij (i, j = 0, 1, 2, 3) for df (i + j). When passing to the limiting elliptic cone, different regions may fuse together, but their corresponding weights need not converge to 0. Below we give the 10 of the 16 weights w_ij. They are derived in the Appendix D. The remaining six weights can be obtained by symmetry. Computationally, these weights can be calculated using numerical integration. Separate programs in R (R Development Core Team, 2010) have been coded to calculate the weights in Sections 2.2, 3.2 and 3.3. They are available from the first author upon request. We have

$$\begin{array}{l}{w}_{33}=\frac{{\mid {\mathcal{I}}_{\text{A}}^{\ast }\mid }^{\frac{1}{2}}}{8{\pi }^3{\mid {\mathit{\Lambda }}_{\text{C}}{\mathit{\Lambda }}_{\text{A}}\mid }^{\frac{1}{2}}}\\ \times {\int }_{{\psi }_a=0}^{2\pi }{\int }_{{\psi }_c=0}^{2\pi }{\int }_{{\phi }_a=\frac{\pi }{4}}^{\frac{\pi }{2}}{\int }_{{\phi }_c=\frac{\pi }{4}}^{\frac{\pi }{2}}\frac{cos{\phi }_{a}cos{\phi }_c(2t{\tau }^2-3\tau sint+t)}{{({\alpha }_1{\alpha }_2)}^{3/2}{sin}^{5}t}d{\phi }_{c}d{\phi }_{a}d{\psi }_{c}d{\psi }_a\\ w_{23}=\frac{1}{16{\pi }^2{\mid {\mathit{\Lambda }}_{\text{C}}\mid }^{\frac{1}{2}}}{\int }_{{\psi }_a=0}^{2\pi }{\int }_{{\psi }_c=0}^{2\pi }{\int }_{{\phi }_c=\frac{\pi }{4}}^{\frac{\pi }{2}}{\left(\frac{cos{\phi }_c{\mid {\stackrel{\sim }{\mathbf{J}}}_{\text{A}}^{\prime }{\mathcal{I}}_{\text{A}}^{\ast }{\stackrel{\sim }{\mathbf{J}}}_{\text{A}}\mid }^{\frac{1}{2}}}{{(1+\tau )}^2{\alpha }_1{\alpha }_2^{3/2}}\right)}_{{\phi }_a=\pi /4}d{\phi }_{c}d{\psi }_{c}d{\psi }_a\\ w_{13}=\frac{1}{16{\pi }^3{\mid {\mathit{\Lambda }}_{\text{C}}\mid }^{\frac{1}{2}}}{\int }_{\psi =0}^{2\pi }{\int }_{{\psi }_c=0}^{2\pi }{\int }_{{\phi }_c=\frac{\pi }{4}}^{\frac{\pi }{2}}\times {\left(\frac{{\mid {\stackrel{\sim }{\mathbf{J}}}_{\text{A}}^{\ast \prime }{\mathcal{I}}_{\text{A}}^{\ast -1}{\stackrel{\sim }{\mathbf{J}}}_{\text{A}}^{\ast }\mid }^{\frac{1}{2}}{({\mathit{r}}_a^{\prime }{\mathcal{I}}_{\text{A}}^{\ast }{\mathit{r}}_a)}^{\frac{1}{2}}cos{\phi }_c(2t-sin(2t))}{{\alpha }_1^{\ast }\sqrt{{\alpha }_1{\alpha }_2^3}{sin}^{3}t}\right)}_{\begin{array}{c}{\phi }_a={\phi }_a^{\ast }=\pi /4\\ {\psi }_a={\psi }_a^{\ast }=\psi \end{array}}d{\phi }_{c}d{\psi }_{c}d\psi \\ w_{03}=\left(\frac{1}{2}-\frac{1}{\pi }{\int }_0^{\pi /2}\varsigma ({({\mathcal{I}}_{\text{A}}^{\ast }{\mathit{\Lambda }}_a)}^{-1},{\psi }_a)d{\psi }_a\right)\left(\frac{1}{2}-\frac{1}{\pi }{\int }_0^{\pi /2}\varsigma ({\mathit{\Lambda }}_c,{\psi }_c)d{\psi }_c\right)\end{array}$$

where function ς was defined in Equation (3);

$$w_{22}=\frac{1}{8{\pi }^3}{\int }_{{\psi }_a=0}^{2\pi }{\int }_{{\psi }_c=0}^{2\pi }{\left(t^{\ast }\frac{sint-\mathit{t}cost}{{\alpha }_1{\alpha }_2{sin}^{3}t}{\mid {\stackrel{\sim }{\mathbf{J}}}_{22}^{\prime }\overline{\mathcal{I}}{\stackrel{\sim }{\mathbf{J}}}_{22}\mid }^{\frac{1}{2}}\right)}_{\begin{array}{c}{\phi }_a={\phi }_c=\pi /4\\ {\psi }_a={\psi }_a^{\ast },{\psi }_c={\psi }_c^{\ast }\end{array}}d{\psi }_{c}d{\psi }_a$$

where J̃₂₂ = diag{J̃_A, J̃_C} is a 6×4 matrix;

$$w_{12}=\frac{1}{16{\pi }^2}{\int }_{{\psi }_a=0}^{2\pi }{\int }_{{\psi }_c=0}^{2\pi }{\left(\frac{{\mid {\stackrel{\sim }{\mathbf{J}}}_{12}^{\ast \prime }{\mathcal{I}}^{-1}{\stackrel{\sim }{\mathbf{J}}}_{12}^{\ast }\mid }^{\frac{1}{2}}}{{\alpha }_2^{\ast \frac{1}{2}}{\alpha }_1^{\ast }(1+{\tau }^{\ast })}\frac{{\mid {\stackrel{\sim }{\mathbf{J}}}_{12}^{\prime }\overline{\mathcal{I}}{\stackrel{\sim }{\mathbf{J}}}_{12}\mid }^{\frac{1}{2}}}{{\alpha }_1^{\frac{1}{2}}{\alpha }_2(1+\tau )}\right)}_{\begin{array}{c}{\psi }_a={\psi }_a^{\ast },{\psi }_c={\psi }_c^{\ast }\\ {\phi }_a={\phi }_c={\phi }_a^{\ast }={\phi }_c^{\ast }=\pi /4\end{array}}d{\psi }_{c}d{\psi }_a$$

where J̃₁₂ = diag{r_a, J̃_C} and ${\stackrel{\sim }{\mathbf{J}}}_{12}^{\ast }=\text{diag}\{{\stackrel{\sim }{\mathbf{J}}}_{\text{A}}^{\ast },{\mathit{r}}_c^{\ast }\}$ are 6×3 matrices;

$$w_{11}=\frac{1}{8{\pi }^3}{\int }_{{\psi }_a=0}^{2\pi }{\int }_{{\psi }_c=0}^{2\pi }{\left(t\frac{sin{t}^{\ast }-t^{\ast }cos{t}^{\ast }}{{\alpha }_1^{\ast }{\alpha }_2^{\ast }{sin}^3{t}^{\ast }}{\mid {\stackrel{\sim }{\mathbf{J}}}_{11}^{\ast \prime }{\overline{\mathcal{I}}}^{-1}{\stackrel{\sim }{\mathbf{J}}}_{11}^{\ast }\mid }^{\frac{1}{2}}\right)}_{\begin{array}{c}{\phi }_a^{\ast }={\phi }_c^{\ast }=\pi /4\\ {\psi }_a={\psi }_a^{\ast },{\psi }_c={\psi }_c^{\ast }\end{array}}d{\psi }_{c}d{\psi }_a$$

where ${\stackrel{\sim }{\mathbf{J}}}_{11}^{\ast }=\text{diag}\{{\stackrel{\sim }{\mathbf{J}}}_{\text{A}}^{\ast },{\stackrel{\sim }{\mathbf{J}}}_{\text{C}}^{\ast }\}$ is a 6×4 matrix;

$$\begin{array}{l}{w}_{20}=\frac{{\mid {\mathit{\Lambda }}_{\text{C}}\mid }^{\frac{1}{2}}}{16{\pi }^3{\mid {\mathcal{I}}_{\text{C}}^{\ast }\mid }^{\frac{1}{2}}}\times {\int }_{\psi =0}^{2\pi }{\int }_{{\psi }_c^{\ast }=0}^{2\pi }{\int }_{{\phi }_c^{\ast }=\frac{\pi }{4}}^{\frac{\pi }{2}}{\left(\frac{{\mid {\stackrel{\sim }{\mathbf{J}}}_{\text{A}}^{\prime }{\stackrel{\sim }{\mathbf{J}}}_{\text{A}}\mid }^{\frac{1}{2}}{({\mathit{r}}_a^{\ast \prime }{\mathit{r}}_a^{\ast })}^{\frac{1}{2}}cos{\phi }_c^{\ast }(2t^{\ast }-sin(2t^{\ast }))}{{\alpha }_1\sqrt{{\alpha }_1^{\ast }{\alpha }_2^{\ast 3}}{sin}^3{t}^{\ast }}\right)}_{\begin{array}{c}{\phi }_a={\phi }_a^{\ast }=\pi /4\\ {\psi }_a={\psi }_a^{\ast }=\psi \end{array}}d{\phi }_c^{\ast }d{\psi }_c^{\ast }d\psi \\ w_{10}=\frac{{\mid {\mathit{\Lambda }}_{\text{C}}\mid }^{\frac{1}{2}}}{16{\pi }^2{\mid {\mathcal{I}}_{\text{C}}^{\ast }\mid }^{\frac{1}{2}}}{\int }_{{\psi }_a^{\ast }=0}^{2\pi }{\int }_{{\psi }_c^{\ast }=0}^{2\pi }{\int }_{{\phi }_c^{\ast }=\frac{\pi }{4}}^{\frac{\pi }{2}}{\left(\frac{cos{\phi }_c^{\ast }{\mid {\stackrel{\sim }{\mathbf{J}}}_{\text{A}}^{{\ast }^{\prime }}{\stackrel{\sim }{\mathbf{J}}}_{\text{A}}^{\ast }\mid }^{\frac{1}{2}}}{{(1+{\tau }^{\ast })}^2{\alpha }_1^{\ast }{\alpha }_2^{\ast 3/2}}\right)}_{{\phi }_a^{\ast }=\pi /4}d{\phi }_c^{\ast }d{\psi }_c^{\ast }d{\psi }_a^{\ast }\\ w_{00}=\frac{{\mid {\mathit{\Lambda }}_{\text{C}}{\mathit{\Lambda }}_{\text{A}}\mid }^{\frac{1}{2}}}{8{\pi }^3{\mid {ℐ}_{\text{A}}^{\ast }\mid }^{\frac{1}{2}}}\\ \times {\int }_{{\psi }_a^{\ast }=0}^{2\pi }{\int }_{{\psi }_c^{\ast }=0}^{2\pi }{\int }_{{\phi }_a^{\ast }=\frac{\pi }{4}}^{\frac{\pi }{2}}{\int }_{{\phi }_c^{\ast }=\frac{\pi }{4}}^{\frac{\pi }{2}}\frac{cos{\phi }_a^{\ast }cos{\phi }_c^{\ast }(2t^{\ast }{\tau }^{\ast 2}-3{\tau }^{\ast }sin{t}^{\ast }+t^{\ast })}{{({\alpha }_1^{\ast }{\alpha }_2^{\ast })}^{3/2}{sin}^5{t}^{\ast }}d{\phi }_c^{\ast }d{\phi }_a^{\ast }d{\psi }_c^{\ast }d{\psi }_a^{\ast }.\end{array}$$

3.3. Complete Normal Data

With complete normal data, the FIM 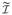is highly structured at C = E = 0 (see Equation (B.1) in Appendix B). Exploiting this structure, we have the following conclusion:

Proposition 2

With complete normal data, $\overline{\mathcal{I}}(\mathit{\theta })=\left(\begin{array}{cc}1& \rho \\ \rho & 1\end{array}\right)\otimes \mathbf{I}$ and Λ_A = Λ_C = diag{−1, −1, 1}, where $\rho =(w_{\text{A}}{w}_{\text{C}}{\alpha }_{\text{DZ}}+{\alpha }_{\text{MZ}})/\sqrt{(w_{\text{A}}^2{\alpha }_{\text{DZ}}+{\alpha }_{\text{MZ}})(w_{\text{C}}^2{\alpha }_{\text{DZ}}+{\alpha }_{\text{MZ}})}$, and α_MZ and α_DZ are sample size proportions. The asymptotic χ̄² distribution is determined only by sample size ratio through ρ and is not related to the nuisance parameter E.

In this case, 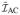= ρI and we further have ${\mathcal{I}}_{\text{A}}^{\ast }={\mathcal{I}}_{\text{C}}^{\ast }=(1-{\rho }^2)\mathbf{I}$, α₁ = α₂ = 1, ${\alpha }_1^{\ast }={\alpha }_2^{\ast }={(1-{\rho }^2)}^{-1}$

and τ =−τ^* = ρ(cosφ_a cosφ_c cosΔψ + sinφ_a sinφ_c). Note the weights are related to ψ_a and ψ_c only through Δψ = ψ_a − ψ_c, so the number of integrals involved can all be reduced. Especially, for w_ij(i, j = 1, 2), $\tau =-{\tau }^{\ast }=\frac{1}{2}\rho (1+cos\mathrm{\Delta }\psi )$ and more simplification is possible. We have

$$\begin{array}{l}{w}_{33}=\frac{{(1-{\rho }^2)}^{\frac{3}{2}}}{2{\pi }^2}{\int }_{\mathrm{\Delta }\psi =0}^{\pi }{\int }_{{\phi }_a=\frac{\pi }{4}}^{\frac{\pi }{2}}{\int }_{{\phi }_c=\frac{\pi }{4}}^{\frac{\pi }{2}}\frac{t(1+2{\tau }^2)-3\tau sint}{{sin}^{5}t}cos{\phi }_{a}cos{\phi }_{c}d{\phi }_{c}d{\phi }_{a}d\mathrm{\Delta }\psi \\ w_{23}=\frac{1-{\rho }^2}{4\sqrt{2}\pi }{\int }_{\mathrm{\Delta }\psi =0}^{\pi }{\int }_{{\phi }_c=\pi /4}^{\pi /2}\frac{cos{\phi }_c}{{(1+\tau )}^2}d{\phi }_{c}d\mathrm{\Delta }\psi \\ w_{13}=\frac{{(1-{\rho }^2)}^{\frac{1}{2}}}{2\sqrt{2}{\pi }^2}{\int }_{\mathrm{\Delta }\psi =0}^{\pi }{\int }_{{\phi }_c=\pi /4}^{\pi /2}\frac{cos{\phi }_c(t-\tau sint)}{{sin}^{3}t}d{\phi }_{c}d\mathrm{\Delta }\psi \\ w_{03}={\left(\frac{1}{2}-\frac{\sqrt{2}}{4}\right)}^2=0.02145\\ w_{22}=\frac{{(1-{\rho }^2)}^{\frac{1}{2}}}{4{\pi }^2}{\int }_{\mathrm{\Delta }\psi =0}^{\pi }(\pi -t)\frac{sint-\tau t}{{sin}^{2}t}d\mathrm{\Delta }\psi \end{array}$$

$$\begin{array}{l}{w}_{12}=\frac{1}{8}-\frac{{\rho }^2}{16\pi }{\int }_{\mathrm{\Delta }\psi =0}^{\pi }\frac{{sin}^2\mathrm{\Delta }\psi }{1-\frac{1}{4}{\rho }^2{(1+cos\mathrm{\Delta }\psi )}^2}d\mathrm{\Delta }\psi \\ w_{11}=\frac{{(1-{\rho }^2)}^{\frac{1}{2}}}{4{\pi }^2}{\int }_{\mathrm{\Delta }\psi =0}^{\pi }t\frac{sint+\tau (\pi -t)}{{sin}^{2}t}d\mathrm{\Delta }\psi \\ w_{20}=\frac{{(1-{\rho }^2)}^{\frac{1}{2}}}{2\sqrt{2}{\pi }^2}{\int }_{\mathrm{\Delta }\psi =0}^{\pi }{\int }_{{\phi }_c=\pi /4}^{\pi /2}\frac{cos{\phi }_c(\pi -t+\tau sint)}{{sin}^{3}t}d{\phi }_{c}d\mathrm{\Delta }\psi \\ w_{10}=\frac{1-{\rho }^2}{4\sqrt{2}\pi }{\int }_{\mathrm{\Delta }\psi =0}^{\pi }{\int }_{{\phi }_c=\pi /4}^{\pi /2}\frac{cos{\phi }_c}{{(1-\tau )}^2}d{\phi }_{c}d\mathrm{\Delta }\psi \\ w_{00}=\frac{{(1-{\rho }^2)}^{\frac{3}{2}}}{2{\pi }^2}{\int }_{\mathrm{\Delta }\psi =0}^{\pi }{\int }_{{\phi }_a=\frac{\pi }{4}}^{\frac{\pi }{2}}{\int }_{{\phi }_c=\frac{\pi }{4}}^{\frac{\pi }{2}}\frac{(\pi -t)(1+2{\tau }^2)+3\tau sint}{{sin}^{5}t}cos{\phi }_{a}cos{\phi }_{c}d{\phi }_{c}d{\phi }_{a}d\mathrm{\Delta }\psi .\end{array}$$

These formulas are applied to the equal sample size case and the result is shown in Table 2. The final weight w_k for the χ̄² distributions can be determined by w_k = Σ_i+j=k w_ij. Table 1 displays weights for various sample size ratios in an ACE or ADE model. Note only cases with n_MZ > n_DZ are shown because in practice available observations from MZ twins are inmost cases more than those from DZ twins. Along with the weights are the 95th and 99th percentiles of the χ̄² distribution. The ${\chi }_6^2$ distribution is also included for comparison. We can see the weights for the different sample size ratios are very close to each other. There is a trend that the weights for higher dfs increases and those for lower dfs decreases when the sample sizes become similar. This suggests that the χ̄² distribution for equal sample size is the most conservative. When compared to the ${\chi }_6^2$ distribution, all χ̄² distributions put more weights on lower dfs while their weights for ${\chi }_6^2$ are negligible. As a result, they have much lower critical values. In fact, the 95th percentile of ${\chi }_6^2$ distribution (12.6) is more than twice that of any of the χ̄² distributions and corresponds to the 99.7th percentile of the most conservative χ̄² distribution in the table, so the incorrect use of LRT at the level of α = 0.05 has an actual Type I error rate of at most 0.003. This suggests that the incorrect use of ${\chi }_6^2$ would result in very conservative results. Comparing ACE and ADE models, the distributions for the ADE models are stochastically smaller. In particular, an ADE model with equal sample sizes has the same weights as an ACE model with n_MZ = 4n_DZ. This is because they happen to share the same value of ρ in Proposition 2.

Table 2.

The weights w_ij(i, j = 0, 1, 2, 3) for equal sample sizes when testing A = C = 0 calculated from equations in Section 3.3.

	0	1	2	3
0	0.1113	0.1485	0.1265	0.0214
1	0.1485	0.0916	0.0778	0.0097
2	0.1265	0.0778	0.0245	0.0023
3	0.0214	0.0097	0.0023	0.0002

Table 1.

The weights (in percentages) of the χ̄² distribution for testing A = C = 0 in a bivariate ACE model and for testing A = D = 0 in a bivariate ADE model.

Model	Sample size proportions		Weights							Percentiles
	αMZ	αDZ	0	1	2	3	4	5	6	95	99
Naive LRT			0	0	0	0	0	0	1.00	12.59	16.81
ACE	0.5	0.5	11.13	29.69	34.47	19.85	4.38	0.46	0.02	6.16	9.68
	0.6	0.4	11.39	30.12	34.56	19.49	4.03	0.39	0.02	6.11	9.61
	2/3	1/3	11.62	30.50	34.64	19.17	3.73	0.33	0.01	6.06	9.56
	0.7	0.3	11.75	30.71	34.68	18.98	3.56	0.31	0.01	6.04	9.53
	3/4	1/4	11.97	31.08	34.75	18.66	3.27	0.26	0.01	6.00	9.47
	0.8	0.2	12.22	31.50	34.82	18.29	2.95	0.21	0.01	5.95	9.41
ADE	0.5	0.5	12.22	31.50	34.82	18.29	2.95	0.21	0.01	5.95	9.41
	0.6	0.4	12.58	32.07	34.92	17.78	2.50	0.15	0.00	5.88	9.32
	2/3	1/3	12.81	32.44	34.98	17.44	2.21	0.12	0.00	5.83	9.27
	0.7	0.3	12.93	32.63	35.01	17.26	2.06	0.11	0.00	5.81	9.24
	3/4	1/4	13.11	32.92	35.05	16.99	1.84	0.09	0.00	5.78	9.20
	0.8	0.2	13.30	33.22	35.09	16.71	1.61	0.07	0.00	5.74	9.15

4. Simulation Studies

4.1. Study 1

In the first simulation, we examine the accuracy of the weights derived in Section 2.2 for testing a single variance component in a bivariate ACE model. Four different sample size combinations are assumed: (n_MZ, n_DZ) = (100, 100), (150, 50), (500, 500), (750, 250). They vary in terms of the total sample size (N = 200 or 1000) and the ratio between the two groups (n_MZ/n_DZ = 1 or 3). For each sample size combination, 10,000 samples of sample covariance matrices are drawn from the ACE model with A = 0 and $\mathbf{C}=\mathbf{E}=\left(\begin{array}{cc}1& 0.5\\ 0.5& 1\end{array}\right)$. Each sample is fitted to both the ACE and the CE model using OpenMx (Boker, Neale, Maes, Wilde, Spiegel, Brick, et al., 2011) and the statistic T is produced for each sample. The 1st–99th percentiles of T are then plotted against those of the analytical asymptotic χ̄² distribution with weights given in Corollary 2. The four QQplots are displayed in Figure 2. The χ̄² distribution fits the simulated distribution very well in all four conditions.

Figure 2.

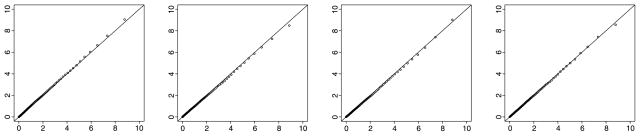
Plots of the 1st–99th percentiles of the simulated sampling distribution of T against those of the χ̄² distribution in Simulation Study 2. The sample sizes (n_MZ, n_DZ) are (from left to right) (100, 100), (150, 50), (500, 500) and (750, 250). The true and null model is CE and the alternative model is ACE.

To obtain a clearer understanding of the origin of the mixture distribution in this case, we further examine the estimates  in the full ACE model. According to our analysis in Section 2.2, samples that give a full rank  contribute to the ${\chi }_3^2$ component and those that yield  = 0 contribute to the ${\chi }_0^2$ component, so the distribution of the rank of  should correspond to the weights in the mixture. The rank of  is determined for each sample of size n_MZ = n_DZ = 500 and we find 14.61 % produced  = 0, 70.84 % gave an  of rank 1, and 14.55 % yielded an  of full rank. These percentages are very close to the weights w₀, w₁ + w₂ and w₃ as given in Corollary 2, confirming our previous analysis.

4.2. Study 2

The second simulation studies (1) the accuracy of the χ̄² distribution in testing a single bivariate variance component when a nuisance parameter is on the boundary, an issue raised in Section 2.4, and (2) the accuracy of the weights given in Section 3.3 for testing both variance components in a bivariate ACE model. In this study, the true model is an ACE model with A = C = 0. The same sample size combinations, number of replications and true value of E are assumed as in the first study. Each simulated sample is fitted to the E, AE, CE and ACE models, and a test statistic T can be computed for five tests: AE vs. ACE, CE vs. ACE, E vs. AE, E vs. CE, and E vs. ACE. The 1st–99th percentiles of T are plotted against those of a χ̄² distribution. For the first four tests, the χ̄² distribution is a mixture of χ²’s with zero–three dfs with weights given by Corollary 2. For the test of E vs. ACE, the χ̄² distribution is a mixture of χ²’s with zero–six dfs with weights given in Table 1.

In Figure 3, the first and second panels display the QQplots for testing the AE and CE models against the ACE model when the true model is E. The plots show that the χ̄² is stochastically much larger than the empirical distribution. The use of this χ̄² distribution would give a larger critical value and more conservative results, though it is still less conservative than using the ${\chi }_3^2$ distribution. In this case, one possible solution is to constrain the boundary nuisance parameter on the boundary and test the E model against the AE and CE models. The QQplots for these tests are displayed in the third and fourth panels and show that the χ̄² distribution is now appropriate. These results confirm our discussion in Section 2.4.

Figure 3.

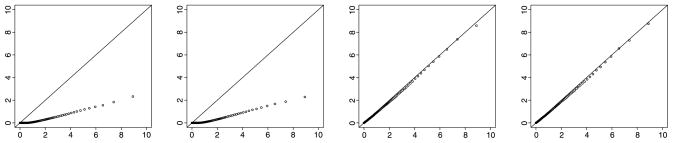
Plots of the 1st–99th percentiles of the simulated sampling distribution of T against those of the χ̄² distribution in Simulation Study 2. The true model is E. The null and alternative models are (from left to right) AE vs. ACE, CE vs. ACE, E vs. AE and E vs. CE. The sample sizes are n_MZ = n_DZ = 500 for the left two panels and n_MZ = 150 and n_DZ = 50 for the right two panels.

Another focus of the present simulation is the test of two components. The QQplots are displayed in Figure 4, which show that the χ̄² distribution with weights calculated in Table 1 fits the empirical distribution very well under all four sample size combinations. Similar to but more complex than testing a single component, these weights come from the w_ij ’s, which are proportions of (Â, Ĉ) that lie on the different types of boundary of Θ_A ×Θ_C with different ranks for the two matrices. These proportions for n_MZ = n_DZ have been tabulated in Table 2. Note weights with 1 and 2 in their subscripts need to be combined to give the proportions of  or Ĉ of rank 1, because the edges and faces of a polyhedral cone are no longer distinguishable in its limiting circular cone. For example, the proportion of the sample with both  and Ĉ of rank one corresponds to the sum w₁₁ + w₁₂ + w₂₁ + w₂₂. This is again confirmed in this simulation. Table 3 displays the observed proportions of replications for n_MZ = n_DZ = 500 that fall into different rank conditions, and the proportions are close to those given by analytical results.

Figure 4.

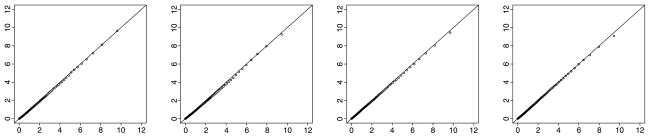
Plots of the 1st–99th percentiles of the simulated sampling distribution of T against those of the χ̄² distribution in Simulation Study 2. The sample sizes (n_MZ, n_DZ) are (from left to right) (100, 100), (150, 50), (500, 500) and (750, 250). The true and null model is E and the alternative model is ACE.

Table 3.

Ranks of  and Ĉ of the ACE model in Simulation Study 2 with n_MZ = n_DZ = 500. The total count is 10,000.

Rank Â	0			1			2
Rank Ĉ	0	1	2	0	1	2	0	1	2
Obs. proportions	12.27	27.41	1.77	28.00	26.20	1.20	1.92	1.23	0.00
Exp. probabilities	11.13	27.50	2.14	27.50	27.17	1.20	2.14	1.20	0.02

4.3. Study 3

The previous simulation study confirms the validity of weights given in Section 3.3 for complete normal data. In this study, we check the validity of the analytical results in Section 3.2 for more general situations, in which the weights are determined directly from the FIM. The FIM 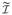is specified as follows: the two diagonal blocks 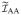and 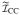are correlation matrices with equal correlations 0.7 and 0.5, respectively, and the off diagonal block 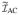is a 3×3 matrix with equal elements of 0.3. Clearly this matrix does not satisfy the structure for complete normal data as given in Appendix B. The weights are calculated as 0.1129, 0.2982, 0.3203, 0.1888, 0.0656, 0.0130 and 0.0012 for dfs from 0 to 6. The sums of weights for odd and even dfs are both 0.5000, satisfying Property 3 in Appendix A.

We now check this result against a Monte Carlo sample from χ̄² obtained by fitting a random sample of size 10,000 from N(0, 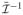) to the model N(θ, 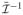) with n.n.d. constraints on θ = (a′, c′)′. This method of sampling from the asymptotic distribution follows directly from Chernoff (1954, Theorem 2). The restricted optimization was carried out in R using the nlm function. This sample is compared to a sample of size 10⁶ generated from a χ̄² distribution with weights calculated above and a QQplot is displayed in Figure 5. The QQplot shows that the χ̄² gives an accurate description of the Monte Carlo sample.

Figure 5.

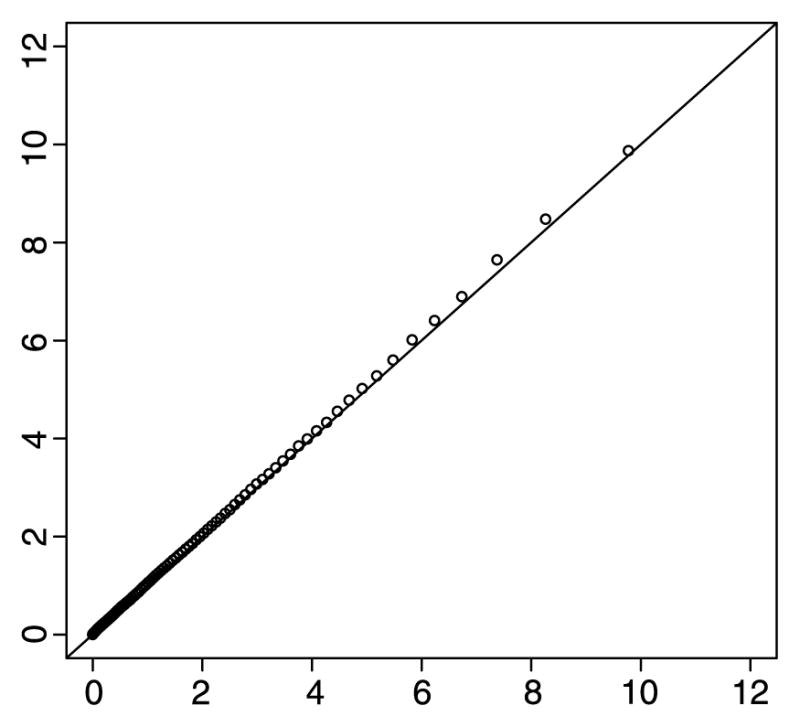
Plot of 1st–99th percentiles of the simulated sample in Simulation Study 3 against those of a χ̄² distribution based on calculated weights.

5. An Example

After confirming the analytical asymptotic distributions with three simulation studies, we apply these results to a data set from the Medical College of Virginia Twin Study (Schieken, Eaves, Hewitt, Mosteller, Bodurtha, Moskowitz, et al., 1989) to demonstrate their use. The data are skinfold measures made on 11 year-old male twins through standard anthropometric techniques. The covariance matrices of four variables, two measures obtained for biceps (BIC) and subscapular (SSC) skinfolds on the twins, are presented in Table 4 for both MZ and DZ twins. The sample sizes are 84 and 33 for the MZ and DZ twins, respectively.¹

Table 4.

The covariance matrices for skinfold measures on twins.

	MZ twin pairs (nMZ = 84)				DZ twin pairs (nDZ = 33)
	BIC1	SSC1	BIC2	SSC2	BIC1	SSC1	BIC2	SSC2
BIC1	0.1285				0.1538
SSC1	0.1270	0.1759			0.1999	0.3007
BIC2	0.0982	0.1069	0.1233		0.0435	0.0336	0.1782
SSC2	0.0999	0.1411	0.1295	0.1894	0.0646	0.0817	0.2095	0.3081

BIC = bicep; SSC = subscapular.

The sample is fitted to the full ACE, AE and E models using OpenMx (Boker et al., 2011). The estimates of the variance components are shown in Table 5. The full ACE model gives a Ĉ with very small entries, suggesting the AE model may hold in the population. The test statistic for testing the AE model against the full ACE model is T = 3.175, yielding a p-value of 0.365 under the traditional ${\chi }_3^2$ distribution of LRT. To use the χ̄² distribution proposed in this research, we have to use the estimates  and Ê under the AE model. As  is not close to singular, the procedure proposed in Section 2.2 is valid. The eigenvalues of (A+E)⁻¹A are 0.822 and 0.615 and the three eigenvalues that determine the shape of the elliptic cone are given by −1.0038, −1 and 1.0038 (which are normalized such that the sum is −1), satisfying Corollary 1. Because the three eigenvalues have similar magnitudes, the weights are close to those specified in Corollary 2. In fact, we have w₃ = 0.1466, w₂ = 0.3537, w₁ = 0.3534 and w₀ = 0.1463. The critical value for a 5 % level test is 5.486. The observed statistic is smaller than the critical value, yielding a non-significant result. However, the p-value is 0.152, much smaller than the one given by a ${\chi }_3^2$ distribution.

Table 5.

Estimates of the bivariate variance components and −2 ln L of three models when fitted to the skinfold data.

	ACE model		AE model		E model
A	0.1062		0.1172
	0.1401	0.1893	0.1359	0.1910
C	0.0116
	−0.0040	0.0014
E	0.0285		0.0283		0.1371
	0.0264	0.0441	0.0266	0.0439	0.1495	0.2165
−2 ln L	−802.5753		−799.4005		−670.9482

The test statistics for testing the E model against the AE and ACE models are both above 100, far beyond the critical values set by the ${\chi }_3^2$ and ${\chi }_6^2$ distributions. Because the naive use of LRT is more conservative, a significant result would remain significant if the correct sampling distribution were used.

6. Summary and Discussion

6.1. A Brief Summary

Testing whether a particular variance component exists is one of the main purposes of the use of the ACE or ADE models. Unfortunately the traditional LRT for such purposes has been found invalid due to the boundary condition imposed by the n.n.d. of variance components, which implies that a regularity condition of LRT is violated (Carey, 2005; Visscher, 2006). The present research resolves the issue of testing the existence of one or two variance components in bivariate ACE and ADE models by deriving the correct asymptotic sampling distribution for the test statistic T. Our analysis shows that the geometry of the boundary condition involved is more complicated than those studied by Self and Liang (1987) and those in a univariate ACE or ADE models as discussed by Dominicus et al. (2006), and that the desired distribution is a mixture of χ² distributions which can be calculated by projecting a multivariate normal distribution onto an elliptic cone (for testing a single component) or an oblique Cartesian product of two elliptic cones (for testing two components). The correct distributions are stochastically smaller than the χ² distributions assumed by traditional LRTs and are more powerful. We provide formulas and computer program for the computation of the mixture weights, and our analytical derivations are confirmed by simulation studies.

Because our analytical results are entirely based on the FIM 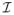of the model, it is appropriate for all practical situations in general, including the presence of missing data, ordered categorical data and covariates, as long as the central limit theorem holds. For complete normal data, several invariance properties are established in Sections 2.3 and 3.3 using the special structure of 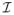. Interestingly, for a special type of missing data pattern, these invariance results are still valid. This special type is missing by person, or that variables related to one twin are always missing together. In this case, the FIM under the E model still have the desired structure (see Appendix B for the proof), so the results in Section 3.3 are still valid, though in this case n_MZ, n_DZ, α_MZ and α_DZ should be the sample sizes or percentages of complete MZ or DZ twin pairs. The invariance properties discussed in Section 2.3 are also valid.

6.2. Generalization to Higher Dimensions and Other Models

The current research tackles the bivariate ACE and ADE models only, which may be a bit disappointing as most readers would wish that such a study would resolve the LRTs for multivariate ACE or ADE models in general, once and for all. However, this is unfortunately not an easy task. The current research exploits the fact that the n.n.d. for 2 × 2 matrices is defined by a quadratic form on the three distinct elements, which is not true for higher dimensions. In higher dimensions, this restriction is represented by non-negative eigenvalues of the variance components and gives rise to more complicated geometry. Kuriki and Takemura (2000) studies this geometry and gives the weights for testing a single p×p variance component under the assumption that the non-duplicated elements in the covariance matrix have independent distributions with some specified variances, which is not the case for most practical situations.

Although an analytical expression is hard to derive for higher dimensions, Chernoff (1954, Theorem 2) does suggest a Monte Carlo strategy for simulation of the asymptotic distribution. Normally distributed vectors a can first be simulated from N(0, 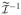), the asymptotic distribution for non-restricted estimates, and then fitted to the restricted space defined by the n.n.d. by minimizing the quadratic form (a₁ − a)′ 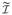(a₁ − a). The minimizer gives the desired sampling distribution. This method was employed by Silvapulle and Sen (2005, Section 3.5) for inequality constrained normal means and by Han and Chang (2010) for a genetic linkage model. It has also been used in Section 4.3 to validate the analytical results. Though expected to be computationally intensive when compared to analytical solutions, this simulation based approach is more efficient than bootstrapping, as only the parameters of interest are involved and the optimization is performed on a quadratic form. This method is also available for situations where the sampling distribution is not a mixture of χ²’s due to concavity of Θ₁ or Θ₀. Research along this line is beyond the scope of this article and will be published separately.

Though the current research concerns only the test of variance components in ACE and ADE models, its application can be more general. Mathematically, any test on three parameters θ₁, θ₂ and θ₃ with an alternative hypothesis of the shape ${\theta }_1{\theta }_3-{\theta }_2^2\ge 0({\theta }_1,{\theta }_3\ge 0)$ can be solved by the method laid out in Section 2.2. One of such problems is the test of two random effects in random coefficient models. Application to this area of study is beyond the scope of the current article.

Appendix A. Some Properties of the χ̄² Distribution

Property 1

When the approximating cone 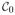of Θ₀ is a subset of the largest linear² subspace of the approximating cone 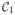of Θ₁ and both cones are convex, the statistic T has an asymptotic χ̄² distribution. See Dr. Alexander Shapiro’s website for his proof.³ For the special case of Θ₀ = 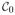= 0, we denote the weight w_k of ${\chi }_k^2$ by w_k(p, 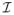(θ₀)⁻¹, 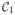), where p is the dimension of Θ₁ and 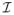(θ₀) is the FIM of the alternative model.

Property 2

If nuisance parameters ξ are present but are not on their boundary, when testing ψ = 0 against a constrained alternative ψ ∈ Ψ, the equation for the weights of the χ̄² distribution is given by w_k = w_k(q, 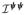, 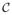), where q is the length of ψ, 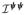is the block of 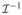that corresponds to ψ, and 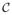is the approximating cone to Ψ in ℝ^q.

Property 3

The weights {w_k} for odd and even k sum up to 0.5, respectively (Shapiro, 1987). See Dr. Alexander Shapiro’s website for proofs he receives from correspondence.⁴

Property 4

w_k(p, 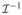, 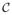) = w_p−k(p, 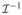, 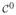), where 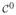is the polar cone of 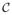, defined as the subset of ℝ^p whose projection onto 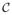is the apex of 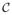, or 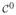= {x|x′ 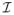y ≤ 0,∀y ∈ }.

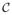For more properties of the weights of a χ̄² distribution, see Silvapulle and Sen (2005, Section 3.6).

Appendix B. The Fisher Information Matrix

We derive the FIM 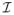(θ₀) of a p-variate ACE model with complete normal data. In general, the typical element of the FIM of a covariance structure model is given by ${(\mathcal{I})}_{\alpha \beta }=\frac{1}{2}\text{tr}\{{\mathrm{\Delta }}_{\alpha }{\mathit{\sum }}^{-1}{\mathrm{\Delta }}_{\beta }{\mathit{\sum }}^{-1}\}$, where Σ = Σ(θ) is the covariance structure and Δ_α = ∂Σ/∂θ_α. For the DZ twin group in an ACE model, ${\mathit{\sum }}_{\text{DZ}}^{-1}$ takes the shape $\left(\begin{array}{cc}{\mathit{\sum }}_1^{\text{DZ}}& {\mathit{\sum }}_2^{\text{DZ}}\\ {\mathit{\sum }}_2^{\text{DZ}}& {\mathit{\sum }}_1^{\text{DZ}}\end{array}\right)$, where all blocks are symmetric. If we define the p × p binary matrix K_ij = ∂C/∂c_ij (e.g., ${\mathbf{K}}_{12}={\mathbf{K}}_{21}=\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)$ for p = 2), we have $\partial {\mathit{\sum }}_{\text{DZ}}/\partial c_{ij}=\left(\begin{array}{cc}1& w_{\text{C}}\\ w_{\text{C}}& 1\end{array}\right)\otimes {\mathbf{K}}_{ij}$ and the derivatives w.r.t. A and E can be obtained similarly. If we further define K as the p² × p(p + 1)/2 matrix whose columns are the vecK_ij ’s (e.g., K = diag{1, 1_2×1, 1} for p = 2) and ${\mathbf{Q}}_1^{\text{DZ}}={\mathbf{K}}^{\prime }({\mathit{\sum }}_1^{\text{DZ}}\otimes {\mathit{\sum }}_1^{\text{DZ}}+{\mathit{\sum }}_2^{\text{DZ}}\otimes {\mathit{\sum }}_2^{\text{DZ}})\mathbf{K}$ and ${\mathbf{Q}}_2^{\text{DZ}}={\mathbf{K}}^{\prime }({\mathit{\sum }}_1^{\text{DZ}}\otimes {\mathit{\sum }}_2^{\text{DZ}}+{\mathit{\sum }}_2^{\text{DZ}}\otimes {\mathit{\sum }}_1^{\text{DZ}})\mathbf{K}$, the FIM for the DZ twins can be expressed as

$${\mathcal{I}}^{\text{DZ}}=\left(\begin{array}{ccc}1+w_{\text{A}}^2& 1+w_{\text{A}}{w}_{\text{C}}& 1\\ 1+w_{\text{A}}{w}_{\text{C}}& 1+w_{\text{C}}^2& 1\\ 1& 1& 1\end{array}\right)\otimes {\mathbf{Q}}_1^{\text{DZ}}+\left(\begin{array}{ccc}2w_{\text{A}}& w_{\text{A}}+w_{\text{C}}& w_{\text{A}}\\ w_{\text{A}}+w_{\text{C}}& 2w_{\text{C}}& w_{\text{C}}\\ w_{\text{A}}& w_{\text{C}}& 0\end{array}\right)\otimes {\mathbf{Q}}_2^{\text{DZ}}.$$

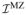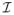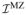The FIM for the MZ twins can be obtained similarly by altering the weights. Let α_MZ and α_DZ be sample size proportions of the two types of twin, with α_MZ + α_DZ = 1. The overall FIM (of sample size one) is given by α_MZ + α_DZ .

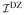A special case of interest is when ${\mathit{\sum }}_1^{\text{MZ}}=a_1\mathbf{X},{\mathit{\sum }}_2^{\text{MZ}}=a_2\mathbf{X},{\mathit{\sum }}_1^{\text{DZ}}=a_3\mathbf{X}$ and ${\mathit{\sum }}_2^{\text{DZ}}=a_4\mathbf{X}$ are scalar multiples of the same matrix X. In this case, ${\mathbf{Q}}_1^{\text{MZ}},{\mathbf{Q}}_1^{\text{DZ}},{\mathbf{Q}}_2^{\text{MZ}}$ and ${\mathbf{Q}}_2^{\text{DZ}}$ are all scalar multiples of K′(X⊗X)K, so the FIM takes the shape 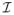= Y⊗ [K′(X⊗X)K], where Y is some 3 × 3 matrix. When A = C = 0, we have a₁ = a₃ = 1, a₂ = a₄ = 0 and X = E⁻¹, and the FIM becomes

$$\mathcal{I}=({\mathbf{1}}_{3\times 3}+{\alpha }_{\text{DZ}}{w}_{\text{DZ}}{w}_{\text{DZ}}^{\prime }+{\alpha }_{\text{MZ}}{w}_{\text{MZ}}{w}_{\text{MZ}}^{\prime }+{\alpha }_{\text{MZ}}{w}_{\text{MZ}}{w}_{\text{MZ}}^{\prime })\otimes \{{\mathbf{K}}^{\prime }{(\mathbf{E}\otimes \mathbf{E})}^{-1}\mathbf{K}\},$$ (B.1)

where 1_3×3 is a 3×3 matrix of 1’s, w_DZ = (w_A,w_C, 0)′ and w_MZ = (1, 1, 0)′.

When data are missing by person, variables related to one twin are missing or present together. The covariance matrix of variables for the singletons is Σ₀ = A+C+E for both MZ and DZ twins, and the FIM for the singletons is given by ${\mathcal{I}}^0=\frac{1}{2}({\mathbf{1}}_{3\times 3})\otimes [{\mathbf{K}}^{\prime }{({\mathit{\sum }}_0\otimes {\mathit{\sum }}_0)}^{-1}\mathbf{K}]$. The FIM for the entire data set is the weighted sum of 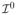and the complete data FIM given earlier. Especially, when A = C = 0, we have Σ₀ = E, and ${\mathcal{I}}^0=\frac{1}{2}({\mathbf{1}}_{3\times 3})\otimes [{\mathbf{K}}^{\prime }{(\mathbf{E}\otimes \mathbf{E})}^{-1}\mathbf{K}]$. Summing over the twin and singleton groups, we have

$$\mathcal{I}=\left\{\left(\alpha +\frac{1}{2}\beta \right){\mathbf{1}}_{3\times 3}+{\alpha }_{\text{DZ}}{w}_{\text{DZ}}{w}_{\text{DZ}}^{\prime }+{\alpha }_{\text{MZ}}{w}_{\text{MZ}}{w}_{\text{MZ}}^{\prime }\right\}\otimes \{{\mathbf{K}}^{\prime }{(\mathbf{E}\otimes \mathbf{E})}^{-1}\mathbf{K}\},$$

where α = α_DZ +α_MZ are proportions of complete twin data and β is the proportion of data with only a single twin.

Appendix C. Lemmas and Proofs

Lemma 1

Let Ω = {r|r′Qr < 1, r₁ > 0, r₂ > 0}, where $\mathbf{Q}=\left(\begin{array}{cc}{a}_1& a_3\\ a_3& a_2\end{array}\right)\ge \mathbf{0}$ and r = (r₁, r₂)′. Denote $\tau =a_3/\sqrt{a_1{a}_2}$ and t = arccos τ. We have

$$\begin{array}{l}{\int }_{\mathrm{\Omega }}{r}_1^2{r}_2^{2}d\mathit{r}=\frac{t-3\tau sint+2t{\tau }^2}{48{sin}^{5}t{(a_1{a}_2)}^{3/2}},{\int }_{\mathrm{\Omega }}{r}_1{r}_2^{2}d\mathit{r}=\frac{1}{15{(1+\tau )}^2{a}_1{a}_2^{3/2}},\\ {\int }_{\mathrm{\Omega }}{r}_2^{2}d\mathit{r}=\frac{2t-sin(2t)}{16\sqrt{a_1{a}_2^3}{sin}^{3}t},{\int }_{\mathrm{\Omega }}{r}_1{r}_{2}d\mathit{r}=\frac{sint-\mathit{t}cost}{8a_1{a}_2{sin}^{3}t}\\ \mathit{and}{\int }_{\mathrm{\Omega }}{r}_{2}d\mathit{r}=\frac{1}{3a_1^{1/2}{a}_2(1+\tau )}.\end{array}$$

Proof

One only need to prove for the case of a₁ = a₂ = 1 and a₃ = τ. This can be done through integration with the reparametrization (r₁, r₂) = R sin(t/2 ± θ)/sin t. The region Ω becomes {0 ≤ R ≤ 1, |θ| ≤ t/2} under the new coordinate system.

Lemma 2

The matrices K = diag{1, 1_2×1, 1}, $\mathbf{B}=\text{diag}\{1,\frac{1}{2}\times {\mathbf{1}}_{2\times 1},1\}$ and $\mathbf{M}={\mathbf{KB}}^{\prime }=\text{diag}\{1,\frac{1}{2}{\mathbf{1}}_{2\times 2},1\}$ satisfies

1. K′B = I, K′M= K′ and MB = B;

2. M is exchangeable with X⊗X for arbitrary X;

3. {K′(X⊗X)⁻¹K}⁻¹ = B′(X⊗X)B for arbitrary X.

Proof

See Gupta and Nagar (1999, Section 1.2) or check by simple algebra.

Proof of Proposition 1

Given the relationship between the two sets of parameters, following the calculations in Appendix B, we have ${\mathit{\sum }^{\sim }}_i^j={\mathbf{X}}^{-1}{\mathit{\sum }}_i^j{{\mathbf{X}}^{-1}}^{\prime }$ and ${\stackrel{\sim }{\mathbf{Q}}}_i^j={\mathbf{YQ}}_i^j{\mathbf{Y}}^{\prime }$ for i = 1, 2 and j = MZ,DZ, where Y = K′(X⊗X)⁻¹B with K and B defined in Lemma 2 in Appendix C. The relationship between blocks of the FIM can be further found as 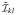= Y 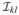Y′ for k, l = a, c, e. From Equation (1), we have 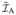= Y 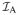Y′. For any decomposition 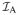= LL′, we have 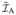= L̃L̃′, where L̃ = YL, and therefore L̃⁻¹VL̃⁻¹′= L⁻¹Y⁻¹VY⁻¹′L⁻¹′. From Lemma 2, we have Y⁻¹ = (K′(X⊗X)⁻¹B)⁻¹ = K′(X⊗X)B, and simple algebra gives Y⁻¹VY⁻¹′= |X|²V. Therefore we have L̃⁻¹VL̃⁻¹′= |X|²L⁻¹VL⁻¹′, which implies Λ̃ = |X|²Λ, so the weights in the χ̄² distribution must be the same for the two cases.

Proof of Corollary 1

The conclusion follows from Proposition 1, if we choose $\mathbf{X}={(\mathbf{C}+\mathbf{E})}^{-\frac{1}{2}}\mathbf{U}$, where U’s columns are eigenvectors of ${(\mathbf{C}+\mathbf{E})}^{-\frac{1}{2}}\mathbf{C}{(\mathbf{C}+\mathbf{E})}^{-\frac{1}{2}}$. Note now both C̃ and Ẽ are diagonal matrices. Following our calculations in Appendix B, all nine blocks of the FIM must be diagonal and therefore 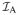and L must be diagonal. Simple algebra shows that the eigenvalues −λ₁,−λ₂ < 0 < λ₃ of L⁻¹VL⁻¹′ must satisfy λ₃ = λ₂ or λ₃ = λ₁, and the conclusion follows.

Proof of Corollary 2

From Corollary 1, the pair of true values C̃ = γI/(1 + γ) and Ẽ = I/(1 + γ) would yield the same sampling distribution. Because C̃ and Ẽ are both scalar matrices, as a special case treated in Appendix B, the FIM takes the form 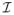= Y ⊗ [K′I_4×4K] = Y ⊗ diag{1, 2, 1} for some 3 × 3 matrix Y, and consequently 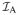= ( 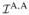)⁻¹ ∝ diag{1, 2, 1}. Simple algebra gives λ₁ = λ₂ = λ₃ and Equations (5) and (6) give $w_0=w_3=\frac{1}{2}-\frac{\sqrt{2}}{4}$.

Proof of Proposition 2

From Equation (B.1), $\stackrel{\sim }{\mathcal{I}}=\left(\begin{array}{cc}{\tau }_{\text{A}}^2& \rho {\tau }_{\text{A}}{\tau }_{\text{C}}\\ \rho {\tau }_{\text{A}}{\tau }_{\text{C}}& {\tau }_{\text{C}}^2\end{array}\right)\otimes \{{\mathbf{K}}^{\prime }{(\mathbf{E}\otimes \mathbf{E})}^{-1}\mathbf{K}\}$, where ${\tau }_{\text{A}}^2=w_{\text{A}}^2{\alpha }_{\text{DZ}}+{\alpha }_{\text{MZ}}$ and ${\tau }_{\text{C}}^2=w_{\text{C}}^2{\alpha }_{\text{DZ}}+{\alpha }_{\text{MZ}}$. Consider the decomposition E = X′X and define $\mathbf{B}=\text{diag}\{1,\frac{1}{2}\times {\mathbf{1}}_{2\times 1},1\},\mathbf{D}=\text{diag}\{1,\sqrt{2},1\}$, L = K′(X ⊗ X)⁻¹BD and $\mathbf{M}={\mathbf{BD}}^2{\mathbf{B}}^{\prime }=\text{diag}\{1,\frac{1}{2}{\mathbf{1}}_{2\times 2},1\}$. Using Lemma 2, we have the relationship LL′= K′(X ⊗ X)⁻¹M(X′ ⊗ X′)⁻¹K = K′(E ⊗ E)⁻¹K. We then consider the transformation $(\overline{\mathit{a}},\overline{\mathit{c}})=({\tau }_{\text{A}}^{-1}{\mathbf{L}}^{\prime }\mathit{a},{\tau }_{\text{C}}^{-1}{\mathbf{L}}^{\prime }\mathit{c})$. Under the new parametrization, $\overline{\mathcal{I}}=\left(\begin{array}{cc}1& \rho \\ \rho & 1\end{array}\right)\otimes \mathbf{I}$ and the quadratic forms defining the cones become ā′V̄ā ≥ 0 and c̄′V̄c̄ ≥ 0 with V̄ = L⁻¹VL⁻¹′. Again, remember L⁻¹ = D⁻¹K′(X ⊗ X)B (Lemma 2) and simple algebra gives $\overline{\mathbf{V}}=\frac{1}{2}{\mid \mathbf{X}\mid }^2\left[\begin{array}{ccc}0& 0& 1\\ 0& 1& 0\\ 1& 0& 0\end{array}\right]$, so its three eigenvalues must be of the same size. This implies that both Θ_A and Θ_C are circular cones with the height equal to the base radius, and the weights are entirely determined by ρ in .

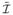Appendix D. Calculation of Weights for Testing Two Components

We derive the weights w_ij using the notations and coordinate systems defined in Section 3.1. Under the elliptic coordinate system, the FIM becomes G = J′ 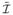J, which is no longer a constant. The unit ball in ℝ⁶ is given by $\mathcal{B}=\{{\overline{\mathit{\theta }}}^{\prime }\overline{\mathcal{I}}\overline{\mathit{\theta }}\le 1\}=\{{\alpha }_1{r}_a^2+{\alpha }_2{r}_c^2+2{\alpha }_3{r}_a{r}_c\le 1\}$, where the α’s are given in Equation (10).

The polar cone of Θ₁ was defined in Section 3.1. As a brief proof, we note the inner product between (r_a,ψ_a,φ_a, r_c,ψ_c,φ_c) ∈ Θ₁ and $(r_a^{\ast },{\psi }_a^{\ast },{\phi }_a^{\ast },r_c^{\ast },{\psi }_c^{\ast },{\phi }_c^{\ast })\in {\mathrm{\Theta }}_1^0$ is given by

$$\begin{array}{l}{\overline{\mathit{\theta }}}^{\prime }{\overline{\mathit{\theta }}}^{\ast }=r_a^{\ast }{r}_a\{cos{\phi }_{a}cos{\phi }_a^{\ast }cos({\psi }_a^{\ast }-{\psi }_a)-sin{\phi }_{a}sin{\phi }_a^{\ast }\}\\ +r_c^{\ast }{r}_c\{cos{\phi }_{c}cos{\phi }_c^{\ast }cos({\psi }_c^{\ast }-{\psi }_c)-sin{\phi }_{c}sin{\phi }_c^{\ast }\}\\ \le r_a^{\ast }{r}_a\{cos{\phi }_{a}cos{\phi }_a^{\ast }-sin{\phi }_{a}sin{\phi }_a^{\ast }\}+r_c^{\ast }{r}_c\{cos{\phi }_{c}cos{\phi }_c^{\ast }-sin{\phi }_{c}sin{\phi }_c^{\ast }\}\\ =r_a^{\ast }{r}_{a}cos({\phi }_a+{\phi }_a^{\ast })+r_c^{\ast }{r}_{c}cos({\phi }_c+{\phi }_c^{\ast })\le 0\end{array}$$

because $\pi /4\le {\phi }_a,{\phi }_a^{\ast },{\phi }_c,{\phi }_c^{\ast }\le \pi /2$. The unit ball in ℝ⁶ is given by $\mathcal{B}=\{{\overline{\mathit{\theta }}}^{\ast \prime }{\overline{\mathcal{I}}}^{-1}{\overline{\mathit{\theta }}}^{\ast }\le 1\}=\{{\alpha }_1^{\ast }{r}_a^{\ast 2}+{\alpha }_2^{\ast }{r}_c^{\ast 2}+2{\alpha }_3^{\ast }{r}_a^{\ast }{r}_c^{\ast }\le 1\}$ in this new coordinate system.

Below we calculate the 10 weights by discretizing the cones. The elliptic cone Θ_A is discretized by S equally spaced angles ψ_s between 0 and 2π, with s = 0, 1, …, S and ψ₀ = 0 and ψ_S = 2π. They corresponds to generatrices ${\mathit{g}}_s={(\sqrt{{\kappa }_1^{\text{A}}}cos{\psi }_s,\sqrt{{\kappa }_2^{\text{A}}}sin{\psi }_s,\sqrt{{\kappa }_3^{\text{A}}})}^{\prime }$, which discretizes the circular cone into a polyhedral cone with S faces. Θ_C is similarly discretized with subscripts r = 0, 1, …, R. The weights will first be calculated using the polyhedral cones and then limits are taken to obtain weights w_ij for the original problem.

D.1. The Derivation of w₃₃ and w₀₀

The region of ℝ⁶ that corresponds to w₃₃ is simply Θ₁ = Θ_A ×Θ_C. Its volume V_|| inside 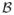can be calculated by integrating ${\mid \mathbf{G}\mid }^{\frac{1}{2}}=\mid {\mathbf{J}}_{\text{A}}\mid \mid {\mathbf{J}}_{\text{C}}\mid {\mid \overline{\mathcal{I}}\mid }^{\frac{1}{2}}={\mid {\mathit{\Lambda }}_{\text{C}}{\mathit{\Lambda }}_{\text{A}}\mid }^{-\frac{1}{2}}{\mid {\mathcal{I}}_{\text{A}}^{\ast }\mid }^{\frac{1}{2}}{r}_a^2{r}_c^{2}cos{\phi }_{a}cos{\phi }_c$ over .

$$\begin{array}{l}{V}_{\Vert }={\int }_{{\psi }_a=0}^{2\pi }{\int }_{{\psi }_c=0}^{2\pi }{\int }_{{\phi }_a=\frac{\pi }{4}}^{\frac{\pi }{2}}{\int }_{{\phi }_c=\frac{\pi }{4}}^{\frac{\pi }{2}}\int {\int }_{\mathcal{B}}{\mid \mathbf{G}\mid }^{\frac{1}{2}}{dr}_a{dr}_{c}d{\phi }_{c}d{\phi }_{a}d{\psi }_{c}d{\psi }_a\\ =\frac{{\mid {\mathcal{I}}_{\text{A}}^{\ast }\mid }^{\frac{1}{2}}}{{\mid {\mathit{\Lambda }}_{\text{C}}{\mathit{\Lambda }}_{\text{A}}\mid }^{\frac{1}{2}}}{\int }_{{\psi }_a=0}^{2\pi }{\int }_{{\psi }_c=0}^{2\pi }{\int }_{{\phi }_a=\frac{\pi }{4}}^{\frac{\pi }{2}}{\int }_{{\phi }_c=\frac{\pi }{4}}^{\frac{\pi }{2}}\frac{cos{\phi }_{a}cos{\phi }_c(2t{\tau }^2-3\tau sint+t)}{48{sin}^{5}t{({\alpha }_1{\alpha }_2)}^{3/2}}d{\phi }_{c}d{\phi }_{a}d{\psi }_{c}d{\psi }_a\end{array}$$

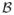where the double integral over (r_a, r_c) has been simplified using Lemma 1. The weight w₃₃ is given by w₃₃ = V_||/V₆ where V₆ = π³/6 is the volume of a 6-dimensional ball. w₀₀ is the proportion of the ball 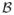that falls into the polar cone. It can be similarly calculated by integrating over ${\mid {\mathbf{G}}^{\ast }\mid }^{\frac{1}{2}}=\mid {\mathbf{J}}_{\text{A}}^{\ast }\mid \mid {\mathbf{J}}_{\text{C}}^{\ast }\mid {\mid \overline{\mathcal{I}}\mid }^{-\frac{1}{2}}={\mid {\mathit{\Lambda }}_{\text{C}}{\mathit{\Lambda }}_{\text{A}}\mid }^{\frac{1}{2}}{\mid {\mathcal{I}}_{\text{A}}^{\ast }\mid }^{-\frac{1}{2}}{r}_a^{\ast 2}{r}_c^{\ast 2}cos{\phi }_a^{\ast }cos{\phi }_c^{\ast }$.

D.2. The Derivation of w₂₃ and w₁₀

The region of ℝ⁶ that corresponds to w₂₃, after projected onto Θ₁, lies on a face of the discretized Θ_A and the interior of Θ_C. Consider the face of Θ_A, 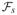, lying between generatrices ${\mathit{g}}_{s\pm \frac{1}{2}}$. The normal vector to 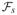× Θ_C is given by ${\psi }_a^{\ast }={\psi }_s,{\phi }_a^{\ast }=\pi /4,r_c^{\ast }=0$. For each s, the proportion of the unit ball 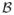that falls into this region can be calculated as the product of two proportions: (1) p_⊥ (s) = 1/2, because the normal vector determines a unidimensional subspace and half of it has the same direction of the normal vector; (2) p_|| (s), the proportion of the 5-dimensional subspace spanned by 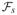×Θ_C inside 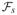×Θ_C.

To calculate p_||(s), we note that ${ℱ}_s\times {\mathrm{\Theta }}_{\text{C}}=\{{\psi }_{s-\frac{1}{2}}<{\psi }_a<{\psi }_{s+\frac{1}{2}},{\phi }_a=\pi /4,\pi /4<{\phi }_c<\pi /2\}$, so its volume inside is given by

$$\begin{array}{l}{V}_{\Vert }(s)={\int }_{{\psi }_a={\psi }_{s-\frac{1}{2}}}^{{\psi }_{s+\frac{1}{2}}}{\int }_{{\psi }_c=0}^{2\pi }{\int }_{{\phi }_c=\pi /4}^{\pi /2}\int {\int }_{\mathcal{B}}{({\mid \stackrel{\sim }{\mathbf{G}}\mid }^{\frac{1}{2}})}_{{\phi }_a=\pi /4}{dr}_a{dr}_{c}d{\phi }_{c}d{\psi }_{c}d{\psi }_a\\ =\frac{2}{15{\mid {\mathit{\Lambda }}_{\text{C}}\mid }^{\frac{1}{2}}}{\int }_{{\psi }_a={\psi }_{s-\frac{1}{2}}}^{{\psi }_{s+\frac{1}{2}}}{\int }_{{\psi }_c=0}^{2\pi }{\int }_{{\phi }_c=\pi /4}^{\pi /2}{\left(\frac{cos{\phi }_c{\mid {\stackrel{\sim }{\mathbf{J}}}_{\text{A}}^{\prime }{\mathcal{I}}_{\text{A}}^{\ast }{\stackrel{\sim }{\mathbf{J}}}_{\text{A}}\mid }^{\frac{1}{2}}}{{(1+\tau )}^2{\alpha }_1{\alpha }_2^{3/2}}\right)}_{{\phi }_a=\pi /4}d{\phi }_{c}d{\psi }_{c}d{\psi }_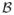a\end{array}$$

where G̃ is the 5×5 block of G corresponding to the first, second, fourth, fifth and sixth columns and rows and we have ${\mid \stackrel{\sim }{\mathbf{G}}\mid }^{\frac{1}{2}}=\mid {\mathbf{J}}_{\text{C}}\mid r_a{\mid \left(\begin{array}{cc}{\stackrel{\sim }{\mathbf{J}}}_{\text{A}}^{\prime }& {\mathbf{0}}_{2\times 3}\\ {\mathbf{0}}_{3\times 3}& {\mathbf{I}}_{3\times 3}\end{array}\right)\overline{\mathcal{I}}\left(\begin{array}{cc}{\stackrel{\sim }{\mathbf{J}}}_{\text{A}}& {\mathbf{0}}_{3\times 3}\\ {\mathbf{0}}_{3\times 2}& {\mathbf{I}}_{3\times 3}\end{array}\right)\mid }^{\frac{1}{2}}=r_a{r}_c^{2}cos{\phi }_c{\mid {\mathit{\Lambda }}_{\text{C}}\mid }^{-\frac{1}{2}}{\mid {\stackrel{\sim }{\mathbf{J}}}_{\text{A}}^{\prime }{\mathcal{I}}_{\text{A}}^{\ast }{\stackrel{\sim }{\mathbf{J}}}_{\text{A}}\mid }^{\frac{1}{2}}$. Note the double integral over 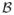has been simplified using Lemma 1. We have $w_{23}=lim{\sum }_s{p}_{\perp }(s)p_{\Vert }(s)=\frac{1}{2}lim{\sum }_s{V}_{\Vert }(s)/V_5$, where $V_5=\frac{8}{15}{\pi }^2$ is the volume of a 5-dimensional unit ball. The weight w₁₀ can be obtained by the duality between Θ₁ and ${\mathrm{\Theta }}_1^0$ as given in Property 4 in Appendix A.

D.3. The Derivation of w₁₃ and w₂₀

The projection of the region of ℝ⁶ that corresponds to w₁₃ onto Θ₁ lies on a 4-face g_s ×Θ_C for some s. This 4-face of Θ₁ is sandwiched by the two 5-faces ${ℱ}_{s\pm \frac{1}{2}}\times {\mathrm{\Theta }}_{\text{C}}$, whose normal vectors determine a plane orthogonal to this 4-face. The proportion of ℝ⁶ that project onto this 4-face is the product of (1) p_⊥ (s), the proportion of the aforementioned plane sandwiched between the two normal vectors of the two adjacent 5-faces, and (2) p_||(s), the proportion of the 4-dimensional space spanned by g_s × Θ_C that lies inside it.

To calculate p_⊥ (s), we note the space between the two normal vectors of ${ℱ}_{s\pm \frac{1}{2}}\times {\mathrm{\Theta }}_{\text{C}}$ can be represented by { ${\psi }_{s-\frac{1}{2}}\le {\psi }_a^{\ast }\le {\psi }_{s+\frac{1}{2}},{\phi }_a^{\ast }=\pi /4,r_c^{\ast }=0$} , so its area inside is given by

$$\begin{array}{l}{V}_{\perp }(s)={\int }_{{\psi }_a^{\ast }={\psi }_{s-\frac{1}{2}}}^{{\psi }_{s+\frac{1}{2}}}{\int }_{{\alpha }_1^{\ast }{r}_a^{\ast 2}<1}{r}_a^{\ast }{({\mid {\stackrel{\sim }{\mathbf{J}}}_{\text{A}}^{\ast \prime }{\mathcal{I}}_{\text{A}}^{\ast -1}{\stackrel{\sim }{\mathbf{J}}}_{\text{A}}^{\ast }\mid }^{\frac{1}{2}})}_{{\phi }_a^{\ast }=\pi /4}d{r}_a^{\ast }d{\psi }_a^{\ast }\\ ={\int }_{{\psi }_a^{\ast }={\psi }_{s-\frac{1}{2}}}^{{\psi }_{s+\frac{1}{2}}}{\left(\frac{{\mid {\stackrel{\sim }{\mathbf{J}}}_{\text{A}}^{\ast \prime }{\mathcal{I}}_{\text{A}}^{\ast -1}{\stackrel{\sim }{\mathbf{J}}}_{\text{A}}^{\ast }\mid }^{\frac{1}{2}}}{2{\alpha }_1^{\ast }}\right)}_{{\phi }_a^{\ast }=\pi /4}d{\psi }_a^{\as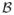t }\end{array}$$

and p_⊥ (s) = V_⊥ (s)/V₂, where V₂ = π is the area of the unit disk.

For p_||(s), we note g_s × Θ_C = {ψ_a = ψ_s,φ_a = π/4,π/4 < φ_c < π/2}. The volume of its part inside is given by

$$\begin{array}{l}{V}_{\Vert }(s)={\int }_{{\psi }_c=0}^{2\pi }{\int }_{{\phi }_c=\pi /4}^{\pi /2}\int {\int }_{\mathcal{B}}{({\mid \stackrel{\sim }{\mathbf{G}}\mid }^{\frac{1}{2}})}_{\begin{array}{c}{\phi }_a=\pi /4\\ {\psi }_a={\psi }_s\end{array}}{dr}_a{dr}_{c}d{\phi }_{c}d{\psi }_c\\ ={\left(\frac{{\mathit{r}}_a^{\prime }{\mathcal{I}}_{\text{A}}^{\ast }{\mathit{r}}_a}{\mid {\mathit{\Lambda }}_{\text{C}}\mid }\right)}_{\begin{array}{c}{\phi }_a=\pi /4\\ {\psi }_a={\psi }_s\end{array}}^{\frac{1}{2}}{\int }_{{\psi }_c=0}^{2\pi }{\int }_{{\phi }_c=\pi /4}^{\pi /2}{\left(\frac{cos{\phi }_c(2t-sin(2t))}{16\sqrt{{\alpha }_1{\alpha }_2^3}{sin}^{3}t}\right)}_{\begin{array}{c}{\phi }_a=\pi /4\\ {\psi }_a={\psi }_s\end{array}}d{\phi }_{c}d{\psi }_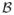c\end{array}$$

where G̃ is the 4 × 4 block of G corresponding to its first, fourth, fifth and sixth columns and rows with ${\mid \stackrel{\sim }{\mathbf{G}}\mid }^{\frac{1}{2}}=\mid {\mathbf{J}}_{\text{C}}\mid r_a{\mid \left(\begin{array}{cc}{\mathit{r}}_a^{\prime }& {\mathbf{0}}_{1\times 3}\\ {\mathbf{0}}_{3\times 3}& {\mathbf{I}}_{3\times 3}\end{array}\right)\overline{\mathcal{I}}\left(\begin{array}{cc}{\mathit{r}}_a& {\mathbf{0}}_{3\times 3}\\ {\mathbf{0}}_{3\times 1}& {\mathbf{I}}_{3\times 3}\end{array}\right)\mid }^{\frac{1}{2}}=r_a{r}_c^{2}cos{\phi }_c{\mid {\mathit{\Lambda }}_{\text{C}}\mid }^{-\frac{1}{2}}{({\mathit{r}}_a^{\prime }{\mathcal{I}}_{\text{A}}^{\ast }{\mathit{r}}_a)}^{\frac{1}{2}}$. Again, the double integral w.r.t. (r_a, r_c) was simplified with Lemma 1. The weight w₁₃ is given by w₁₃ = limΣ_s V_⊥ (s)V_||(s)/V₂V₄, where $V_4=\frac{1}{2}{\pi }^2$ is the volume of a 4-dimensional unit ball. The weight w₂₀ can be obtained from the duality between ${\mathrm{\Theta }}_1^0$ and Θ₁.

D.4. The Derivation of w₀₃

The projection of the region that corresponds to w₀₃ lies on the 3-face 0 × Θ_C, which is adjacent to 5-dimensional surface ∂Θ_A × Θ_C of Θ₁. The collection of normal vectors of this surface is the elliptic cone { ${\phi }_a^{\ast }=\pi /4,r_c^{\ast }=0$}. Let p_⊥ be the proportion of the 3-dimensional space spanned by this elliptic cone that falls inside this cone and p_|| be the proportion of the 3-dimensional space spanned by the 3-face 0 × Θ_C that falls inside 0 × Θ_C. We have

$$p_{\perp }=\frac{1}{2}-\frac{1}{\pi }{\int }_0^{\pi /2}\varsigma \left({\left({\overline{\mathcal{I}}}_{\text{A}}^{\ast }{\mathit{\Lambda }}_a\right)}^{-1},{\psi }_a\right)d{\psi }_a\text{and}{p}_{\Vert }=\frac{1}{2}-\frac{1}{\pi }{\int }_0^{\pi /2}\varsigma ({\mathit{\Lambda }}_c,{\psi }_c)d{\psi }_c$$

where function ς is defined in Section 2.2. The weight w₀₃ is given by w₀₃ = p_⊥p_||.

D.5. The Derivation of w₂₂ and w₁₁

Both Θ_A and Θ_C need to be discretized to calculate w₂₂. The projection of the region of ℝ⁶ that corresponds to w₂₂ lies on the 4-face ${ℱ}_s^{\text{A}}\times {ℱ}_r^{\text{C}}$ for some r and s, where ${ℱ}_s^{\text{A}}$ is a face of the discretized Θ_A between edges ${\mathit{g}}_{s\pm \frac{1}{2}}^{\text{A}}$, and ${ℱ}_r^{\text{C}}$ is similarly defined. This 4-face is adjacent to 5-faces ${ℱ}_s^{\text{A}}\times {\mathrm{\Theta }}_{\text{C}}$ and ${\mathrm{\Theta }}_{\text{A}}\times {ℱ}_r^{\text{C}}$, whose normal vectors are given by { ${\psi }_a^{\ast }={\psi }_s,{\phi }_a^{\ast }=\pi /4,r_c^{\ast }=0$} and { ${\psi }_c^{\ast }={\psi }_r,{\phi }_c^{\ast }=\pi /4,r_a^{\ast }=0$}, respectively. The proportion of the 2-dimensional subspace between these two normal vectors is given by $p_{\perp }(s,r)={(t^{\ast }/2\pi )}_{{\psi }_c^{\ast }={\psi }_r,{\psi }_a^{\ast }={\psi }_s}$.

The 4-face ${ℱ}_s^{\text{A}}\times {ℱ}_r^{\text{C}}$ can be expressed as { ${\psi }_{s-\frac{1}{2}}<{\psi }_a<{\psi }_{s+\frac{1}{2}},{\phi }_a=\pi /4,{\psi }_{r-\frac{1}{2}}<{\psi }_c<{\psi }_{r+\frac{1}{2}},{\phi }_c=\pi /4$}. To calculate its volume inside 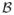, we note the metric tensor G̃ is now given by the first, second, fourth and fifth rows and columns of G, and $\mid \stackrel{\sim }{\mathbf{G}}\mid =r_a^2{r}_c^2\mid {\stackrel{\sim }{\mathbf{J}}}^{\prime }\overline{\mathcal{I}}\stackrel{\sim }{\mathbf{J}}\mid$, where J̃ = diag{J̃_A, J̃_C} is a 6×4 matrix. We have

$$\begin{array}{l}{V}_{\Vert }(s,r)={\int }_{{\psi }_a={\psi }_{s-\frac{1}{2}}}^{{\psi }_{s+\frac{1}{2}}}{\int }_{{\psi }_c={\psi }_{r-\frac{1}{2}}}^{{\psi }_{r+\frac{1}{2}}}\int {\int }_{\mathcal{B}}{({\mid \stackrel{\sim }{\mathbf{G}}\mid }^{\frac{1}{2}})}_{{\phi }_a={\phi }_c=\pi /4}{dr}_a{dr}_{c}d{\phi }_{c}d{\psi }_{c}d{\psi }_a\\ ={\int }_{{\psi }_a={\psi }_{s-\frac{1}{2}}}^{{\psi }_{s+\frac{1}{2}}}{\int }_{{\psi }_c={\psi }_{r-\frac{1}{2}}}^{{\psi }_{r+\frac{1}{2}}}{\left(\frac{sint-\mathit{t}cost}{8{\alpha }_1{\alpha }_2{sin}^{3}t}{\mid {\stackrel{\sim }{\mathbf{J}}}^{\prime }\overline{\mathcal{I}}\stackrel{\sim }{\mathbf{J}}\mid }^{\frac{1}{2}}\right)}_{{\phi }_a={\phi }_c=\pi /4}d{\psi }_{c}d{\psi }_a\end{array}$$

where the double integral w.r.t. (r_a, r_c) has been solved by Lemma 1. This 4-face takes a proportion of p_||(s, r) = V_||(s, r)/V₄ out of the 4-dimensional space it spans. Combining the above two proportions, we have w₂₂ = limΣ_sΣ_r p_⊥ (s, r)p_||(s, r). The weight w₁₁ can be obtained similarly.

D.6. The Derivation of w₁₂

The projection of the region of ℝ⁶ that corresponds to w₁₂ lies on the 3-face ${\mathit{g}}_s^{\text{A}}\times {ℱ}_r^{\text{C}}=\{{\psi }_{r-\frac{1}{2}}<{\psi }_c<{\psi }_{r+\frac{1}{2}},{\phi }_a={\phi }_c=\pi /4,{\psi }_a={\psi }_s\}$ for some r and s. Its volume inside is given by

$$\begin{array}{l}{V}_{\Vert }(r,s)={\int }_{{\psi }_c={\psi }_{r-\frac{1}{2}}}^{{\psi }_{r+\frac{1}{2}}}\int {\int }_{\mathcal{B}}{({\mid \stackrel{\sim }{\mathbf{G}}\mid }^{\frac{1}{2}})}_{\begin{array}{c}{\psi }_a={\psi }_s\\ {\phi }_a={\phi }_c=\pi /4\end{array}}{dr}_a{dr}_{c}d{\psi }_c\\ ={\int }_{{\psi }_c={\psi }_{r-\frac{1}{2}}}^{{\psi }_{r+\frac{1}{2}}}{\left(\frac{{\mid {\stackrel{\sim }{\mathbf{J}}}^{\prime }\overline{\mathcal{I}}\stackrel{\sim }{\mathbf{J}}\mid }^{\frac{1}{2}}}{3{\alpha }_1^{\frac{1}{2}}{\alpha }_2(1+\tau )}\right)}_{\begin{array}{c}{\psi }_a={\psi }_s\\ {\phi }_a={\phi }_c=\pi /4\end{array}}d{\psi }_c\end{array}$$

where G̃ is given by the first, fourth and fifth columns and rows of G and $\mid \stackrel{\sim }{\mathbf{G}}\mid =r_c^2\mid {\stackrel{\sim }{\mathbf{J}}}^{\prime }\overline{\mathcal{I}}\stackrel{\sim }{\mathbf{J}}\mid$ with J̃ = diag{r_a, J̃_C}.

The part of ℝ⁶ whose projection lies on ${\mathit{g}}_s^{\text{A}}\times {ℱ}_r^{\text{C}}$ is sandwiched between ${\mathit{g}}_s^{\text{A}}\times {ℱ}_r^{\text{C}}$ and { ${\psi }_{s-\frac{1}{2}}<{\psi }_a^{\ast }<{\psi }_{s+\frac{1}{2}},{\phi }_a^{\ast }={\phi }_c^{\ast }=\pi /4,{\psi }_c^{\ast }={\psi }_r$}. The latter is a part of the 3-dimensional subspace orthogonal to ${\mathit{g}}_s^{\text{A}}\times {ℱ}_r^{\text{C}}$. Similar to the derivation of V_||(r, s), we can obtain the volume of this part of the normal space inside as

$$V_{\perp }(r,s)={\int }_{{\psi }_a^{\ast }={\psi }_{s-\frac{1}{2}}}^{{\psi }_{s+\frac{1}{2}}}{\left(\frac{{\mid {{\stackrel{\sim }{\mathbf{J}}}^{\ast }}^{\prime }{\overline{\mathcal{I}}}^{-1}{\stackrel{\sim }{\mathbf{J}}}^{\ast }\mid }^{\frac{1}{2}}}{3{\alpha }_2^{\ast \frac{1}{2}}{\alpha }_1^{\ast }(1+{\tau }^{\ast })}\right)}_{\begin{array}{c}{\psi }_c^{\ast }={\psi }_r\\ {\phi }_a^{\ast }={\phi }_c^{\ast }=\pi /4\end{array}}d{\psi }_a^{\ast }$$

where ${\stackrel{\sim }{\mathbf{J}}}^{\ast }=\text{diag}\{{\stackrel{\sim }{\mathbf{J}}}_{\text{A}}^{\ast },{\mathit{r}}_c^{\ast }\}$. The weight w₁₂ is given by $w_{12}=lim{\sum }_s{\sum }_r{V}_{\perp }(r,s)V_{\Vert }(r,s)/V_3^2$, where V₃ = 4π/3 is the volume of a 3-dimensional unit ball.