Varying Degrees of Nonlinear Mechanical Behavior Arising From Geometric Differences of Urogynecological Meshes

Abstract

Synthetic polypropylene meshes were designed to restore pelvic organ support for women suffering from pelvic organ prolapse; however, the FDA released two notifications regarding the potential complications associated with mesh implantation. Our aim was to characterize the structural properties of Restorelle and UltraPro subjected to uniaxial tension along perpendicular directions, and then model the tensile behavior of these meshes utilizing a co-rotational finite element model, with an imbedded linear or fiber-recruitment local stress-strain relationship. Both meshes exhibited highly nonlinear stress-strain behavior; Restorelle had no significant differences between the two perpendicular directions, while UltraPro had a 93% difference in the low (initial) stiffness (p=0.009) between loading directions. Our model predicted that early alignment of the mesh segments in the loading direction and subsequent stretching could explain the observed nonlinear tensile behavior. However, a nonlinear stress-strain response in the stretching regime, that may be inherent to the mesh segment, was required to better capture experimental results. Utilizing a nonlinear fiber recruitment model with two parameters A and B, we observed improved agreement between the simulations and the experimental results. An inverse analysis found A=120 MPa and B=1.75 for Restorelle (RMSE=0.36). This approach yielded A=30 MPa and B=3.5 for UltraPro along one direction (RMSE=0.652), while the perpendicular orientation resulted in A=130 MPa and B=4.75 (RMSE=4.36). From the uniaxial protocol, Restorelle was found to have little variance in structural properties along these two perpendicular directions; however, UltraPro was found to behave anisotropically.

Introduction

In the field of urogynecology, synthetic polypropylene meshes saw a dramatic increase in use over the last decade. It had been estimated that these devices were implanted in over 200,000 women annually when their use peaked. They are designed to restore pelvic organ support for women suffering from pelvic organ prolapse (Olsen et al., 1997). Because they are essentially modified abdominal hernia meshes, their use in the field of Urogynecology has undergone little oversight. Evidence had suggested that the number of patients experiencing post-surgical morbidity had been grossly underreported, which lead to the Food and Drug Administration to release two Public Health Notifications about the potential complications associated with urogynecological mesh implantation (FDA Public Health Notification, 2009 & 2011). These complications often include scarring, pain, mesh exposure and dyspareunia and can greatly reduce the quality of life for women (Chen et al., 2007; Fenner, 2000). Recent data from our laboratory suggest that the mechanics of the mesh plays a significant role in dictating the host response following implantation (Feola et al., 2013; Liang et al., 2013). However, other than some fundamental mechanical testing experiments, little has been done to more rigorously analyze the mechanical response of these meshes.

The latest generations of meshes are all made of polypropylene; yet, their knit patterns, quantity of material, and geometry can yield a wide array of mechanical behavior. A study by Saberski et al. found that several polypropylene meshes were anisotropic in response to uniaxial tensile testing protocols in perpendicular directions, while others were not (Saberski et al., 2011). Since the material used to create different mesh product is the same (polypropylene), it is the different textile properties that gives rise to the large variations in mechanical behavior observed in previous studies (Feola et al., 2013; Shepherd et al., 2012). Understanding the relationship between mesh textile properties and its mechanical behavior is critical to improve mesh design.

The textile field has a deep history of utilizing constitutive and finite element modeling techniques to understand the mechanics of various products (Kaiser, 2008; Yeoman et al., 2010). However, the application of these approaches to the field of Urogynecology and the commonly used synthetic meshes utilized in prolapse repair is relatively new. In this study, we propose to employ a co-rotational finite element technique that allows for large rotations and displacements, but small material strains to model mesh mechanical behavior (Battini and Pacoste, 2002; Crisfield, 1997). A constitutive law can then be described independently as a linear or nonlinear function using this method. This approach may be better suited for prolapse meshes that are macroporous and undergo large-scale segment rotations and realignment in response to uniaxial extension (Shepherd et al., 2012).

We hypothesized that much of the difference in mechanical behavior between two different mesh designs could be attributed to the overall geometry of the mesh. Thus, we aimed to characterize the ex vivo structural properties of a bidirectionally isotropic mesh [Restorelle™ (marketed as Minimesh™ by Mpathy Inc.) and an anisotropic mesh [UltraPro™ (marketed as Prolift +M™ by Gynecare Inc.)] subjected to uniaxial tension along two perpendicular directions. Next, we utilized the co-rotational finite element model to determine if their differences in structural behavior can be solely attributed to the different geometries of these meshes. We first employed a linear stress-strain law for the mesh fibers to evaluate the contribution of segment rotation and alignment towards the nonlinear structural response of the mesh. Use of an inverse approach to fit the model to experimental data allowed the contribution of geometry to the mechanical nonlinearity to be assessed. A nonlinear fiber recruitment constitutive model was used to simulate the mesh structural response. We found that this model was necessary for better agreement of model predictions and experimental observations, pointing to the inherent nonlinearity of the mesh segments due to the presence of knits and crimps. We finally utilized our model to study the origin of direction-dependence of the mesh structural response, and found that it may depend on the architecture of the mesh.

Methods

Uniaxial Testing

Manufacturers provided sterile sheets of the Restorelle and UltraPro for uniaxial tensile testing. The methods for tensile testing have previously been described (Jones et al., 2009; Shepherd et al., 2012). Mesh samples were attached to a custom set of clamps to form a clamp-mesh-clamp construct. Clamp to clamp distances were measured. To ensure that samples were tested consistently, an aspect ratio (width to height ratio) of five was maintained for all samples. To determine the ex vivo structural properties of each mesh, samples of clinically relevant size (75×15 mm) of Restorelle (n=5) and UltraPro (n=4) were tested in response to uniaxial extension along orientation 1 (O1) and orientation 2 (O2) as shown in Figure 1. Orientation 1 indicates the direction implanted along the longitudinal axis of the vagina during placement for an abdominal sacral colpopexy procedure.

Figure 1.

Macroscopic images of Restorelle (left) and UltraPro (right) meshes illustrating orientation 1 (O1 or warp) and orientation 2 (O2 or weft).

After each mesh sample was cut and placed within the custom designed clamps, the constructs were placed into a 37°C saline bath fixed to the base of the Instron™ testing machine (Instron⁵⁵⁶⁵, Norwood, MA) screw driven testing apparatus (Shepherd et al., 2012). Samples were allowed 15-20 minutes to equilibrate prior to testing. Samples were preload (0.1N) at a rate of 10 mm/min, and the final clamp-to-clamp distance was recorded as the reference length. Next, each mesh was loaded to failure at a rate of 50 mm/min.

The load-displacement curves yielded a nonlinear response that can be approximated as bilinear, which is commonly seen with prolapse meshes (Shepherd et al., 2012). The failure load (N) and corresponding relative elongation (%), defined as the elongation divided by the reference length, were recorded. The slope in the toe region of the curve was defined as the low stiffness (N/mm), while the slope in the linear region of the curve we define as the high stiffness (N/mm). These values were determined by assuming the response is bi-linear and fitting lines to each region. The inflection point was defined as the intercept of these two lines.

Finite Element Modeling

Prior to the simulation, the geometry of each mesh was approximated using a custom made Matlab script (MathWorks Version 7.11, 2010). In short, two populations of fibers, with a similar diameter, were assumed for each of these meshes to create a computer representation of the mesh based on the actual micrographs.

All generated mesh renderings were standardized to the average size of each mesh tested experimentally (75 × 15 mm). The number of finite element nodes along each mesh segment was set to 10, as changes in the simulated load-elongation response after increasing the node number to 20 was negligible. Individual segments between each node were modeled as Timoshenko beam elements, which account for first-order shear deformation. Constitutive relationships, both linear and nonlinear, were prescribed to these beam elements. In addition to implementing a unique local stress-strain relationship, this co-rotational and finite element approach accounts for the fiber geometry and nodal interaction. Interaction between mesh segments can affect the degree to which overlapping nodes, or joints, can transfer bending moments generated during rotation of the mesh. Since these meshes are not rigidly locked at the overlapping knits, it is important that simulations consider the interaction of these joints. Therefore, we implemented a ‘hinge’ parameter that can range from 0, or no moment transferred, to 1, indicating the entire moment is transferred. Although it is unclear how much of the moment is transferred between nodes, it is known that these are not rigid interactions. Subsequently, this parameter was set to 0.5 to allow 50% of the moment forces to be transferred at the joints.

Lastly, the cross-sectional area of each segment was estimated based on the width and number of individual fibers within each of the mesh strands. Reexamining Figure 1, it is evident that each strand of the Restorelle and UltraPro meshes consist of multiple fibers of polypropylene. A single representative fiber diameter was calculated from these multiple fibers. In short, the number and diameter of the individual fibers was determined and the cumulative area those fibers was utilized as the representative area. The areas for Restorelle and UltraPro were calculated to be 0.11 mm and 0.19 mm, respectively.

For the first simulation, the local stress-strain relationship was assumed to be linear according to:

$$\sigma =E\ast \varepsilon$$ (1)

Here, E represents the elastic modulus relating the stress and strain. Using this model, any degree of nonlinearity or anisotropy described by the model in terms of the force-displacement relationship would be strictly a function of mesh geometry. In the second set of simulations, the local stress-strain relationship was assumed to be nonlinear and described by a two-parameter exponential model:

$$\sigma =A\ast [e^{B\ast \varepsilon }-1]$$ (2)

This adds a mechanism for nonlinearity as a result of local segment deformation. Here A, in MPa, is a scaling factor and B governs the nonlinearity of the curve. As earlier mentioned, each strand of these polypropylene meshes consists of multiple fibers, and this phenomenological fiber-recruitment model describes the mechanical behavior resulting from twisting/braiding of these individual mesh fibers. As the mesh is elongated, these fibers progressively become taut, and additional fibers are recruited to resist the load. Elastic modulus (E) and parameters (A & B) for each simulation were determined by optimizing the simulated load-elongation responses to match the average curves from the uniaxial tension protocol via an inverse finite element modeling approach. For simulations, we used a custom designed and compiled finite element software. The software is based on a rigorous validated framework and yields unique results for forward modeling and simulation. The software has been extensively validated on different biomechanical systems (Henderson et al., 2014 and Pal et al., 2014). The boundary conditions of the mesh were designed to mimic clamping of the mesh at either end. While the long edge of the mesh was left free of constraints, all nodes of the mesh along the simulated clamped edge were rigidly constrained. The opposite simulated clamped edge was constrained along the 2 orthogonal directions, and the remaining axis was used to subject the mesh to a prescribed elongation: Restorelle, assumed to be a bidirectionally isotropic mesh, was displaced along an axis (O1=O2) for 52 mm, while UltraPro was simulated to extensions of 73 mm and 41 mm for O1 and O2, respectively.

Statistics

For the uniaxial protocol, sample sizes were based on data from a previous study of synthetic prolapse meshes (Shepherd et al., 2012). Structural properties determined from the uniaxial protocol were found to be normally distributed and are presented as mean ± standard deviation. A Student's t-test was utilized to compare Restorelle and UltraPro structural properties between orientation 1 and orientation 2 for each mesh. A significance level of 0.05 was set for all structural properties. A lack of statistical differences between orientation 1 and 2 led to the assumption of a bidirectionally isotropic material for finite element simulations (O1=O2). For the finite element predictions, we desired to have accurate predictions compared to our experimental data defined by root mean squared error (RMSE < 10) and the normalized root mean squared error (NRMSE < 10%).

Results

From the uniaxial load to failure protocol, we found that the directional dependence on the structural properties varied between Restorelle and UltraPro. Figure 2 illustrates the average load-relative elongation curves of the Restorelle and UltraPro meshes loaded to failure along two perpendicular directions: orientation 1 and orientation 2. This figure also illustrates the similar structural properties of Restorelle found between orientation 1 and orientation 2 (Table 1) with only a 3.4% difference found between the failure loads (p=0.44), a 5.7% difference in the low stiffness (p=0.37) values, and a 2.6% difference in the high stiffness (p=0.49) values (O1 vs. O2). This demonstrates that Restorelle behaves similar to a bidirectionally isotropic material, O1=O2, when loaded to failure along orientation 1 and orientation 2. However, when examining the structural properties of the UltraPro mesh we found significant differences between orientation 1 and orientation 2 (Table 1). For the UltraPro mesh, orientation 1 failed at a considerably lower load with an 88% difference in the failure load (p<0.001). Orientation 1 was significantly less stiff compared to orientation 2 with a 93% difference in the low stiffness values (p=0.009) and a 91% difference in the high stiffness values (p<0.001). These results indicate that UltraPro is indeed an anisotropic mesh, which has significantly different structural properties depending on the loading direction.

Figure 2.

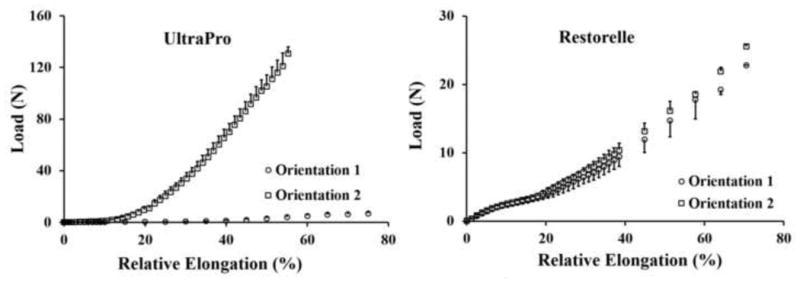
The average load versus relative elongation of Restorelle (left) and UltraPro (right) illustrating the response along orientation 1 and orientation 2. The error bars represent the standard deviation.

Table 1.

The structural properties of Restorelle (n=5) and UltraPro (n=4) subjected to a uniaxial tensile testing protocol. Mesh samples were loaded to failure along two perpendicular directions orientation 1 (O1) and orientation 2 (O2), and compared utilizing a Student's t-test (p-value<0.05). O1 represents the direction prolapse meshes are typically implanted.

Mesh	Failure Load (N)	Relative Elongation (%)	Low Stiffness (N/mm)	High Stiffness (N/mm)	Inflection Point (%)
Restorelle Orientation 1	22.7 ± 2.82	68.4 ± 6.34	0.177 ± 0.033	0.582 ± 0.082	29.1 ± 2.1
Restorelle Orientation 2	24.3 ± 3.32	68.4 ± 7.12	0.198 ± 0.038	0.613 ± 0.051	28.8 ± 2.2
P-value	0.44	0.99	0.37	0.49	0.80
UltraPro Orientation 1	7.83 ± 0.69	87.9 ± 5.62	0.009 ± 0.002	0.236 ± 0.019	46.5 ± 5.2
UltraPro Orientation 2	122.3 ± 13.8	54.4 ± 3.27	0.258 ± 0.085	4.75 ± 0.295	22.6 ± 1.86
P-value	<0.001	<0.001	0.009	<0.001	<0.001

Based the bidirectional isotropy of Restorelle, only loading along orientation 1 was simulated in the finite element simulations. On the other hand, loading along orientation 1 and orientation 2 was simulated for UltraPro in separate simulations. A linear stress-strain relationship was utilized on the local segment level for the initial simulations. Using inverse optimization to fit the experimental data, a modulus (E) value of 200 MPa was determined for Restorelle. The initial portion of the load-displacement curve matches the experiments well, suggesting the linear constitutive law (Equation 1) is appropriate in this region as segment rotation and realignment to the loading direction is dominating the mechanical behavior. However, the overall quality of fit resulted in a RMSE of 4.92 and a NRMSE of 21.1%, largely due to the slight degree of nonlinear behavior being observed experimentally at higher mesh elongations, which was not being captured by the assumption of linear segment stress-strain behavior (Figure 3).

Figure 3.

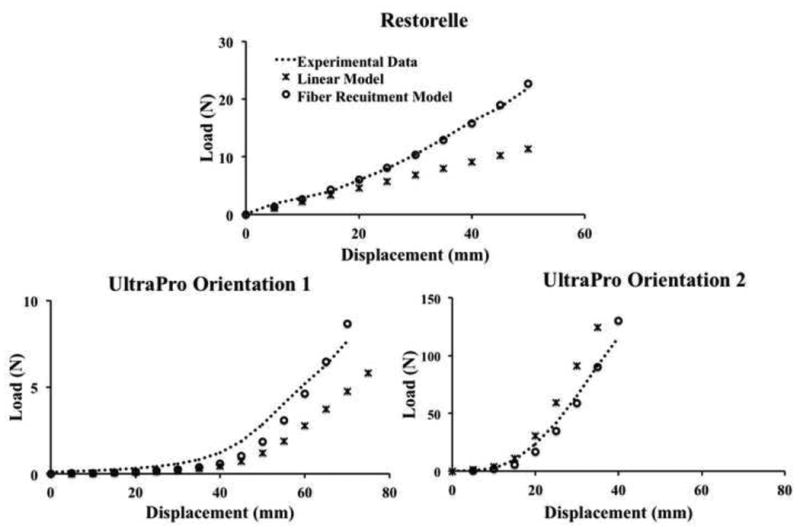
Load-displacement curves of the average experimental data (dashed line) for Restorelle and UltraPro along orientation 1 and 2 compared to their respective simulated data for the linear stress-strain relationship (*) and fiber-recruitment model (o)

For UltraPro, the inverse analysis provided a segment modulus value of 90 MPa along orientation 1 and the linear segment constitutive assumption was able to capture a large degree of the nonlinearity of the mesh (RMSE=1.27 and NRMSE=16.5%), suggesting that changes in the geometry may account for much of its nonlinear structural behavior. While the simulated data behaves similar to the experimental results (Figure 3), the model could not fully account for the nonlinearity following the inflection point (∼40 mm). Interestingly, the inverse analysis along the perpendicular direction (orientation 2) resulted in a segment modulus value that was an order of magnitude higher (E=1,500 MPa) compared to orientation 1. While the simulated curve initially described the experimental data very well (Figure 3), after ∼ 20 mm the simulated and experimental curves again begin to deviate from each other with the simulated data now overshooting the nonlinearity observed experimentally. Nevertheless, it resulted in a RMSE=9.74 and NRMSE=8.1%.

Our initial approach did not have the accuracy expected, as the NRMSE for both Restorelle and UltraPro simulated along orientation 1 were greater than 10%. In addition, although UltraPro simulated along orientation 2 had a RMSE<10 and NRMSE<10%, it was borderline on both calculations. Thus, the use of a non-linear two-parameter fiber recruitment model for the segment constitutive description was employed and demonstrated improved agreement between the simulations and the experimental results. For Restorelle, an A of 120 MPa and a B of 1.75 provided the best representation of the experimental data (RMSE=0.36 and NRMSE=1.5%). The inverse analysis of the UltraPro mesh along orientation 1 yielded improved RMSE to 0.652 and the NRMSE to 8.5% with an A=30 MPa and B=3.5. The perpendicular orientation resulted in an A of 130 MPa and B of 4.75. Simulations of the UltraPro mesh along orientation 2 utilizing the fiber recruitment model lowered the RMSE to 4.36 and a NRMSE 4.7%. These findings suggest that there may be additional aspects to the knit pattern that are directionally dependent and not captured using this modeling approach. However, the major contributors to the mechanical behavior of these meshes are being described by this approach.

A distinct advantage of utilizing a finite element approach is that from these simulations, we can simulate a visually deformed mesh at increments of deformation and observe the orientation of the segments. In Figure 4, 5 and 6, we illustrate the simulated deformation of Restorelle, UltraPro along orientation 1, and UltraPro tensioned along orientation 2. Each simulated graft was captured and plotted at 0%, 50% and 100% of the total deformation. For Restorelle, the mesh simply elongates with no rotation of strands due to the initial square geometry of the mesh (Figure 4). This resulted in a linear load-elongation curve when assuming a linear stress-strain relationship on the local level. The lack of rotation in the finite element simulation in response to uniaxial tension translates to an elongation of the mesh network with minimal change in the predicted width. The observed nonlinear behavior in the experimental force response, therefore, clearly shows that there exists some inherent nonlinearity in the strands of fibers.

Figure 4.

Graphical representation of mesh deformation simulated from the finite element model of Restorelle (left) relative to an experimental elongation of the mesh (right) from 0 to 100% of the maximal elongation of each mesh prior to failure. Note that the experimental images where taken just prior to 100% of the maximal elongation.

Figure 5.

Simulations of mesh deformation of UltraPro along orientation 1 (left) compared to experimental loading of the mesh at various stages of elongation (right). Each mesh undergoes a large degree of fiber rotation in response to elongation from 0% to 50% and from 50% to 100% of the elongation prior to failure. Note that the experimental images where taken just prior to 100% of the maximal elongation.

Figure 6.

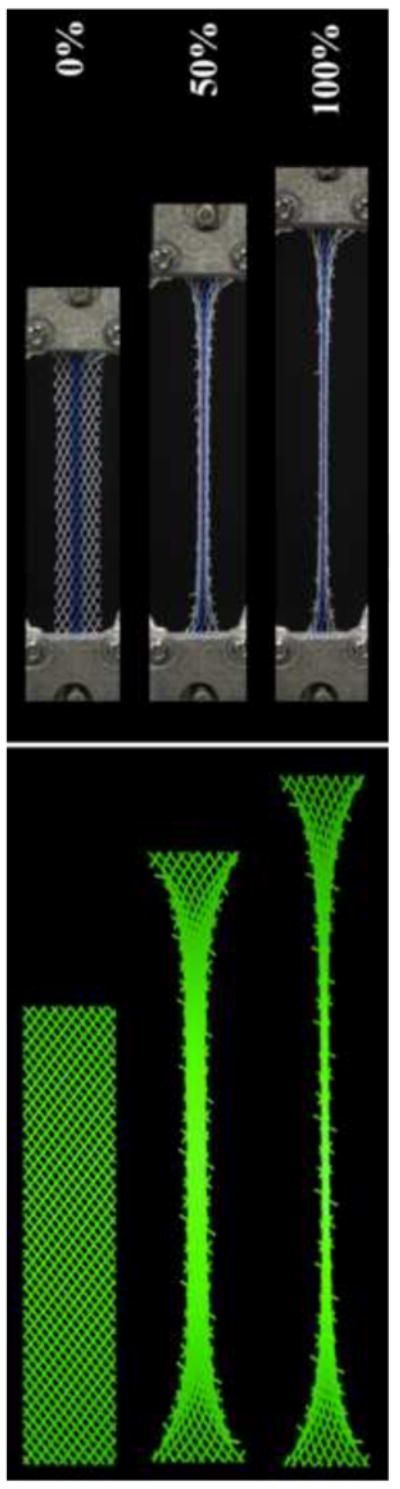
Simulations of mesh deformation of UltraPro along orientation 2 (left) and experimental loading of the mesh (right). Similar to UltraPro along orientation 1 there is a large degree of fiber rotation as the mesh is elongated.

Examining UltraPro subjected to uniaxial loading in perpendicular directions (Figure 5 and 6), it can be seen that the mesh architecture changes greatly while the mesh is being loaded. Further, at 50% relative elongation, the UltraPro samples along orientation 2 are predicted to have a more horizontally contracted and vertically aligned appearance as compared to both Restorelle and UltraPro when loaded along orientation 1. Therefore, the polypropylene fibers of UltraPro may be quicker to engage and resist deformation along orientation 2, which may partially explain why the load-elongation response is so different along each orientation.

Discussion

In this study, we utilized a combined experimental and computational modeling approach to assess the degree to which mesh geometry could account for differences in mechanical behavior between two urogynecological meshes, Restorelle and UltraPro. Experimentally, we found that the mechanical behavior of Restorelle was not significantly different between orientation 1 and orientation 2. These results suggest that Restorelle may be considered as bidirectionally isotropic material only when specifically examined along the two mutually orthogonal directions examined in this study. UltraPro, on the other hand, was found to display mechanical behavior that was vastly different depending on the loading direction. These results are similar to those previously reported (Saberski et al., 2011; Ozog et al., 2011), and confirm that it is important to consider the biomechanical properties of these grafts prior to implantation. Based on a co-rotational inverse finite element modeling approach, it was found that there is a significant degree of material nonlinearity inherent to each segment, but also that changes in mesh geometry could account for a large degree of structural nonlinearity and anisotropy observed experimentally for the UltraPro mesh.

Previous work has been invested to develop FE models of synthetic meshed used in hernia repair (Yeoman et al., 2010; Hernandez-Gascon et al., 2011). Yeoman et al., (2010) proposed a nonlinear anisostropic strain energy functional that can capture response of a variety of knit fabrics. Hernandez-Gascon et al., (2011) introduced a strain energy function that can reproduce the anisotropic response of the knitted fabric. All of these models, however, are often complex and offer limited insight into what dictates the structural properties of these meshes. The approach in this study is particularly advantageous because it incorporates the mesh geometry, fiber interaction, and moments created by mesh realignment. Significantly, our model revealed deformed shapes of the mesh during the loading process. Qualitatively comparing our simulations to experimental findings, we saw similar changes in the macrostructure of the mesh. For UltraPro, the large-scale rotations of the segments observed for our simulations matched well with those observed experimentally. Our simulations captured that the degree of rotation is direction-dependent, which may partially explain the origin of anisotropy for these meshes. For Restorelle, the overall geometry from our simulations again matched reasonably well with those obtained experimentally. However, our simulations show that rotation of a mesh segment should not occur when the mesh is loaded along the directions modeled in this study. However, there were minor rotations and thinning within the middle of the mesh that could be observed in response to experimental loading. These differences could originate for several reasons. When performing the experiments there is always a risk of cutting artifact during preparation and alignment issues. However, the consistency of this response from experiment to experiment points to this arising more from the unique knit pattern of this mesh, which this current study did not attempt to capture. This is supported by a closer inspection of Figure 1 showing a sidedness (left to right and top to bottom) of the knit entering and exiting a “knot” joining the fibers along orientation 1 and 2.

The inherent constitutive nonlinearity of the segments may be attributed to the twisting/braiding of individual fibers of polypropylene, which creates a recruitment effect. This is further supported by the fact that this nonlinearity appeared to be most significant at larger elongations at which most of the rotational rearrangement of the mesh had already taken place, and the segments are primarily being stretched axially. In addition, previous work has shown that single strands of a polypropylene display an initially linear stress-strain behavior (Shuttleworth et al., 1999), and experimental work within our own laboratory has confirmed these results (data not shown). Therefore, the nonlinearity appearing in the uniaxial tensile behavior seems to primarily result from multiple fibers being recruited and the rotation of the strands within each mesh. Our model captures the toe region of the experimental curves well and suggests that the unaccounted anisotropy may also be due to directionally-dependent difference in the segments (i.e. degree of twisting in the fibers) or a preferential rotation direction caused by the knitting (“knots”) joining the two populations of parallel segments that comes into play at larger elongations.

Since it has been shown that the mechanical behavior of these prolapse meshes likely contributes to the host response after implantation, simulations provide us with insight into the important parameters that govern the mechanical behavior of these meshes. Previous research from our laboratory compared these two meshes to an even stiffer mesh after implantation in the non-human primate (Feola et al., 2013). In that study Restorelle and UltraPro helped preserve the passive biomechanical properties of the underlying and integrated tissue compared to the stiffer Gynemesh PS mesh. However, the active response (smooth muscle contractility) was negatively impacted by both Gynemesh PS and Restorelle. In the current study, we have shown that a large portion of the non-linear response of these polypropylene meshes in response to uniaxial tension is related to the mesh geometry. These findings combine to suggest that the knit pattern and pore geometry greatly impacts the mechanics of the mesh and, in turn, may be critical in terms of the host response. Thus, studies that more directly relate mesh geometry and mechanical behavior to the host response are important for the design of future polypropylene meshes,

This present study represents the initial work towards the development of a finite element model for the more detailed characterization of synthetic meshes, specifically of polypropylene meshes used in prolapse repair. This model illustrated that the geometry of Restorelle and UltraPro meshes accounts for much of their nonlinearity and anisotropic behavior. Further, we have illustrated that recruitment plays an important role, especially at larger elongations. In general, the degree of connectivity, or overlapping fibers, the location of local stress and strain increases, and the overall mesh fiber orientation or realignment due to loading can be examined through this approach. An accurate modeling program would be advantageous in addressing complicated questions including how fiber interactions affect the stiffness of the mesh. Further, it can help relate the textile properties to the structural properties of these meshes in response to different loading conditions, which would be a substantial step in the field. This will likely require a multi-scale model whereby each fiber within each strand is modeled to provide a higher degree of accuracy. Such an approach could include the degree of anisotropy, orientation, connectivity, multiple fiber diameters, and can be extended to 3D to capture out-of-plane deformations of these material. This may be advantageous to better describe the mechanical behavior of other meshes with more complicated knit patterns. Farther down the line, this combination may allow us to direct the manufacturing design of the next generation of meshes by describing, in full, which textile properties are essential to obtain the ideal mesh structural properties.