Summary
Partial area under the ROC curve (PAUC) has been proposed for gene selection in Pepe et al. (2003) and thereafter applied in real data analysis. It was noticed from empirical studies that this measure has several key weaknesses, such as an inability to reflect nonuniform weighting of different decision thresholds, resulting in large numbers of ties. We propose the weighted area under the ROC curve (WAUC) in this paper to address the problems associated with PAUC. Our proposed measure enjoys a greater flexibility to describe the discrimination accuracy of genes. Nonparametric and parametric estimation methods are introduced, including PAUC as a special case, along with theoretical properties of the estimators. We also provide a simple variance formula, yielding a novel variance estimator for nonparametric estimation of PAUC, which has proven challenging in previous work. The proposed methods permit sensitivity analyses, whereby the impact of differing weight functions on gene rankings may be assessed and results may be synthesized across weights. Simulations and re-analysis of two well-known microarray datasets illustrate the practical utility of WAUC.
Keywords: Gene selection, Empirical distribution, Location-scale model, Partial area under the curve, Random threshold, Weighted area under the curve
1. Introduction
Receiver Operating Characteristic (ROC) curve is an important statistical tool for evaluating the accuracy of continuous diagnostic tests, such as biomarkers for cancer, serum cholesterol, temperature and blood pressure (Walter (2005) and Pepe (2003)). The area under the ROC curve (AUC) is a popular summary measure of accuracy for the test. However, the AUC may be too global a summary measure, and may not reflect the region of the curve which is of the greatest interest. In some cases, it may be of interest to assess tests across different ranges, corresponding to different hypothetical operating scenarios for the test. For a particular clinical application, a decision threshold may be chosen so that the diagnostic test will have either satisfactory specificity (eg, > 90%) or sensitivity. In these circumstances, the average accuracy of the test over the specified range of specificities is a more meaningful summary measure than the area under the entire ROC curve. For such settings, partial area under the ROC curve (PAUC) has been studied as an appropriate summary measure of the diagnostic test’s accuracy. A related measure is PAUC index (Zhou et al. (2002)) which equals PAUC divided by the length of the specified interval of specificity. Normalized in this way, PAUC index has a probabilistic interpretation similar to AUC.
AUC and PAUC have recently been applied to the biological field for selecting differentially expressed genes from microarray experiments. In fact, using the two-sample Mann-Whitney-Wilcoxon rank sum statistic (which is equivalent to AUC) to compare the diagnostic performance of different genes has been widely accepted in clinical practice (eg., Joober et al. (1999) and de Alava et al. (2000), among others). Pepe et al. (2003) proposed to use PAUC to rank genes when the comparison of discrimination accuracy must be conditional on having acceptable specificity levels. For a recent application of selecting genes based on PAUC, see Chatterjee et al. (2006).
There are three weaknesses linked with PAUC (or PAUC index) which drive us to develop more general measures in this paper. Firstly, considering a range of high specificity values such as (0.9, 1) may yield very low sensitivities over the range of interest and hence very low PAUC for a large percentage of genes. In such scenarios, ranking genes based on PAUC will be noninformative. Thus, ordering genes based on PAUC may not adequately reflect the importance of these genes for differentiating two classes. Secondly, the PAUC only focuses on a truncated region of the ROC curve and thus completely ignores the performance of the gene outside the specified interval. It might be more natural to still keep some ROC information from the entire [0,1] interval, but with relatively less weights. Thirdly, as witnessed in our real data analysis, it could happen that many genes achieve the same PAUC value due to the discreteness of nonparametric estimates. We find that in the well-known lymphoma data (Ship et al. (2002)) more than 400 genes achieve the perfect PAUC value (PAUC index equals one) over the specificity range (0.9, 1). It is thus difficult to assess the relative importance of genes under such a measure.
Both AUC and PAUC (or more appropriately, PAUC index) can be regarded as an integration of the ROC curve with uniform weights over (0, 1) and its subinterval. In this paper we consider flexible weight functions for AUC. The specification of such general weight functions can be helpful if one conceptualizes the decision threshold in a particular application as being random across patients, with the weight in the weighted AUC (WAUC) corresponding to the probability distribution of the threshold. With a proper choice of weight function, WAUC overcomes the three potential problems of PAUC and still achieves the desired interpretation as the weighted average of sensitivity in the relevant range of specificity. Such an approach allows us to place more emphasis over the important range of specificity values by using a density function peaked over this range as the weight function. Provided the density is positive over (0, 1), the resulting WAUC still keeps, to some degree, information of the overall ROC curve.
From a practical perspective, this generalization is nontrivial, as it permits one to assess the sensitivity of gene rankings to the choice of weight function. Here, different weights correspond to different beliefs regarding the relative importance of different portions of the ROC curve. For some choice of weights, the rankings may be noninformative, while for others, distinctive patterns may emerge, as discussed above. Synthesizing results from different weights gives a more complete picture of the clinical utility of the diagnostic information in the gene expression levels. This is discussed in Section 2.4.
The idea of weighting the AUC has precedent in Wieand et al. (1989) to streamline the theoretical properties of nonparametric estimation of AUC and PAUC. However, not much practical attention has been placed on the development of appropriate statistical procedures about general weighted AUC measures. Bandos et al. (2005) used a specific weighting system when estimating AUC to incorporate the clinical importance (utility) when evaluating the accuracy of a diagnostic test. Their method is a special case of our development with weight function depending on observed test results. We provide a general framework on how to conduct a diagnostic accuracy study with WAUC and supply necessary asymptotic results as a basis for statistical inference.
This paper has the following contributions. (i) A framework for ROC analysis incorporating the specificity distribution is constructed. This allows more flexible evaluation of diagnostic accuracy when the practical emphasis varies across the range of specificity. (ii) Variance formula for the nonparametric WAUC estimator is explicitly derived (see (10) in Section 2.2). Since PAUC is one special case of WAUC, the formula immediately facilitates the calculation of standard error for nonparametric PAUC estimator without using bootstrap resampling or other ad hoc procedures, as in previous work. (iii) A simple analytic form for WAUC is provided for parametric location-scale model (see (13) in Section 2.3). Such a result exhibits a reasonable generalization of currently widely-used computation method for binormal AUC. (iv) The proposed methodology for weighted analysis is illustrated with simulated and real data sets in Section 3. Specifically, two well-known microarray data sets have been re-analyzed in Section 3.2. Our numerical results have confirmed the theoretical and practical advantages in WAUC over AUC and PAUC.
2. Methods
2.1. Definition of Weighted Area Under the ROC Curve
Denote the observed continuous diagnostic test results as
for nD disease-present subjects and nD̄ disease-absent subjects. Assume that {TDi, i = 1, · · ·, nD} are identically distributed with population survivor function SD(c) = se(c) = P(TDi ≥ c). Similarly {TD̄j, j = 1, · · ·, nD̄} are such that SD̄(c) = 1 − sp(c) = P (TD̄j ≥ c). The ROC curve, expressed as a function of specificity (Pepe, 2003), is as follows:
We propose the weighted area under the ROC curve (WAUC) which is defined by
This measure can be reduced to some familiar measures for special choices of f(sp). When f(sp) = 1 for sp ∈ [0, 1], WAUC is simply the ordinary AUC. When , WAUC is the partial AUC index restricted in [a, b].
If we take f to be the probability density function of sp, then the weighting of ROC curve may be interpreted as the corresponding threshold c following a certain probability distribution. When we intend to highlight a portion of specificity values with larger weights in the computation of ROC curve, we essentially adjust probability of the random threshold accordingly. In fact, sp ~ f(sp) if and only if c ~ f(SD̄(c))sD̄ (c), where sD̄ is the derivative of SD̄. Therefore the stochastic appearance of sp in this paper can be understood as a consequence of the consideration of such an underlying random threshold.
In general, WAUC may be interpreted as the weighted average of sensitivity with weights emphasizing specificity of interest. When f is a probability density function, the WAUC corresponds to the expected sensitivity under the assumed specificity distribution, with a WAUC value > .5 indicating that in the long run the test classifies diseased patient more often right than wrong under f. However, one should realize that the minimum acceptable WAUC is generally different from .5 if the weight function is not symmetrical around .5. A useless diagnostic test whose distributions for diseased and non-diseased population are the same has se = 1 − sp and the WAUC value which is
Such a null value is 1 − (a+ b)/2 for f being uniform on [a, b]. Standard AUC has W0 = 0.5 while PAUC index on the interval [a, 1] has W0 = (1 − a)/2. A test can only be considered useful if its WAUC exceeds W0.
2.2. Nonparametric inference
The survivor functions for TD and TD̄ can be estimated empirically as
| (1) |
| (2) |
Using the above notation, the estimated ROC curve is
| (3) |
The WAUC for a weight function f is estimated by
| (4) |
We now consider the statistical properties of this estimator. It has been shown in Hsieh and Turnbull (1996) that
| (5) |
under the following technical conditions:
SD(c) and SD̄ (C) have continuous derivatives;
the slope of ROC(sp) is bounded on any subinterval (a, b) of (0, 1);
(6)
The distributional conditions (a) and (b) are easily satisfied for most practical test data. Condition (c) requires that one class is not dominating in the whole sample. It is then straightforward to show that estimator (4) is strongly consistent to the WAUC if we notice
| (7) |
and apply the dominated convergence theorem (Durrett (2005)) on the right hand side.
Furthermore, following the results in Hsieh and Turnbull (1996), we have
| (8) |
where
| (9) |
The derivation of the variance is contained in Appendix.
In practice, the variance estimator can be computed by replacing ROC(sp) in the above formula with its estimator. As we see in the following expression, integration of the empirical ROC curve reduces to finite summations. The estimator is thus
| (10) |
where the function is the integral of the weight function. Since PAUC is a special case related to WAUC, this general variance formula also provides a feasible solution for computing the variance of nonparametric estimator of PAUC (Dodd and Pepe (2003)). To our knowledge this handy analytic formula has never appeared in diagnostic medicine literature. Most practitioners usually relied on a time-consuming bootstrap procedure to evaluate the variability of PAUC. We strongly recommend researchers to implement this simple formula in their simulation studies and data analysis for PAUC.
2.3. Parametric inference
It is often convenient and appealing to postulate a parametric form for SD(c) and SD̄(c) and conduct ROC analysis based on such parametric distributions. Typically a normal distribution is considered for both SD(c) and SD̄(c), possibly after some given transformation of the original test results TD,i and TD̄,j. The resulting parametric ROC curve is termed as a binormal curve (Zhou et al. (2002)).
In this paper we assume {TD} and {TD̄} both come from a location-scale family {Q(μ,σ) : μ ∈ ℝ, σ > 0}, with different location parameter μ and scale parameter σ. The distribution function of a member in this family satisfies
for a known distribution function Q(·).
Assume that TD ~ Q(μD,σD) and TD̄ ~ Q(μD̄,σD̄). Under the assumed distributions, the parametric ROC curve can be represented as
| (11) |
where
| (12) |
Under the assumed parametric model (11), the weighted AUC is derived to be
| (13) |
where the expectation is taken with respect to Z which follows the Q distribution.
A Monte Carlo approach can be implemented to evaluate (13) numerically: simulate a large number of zm (m = 1, · · ·, M) from Q and compute . When M is large enough, this finite summation gives a close approximation of (13).
Formula (13) may be applied with general Q and weight functions for parameterized ROC curve. Under some specifications, this general formula may become familiar quantities that have been widely used in practice. The following is a special result for the unweighted AUC. When F is the identity function (f being uniform on [0,1] and consequently WAUC being AUC) and Q is a symmetric distribution such as the standard normal distribution or the standard logistic distribution, the expression (13) reduces to
| (14) |
after simple algebra. A special case of (14) has been reported frequently in diagnostic accuracy studies where the binormal assumption for ROC curve has been assumed.
The proofs of (11) and (13) are contained in the Appendix. A proof of (14) for Q being standard normal is contained in Pepe (2003); the general proof is similar and is omitted.
If consistent parameter estimates â and b̂ are available, we can estimate WAUC consistently by
| (15) |
For binormal model, maximum-likelihood methods (Zhou et al. (2002)) are widely used. In fact, if the normal assumption is correct, the mean and variance parameters in the diseased and healthy population can be estimated with their sample versions and plugged into (12).
Furthermore, suppose (â, b̂) are asymptotically normal. This leads to the asymptotic normal distribution of with mean WAUC and variance
| (16) |
where we assume the density q(z) of Q(z) exists. To implement this formula in an MLE procedure, the asymptotic variances var(â), var(b̂) and covariance cov(â, b̂) can be estimated consistently from the observed inverse information matrix (Hessian matrix of the log-likelihood function).
2.4. Choice of weight function
The WAUC offers a sensible measure of diagnostic performance when a clinically relevant range of specificity has been specified. The relative importance of the specificity values is characterized by the weight function in the computation of WAUC. Instead of assigning non-informative equal weights to all possible values in (0, 1), a general weight function can be any probability density or weight function defined within this range. Depending on the focus of study, we can choose right-skewed, symmetric or left-skewed distributions.
The class of Beta density function (Gupta and Nadarajah (2004)) provides abundant choices for the weight function. The Beta(α, β) density is given by
for α > 0, β > 0 and 0 ≤ x ≤ 1 where the boundary values at x = 0 or x = 1 are defined by continuity (as limits). The relative importance can be adjusted by modifying the parameter values (α, β) in the density function.
When assessing his or her knowledge about the specificity weight (or equivalently, the distribution of the random threshold in the population), one naturally tends to anchor on the uniform distribution and begin to establish departures from uniformity (Tversky and Kahneman (1981)). We notice that the uniform distribution on (0, 1) is a special case of the Beta density when α = β = 1. We therefore propose the following weight elicitation procedure, following a similar idea in Chaloner and Duncan (1983):
-
Step 1
Choose the distribution mode which is the most likely value of specificity in the weighting scheme.
-
Step 2
Choose the distribution variance which describes the relative likelihood of mode to adjacent values. When only vague information is available for the spread pattern, one chooses the value close to that of the uniform distribution.
-
Step 3
Choose a sensible Beta density that satisfies the two conditions the most.
The mode elicitation method in Step 1 has intuitive appeal to data analysts and excludes certain Beta densities with no modes for sp ∈ (0, 1). The first two steps effectively mimic the human cognitive processing and creat a distribution that can reflect one’s view of the relative importance of specificity values. We note that the mode and variance of the Beta density are given by (α − 1)/(α + β − 2) and αβ/[(α + β + 1)(α + β)2], respectively. Given desired values of the mode and variance at Steps 1 and 2, we may solve a system of two equations to find the two parameters α and β exactly. Finally for the sake of interpretability we usually have to adjust the solved values to sensible parameters to strike a balance between mathematical precision and practical utility.
In this paper, we prefer the mode of the weight to be near large values of the specificity, say 85% or 90%. This suggests that α has to be much greater than β and both parameters must be above one. As for the variance, we would imagine the overall distribution displays a comparable variation relative to the non-informative uniform distribution which is the standard weight for the ordinary AUC. This requirement implies that α and β may not be too extreme. We note that if these two parameters are too large, the variance would be very small and the distribution would be indistinguishable from a degnerate point mass at the mode. This kind of weight simply gives the sensitivity of the test at a particular specificity and may be too restrictive for a meaningful comparison of the test accuracy. To qualify the two demands, we suggest using Beta(8, 2) in the following simulation and data analysis. Winkler (1967) and Colombo and Constantini (1980) had earlier discussions on the selection of Beta parameters. Hahn (2006) summarized the recent development on this issue.
We remark that using whole number Beta parameters is not a necessary requirement in the final step. Sometimes the exact solutions obtained from solving the equations set at the first two steps may involve complex numbers. Therefore the adjustment at the final step ensures that the chosen parameters are those best satisfy the conditions specified in the first two steps. Using whole numbers is just a relatively simple approach to do the adjustment. It is always acceptable to consider non-integer Beta parameters.
In addition to the Beta weight, one may also consider a class of conceptually simple weight functions by keeping a uniform distribution in the interval [0.9,1] and decreasing weights gradually below 0.9. Herein we consider a linearly decreasing weight between 0.9 and 0.5. The resulting distribution after proper rescaling is a trapezoid density function. The advantage of this weight function is that it does not downweight the area of extremely large specificity. We compare this weight in the real examples and find similar performance as the Beta weight.
We realize that in practice assessors may choose different weight distributions and yield different WAUC values for a test. This might be due to varying degree of belief from each assessor (Hogarth (1975) and Kahneman et al. (1982)). The conclusion from each weighted ROC analysis thus needs to be construed with respect to the weight function considered by the assessor. A relatively objective approach is to obtain independent estimates from different assessors and combine their results with a method called recoiling quantitative opinions proposed by Berger (1985), pages 272–286. The aggregated WAUC value is then representative of how people in the general population perceive the relative importance of the specificity values. Such aggregated analyses may be carried out by noting that the WAUC is a linear functional of the ROC curve and the implied weight function for the aggregated WAUC is thus just a weighted average of the weight functions for the different assessors.
3. Numerical results
3.1. Simulations
We include two parts of simulation studies. In Section 3.1.1, we investigate the finite sample performance of the proposed WAUC estimators under various test distributions. We notice that the nonparametric estimates are usually robust while parametric estimates may be misleading under model mis-specification. In Section 3.1.2, we conduct hypothetical selections between two diagnostic tests for two different cases. This numerical experiment is pertinent to our real data analysis. Through simulations we find out that neither AUC nor PAUC can select the best test in the two cases while WAUC can always maintain a satisfactory performance.
3.1.1. Consistency of estimations
We consider two types of distributions to simulate test results. Under known distributions, the true WAUCs under four kinds of weights are computed by using (14) with numerical integrations. For the two cases, we choose sample size nD = nD̄ = n and conduct 1000 simulations. At each simulation, we estimate the WAUC’s and their standard errors under four weights. Nonparametric estimators are computed as described in Section 2.2. Parametric estimators are computed as described in Section 2.3 with a known distribution Q. Because of its wide applications in clinical practice, we use the normal distribution as Q to compute the parametric estimators.
In the first case, we generate the test results TDi ~ N (1, 1) and TD̄j ~ N (0, 0.5). After 1000 simulations, we summarize the results in Table 1. The average of the estimated WAUC’s is reported as . The standard deviation of the estimated WAUC’s is reported as . The average of the estimated standard errors is reported as . Coverage probability of the asymptotical normal confidence interval for WAUC is also reported.
Table 1.
Simulation results for data from normal distribution: U(a,b) refers to uniform distribution on interval (a,b). Beta(a,b) refers to beta distribution with parameters a and b.
| f(sp) | n | WAUC | Nonparametric Method | Parametric Method | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||||
|
|
|
|
|
|
|
||||||
| U(0,1) | 50 | 0.81 | 0.80 | 0.047 | 0.045 (94%) | 0.81 | 0.046 | 0.042 (93%) | |||
| 100 | 0.81 | 0.029 | 0.032 (97%) | 0.82 | 0.028 | 0.029 (94%) | |||||
|
| |||||||||||
| U(0.5,1) | 50 | 0.72 | 0.74 | 0.063 | 0.054 (85%) | 0.72 | 0.057 | 0.055 (93%) | |||
| 100 | 0.73 | 0.044 | 0.041 (92%) | 0.72 | 0.042 | 0.039 (95%) | |||||
|
| |||||||||||
| Beta(2,8) | 50 | 0.92 | 0.91 | 0.033 | 0.035 (94%) | 0.92 | 0.030 | 0.030 (91%) | |||
| 100 | 0.92 | 0.024 | 0.024 (95%) | 0.92 | 0.021 | 0.021 (93%) | |||||
|
| |||||||||||
| Beta(8,2) | 50 | 0.69 | 0.71 | 0.065 | 0.061 (89%) | 0.69 | 0.060 | 0.058 (93%) | |||
| 100 | 0.70 | 0.044 | 0.044 (94%) | 0.69 | 0.040 | 0.041 (95%) | |||||
It is noted from Table 1 that both nonparametric and parametric methods work fairly well under all kinds of weight function for sp. The parametric estimators are usually more efficient as they tend to have smaller standard errors than their nonparametric counterparts. Nonetheless, the improvement is quite small.
We then consider a second case for test distributions. We simulate TDi from a negative aging Weibull(0.5, 4) and TD̄j from a positive aging Weibull(2, 2) respectively, where the density of Weibull(a,b) is given by
We report the results of 1000 simulations in Table 2, with the columns labeled as in Table 1.
Table 2.
Simulation results for data from Weibull distribution: U(a,b) refers to uniform distribution on interval (a,b). Beta(a,b) refers to beta distribution with parameters a and b.
| f(sp) | n | WAUC | Nonparametric Method | Parametric Method | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||||
|
|
|
|
|
|
|
||||||
| U(0,1) | 50 | 0.52 | 0.53 | 0.059 | 0.063 (96%) | 0.65 | 0.027 | 0.054 (36%) | |||
| 100 | 0.52 | 0.045 | 0.045 (94%) | 0.64 | 0.024 | 0.038 (8%) | |||||
|
| |||||||||||
| U(0.5,1) | 50 | 0.54 | 0.54 | 0.069 | 0.066 (93%) | 0.63 | 0.029 | 0.054 (3%) | |||
| 100 | 0.54 | 0.048 | 0.047 (95%) | 0.62 | 0.023 | 0.038 (1%) | |||||
|
| |||||||||||
| Beta(2,8) | 50 | 0.37 | 0.38 | 0.064 | 0.063 (93%) | 0.33 | 0.033 | 0.053 (92%) | |||
| 100 | 0.37 | 0.047 | 0.045 (94%) | 0.33 | 0.028 | 0.037 (86%) | |||||
|
| |||||||||||
| Beta(8,2) | 50 | 0.56 | 0.55 | 0.066 | 0.067 (95%) | 0.63 | 0.030 | 0.054 (7%) | |||
| 100 | 0.56 | 0.048 | 0.048 (94%) | 0.62 | 0.022 | 0.038 (0%) | |||||
Because the Weibull distribution is heavily skewed, the parametric method using normal distribution may not be appropriate, as witnessed in Table 2. Nonparametric estimator performs well, as expected, given that it does not rely on any distributional assumptions.
Since log of a Weibull variable is in a location-scale family (Gumbel distribution), we perform a separate parametric estimation procedure for WAUC based on log of the test results with a known Q to be the Gumbel distribution. The resulting estimators and their standard errors closely approximate the true WAUC and empirical standard deviation of , respectively. Coverage rates are also largely improved to be close to the nominal level. The results are not reported here since they are similar to those obtained in the first case with correct parametric distribution.
In summary, the parametric estimator, while most efficient, may produce unacceptable bias when data do not follow the assumed distributions, usually normal. The nonparametric method produces substantially more robust estimation. Though nonparametric method may be less efficient than binormal model when normality hold, the loss in efficiency is not great in our simulations. We recommend that nonparametric approach be used as a standard reference calculation for routine practice. If there are large differences between the binormal estimator and the nonparametric estimator, then one should be cautious in utilizing the parametric approach, as there may be substantial model misspecification.
3.1.2. Comparison of tests using AUC, PAUC and WAUC
We consider two cases of test comparison in the following. In each case, we generate two tests according to the specified distribution. We intend to compare the test accuracy based on the generated samples.
-
Case I
Test 1 has TD̄ ~ N (0, 1) and TD ~ .2N (5, 1) + .8N (0, 1); Test 2 has TD̄ ~ N (0, 1) and TD ~ .4N (5, 1) + .6N (0, 1).
-
Case II
Test 1 has TD̄ ~ N (0, 1) and TD ~ .75N (2, 1) + .25N (0, 1); Test 2 has TD̄ ~ N (0, 1) and TD ~ N (1.07, 1).
For each case, we compute three accuracy measures: AUC, PAUC, and WAUC for Tests 1 and 2 over 1000 simulations. The partial region for PAUC is from .9 to 1. The weight for WAUC is Beta(8,2). Sample size is nD = nD̄ = 60 for each sample. Since investigators usually want to determine the relative importance of the two tests, we thus report the frequencies that Test 1 is preferred over Test 2 under these criteria. A good accuracy criterion should favor the better test more frequently.
In Case I, both tests for diseased subjects have a chance to be identically distributed as tests for non-diseased subjects. Such a chance is much larger for Test 1 than for Test 2. We therefore would prefer Test 2 in practice. The percentages of favoring Test 1 under AUC, PAUC and WAUC are 9.9%, 36.5%, and 12.6%, respectively. Using PAUC to select between these two tests would make a mistake with a probability that is three times larger than the error rates for AUC and WAUC in this case. The performance of AUC and WAUC is quite similar.
In Case II, simulation results indicate that the percentages of favoring Test 1 under AUC, PAUC and WAUC are 82.7%, 24.3%, and 30.0%, respectively. In this case, Test 1 has a slightly better AUC value (.8579) than Test 2 (.8576). However, in the region of high specificity, Test 2 actually has a better performance for differentiating the diseased subjects. An investigator aiming at ensuring high specificity would prefer Test 2 over Test 1. PAUC and WAUC favor Test 2 most of the time and therefore are much more successful than AUC.
In both cases, if we look at the sole values of AUC or PAUC, we might miss the more accurate test and select the unfavorable one. In fact, the appropriate criteria that should be used are AUC for Case I and PAUC for Case II. On the other hand, WAUC seems to be a good comprimize between AUC and PAUC and can identify the best test with the same frequency as the other appropriate criteria. This observation has also been made when we tried other settings of tests comparison. The cause of its satisfactory performance is that WAUC stresses the partial ROC curve for large values of specificity while also keeping a connection to the complete ROC curve. This is a quality unattainable for either AUC or PAUC.
We next move to a more complex simulation setting of gene selection analoguous to the real problems in the next session. We still consider the above two cases. In Case I, we generate 40 genes with the same distribution as Test 2, 10 genes with the same distribution as Test 1 and 50 genes which does not differentiate the diseased and healthy subjects. We compute AUC, PAUC and WAUC values for the 100 genes and select the top ten only. We expect to identify the 10 genes with the same distribution as Test 1 in the top ten list in each simulation. After a large number of simulations, we report the proportion that the 10 preferred genes are indeed selected in the top ten. Under AUC and WAUC, the proportions are 92.5% and 88.3%. However, the proportion is only 42.0% under PAUC. Using PAUC thus cannot choose all of the ten important genes most of the time. Similarly, in Case II, we generate 40 genes with the same distribution as Test 1, 10 genes with the same distribution as Test 2 and 50 genes which does not differentiate the subjects. Again we report proportions of selecting the 10 best genes (with the same distribution as Test 2) as top ten among the 100 genes under the three criteria. Under PAUC and WAUC, the proportions are 96.9% and 94.5%. The proportion is only 34.6% under AUC. WAUC appears to be more successful than AUC and PAUC since it can select correctly the best genes at the top of the ranked list most of the time.
3.2. Microarray data
Microarrays enable the simultaneous measurement of the expression levels of tens of thousands of genes and have found widespread application in biological and biomedical research. The use of microarray to discover genes, which are differentially expressed between the diseased and healthy patients has many applications. These include the identification of disease biomarkers that may be important in the diagnoses of the different types and subtypes of diseases. Numerous feature selection methods have been applied to the detection of differentially expressed gene lists. We focus on the method based on ROC analysis in this paper.
3.2.1. Ovarian cancer data
We revisit the ovarian cancer data which has been studied in Pepe et al. (2003). Ovarian tissue from 30 subjects with cancer, and 23 subjects without cancer, were analyzed for mRNA expression, using glass arrays spotted for 1536 gene clones. The microarray data set provided a valuable source of information to identify differential biomarkers for ovarian cancer.
Pepe et al. (2003) did a pilot analysis by examining the first 100 genes in the whole data set. For comparison, we computed WAUC under three different weight functions for the same 100 genes: U(0,1), U(0.9,1), and Beta(8,2). U(0,1) gives the ordinary AUC. U(0.9,1) leads to a PAUC index over a range of high specificity values. Beta(8,2) gives a negatively skewed weight for WAUC with an emphasis on high specificity values.
We sorted the genes according to their WAUC values. The top 20 genes under three criteria were reported in Table 3 along with their nonparametric estimated WAUC values. For the sake of comparison, we also included the rankings resulted from using two sample T-tests and Wilcoxon rank sum tests. We note that these two tests tend to comparing the overall accuracy of the diagnostic markers and usually cannot be used to compare the markers when we restrict our attentions to ROC regions with high specificity. It was not a surprise that the results from these two tests are quite close to that obtained under the ordinary AUC. The correlation between gene ranks according to T-test P-value and ranks according to AUC is −.914; the correlation between gene ranks according to Wilcoxon test P-value and ranks according to AUC is −.908. The correlation between the two tests is .992. In addition to the global comparison, we are also interested in comparing the accuracy of the genes under the requirement of high specificity.
Table 3.
Gene number and estimated weighted area under the ROC curve under four different weights for the top 10 genes from Ovarian cancer dataset.
| Rank | U(0,1) | U(.9,1) | Beta(8,2) | Trapezoid | T test | Wicoxon test | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| ||||||||||||
| Gene | WAUC | Gene | WAUC | Gene | WAUC | Gene | WAUC | Gene | P-value | Gene | P-value | |
| 1 | 93 | .971 | 93 | .900 | 93 | .922 | 93 | .938 | 9 | 2.8 × 10−11 | 93 | 5.7 × 10−9 |
| 2 | 42 | .870 | 65 | .589 | 42 | .759 | 76 | .804 | 87 | 2.5 × 10−10 | 9 | 9.1 × 10−8 |
| 3 | 76 | .864 | 5 | .513 | 76 | .752 | 65 | .785 | 49 | 6.5 × 10−10 | 87 | 1.1 × 10−7 |
| 4 | 65 | .854 | 23 | .452 | 65 | .737 | 42 | .783 | 95 | 1.5 × 10−9 | 88 | 3.9 × 10−7 |
| 5 | 16 | .804 | 52 | .423 | 16 | .674 | 16 | .697 | 71 | 1.1 × 10−8 | 71 | 4.0 × 10−7 |
| 6 | 5 | .789 | 42 | .407 | 5 | .647 | 5 | .687 | 88 | 2.4 × 10−8 | 95 | 4.5 × 10−7 |
| 7 | 52 | .784 | 51 | .404 | 39 | .570 | 39 | .685 | 50 | 2.4 × 10−8 | 49 | 6.2 × 10−7 |
| 8 | 97 | .780 | 35 | .341 | 35 | .559 | 23 | .650 | 93 | 8.5 × 10−8 | 40 | 1.4 × 10−6 |
| 9 | 39 | .752 | 73 | .327 | 97 | .549 | 35 | .637 | 40 | 8.4 × 10−7 | 50 | 3.3 × 10−6 |
| 10 | 75 | .736 | 76 | .318 | 23 | .543 | 97 | .597 | 65 | 1.6 × 10−6 | 91 | 4.1 × 10−6 |
Pepe et al. (2003) illustrated the advantage for PAUC which corresponds to .1 times of WAUC under U(.9, 1). They demonstrated their point by comparing two genes whose positions in the original data set are 5 and 97. The estimated density (using the kernel method, Simonoff (1996)) of the two gene expression profiles were plotted in Figure 1. Both of them have very high and similar overall AUC values. Pepe et al. (2003) argued that gene 97 does not have a good performance comparing to gene 5 under the PAUC criterion. Gene 5 has much larger average sensitivity over the range of high specificity values, with gene 97 having corresponding WAUC < .3. PAUC is thus a better measure than AUC since in population screening we require a high specificity for the gene to separate the normal subjects out correctly.
Fig. 1.

Distribution of gene expressions for the diseased and normal populations from the Ovarian cancer dataset. The area under the density for the diseased population is shaded.
Although PAUC, or equivalently WAUC under weight U(.9, 1), may provide the relative accuracy of the genes under the purpose of ensuring high specificity, the absolute accuracy of WAUC appears to be quite low for most genes under this weight function. In fact, all genes except 93, 65 and 5 (the top 3) have WAUC values lower than .5. Note however that the null value W0 for this weight is 0.05. WAUC values in (0.05, 0.5) are acceptable but reflect that for this specificity distribution diseased subjects are classified incorrectly more than 50% of the time. Within the truncated region of sp, which corresponds to a truncated range for the gene distribution, the gene expression value for diseased population might not be consistently higher than that from normal population. This implies that the usual probabilistic interpretation of AUC, the probability of correctly ordering the two populations, may not be reflected well for most genes from the face-value of PAUC. The reason lies in that PAUC completely ignores the ROC value outside the specified narrow range.
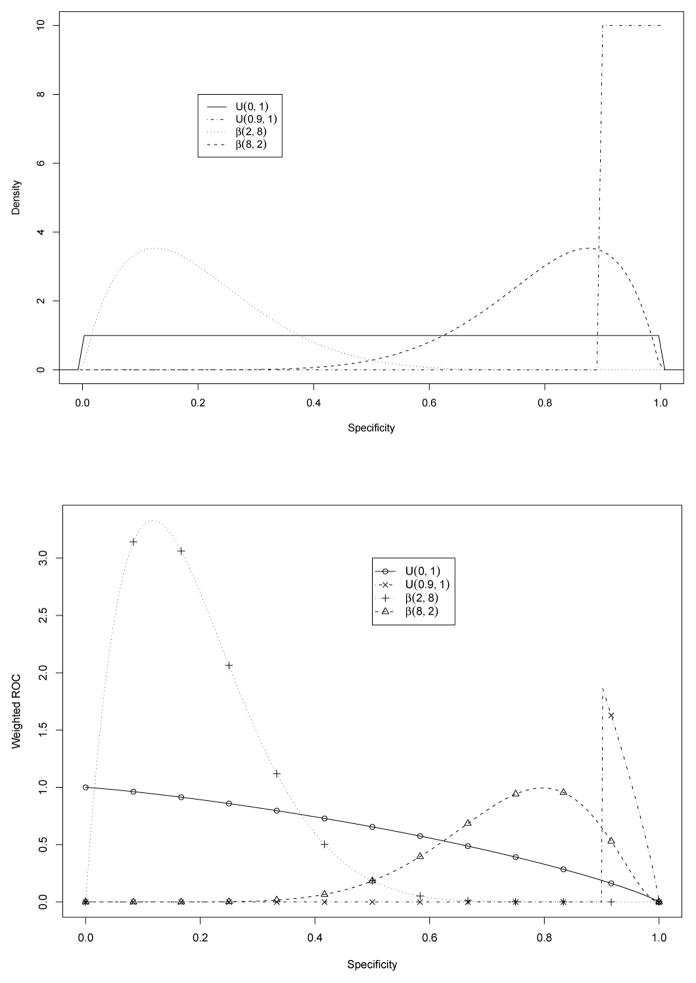
It may be more flexible to use a less extreme weight choice, say, a continuous weight function defined over the entire region of (0, 1). In this example, WAUC under Beta weights confirms the importance of gene 97 (still among the top ten). Beta(8,2) gives high weight for large sp and therefore WAUC for gene 5 is still higher than that of gene 97. The influence of the weights is illustrated in Figure 2. A Beta(2,8) weight has also been included in the figure. Such a weight generally leads to large WAUC values since low specificity lends greater support for high sensitivity.
Fig. 2.
Weight functions (upper panel) and weighted ROC curves (lower panel). In the lower panel, the solid line is the original ROC curve, also corresponding to U(0,1). 13 points (circles) on this curve are marked and their corresponding weighted values are symboled with different point characters on the other three weighted ROC curves.
We also note that the top ten genes selected by WAUC under the trapezoid weight are identical to those selected under Beta(8,2) weight. The relative order of these ten genes are slightly different. The trapezoid weight, constructed by extending the truncated uniform distribution to the entire interval [0,1], thus shows a satisfactory performance as the Beta(8,2) weight.
The rankings of genes obtained under different weight functions suggest the importance of genes may vary under different weight functions, reflecting different beliefs about the relative importance of different regions of the ROC. Using the more flexible WAUC, we can see how the selection of important genes changes under different weights. Previous methods using AUC or PAUC might mask the significance of many excellent genes by assigning relatively low ranks under rigid uniform weights. Since valuable genetic data are usually expensive to obtain, we believe that WAUC can potentially benefit the cost-effectiveness of similar clinical studies by highlighting genes which may be of potential interest (under certain weight functions). Such results may suggest that it is worthwhile to allocate resources to further research on certain genes, which might have otherwise been overlooked by existing analyses using AUC of PAUC.
We conducted similar ROC analysis by using the complete data set which involves 1536 genes in total. The results for WAUC under U(0.9,1) weight (or PAUC index) indicate that a total of 199 genes have perfect WAUC values. The second highest WAUC value is .996 which is achieved by the next 63 genes. In this case, using such a WAUC produces an extreme number of ties when ranking genes. It is difficult to judge the relative accuracy for genes who have the same WAUC values.
Eyeballing the distribution (left panel of Figure 3) of gene 1348, which has perfect WAUC under U(0.9,1) weight, we notice that there is no cancer subject whose test value falls into the upper 10 percentile of healthy group. Therefore none from the cancer group was mis-labeled under such truncated region. However, the overall classification performance of this gene is not great. In most of the domain, the two distributions overlap, indicating very weak differential power for the gene. The overall AUC (or WAUC under uniform weight on (0,1)) is only 0.602, only slightly better than W0 = 0.5.
Fig. 3.
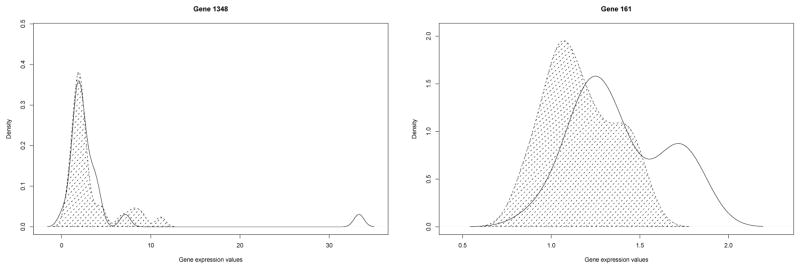
Distribution of gene expressions for the diseased and normal populations from the Ovarian cancer dataset. The area under the density for the cancer patients is shaded.
The WAUC values under the trapezoid weights produce more meaningful rankings. The highest WAUC values are .993 achieved by three genes 161, 612 and 1409, respectively. The second highest WAUC values are .990 achieved by four genes 111, 173, 179 and 510. This was followed by gene 349 with WAUC .988 and genes 87 and 436 with WAUC .987. The results from Beta(8,2) weight are quite similar. The highest WAUC is 1.0 achieved by gene 510, followed by two genes 612 and 1409 with WAUC .999, then followed by five genes 148, 161, 173, 732 and 966 with WAUC .998, and then followed by two genes 179 and 111 with WAUC .997 and .996, respectively. Seven among the top ten genes are identical under the two weights. The overall correlation between these two ranking is .99. As an example, the distribution of gene 161 was shown in the right panel of Figure 3. Clearly this gene differentiate the two groups much better than gene 1348. Gene 161 also has WAUC equal to 1 under U(0.9,1). Clearly, not all genes with high ranks under WAUC with U(0.9,1) wieght deserve the same amount of attention. WAUC with U(0.9,1) might mislead us to believe too many genes to have the same accuracy while in fact they may not.
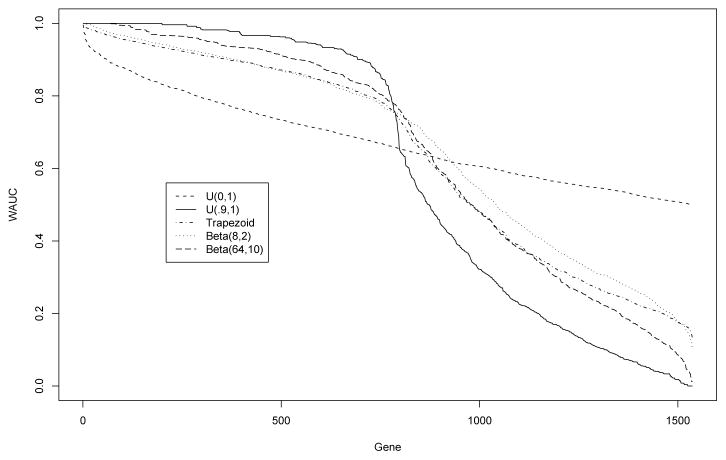
For the sake of comparison, we consider another beta weight Beta(64,10) which has the same mode as Beta(8,2) but a much smaller variance (.00156). We note the variance for Beta(8,2) is .015. The WAUC under Beta(64,10) gives that 42 genes are ranked equally as the most important with 100% WAUC and followed by another 34 genes with the second highest WAUC 99.9%. This weight favors large value of specificity but restricts the variation of specificity distribution. It thus also creats many ties in the ranking of genes. Therefore such a weight is not as desirable as Beta(8,2) which allows relatively more variability and leads to sensible rankings.
The sorted WAUC values for the genes under five discussed weights were shown in Figure 4. While the WAUC values under trapezoid and Beta(8,2) weights are decreasing strictly, those under U(0.9,1) and Beta(64,10) decrease as a step function. Thus, while the WAUC under U(0.9,1) may be successful in some cases to rank genes for the aforementioned goal, it can potentially create large number of ties due to the truncated nature of the estimator. Similar problem occurs for Beta(64,10) due to its limited variation. It is more flexible to consider weights like Beta(8,2) or the trapezoid density used in this paper when we want to focus on high specificity region of the ROC curve and provide strictly ordered rankings for all the genes.
Fig. 4.
Sorted WAUC values for 1538 genes in the Ovarian cancer dataset.
4. Discussion
Using the WAUC to select genes, we can maintain all the nice properties mentioned in Pepe et al. (2003) for the PAUC. In addition, we can eliminate possible problems associated with the PAUC. Therefore, the WAUC may be a more general measure of accuracy for biological studies.
The choice of weight function should ideally reflect the relative importance of specificity values. Besides borrowing knowledge from subject matter experts, we can further consider a hierarchical approach to specifying parameters in the weight function, as with the Beta distribution, where prior distribution may be placed on α and β. As discussed in Section 2.4 and in the microarry examples in Section 3.2.1 and 3.2.2, this framework is useful in facilitating sensitivity analyses, whereby the impact of different weights on rankings may be formally evaluated.
If attention is to be confined to a truncated region of specificity, as with PAUC, our approach enables a more flexible weight to be employed, versus simply using a flat weight within this region. This expands the current PAUC methodology to allow more general sensitivity analyses of the ROC, for thresholds exceeding the lower specificity bound. A Beta distribution (or any other familiar continuous distribution) can be re-shaped to represent the relative importance of specificities within the truncated region.
The proposed methods in this paper can be applied for situations where high sensitivities are desirable. Since ROC curve can also be regarded as specificity varying as a function of sensitivity, all the mathematical derivations can be easily modified to achieve similar results for weight functions of sensitivity.
The connection between WAUC and p-values may also be easily established. Using the asymptotic results in Section 2, one can compute p-value for each gene to test the null hypothesis that the WAUC is greater than certain cut off value. Genes may then be sorted according to the p-values of this test in the same way as the t test or Wilcoxon test. However, the choice of the cut off value under the null hypothesis may be different for different problems. Comprehensive development on ranking methods based on such p-values requires further research efforts.
An important topic is comparing WAUC values from two markers under the same weight, in particular, the development of formal testing procedures. In general, marker measurements taken on a common set of individuals are correlated and one cannot directly use (8) and (9) to derive a nonparametric test or use (16) to derive a parametric test. While the difference of two WAUCs will still be normally distributed, for paired data, the variance formula may be quite complicated, involving a covariance term for the two markers. However, bootstrap variance estimation for the difference of the two WAUCs may be easily computed, analogously to bootstrapping the difference of two correlated AUCs. The derivation of a simple plug in variance estimator for the difference is beyond the scope of the current paper, but a worthwhile topic for future research.
Acknowledgments
We thank the Editor, the Associate Editor, and two reviewers for constructive comments on the manuscript. In particular, the AE has suggest the use of the trapezoid weight.
Appendix
Derivation of (9)
Hsieh and Turnbull (1996) studied the asymptotic behavior of . Assume the same technical condition (6), the stochastic process (indexed by sp) is asymptotically equal to
| (17) |
uniformly for sp on (a, b), where B1 and B2 are two independent versions of Brownian bridges (Billingsley (1999)), sD and sD̄ are the derivative of SD and SD̄, respectively.
Hence, the asymptotic variance of is
Proof of (11)
Proof
For any threshold c,
For an sp, we notice that c = μD̄ + σD̄Q−1(sp) is the corresponding threshold for the test positive criterion. Hence
where a and b are as given in (12).
Proof of (13)
Proof
Assume the density function q(z) of Q(z) exists,
Contributor Information
Jialiang Li, Department of Statistics and Applied Probability, National University of Singapore, Singapore 117546.
Jason P. Fine, Department of Biotatistics, University of North Carolina, Chapel Hill, USA
References
- Bandos AI, Rockette HE, Gur D. Incorporating utility-weights when comparing two diagnostic systems. Acad Radiol. 2005;12:1293–130. doi: 10.1016/j.acra.2005.05.028. [DOI] [PubMed] [Google Scholar]
- Berger J. Statistical Decision Theory and Bayesian Analysis. Springer Verlag; New York: 1985. [Google Scholar]
- Billingsley P. Convergence of Probability Measures. Wiley; 1999. [Google Scholar]
- Chaloner KM, Duncan GT. Assessment of a Beta prior distribution: PM elicitation. The Statistician. 1983;32:174–180. [Google Scholar]
- Chatterjee M, Mohapatra S, Ionan1 A, Bawa G, Ali-Fehmi R, Wang X, Nowak J, Ye B, Nahhas FA, Lu K, Witkin SS, Fishman D, Munkarah A, Morris R, Levin NK, Shirley NN, Tromp G, Abrams J, Draghici S, Tainsky MA. Diagnostic markers of ovarian cancer by high-throughput antigen cloning and detection on arrays. Cancer Research. 2006;66:1181–119. doi: 10.1158/0008-5472.CAN-04-2962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colombo AG, Constantini D. Ground-hypotheses for beta distribution as Bayesian prior. IEEE Transactions on Reliability. 1980;1:17–21. [Google Scholar]
- de Alava E, Panizo A, Antonescu CR, Huvos AG, Pardo-Mindn FJ, Barr FG, Ladanyi M. Association of EWS-FLI1 type 1 fusion with lower proliferative rate in Ewing’s sarcoma. American Journal of Pathology. 2000;156:849–855. doi: 10.1016/S0002-9440(10)64953-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dodd LE, Pepe MS. Partial AUC estimation and regression. Biometrics. 2003;59:614–623. doi: 10.1111/1541-0420.00071. [DOI] [PubMed] [Google Scholar]
- Durrett R. Thomson Learning. 3 2005. Probability: Theory and Examples. [Google Scholar]
- Gupta AK, Nadarajah S. Handbook of Beta Distribution and Its Applications. Marcel Dekker, Inc; New York: 2004. [Google Scholar]
- Hahn ED. Re-examining informative prior elicitation through the lens of Markov chain Monte Carlo methods. Journal of Royal Statistical Society, Series A. 2006;169:37–48. [Google Scholar]
- Hogarth RM. Cognitive process and the assessment of subjective probabilities. Journal of American Statistical Association. 1975;70:271–289. [Google Scholar]
- Hsieh F, Turnbull BW. Nonparametric and semiparametric estimation of the receiver operating characteristic curve. Annals of Statistics. 1996;24:25–4. [Google Scholar]
- Joober R, Benkelfat C, Toulouse A, et al. Analysis of 14 CAG repeat-containing genes in schizophrenia. American Journal of Medical Genetics. 1999;88:694–699. [PubMed] [Google Scholar]
- Kahneman D, Slovic P, Tversky A. Judgement under Uncertainty, Heuristics and Biases. Cambridge University Press; London: 1982. [DOI] [PubMed] [Google Scholar]
- Pepe MS. The Statistical Evaluation of Medical Tests for Classification and Prediction. Oxford University Express; 2003. [Google Scholar]
- Pepe MS, Longton G, Anderson GL, Schummer M. Selecting differen-tially expressed genes from microarray experiments. Biometrics. 2003;59:133–142. doi: 10.1111/1541-0420.00016. [DOI] [PubMed] [Google Scholar]
- Ship MA, Ross KN, Tamayo P, Wang AP, Kutok JL, Aguiar RC, Gaasenbeek M, Angelo M, Reich M, Pinkus GS. Diffuse large B-cell lym-phoma outcome prediction by gene-expression profiling and supervised machine learning. Nat Med. 2002;8:68–74. doi: 10.1038/nm0102-68. [DOI] [PubMed] [Google Scholar]
- Simonoff JS. Smoothing Methods in Statistics. Springers; New York: 1996. [Google Scholar]
- Tversky A, Kahneman D. The framing of decisions and teh psychology of choice. Science. 1981;211:453–458. doi: 10.1126/science.7455683. [DOI] [PubMed] [Google Scholar]
- Walter SD. The partial area under the summary ROC curve. Statistics in Medicine. 2005;24:2025–2040. doi: 10.1002/sim.2103. [DOI] [PubMed] [Google Scholar]
- Wieand S, Gail MH, James BR. A family of nonparametric statistics for comparing diagnostic markers with paired or unpaired data. Biometrika. 1989;76:585–592. [Google Scholar]
- Winkler RL. The assessment of prior distribution in Bayesian analysis. Journal of American Statistical Association. 1967;62:776–800. [Google Scholar]
- Zhou XH, Obuchowski NA, McClish DK. Statistical Methods in Diagnostic Medicine. Wiley; New York: 2002. [Google Scholar]