Estimating Vaccine Efficacy under the Heterogeneity of Vaccine Action in a Nonrandomly Mixing Population

Abstract

Vaccines often have heterogeneous actions because of possible variation in the immune systems of hosts. One must consider such heterogeneity of vaccine action when developing a vaccine efficacy parameter. Addressing this issue the summary model of vaccine action has been proposed in the literature to estimate vaccine efficacy in a randomly mixing population. However, nonrandom mixing is common, particularly in a small-group-mixing population. This article extends the summary model of vaccine action to such a nonrandomly mixing population. The interpretation and estimation of the summary vaccine efficacy were discussed in light of other two models of vaccine action: the leaky and all-or-nothing model. Vaccine efficacy under all models is defined as the relative reduction in transmission probability due to vaccine. Estimation of the transmission probabilities is described based on a deterministic epidemic model of an acute transmitted disease. This article further discusses, based on the above vaccine models, the estimation of vaccination coverage required to control epidemic. Methods are illustrated using data simulated by considering different patterns of mixing and vaccine action. Results confirm that the summary model performs better than other two models when vaccine action is heterogeneous.

1. INTRODUCTION

The design and implementation of a vaccination program for the control of infectious diseases requires a consistent estimate of vaccine efficacy. Accordingly, estimation of vaccine efficacy has received much attention in the literature. Most such literature often ignores the fact that the immune response tends to vary among the hosts, and thus the vaccines have heterogeneous action. Halloran et al. (1992) pointed out that one should consider such heterogeneity of vaccine action when developing a vaccine efficacy parameter. To address this issue, some studies (Halloran et al., 1996; Longini and Halloran, 1996; Becker and Utev, 2002), including Halloran et al. (1992) discussed the estimation of vaccine efficacy in a randomly mixing population. However, nonrandom mixing is common in practice; for example, in a population stratified into different small groups such as households, where within-group mixing is usually higher than between groups and thus the overall mixing is nonrandom. Therefore, two important issues one needs to consider when estimating vaccine efficacy in a small-group-mixing population are heterogeneous vaccine action and nonrandom mixing.

A few studies have estimated vaccine efficacy in a nonrandomly mixing population (Haber et al., 1991a, 1995; Halloran et al., 1996; Longini and Halloran, 1996; Davis et al., 2006); however, these studies have ignored the heterogeneity of vaccine action across the vaccinated strata. Moreover, some other studies (Becker and Starczak, 1997; Ball and Lyne, 2002; Ball et al., 2004a,b; Ball and Lyne, 2006; Pellis et al., 2009) have modeled the epidemic in such a stratified population and discussed the estimation of optimal vaccination coverage under models that do not allow for the heterogeneity of vaccine action. The present work is designed to estimate vaccine efficacy under the heterogeneity of vaccine action in a population that is stratified into households, for a particular outbreak of acute, directly transmitted, infectious disease. In addition, this article focuses on estimation of optimal vaccination coverage, a fraction of population that needs to be vaccinated to control epidemic.

The article is organized as follows. In section 2, we briefly discuss some existing measures of vaccine efficacy under the heterogeneity of vaccine action. A deterministic model of an acute transmitted disease in a nonrandomly mixing population is discussed in section 3. Estimation of vaccine efficacy in a stratified population is described in section 4, and section 5 discusses the variance approximation of the estimator. Section 6 discusses the estimation of vaccination coverage required to control epidemic. For illustration the methods, a simulation study is described in section 7. Finally, section 8 includes a brief discussion and conclusion of the paper.

2. MEASURES OF VACCINE EFFICACY UNDER THE HETEROGENEITY OF VACCINE ACTION

Measures of protective vaccine efficacy (VE) depend on the nature of the host's response to the vaccine. Greenwood and Yule (1915) first recognized the VE estimation problem and discussed the need to model the possible heterogeneity in host susceptibility in both vaccinated and unvaccinated individuals. Since then, some researchers have modeled unmeasured heterogeneity through stratification (Smith et al., 1984; Halloran et al., 1992, 1996; Longini and Halloran, 1996), while others have modeled it by considering the susceptibility to follow probability distributions (Brunet et al., 1993; Struchiner et al., 1995). Smith et al. (1984) defined two models of vaccine action: model 1 assumes that the vaccine equally reduced the probability of infection given exposure to infection in all of the vaccinated individuals whereas model 2 assumes that the vaccine may give complete protection to a fraction of the vaccinated while the remaining fraction receive no protection. These models are increasingly by being used in practice.

Haber et al. (1991b) obtained expressions for the protective effects of two vaccine mechanisms of Smith et al. (1984) based on a deterministic epidemic model of an acute directly transmitted disease, where vaccine efficacy was defined as the relative reduction in the transmission probability due to the vaccine. For a randomly mixing population, the transmission probabilities were estimated from the observed attack rates in the vaccinated and unvaccinated by solving their proposed model. These methods have been extended further to a nonrandomly mixing population (Haber et al., 1991a, 1995). In the subsequent year, Halloran et al. (1992) described models 1 and 2 of Smith et al. (1984) as the “leaky” and “all-or-nothing” model, respectively and indicated that in the case of the all-or-nothing model, there are two vaccinated strata, each with different vaccine actions. Based on this premise, Halloran et al. (1992) discussed several models of vaccine action and derived a general expression for a summary vaccine efficacy parameter, where vaccine efficacy was defined as the relative reduction in susceptibilities to infection due to vaccine. Extending the results of Haber et al. (1991b) for a randomly mixing population, the authors discussed the interpretation and estimation of summary vaccine parameter in light of the leaky model and all-or-nothing model.

The present article extends the summary vaccine efficacy parameter to a nonrandomly mixing population that is stratified into households, for an outbreak of an acute directly transmitted disease. For comparative purposes, the leaky and all-or-nothing models of Smith et al. (1984) are briefly discussed. Vaccine efficacy under all models is defined as the relative reduction in the transmission probability due to vaccine. The transmission probability to a susceptible person can be defined as the probability that this person will become infected by a single infected person during one short unit of time (Haber et al., 1991b). Estimation of the transmission probabilities from the observed attack rates is discussed based on a deterministic model.

3. A DETERMINISTIC MODEL OF AN ACUTE TRANSMITTED DISEASE IN A NONRANDOMLY MIXING POPULATION

In this section, the deterministic model proposed by Haber et al. (1995) is adapted to model the transmission of a infectious disease in a population stratified into households. Let M_k be the number of households of sizes k (k = 1, 2, …, L), and therefore, M = Σ^L_k=1 M_k is the total number of households in the community. Assume that there is a stronger homogeneous mixing among the members within a household than for members between households. Let λ_ij (i, j = 1, …, M) be the number of contacts with members of household j that a person from household i makes per unit of time, and let λ_i = Σ^M_j=1 λ_ij. The proportion of contacts made by a person from household i with persons of household j is ρ_ij = λ_ij/λ_i. There are certain constraints on the ρ_ij inherent in their meaning:

Let β_i be the probability that a contact between a susceptible from household i and an infective results in transmission of infection. Assume that this probability does not depend on the household of the infected person. Further assume that the infection can be described by the SIR (susceptible → infective → removed) model (Bailey, 1975). In this model, a susceptible person who becomes infected remains infectious to others for a certain time period and then becomes immune.

As households are small in size, we measure all components of the SIR deterministic model in terms of proportion instead of the actual numbers (Becker and Utev, 1997; Ball and Lyne, 1999). Let S_i(t), I_i(t), and R_i(t) denote the proportions of susceptible, infected, and naturally immune persons, respectively in household i at time t, where S_i(t) + I_i(t) + R_i(t) = 1. Assume that the total number of persons in household i is fixed over the time of epidemic. Then the deterministic description of disease transmission is given by:

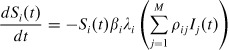(1)

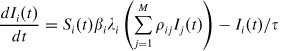(2)

(3)

where τ is the average length of an exponentially distributed infectious period.

Substituting I_j(t) from equation (3) into equation (1) yields

(4)

Let T be the time at which the observation is made after the end of the outbreak. Integrating both sides of equation (4) from 0 to T and exponentiating, we have

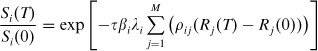(5)

Let A_i = [S_i(0) − S_i(T)]/S_i(0) denote the observed attack rate in household i at time T, and let Z_i = R_i(T) − R_i(0) be the proportion of persons who recovered from the disease during (0, T). Using these values, equation (5) becomes

(6)

where D_i = λ_i Σ^M_j=1 ρ_ijZ_i. Therefore, the transmission probabilities can be estimated as

(7)

The ^β's for all households of size k are equal, because all D_i's as well as A_i's for those households are equal. Therefore, the transmission probability for a household of size k can be estimated by taking the average over transmission probabilities obtained for all households of size k as

(8)

4. ESTIMATION OF VACCINE EFFICACY

Let us assume that vaccination is not random, but that all of the individuals belonging to the same household are either vaccinated or not. Let v be the vaccination status, where v = 0 if unvaccinated, and v = 1 if vaccinated. Incorporating the vaccination status, equation (8) can be written as

(9)

4.1. Leaky Vaccine Model

Under the definition of the leaky vaccine model, the vaccine efficacy in a household of size k can be estimated as

(10)

If vaccination does not affect the number of contacts made by an individual and consequently the distribution of an individual's contacts, then D_k,0 = D_k,1, and therefore, equation (10) becomes

(11)

If the number of contacts made by an individual depends on his/her vaccination status, then (11) provides a biased estimate of true VE^(M1)_k, because the assumption of equal exposure to infection of vaccinated and unvaccinated individuals is violated (Haber et al., 1995). In practice, it is likely that the vaccinated individuals have more contacts than unvaccinated individuals, because they may feel that they are protected from infection (Fine and Clarkson, 1987; Comstock, 1990). Therefore, it is wise to use equation (10) rather than equation (11) to estimate vaccine efficacy in a population stratified into households.

4.2. All-or-Nothing Vaccine Model

Under this vaccine model, a fraction α_i of vaccinees in household i is completely protected by the vaccine while the remaining fraction (1 − α_i) receive no protection but have equal transmission probabilities to those of unvaccinated persons from household j. Let β = β_i,1 = β_i,0 be the common value of such transmission probabilities. Therefore, using equation (6) the observed attack rates for the unvaccinated and vaccinated household of size k can be written as:

(12)

(13)

Under the vaccine action as in the all-or-nothing model, it has been shown in Haber et al. (1991b) that VE_k = α_k. Solving equations (12) and (13) for α_k we have the estimated vaccine efficacy for the household of size k as:

(14)

If vaccination does not affect the number of contacts and so the distribution of contacts made by an individual, equation (14) reduces to:

(15)

The estimator (15) underestimates the true VE^(M2) if vaccination alters an individual's contact rate in practice. Moreover, the estimators (10) and (15) under the leaky and all-or-nothing vaccine models, respectively, are similar to those discussed in Haber et al. (1995) for a non-randomly mixing population that is partitioned into two large groups.

4.3. Summary Vaccine Model

The transmission probability defined in the earlier section is a function of susceptibility of the susceptible, and therefore, defining vaccine efficacy, under the summary model of vaccine action, based on relative transmission probabilities is equivalent to those based on relative susceptibilities (Halloran et al., 1992). According to the vaccine mechanism under the summary model, suppose a vaccinated household i is separated into two strata in terms of host response to the vaccine, where stratum 1 consists of a fraction α_i of vaccinees, and stratum 2 consists of the remaining fraction 1 – α_i. Accordingly, let β⁽¹⁾_i,1 and β_i,1⁽¹⁾ be the transmission probabilities among the vaccinees in strata 1 and 2, respectively. Let β_j,0 be the transmission probabilities among the members of unvaccinated household j. If the vaccine acts as in the summary model, then the following conditions hold true:

In this case, equations (1)–(5) are remain unchanged. Let S⁽¹⁾_i,1 and S⁽²⁾_i,1 denote the proportions of vaccinated susceptible in strata 1 and 2, respectively in household i. Then equation (5) can be written for strata 1 and 2, respectively, as

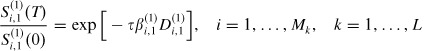(16)

(17)

Let us define the observed attack rates for vaccinated strata 1 and 2, respectively, as

As both strata are part of the same household, they have common mixing distribution and recovery rate in the interval (0, T). In this case, D⁽¹⁾_i,1 = D⁽²⁾_i,1 = D_i,1. Substituting these values in (16) and (17) and solving for the transmission probability for strata 1 and 2 we have:

(18)

(19)

Using the same argument that was used to derive equation (8), equations (18) and (19) can be replaced by their average estimates obtained over all households size k as

(20)

(21)

Similarly, α_i can be replaced by α_k.

4.4. Strata Are Identifiable and α Known

Suppose that α_k and two strata of vaccinated individuals are identifiable, and therefore, A⁽¹⁾_k,1 and A⁽²⁾_k,1 are also known. Then by using equations (9), (20) and (21) the summary vaccine efficacy for a household of size k can be estimated as

(22)

(23)

If vaccination does not alter the mixing distribution, then D_k,0 = D_k,1, and (23) becomes

(24)

Similar to the estimators (11) and (15) under the leaky and all-or-nothing models, respectively, the estimator (24) provides biased estimate of the true VE_k if vaccination alters an individual's contact rate.

4.5. Strata Are Not Identifiable and α Unknown

If strata are not identifiable and α is unknown, then one can derive bounds for VE_k as

where VE_k^(M2) and VE_k^(M1) are the vaccine efficacy under the all-or-nothing and leaky models, respectively. The upper bound assumes that all vaccinated individuals are equally affected by the vaccine, and the lower bound assumes that some of them are completely protected while the remainder have no protection. The proof of this inequality is given in the appendix.

5. VARIANCE OF THE VACCINE EFFICACY ESTIMATOR

We derive an expression for the variance of the vaccine efficacy estimators given in (10), (14), and (23) under the leaky, all-or-nothing, and summary vaccine models, respectively. In the case of the leaky vaccine model, the estimator (10) is a function of the simpler estimator (11) multiplied by the constant term D_k,0/D_k,1. That is, if *_k denotes the simpler estimator in (11), then variance of the estimator in (10) can be expressed as

(25)

where the following approximation for the variance of *_k can be derived as in Haber et al. (1991a) (when there is no subsampling):

(26)

For the estimator (14) under the all-or-nothing model, the following variance approximation can be derived using the delta method (Haber et al., 1995):

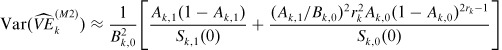(27)

where r_k = D_k,1/D_k,0, and B_k,0 = 1 − (1 − A_k,0)^r_k.

In the summary measure of vaccine efficacy, the estimator in (23) can be expressed as

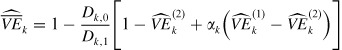(28)

where are the vaccine efficacy estimators in vaccinated strata 1 and 2, respectively. As strata 1 and 2 are independent, ⁽¹⁾_k and ⁽²⁾_k are independent. Therefore, the variance of the summary vaccine estimator can be approximated as

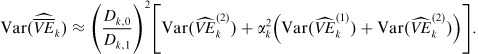(29)

By definition, both ⁽¹⁾_k and ⁽²⁾_k are closely related to the simpler estimator (11) of vaccine efficacy in the leaky vaccine model. Therefore, using the same approach applied in estimating Var(*_k) given in (26) the variances of ⁽¹⁾_k and ⁽²⁾_k can be obtained, respectively, as:

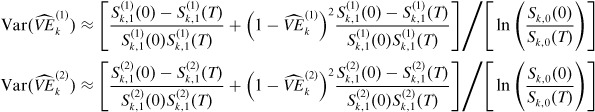The preceding expression for the variance of the summary vaccine estimator is appropriate when vaccinated strata are identifiable and α_k is known. When α_k is unknown and the strata are not identifiable, the approximate variance of this estimator can be obtained by taking an average over Var(^(M1)_k) and Var(^(M2)_k). All of these variance expressions derived thus for can be used to obtain confidence intervals for the corresponding true vaccine efficacy.

6. ESTIMATION OF THE VACCINATION COVERAGE

For designing an effective vaccination program, it is important to estimate the vaccination coverage required to control an epidemic. In this section, we discuss estimation of such threshold parameter based on the deterministic approach discussed in section 3. We derive a threshold value f*_k for the fraction f_k of vaccinated households of size k such that for f_k ≥ f*_k there will be no epidemic, and for f_k ≤ f*_k there will be an epidemic (Kermack and McKendrick, 1927; Haber et al., 1991b).

Let us define the dynamic variable I_k(t) = I_k,0(t) + I_k,1(t), the total number of infectives at time t in all households of size k. Then taking differentiation we have

(30)

Using equation (2) and I_k(t) = I_k,0(t) + I_k,1(t), equation (30) can be rewritten as

(31)

where M_k,0 and M_k,1 are the number of unvaccinated and vaccinated households of size k, respectively, and M_k,0 + M_k,1 = M_k. Also 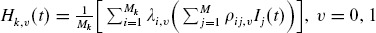. It has been discussed in the literature that I_k(t) is either strictly decreasing (in the case of no epidemic) or strictly increasing to a maximum and strictly decreasing thereafter (in the case of an epidemic) (Hethcote, 1976; Haber et al., 1991b). Therefore, it can be proved that there will not be an epidemic if .

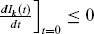6.1. When the Leaky Model is Operating

Let us consider the leaky model is operating in practice, and assume that no one in the population has naturally acquired immunity. Evaluating equation (31) at t = 0, and using the initial condition S_k,0(0) = S_k,1(0) = 1, we have

(32)

where I_k(0) = 0⁺ is very small number.

As assumed that there is one infective in the population at t = 0, so I_k(0) = 1. This implies the term Σ^M_j=1 ρ_ij,vI_j(0) = 1, and hence, the term H_k,v(0) = λ_k,v. Moreover, the assumption on mixing due to vaccination is no longer valid before the vaccination starts, and therefore, λ_k,0 = λ_k,1 = λ_k. Assume that the transmission parameters (β_k,0 and β_k,1 or α or β⁽¹⁾_k,1 and β_k,1⁽²⁾) are known from a previous study on a similar population. Substituting I_k(0) = 1, H_k,v = λ_k, M_k,0 = M_k(1 − f_k), and M_k,1 = M_kf_k in (32) we have

(33)

In a situation where there will be no epidemic, we have 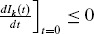. Therefore, solving equation (33) for f_k gives

(34)

Since β_k,0 ≥ β_k,1 under the leaky model, the inequality (34) will be satisfied when f*_k ≥ f_k, and the threshold value f*_k is given by

(35)

where R_0,k = τkM_kλ_kβ_k,0 is the basic reproduction number for the households of size k.

6.2. When the All-or-Nothing Model is Operating

In this model, we use S_k,1(0) = (1 − α_k) and β_k,0 = β_k,1. Then an epidemic will not be occur if

(36)

Solving equation (36) for f*_k yields

(37)

6.3. When the Summary Model is Operating

In the summary model, we use S⁽¹⁾_k,1(0) = α_k, S⁽²⁾_k,1(0) = (1 − α_k), and β_k,1⁽¹⁾ ≤ β_k,1⁽²⁾ ≤ β_k,0. Then an epidemic will not be occur if

(38)

where β_k,1 = α_kβ⁽¹⁾_k,1 + (1 − α_k)β_k,1⁽²⁾. Solving equation (38) for f*_k yields

(39)

We can see that the denominator of f*_k in the case of all models is the vaccine efficacy. Therefore, the equations (35), (37), and (39) can be replaced by a single equation as follows:

(40)

The threshold f*_k depends on the vaccine efficacy and the R_0,k. We can see that f*_k is positive only if R_0,k > 1 (which is the condition required to guarantee that an epidemic will occur in the absence of vaccination). From the previous study if we know R_0,k for an acute directly transmitted disease, then f*_k depends on the vaccine efficacy. If vaccine action is truly heterogeneous, then all models except the summary one provide a biased estimate of vaccine efficacy, which leads to bias in f*_k. However, in practice, the model for the vaccine action is unknown; in this case a optimistic approach is to use the largest f*_k (Haber et al., 1991b). Moreover, if f*_k > 1, then it implies that an epidemic will occur regardless of the value of f_k, which could be possible if the disease is extremely infectious.

Finally, the overall fraction of households in the community that needs to be vaccinated can be estimated as follows:

(41)

which has an interpretation similar to f*_k.

7. SIMULATION STUDY

7.1. Simulation Design

A simulation study was conducted to illustrate the methods described in the earlier sections. We simulated an epidemic path of number of susceptibles, infectious, and recovered individuals based on the SIR epidemic process in a population partitioned into households. We considered a population of 500 households, where there were 5, 15, 35, 35, and 10% of households of sizes 1, 2, 3, 4, and 5, respectively; 50% of households were assumed to be vaccinated. We further assumed that initially there was one infective in the population from which the epidemic started, and that there were no naturally immune persons. The length of infectious period was assumed to be a random variable with mean τ = 5.

In simulation, we considered two matrices of mixing distribution denoted by {ρ_rk,v}. In the first matrix (Table 1), there is higher mixing within households than between households, and an individual's contacts do not depend on vaccination status. In the second matrix, there is a higher mixing within households than between households, and individuals are more likely to contact individuals of the same vaccination status. In both matrices, the mixing distribution, ρ_rk,v, is proportionally related to the size of the household. However, the mixing distribution of all households of the same size is equal. One should note the symmetry condition ρ_rk,v = ρ_kr,v.

Table 1.

Values of ρ_rk,v used in simulation, where v = 0 for unvaccinated, v = 1 for vaccinated

		k = 1			k = 2		k = 3		k = 4		k = 5
		v	0	1	0	1	0	1	0	1	0	1
ρrk,0 = ρrk,1	r = 1	0	0.24	0.24	0.08	0.08	0.10	0.10	0.14	0.14	0.20	0.20
		1	0.24	0.24	0.08	0.08	0.10	0.10	0.14	0.14	0.20	0.20
	r = 2	0	0.08	0.08	0.30	0.30	0.12	0.12	0.16	0.16	0.23	0.23
		1	0.08	0.08	0.30	0.30	0.12	0.12	0.16	0.16	0.23	0.23
	r = 3	0	0.10	0.10	0.12	0.12	0.36	0.36	0.20	0.20	0.28	0.28
		1	0.10	0.10	0.12	0.12	0.36	0.36	0.20	0.20	0.28	0.28
	r = 4	0	0.14	0.14	0.16	0.16	0.20	0.20	0.42	0.42	0.32	0.32
		1	0.14	0.14	0.16	0.16	0.20	0.20	0.42	0.42	0.32	0.32
	r = 5	0	0.20	0.20	0.23	0.23	0.28	0.28	0.32	0.32	0.48	0.48
		1	0.20	0.20	0.23	0.23	0.28	0.28	0.32	0.32	0.48	0.48
ρrk,0 < ρrk,1	r = 1	0	0.32	0.22	0.15	0.10	0.20	0.14	0.24	0.16	0.28	0.19
		1	0.22	0.42	0.10	0.19	0.14	0.29	0.16	0.31	0.19	0.33
	r = 2	0	0.15	0.10	0.36	0.16	0.20	0.18	0.25	0.19	0.27	0.21
		1	0.10	0.19	0.16	0.48	0.18	0.33	0.19	0.35	0.21	0.37
	r = 3	0	0.20	0.14	0.20	0.18	0.42	0.20	0.25	0.22	0.32	0.24
		1	0.14	0.29	0.18	0.33	0.20	0.56	0.22	0.39	0.24	0.40
	r = 4	0	0.24	0.16	0.25	0.19	0.25	0.22	0.48	0.25	0.30	0.26
		1	0.16	0.31	0.19	0.35	0.22	0.39	0.25	0.65	0.26	0.43
	r = 5	0	0.28	0.19	0.27	0.21	0.32	0.24	0.30	0.26	0.54	0.30
		1	0.19	0.33	0.21	0.37	0.24	0.40	0.26	0.43	0.30	0.75

We simulated a separate epidemic path under each of the vaccine models described in section 4. When the leaky model was operating, the transmission probabilities β_1,0 = β_2,0 = β_3,0 = β_4,0 = β_5,0 = 0.80 for the unvaccinated group and β_1,1 = β_2,1 = β_3,1 = β_4,1 = β_5,1 = 0.20 for the vaccinated group were used. These confirmed the true VE under the leaky model as 0.75. For the all-or-nothing model, the proportion of completely immune vaccinated individuals was considered as α₁ = α₂ = α₃ = α₄ = α₅ = 0.60. The remaining proportion of vaccinees had similar transmission probabilities to the unvaccinated individuals as in the leaky model. Therefore, the true VE for the all-or-nothing model is 0.60. The transmission probabilities for the vaccinated strata 1 and 2 under the summary vaccine were β⁽¹⁾_1,1 = β⁽¹⁾_2,1 = β⁽¹⁾_3,1 = β_4,1⁽¹⁾ = β⁽¹⁾_5,1 = 0.22 and β⁽²⁾_1,1 = β⁽²⁾_2,1 = β⁽²⁾_3,1 = β⁽²⁾_4,1 = β_5,1⁽²⁾ = 0.30, respectively. The transmission probabilities for the unvaccinated group were similar to those under the leaky model. Therefore, the true VE under the summary model . For each scenario, 500 simulations were performed, and the estimate of VE was taken from the average over 500 simulations. Models were compared by assessing 90% nominal coverage of confidence interval for the true vaccine efficacy parameter. Coverage was calculated as the percentage of simulations in which the true value was enclosed by the estimated confidence interval.

One of the main objectives of the study was to estimate vaccine efficacy under the heterogeneity of vaccine action in a nonrandomly mixing population. Among the already-described epidemic processes simulated based on three vaccine models, only the process under the summary model was generated considering the heterogeneity of vaccine action across the vaccinees. Using the outcomes of this epidemic process (where the true VE = 0.685), estimates of VEs with their corresponding coverage probabilities under each of the vaccine models were obtained, and results were compared to assess models’ performance under the heterogeneity of vaccine action.

7.2. Results

Depending on mixing patterns, there are two estimators of VE under each of the vaccine models. When the individual vaccine model was operating as the true model, results of simulation based on the first ρ matrix indicate that both estimators of the model provided unbiased estimate with good coverage (Table 2). Based on the second ρ matrix, the estimators (10) in the leaky model, (14) in the all-or-nothing model, and (23) in the summary model provided accurate estimates of the corresponding true VE with good coverage. However, the estimators (11), (15), and (24) in the leaky, all-or-nothing, and summary models, respectively, underestimated the true VE and provided worse coverage, because these estimators ignore the change in mixing due to vaccination. Moreover, between the models of vaccine action, the summary and all-or-nothing models performed equally but slightly better than the leaky model, given that the respective model acted as the true model. This holds true under all types of mixing pattern considered.

Table 2.

Estimates of vaccine efficacy, under all vaccine models, when individual model was operating as true model: mean estimate (), standard error (SE), and coverage (Cov %)

		Leaky model (true VE = 0.75)						All-or-nothing model (true VE = 0.60)						Summary model (true VE = 0.685)
		Estimator (10)			Estimator (11)			Estimator (14)			Estimator (15)			Estimator (23)			Estimator (24)
	HH size		SE	Cov		SE	Cov		SE	Cov		SE	Cov		SE	Cov		SE	Cov
ρrk,0 = ρrk,1	k = 1	0.787	0.034	69	0.771	0.039	65	0.621	0.022	73	0.625	0.024	67	0.694	0.022	74	0.667	0.025	71
	k = 2	0.775	0.026	72	0.763	0.033	69	0.619	0.020	75	0.614	0.023	72	0.692	0.023	73	0.668	0.021	74
	k = 3	0.738	0.020	77	0.747	0.031	74	0.616	0.018	77	0.620	0.027	78	0.689	0.018	79	0.679	0.017	77
	k = 4	0.741	0.019	83	0.732	0.022	81	0.608	0.012	88	0.591	0.020	88	0.683	0.010	89	0.683	0.011	86
	k = 5	0.746	0.019	86	0.741	0.021	85	0.604	0.013	91	0.596	0.021	87	0.604	0.013	91	0.692	0.021	87
ρrk,0 < ρrk,1	k = 1	0.772	0.036	70	0.691	0.062	60	0.617	0.027	71	0.524	0.041	61	0.693	0.024	73	0.612	0.035	64
	k = 2	0.769	0.023	71	0.683	0.060	62	0.618	0.021	76	0.538	0.033	62	0.691	0.025	72	0.631	0.033	68
	k = 3	0.729	0.024	77	0.687	0.053	65	0.611	0.019	76	0.551	0.025	70	0.687	0.017	77	0.637	0.026	70
	k = 4	0.745	0.018	84	0.662	0.046	68	0.603	0.010	89	0.573	0.029	70	0.681	0.012	88	0.641	0.021	73
	k = 5	0.751	0.015	87	0.665	0.041	71	0.602	0.008	92	0.573	0.019	76	0.682	0.009	90	0.662	0.022	76

To assess models’ performance under the heterogeneity of vaccine action, further simulation was conducted under a common true model of heterogeneous vaccine actions (i.e., the summary model was operating as true model in this case), and estimates of VE under each of the vaccine models were obtained. Results (Table 3) of simulation based on the first matrix of mixing pattern show that the leaky and all-or-nothing models possessed a biased estimate; however, the summary model provided an unbiased estimate with good coverage. Simulation based on the second matrix indicates that the estimator ignoring the change in mixing due to vaccination still provided a biased estimate.

Table 3.

Estimates of vaccine efficacy, for all vaccine models when summary model was operating as true model (true VE = 0.685): mean estimate (), and coverage (Cov %)

		Leaky model				All-or-nothing model				Summary model
		Estimator (10)		Estimator (11)		Estimator (14)		Estimator (15)		Estimator (23)		Estimator (24)
	HH size		Cov		Cov		Cov		Cov		Cov		Cov
ρrk,0 = ρrk,1	k = 1	0.723	63	0.725	62	0.644	63	0.640	62	0.694	74	0.667	71
	k = 2	0.724	65	0.720	65	0.645	64	0.642	63	0.692	73	0.668	74
	k = 3	0.720	66	0.718	64	0.646	65	0.645	65	0.689	79	0.679	77
	k = 4	0.719	67	0.718	67	0.648	65	0.648	65	0.683	89	0.683	86
	k = 5	0.718	68	0.715	68	0.651	67	0.651	66	0.604	91	0.692	87
ρrk,0 < ρrk,1	k = 1	0.749	67	0.727	68	0.650	65	0.621	56	0.693	73	0.612	64
	k = 2	0.745	66	0.728	69	0.652	68	0.622	57	0.691	72	0.631	68
	k = 3	0.742	67	0.723	68	0.647	67	0.623	58	0.687	77	0.637	70
	k = 4	0.740	68	0.721	70	0.648	68	0.624	58	0.681	88	0.641	73
	k = 5	0.740	69	0.720	72	0.651	69	0.631	59	0.682	90	0.662	76

For the household of larger size, all types of estimator provided comparatively more accurate estimates of the true value than those for the household of smaller size, which implies the usual problem related to sample size in getting a consistent estimate.

Estimates of VE under each of the vaccine models have different interpretations. For example, the estimate 0.600 under the all-or-nothing model can be interpreted as 60% of the vaccinated individuals begin completely protected from infection. The interpretation of the estimate 0.75 under the leaky model is that the transmission probability given exposure to one infective is reduced by 75%. The estimate under the summary model has, in terms of average, similar interpretation to those under the leaky model.

In section 6, we discussed the estimation of the vaccination coverage, where the estimator f*_k we derived is the function of the basic reproduction number R₀ and the vaccine efficacy. In this section, the methods were illustrated using the estimated vaccine efficacy from the simulation study and the basic reproduction number assumed at R₀ = 2. The estimated vaccination coverage under all models of vaccine action is presented in Table 4.

Table 4.

Estimates of the vaccination coverage under all models (using estimates of VE from table 2 when ρ_rk,0 < ρ_rk,1); the basic reproduction number was assumed at R₀ = 2

HH size	f* (Leaky)	f* (All-or-nothing)	f* (Summary)
k = 1	0.664	0.833	0.727
k = 2	0.664	0.832	0.729
k = 3	0.664	0.834	0.729
k = 4	0.665	0.834	0.728
k = 5	0.666	0.834	0.728
Overall	0.664	0.834	0.728

Under each model, there was no substantial difference among the household specific estimates of f*_k (k = 1, …, 5). However, between the models, the largest overall estimate was observed for the all-or-nothing model, which was followed by the estimate for the summary model, while the smallest one was observed for the leaky model. We do not know which model is operating in practice. In this case, the optimistic approach is to use the largest one. Moreover, following others studies (Ball et al. 1999), it is also suggested that larger households should be vaccinated first, because members of a larger household are expected to be infected more rapidly than those of a smaller household because of the existence of higher mixing in larger household than smaller one. Otherwise, the epidemic will spread very fast.

8. DISCUSSION AND CONCLUSION

Estimation of vaccine efficacy parameters depends on several assumptions, particularly those related to population structure and their mixing patterns, the routes of transmission of the infection agent, and vaccine response (Haber et al., 1991a). Most published studies on vaccine efficacy assume random mixing throughout the population. However, nonrandom mixing is common in a population that is stratified into small groups such as households. Although some studies consider nonrandom mixing, the heterogeneity of vaccine response among the hosts is often ignored. This work discussed the estimation of vaccine efficacy under the heterogeneity of vaccine action in a nonrandomly mixing population, for an acute directly transmitted disease. To allow for the heterogeneity of vaccine action in a nonrandomly mixing population, three models of vaccine actions were discussed, particularly focusing on the summary model proposed by Halloran et al. (1992) for a randomly mixing population. Estimation and interpretation of the summary vaccine efficacy were discussed in light of other two models: the leaky and all-or-nothing models suggested in Smith et al. (1984). Vaccine efficacy under all models was defined assuming a vaccine that lowers the transmission probability to vaccinated individuals. A deterministic approach proposed in Haber et al. (1995) was applied in estimating the transmission probabilities in terms of a log transformation of final attack rates.

To illustrate the methods, a simulation study was conducted under each of the vaccine models, depending on whether vaccination along with stratification alters the mixing pattern or not. The estimators under each of the vaccine models ignoring the change in mixing pattern due to vaccination underestimate their corresponding true VE. The simulation results, based on all types of mixing pattern, further confirmed that all models of vaccine action performed almost equally when the individual model was operating as true model of vaccine action. These results, particularly under the leaky and all-or-nothing models, are analogous to those in Haber et al. (1995) for a nonrandomly mixing population that is partitioned into two large groups. However, population in practice consists of several small groups such as households, where nonrandom mixing is obvious. This work provided information on estimating vaccine efficacy in such a small-group-mixing population.

One of the main objectives of the study was to estimate and assess performance of the vaccine models under the heterogeneity of vaccine action. This was accomplished by conducting a further simulation study based on a true model that considers heterogeneous vaccine actions. Results, from simulation based on all types of mixing pattern, confirm that the summary model performed better than both the leaky and all-or-nothing models. The reason is simple: The leaky and all-or-nothing models do not properly take into account the heterogeneity of vaccine action, while the summary model does. In practice, vaccine may have heterogeneous effects because of varying immune systems among the hosts (Halloran et al., 1992). Therefore, it is worthwhile to estimate vaccine efficacy based on the summary model. The estimator (23) we derived under the summary model of vaccine action for a nonrandomly mixing population has interpretation similar to those derived in Halloran et al. (1992) for a randomly mixing population. In addition, we derived an approximate expression for standard error of this estimator, which is useful to have an idea of its sampling distribution and to make an inferential statement. Further, following Halloran et al. (1992), a bound for the summary vaccine efficacy was derived when vaccinated strata was not identifiable, where the lower and upper bounds were represented by the vaccine efficacy under the all-or-nothing and leaky models, respectively.

This article further discussed, under the preceding models of vaccine action, the estimation of vaccination coverage required to control an epidemic. We derived a threshold value f*_k that depends on the basic reproduction number R₀ and the vaccine efficacy, and that has interpretation similar to those in other studies (Becker and Starczak, 1997; Ball and Lyne, 2002, 2006; Pellis et al., 2009). The methods were illustrated by using the vaccine efficacy obtained from the simulation study and assuming R₀ = 2. The numerical result shows that the estimates of f*_k were not identical for all models of vaccine action. In this case, the optimistic approach is suggested to use the largest value of f*_k. This kind of information would be useful for health policymakers to design an appropriate vaccination program.

Because of the unavailability of real field data, this article was unable to provide an application of the methods discussed. Therefore, providing an application of these methods to real field data could be a future research project. Further, these methods could be extended to a nonrandomly mixing population that is stratified in two levels: by households, then by homestay and outgoing groups, where unequal mixing between outgoing and home-stay groups is possible. Moreover, it would be reasonable to consider the heterogeneity of vaccine response for each individual rather than for a group of individuals, as vaccine responses vary from individual to individual. In this case, vaccine efficacy could be estimated by using a gamma frailty model, which takes into account the individual heterogeneity.

APPENDIX

Proof of the Inequality: VE^(M2)_k ≤ VE_k ≤ VE^(M1)_k

We assumed that overall mixing in the population is nonrandom due to stratification and vaccination. Also we let all other assumptions described earlier remain the same. We further assumed that α as well as the attack rates in vaccinated strata 1 and 2 are unknown. First, we prove that VE^(M1)_k ≥ VE_k,

Here ln(1 − A_k,0) is negative for 0 ≤ A_k,0 ≤ 1. Therefore, we have to prove

(42)

We assumed here that . That is, the crude estimate is equal to the weighted average. However, the last inequality remains unchanged. It is obvious that ln(1 − A_k,1) is a concave function as ln(1 − x) is concave for x ∊ ℛ, and therefore, equation (42) is true, which implies that VE^(M1)_k ≥ VE_k. For details, see Halloran et al. (1992). Similarly, it can be proved that VE^(M2)_k ≤ VE_k. Finally, we have

Hence, if we cannot identify the strata and do not know α, we have an upper and lower bound for the true summary vaccine efficacy, VE_k.