Mechanical Characterization of Tissue-Engineered Cartilage Using Microscopic Magnetic Resonance Elastography

Abstract

Knowledge of mechanical properties of tissue-engineered cartilage is essential for the optimization of cartilage tissue engineering strategies. Microscopic magnetic resonance elastography (μMRE) is a recently developed MR-based technique that can nondestructively visualize shear wave motion. From the observed wave pattern in MR phase images the tissue mechanical properties (e.g., shear modulus or stiffness) can be extracted. For quantification of the dynamic shear properties of small and stiff tissue-engineered cartilage, μMRE needs to be performed at frequencies in the kilohertz range. However, at frequencies greater than 1 kHz shear waves are rapidly attenuated in soft tissues. In this study μMRE, with geometric focusing, was used to overcome the rapid wave attenuation at high frequencies, enabling the measurement of the shear modulus of tissue-engineered cartilage. This methodology was first tested at a frequency of 5 kHz using a model system composed of alginate beads embedded in agarose, and then applied to evaluate extracellular matrix development in a chondrocyte pellet over a 3-week culture period. The shear stiffness in the pellet was found to increase over time (from 6.4 to 16.4 kPa), and the increase was correlated with both the proteoglycan content and the collagen content of the chondrocyte pellets (R²=0.776 and 0.724, respectively). Our study demonstrates that μMRE when performed with geometric focusing can be used to calculate and map the shear properties within tissue-engineered cartilage during its development.

Introduction

Articular cartilage serves as a load-bearing and low-friction surface that facilitates synovial joint motions. The ability of cartilage to resist compressive loads and internal shear stresses relies on the functional integrity of its extracellular matrix (ECM). The ECM consists of a solid network of macromolecular polymers (proteoglycan and collagen) surrounded by a fluid phase of water.¹ The frictional interactions between the solid and fluid phases establish the viscoelastic behavior of cartilage, which is important for normal lubrication and load transmission in the joint.² In the event of injury, when this integrity is breached, the avascular nature of cartilage limits the self-repair of the damaged cartilage. Therefore, implantation of tissue-engineered cartilage is being explored as a potential therapy.^3,4

Current efforts in cartilage tissue engineering have focused on optimizing the mechanical properties of the implant to withstand the loading conditions after transplantation.⁵ While a variety of culture systems, growth factors, and mechanical stimuli have been developed to fulfill this requirement,^6–10 optimal strategies are not yet fully established. Ideally, the successful engineering of cartilage implants should restore the viscoelastic properties of native cartilage. Cartilage exhibits flow-dependent and flow-independent viscoelasticity under different forces.⁵ Compressive loading causes interstitial fluid flow within the matrix, so the resulting viscoelastic behavior of cartilage is mainly due to the resistance to fluid flow through the ECM. In contrast, the interstitial fluid flow is minimal in shear, and the measured properties largely depend on the deformations of the solid ECM rather than the fluid exudation and redistribution.¹¹ Given that the viscoelastic properties of the solid ECM from flow-independent measurements are highly sensitive to biochemical alterations of the matrix constituents,² it is therefore important to frequently monitor the flow-independent viscoelastic properties of the engineered cartilage throughout its development.

Shear testing by small torsional displacements has been widely used to study the viscoelastic properties of the solid ECM of engineered cartilage under flow-independent conditions.^11,12 However, such methods only give bulk or average properties of the sample rather than the specific mechanical properties of local tissues. To address this problem, imaging-based methods, such as magnetic resonance imaging (MRI), have emerged as a promising way to nondestructively visualize the deformation and to measure the mechanical properties of soft tissues.¹³ MRI spin-tagging registration and MRI phase contrast methods have been used to track the deformation of cartilage explants (native and engineered) under static or cyclic compressive loading.^14–16 Although these MR-based methods can help elucidate the compressive properties of engineered tissues, they cannot decouple the solid matrix viscoelastic effects from the flow-dependent viscoelastic effects under compression. In contrast, magnetic resonance elastography (MRE) has been proposed as a nondestructive way to measure the shear modulus (or shear stiffness) of soft tissues under dynamic shear loading.^17–19 MRE uses small shear displacements (∼μm) and enables direct assessment of shear properties of the solid ECM. The measured shear modulus (or stiffness) thus reflects the deformation of the solid ECM network produced by cells.

Microscopic magnetic resonance elastography (μMRE) has extended MRE to the submillimeter scale to image shear waves in biological tissues and engineered tissues with high spatial resolution.^20–23 μMRE is achieved by coupling a mechanical actuator to the targeted sample. A phase-contrast MRI technique is used to visualize and quantitatively measure propagating shear waves in the sample subjected to harmonic mechanical excitation. From the observed wave pattern the local shear stiffness can be calculated on a pixel by pixel basis to provide a quantitative tissue stiffness map. Such maps can be used to depict changes of the ECM stiffness during tissue development. In previous studies conducted on larger engineered bone and fat tissues (4–5 mm), μMRE was applied using surface excitation at frequencies between 20 Hz and 2 kHz to assess changes in shear stiffness at different growth stages.^20–23 However, using μMRE to evaluate even smaller sizes (2–3 mm) of stiffer engineered cartilage tissues (e.g., above 100 kPa) is challenging as it requires a higher excitation frequency (>2.5 kHz) to shorten the shear wavelength.²⁴ One drawback of an increased excitation frequency is an increased wave attenuation in the targeted tissue.²⁵ To overcome rapid wave attenuation at higher frequencies in a relatively small and stiff material, we have developed a geometric focusing method for in vitro μMRE by utilizing the focusing effect of cylindrically inward propagating waves.²⁶ In geometric focusing μMRE, the samples are embedded into an agarose gel in a test tube. A small, harmonic shear displacement is applied to the samples by vibrating the entire tube axially at the desired high frequency (1–10 kHz) (Fig. 1). This motion generates a uniform axisymmetric shear wave that propagates concentrically inward. The waves attenuate as they travel away from the tube wall due to viscous loss in the gel and the embedded sample, but this attenuation is largely overcome by the geometric focusing. Previous studies have demonstrated the potential of this approach to assess the shear viscoelastic properties of the soft gel phantoms (Ecoflex and agarose) using shear waves in the frequencies range from 200 Hz to 7.75 kHz.^26,27

FIG. 1.

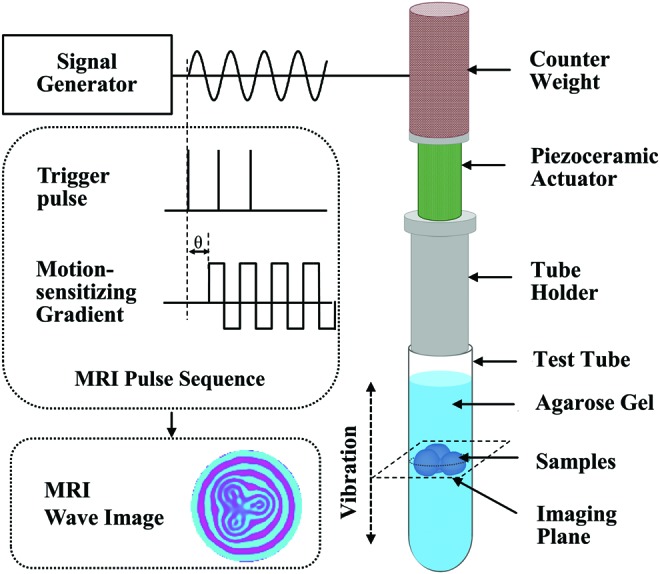
Microscopic magnetic resonance elastography (μMRE) setup. The magnetic resonance imaging (MRI) pulse sequence that encodes the mechanical motion through the application of motion-sensitizing gradient (MSG) is shown at the middle left. The piezoceramic actuator applies concentrically focused shear waves to the gel-embedded samples by vibrating the entire test tube axially at the desired frequency (right). The MSG and the actuator are synchronized using trigger pulses sent from the MRI scanner. An example of a shear wave image of gel-embedded alginate beads at driving frequency of 5 kHz is shown at the bottom left. Color images available online at www.liebertpub.com/tec

The objective of this study was to apply this geometric focusing μMRE method (at 5 kHz) to quantify the biomechanical shear properties of tissue-engineered cartilage in vitro, demonstrating the sensitivity of μMRE measurement over a range of material properties. Specifically, we first tested this new technique by monitoring the changes of shear stiffness in a calcium cross-linked alginate bead model, whose mechanical behaviors can be modified by exposure to different ion concentrations.²⁸ Then, we used geometric focusing μMRE to evaluate changes in the shear stiffness of scaffold-free engineered cartilage tissues (chondrocyte pellets) during a 3-week culture period. The μMRE results were correlated with biochemical analyses of the proteoglycan and collagen content in the chondrocyte pellets.

Theory (MRE)

MRE was originally developed as a noninvasive way to measure internal organ stiffness through the visualization of mechanically induced low-frequency spin motion.¹⁷ μMRE typically employs an MRI system with a higher magnetic field (11.7 T vs. 1.5 T) to obtain a better signal-to-noise ratio and thus extends MRE to the submillimeter scale.²⁰ To obtain higher spatial resolution, μMRE also uses stronger MR imaging gradients (200 G/cm vs. 5 G/cm) and more compact mechanical actuators to generate higher excitation frequencies than those used in the clinic.²⁹ The principle of MRE can be briefly described as follows.

MRE systems have three essential components: a triggered mechanical actuator, an MRI programmed with a special pulse sequence to synchronize the mechanical excitations, and an inversion algorithm to covert the MRI acquired wave motion into elastic or viscoelastic maps (elastogram). The actuator must be coupled to the tissue of interest in a manner to induce dynamic shear wave motion, typically in the low audible frequency range (20 Hz to several kHz). The MRI pulse sequence is used to encode the wave motion in the sample (Fig. 1). The encoding is obtained through the application of bipolar motion-sensitizing gradients (MSGs) that are synchronized with the mechanical excitations. When the oscillating MSGs are set to the same frequency as the mechanical harmonic motion, phase accumulation will occur in the phase component of the complex MR image.^20,30 This phase accumulation depends on the duration of the MSGs, the strength of the gradient field, the amplitude of the mechanical motion, the angle between the directions of mechanical motion and the MSGs, and the phase difference (θ) between the mechanical motion and the MSGs. The phase accumulation φ, for a given point in the image can be written in following general form,

where γ is the gyromagnetic ratio characteristic of the nuclei (42.57 MHz/T for H nuclei), G(t) is the time-dependent magnetic gradient vector, r(t) is the time-dependent displacement vector, and Δt is the duration of the MSGs. In essence, the phase accumulation ϕ provides a quantitative snapshot of the tissue displacement caused by propagating mechanical waves through its encoding in MR phase images. Acquisition of shear wave images at different time offsets of mechanical motion enables the reconstruction of complex valued shear wave propagation images.

The acquired wave images are used by the inversion algorithms to fit data to a shear viscoelastic model of the tissue.³¹ Assuming linear isotropy and infinitesimal harmonic shear motion at frequency ω=2πf, the viscoelastic behaviors of a homogeneous solid can be described by two complex Lamé constants λ and μ that predominantly control the longitudinal and shear strains, respectively. In soft tissue-like materials, the effect of first Lamé parameter λ can be simply neglected if the excitation is primarily shear.¹⁸ The second Lamé parameter is the shear modulus and can be written as μ*=μ_r+jωμ_i. Here, the Voigt model is used to extract the mechanical properties. μ_r and μ_i denote shear elasticity and shear viscosity.²⁰ The shear wave speed c_s and wavelength λ_s=c_s/f are then related to the complex shear modulus μ*:

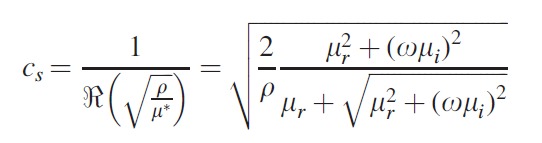(2)

where ω is the angular frequency of the mechanical motion and ρ is density. The wave speed itself can be reported as effective shear stiffness, defined as

and represents the shear modulus of an elastic material that exhibits the observed wave speed. In tissue exhibiting only a modest amount of attenuation (e.g., μ_i<0.1μ_r), shear stiffness is an approximation of the real part or magnitude of the complex shear modulus.¹⁹ For example, for 0.75% w/v agarose gel, the value of shear stiffness μ_s=9.15 kPa is close to the magnitude of the shear modulus |μ*|=8.99 kPa at a driving frequency of 550 Hz.²⁰ In the current study, shear stiffness μ_s is used as a simple means of comparing measurements in different materials.

The shear stiffness μ_s can be calculated if the wavelength λ_s is measured, as the frequency is known and the density of most soft tissues is close to the density of water (1000 kg/m³). A variety of approaches can be used to estimate the localized wavelength.³¹ In this study, the propagating wavelength λ_s is estimated at each pixel in the acquired wave image using the local frequency estimation (LFE) inversion algorithm applied to the wave images.³²

Materials and Methods

Alginate bead formation

Homogeneous alginate beads (∼2.5 mm diameter) were made using an extrusion-dripping method.³³ Briefly, alginate (Sigma) was dissolved in a 0.15 M NaCl solution. Low viscosity sodium alginate solutions (1.2% w/v) were slowly extruded through a 22-gauge needle into spherical drops that immediately fell into a CaCl₂ solution (102 mM). The resulting beads were allowed to polymerize in this solution for 10 min before two consecutive washes with 0.15 M NaCl solution to remove free calcium ions.

Chondrocyte pellet culture

Chondrocytes were harvested from the full depth of articular cartilage acquired from the metacarpophalangeal joints of 18-month-old bovines according to a published protocol.³³ Briefly, chondrocytes were released from the chopped slices of cartilage by enzymatic digestion using 0.2% pronase (Calbiochem) for 1 h followed by treatment with 0.025% bacterial collagenase P (Roche Applied Science) overnight at 37°C. Enzymes and digestion products were removed by passing the mixture through a 70-μm filter and centrifuging at 1200 rpm for 10 min. The collected chondrocytes were resuspended in Delbecco's Modified Eagle Media/Ham's F-12 Nutrient Mixture (DMEM/F12) culture medium (Mediatech, Inc.) containing 20% fetal bovine serum (Atlanta Biologicals) and 25 μg/mL ascorbic acid-2-phosphate (Sigma). Next, chondrocytes (5×10⁵) in culture medium were transferred into 1.5 mL microfuge tubes, and centrifuged at 1000 rpm for 6 min to form a pellet. The resulting cell pellets were cultured within the same tube for 3 days in a 37°C, 5% CO₂, and 100% humidity incubator, and then were transferred into a 15 mL conical tube at day 3, and continued to grow for 3 weeks. The tube lids were loosely capped to allow for gas exchange. The culture medium was changed every day for the first 3 days and every second day for the remainder of the culture period. At the end of each week, sample pellets (∼2.5 mm diameter) were removed for μMRE and biochemical analysis.

μMRE sample preparation and experimental design

For each μMRE experiment, three samples were embedded in 1% (w/v) agarose gel (Lonza) in a 10 mm customized MRE plastic tube. The agarose gel was used to promote the transfer of shear wave motions into the enclosed samples. The temperature of the agarose was ∼37°C to minimize damage to the embedded samples. The agarose was allowed 10 min to gel prior to the start of the measurements.

In the first experiment, the mechanical properties of the embedded alginate beads were modified by changes in the surrounding agarose gel. Two groups of agarose gels were prepared by dissolving agarose 1% (w/v) in tissue culture medium (DMEM/F12) or in a 1 mM CaCl₂ solution. The medium-based gel was used to induce changes in the mechanical properties of the alginate beads, while the calcium-based gel was used as a control in which the concentration of CaCl₂ was chosen to match its respective concentration (1 mM) in culture medium.^29,34 The shear stiffness of the beads was measured every 30 min for 7 h by μMRE.

In the second experiment, the chondrocyte pellets were taken weekly for μMRE analysis. The 1% (w/v) medium-based agarose gel was used to enclose the pellets. The medium-based agarose was required here to maintain chondrocyte cell viability by minimizing osmotic and pH changes between gel and enclosed living constructs. To confirm the mechanical stability of our gel/pellet preparations, the shear stiffness of the week 1 pellets were measured every 30 min for 4 h.

MRI and μMRE experiments

All experiments were performed using a vertical bore (54 mm diameter) Bruker DRX 11.74 T (500 MHz for protons) Avance MR Spectrometer (Oxford Instruments). A Bruker linear triple-axis gradient system with a maximum magnetic field gradient strength of 200 G/cm and a micro-imaging probe were used for all experiments. The Bruker 10 mm saddle coil was used for imaging.

The μMRE experiments were conducted as previously described.²⁷ Briefly, as shown in Figure 1, steady state harmonic mechanical motions (5 kHz) were generated using a piezoceramic stack actuator that provides 11.6 μm displacements at 100 V. The mechanical actuator assembly was fixed to the top of a 10 mm diameter MRE cylindrical tube that contains the gel-embedded pellets or beads, while the radio frequency (RF) saddle coil was positioned on the outside of the test tube, and with its center aligned with the middle of the sample. A key aspect of this assembly is that the vertical motion of the wall of the MRE tube serves as the source of the concentrically focused shear wave propagating uniformly into the gel/bead or pellet sample. Before starting the MRE pulse sequence, the MR system sent a trigger to a function generator (33220A Function/Arbitrary Waveform Generator, 20 MHz; Agilent Technologies Test and Measurement) to initiate the mechanical motion. The mechanical actuator was synchronized with the MSGs.

For data acquisition, a gradient echo based MRE pulse sequence was used with the following imaging parameters: pulse repetition time/echo time=1000/6 ms; flip angle=30°; field of view=10 mm; slice thickness=0.5 mm; two slices; in-plane resolution=78×78 μm; and MSG strength=120 G/cm. To monitor the propagation of the shear wave, eight temporal measurements were obtained by shifting the phase offset (θ) between the mechanical motion and the MSGs over the vibration period. At each of the time steps, two MR phase images were acquired. One was acquired with the MSGs as illustrated in Figure 1, and another was acquired after reversing the polarity of the MSGs. The phase difference (mechanical motion) image was formed by subtraction of two phase images.³⁰ From the wave image, the shear wavelength λ_s was estimated using the LFE inversion algorithm with directional filtering. A custom-made MATLAB (MathWorks, Inc.) program was used to calculate the shear stiffness and to create stiffness maps. Regions of interest (ROIs) in each slice were selected to cover the entire bead or pellet. The shear stiffness of each bead or pellet was averaged over all pixels in the selected ROIs. The T2-weighted MR images were also acquired using a spin echo sequence with the following imaging parameters: pulse repetition time/echo time=3000/64 ms; field of view=10 mm; slice thickness=0.5 mm; and in-plane resolution=78×78 μm.

Biochemical analyses

Each week, separate pellets (n=5) were first blotted dry and weighed to obtain the wet weight (WW). The pellets were subsequently treated with papain (100 μg/0.5 mL; Sigma) at 60°C and digested overnight. The total proteoglycan content was measured using the dimethyl-methylene blue (DMB) assay, which is based on a ratio of absorbance at 530/595 nm.³³ The total collagen content was measured from aliquots of the papain digest of the pellets after acid hydrolysis (6.0 N HCl, 108°C, 24 h) using a colorimetric hydroxyproline assay.³⁵ Using purified hydroxyproline standards, the total collagen content was calculated from 8.2 times the total hydroxyproline content.³³ The measured proteoglycan and collagen content were then normalized to the WW of pellets.

Statistical analyses

Both the MRE data and biochemical data are reported as mean±standard deviation. A one-way analysis of variance was performed to compare the means measured at each week over the 3-week culture period. Pearson's correlation analysis was applied to assess the relationship between shear stiffness and the corresponding ECM components (proteoglycan and collagen content) of the pellets. Statistical significance was defined as p<0.05. All statistical tests were computed using SPSS software (SPSS, Inc.).

Results

μMRE results of alginate beads

The μMRE-derived shear stiffness of alginate beads was measured over 7 h following embedding in two different formulations of agarose gels (Fig. 2). The shear stiffness of beads embedded in the medium-based gel decreased from 8.45±0.23 kPa to 2.01±0.09 kPa over 7 h, while no change in shear stiffness was observed in beads suspended in a calcium-based agarose gel.

FIG. 2.

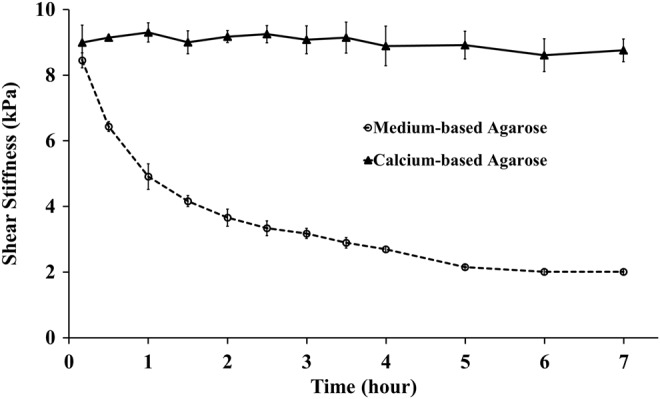
μMRE-derived shear stiffness at 5 kHz of alginate beads embedded in calcium-based (▴) and medium-based (○) agarose gels plotted versus time. The beads enclosed in the calcium-based gel were mechanically stable, while the beads suspended in the medium-based gel became softer. The plotted values represent mean±standard deviation (n=6 per group). μMRE, microscopic magnetic resonance elastography.

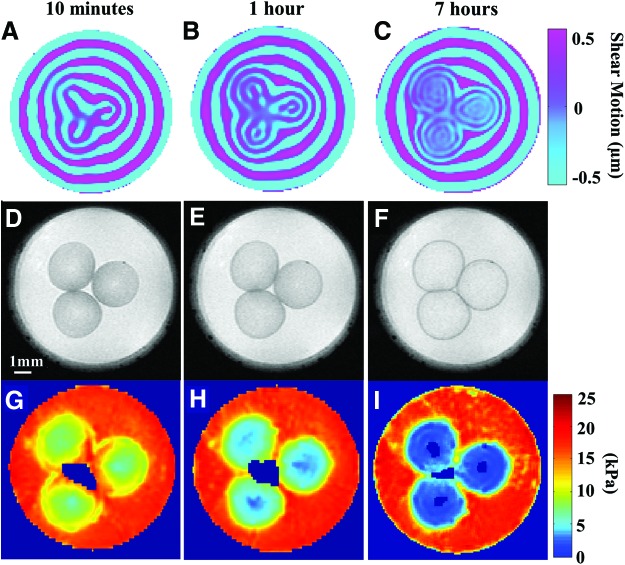
Shear wave images of alginate beads embedded in the medium-based agarose gel for 10 min, 1 h, and 7 h are displayed in Figure 3A, B, and C, respectively. The corresponding T2-weigthed MR images (with a voxel resolution of 78×78×500 μm³) are shown in Figure 3D–F. Finally, the computed shear stiffness maps at 10 min, 1 h, and 7 h generated by the LFE algorithm are presented in Figure 3G–I. In these figures, it is observed that the shear wavelength decreases over time with the swelling of beads. The shorter wavelength reflects softer samples with averaged shear stiffness at the measured times of 8.45±0.23 kPa, 4.91±0.39 kPa, and 2.01±0.09 kPa, based on the wavelengths of 0.6, 0.43, and 0.28 mm, respectively.

FIG. 3.

μMRE results of alginate beads embedded in the medium-based agarose gel. The first column displays alginate beads measured 10 min after embedding in the medium-based gel; the middle column displays beads at 1 h after embedding, and the last column presents beads embedded for 7 h. The first row (A–C) displays the shear wave images obtained from phase part of the complex MR images across an axial slice of the beads. The second row (D–F) displays the corresponding T2-weighted MR images with a resolution of 78×78×500 μm³. The third row (G–I) displays the shear stiffness maps obtained using the local frequency estimation (LFE) estimation. Color images available online at www.liebertpub.com/tec

μMRE results of chondrocyte pellets

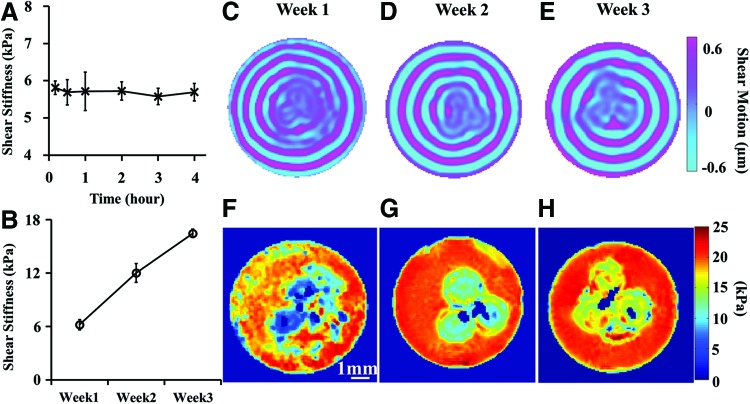
Although the medium-based agarose gel induced stiffness changes in alginate beads, no change in shear stiffness was observed for chondrocyte pellets after embedding in the medium-based agarose gel over 4 h (Fig. 4A). The shear stiffness of the chondrocyte pellets was measured over 3 weeks. Shear wave images of chondrocyte pellets acquired each week are shown in Figure 4C, D, and E, respectively. We observed an increase in the wavelength within the constructs with tissue development. The corresponding shear stiffness maps generated by the LFE algorithm are presented in Figure 4F–H. As shown in Figure 4B, the shear stiffness of the pellets increased from 6.19±0.57 kPa at week 1 to 12.01±1.06 kPa at week 2, to 16.45±0.46 kPa by the end of the third week, based on the wavelengths of 0.5, 0.63, and 0.8 mm, respectively. There was a significant increase in shear stiffness between successive weeks (p<0.05).

FIG. 4.

μMRE results of chondrocyte pellets measured at 5 kHz weekly. (A) Shear stiffness of pellets embedded in the medium-based agarose gel plotted versus time at week 1. (B) Shear stiffness of pellets during the 3-week culture period. The plotted values represent mean±standard deviation (n=6; three pellets per time point, two slices per pellet). The averaged shear stiffness showed a significant difference at all stages of development (p<0.05). (C–E) Shear wave images acquired each week from phase part of the complex MR images across an axial slice of pellets. (F–H) Shear stiffness maps obtained each week by LFE estimation. Color images available online at www.liebertpub.com/tec

Biochemical results of chondrocyte pellets

A progressive accumulation in both collagen and proteoglycan (% WW, normalized to the WW of pellets) was observed during the 3-week culture period (Fig. 5). The collagen content rose progressively during the culture period (week 1: 0.08±0.03%; week 2: 0.10±0.04%; and week 3: 0.16±0.03%). The proteoglycan content increased from 0.53±0.08% at week 1 to 0.88±0.1% at week 3. The collagen and proteoglycan content showed significant increase at all stages of development (p<0.05).

FIG. 5.

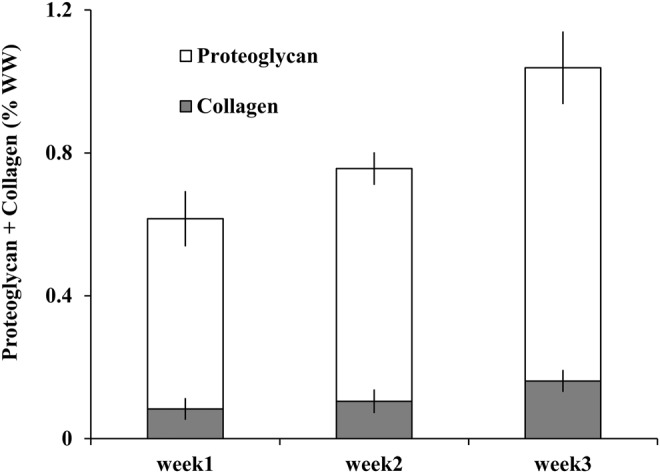
Accumulation of proteoglycan and collagen in the pellets over 3 weeks. The values are normalized to the wet weight (WW) of the pellets. The plotted values represent mean±standard deviation (n=5 per time point). The proteoglycan and collagen content showed a significant difference at all stages of development (p<0.05).

Correlation of matrix contents with mechanical properties

Pearson's correlation analysis revealed that the shear stiffness of the chondrocyte pellets was linearly related to proteoglycan and to collagen content (Fig. 6), while shear stiffness increased with increasing matrix content over the 3-week culture period. Specifically, the measured shear stiffness was highly correlated with both proteoglycan and collagen (R²=0.776 and 0.724, respectively).

FIG. 6.

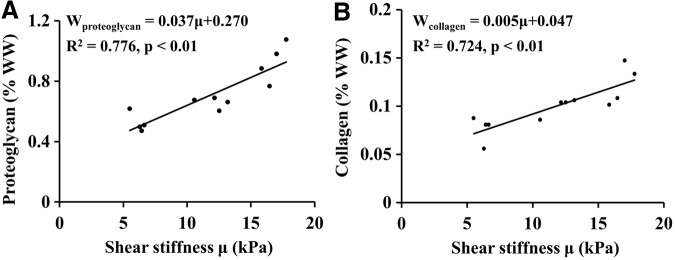
Correlations between MRE-derived shear stiffness and the corresponding (A) proteoglycan and (B) collagen contents. The regression equation, correlation coefficient, and its p-value are shown in each graph.

Discussion

The present study shows that μMRE with geometric focusing is able to nondestructively measure the shear stiffness of tissue-engineered cartilage under high-frequency (e.g., 5 kHz) shear loading. Micrometer shear wave motion was introduced into the constructs using geometric focusing excitation. The acquired MR wave images encode shear displacements and wave motion. Measurement of cyclic shear wave motions in the constructs provides the quantitative shear stiffness maps. Such maps can be used to monitor the formation of the ECM during tissue development.

Given that reliable estimation of shear stiffness requires the ability to detect at least half a wavelength in the measurement region,^24,36 MRE measurement of tissue-engineered cartilage is often challenged by the small size (diameter less than 5 mm) and high stiffness (shear modulus greater than 50 kPa) of the material. The small and stiff samples need a higher driven frequency to reduce the spatial wavelength. For example, the shear wavelength of 0.7% agarose gel is much smaller at a driven frequency of 5 kHz (0.7 mm) than at 550 Hz (5.5 mm).^20,27 Considering a stiff sample (100 kPa) with a diameter of 2 mm, which are typical properties for tissue-engineered cartilage, and using 1000 kg/m³ for the density, then according to Equation (3), the mechanical actuator should be driven at a frequency of 2.5 kHz or higher to ensure that at least half a wavelength is visible. While previous μMRE studies reported by Othman and colleagues have used surface excitation of gels in nuclear magnetic resonance (NMR) tubes to study the development of engineered bone and fat constructs at frequencies up to 2 kHz,^20–23 the wave penetration using surface excitation is diminished by an increase in wave attenuation at higher frequencies. The advantage of geometric focusing μMRE is its ability to compensate for rapid wave attenuation at higher frequencies (>2.5 kHz). Yasar et al. have used the agarose and Ecoflex phantoms to show that geometrically focused shear waves at 5 kHz result in a more uniform amplitude throughout the entire region within the tube, compared with the application of shear waves from the medium surface, which attenuate exponentially in amplitude.^26,27

In this study, μMRE with geometric focusing was first applied to alginate beads embedded in agarose gel, demonstrating its sensitivity to the changes of shear properties. The calcium cross-linked alginate beads were used because their mechanical properties could be easily modified. LeRoux et al. have reported that the dynamic shear modulus of the 2% (w/v) alginate gel fell by 84% over 15 h in a bath of physiological NaCl and CaCl₂ when compared with the gels placed in a CaCl₂ solution.³⁴ And the concentrations of NaCl (0.15 M) and CaCl₂ (1.8 mM) in their study were chosen to match their respective concentrations in DMEM culture media. Since, in vitro μMRE requires mechanical coupling between the sample and the mechanical actuator, a hydrogel (e.g., agarose gel) is needed to transfer the shear wave motion from the actuator to the embedded samples. In our study, we found that by preparing the agarose with tissue culture medium, the shear stiffness of beads decreased over time. This decrease in shear stiffness is likely due to the loss of cross-linking over time from the competition between the calcium ions and noncross-linking cations (e.g., K⁺, Na⁺, Mg²⁺, etc.) in the medium. As the cross-links were lost, the alginate beads swelled over time (Fig. 3D–F) with an associated decrease in the solid volume fraction of alginate. In contrast, the alginate beads were found to be mechanically stable in agarose gel formed with 1 mM CaCl₂. The shear stiffness of the alginate beads embedded in medium-base gel were within the range (dynamic shear modulus of 1–2 kPa after 15 h in 0.15 M NaCl) reported by LeRoux et al.³⁴ and Wan et al.¹²

For the chondrocyte pellet experiments, we prepared agarose gel with the tissue culture medium to maintain chondrocyte cell viability by minimizing osmotic and pH changes between the cell pellets and the supporting gels. The mechanical stability of pellets embedded in the medium-based gel was confirmed by the μMRE measurements of pellets over 4 hours. However, to be safe, all μMRE experiments were conducted in less than one hour to minimize any potential interference.

The shear stiffness values of chondrocyte pellets measured from μMRE method are also comparable with other ex vivo, but non-MRE, mechanical studies.^11,12,37 Graff et al., for example, measured an increase from 15.6 to 50.7 kPa in the equilibrium compressive moduli of chondrocyte pellets over a 3-week culture period.³⁷ It should be noted that in Graff et al.'s study, the investigators used a high cell density (1.6 million cells/pellet) that exhibited a high synthetic rate—more than three-folds of proteoglycan and collagen content per pellet—than was used in our study (0.5 million cells/pellet). Stading and Langer measured the complex shear modulus of polyglycolic (PGA)-based constructs under dynamic shear tests over an 8-week culture period. Their study found that the storage modulus increased from 1 kPa at week 1 to 15 kPa at week 8.¹¹ In another study reported by Wan et al., the dynamic shear moduli of cell-seeded alginate constructs (30 million cells/mL) increased from 4 kPa at day 1 to 20 kPa at day 40.¹²

For structure–function correlations, Stading and Langer reported a power law relationship between the shear properties and ECM components in a PGA-based cartilage construct over a 56-day culture period.¹¹ And, Wan et al. empirically determined an exponential relationship in their alginate-based cartilage constructs cultured over 40 days.¹² In the present study, however, a linear relationship was found between the shear stiffness and ECM components in the chondrocyte pellets over 21 days. The linear dependence reported here may therefore only reflect the contributions of ECM constituents to the shear stiffness of the chondrocyte pellets over a shorter culture period (21 days), and a nonlinear relationship may develop following a longer culture time. As chondrocytes proliferated and secreted both proteoglycan and collagen, the development of a continuous matrix in the pellets was monitored by the shear stiffness, which expresses the elastic stiffness resulting from the solid ECM deformation. If the matrix were absent, the shear stiffness would only reflect the elastic properties of the chondrocyte pellets. Therefore, as the ECM structure develops in the sample, the shear stiffness would be expected to increase with increasing proteoglycan and collagen contents.

In this study, we used the LFE algorithm to estimate the wavelength and calculate the shear stiffness. The LFE technique has been shown to be a robust, noise-insensitive inversion because of the sophisticated multiscale data averaging in the estimation.³² By using this method, the correct estimation is reached using only half a wavelength in a given region. It should be noted that there are “holes” in the stiffness maps (Figs. 3I and 4F–H), which correspond to regions that LFE failed to estimate the wavelength. For example, in Figure 3I, the shear stiffness cannot be calculated in the center of the beads. Although geometric focusing is designed to compensate for wave attenuation, when the stiffness of the beads decreased to 2 kPa, the shear waves may dampen too fast in the center of the beads for accurate wavelength estimation. In Figure 4F, the stiffness of the chondrocyte pellet at the right bottom corner cannot be determined. This may be due to the presence of a noticeable air bubble next to the right edge (image not shown), which was accidently trapped while making the gel. Since an air bubble can generate a magnetic susceptibility artifact that extends beyond its diameter and shear waves cannot propagate in the air, the air bubble could result in a noticeable wave distortion in the pellet next to it, and significantly affect the stiffness reconstruction around it.

Although LFE is a robust inversion with accurate and isotropic local frequency estimates, it has two limitations.²⁴ The first is that it has limited resolution, particularly at sharp boundaries, where the stiffness map is blurred. The second problem is that the LFE calculates only the local wavelength and does not account for attenuation. Therefore, the LFE-derived wavelength only estimates the magnitude of shear modulus rather than the complex shear modulus. To extract the attenuation and shear modulus with a higher confidence level, other inversion algorithms such as, direction inversion of wave equation and finite element analysis,²⁴ should be investigated in the future studies. Such inversion methods require all the components of motion within samples in three orthogonal directions to ensure the accurate calculation. However, the μMRE acquisition in the current work was performed in a single direction (out of plane) that captured only one component of the displacement. Future μMRE experiments should be performed so that the MSG directions are varied to capture all three orthogonal components of displacement.

In addition to the restrictions on sample size and stiffness—discussed above—our μMRE system with geometric focusing exhibits other limitations characteristic of MRI systems. For example, the inner diameter of the sample container (d) places a constraint on the maximum measurable wavelength λ_s≤2d, while the MR system resolution (Δx) places a constraint on the minimum measureable wavelength λ_s≥2Δx. In addition, to apply geometric focusing μMRE to even stiffer materials, such as fully developed engineered constructs with the stiffness of native cartilage (MPa), higher mechanical excitation frequencies (i.e., above 9 kHz) are required. Further, while μMRE itself is a nondestructive evaluation method, the current μMRE technique requires embedding the engineered constructs in a hydrogel for MRE force transduction. This prevents completely noninvasive measurements on intact tissue constructs. Further improvements in MRI hardware and the MRE mechanical excitation setup are needed to overcome these shortcomings, such as, an MRI compatible bioreactor with a small MRE actuator attached. Nevertheless, the primary advantages of μMRE are that it does not require tissue sectioning and that it can provide a quantitative tissue stiffness map throughout an engineered construct. Thus, μMRE has the potential to address many of the needs expressed by tissue engineers for direct monitoring and mapping of the mechanical properties of engineered tissue in vitro and in situ.

Conclusion

This work demonstrates that μMRE with geometric focusing can be used to nondestructively assess the shear properties of tissue-engineered cartilage at high-frequencies (e.g., 5 kHz). The measured shear stiffness is sensitive to the formation of the solid ECM components (proteoglycan and collagen) during tissue development.

Acknowledgments

The authors thank Lawrence Madsen and Kathryn Solka, from the Department of Biochemistry of Rush University for their kind help in sample preparation, and Dr. Robert Kleps, Director of the NMR Research Service Facility, Research and Resource Center at the University of Illinois at Chicago, for his technical assistance. This study was supported in part by the NIBIB Grant (EB007537).

Disclosure Statement

No competing financial interests exist.