Robust measurement of individual localized changes to the aging hippocampus

Abstract

Alzheimer’s Disease (AD) is characterized by a stereotypical spatial pattern of hippocampus (HP) atrophy over time, but reliable and precise measurement of localized longitudinal change to individual HP in AD have been elusive. We present a method for quantifying subject-specific spatial patterns of longitudinal HP change that aligns serial HP surface pairs together, cuts slices off the ends of the HP that were not shared in the two delineations being aligned, estimates weighted correspondences between baseline and follow-up HP, and finds a concise set of localized spatial change patterns that explains HP changes while down-weighting HP surface points whose estimated changes are biologically implausible. We tested our method on a synthetic HP change dataset as well as a set of 320 real elderly HP measured at 1-year intervals. Our results suggests that the proposed steps reduce the amount of implausible HP changes indicated among individual HP, increase the strength of association between HP change and cognitive function related to AD, and enhance the estimation of reliable spatially-localized HP change patterns.

1. Introduction

Alzheimer’s Disease (AD) is the most common form of dementia in the elderly. Its pathological process preferentially damages the hippocampus (HP), a brain region crucial to a variety of cognitive functions. Because this HP damage is visible on structural magnetic resonance images (MRI) of the brain, longitudinal MRI-based measurements of HP change have been proposed as markers of the effects of AD pathology, with possible uses in clinical diagnosis of AD and quantification of treatment effects in clinical trials [2,16,5]. Furthermore, HP atrophy associated with AD occurs with a stereotypical spatial progression: among HP sub-regions, AD-related damage begins in one region (called CA1) and spreads to another (subiculum) and yet another (CA2-4 and dentate gyrus). Therefore, numerous approaches for quantifying spatial patterns of localized HP atrophy have been proposed as measures that may be more specific to AD-related damage than total HP volume (for example, [6,25]). These efforts have suggested that localized HP damage to CA1 and subiculum may be preferentially associated with the pathology and cognitive consequences of AD [4].

However, quantitative measurements of how individual hippocampi evolve over time in response to AD pathology, based on serial MRI, have been rare. Most reports of localized HP changes related to AD are cross-sectional in nature, showing spatial patterns of differences between groups of HP that are each measured at a single time point [6,12]. Among reports of localized longitudinal HP change related to AD, most show population mean spatial maps of localized HP thickness at baseline and follow-up, without providing information about localized changes within any individual [22]. The few reports that do quantify individual-level change to localized hippocampal regions are mathematically rigorous [23,19], but assume one-to-one correspondences in hippocampal boundaries between time points, despite evidence that there can be substantial variability between tracings in terms of what portions of the anatomy are included within the hippocampus boundary [11,14]. In contrast to modeling longitudinal changes to individual closed surfaces such as the HP, several techniques measure individual longitudinal change trajectories at a voxel level [18,24]; for each individual, dense deformation fields among series of images are estimated, with various methods used to encourage the deformation fields to be spatially and temporally smooth. These exploratory quantifications of change are unbiased, highly automated, and general, but the need to detect subtle, localized shape changes to complex-shaped regions require deformation quantification at a very fine scale, making the methods computationally complex. Such longitudinal localized HP change measurements at an individual level will be important for eventually applying localized HP change measures to AD clinical diagnosis and to clinical trials.

The relative lack of scientific findings related to individual trajectories of longitudinal localized patterns of HP change is due to a series of unique technical challenges. The hippocampus is a small structure relative to typical voxel sizes in conventional structural MRI, especially when it is atrophied, and changes over short periods of time can be subtle, even in AD; this makes precise delineation of the HP in each image, and highly precise quantification of change, imperative. However, the HP is notoriously difficult to delineate in a reliable fashion; there are scores of manual tracing protocols [11] and even highly trained experts agree about where to trace the HP boundary to varying degrees on varying HP sub-regions [14,3]. Therefore, beyond precisely aligning baseline HP to corresponding follow-up HP, any method for measuring localized HP changes related to AD must be robust to discrepancies between baseline and follow-up in what tissue was or was not included in the delineation. In this work, we take advantage of prior knowledge of the AD pathological process to overcome discrepancies in hippocampus boundaries between baseline and follow-up. Specifically, it is generally agreed that during late-life aging and AD, the hippocampus atrophies rather than grows; we therefore attribute longitudinal hippocampal growth to erroneous boundary discrepancies and discount the impact of such apparent growth on longitudinal change estimates.

In this paper, we present a robust method for measuring longitudinal, localized patterns of spatial change to individual aging HP. We align follow-up to baseline HP by deforming the follow-up HP along its central cylindrical axis, and cut off ends of the structure that are not shared between the two delineations. Then we estimate weighted correspondences between baseline and follow-up HP. After baseline alignment to a template, rate of change in localized HP radius is quantified at a grid of surface points on the template, and points whose change rates are biologically implausible with respect to the aging and AD processes (i.e., regions whose local radius appears to increase with time) are down-weighted in subsequent quantification of localized spatial patterns of radius change. Those spatial patterns are estimated through a new version of Localized Components Analysis (LoCA) which searches for a concise set of localized HP regions whose change accounts for the greatest amount of HP change variability across the population [25]. Experiments on real data from real and synthetic data suggest that by downweighting biologically-implausible change, this new approach to longitudinal hippocampal change estimation provides more reliable change estimates that are more tightly linked to relevant clinical outcome measures.

2. Methods

Fig. 1 shows our framework for calculating individual hippocampus change. The cylinder-like HP surface is represented by a central axis, n_t slices along that axis, and n_θ surface points on each slice. The position of the central axis within each slice is calculated by taking the center of mass of all surface points in that slice. The central axis in this paper is estimated as the trajectory of mass centers of sample slices. Each surface point is represented by its cylindrical coordinates (t,θ), where t is the index of the slice and θ is the angle between a vector from the central axis to the surface point, and a vector in a canonical direction. The first step in the process is to align each individual’s follow-up HP to the corresponding baseline HP by shifting the follow-up HP along its central axis and cutting off slices at the ends that are not shared between the two segmentations (Fig. 1a and b). Template alignment similarly shifts each baseline HP along its central axis to align it to the HP of a typical healthy individual (the template HP) and cuts off non-shared slices; it also deforms the baseline HP to correct for major differences in HP shape between individuals. For each surface point on each baseline HP, a set of weighted (soft) correspondences are then estimated between that point and points on the corresponding follow-up HP; the rate of HP change over time at each baseline surface point is calculated in terms of differences in local HP radius (i.e., the length of the vector from the central axis to the point) between baseline and the follow-up surface points that it softly corresponds to (Fig. 1b). Hard correspondences between baseline HP and the template HP allow for comparison of HP change rate across individuals at standardized surface locations.¹ At each location on the template HP we find individuals whose estimated radius change there is biologically implausible (Fig. 1c); we then estimate a set of shape components, or spatially localized spatial patterns of coherent HP change(Fig. 1d), while down-weighting the influence of such implausible change. The following sections describe each step in detail.

Fig. 1.

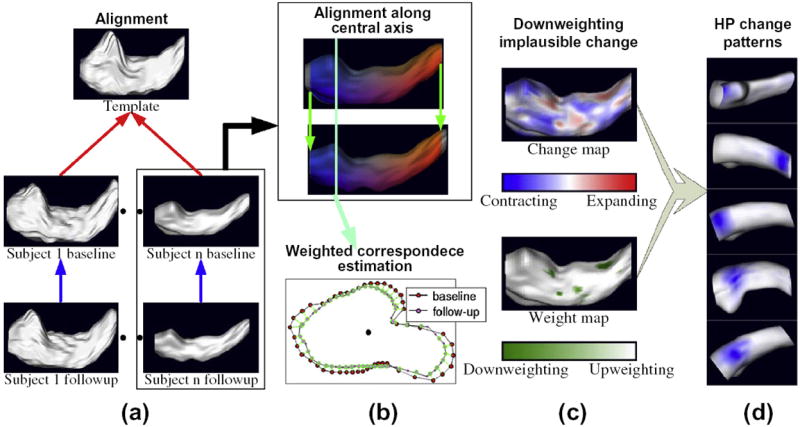
Framework for measuring longitudinal localized hippocampus change. (a) Follow-up HP are aligned to baseline HP (blue arrows) and baseline HP are aligned to a common template (red). (b) The alignment consists of deforming and shifting HP along their central axes, cutting off structure end slices not shared between the pair (top), and establishing weighted correspondences at each surface point (bottom). (c) Rates of local HP radius decrease are estimated (top) and points with implausible change rates are down-weighted. (d) Spatial patterns of coherent HP change (blue spots) are generated by a version of LoCA that accounts for the down-weighting. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

2.1. Alignment along central axis

2.1.1. Motivation

The anterior and posterior anatomical boundaries of the HP are notoriously difficult to identify in typical MRI scans, and therefore longitudinal series of HP tracings are plagued by inconsistencies in where those boundaries are drawn. These boundary inconsistencies cause portions of the structure to be present at some time points and absent at others, and therefore cause errors in the estimation of point correspondences between time points. Aligning follow-up to baseline HP identifies the portion of the HP that is shared between the two time points, with a goal of deleting the remainder of the tracings that were traced at one time point but not the other. Alignment of baseline HP to a template then aims to extend this analysis to identify the portion of the HP that was traced across all individuals.

2.1.2. Alignment definition

For both the alignment of baseline to follow-up, and the alignment of baseline to template, the purpose of alignment along the central HP axis is to estimate a function f that maps slices t of one HP to slices f(t) of the other. For both alignments, we allow f(t) to be undefined for t at the ends of the HP, to account for the very common differences between HP (even of the same individual) in terms of the starting and stopping points of the segmentation (see Fig. 2e and f). Differences between baseline and follow-up HP in the region starting and stopping points represent inconsistencies in the segmentation algorithm; analogous differences between baseline and template HP may additionally represent real anatomical differences. For the alignment of baseline HP to the template, a deformable model is used to account for differences in HP morphology between individuals. For the alignment of follow-up HP to baseline, f is simply a translation designed to cut off non-shared HP slices from both segmentations; a deformable alignment between the two could in fact remove real HP change that had occurred over time.

Fig. 2.

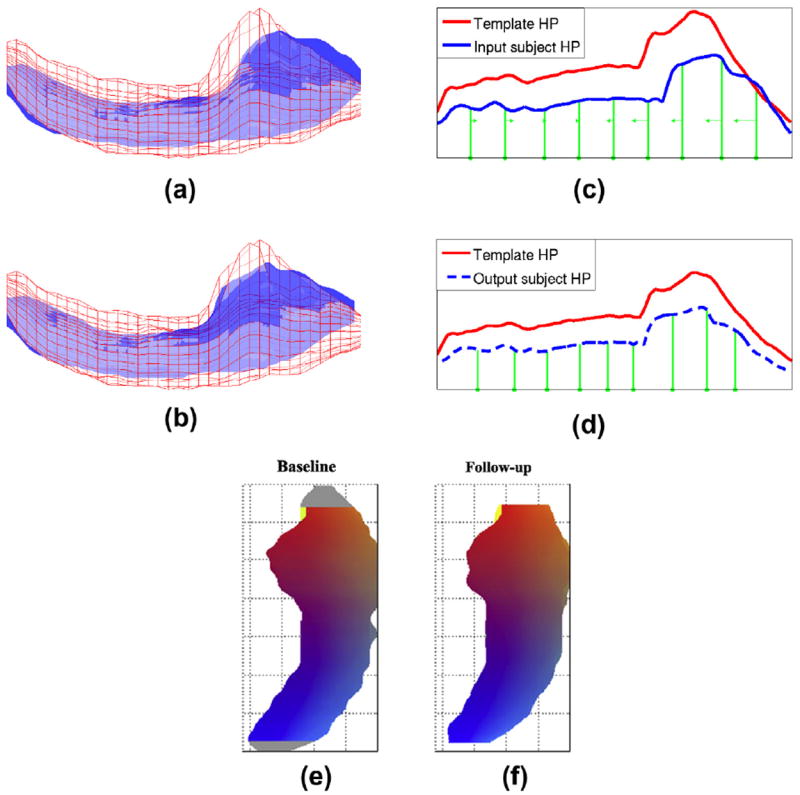
A baseline subject HP (blue surface) and a template HP (red wireframe) are shown overlaid before (a) and after (b) alignment from an inferior viewpoint. The curves plotting maximum distance from surface points to the central axis in each slice drive the alignment, and are more similar after alignment (d) than before (c). Green lines show positions of control slices before alignment (c) and after (d), with the direction and magnitude of control slice motion indicated by arrows. (e) (f) After baseline and follow-up HP are aligned, it is very common for end slices to occur in one HP that have no obvious counterpart in the other (gray). There slices are removed prior to change rate estimation. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

2.1.3. Control point definition

For deformable alignment, we place p slices spaced at uniform intervals along the central axis of an individual baseline HP and the template baseline HP respectively. Let the slice positions of these p control slices along the baseline HP be denoted {c₁, c₂, - ⋯, c_p}. Moving these control points to new positions $\left\{c_1^{\prime },c_2^{\prime },\cdots ,c_p^{\prime }\right\}$ defines a deformable mapping between baseline and template slices: $f(t)={\sum }_{i=0}^p{c}_i^{\prime }{k}_i(t)$ for kernel functions k_i(t). The kernel functions insure that slice c_i in the baseline HP maps to slice $c_i^{\prime }$ in the template HP, and slices between c_i and c_i+1 are smoothly mapped to slices between $c_i^{\prime }$ and $c_{i+1}^{\prime }$. In our experiments we used linear kernel functions:

$$k_i(t)=\{\begin{array}{ll}\frac{t-c_{i-1}}{c_i-c_{i-1}},& c_{i-1}\le t\le c_i,i>1\\ \frac{c_{i+1}-t}{c_{i+1}-c_i},& c_i\le t\le c_{i+1},i<p\\ 0,& \mathrm{otherwise}\end{array}$$

2.1.4. Similarity metric

Thus, the deformable alignment amounts to estimating $\left\{c_1^{\prime },c_2^{\prime },\cdots ,c_p^{\prime }\right\}$, and the alignment of follow-up to baseline is an estimation of a translation along the central axis. These transformations are optimized to maximize HP similarity. To calculate this similarity, we first define a function d(t) along the length of the HP axis that gives the maximum local radius of all surface points on slice t− that is, the maximum distance from boundary points on slice t to the central axis (Fig. 2c and d). The similarity metric that drives alignment is the Pearson correlation coefficient between the d(t) for the transformed HP and the d(t) for the template one.² The summary curves provide a computationally efficient means for evaluating shape similarity while capturing the anatomically salient characteristics of HP morphology.

2.1.5. Alignment optimization

The basic approach of modifying the transformation to maximize HP similarity is modified to account for additional factors. First, while we want to cut off slices of tissue that are not shared between HP, we also want to prevent the alignment from aggressively cutting off too many slices in the pursuit of higher similarity values. Therefore, the similarity metric is a linear combination of terms that try to maximize HP similarity, and the amount of HP that overlaps between the two, respectively. That is, we maximize λρ + (1 − λ)γ, where ρ is the correlation between d curves; γ is the percentage of HP slices on the fixed HP that overlap with the transformed one; and λ is a constant between 0 and 1. In addition, we encourage the transformations to stay numerically well conditioned by imposing lower and upper bounds on the distance $c_i^{\prime }-c_{i-1}^{\prime }$ between adjacent transformed control slices. We use the fminsearch routine in Matlab to maximize the alignment objective function with respect to the transformation parameters, and to solve the new positions of the moving control point slices $\left\{c_1^{\prime },c_2^{\prime },\cdots ,c_p^{\prime }\right\}$. See Fig. 2a and b for an example baseline HP whose similarity to the template increases substantially after alignment.

2.2. Weighted correspondence estimation

2.2.1. Motivation

Given pairs of follow-up and baseline HP whose slices have been aligned, previous approaches have established correspondences across HP between surface points that have corresponding cylindrical coordinates [22]; in theory, the rate of HP change can be calculated by computing the difference in local HP radius at those corresponding surface points. However, because each HP slice is based on a relatively small number of image voxels, the number of non-redundant surface points is also small, thus causing many surface points to have no single natural correspondence on the other HP (see Fig. 3). Therefore, we use weighted correspondences to assess the change rate in local HP radii: we map each surface point to a weighted average point on the other HP, where the weights are based on proximity to the surface point and proximity to the surface normal vector at that surface point.

Fig. 3.

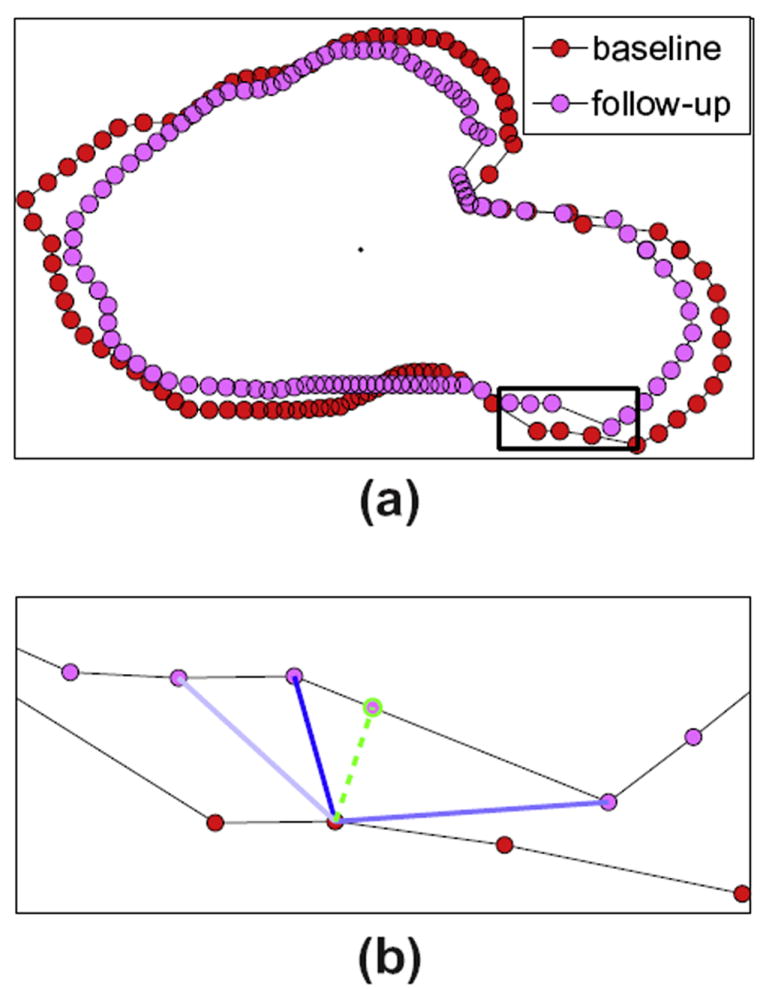
(a) Corresponding slices from a baseline and follow-up HP are shown overlaid. (b) Expanded view of a sub-region of these slices illustrating weighted correspondence. A point on the baseline HP is mapped to the green point on the follow-up HP, which was found by a weighted average of the positions of follow-up points (pink) by their distance to the baseline point and how they deviate from the surface normal direction at the baseline point. Higher weights are indicated by darker blue lines to the baseline point. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

2.2.2. Mathematical definition

More formally, we map each surface point in the baseline HP that has cylindrical coordinates (t, θ₀) to a weighted average point Σ_θ ϖ(θ₀, θ)pos(f(t), θ), where pos(t, θ) is the Cartesian coordinates of HP surface point (t, θ).

2.2.3. Weight estimation

The weighting function ϖ(θ₀,θ) is a sum of two terms that depend on the proximity of pos(f(t), θ) and pos(t, θ₀) and the similarity of vector from pos(t, θ₀) to pos(f(t), θ) to the surface normal vector at pos(t, θ₀). For proximity, we use a logistic function $l(x)=2-\frac{2}{1+e^{-\frac{x}{T}}}$ governed by a slope parameter T, and for similarity in surface normal orientation we calculate the inner product between the surface normal at pos(t,θ₀) and the vector between pos(t, θ₀) and pos(f(t), θ). Let i(θ, θ₀) denote this inner product, and let dis(θ, θ₀) denote the Euclidean distance between pos(t, θ₀) and pos(f(t), θ). The weighting function is then ϖ(θ₀, θ) = β l(dis(θ, θ₀)) + (1 − β)i(θ, θ₀), in our experiment, β was set to 0.8. The plot of the logistic function l() is shown in Fig. 4, the parameter T controls how fast l(x) goes to zero. It is natural to think that if a baseline slice is thick, i.e., the average radius is large, then the radius change over time can be large. Therefore we set T to be constantly proportional to the average thickness of the corresponding baseline slice.

Fig. 4.

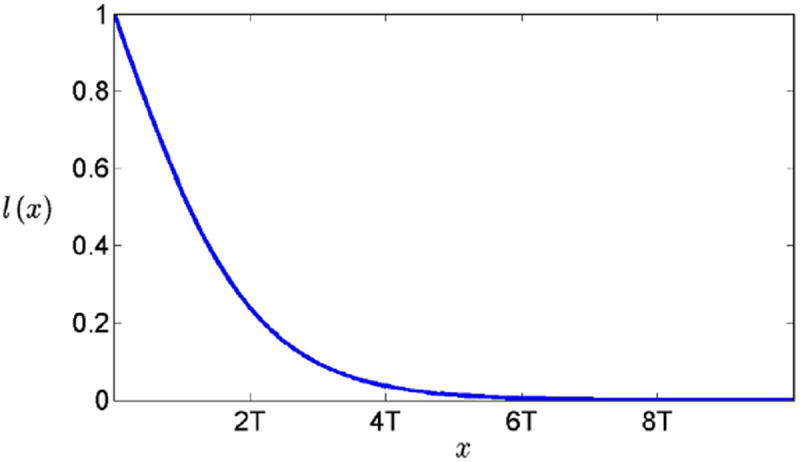
Logistic function used to establish weighted correspondences between HP surface points.

After weight estimation, for every baseline point, the follow-up boundary points with the highest N weights are picked. The weights of these follow-up points are normalized so that they sum up to 1. The image of a baseline point is the weighted average of the Cartesian coordinates of these N points.

2.3. Downweighting

2.3.1. Motivation

The weighted correspondences allow us to calculate the difference in local radius between each baseline HP surface point and its weighted correspondence point on the follow-up HP; dividing this difference by the interval between baseline and follow-up scans provides a rate of local HP change. The alignment of baseline HP to the template allows us to assemble measurements of rates of local radius change across all individuals at the template surface points. However, because noise in HP boundary measurements is high, and because the alignment procedure does not perfectly align the HP, some individuals are likely to have spurious weighted correspondences at some surface points, even after alignment and weighted correspondence estimation, leading to spurious estimates of local radius change. Therefore, for each surface point we discount rates of change that are outliers over the population, and also use biological knowledge about the aging and AD processes to discount the influence of such points on estimated spatial patterns of change. Specifically, there is overwhelming evidence that aging and AD pathology decrease the size of the HP by promoting death of neurons, without increasing its size (see, e.g., [7,10,20]) ; thus, at each HP surface location, positive rates of radius change, suggesting HP growth, are considered implausible and are thus downweighted.

2.3.2. Outlier penalization

Let r_i,t,θ denote the radius change rate of subject i at template HP cylindrical coordinate (t, θ). We calculate the mean and standard deviation of r_{i,t, θ} over i, μ_{t, θ} and σ_{t, θ}, and for each i calculate a weight w_i,t,θ for point (t,θ) that tends toward zero as change rates become greater than the mean plus one standard deviation:

$$W_{i,t,\theta }=\{\begin{array}{cc}l\left(\frac{r_{i,t,\theta }-{\mu }_{t,\theta }}{{\sigma }_{t,\theta }}\right),& r_{i,t,\theta }>{\mu }_{t,\theta }+{\sigma }_{t,\theta }\\ 1,& \mathrm{otherwise}\end{array}$$

The logistic function l() is defined as above. In our experiments we set the logistic slope T to .25. These weights are incorporated into the following step that estimates spatially-localized patterns of coherent local HP radius change. The algorithm makes less of an attempt to account for HP change in individual points that have low w_i,t,θ, i.e. surface points whose change rates are implausible high outliers.

2.4. Localized change components

2.4.1. Motivation

Now we have radius change estimates and a weighting for their plausibility at each surface point and individual. Our goal is to reduce the large number of such numerical measurements to a small, intuitive set of summary measures that describe spatial patterns of hippocampus change that are shared across the population. Therefore, we apply a modified version of a linear subspace method, LoCA, to aggregate radius changes according to their weights over spatial neighborhoods and provide a compact set of HP shape change patterns.

2.4.2. Traditional LoCA

After downweighting, the HP of subject i can be represented by a vector v_i of the local radius change rates r_i,t,θ, and a weight vector w_i of the corresponding w_i,t,θ. We then use a new version of Localized Components Analysis (LoCA), called Weighted LoCA, to estimate a linear subspace for the set of v,w pairs [1]. LoCA attempts to find an orthogonal set of basis vectors e₁, ⋯, e_n that provide a concise and spatially localized explanation for the set of v_i vectors. A basis vector represents a vectorized matrix of shape changes on its surface grid. Because the basis vectors capture a dominant pattern of local HP radius change, we refer to them as HP change patterns. After estimation of the e vectors, individual HP are represented by several change pattern coefficients α_i,j, where v_i ≈ e₀ + Σ_jα_i,j * e_j. Each α_i,j quantifies the degree to which a particular HP change pattern e_j is indicated in the HP local radius change vector v_i. LoCA generates the initial basis vectors from the covariance matrix of the v_i, and iteratively optimizes them to minimize an energy function that is a linear combination of 2 terms: a conciseness term and a locality term. The former one, like PCA, attempts to make the smallest number of e vectors account for the largest amount of variance in the v_i as possible; the variance accounted by vector v_j can be computed as the variance of the change pattern coefficients α_i,j. The locality term penalizes basis vectors that are not spatially localized. Generally speaking, spatial locality means that all non-zero entries of a basis vector correspond to surface points that form a spatially localized subregion. The LoCA optimization process iteratively rotates pairs of basis vectors in the plane they span in an attempt to optimize the conciseness and locality terms. Extensive simulations have suggested that the LoCA energy function is smoothly varying and well behaved, often with a single global minimum; optimization based on a widely available gradient-free optimizer almost always converges to the global minimum (see Section 2.0.7 and Section 3.0.8 of [25].

2.4.3. Weighted LoCA

The addition of the weight vectors w_i,t,θ modifies this optimization in three ways. First, the calculation of e₀, the population average HP change rate vector, becomes a weighted average. That is, the entry e₀[k] representing the average change rate in template HP point k is calculated by: ${\mathbf{e}}_0[k]=\frac{{\sum }_i{\mathbf{w}}_i[k]{\mathbf{v}}_i[k]}{{\sum }_i{\mathbf{w}}_i[k]}$. Similarly, the covariance matrix becomes a weighted covariance matrix whose entries C[j,k] are: $C[j,k]=\frac{{\sum }_i{\mathbf{w}}_i[j]{\mathbf{v}}_i[j]{\mathbf{w}}_i[k]{\mathbf{v}}_i[k]}{{\sum }_i{\mathbf{w}}_i[k]{\mathbf{w}}_i[j]-1}$. Third, while calculating conciseness energy term, the coefficient α_i,j becomes a weighted inner product between vectors v_i and e_j, that is α_i,j = Σ_k(v_i[k] − e_o[k])w_i[k]e_j[k]. If v_i[k] represents implausible longitudinal change, its weight vector entry w_i[k] will be less than 1. If e_j affects that surface point, i.e. e_j[k] > 0, the reduced weighting will make the coefficient α_i,j smaller, and thus v_i[k] will contribute less to the variance accounted for by e_j. Because basis vectors are more significant (high ranked) if they account for more variance, the downweighting therefore reduces the importance of basis vectors covering the region where estimates of change are less confident. Note that if the elements of the weight vector are all 1, weighted LoCA reduces to the original definition of LoCA.

3. Experiments

Our experiments used synthetic and real data to evaluate the effectiveness of the proposed method for quantifying localized HP change patterns. We first tested whether the downweighting strategy and weighted LoCA increase the ability to detect ground-truth longitudinal change patterns in noisy synthetic hippocampi. Then we tested the overall method on hippocampi from clinical groups consisting of AD patients, amnestic mild cognitive impairment (MCI) patients, and normal controls from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) [15,13]. We assessed the localized change patterns calculated after application of each subsequent step of the algorithm to show stepwise improvements in performance. Performance was assessed in terms of plausibility of group average longitudinal change maps within each clinical group, plausibility of the 5 most significant localized change patterns estimated, and strengths of association between change pattern coefficients and cognitive outcome measures. We note that the baseline version of the algorithm, without alignment, weighted correspondences, or outlier removal, corresponds to a trivial longitudinal extension of the LoCA algorithm [25], and that point-by-point mapping of hippocampus changes without these algorithmic enhancements has been presented as a competing method for quantifying localized change [22].

3.1. Synthetic HP dataset

3.1.1. Data generation

Starting with the population-average HP from the ADNI data set described below, we generated longitudinal series of synthetic hippocampi by adding the following three sources of variability to the shape: 1. a shape change pattern that represents linear longitudinal atrophy to an HP sub-region, such as may accompany aging or AD; 2. white noise across the entire surface that simulates global and random measurement error, for example due to limits in image resolution; 3. systematic noise due to inconsistency in the anatomical definition of HP sub-region boundaries. More formally, the change vector for subject i is computed as ${\mathbf{v}}_i={\mathbf{e}}_0+{\sum }_{j=1}^k{\alpha }_{i,j}\ast {\mathbf{e}}_j+n_w+n$, where e₀ is the average HP change pattern over the population, and the change patterns e_j are predefined and spatially localized. In our experiment, we chose k = 3 and |e_j| = 1 for all j = 1, …, k. Each coefficient α_i,j is drawn randomly from a zero mean normal distribution. To allow the algorithm to distinguish the e_j from each other, the variances of α_i,j for differing e_j differed: α_i,1 ~ N(0, 1.5), α_i,2 ~ N(0, 1.25) and α_i,3 ~ N(0, 1). n_w is Gaussian white noise whose magnitude is constant across the entire HP surface. The n noise vector specifically induces spurious positive hippocampus changes in the portion of the HP surface covered by e₁. Specifically, n is generated by drawing from a zero mean normal distribution and taking the absolute value. Entries in n are then set to zero if the corresponding entry in e₁ is zero. We estimated the weight vector w_i for each v_i using the same calculation introduced in Section 2.3. The result using traditional LoCA on {v_i} is compared with that generated by applying weighted LoCA on {(v_i, w_i)}.

3.1.2. Change pattern estimate

In Fig. 5, the first row, from left to right, lists the three ground truth change patterns e₁, e₂ and e₃. The change pattern e₁ covers the lateral posterior region of HP where the change estimates were affected by the systematic noise. The second and third rows illustrate two typical results generated by running weighted LoCA on the synthetic data with and without downweighting. Only the change patterns that account for more than 5% of total variance are shown. In the third row, the generated change patterns are basically the same as the ground truth. In the second row, there are two change patterns (column 2 and 4) that both cover the lateral posterior region, representing an artifactual reporting of one true underlying region of atrophy into two separate change patterns. This suggests that surface noise can induce a set of change patterns that are less concise than they could be. Because the LoCA optimization is a random process, we ran our program on simulated data with and without downweighting for 20 times respectively. In 14 sets of results based on synthetic data without downweighting, the change pattern e₁ was split into two change patterns. In contrast, this happened 10 times if we downweighted the noisy data. By analyzing the ground truth coefficients α_i,1 and the corresponding coefficients generated from the downweighted data, we found that the correlation coefficient between the two sets of coefficients during the 20 runs is always higher than 0.999. Together, these observations suggest that weighted LoCA together with the downweighting strategy extracts reliable local change patterns from noisy data in a more stable way.

Fig. 5.

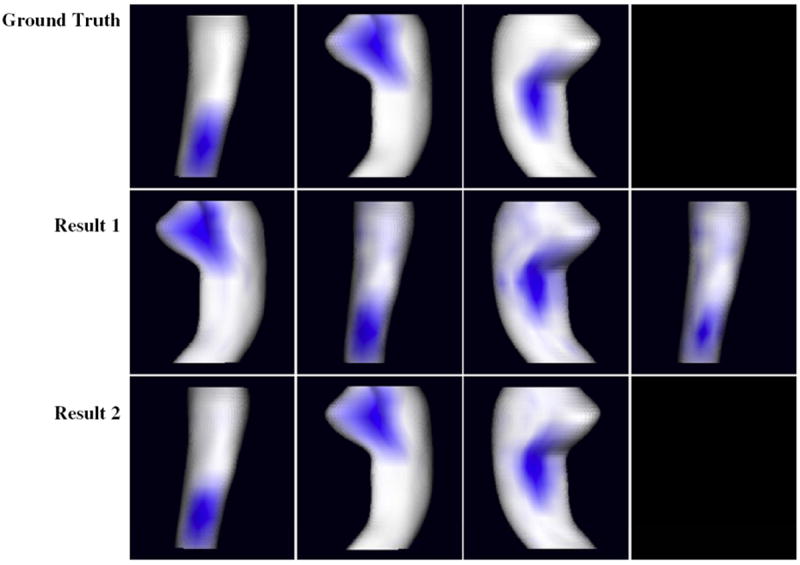
For synthetic dataset, the ground truth change patterns and two sets of typical LoCA change patterns accounting for more than 5% of HP change rate variability are shown. The magnitudes of change pattern entries are illustrated by intensities of blue color. For each rendering, the change pattern accounts for a coherent pattern of change in the region shown in blue. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

3.2. ADNI HP dataset

We tested our methods on a set of 79 AD patients; 146 patients with amnestic mild cognitive impairment (MCI), an AD precursor condition; and 95 normal controls from ADNI who had baseline and 12-month follow-up MRIs, and semi-automated HP segmentations. MCI is a clinical condition characterized by cognitive impairment that is not adequate to meet clinical criteria for AD. Individuals with MCI show many of the cardinal signs of eventual dementia, including reduced hippocampus volume on MRI and other biomarker measurements consistent with dementia[17].

ADNI

Data were obtained from the ADNI (www.loni.ucla.edu/ADNI). The ADNI was a 5-year study with a primary goal of testing whether serial MRI, positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (MCI) and early Alzheimer’s Disease (AD). Subjects were recruited from over 50 sites across the US and Canada. The initial goal of ADNI was to recruit 800 adults, ages 55–90, including approximately 200 cognitively normal older individuals to be followed for 3 years, 400 people with MCI to be followed for 3 years, and 200 people with early AD to be followed for 2 years.

3.2.1. MRI acquisition

Acquisition of 1.5T MRI data at each performance site followed a previously-described standardized protocol that was rigorously validated across sites. The protocol included a high-resolution T1-weighted sagittal volumetric magnetization prepared rapid gradient echo (MP-RAGE) sequence. The ADNI MRI core optimized the acquisition parameters of these sequences for each make and model of scanner included in the study. Before being allowed to scan ADNI participants, all performance sites were required to pass a strict scanner validation test, including MP-RAGE scans of human subjects and a spherical fluid-filled phantom. Additionally, each scan of ADNI participants included a scan of the phantom, which was required to pass strict validation tests. All vetted raw scan data was transferred to the University of California, San Francisco for semi-automated HP volumetry.

HP delineation

Semi-automated delineation of all ADNI baseline and 1-year follow-up hippocampi was carried out using a commercially available high dimensional brain mapping tool (Medtronic Surgical Navigation Technologies, Louisville, CO), that has previously been validated and compared to manual tracing of the hippocampus. Measurement of hippocampus volume is achieved first by placing manually 22 control points as local landmarks for the hippocampus on the individual brain MRI data: one landmark at the head, one at the tail, and four per image (i.e., at the superior, inferior, medial and lateral boundaries) on five equally spaced images match the individual brains to a template brain. The fluid transformation is used to label hippocampus pixels in the native space of the subject scan, resulting in a binary image representation of the HP structure. The number of hippocampus voxels in this space is counted to obtain the total HP volume. This method of measuring hippocampus volume agrees strongly with fully-manual delineations, with a documented intraclass correlation coefficient between semi-automated and manual volumes of .94. Binary images for each hippocampus were uploaded to the ADNI database at the UCLA Laboratory for Neuroimaging (LONI) and transferred to the UC Davis Imaging of Dementia and Aging Laboratory (IDeA Lab) for further analysis. Hippocampus volume change rate for each individual was calculated by taking the difference between corresponding baseline and follow-up volumes, and dividing by the inter-scan interval.

3.2.2. Average HP change

We performed alignment along central axis, weighted correspondence and downweighting on 320 raw HP surface to estimate radius changes at sampled HP locations over all subjects. What percentage of the HP was cut off due to non-shared slices is summarized across all individuals in histogram form in Fig. 6. At least 88% of HP slices were kept after alignment, and most HP retained 96% or more of their slices. This suggests that our alignment objective function successfully prevented the optimization process from aggressively cutting off large portions of the structure. As expected, local HP radii decreased on average faster among AD patients than MCI patients, and faster among MCI patients than controls (Fig. 7). However, if none of the processing steps described above are applied to the segmentations, many local regions appear to grow over time (red), even in the AD group, in clear violation of the conventional wisdom that HP radii should be either stable or decreasing in each group. Each additional step of processing had a visible effect in reducing the magnitude and extent of local HP growth regions, thus increasing the plausibility of the change measurements. The final maps of change calculated after all processing steps among MCI and AD groups suggest prominent atrophy on average in the anterior medial head and lateral body sub-regions, both of which appear to correspond to the CA1 HP sub-field that is preferentially damaged by early AD pathology [6]. The relatively spared (white) HP region in MCI and AD appears to lie within the CA2-4 or dentate gyrus sub-fields, which are relatively preserved by early AD. In addition, the final mean change maps agree with prior studies by suggesting that even among cognitively normal individuals the HP atrophies mildly over time [21].

Fig. 6.

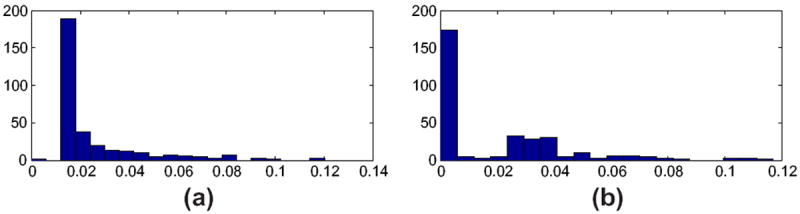
(a) The histogram plots the ratio of the number of template HP slices that were removed during alignment from each individual baseline HP to the template, to the total number of slices in template HP, across all baseline HP. (b) The histogram plots the ratio of the number of baseline HP slices that were removed during alignment of individual follow-up to baseline, to the total number of slices in the baseline HP, across all individuals.

Fig. 7.

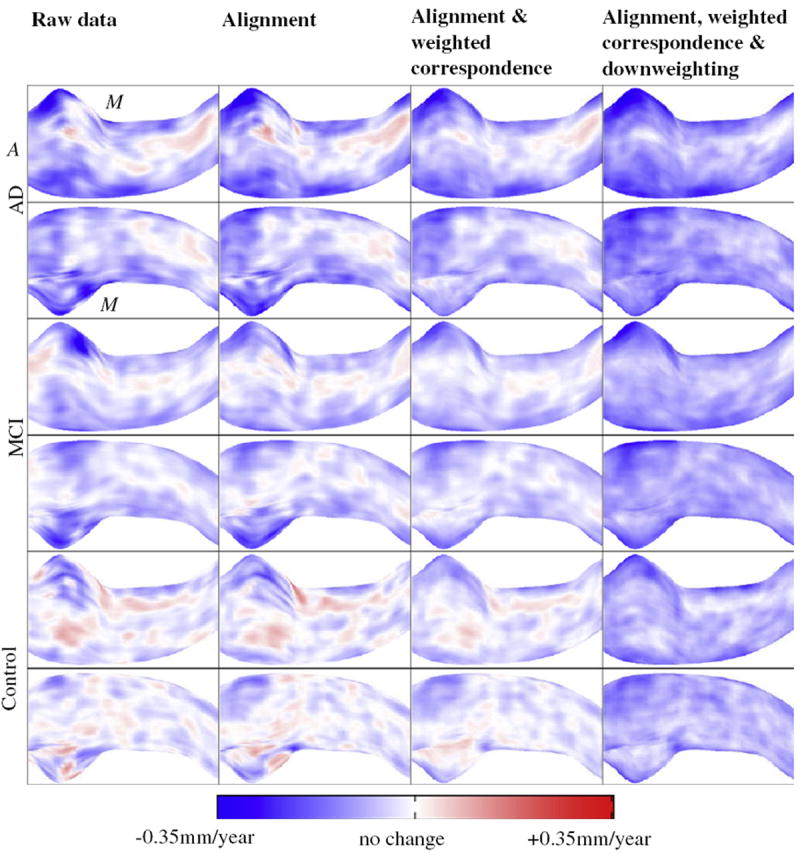
Color-coded maps of average local radius change rates among ADNI control, MCI, and AD groups calculated after application of varying sets of algorithm steps. Red points indicate positive change, i.e. HP growth over time, while blue points indicate local atrophy. Odd and even rows render the HP from superior and inferior viewpoints respectively (anterior and medial directions are marked with A, M). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

3.2.3. Localized HP change patterns

We ran weighted LoCA on four versions of HP change maps that represented differing levels of processing to assess whether the various steps ease the estimation of plausible, spatially localized HP change patterns. Weighted LoCA was applied to: 1. the raw data, 2. the data after applying only the down-weighting step in Sections 2.4 and 3. the data after applying alignment, weighted correspondence estimation, and 4. the data after applying alignment, weighted correspondence estimation, and down-weighting. The individual radius change rate map of each subject can be expressed as the sum of a population average change rate map plus a linear combination of spatial change patterns estimated by LoCA. The five LoCA change patterns that account for the highest percentage of variability in HP change rate for each method are shown in Fig. 8, with blue areas representing a spatial pattern of coherent HP change that was indicated by the data set. The renderings suggest that the processing steps eased the estimation of biologically plausible, localized change patterns. In particular, some of the change patterns based on the raw data and downweighting only are not spatially localized, including blue areas at both the top and bottom of the structure simultaneously(raw data columns 1 and 3; downweighting columns 3 and 5). The goal of LoCA is to exclude such patterns, which are more difficult to interpret anatomically. In addition, the change patterns based on raw data and downweighting only suggest that substantial HP radial change is only occurring in the HP head (top of each sub-figure), while change patterns covering a broader extent of the structure, especially the CA1 and subiculum regions preferentially damaged by early AD pathology, are found from the aligned and downweighted data. Furthermore, downweighting helps to prevent reporting of change patterns that are biologically implausible. Note, for example, that the fifth change pattern based on the aligned but not downweighted data covers the same region where HP radii were erroneously reported to grow on average over 1 year in the control group (red area in subfigure row 5 and column 3 of Fig. 7), and this region is not accounted for in the downweighted LoCA change patterns. Together, these observations suggest that biologically-plausible local change patterns may be easier to discover from the data due to the processing steps.

Fig. 8.

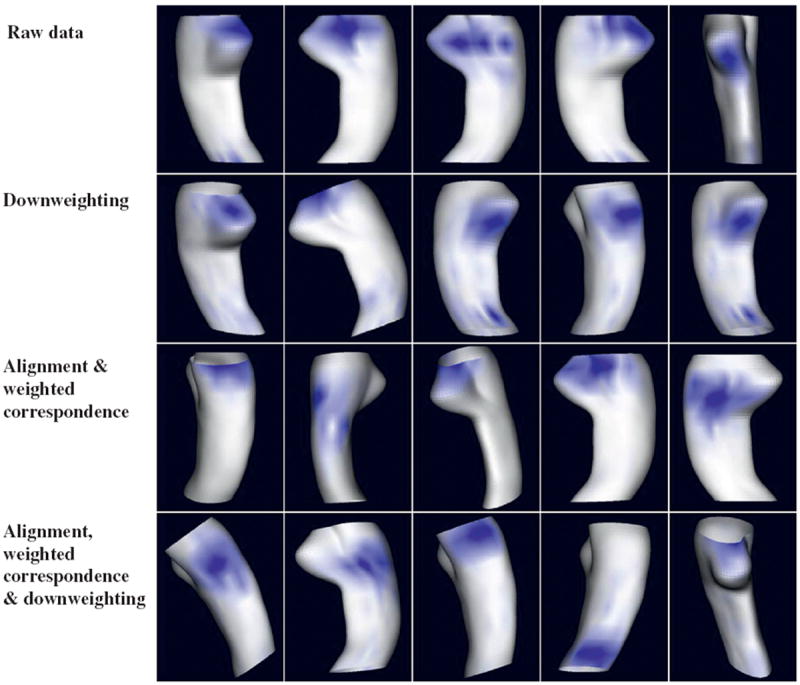
For 4 differing algorithm variants, the 5 LoCA change patterns accounting for the greatest amount of HP change rate variability are shown. For each rendering, the change pattern accounts for a coherent pattern of change in the region shown in blue. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

3.2.4. Relation between HP change and cognition

Given LoCA change patterns, the HP change pattern of each individual can be expressed in terms of change pattern coefficients: these quantify the degree to which any particular change pattern (such as the ones shown in Fig. 8) is evident in that individual. To test whether the processing steps encourage the discovery of clinically relevant HP change patterns, we analyzed associations between cognitive measures collected by ADNI at baseline, and HP change pattern coefficients. Based on the natural history of AD, we would expect diminished cognitive scores to indicate greater levels of AD pathology and therefore greater subsequent HP atrophy; thus, HP change patterns that more strongly associate with baseline cognition may be more clinically relevant as indicators of AD-related HP injury. For each cognitive measure and algorithm variant, we estimated single linear regression models with the coefficients for each of the top 5 change patterns shown in Fig. 8 as predictors, and the cognitive measures as the outcome. We use the minimum P values (as indicated as p_min) for the significance of top 5 change patterns as predictors of AD-relevant cognitive test scores to quantify the strength of association between the change patterns and the cognitive measure. For each of the 3 cognitive measures, the p_min for the data based on alignment and downweighting was smaller than the any of the p_min based on aligned only data, downweighting only data or raw data (Fig. 9), suggesting that the full algorithm enhances the discovery of HP change patterns that are more relevant in terms of stronger associations with real-world outcome measures.

Fig. 9.

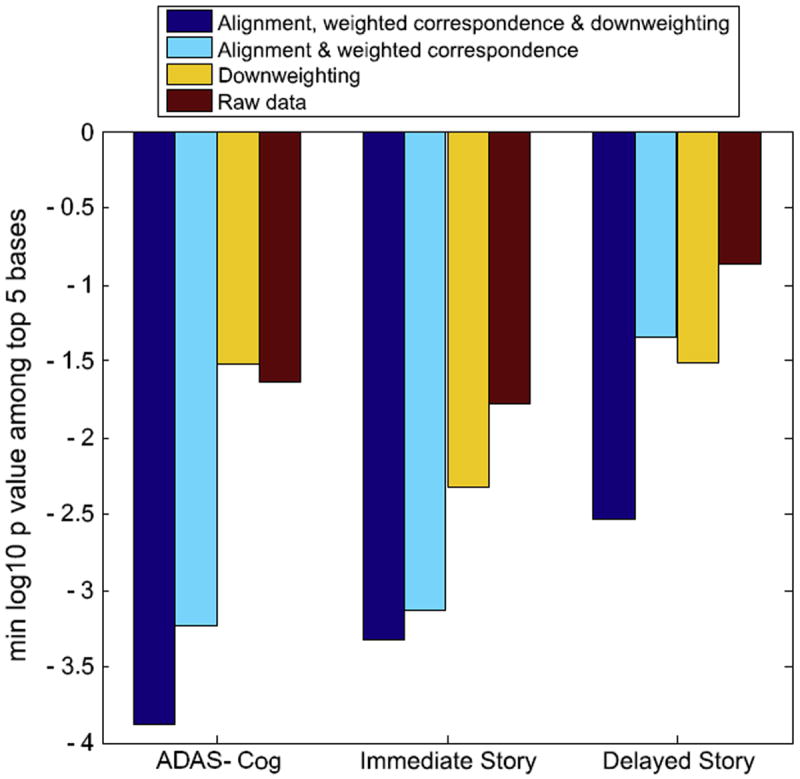
For 4 different algorithm variants, the decadic logarithm of the minimum P values demenstrating the significance of top 5 change patterns as predictors of AD-relevant cognitive test scores. The P values are derived from univariate regression models.

4. Discussion

In this paper, we proposed a sequence of processes to estimate biologically reliable and localized patterns of spatial change to individual aging HP. The first two steps, alignment and weighted correspondence estimation, refine the one-to-one surface correspondences and reduce the amount of implausible HP changes indicated among individual HP. The next step, downweighting, discounts the impact of the remaining outlier HP change measures by giving them low confidences. Weighted LoCA effectively decreases the influence of low-weight points on initializing change patterns and estimating significance of change patterns.

The hippocampus is a very small brain structure relative to conventional MRI voxel sizes, it is difficult to delineate in a reliable way, and its changes can be subtle even in degenerative disease. Our results on the ADNI dataset suggest that a precise sequence of HP-specific algorithmic steps, including alignment, weighted correspondence estimation, downweighting and weighted LoCA may be required to overcome these issues and estimate rates of localized HP change that are both biologically plausible and clinically relevant. Our experiment on simulated data shows that by downweighting the measures that appear to be biologically implausible, weighted LoCA provides reliable change patterns in a more stable way.

Unlike other methods that measure individual-level HP changes, our method does not require precise initial HP delineation correspondence. The alignment step effectively cuts off slices of tissue that are not shared between HP by maximizing the HP shape similarity along its central axis. A novelty in our method is the downweighting mechanism together with weighted LoCA that discounts the impact of outlier measures, and that has been shown to be more stable against outliers.

One of the unique aspects of this method is that outlier HP points that show significant growth over time are down-weighted during the estimation of spatial change patterns. We do so due to overwhelming evidence that in observational studies of aging covering the spectrum from cognitive health to clinical impairment, the hippocampus either maintains a relatively constant size or shrinks (see, e.g. [7,10,20]). However, in certain other contexts it may be unrealistic to make the assumption that localized hippocampus growth in the aging brain is artifactual. Clinical trials may administer aggressive treatments that spur hippocampus growth for example [9]. It is important to note that the downweighting component of this algorithm may be inappropriate for such settings.

Future work should extend the technique to longer series of longitudinal scans. For such data sets, groupwise alignment of HP from all scans in a longitudinal series, in one unified optimization, may provide superior correspondence estimation that is not biased by assigning privileged status to the baseline time point; however, such groupwise optimization is likely to be computationally complex. In addition, robust estimation of intra-individual variability in localized changes should be captured from such data along with inter-individual variability, following the powerful mixed models regression approach to change assessment [8]. Such enhancements are beyond the scope of the current work, which took a principled first step by enhancing longitudinal shape change estimation from a serial pair of HP.