High-Resolution Cardiovascular MRI by Integrating Parallel Imaging With Low-Rank and Sparse Modeling

Abstract

Magnetic resonance imaging (MRI) has long been recognized as a powerful tool for cardiovascular imaging because of its unique potential to measure blood flow, cardiac wall motion, and tissue properties jointly. However, many clinical applications of cardiac MRI have been limited by low imaging speed. In this paper, we present a novel method to accelerate cardiovascular MRI through the integration of parallel imaging, low-rank modeling, and sparse modeling. This method consists of a novel image model and specialized data acquisition. Of particular novelty is the proposed low-rank model component, which is specially adapted to the particular low-rank structure of cardiovascular signals. Simulations and in vivo experiments were performed to evaluate the method, as well as an analysis of the low-rank structure of a numerical cardiovascular phantom. Cardiac imaging experiments were carried out on both human and rat subjects without the use of ECG or respiratory gating and without breath holds. The proposed method reconstructed 2-D human cardiac images up to 22 fps and 1.0 mm × 1.0 mm spatial resolution and 3-D rat cardiac images at 67 fps and 0.65 mm × 0.65 mm × 0.31 mm spatial resolution. These capabilities will enhance the practical utility of cardiovascular MRI.

I. Introduction

CARDIOVASCULAR diseases such as congenital heart disease or coronary artery disease are a major cause of death around the globe. It has long been a dream of imaging scientists to develop advanced imaging methods capable of capturing the structural and functional changes of the beating heart in real time. Over the last five decades, significant progress has been made, leading to the successful development and application of several noninvasive cardiac imaging modalities, including echocardiography [1], cardiac CT [2], cardiac PET (positron emission tomography) [3], cardiac SPECT (single photon emission computed tomography) [4], and cardiac MRI (magnetic resonance imaging) [5]. Cardiovascular MRI has a unique potential to allow multiple comprehensive cardiac assessments in a single integrated examination [6], such as measurement of blood flow and cardiac wall motion, assessment of tissue properties, etc. [7], [8]. However, the low imaging speeds of existing MRI technology have limited its research and clinical impact.

Significant efforts have been made over the last three decades to develop high-speed MRI technology, resulting in a large number of methods. These methods can be grouped into three categories: 1) fast scanning methods using special pulse sequences [9]–[13]; 2) parallel imaging methods using phased array coils [14]–[17]; and more recently, 3) sparse sampling methods [18]–[36].

Sparse sampling methods for cardiac MRI can be partitioned into two subcategories: those exploiting the sparsity of cardiovascular images in various domains [22], [24], [25], [26], [27], and those exploiting the partial separability (PS)-induced low-rank properties of cardiac images [30]–[33]. Because sparsity and low-rankness are complementary properties, methods have been proposed recently which jointly enforce both the PS model and signal sparsity. Examples include PS-Sparse [34], [35] and k-t SLR [36].

In this paper, we present a novel method that synergistically integrates fast scanning, parallel imaging, and both low-rank and sparse modeling. We have successfully used the technique to perform 2-D human cardiac imaging up to 22 fps and 1.0 mm × 1.0 mm spatial resolution and 3-D rat cardiac imaging at 67 fps and 0.65 mm × 0.65 mm × 0.31 mm spatial resolution without the use of ECG gating, respiratory gating, or breath holds. This unprecedented 3-D capability enables simultaneous whole-heart imaging of cardiac motion, respiratory motion, and first-pass myocardial perfusion. This in turn allows multiple cardiac assessments including measurement of ejection fraction, cardiac output, and myocardial blood flow in a single experiment. We believe that this capability would improve the practical impact of cardiovascular MRI.

The rest of the paper is organized as follows. Section II describes the proposed method in detail. Section III shows some representative results obtained using the proposed method, and Section IV contains the conclusion of the paper.

II. Proposed Method

The proposed method achieves high-speed cardiac imaging by using a novel data acquisition scheme that sparsely samples (k, t)-space. The sparse sampling scheme is enabled by a new image model capable of reconstructing high-quality images from highly undersampled data. This model effectively integrates: 1) sparse sampling based on “regional” PS (a form of low-rank modeling); 2) sparse sampling based on compressed sensing (CS) (a form of sparse modeling); and 3) sparse sampling based on sensitivity encoding using phased array coils (often known as parallel imaging). In this section, we describe our proposed method in detail.

A. Spatiotemporal Image Model

We represent the spatiotemporal changes of cardiac images using an Lth-order PS model [30], [31],

$$\rho (\mathbf{r},t)=\sum _{l=1}^L{\psi }_l\left(\mathbf{r}\right){\phi }_l\left(t\right).$$ (1)

Equivalently, the (k, t)-space signal $d(\mathbf{k},t)=F_{\mathbf{r}}\left\{\rho (\mathbf{r},t)\right\}=\int \rho (\mathbf{r},t)e^{-i2\pi \mathbf{k}\cdot \mathbf{r}}$ dr can be expressed as

$$d(\mathbf{k},t)=\sum _{l=1}^L{\tilde{\psi }}_l\left(\mathbf{k}\right){\phi }_l\left(t\right)$$ (2)

where ${\tilde{\psi }}_l\left(\mathbf{k}\right)=F_r\left\{{\psi }_l\left(\mathbf{r}\right)\right\}$. The Lth-order PS model in (1) implies that the following Casorati matrix

$$\mathbf{C}\left(d\right)=\left[\begin{array}{cccc}\hfill d({\mathbf{k}}_1,t_1)\hfill & \hfill d({\mathbf{k}}_1,t_2)\hfill & \hfill \dots \hfill & \hfill d({\mathbf{k}}_1,t_N)\hfill \\ \hfill d({\mathbf{k}}_2,t_1)\hfill & \hfill d({\mathbf{k}}_2,t_2)\hfill & \hfill \dots \hfill & \hfill d({\mathbf{k}}_2,t_N)\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill d({\mathbf{k}}_M,t_1)\hfill & \hfill d({\mathbf{k}}_M,t_2)\hfill & \hfill \dots \hfill & \hfill d({\mathbf{k}}_M,t_N)\hfill \end{array}\right]$$

which can be constructed for any arbitrary set of indices ${\left\{m\right\}}_{m=1}^M\mathrm{and}{\left\{n\right\}}_{n=1}^N$ has a rank of no more than L [31], [33]. The same is true for the Casorati matrix C(ρ). It has been observed that cardiac (k, t)-space signals are often partially separable to a low order (as illustrated in Fig. 1) because the high degree of spatiotemporal correlation makes ${\left\{d({\mathbf{k}}_m,t)\right\}}_{m=1}^M$ linearly dependent (M > L).

Fig. 1.

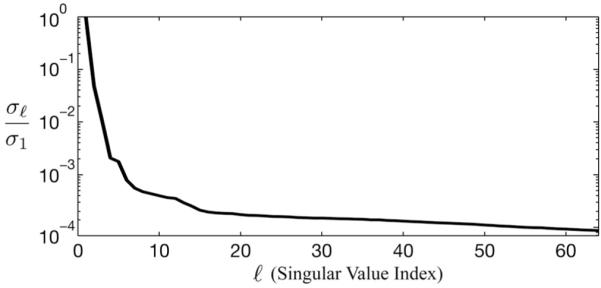
Plot of the normalized singular values (denoted by ρ) of the Casorati matrix of a typical cardiac dataset. As can be seen, the singular values decay very quickly, resulting in an effective rank of about L = 16.

The basic PS model assumes that the entire image shares a common temporal subspace of same dimension. There are several ways to extend the basic PS model for cardiac imaging [37], [38]. For example, noting that cardiac and noncardiac anatomy undergo different types of motion, the spatiotemporal signal changes can be more efficiently represented by a regional PS model as

$$\rho (\mathbf{r},t)=\{\begin{array}{cc}\sum _{l=1}^{L_1}{\psi }_l\left(\mathbf{r}\right){\phi }_l\left(t\right),\hfill & \text{if}\mathbf{r}\notin \Omega \hfill \\ \sum _{l=1}^{L_2}{\psi }_l\left(\mathbf{r}\right){\phi }_l\left(t\right),\hfill & \text{if}\mathbf{r}\in \Omega \hfill \end{array}\phantom{\}}$$ (3)

where ${\left\{{\phi }_l\left(t\right)\right\}}_{l=1}^{L_2}\mathrm{and}{\left\{{\varphi }_l\left(t\right)\right\}}_{l=1}^{L_1}$ span the temporal subspace for the cardiac region (Ω) and the noncardiac region, respectively. In practice, we may further assume that $\mathrm{span}{\left\{{\phi }_l\left(t\right)\right\}}_{l=1}^{L_2}\supset \mathrm{span}{\left\{{\varphi }_l\left(t\right)\right\}}_{l=1}^{L_1}$ since any background motion (e.g., respiratory motion) also affects the cardiac region. Therefore, we can rewrite (3) as

$$\rho (\mathbf{r},t)=\{\begin{array}{cc}\sum _{l=1}^{L_1}{\psi }_l\left(\mathbf{r}\right){\phi }_l\left(t\right),\hfill & \text{if}\mathbf{r}\notin \Omega \hfill \\ \sum _{l=1}^{L_2}{\psi }_l\left(\mathbf{r}\right){\phi }_l\left(t\right),\hfill & \text{if}\mathbf{r}\in \Omega \hfill \end{array}\phantom{\}}$$ (4)

where it is assumed that L₂ ≥ L₁ Equation (4) implies that ${\left\{{\phi }_l\left(t\right)\right\}}_{l=1}^{L_2}$ span the entire temporal subspace for d(k, t) or ρ(r, t), while temporal signal changes in noncardiac regions live only in the subspace spanned by ${\left\{{\phi }_l\left(t\right)\right\}}_{l=1}^{L_2}$. The basic PS model corresponds to L₁ = L₂.

Given a (k, t)-space dataset ${\left\{d({\mathbf{k}}_m,t_n)\right\}}_{m=1,n=1}^{M,N}$, we can express the singular value decomposition (SVD) of its Casorati matrix C(d) as

$$\mathbf{C}\left(d\right)=\sum _{l=1}^L{\sigma }_l{\mathbf{u}}_l{\mathbf{v}}_l^H$$ (5)

where σ_ℓ is the ℓth singular value, and where u_ℓ and v_ℓ are the ℓth left and right singular vectors, respectively. Clearly, we have L = L₂. An experimental “fact” that can be taken advantage of for constructing the PS model in (4) is that the dominant right singular vectors tend to capture the “low-frequency” (e.g., respiratory) temporal signal changes, while the “high-frequency” components represent mainly cardiac signal changes (as illustrated in Fig. 2 below and also in Fig. 4 in Section III-A). Therefore, one set of temporal basis functions for ρ(r, t) can be defined in the form ${\widehat{\phi }}_l\left(t_n\right)={\mathbf{V}}_{nl}^{\ast }$ (note that the ℓth column of v is equal to v_ℓ), which is already partitioned according to the assumptions in (4).

Fig. 2.

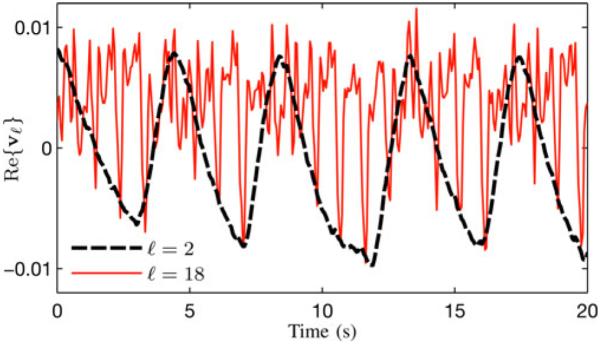
Separation of respiratory and cardiac signal changes in the SVD of a typical human cardiac MR dataset. The Casorati matrix was created from data measured at a limited number of k-space locations. The figure plots the real parts of v₂ and v₁₈, respectively. Both vectors are complex, but only the real parts are shown for the purposes of simplicity. As can be seen, v₂ contains the low-frequency signal changes (related to respiratory motion), whereas v₁₈ captures faster cardiac motion.

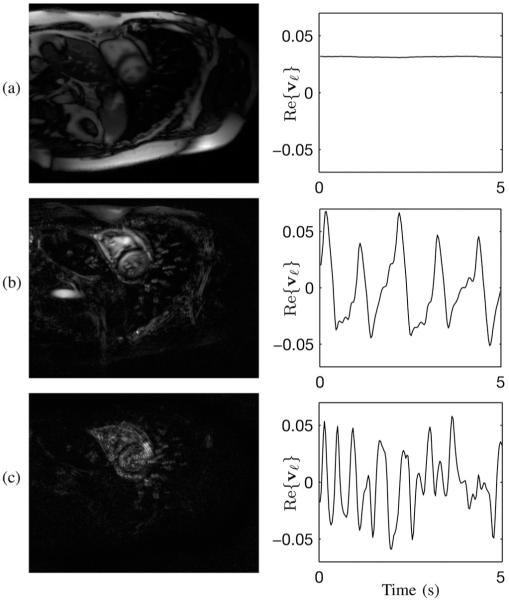
Fig. 4.

Representations of |u_ℓ| and Re{v_ℓ} from C(ρ) for (a) ℓ = 1, (b) ℓ = 5, and (c) ℓ = 19.

B. Data Acquisition

The (k, t)-space signal from a parallel array of Q coils can be expressed as

$$\begin{array}{cc}\hfill d_q(\mathbf{k},t)& =F_{\mathbf{r}}\left\{S_q\left(\mathbf{r}\right)\rho (\mathbf{r},t)\right\}\hfill \\ \hfill & =\int S_q\left(\mathbf{r}\right)\rho (\mathbf{r},t)e^{-i2\pi \mathbf{k}\cdot \mathbf{r}}d\mathbf{r}\hfill \end{array}$$ (6)

where S_q (r) is the sensitivity weighting function and ρ_q (r, t) = S_q (r)(r, t) the sensitivity-weighted image of the qth coil. Conventional imaging methods sample k-space at the Nyquist rate and reconstruct each ρ_q (r, t) using conventional reconstruction methods. These individual coil images ${\left\{{\rho }_q(\mathbf{r},t)\right\}}_{q=1}^Q$ are then typically combined using the sum-of-squares algorithm, producing $\rho (\mathbf{r},t)=\sqrt{{\Sigma }_{q=1}^Q\mid {\rho }_q(\mathbf{r},t){\mid }^2}$. However, sampling highdimensional k-space at the Nyquist rate results in low imaging speeds which often violate the temporal Nyquist rate associated with rapid cardiac and respiratory motions. Parallel imaging, low-rank modeling, and sparse representation each provide a complementary avenue for signal recovery from undersampled (k, t)-space data. Here, we integrate these capabilities to achieve high spatiotemporal resolution for cardiac imaging.

The proposed data acquisition scheme is characterized by the collection of two datasets denoted as D₁ and D₂ here. For simplicity, we ignore the readout direction of k-space. D₁ contains data in a few k-space locations at a high temporal rate (satisfying the temporal Nyquist criterion), and D₂ contains data from sparse (k, t)-space locations. This scheme is motivated by the signal model in (4): D₁ can just be navigator data (or training data) used to determine the temporal basis functions ${\left\{{\widehat{\phi }}_l\left(t\right)\right\}}_{l=1}^L$ and D₂ should contain imaging data with proper contrast-weighting for determining ${\left\{{\widehat{\varphi }}_l\left(\mathbf{r}\right)\right\}}_{l=1}^L$. Using navigator (or training) data for model estimation in MR dynamic imaging was introduced in [18], and the idea was later used in several other publications (e.g., [19], [30]-[32]).

Let $D_1={\left\{d_q({\mathbf{k}}_{j,1},t_{j,1})\right\}}_{j=1,q=1}^{J_1,Q}$. Here, ${\left\{{\mathbf{k}}_{j,1}\right\}}_{j=1}^{J_1}$ covers a few k-space locations to ensure that the temporal Nyquist criterion is satisfied, without being subject to the spatial Nyquist constraint or any spatial resolution considerations. In practice, ${\{{\mathbf{k}}_{j,1}\}}_{j=1}^{J_1}$ often sample the central k-space based on signal-to-noise considerations. For each k_j,1, we assume that d_q (k_j,1, t) is measured for t = t₁, t₂,…, t_N, and that this sampling rate satisfies the temporal Nyquist criterion for the underlying signal. The data in D₁ can be rearranged into Q Casorati matrices C_q = C(d_q), for q = 1, 2,… , Q. All the C_q’s share the same temporal subspace as ρ(r, t), as the inclusion of time-invariant coil sensitivity weightings S_q (r) in (6) does not alter partial separability of the (k, t)-space data. We can then compute the SVD of the expanded Casorati matrix ${\left[{\mathbf{C}}_1^T{\mathbf{C}}_2^T\dots {\mathrm{C}}_Q^T\right]}^T={\Sigma }_{l=1}^L{\sigma }_l{\mathbf{u}}_l{\mathbf{v}}_l^H$ and define the temporal basis functions as ${\widehat{\phi }}_l\left(t_n\right)={\mathbf{V}}_{nl}^{\ast }$ Having this set of prede-fined temporal basis functions is enormously useful in low-rank modeling [35] because: 1) it reduces the number of degrees-of-freedom in the PS model; 2) it simplifies the model-fitting inverse problem so that only the spatial coefficients ${\left\{{\widehat{\phi }}_l\left(\mathbf{r}\right)\right\}}_{l=1}^L$ need to be determined; and perhaps more importantly, 3) it improves the quality of the resulting reconstructions.

With ${\left\{{\widehat{\phi }}_l\left(t\right)\right\}}_{l=1}^L$ being defined, we have a lot of flexibility in acquiring $D_2={\left\{d_q({\mathbf{k}}_{j,2},t_{j,2})\right\}}_{j=1,q=1}^{J_2,Q}$ to obtain sufficient data for determining the spatial coefficients of the PS model without being subject to the Nyquist constraint along both the spatial and temporal directions. The following practical factors should be considered in deciding the (k, t)-space sampling locations ${\left\{({\mathbf{k}}_{j,2},t_{j,2})\right\}}_{j=1,}^{J_2}$ in a specific data acquisition scheme.

First, with sensitivity-encoding using Q receiver coils, we can undersample k-space by a factor of P ≥ Q according to multi-channel sampling theory [17]. In practice, we choose P « Q to avoid the well-known ill-conditioning problem associated with conventional parallel imaging. In conventional parallel imaging, there is a tradeoff between k-space undersampling and temporal undersampling. By integrating parallel imaging with low-rank modeling, the proposed method avoids this tradeoff: temporal undersampling is allowed in PS model-based image reconstruction (as discussed in Section II-C). Therefore, the proposed method allows more flexibility in placing ${\left\{({\mathbf{k}}_{j,2},t_{j,2})\right\}}_{j=1,q=1}^{J_2,Q}$ and enables sparser sampling of (k, t)-space than conventional parallel imaging.

Second, in parallel imaging, image reconstruction requires either explicit knowledge of each S_q (r) [15] or implicit knowledge, often in the form of auto-calibration signal (ACS) lines measured from Nyquist samples in the central region of k-space [16]. The proposed method can use either strategy, although we use the latter in our implementation. Third, the proposed method utilizes a spatial-spectral sparsity constraint to regularize the PS model to avoid any potential ill-conditioning problem associated with (k, t)-space undersampling [35]. Sparse modeling is most effective with “incoherent” data acquisition [23]. In our proposed method, one can gain the desired incoherence by sampling (k, t)-space in a randomized order [22]. Simply put, for a given k_j,2 , temporal sampling should not be periodic, i.e., t_j,2 ≠ jΔt. Further details of our implementation can be found in Section III.

C. Image Reconstruction

Equation (1) admits the factorization C(ρ) = ΨΦ, where Ψ_ij = ψ_j(r_i) and Φ_ij = φ_j(t_j) Given a predetermined $\widehat{\Phi }$ we can reconstruct $\widehat{\mathbf{C}}\left(\rho \right)$ (ρ) by solving for $\widehat{\Psi }$. We do this by solving the following optimization problem:

$$\begin{array}{cc}\hfill \widehat{\Psi }=& \arg \underset{\Psi }{\min }\sum _{q=1}^Q{D}_q\left(\Psi \right)+{\lambda }_1\Vert R\left\{\Psi \right\}{\Vert }_{1,2}\hfill \\ \hfill & +{\lambda }_2\Vert \mathrm{vec}\left(\Psi \widehat{\Phi }{\mathbf{W}}_t\right){\Vert }_1\hfill \end{array}$$ (7)

where

$$D_q\left(\Psi \right)=\sum _j\mid d_q({\mathbf{k}}_j,t_j)-\sum _{l=1}^{L_2}{\widehat{\phi }}_l\left(t_j\right)\times \int S_q\left(\mathbf{r}\right){\psi }_l\left(\mathbf{r}\right)e^{-i2\pi {\mathbf{k}}_j\cdot \mathbf{r}}d\mathbf{r}{\mid }^2$$

and

$$\Vert R\left\{\Psi \right\}{\Vert }_{1,2}=\sum _{l=L_1+1}^{L_2}\left(\sqrt{\sum _{m\mid {\mathbf{r}}_m\in \Omega }\mid {\psi }_l\left({\mathbf{r}}_m\right){\mid }^2}+\sum _{m\mid {\mathbf{r}}_m\notin \Omega }\mid {\psi }_l\left({\mathbf{r}}_m\right)\mid \right).$$ (8)

R{Ψ} concatenates the rightmost columns of Ψ (i.e., Ψ _{L1 +1} through Ψ_L2), and vec(·) is the vector constructed by concatenating the columns of the argument matrix. ∥R{Ψ}∥ enforces the subspace structure in (4), and$\Vert \mathrm{vec}\left(\Psi \widehat{\Phi }{\mathbf{w}}_t\right){\Vert }_1$ is a spatial-spectral sparsity contraint widely used in CS-based cardiac MRI (e.g., [22], [24], [25], [27], [33], [35]).

The constraint ∥R{Ψ}∥_1,2 promotes group sparsity of ${\left\{{\psi }_l\left(\mathbf{r}\right)\right\}}_{l=L_1+1}^{L_2}$ in order to enforce the subspace structure in (4). Defining x_(i) as the ith group of some vector x, then the mixed (1,2)-norm is defined as $\Vert \mathbf{x}{\Vert }_{1,2}={\Sigma }_{i=1}^I\Vert {\mathbf{x}}_{\left(i\right)}{\Vert }_2$ [39], [40]. Equation (8) distributes the higher-order spatial coefficients ${\left\{{\psi }_l\left(\mathbf{r}\right)\right\}}_{l=L_1+1}^{L_2}$ into different groups. For each L₁ < l ≤ L₂, each set of cardiac spatial coefficients {ψ_l(r_m)}_m|r_m ∈Ω comprises a group, as does each individual noncardiac spatial co-efficient ψ_l(r_m), r_m ∉ Ω. As a result, the cardiac region takes on an effective model order up to L₂ and each noncardiac voxel individually takes on an effective model order of L₁ or slightly higher. This grouping promotes a uniformly high model order over the cardiac region and a spatially varying low model order over the noncardiac region, introducing flexibility to the choices of L₁ and L₂ . This flexibility is desirable for model order selection and region identification in practical applications because: if either L₁ or L₂ is chosen too small, then the representational power of the model is reduced, leading to model bias; if either L₁ or L₂ is chosen too high, then the model becomes sensitive to noise and reconstruction quality will be heavily dependent on regularization. Similarly, this flexibility also allows imprecise specification of Ω, as voxels incorrectly placed outside Ω would also be allowed to take on a higher model order. Voxels incorrectly placed inside Ω will have higher model orders than necessary, but the model overfitting problem would still be addressed by spatial-spectral sparsity regularization. The group sparsity constraint reduces these potential pitfalls while still allowing the option to exactly enforce the basic PS model by using L₁ = L₂.

Note that when λ₁ = 0 or L₁ = L₂, the reconstruction problem in (7) integrates the ℓ₁-norm regularized basic PS model [34], [35] with parallel imaging. If we further select L₁ = L₂ min{M, N}, i.e., reconstruct a full-rank image, then we would obtain an (r, f)-space sparsity inverse problem similar k-t SPARSE-SENSE [27].

We solve the convex optimization problem in (7) by using an additive half-quadratic minimization algorithm [41], [42] extended to handle (1,2)-norm regularization and combined with a continuation procedure [43]. This algorithmic approach has previously been shown to be efficient for similar problems [35]. For simplicity of notation, we define the operator $T\left\{\Psi \right\}={\left[\frac{{\lambda }_1}{\lambda }R{\left\{\Psi \right\}}^T\frac{{\lambda }_2}{\lambda }\mathrm{vec}{\left(\Psi \widehat{\Phi }{\mathbf{w}}_t\right)}^T\right]}^T$ in order to express the regularization constraints in (7) using an alternative (1,2)-norm expression with groupings such that

$$\lambda \Vert T\left\{\Psi \right\}{\Vert }_{1,2,\mathrm{alt}}={\lambda }_1\Vert R\left\{\Psi \right\}{\Vert }_{1,2}+{\lambda }_2\Vert \mathrm{vec}\left(\Psi \widehat{\Phi }{\mathbf{w}}_t\right){\Vert }_1.$$ (9)

Using this simplified notation, (7) becomes

$$\widehat{\Psi }=\arg \underset{\Psi }{\min }\sum _{q=1}^Q{D}_q\left(\Psi \right)+\lambda \Vert T\left\{\Psi \right\}{\Vert }_{1,2,\mathrm{alt}}$$ (10)

which is a straightforward (1,2)-norm regularized inverse problem.

The sensitivity encoding functions ${\left\{S_q\left(\mathbf{r}\right)\right\}}_{q=1}^Q$ must also be known in order to solve (7). In our implementation, we obtain these functions from GRAPPA [16] reconstructions of the time-averaged measured data. We first average the measured (k, t)-space data at each k-space location over time, yielding a static k-space dataset ${\left\{{\stackrel{‒}{d}}_q\left({\mathbf{k}}_m\right)\right\}}_{m=1}^M$ We treat each of these datasets as measurements of a function ${\stackrel{‒}{d}}_q\left(\mathbf{k}\right)$ which in our implementation is downsampled in the k_y direction by a factor of P (except over the ACS region, which has N_ACS Nyquist-sampled k-space lines). We then use GRAPPA to reconstitute each ${\stackrel{‒}{d}}_q\left(\mathbf{k}\right)$ for which inverse Fourier reconstruction yields ${\stackrel{‒}{\rho }}_q\left(\mathbf{r}\right)$ The sensitivity encoding functions are then defined as $S_q\left(\mathbf{r}\right)={\stackrel{‒}{\rho }}_q\left(\mathbf{r}\right)∕{\rho }_{\mathrm{ref}}\left(\mathbf{r}\right)$ where ρ_ref (r) is a coil reference image usually produced from ${\left\{{\stackrel{‒}{\rho }}_q\left(\mathbf{r}\right)\right\}}_{q=1}^Q$ by the sum-of-squares algorithm. This strategy, which extends themethod in [44] to produce full-resolution sensitivity encoding functions, combines advantages of GRAPPA reconstruction (e.g., robustness to overlapping geometry) with the simple joint-channel reconstruction of the SENSE [15] inverse problem.

III. Results and Discussion

All data in this paper were collected according to the strategy outlined in Section II-B, with implementation as follows. Successive readouts of ${\left\{d_q(\mathbf{k},t)\right\}}_{q=1}^Q$ alternated between D₁ and D₂ such that J₁ = J₂ = J and t_j,2 = (t_{j, 1} + T_R) ∀j, where T_R is the time between readouts. Assuming that k_x was the readout direction, then D₁ contains (k, t)-space data from N_d unique (k_y , k_z)-space locations, sampled in repeating order: k_j,2 = k_{(j−Nd), 2} ∀ j < N_d. For D₂, each k_y,j,2 was drawn from a set consisting of 1) N_ACS central k_y-space locations with a sampling rate Δk_y satisfying the Nyquist criterion and 2) additional k_y-space locations at the sampling rate PΔk_y. No k-space undersampling was performed in the k_z direction. We produced the sampling schedule ${\left\{({\mathbf{k}}_{j,2},t_{j,2})\right\}}_{j=1,q=1}^{J_2,Q}$ from successive random permutations of the resulting (k_y, k_z)-space locations. Fig. 3 illustrates a 2-D example of the sampling patterns implemented throughout this paper.

Fig. 3.

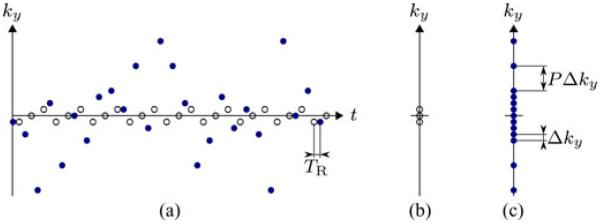
Illustrative example of the sampling patterns implemented throughout this paper. Subfigure (a) depicts the (k, t)-space sampling schedules for D₁ (outlined circles) and D₂ (filled circles) for 2-D imaging with parameters N_d = 3, N_ACS = 9, and P = 4. Subfigures (b) and (c) depict the k-space sampling locations ${\left\{{\mathbf{k}}_{j,1}\right\}}_{j=1}^{J_1}\mathrm{and}{\left\{{\mathbf{k}}_{j,2}\right\}}_{j=1}^{J_2}$ respectively.

A. Analysis of the Low-Rank Model

Here, we present an analysis of low-rank structure in a numerical cardiovascular phantom ρ(r, t). This analysis demonstrates the utility of the model in (4) when combined with the proposed data acquisition/subspace definition scheme using the SVD of D₁ to define $\widehat{\Phi }$. The phantom was generated from in vivo human short axis MR images, and it features variable-rate cardiac and respiratory motion. D₁ was collected with N_d = 5. Section III-B describes this phantom in greater detail.

The SVD of C(ρ) yields insight into the low-rank structure of cardiovascular images. As ℓ increases, signal in the spatial “eigenmaps” ${\left\{{\mathbf{u}}_l\right\}}_{l=1}^L$ becomes more concentrated in the cardiac region than in the noncardiac region. Fig. 4 shows image representations of |u_ℓ| and Re{v_ℓ} for ℓ = 1, 5, 19 from the cardiac phantom. Each eigenmap contains cardiac signal; however, by ℓ = 19, the noncardiac signal is highly sparse, limited to only a few voxels over the vasculature.

In the following paragraphs, we will denote C₁ and C₂ as the mutually exclusive submatrices of C(ρ) which represent the cardiac and noncardiac regions of the image, respectively. Formally, these submatrices are described as C₁ = [C(ρ)_mn]_{m |rm ∊Ω, n= 1,2,…,N} and C₂ = [C (ρ)_mn]_{m |rm ∉Ω, n= 1,2,…,N}. We further denote $\mathrm{R}\left({\widehat{\Phi }}^H\right)$ as the column space of $\left({\widehat{\Phi }}^H\right)$ and E₁ and E₂ as the rank-L Eckart-Young column spaces for ${\mathbf{C}}_1^H\mathrm{and}{\mathbf{C}}_2^H$ respectively. The root-mean-square (RMS) error of a matrix X approximating some C is given by the Frobenius norm ∥C - X∥_F, and the corresponding normalized RMS (NRMS) error is given by ∥C - X∥_F/∥C∥_F.

Here, we compare the approximation errors resulting from different low-rank approximations of ${\mathbf{C}}_1^H\mathrm{and}{\mathbf{C}}_2^H$ The lowest RMS approximation errors achievable by an Lth-order PS model with predetermined $\widehat{\Phi }$ result from projecting ${\mathbf{C}}_1^H\mathrm{and}{\mathbf{C}}_2^H$ onto $\mathrm{R}\left({\widehat{\Phi }}^H\right)$. The lowest possible rank-L approximation errors foreach region result from projecting ${\mathbf{C}}_1^H\mathrm{and}{\mathbf{C}}_2^H$ onto E₁ and E₂, respectively; these approximation errors can be calculated directly from the singular values of C₁ and C₂

Fig. 5 shows the corresponding NRMS error values as a function of model order L. The error curves from the Eckart–Young approximation are an indicator of the intrinsic rank properties of each region. It is evident that very low-order representations of the noncardiac region can match the accuracy of moderately low-order representations of the cardiac region. Here, a rank-6 approximation of C₂ is as accurate as a rank-54 approximation of C₁ (as measured by NRMS error). When compared to the ideal regional subspaces, there only is a small loss of accuracy associated with use of the suboptimal estimate $\widehat{\Phi }$ the relatively small size of this loss suggests that the intrinsic rank properties of cardiovascular images can be successfully and practically exploited using the nested subspace strategy represented in (4) as combined with the proposed data acquisition/subspace definition scheme using the SVD of D₁ to define $\widehat{\Phi }$.

Fig. 5.

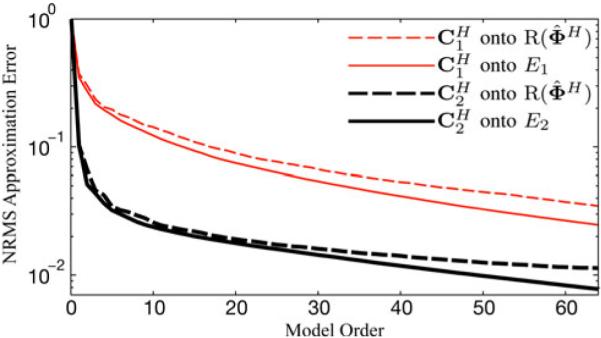
NRMS error of low-rank approximations from projecting the cardiac and noncardiac matrices ${\mathbf{C}}_1^H\mathrm{and}{\mathbf{C}}_2^H$ onto different temporal subspaces. In both cases, the noncardiac region can be estimated with a low-order model as accurately as the cardiac region can with a higher-order model.

B. Simulation Results

We have evaluated the proposed method using the same numerical cardiac phantom. The source images for this phantom were collected using retrospective ECG and respiratory gating, resulting in images of a single representative cardiac cycle. These images were looped and time-warped to simulate a variable-rate heartbeat, and then spatially deformed to simulate variable-rate respiration. The phantom image sequence contains one complex-valued 200 × 256 frame every 3 ms over a duration of 30 s. We provide reconstruction examples using the proposed method as well as sliding window reconstructions (i.e., direct Fourier reconstructions of the sparsely sampled (k, t)-space data after nearest-neighbor temporal interpolation), and CS model reconstructions.

In all simulations, we sparsely sampled (k, t)-space data from the numerical phantom. The sampling pattern was limited to a single (k, t)-space readout line every 3 ms (the effective T_R ) to represent real-world sampling conditions. Data were collected with Q = 1, P = 1, and N_d = 5.

Reconstructions were performed according to (7) with a variety of parameters. Regularization parameters were chosen for the minimum NRMS reconstruction error $\Vert \mathbf{C}\left(\rho \right)-\widehat{\Psi }\widehat{\Phi }{\Vert }_F∕\Vert \mathbf{C}\left(\rho \right){\Vert }_F$ after a comprehensive sweep. All reconstructions have a frame rate of 33 fps, which is equal to the temporal resolution of the training data (i.e., 1/2N_d T_R ).

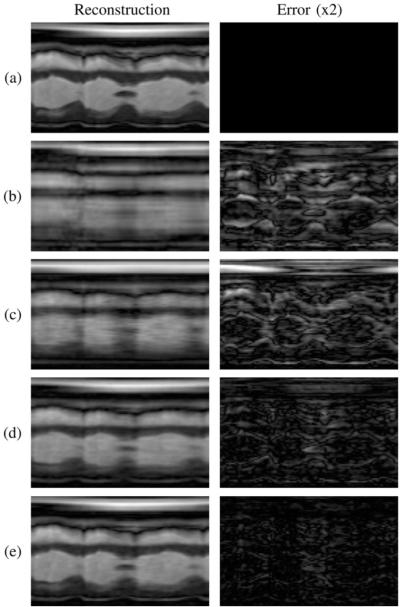
Table I presents the NRMS reconstruction errors over a range of values for L₁ and L₂ . Entries where L₁ = L₂ are denoted by “*,” and the full-rank (i.e., CS) reconstruction is denoted by “†.” The smallest overall reconstruction error appears in bold. Model order combinations where L₁ > L₂ are inconsistent with the assumption in (4) that L₂ ≥ L₁ and are therefore grayed out. The left column of Fig. 6 depicts 2-D spatiotemporal slices from the phantom (i.e., the gold standard) and the noiseless reconstructions which yielded the smallest NRMS error for each method. The right column depicts the error image for each reconstruction, scaled by a factor of 2 for clarity.

TABLE I.

Normalized RMS Reconstruction Errors in Simulations

		L1 (Non-cardiac)
		16	25	32	64	1000
L2(Cardiac)	16	3.67%*
	25	3.37%	3.46%*
	32	3.32%	3.35%	3.42%*
	64	3.35%	3.28%	3.53%	3.81%*
	1000					9.31%†

^*denotes a result where L₁ = L₂, and

^†denotes the full-rank (i.e., CS) result. The model order combinations corresponding to are grayed out. The smallest reconstruction error appears in bold.

Fig. 6.

(a) Gold standard, (b) sliding window reconstruction, and reconstructions using (c) the full-rank (i.e., CS) model, (d) the proposed model with L₁ = L₂, and (e) the proposed model with L₁ < L₂. The error images are scaled by a factor of 2.

Fig. 7 depicts normalized singular value curves of the cardiac region ${\widehat{\mathbf{C}}}_1$ and the noncardiac region ${\widehat{\mathbf{C}}}_2$ of the proposed reconstruction with L₁ = 25 and L₂ = 64. The constraint ∥R{Ψ}∥1,2 successfully promoted sparsity of the noncardiac spatial co-efficients indexed above L₁ = 25, yielding effective ranks of L₂ = 64 for the cardiac region and L₁ = 25 for the noncardiac region.

Fig. 7.

Normalized singular value curves from the cardiac and noncardiac regions of the proposed reconstruction with L₁ = 25 and L₂ = 64. The proposed method successfully enforced the desired effective ranks.

C. 2-D Human Imaging

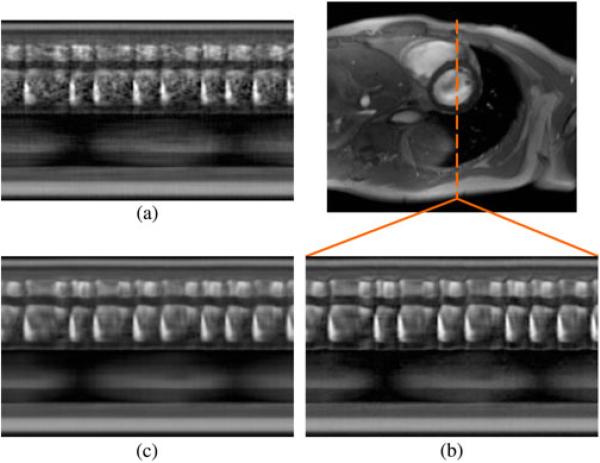
We also demonstrate the proposed method in vivo in human subjects. We implemented the data acquisition scheme on a Siemens TRIO 3 T scanner using a customized FLASH pulse sequence. Typical imaging parameters were as follows: T_R = 4.6 ms, T_E = 2.5 ms, flip angle (FA) = 18°, field-of-view (FOV) = 328 mm × 350 mm, matrix size 330 × 352, in-plane spatial resolution = 1.0 mm × 1.0 mm, slice thickness = 6.0 mm, Q = 12, N_d = 5, N_ACS = 42, and P = 3. The total acquisition time was 3 min. All data were collected continually with neither ECG gating nor breath holding. The experiments were approved by the local Institutional Review Board, and all subjects gave informed consent prior to scanning. We reconstructed the sparsely sampled (k, t)-space data according to the proposed model with L₁ = 16 and L₂ = 48, the proposed model with L₁ = L₂ = 48, and the full-rank (i.e., CS) model. All regularization parameters λ₁ and λ₂ were set according to Morozov’s discrepancy principle [45]. Specifically, the data discrepancy of our reconstructions matches the expected discrepancy of a perfect, noiseless reconstruction: ${\Sigma }_{q=1}^Q{D}_q\left(\widehat{\Psi }\right)=QJ{\sigma }^2$ where J is the number of measured samples per channel and σ² is the variance of the measurement noise. A data discrepancy ${\Sigma }_{q=1}^Q{D}_q\left(\widehat{\Psi }\right)\ll QJ{\sigma }^2$ is associated with overfitting of noise, and a data discrepancy ${\Sigma }_{q=1}^Q{D}_q\left(\widehat{\Psi }\right)\gg QJ{\sigma }^2$ is associated with model bias. We estimated σ² from our outermost k-space data, which have a low signal-to-noise ratio. Fig. 8 depicts an end-diastolic snapshot from the reconstruction with L₁ = 16 and L₂ = 48 as well as spatiotemporal slices through the left ventricle from all reconstructions. The frame rate of all reconstructions is 22 fps.

Fig. 8.

End-diastolic cardiac snapshot and spatiotemporal slices from human experimental results using (a) the full-rank (i.e., CS) model, (b) the proposed model with L₁ = L₂, and (c) the proposed model with L₁ < L₂.

A similar experimental procedure was used to demonstrate the effectiveness of the proposed method in human subjects with cardiac arrhythmias. The imaging protocol remained the same, with specific imaging parameters as follows: T_R = 4.3 ms, T_E = 2.5 ms, FA = 18°, FOV = 286 mm × 340 mm, matrix size = 130 × 192, in-plane spatial resolution = 2.2 mm × 1.8 mm, slice thickness = 7.0 mm, Q = 12, N_d = 5, N_ACS = 32, and P = 3. The total acquisition time was 2 min. We performed reconstruction according to the proposed model with L₁ = 15 and L₂ = 64, the proposed model with L₁ = L₂ = 64, and the full-rank (i.e., CS) model. All regularization parameters λ₁ and λ₂ were set according to Morozov’s discrepancy principle. Fig. 9 depicts an end-diastolic snapshot from the reconstruction with L₁ = 15 and L₂ = 64 as well as spatiotemporal slices through the left ventricle from all reconstructions. The frame rate of all reconstructions is 23 fps.

Fig. 9.

End-diastolic cardiac snapshot and spatiotemporal slices from arrhyth-mic human experimental results using (a) the full-rank (i.e., CS) model, (b) the proposed model with L₁ = L₂, and (c) the proposed model with L₁ < L₂.

D. 3-D Rat Imaging With First-pass Myocardial Perfusion

To demonstrate the proposed method in vivo in rats, we implemented the data acquisition scheme on a Bruker Avance AV1 4.7 T scanner using a customized FLASH pulse sequence. The images were collected with the following parameters: T_R = 7.5 ms, T_E = 2.4 ms, FA = 18°, FOV = 40 mm × 40 mm × 40 mm, matrix size = 62 × 62 × 128, and spatial resolution = 0.65 mm × 0.65 mm × 0.31 mm, Q = 4, N_d = 1, and P = 1. The total acquisition time was 24 min. All data were collected continually with neither ECG gating/triggering nor breath holding. Dynamic contrast enhancement for first-pass myocardial perfusion imaging was performed by injecting a 0.2 mmol/kg bolus of gadolinium contrast agent (Gd-DTPA) into each subject after the start of data acquisition. The animals used in the left anterior descending (LAD) coronary artery. All animals received humane care in compliance with the Guide for the Care and Use of Laboratory Animals, published by the National Institutes of Health, and the animal protocol was approved by the Carnegie Mellon University Institutional Animal Care and Use Committee.

We reconstructed the sparsely sampled (k, t)-space data according to the proposed model with L₁ = 15 and L₂ = 48 and the proposed model with L₁ = L₂ = 48. The full-rank (i.e., CS) solution was not computed due to memory constraints. All regularization parameters λ1 and λ2 were set according to Morozov’s discrepancy principle. Fig. 10 depicts end-systolic snapshots from the reconstruction with L₁ = 15 and L₂ = 48 as well as spatiotemporal slices from each reconstruction. The frame rate of all reconstructions is 67 fps. Fig. 10 depicts baseline-corrected signal intensity curves from the four apical segments of the myocardium in rats with and without ligation of the LAD coronary artery [46]. Hypoperfusion is apparent in the apical and septal segments, both of which are associated with LAD blood supply [47]; the ligated artery was identifiable using the proposed method.

Fig. 10.

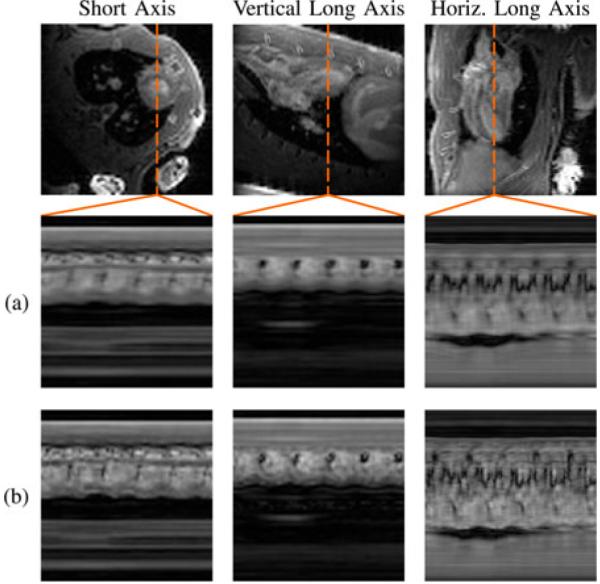
End-systolic cardiac snapshots and spatiotemporal slices from experimental results in rats using (a) the proposed model L₁ = L₂ and (b) the proposed model with L₁ < L₂.

E. Discussion

In simulations, the proposed method with L₁ < L₂ yielded the most accurate reconstruction (in the NRMS error sense) as well as providing the most faithful representation of the true cardiovascular dynamics. For each fixed L₂ , the minimum-error reconstruction occurs for some L₁ < L₂. Each of the low-rank results achieved significantly less error than the full-rank (i.e., CS) method. The superior performance of the proposed method with L₁ < L₂ over that with L₁ = L₂ can be attributed to the variable-rank model which better reflects the nature of cardiovascular images. In contrast, the low-rank model with L₁ = L₂ and the full-rank model do not distinguish between the regions of the image, imposing regionally unspecific model assumptions.

For the human data, the proposed method with L₁ < L₂ shows clear improvement over the proposed method with L₁ = L₂ and the full-rank (i.e., CS) methods. The reconstructions with L₁ < L₂ clearly depict the cardiac and respiratory cycles without the blurring seen in the other reconstructions. All three reconstructions fit the data to the same degree, but the model with L₁ < L₂ is the most flexible: it exhibits the least model bias and captures more subtle temporal variations than do the other models. The other reconstructions show a clear model bias, relying far more heavily on (r, f)-space sparse regularization than did the model with L₁ < L₂.

In 3-D imaging of rat hearts, the proposed method with L₁ < L₂ shows some improvement over the proposed method with L₁ = L₂, although the differences between the reconstructions are less obvious than in the human case. As in the human case, all reconstructions match the measured data to the same degree. The images from the proposed method with L₁ < L₂ are sharper and show slightly less model bias than the images from the proposed method with L₁ = L₂. The increased similarity between the two reconstructions can be partly attributed to the increased reliance of the proposed method with L₁ < L₂ on the (r, f)-space sparse regularization term for more highly under-sampled scenarios such as whole-heart 3-D imaging. The low-rank model allows storage of C(ρ) in the factored form ΨΦ, al-lowing memory-efficient computation even in high-dimensional cases for which C(ρ) cannot be stored in memory. The CS method requires the full C(ρ) to be stored at each iteration, and was therefore not computed due to memory limitations.

The ability to perform high-speed whole-heart 3-D imaging has wide-ranging implications. The improved spatial coverage allows for more comprehensive assessment of the heart than methods which capture only a handful of slices. The ability to image the whole heart in 3-D also eliminates the need for scan plane localization and excessive scout scans, as the reconstructed volumes can be retroactively sliced in arbitrary directions.

The proposed method requires identification of the cardiac region Ω. In our initial implementation, cardiac regions were identified manually from the time-averaged reference image ρ_ref(r). However, it may be preferable to automate this process through image segmentation methods for more practical routine use, especially for 3-D imaging applications.

IV. Conclusion

Cardiovascular MRI can be significantly accelerated by leveraging parallel imaging alongside low-rank and sparse modeling. This paper has described a novel method to integrate these three approaches to sparse sampling, achieving imaging speeds high enough to represent cardiac and respiratory motion without the need for gating or triggering. Very high imaging speeds are even achievable in 3-D: for example, speeds of up to 67 fps at 0.65 mm × 0.65 mm × 0.31 mm spatial resolution were demonstrated in rats, depicting cardiac motion, respiratory motion, and myocardial perfusion in a single experiment. Images generated by the proposed method should allow comprehensive evaluation of the heart through the visualization and measurement of cardiac structures and functions in very high spatial and temporal resolution.

Fig. 11.

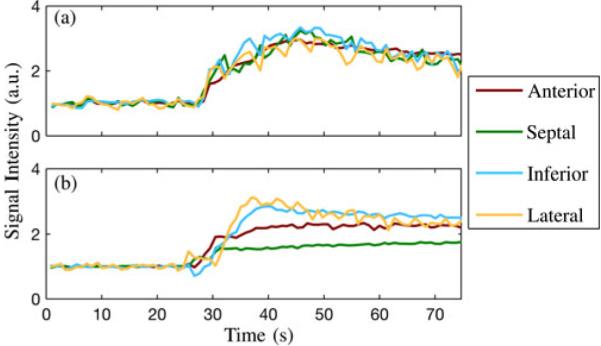
Baseline-corrected signal intensity curves from apical segments of the myocardium in (a) a healthy rat and (b) a rat with a ligated LAD coronary artery.

Biographies

Anthony G. Christodoulou (S’10) received the B.S. and M.S. degrees in electrical engineering from the University of Southern California, Los Angeles, CA, USA, in 2008 and 2009, respectively. He is currently working toward the Ph.D. degree in electrical and computer engineering at the University of Illinois at Urbana-Champaign, Urbana, USA.

His research interests include pulse sequences and image reconstruction with application to real-time cardiac MRI. He received an American Heart Association Predoctoral fellowship (2011–2012) and the IEEE-EMBC 2011 Best Paper award.

Haosen Zhang received the B.E. degree in chemical engineering from Tianjin University, Tianjin, China, and the Ph.D. degree in biomedical engineering from Cleveland State University, Cleveland, OH, USA.

She was a Research Associate at Washington University School of Medicine before she joined Pittsburgh NMR Center for Biomedical Research at Carnegie Mellon University, Pittsburgh, PA, USA, as an MRI Physicist.

Bo Zhao (S’09) obtained the B.S. and M.S. degrees in automation from Tianjin University, Tianjin, China, in 2005 and 2007, respectively. He is currently working toward the Ph.D. degree at the Department of Electrical and Computer Engineering, the University of Illinois at Urbana-Champaign, Urbana, USA.

His research interests include constrained image reconstruction and parameter estimation (novel signal/image modeling, algorithms, and performance characterization) with focus on magnetic resonance imaging.

Mr. Zhao was awarded a Honeywell scholarship (2002–2004) and coauthored the IEEE-EMBC 2011 Best Paper.

T. Kevin Hitchens received the B.S. degree in chemistry from West Virginia University, Morgantown, WV, USA, in 1991, and the Ph.D. degree in chemistry from the University of Virginia, Charlottesville, VA, USA, in 1997, and an M.B.A. from the University of Pittsburgh, Pittsburgh, PA, USA, in 2007.

Following his Ph.D., he accepted a Post-doctoral appointment in the Department of Biological Sciences at Carnegie Mellon University. In 2001, he joined the Pittsburgh NMR Center for Biomedical Sciences at Carnegie Mellon and is currently the Assistant Director.

Chien Ho received the B.A. degree from Williams College, Williamstown, MA, USA, and the Ph.D. degree from, Yale University, New Haven, CT, USA.

He is an Alumni Professor of Biological Sciences at Carnegie Mellon University, Pittsburgh, PA, USA. He has coauthored more than 300 papers and has received several honors and awards, including the ISMRM Gold Medal for his contribution to the development of cell-tracking methodology by MRI.

Zhi-Pei Liang (M‘92–SM‘98–F‘06) received the Ph.D. degree in biomedical engineering from Case Western Reserve University, Cleveland, OH, USA, in 1989.

He is currently the Franklin W. Woeltge Professor of Electrical and Computer Engineering at the University of Illinois at Urbana-Champaign, Urbana, USA. His research interests include image formation theory, algorithms, and biomedical applications.

Dr. Liang served as President of the IEEE Engineering in Medicine and Biology Society from 2011 to 2012. He is a Fellow of ISMRM and AIMBE. He was elected to the International Academy of Medical and Biological Engineering in 2012.