Scaling measurements of the effect of surface slant on perceived lightness

Abstract

The light reflected from an object depends on its reflectance, the illumination, and the pose of the object within the scene. An observer is called lightness constant if the perceived reflectance (lightness) of achromatic objects stays the same despite variation in object-extrinsic factors such as illumination and pose. Here, we used a dissimilarity scaling task to measure lightness constancy as the intensity of the illuminant and the slant of test surfaces were varied. Across two experiments, we had observers rate the dissimilarity of flat grayscale test stimulus pairs. The test stimuli were real illuminated surfaces, not computer simulations. Each test stimulus was seen in its own illuminated chamber, with the two chambers viewed side by side. We varied test surface reflectance, chamber illumination intensity, and the slant of the test in relation to the single light source in each chamber. Data were analyzed using nonmetric multidimensional scaling. The data were well-described by a one-dimensional perceptual representation. This representation was consistent across observers, revealed partial lightness constancy with respect to a change in illumination intensity, and no lightness constancy with respect to changes in surface slant. An additional experiment using a matching procedure and the same stimulus set, however, revealed moderate constancy with respect to changes in surface slant. The difference in results between the two methods is interesting, but not understood.

1. Introduction

Lightness is the perceptual correlate of object surface reflectance. Lightness provides useful information for object identification to the extent that lightness is stable across different scene contexts in which the object is viewed. Achieving such lightness constancy is challenging because the proximal stimulus for lightness, the luminance of the light reflected from the object, depends not only on the object's reflectance but also on object-extrinsic factors such as the scene illumination.

Across scenes where only the intensity of the overall illuminant is changed, human lightness constancy can be very good (for review, see Gilchrist, 2006). Changing the orientation of an object's surface with respect to a directional light source also affects the luminance of the reflected light, even when the light emitted by the illumination sources is held constant. The visual system can stabilize lightness with respect to such geometrical effects (Adelson, 1993; Allred & Brainard, 2009; Beck, 1965; Boyaci, Maloney, & Hersh, 2003; Gilchrist, 1980; Hochberg & Beck, 1954; Knill & Kersten, 1991; Mach, 1886; Pessoa, Mingolla, & Arend, 1996; Radonjić, Todorović, & Gilchrist, 2010; Ripamonti et al., 2004). This form of lightness constancy is not yet well-understood. For example, the degree of lightness constancy can vary considerably with small changes in experimental paradigm (Epstein, 1961) and there can be striking individual differences in performance within a single paradigm (Ripamonti et al., 2004). Although there are hypotheses about the nature of such effects (Bloj et al., 2004; Gilchrist, 1980; Gilchrist, 2006), there is need for a larger empirical foundation to delineate the phenomena.

The primary experimental method used for quantifying lightness constancy has been asymmetric matching. In such experiments, observers report their percepts by indicating when two stimuli seen in different surrounding contexts best match in lightness. Because of the difference in contexts, however, there is no guarantee that the best match will be perfect (see Brainard, Brunt, & Speigle, 1997). Adelson's (2000) haze illusion, for example, captures an effect where two grayscale stimuli of similar lightness can none-the-less appear very different, because one seems to be viewed through atmospheric haze. Based on observations of this sort, Logvinenko and Maloney (2006) suggested that the perceptual representation of achromatic color could be multidimensional, and that asymmetric matching paradigms might be problematic in cases where the degrees of freedom available to the subject did not allow equation of the percepts on all of the underlying dimensions. For example, different subjects might base their matches on different weightings of the underlying perceptual dimensions, leading to individual differences in performance that were not under experimental control. To investigate this possibility, Logvinenko and Maloney (2006) employed a dissimilarity scaling procedure to study the perception of achromatic color with respect to an illumination intensity change. They analyzed their data using nonmetric multidimensional scaling (MDS; Cox & Cox, 2001) and found that an underlying two-dimensional representation was required to account for their data. They interpreted this representation as one that provided perceptual correlates of both surface reflectance and of scene illumination. They also found that a two-dimensional representation was required to explain dissimilarity judgments in the context of a lightness illusion (Logvinenko, Petrini, & Maloney, 2008).

Based upon the work of Logvinenko and Maloney, we wondered whether large individual differences in lightness constancy with respect to changes in surface slant might have their origin in a failure of asymmetric matching to capture contextual effects on an underlying multidimensional representation. We conducted dissimilarity scaling experiments where we varied surface reflectance, surface slant, and illumination intensity, and report these here. For comparison, we also conducted an asymmetric matching experiment using the same stimuli.

2. Experiment 1

2.1. Methods

2.1.1. Overview

Observers in Experiment 1 judged the dissimilarity between pairs of grayscale test cards. Each card was viewed in its own illuminated chamber, with the two chambers located side-by-side. We varied the reflectance of the test cards, the illumination in the chambers, and the slant of the test cards. The following subsections provide detail.

2.1.2. Apparatus

The experimental apparatus consisted of two illuminated chambers positioned side by side (see Figure 1). Each chamber was illuminated independently by two theater stage lamps (SLD Lighting, 3-in. Fresnel #3052), which could be turned on and off by the control computer. One of the two lamps in each chamber had a neutral density filter (Hoya, 72 mm ND 8x filter) that reduced the illumination level to ∼12.5% of that of the unfiltered lamp. The two lamps in each chamber were arranged side-by-side and produced similar illumination geometry. Information regarding the direction of the illumination was available to the observer through visible cast shadows but the lamps themselves were not directly visible.

Figure 1.

Image and schematic of apparatus. All measurements are in meters. Filtered lamps are labeled “L” and unfiltered lamps labeled “H.” The right chamber shows a test card oriented at 42° in the direction away from the light source.

Each chamber contained a rotating stage driven by a stepper motor. A test card was placed on each stage, and the slant of the test card could be adjusted in 1˚ increments under computer-control.

Observers viewed the two chambers from a booth located 1.7 m away. A computer-controlled shutter obscured the observers' view of the chambers during intertrial intervals. The configuration of the two chambers was arranged to closely approximate mirror-symmetry between the two.

A monitor located above the chambers was visible to the observer. On each trial, observers rated dissimilarity by adjusting a slider to display their chosen rating (0–30) on this monitor, and pushed a button when that rating had been set. The monitor also presented instructions to the observers at the start of the experiment.

Doors located in the back of the chamber allowed the experimenter to change the identity of the test cards in each chamber for each trial. A monitor located on the backside of the chamber (and not visible to the observer) informed the experimenter as to which cards should be inserted on each trial.

2.1.3. Experimental conditions

The test cards were constructed from Color-aid paper (chosen from Color-aid Gray Set G912) attached to small stands that interlocked with the rotating stages. The cards differed only in their reflectance. We made two sets of six cards so that any pair of reflectances, including matching reflectances, could be displayed in the two chambers. For convenience, we refer to the two sets as Set A and Set B.

The six test cards were presented in three contexts, for a total of 18 different test–context pairs. For Context 1, the chamber was illuminated by the unfiltered lamp and the test card was presented frontoparallel to the observer (0° slant). We measured the luminance reflected from a Teflon reflectance standard (Labsphere, SRT-99-050) placed on the stage using a PhotoResearch PR-650 spectral radiometer. For Context 1, the luminance reflected from the reflectance standard was 944.6 cd/m². For Context 2, the test was again presented at 0° slant, but the filtered lamp was used. Here, the luminance of the light reflected from the reflectance standard was reduced to 107.4 cd/m². For Context 3, the unfiltered lamp was again used, but the test card was presented at a slant of 42°, with the direction of rotation being away from the direction of the light source relative to the 0° position. For this condition, the luminance of the light reflected from the reflectance standard was 58.31 cd/m², more closely approximating that of Context 2 than that of Context 1. Although both Context 2 and Context 3 produced lower illumination incident on the test card than Context 1, the physical change that accomplished this was different in the two cases.

We measured the reflectance of each card. The reflectance was calculated as the luminance of the test card in Context 1 divided by the luminance of the reflectance in Context 1. The six reflectances used were 0.415, 0.335, 0.270, 0.195, 0.126, and 0.083.

Because the Color-aid paper is not perfectly matte and the test chambers were not perfectly symmetric, we measured the light reflected to the observer for each test card in each context for both chambers for both card Sets A and B. The values provided earlier are averages taken of these measurements.

Supplemental Table S1 provides the complete card measurement data for measurement 1.

2.1.4. Task

For each trial, the observer's task was to provide a numerical rating, ranging from 0 to 30, of the dissimilarity in the appearance of the two test cards, where a rating of 0 would mean that the two cards appeared exactly the same, while a rating of 30 would mean that the two cards appeared as different as the difference between black and white. To make clear what we meant by the latter, at the start of each session observers were shown a pair of test cards outside the range of those used in the experiment. A black card (reflectance of 0.029) was presented in Context 3 in one chamber and white card (reflectance of 0.8725) was presented in Context 1 in the others. Observers were told that this difference should be rated with a dissimilarity of 30.

Before each trial, a card was placed on the platform in each stimulus chamber. The appropriate cards to place for each trial were specified to the experimenter on the display at the back of the apparatus. While the cards were changed, the shutter prevented the observer from viewing the stimuli. Thus the lamp settings and slant of the stimulus were set appropriately for the trial before the shutter opened.

At the start of the session, there were five practice trials. These were chosen randomly from the set of experimental trials. We inserted the practice trials to allow the observer to establish the use of the rating scale before data collection started. Observers, however, were naïve as to the fact that the practice trial data were not recorded, as these trials were not distinguished for the observer from the subsequent experimental trials.

Observers made their ratings using a slider device, with the number of the current rating visible on a computer monitor above the stimulus chambers. Observers provided dissimilarity ratings for all possible combinations of test stimulus–context pairs (one in each chamber), for a total of 324 (18 × 18) trials per set. Each observer completed up to four full replications, for a total of up to 1,296 trials. Set A and Set B of the test cards were alternated between left and right chambers, such that two replications were completed with each test card set in each chamber for observers who completed all four replications. Observers completed approximately 150 trials per hour-long session, a pace that allows completion of four replications across approximately nine sessions.

2.1.5. Observers

Four naïve observers with normal or corrected-to-normal vision participated in this experiment. Three observers (RVX, ROI, and QFO) completed four replications while one observer (WQB) completed two replications.¹ Observers were screened for color deficiency using the Ishihara color plates (Ishihara, 1977). Visual acuity (tested in both eyes) and stereoscopic depth perception were tested using a Keystone Vision Screener II. Observers were excluded from further participation in the experiment if they made more than one mistake on the Ishihara color plates, their visual acuity was less than 20/30, or if their indicated stereopsis corresponded to lower than 75% on the Shepherd–Fry Scale, as reported by the Keystone Vision Screener II.

In addition, before starting the main experiment, observers completed a map scaling task to familiarize them with the type of ratings to be made in the main experiment. In the map scaling task, 10 points on a computer screen were presented in all possible combinations of two at a time (45 combinations) and observers were asked to rate the distance between the two points with a value ranging from 1 (very close) to 30 (most distant). The resulting distance ratings were analyzed using multidimensional scaling (MDS). The configurations returned by MDS were rotated, reflected, translated, and scaled using a distance-preserving Procrustes transformation to match the displayed configuration as closely as possible, and error was measured using the sum of squared difference between each displaced point and the point in the transformed configuration, normalized by the sum of the squared interpoint distances in the actual configuration. Each observer completed the map task twice during the initial experimental session, and observers with an error greater than 0.04 were excluded from further participation in the experiment.

The experiments were carried out in accordance with the relevant institutional and national regulations and legislation, and with the World Medical Association Helsinki Declaration as revised in October 2008 (http://www.wma.net/en/30publications/10policies/b3/).

2.1.6. Instructions

Before participating in the experiment, observers underwent an induction procedure (Allred & Brainard, 2009; Doerschner, Boyaci, & Maloney, 2004) to familiarize them with the difference between surface reflectance on the one hand and the amount of light reflected from a surface on the other. Observers viewed three painted grayscale blocks and were given time to notice how the amount of light reflected from the blocks changed as they were moved in relation to a light source, while the surface reflectance was constant. The induction procedure provided a concrete context for the experimental instructions. The instructions used in the induction procedure are described in the online supplemental material (http://color.psych.upenn.edu/supplements/mdslightness). A picture of the induction procedure apparatus is available in the online supplemental material for Allred and Brainard (2009; http://color.psych.upenn.edu/supplements/slant_contrast).

Two sets of instructions were used, with two observers receiving each set of instructions. For the reflectance condition (Instruction Set A), observers were asked to provide a dissimilarity rating based on the apparent reflectance of the two test cards. For the reflected light condition (Instruction Set B), observers were asked to provide a dissimilarity rating based on the apparent amount of light reflected from the two cards. Observers RVX and WQB received Instruction Set A, while observers ROI and QFO received Instruction Set B. The text for the instructions is also provided in the online supplemental material.

2.1.7. Results

The dissimilarity ratings given by the observers for all test card–context pairs (that is, the dissimilarity matrices that we analyzed) are tabulated for each observer/replication in the online supplemental material (http://color.psych.upenn.edu/supplements/mdslightness), for this and all experiments reported in this paper. Each 18 × 18 raw data matrix was converted into a symmetric dissimilarity matrix by averaging corresponding dissimilarity ratings (where the comparisons were made between the same two test card–context pairs but in opposite chambers; in a few cases, a data recording error resulting in only one of the two measurements being available, in which case it was used in place of the average). The diagonal dissimilarity ratings (comparisons between matched test card-context pairs) were set to zero.

Our first interest was to understand how well the dissimilarity data could be accounted for by a multidimensional scaling (MDS) model, in which each stimulus is represented as a point in a multidimensional space. Within nonmetric MDS models, the dissimilarities between two stimuli are predicted as a monotonic function of the distance between the two corresponding points.

In standard implementations of nonmetric multidimensional scaling, computer routines seek a configuration of points to minimize an error measure referred to as STRESS. Let the variables s and t index the stimuli and let δ_st represent the experimentally obtained dissimilarity between stimuli s and t. A typical definition of STRESS would be

$$\text{STRESS}=\sqrt{{\displaystyle \sum _{s,t}{\left(d_{st}-{\widehat{d}}_{st}\right)}^2/}{\displaystyle \sum _{s,t}{\left(d_{st}\right)}^2.}}$$ (1)

Here, d_st is the distance between the two points in an obtained configuration representing stimuli s and t, typically computed using either a Euclidean or city-block metric, and ${\widehat{d}}_{st}$ is the disparity between stimuli S and t (Kruskal, 1964). The disparities ${\widehat{d}}_{st}$ are obtained as a monotonic function of the dissimilarities δ_st. The monotonic transformation allows for the possibility that the subject's reported dissimilarities are obtained from the underlying perceptual distance using an ordinal scale. The normalization term ${\displaystyle \sum _{s,t}{\left(d_{st}\right)}^2}$ prevents a degenerate representation where all stimuli are mapped to the same point and the nonmonotonic transformation maps all of the disparities to 0. If the MDS model perfectly predicted the data, the STRESS would be 0.

For our analyses, we employed an alternate error measure, which we refer to as iSTRESS (for inverted STRESS). The iSTRESS measure is defined as

$$\text{iSTRESS}=\sqrt{{\displaystyle \sum _r{{\displaystyle \sum _{s,t}\left({\delta }_{r,st}-{\widehat{\delta }}_{st}\right)}}^2/}{\displaystyle \sum _r{{\displaystyle \sum _{s,t}\left({\delta }_{r,st}\right)}}^2,}}$$ (2)

where δ_r,st is the dissimilarity assigned by the observer to the stimulus pair s,t during replication r and ${\widehat{d}}_{st}$ is the predicted dissimilarity between stimuli s and t. The predicted dissimilarities ${\widehat{d}}_{st}$ are obtained as a monotonic function of the solution interpoint distances, d_st.

Clearly, iSTRESS is closely related to STRESS, with the primary difference being that the error is computed with respect to the dissimilarities rather than with respect to the distances inferred from the data. This has the advantage that we can also compute iSTRESS for non-MDS models that account for the data without using the distance concept, and thus compare different types of models using the same error measure. Our primary application of this concept will be to assess the precision of the data and the overall variation in the data, and use these as benchmarks against which to compare MDS models of different dimensions.

A second modification from the standard STRESS equation is that we compute the error measure over replications for individual subjects rather than using mean data. This is of less theoretical significance than the choice to compute the error in the data domain, but does allow us to take measurement precision explicitly into account when evaluating how well the MDS representations account for the data.

Finally, rather than allowing an arbitrary monotonic transformation between representation distances d_st and predicted dissimilarities ${\widehat{d}}_{st}$, we also required that this function be smooth. In particular, we used a power function

$${\widehat{\delta }}_{st}=a{\left(d_{st}\right)}^b$$ (3)

with a > 0 and 0.1 < b < 10. Enforcing smoothness in this relation takes advantage of the fact that perceived lightness is known to vary smoothly as a function of stimulus magnitude and reduces the number of degrees of freedom in the models.

2.2. Results

2.2.1. Representation dimensionality

We found the one-, two-, and three-dimensional MDS representations that minimized iSTRESS for each observer, using the Euclidean distance metric. The value of iSTRESS does not vary appreciably with dimension, indicating that there is little improvement in fit as we move from a one-dimensional representation to a higher dimensional representation (see Figure 2). To calibrate the scale of the variation of iSTRESS with dimension, we also computed iSTRESS for two limiting-case models. The grand mean model fits each measured dissimilarity with a single number obtained as the grand mean (taken over stimulus pairs and replications) of the measured dissimilarities. The iSTRESS value for this model provides an indication, in the context of the iSTRESS metric, of the variance in the data set. Any reasonable model should have a considerably lower iSTRESS than that of the grand mean model. The iSTRESS of the grand mean model for each observer is shown in blue in Figure 2. The mean model fits each measured dissimilarity with its own mean (taken over replications). No model can have a lower iSTRESS value lower than that of the mean model, and it therefore represents the precision of the data. The iSTRESS of the mean model for each observer is shown in green in Figure 2. By comparing the iSTRESS values for the MDS models with that of the two-limiting case models, we see that the one-dimensional MDS representation is capturing most of the variance available to be fit in the data.

Figure 2.

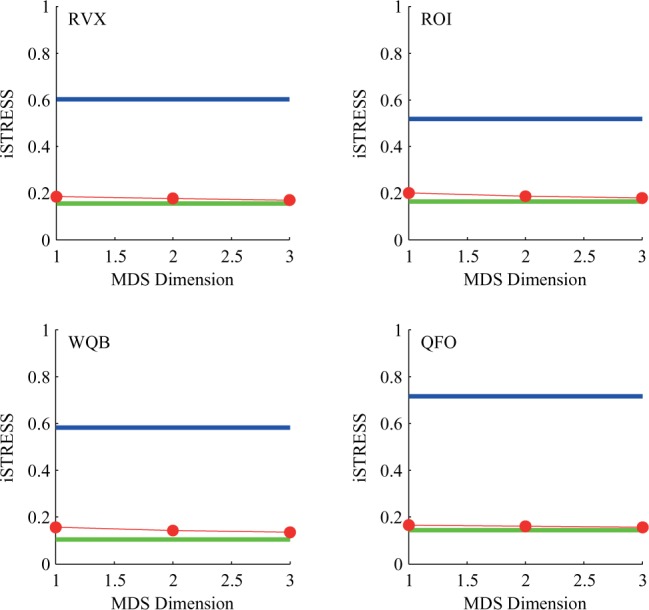
A one-dimensional representation accounts for the Experiment 1 data. Plots of iSTRESS by dimension from MDS analysis for all four observers. The red points show iSTRESS for representations of dimension 1, 2, and 3. The blue line indicates iSTRESS for the grand mean model and the green line for the mean model. Observers whose data are shown in the left panels received Instruction Set A (reflectance) and observers whose data are shown in the right panels received Instruction Set B (reflected light).

Refitting the data using a city-block rather than Euclidean distance metric led to essentially no difference in the iSTRESS values (Madigan, 2011, Appendix Table A.2), and we did not explore the use of the city-block metric further. Relaxing the smoothness constraint led to a slight reduction in stress for each MDS dimension (Madigan, 2011, Appendix Table A.2), but essentially no difference in the recovered representation for the one-dimensional case (Madigan, 2011, Appendix Figure A.4).

Figure 3 shows the one- and two-dimensional solutions obtained via our MDS procedure. Each stimulus is plotted as a point in a two-dimensional space; for this representation of the one-dimensional solutions, the value of the second dimension was set to zero. A comparison of the one- and two-dimensional solutions shows that the two-dimensional representation adds little to the interpretation of the data (see Figure 3). In particular, the variation within the second dimension does not obviously correlate with any salient physical aspect of the stimuli. In addition, while the one-dimensional solution shows good consistency across observers (see also Figures 4 and 5 appearing later), the second dimension of the two-dimensional solution is idiosyncratic with observer. Given the nature of the two-dimensional representation as well as the iSTRESS analysis earlier, we conclude that the data from this experiment do not support the notion that the perceptual representation of lightness is multidimensional.

Figure 3.

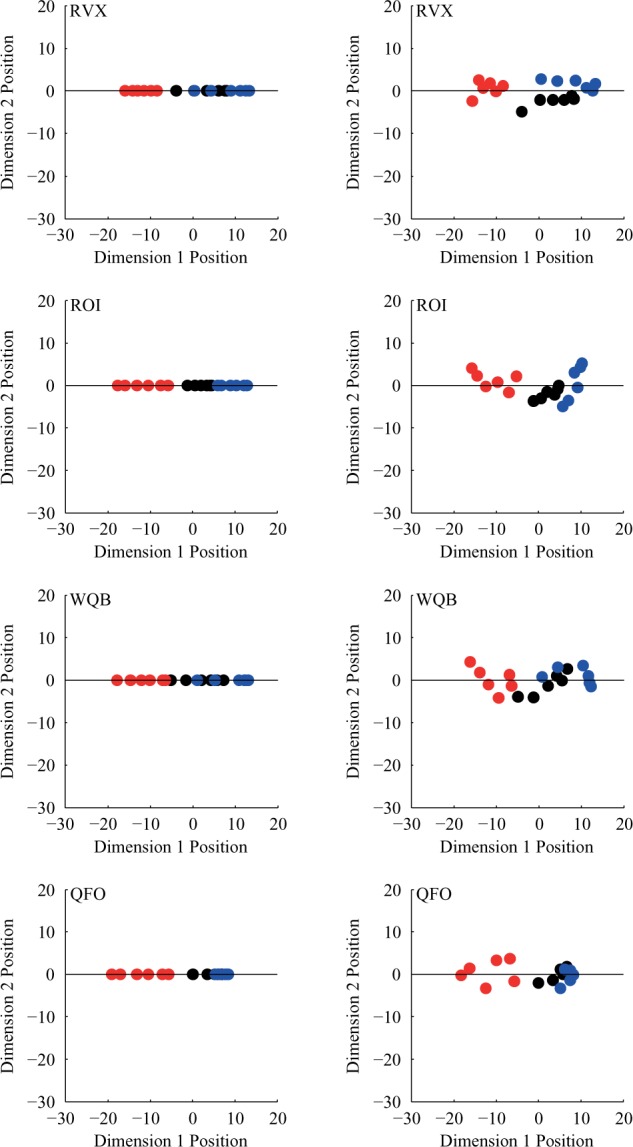
Comparison of the one-dimensional (left panels) and two-dimensional (right panels) MDS solutions for all observers in Experiment 1. In the left panels, the dimension 2 position is set to zero. Each color represents a different context, with blue as Context 1, black as Context 2, and red as Context 3. Observer initials are provided in each panel. The one-dimensional solution for Observer RVX was aligned to the first dimension of the two-dimensional solution for RVX using a Procrustes (relative-distance preserving) transformation. The one-dimensional solutions for the other observers were aligned to the one-dimensional solution for RVX using the same type of transformation, and the two-dimensional solutions for the other observers were similarly aligned to the two-dimensional solution for RVX. Observers RVX and WQB received Instruction Set A (reflectance). Observers ROI and QFO received Instruction Set B (reflected light).

Figure 4.

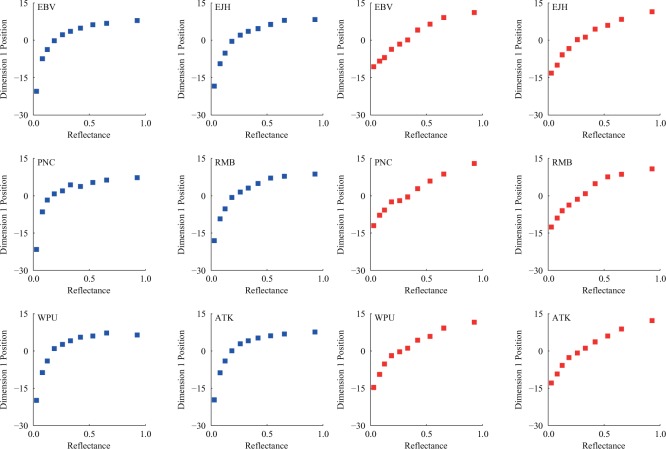
Observers in Experiment 1 were not perfectly lightness constant. Plots of the one-dimensional MDS position against the surface reflectance of the test cards. Each color represents a different context, with blue as Context 1, black as Context 2, and red as Context 3. Observers whose data are plotted in the panels on the left received Instruction Set A (reflectance) while observers whose data are plotted on the right received Instruction Set B (reflected light).

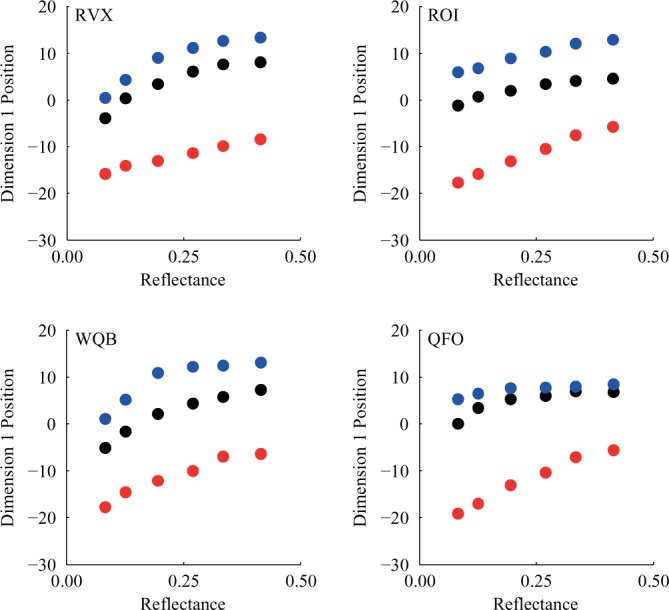
Figure 5.

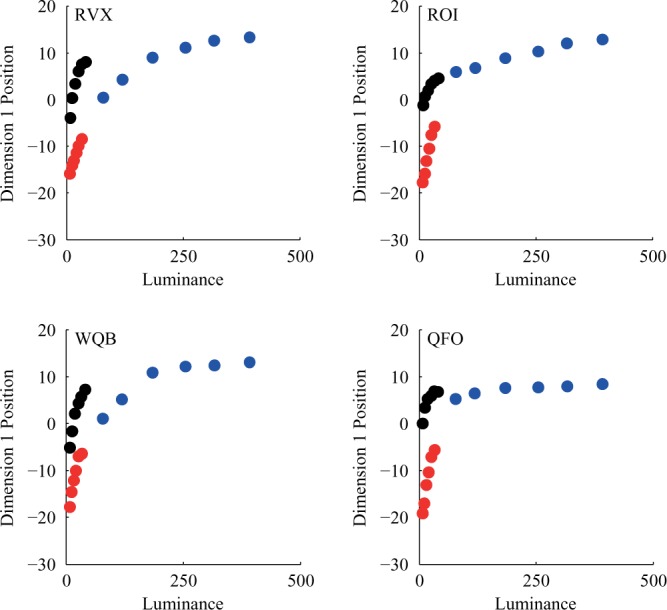
Observers in Experiment 1 were not matching luminance. Plots of the one-dimensional MDS position against luminance reflected from the test cards. Each color represents a different context, with blue as Context 1, black as Context 2, and red as Context 3. Observers on the left received Instruction Set A (reflectance) and observers on the right received Instruction Set B (reflected light). The fact that the data do not fall along a single locus indicates that context has an effect on the relation between stimulus luminance and the perceptual representation. The clear effect is the change in illuminant intensity between Contexts 1/3 (blue/red) and Context 2 (black). The data for Contexts 1 and 3 appear to lie along a single curve, but because of the luminance gap between the stimuli for the two contexts, the data are not definitive in this regard.

2.2.2. Lightness constancy

Given our conclusion that a one-dimensional MDS solution accounts for the data, it is of interest to examine the one-dimensional solutions. These are shown in Figure 4, with position along the solution dimension plotted against stimulus surface reflectance. If an observer were lightness constant, stimuli of the same reflectance seen in different contexts would be represented at the same position in the plot. The observers in our experiment were not perfectly lightness constant.

If, on the other hand, observers were making dissimilarity ratings entirely on the basis of the luminance reflected from the test cards, the data would fall along a single locus when plotted as a function of luminance (Figure 5). This is also not the case. In particular, across the illumination change (Context 1 to Context 2), there is some degree of constancy. For the change in test slant (Context 1 to Context 3), the data are not decisive. This is because the luminance range of the stimuli across the slant change does not overlap, so that a sharp determination of whether the MDS solution plots on a single locus is not possible. It is worth noting that the data from Contexts 2 and 3 are quite different, indicating that the degree of constancy for the two manipulations (illuminant change and slant change) is not the same.

2.2.3. Instructions

The left versus right panels of Figures 4 and 5 contrast our two instruction conditions. Of the four observers in Experiment 1, Observer ROI's (Instruction Set B, judge on the basis of reflected light) responses are most consistent with a luminance comparison across the illumination change. This is consistent with the direction of the instructional manipulation. On the other hand, Observer QFO's data (also Instruction Set B) resemble those of RVX and WQB (Instruction Set A). If there was an effect of instructions in Experiment 1, it was small.

3. Experiment 2

3.1. Methods

3.1.1. Overview

Experiment 2 consisted of two separate subexperiments (referred to as Experiment 2A and Experiment 2B). The methodology of Experiment 2 closely followed that of Experiment 1, with only the stimulus set and observers varying. The stimuli were chosen to provide more information regarding the degree of lightness constancy with regard to slant changes. In particular, we used 10 reflectances in Experiment 2, to more fully characterize performance.

3.1.2. Apparatus

The apparatus was the same as in Experiment 1.

3.1.3. Experimental conditions

We constructed and measured the test cards in the same way as in Experiment 1. The 10 reflectances used in Experiment 2 were 0.938, 0.658, 0.541, 0.424, 0.335, 0.264, 0.187, 0.126, 0.082, and 0.029.

There were six contexts used over Experiment 2A and 2B. The unfiltered lamp was used for all six contexts, with the only difference between the contexts being the slant at which the test cards were presented. Both a slant of frontoparallel to the observer (0° slant) and a slant of 42° away from the light source (Context 1 and Context 3 of Experiment 1, respectively) were used, as well as additional contexts with slants of 42° toward the light source (−42° slant), −21°, 14°, and 28°. The slants chosen included both slants used in Experiment 1. In addition, we included several intermediate steps between the two, as well as two additional slants chosen to produce more luminous test cards than the 0° slant of Experiment 1. The luminance of light reflected from the white reflectance standard and all stimuli for the six contexts is given in Supplemental Table S2.

Experiment 2A conditions. The experimental conditions for Experiment 2A included all 10 reflectances listed above but only the two slant contexts from Experiment 1 (0° and 42°).

The task and practice trials for Experiment 2A were the same as for Experiment 1. Observers did not provide dissimilarity ratings for all possible combinations of test stimulus–context pairs, however. Instead, dissimilarity ratings were made only within each of the two slant contexts, so that there were a total of 200 trials (10 × 10 trials for each of the 0° and 42° slants) per replication. Each observer completed up to four full replications of the experiment, for a total of up to 800 experimental trials. Set A and Set B of the test cards were alternated between left and right chamber, such that replications were completed with each test card set in each chamber.

Experiment 2B conditions. Experiment 2B used only three of the 10 reflectances listed before: 0.424, 0.187, and 0.082, but used all six of the slant contexts. The three reflectances were chosen to have roughly equal perceptual steps between them.

As the example trial was designed to be the most extreme possible luminance difference between two stimuli, it was changed for Experiment 2B. A black card (reflectance of 0.029) was presented at a slant of 42° in one chamber and white card (reflectance of 0.8725) was presented at −42° in the other. Observers were told that this difference should be rated with a dissimilarity of 30.

Observers provided dissimilarity ratings for all possible combinations of test stimulus–context pairs, for a total of 324 (18 × 18) trials per set. Each observer completed up to four full replications of the experiment, for a total of up to 1,296 experimental trials. Set A and Set B of the test cards were alternated between left and right chamber, such that replications were completed with each test card set in each chamber.

3.1.4. Observers

Six naïve observers with normal or corrected-to-normal vision participated in Experiments 2A and 2B. Five observers (EBV, EJH, RMB, WPU, and ATK) completed four replications of Experiment 2A and one (PNC) completed two. One observer completed four replications of Experiment 2B (EBV), two completed two replications (PNC, WPU), two completed one replication (RMB, EJH), and one observer only completed Experiment 2A (ATK). The screening procedures and exclusion criteria for Experiment 2 matched that of Experiment 1. All trials for Experiment 2A were completed before an observer moved on to Experiment 2B.

3.1.5. Instructions

The induction procedure and instruction conditions were the same in Experiment 2, with observers ATK, EJH, and WPU receiving Instruction Set A and observers EBV, PNC, and RMB receiving Instruction Set B.

3.2. Results

3.2.1. Representation dimensionality

As with Experiment 1, we found little improvement in iSTRESS values when moving from a one-dimensional representation to a higher dimensional representation and the one-dimensional representation again captured most of the variance in the data. This is shown in Supplemental Figures S1–S3.

Comparisons of the one-dimensional and two-dimensional representations obtained for Experiments 2A and 2B show that the second dimension adds little interpretive value (see Supplemental Figures S4–S6) and we conclude that a one-dimensional representation is sufficient. Although the form of the two-dimensional solution shows more regularity across subjects than we found in Experiment 1, the points in the two-dimensional representation do not separate systematically with slant (Supplemental Figure S6) but rather fall along a one-dimensional curve in the two-dimensional space. Given the nature of the two-dimensional representation as well as the iSTRESS for the one- and two-dimensional representations, we analyzed the one-dimensional representation. The fact that the solution is one dimensional is not surprising for Experiment 2A, where the dissimilarity judgments were obtained across test reflectance but within slant context. In Experiment 2B, however, dissimilarity judgments were obtained across the multiple slant contexts and the fact that we obtain a one-dimensional solution is consistent with our results from Experiment 1.

3.2.2. Lightness constancy

Figure 6 shows the one-dimensional representations for all observers for the 0-slant context and 42-slant contexts of Experiment 2A. The position along the represented dimension varies with reflectance in a roughly logarithmic relationship. Because each panel of Figure 6 corresponds to a single fixed slant, the position along the represented dimension also varies with luminance in the same fashion. Because the data for each slant context in Experiment 2A were collected separately, these data do not speak to the effect of slant on the underlying perceptual representation. What they do provide are baseline data about the functional relation between reflectance/luminance and the perceptual relation, and we will take advantage of the regularity exhibited by the data in analyses presented later.

Figure 6.

Plots of one-dimensional MDS representation against reflectance of the test cards for Experiment 2A. Lefthand plots (blue symbols) are for the 0° slant condition. Righthand plots (red symbols) are for the 42° slant condition. Observers ATK, EJH, and WPU received Instruction Set A (reflectance). Observers EBV, PNC, and RMB received Instruction Set B (reflected light).

Figure 7 shows the one-dimensional representation for observers in Experiment 2B plotted against reflectance while Figure 8 shows the same representation plotted against luminance. It is clear from Figure 7 that observers are not perfectly lightness constant, as the data separate with slant context. It is clear from Figure 8 that observers are basing their similarity judgments only on stimulus luminance. The fact that the data across slants fall along a single locus indicates that their judgments are being made on the basis of stimulus luminance, with no effect of slant on the relation between luminance and the perceptual representation. The data in Figure 8 are consistent with the data from Experiment 1 shown in Figure 5 for Contexts 1 and 3. Here, however, the fact that we have data from multiple slants pieces together the full locus, without the stimulus gap that existed in Experiment 1.

Figure 7.

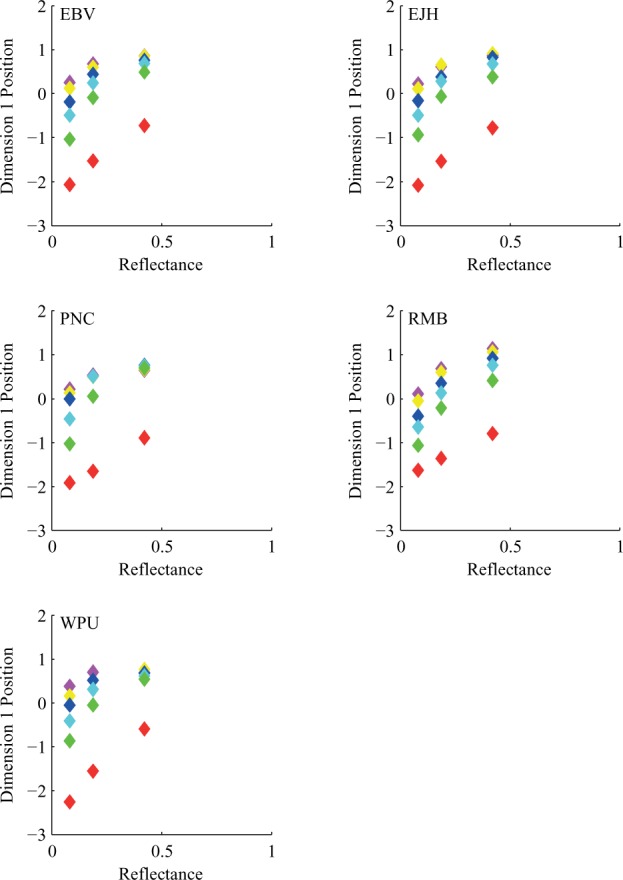
Observers in Experiment 2B were not perfectly lightness constant. Plots of one-dimensional MDS representation against reflectance of the test cards for Experiment 2B. Each color shows a different slant context. The colors are red (42), green (28), cyan (14), blue (0), yellow (−21), and magenta (−42). The separation of the data for the different slants indicates that observers were not making their judgments based only on reflectance. Observers EJH and WPU received Instruction Set A (reflectance). Observers EBV, PNC, and RMB received Instruction Set B (reflected light).

Figure 8.

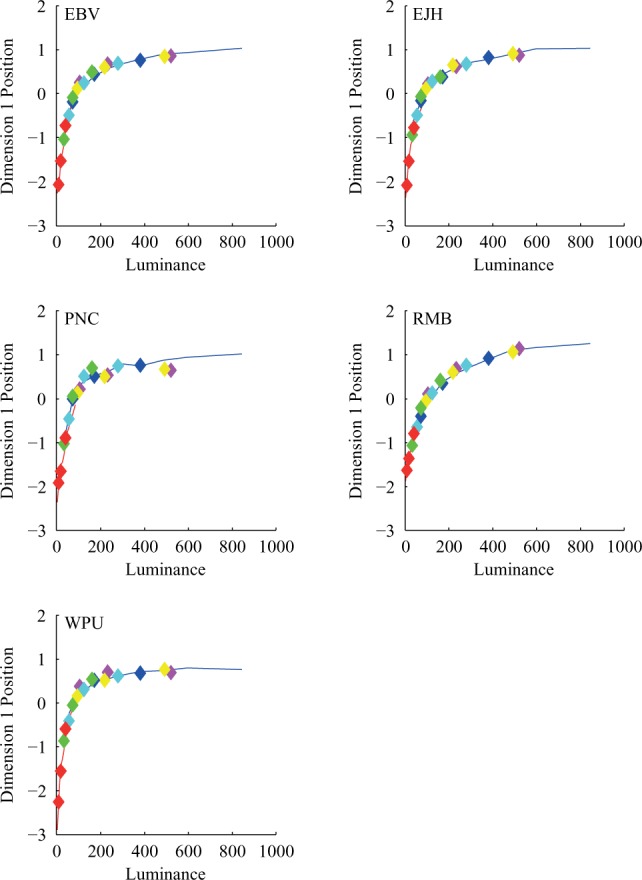
Observers' judgments across slants in Experiment 2B are accounted for by stimulus luminance. Plots of one-dimensional MDS representation against luminance of the test cards for Experiment 2B. Each color shows a different slant context. The colors are red (42), green (28), cyan (14), blue (0), yellow (−21), and magenta (−42). The fact that the data across slants fall along a single locus indicates that observers' judgments are being made on the basis of stimulus luminance, with no effect of slant on the relation between luminance and the perceptual representation. The red and blue lines show the representations from Experiment 2A (Figure 6); distance preserving transformations were applied to bring them into register with the representation derived for 2B. The fact that these lines are difficult to see beneath the data is an indication of the good agreement. Figure S7 provides a fuller view of the transformed solutions. Note that these transformed solutions provide exactly the same account of the dissimilarity data as the untransformed solutions shown in Figure 6, because MDS determines representations only up to a distance preserving transformation. Observers EJH and WPU received Instruction Set A (reflectance). Observers EBV, PNC, and RMB received Instruction Set B (reflected light).

If subjects' judgments of similarity are based on only stimulus luminance across Experiments 2A and 2B, it should be possible to account for the full set of similarity judgments with a single luminance-based perceptual representation. We used a distance preserving transformation to bring the solution for the 0° slant condition of 2A into register with the solution for Experiment 2B and a second distance preserving transformation to do the same thing for the 42° slant condition of 2A. The red and blue lines in Figure 8 show the representations from Experiment 2A (Figure 6; 10 points for each line). The fact that these lines are difficult to see beneath the data is an indication of the good agreement. Figure S7 provides a fuller view of the transformed solutions. For each observer, a single curve in the representation versus luminance plots provides a good account of all the data from Experiment 2.

4. Experiment 3

4.1. Methods

4.1.1. Overview

Observers in Experiment 2 were consistent with each other and the data showed no indication of lightness constancy. The purpose of Experiment 3 was to connect the dissimilarity task and an asymmetric matching task, by having observers who completed Experiment 2 also perform an asymmetric matching task using the full set of stimuli used in Experiment 2.

4.1.2. Apparatus

There was one change made to the apparatus for Experiment 3. An illuminated palette was attached to the wall to the left of the observers. On the palette were 19 1×4 cm patches. One patch was taken from each of the 19 different reflectances represented in the Color-aid Gray Set (G912). The patches were labeled from 1.0 to 10.0 in steps of 0.5. The illumination on the patches varied somewhat across the surface of the palette. The measured luminance and reflectance of the patches are given in Supplemental Table S3.

4.1.3. Experimental conditions

The 10 test cards (reflectances 0.938, 0.658, 0.541, 0.424, 0.335, 0.264, 0.187, 0.126, 0.082, and 0.029) and six contexts (°42°, °21°, 0°, 14°, 28°, 42°) used in Experiment 2 were also used in Experiment 3. The luminances of the test cards in the chambers were not altered significantly when the palette illumination was turned on.

4.1.4. Task

For each trial, the observer's task was to make a match between a stimulus in one of the chambers and the palette to their left. Before each trial, a stimulus was placed on the platform in each stimulus chamber. The appropriate cards to place for each trial were specified to the experimenter on the display at the back of the apparatus. While the cards were changed, the shutter prevented the observers from viewing the stimuli. The slants of the stimuli were then set appropriately for the trial before the shutter opened.

Observers made their match using a slider device, with the number of the current match visible on the computer monitor above the stimulus chambers. Although two stimuli were presented at a time, observers were directed to make matches to each stimulus, one at a time, via an arrow presented on the monitor. The order in which the two visible stimuli were matched was varied randomly trial to trial.

Observers made matches for all test stimulus–context combinations, presented in both the right and left stimulus chambers, for a total of 120 (10 reflectances × 6 contexts × 2 chamber sides) trials per replication. Each observer completed up to two full replications of the experiment, for a total of 240 trials. Set A and Set B of the test cards were alternated between left and right chambers, such that up to two replications were completed with each test card set in each chamber.

Observers were given the option of labeling stimuli as either darker or brighter than the darkest palette patches if they felt they could not make a sufficient match. All trials in which observers made these judgments were excluded from the analysis as described later.

4.1.5. Observers

Four naïve observers with normal or corrected-to-normal vision participated in this study. Three observers completed two replications (EBV, PNC, and RMB) while one completed only a single replication (EJH). These observers also participated in Experiments 2A and 2B.

4.1.6. Instructions

There were again two instruction sets for Experiment 3, with the instructions designed to be close approximations of the previous instructions in content and style. Observers were assigned to the same instruction set they received for Experiment 2. Experiment 3 instructions can be found in the online supplemental material. Each observer in Experiment 3 had undergone the induction procedure at the start of Experiment 2, and this was not repeated for Experiment 3.

4.2. Results

The matches made by the observers are provided in the online supplemental material. We then averaged, for each observer, slant and palette patch, the luminances of all trials on which that palette patch was chosen. This data aggregation procedure finesses the issue of how to quantify out-of-range responses, an issue that would have to be dealt with if instead we had tried to average the palette reflectances chosen for a given test card luminance (see Radonjić, Allred, Gilchrist, & Brainard, 2011 for further discusssion of this point). Figure 9 shows the results.

Figure 9.

Matched palette reflectance for four observers in Experiment 3 against test card luminance. Each context is shown in a different color. The colors are red (42), green (28), cyan (14), blue (0), yellow (−21), and magenta (−42). Curves through the data are the fit of the model described in the text (Equation 4). Observer EJH received Instruction Set A (reflectance). Observers EBV, PNC, and RMB received Instruction Set B (reflected light).

An observer making matches on the basis of stimulus luminance would produce data so that the points from different stimulus contexts were overlapping, such that in cases where mean matched luminance was identical, the plotted palette reflectance would be as well. Observers' results in Experiment 3 do not show this pattern; observers deviate from luminance matching in the direction of lightness constancy. That is, unlike for the scaling data from Experiment 2, observers' judgments could not be explained entirely on the basis of stimulus luminance.

To examine the dependence of matches on slant more quantitatively, we aggregated the data over test reflectance. To do so, we fit a function through the data, for each observer and slant, of the form:

$$r=betacdf\left({\left(gl\right)}^k,a,b\right)$$ (4)

where r is the matched palette reflectance, l is the mean matched luminance, g and k are constants, and a and b are the two parameters of the cumulative beta distribution. Parameters k, a, and b were held fixed across slants for each observer, while parameter g was allowed to vary with slant. This particular functional form is not of theoretical significance. It was chosen because it restricts the reflectance predictions to lie between 0 and 1, because it has enough flexibility to capture the broad trends in the data (although it misses in detail, see Figure 9), and because the resulting gain parameter may be used to summarize the effect of slant. Indeed, for each slant, the quantity 1/g may be interpreted as a relative equivalent illuminant (Bloj et al., 2004; Boyaci et al., 2003; Brainard & Maloney, 2011) for that slant. This is because, given the form of Equation (4), a set of stimuli with luminances that vary with 1/g as a function of slant are predicted to be matched with the same reflectance (see Bloj et al., 2004; Boyaci et al., 2003; Brainard & Maloney, 2011 for an introduction to and discussion of equivalent illuminant models).

Figure 10 plots, for each observer, the quantity 1/g as a function of slant, with the data for each observer normalized to a maximum of 1. This representation makes clear that the deviations from luminance matching shown in Figure 9 are quite systematic, as the plots indicate considerable regularity both within and between observers. For an observer making matches based on test luminance only, the data in each panel of Figure 10 would be constant as a function of test card slant.

Figure 10.

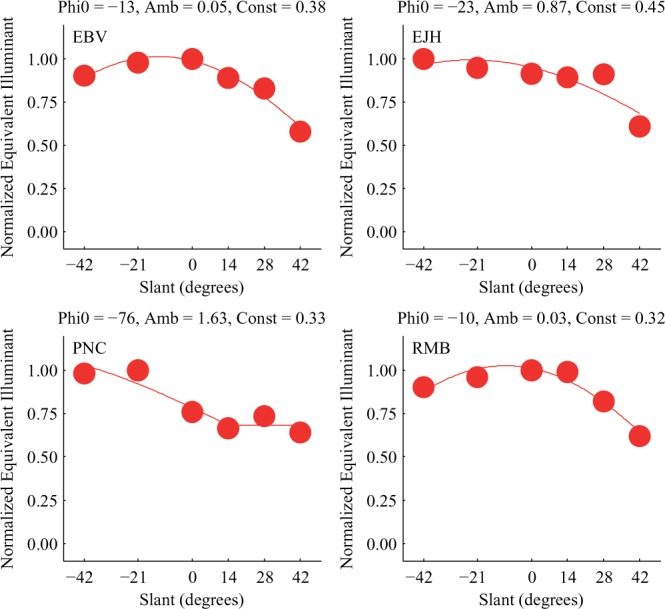
Equivalent illuminant 1/g plotted as a function of slant for each observer, after normalization to a maximum of 1 for each observer. The smooth curve shown in each panel is the fit of the equivalent illuminant model expressed by Equation (5) and the key model parameters and constancy indices for each observer are given in the title for each subplot.

Previous work (Bloj et al., 2004; Boyaci et al., 2003) has shown that data in the form plotted in Figure 10 may be fit with an equivalent illuminant model, where the variation in normalized equivalent illuminant with slant is predicted by a combination of an inferred directional light source and an inferred ambient illumination component:

$$e=w\left(\cos \left(\phi -{\phi }_0\right)+a\right),$$ (5)

where e is the normalized equivalent illuminant, ϕ₀ is the azimuthal position of the inferred directional light source, a is the inferred ambient component, ϕ is the slant of the surface, and the cosine function is truncated for arguments outside the range −90°. We fit the model to the data shown in Figure 10, with the fits indicated by the solid lines. The equivalent illuminant model provides a good description of each observer's data, and the negative values obtained for the parameter ϕ₀ for each observer correspond to the side of the booth at which the directional light source was located. To quantify this further, we followed Bloj et al. (2004) and fit Equation (5) to measurements of the illumination impinging on the test cards as a function of their slant (Supplemental Figure S8). This fit indicated that the illumination in the chambers had an azimuth of approximately −49°. We further used the fit to the illumination and the fits to each observer-equivalent illuminant to assign a constancy index to each observer, following the method introduced by Bloj et al. (2004). The constancy indices for each observer are provided in the titles of the plots shown in Figure 10. The mean constancy index was 0.37, with the range across observers being 0.32–0.45. These indices are within the range but overall lower than those reported by Bloj et al. (2004) for experiments fairly similar to ours: mean 0.57 and range 0.23–0.91.

The range of test card reflectances used in Experiment 3 was greater than that employed in Experiment 2B. We repeated the Experiment 3 analysis with the subset of test cards whose reflectances were in the range of those used in 2B. The results (Supplemental Figures S9 and S10) are quite similar to those obtained for the full test card range, indicating that the differences we find between scaling and matching are unlikely to be due to the difference in test card reflectance range.

5. Discussion

We studied the perception of surface lightness using a dissimilarity scaling method, with a particular interest in the dimensionality of the perceptual representation of lightness. In Experiment 1, we found that observers showed a degree of lightness constancy when the overall intensity of the scene illumination was varied. In contrast to the findings of Logvinenko and Maloney (2006; Logvinenko et al., 2008), however, our dissimilarity data are well-accounted for by a one-dimensional perceptual representation. In both Experiments 1 and 2, we found essentially no lightness constancy with respect to changing the slant of a test surface viewed under directional illumination – the dissimilarity data were well-accounted for by a one-dimensional perceptual representation and the positions of stimuli in this representation were a monotonic function of stimulus luminance across changes in slant. In contrast, use of a matching paradigm (Experiment 3) with the same stimuli revealed moderate lightness constancy with respect to test slant. We found little if any effect of an instructional manipulation intended to bias observers toward or away from making their judgments based on how they perceived test surface reflectance as distinct from the luminance of the light reflected from the tests.

5.1. Dimensionality of lightness representation

Our finding in Experiment 1 that a one-dimensional perceptual representation accounts for the dissimilarity judgments across a change in illumination intensity is different from the report of Logvinenko and Maloney (2006). We do not know the reason for this difference, but we note five differences between our experiments/analysis and theirs.

First, our implementation of MDS employed the iSTRESS goodness-of-fit measure introduced in this paper. We reanalyzed some of Logvinenko and Maloney's data (kindly provided by the authors) and confirmed with our software the regular nature of the two-dimensional solution they obtained as well as the fact that in the two-dimensional solution the points separated by illuminant intensity (Madigan, 2011, Appendix Figure A.6). That our analysis software reproduced their essential result when applied to their data makes it unlikely that analysis differences account for the differences in results.

A second difference between our experiments and theirs is in the instructions. Their instructions were nonspecific regarding what stimulus features the observer should use in making their judgments (L. T. Maloney, personal communication, May 2010). We asked observers to focus on either the apparent reflectance of the test surface or the apparent amount of light reflected from it. It is possible that this led our observers to ignore aspects of the percept or of the broader stimulus context that might otherwise have led to a two-dimensional representation. At the same time, we note that our instructions were intended to direct observers toward the appearance of the test stimulus, which is what we wanted to study, and that which version of instructions observers received had little if any effect on the results.

Third, there was a difference in how the stimuli were grouped for presentation. Only the two cards being compared were visible within each trial of our experiment, while in the experiment reported by Logvinenko and Maloney (2006) all of the stimuli were visible throughout (see their Figure 1). When all of the stimuli are visible at once, a response strategy becomes available to observers that could produce the pattern of results found by Logvinenko and Maloney (2006). In particular, observers could explicitly order the stimuli under each illuminant in terms of their apparent achromatic color and then use the difference in rank ordering, added to a perceived difference in perceived illumination across the display, to form their reported dissimilarity judgments. Application of a strategy of this sort would be much more difficult when only one stimulus at a time is presented in each context.

Fourth, there was a sharp illumination boundary between the stimuli being compared in Logvinenko and Maloney (2006; again see their Figure 1), while in our experiments the comparisons were made across two side-by-side chambers. It may be that the nature of their explicitly-visible illumination boundary somehow led to a two-dimensional representation. On the other hand, the difference in illumination intensity between the two chambers in our Experiment 1 was clearly visible, suggesting that the presence of a perceptible illumination change per se is not a sufficient condition for a two-dimensional solution. In addition, our matching experiment did reveal a degree of lightness constancy for our stimuli. Although this in itself does not imply that the representation should be two-dimensional, it does say that our stimuli provided sufficient information to allow observers to separate illumination and surface reflectance to some extent.

Finally, Logvinenko and Maloney (2006) had a reference stimulus visible throughout that defined perceptually what was meant by the maximal possible dissimilarity. They did this to make it easier for observers to maintain stable use of a dissimilarity scale. Even without a constantly present scale, however, we found that observers' responses led to highly regular solutions.

5.2. Effect of instructions

The question of when and how instructions affect observers' judgments of lightness and color, as well as how such effects should be understood, remains an open issue. Although it is clear that instructions sometimes have a substantial effect on performance (Arend & Reeves, 1986; Arend, Reeves, Schirillo, & Goldstein, 1991; Bauml, 1999; Reeves, Amano, & Foster, 2008; Troost & de Weert, 1991), they do not always do so (Cornelissen & Brenner, 1995; Delahunt & Brainard, 2004; Logvinenko & Tokunaga, 2011; Ripamonti, et al., 2004). Our current results add to the latter list, as we found little if any effect of instructions. This was true both in our scaling experiments and in our matching experiment. Exactly what aspects of the experimental conditions determine whether reliable instructional effects are found is not clear, and awaits further study. One possibility is that the experimental conditions that reveal robust instructional effects are the same as those that reveal a multidimensional representation of surface lightness. Under that view, instructional effects would occur when instructions cause observers to weight the multiple dimensions differently. If this idea holds, then our finding of a one-dimensional lightness representation is consistent with the lack of instructional effects shown by our observers.

5.3. Dissimilarity scaling and lightness constancy

This study is the first, to our knowledge, to use dissimilarity scaling to study lightness constancy with respect to changes in surface slant. The scaling procedure yielded regular results that were consistent across subjects. In this regard, we agree with Logvinenko and Maloney (2006; Logvinenko et al., 2008) that the procedure provides a valuable addition to the set of available methods for studying lightness. Our scaling data revealed essentially no lightness constancy with respect to the slant manipulation, in distinction to our matching data and to many (e.g., Boyaci et al., 2003; Gilchrist, 1980; Hochberg & Beck, 1954; Lee & Brainard, 2014; Radonjić et al., 2010; Ripamonti et al., 2004) but not all (Epstein, 1961) previous studies of this phenomenon. What factors might account for the lack of lightness constancy in our scaling experiments?

In our experiments, the test surface was presented within a fairly sparse context and with no other surfaces in its immediate vicinity. Although there were visible illumination gradients and explicit cast shadows within the experimental chambers that provided information about the illuminant geometry (see Figure 1), it has been hypothesized that it is the presence of nearby coplanar surfaces that provides the primary cue that allows the visual system to compensate for directional illumination (Gilchrist, 2006; Gilchrist et al., 1999; Gilchrist, 1980). On the other hand, Ripamonti et al. (2004) found reasonable lightness constancy with respect to slant using stimuli that shared with ours the feature that the test was placed in isolation on a rotating stage in an experimental chamber, although there was considerable between-observer variation (see also Bloj et al. 2004 for equivalent illumination analysis of the Ripamonti et al. dataset). Ripamonti et al.'s (2004) experimental chamber differed from ours in that it contained a richer set of contextual objects (see their Figure 2). Consistent with Ripamonti/Bloj et al. (2004), however, we do find a moderate degree of lightness constancy with respect to slant when we measure using a matching procedure. This suggests that the lack of lightness constancy we find when using the scaling technique cannot be attributed solely to our particular choice of stimuli. Also consistent with the idea that the presence of cues about the illuminant provided by the immediate surround of the test is not a necessary condition for lightness constancy with respect to slant are the results of Allred and Brainard (2009). They systematically studied how the local contrast around a test surface affected lightness constancy with respect to slant. Although they report that local contrast was an important cue, they also found that a degree of residual lightness constancy remained when the effect of contrast was taken into account, for most of their observers.

Overall, then, we think that some factor other than (or perhaps in addition to) the stimulus conditions must be invoked to explain the difference in lightness constancy revealed by our matching and scaling experiments. We do not know what this factor is. In ongoing work on color constancy that compares results obtained with two methods, Radonjić and Brainard (2013, Vision Sciences Society Abstract) obtained results that suggest that the tendency of subjects to employ what one might call “cognitive strategies” when making responses can vary with the experimental method. It is possible that something of this sort is happening across the scaling and matching methods employed in this paper. At this juncture, however, this must remain speculation that awaits more in-depth investigation, particularly given that our attempt to manipulate performance via instructions had little if any effect in the present studies.

Biography

Sean C. Madigan received his BA in Psychology from Arizona State University in 2005 and his PhD in Psychology from the University of Pennsylvania in 2011. He currently teaches science at Veritas Preparatory Academy in Phoenix, Arizona.

David H. Brainard received his AB in Physics from Harvard University (1982) and his MS (Electrical Engineering) and PhD (Psychology) from Stanford University in 1989. He is currently the RRL Professor of Psychology at the University of Pennsylvania and his research focuses on human color vision and color image processing. He is a Fellow of the Optical Society of America and the Association for Psychological Science.