Abstract
Sparse representation classification (SRC) is one of the most promising classification methods for supervised learning. This method can effectively exploit discriminating information by introducing a 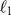 regularization terms to the data. With the desirable property of sparisty, SRC is robust to both noise and outliers. In this study, we propose a weighted meta-sample based non-parametric sparse representation classification method for the accurate identification of tumor subtype. The proposed method includes three steps. First, we extract the weighted meta-samples for each sub class from raw data, and the rationality of the weighting strategy is proven mathematically. Second, sparse representation coefficients can be obtained by
regularization terms to the data. With the desirable property of sparisty, SRC is robust to both noise and outliers. In this study, we propose a weighted meta-sample based non-parametric sparse representation classification method for the accurate identification of tumor subtype. The proposed method includes three steps. First, we extract the weighted meta-samples for each sub class from raw data, and the rationality of the weighting strategy is proven mathematically. Second, sparse representation coefficients can be obtained by 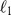 regularization of underdetermined linear equations. Thus, data dependent sparsity can be adaptively tuned. A simple characteristic function is eventually utilized to achieve classification. Asymptotic time complexity analysis is applied to our method. Compared with some state-of-the-art classifiers, the proposed method has lower time complexity and more flexibility. Experiments on eight samples of publicly available gene expression profile data show the effectiveness of the proposed method.
regularization of underdetermined linear equations. Thus, data dependent sparsity can be adaptively tuned. A simple characteristic function is eventually utilized to achieve classification. Asymptotic time complexity analysis is applied to our method. Compared with some state-of-the-art classifiers, the proposed method has lower time complexity and more flexibility. Experiments on eight samples of publicly available gene expression profile data show the effectiveness of the proposed method.
Introduction
The development of high-throughput technologies has enabled scientists to monitor the gene expression levels in tens of thousands of genes simultaneously in a single experiment. This technology has become a symbol of the post-genomic era [1]. Biomedical research indicates that tumor development is related to the change in gene expression levels and that tumor-related biomarkers are usually associated with a few genes. Thus, identifying tumor tissue or disease-related biomarkers accurately is of great practical significance. However, gene expression profile data are characterized by very high dimensionalities and small sample size. The curse of dimensionality problem makes classification challenging.
Some dimensionality reduction methods have recently been proposed to solve the “large 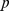 , small
, small  ” problem [2]. Feature extraction and feature selection are two methods of dimensionality reduction; feature extraction transforms original features (genes) into a set of new features by subspace learning [3]–[5]. However, suitable biological interpretation is difficult to obtain from the subspace learning dimensionality reduction results. Feature selection is another commonly used dimensionality reduction method that selects a sub-set of genes that can best predict the response values from the raw data [6]. Although dimensionality reduction can significantly improve computational efficiency, this process can easily lead to over-fitting when a classifier is applied.
” problem [2]. Feature extraction and feature selection are two methods of dimensionality reduction; feature extraction transforms original features (genes) into a set of new features by subspace learning [3]–[5]. However, suitable biological interpretation is difficult to obtain from the subspace learning dimensionality reduction results. Feature selection is another commonly used dimensionality reduction method that selects a sub-set of genes that can best predict the response values from the raw data [6]. Although dimensionality reduction can significantly improve computational efficiency, this process can easily lead to over-fitting when a classifier is applied.
Sparse representation classification (SRC) was proposed by Wright et al. [7] for face recognition. With 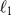 sparsity constraint, a testing face can be approximately represented by parts of the training data that are from the same class. Unlike traditional classification methods such as support vector machine and
sparsity constraint, a testing face can be approximately represented by parts of the training data that are from the same class. Unlike traditional classification methods such as support vector machine and 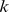 nearest neighbor classifier, SRC is robust to both noise and outliers. However, the orginal training samples may not contain suffiient discriminating information compared with meta-samples [8].
nearest neighbor classifier, SRC is robust to both noise and outliers. However, the orginal training samples may not contain suffiient discriminating information compared with meta-samples [8].
To capture more alternative information from gene expression data, the so-called meta-samples are proposed by [8]–[11]. These samples can be regarded as a set of bases, the linear representation of which can represent the training data. In [11], penalized matrix decomposition is used to extract meta-samples, and clustering is performed on those meta-samples. In [8], the meta-sample based sparse representation classification (MSRC) method is proposed. This method is robust to over-fitting problem and noise. However, MSRC needs two predefined parameters, namely, the number of meta-samples and the sparse penalty factor. These two parameters are data dependent. Thus, model selection methods, such as cross-validation (CV), significantly affect the classification results. In this study, we propose a non-parametric version of MSRC to address this optimal parameter selection problem. The main contributions of this paper are as follows:
The data-dependent sparsity can be automatically adjusted, rather than empirically chosen. Without computationally expensive model selection, our method is scalable and efficient.
The existing MSRC [8] method requires the appropriate selection of the number of meta-samples for each sub class, which is a laborious task. We address this problem by introducing a simple weighting strategy for the meta-sample of each category, and the rationality of weighting strategies is mathematically proved.
Extensive experiments are performed to evaluate the proposed method. Experimental results show the superiority of the non-parametric version of MSRC compared with some state-of-the-art classifiers. Section 3 presents more details.
The remainder of this paper is organized as follows: prior work on sparse representation classification and the fundamentals of the proposed method are described in Section 2. Section 3 presents the experimental results. The proposed method is discussed in Section 4. Section 5 concludes this paper.
Methods
This study primarily aims to establish the manner by which to devise an robust classifier for tumor subtype classification. Given a microarray data set 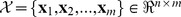 and a set of class labels
and a set of class labels 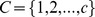 ,
,  is a matrix with
is a matrix with  rows and
rows and  columns. Each column of
columns. Each column of  denotes a sample, whereas each row of
denotes a sample, whereas each row of  denotes a gene. Let
denotes a gene. Let 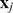 denote the
denote the 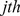 sample, which is a column vector with
sample, which is a column vector with  dimensional. For each element in
dimensional. For each element in  ,
, 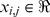 denotes the expression level of the
denotes the expression level of the  gene in the
gene in the 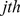 sample. We provide a summary of the abbreviations used in this study in Table 1. For clarity, we use boldface and lowercase type letters for vectors and boldface and capital type letters for matrices.
sample. We provide a summary of the abbreviations used in this study in Table 1. For clarity, we use boldface and lowercase type letters for vectors and boldface and capital type letters for matrices.
Table 1. Notations and abbreviations used in this paper.
| Notation | Description |
| SVD | Singular value decomposition |
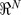
|
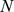 dimensional real number vector dimensional real number vector |
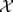
|
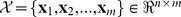 denotes gene expression data set with denotes gene expression data set with  genes, genes,  samples samples |
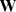
|
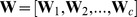 meta-samples associate with meta-samples associate with  classes classes |
|
Number of samples belong to class 
|
|
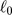 norm norm |

|
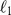 norm norm |
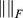
|
Matrix Frobenius norm |
Gene expression profile data are high-throughput data with tens of thousands of genes. However, the number of samples is usually very small, which makes classification challenging. To avoid the curse of dimensionality, differential gene expression analysis [12], [13] is widely used to exclude redundant and irrelevant genes before classification. In our study, we use the Relieff [14] method to select a subset of informative genes for further analysis. In the following subsections, we briefly review meta-sample and sparse representation classification. we then propose weighted meta-sample based parameter free sparse representation classification (PFMSCR).
Meta-samples versus gene expression samples
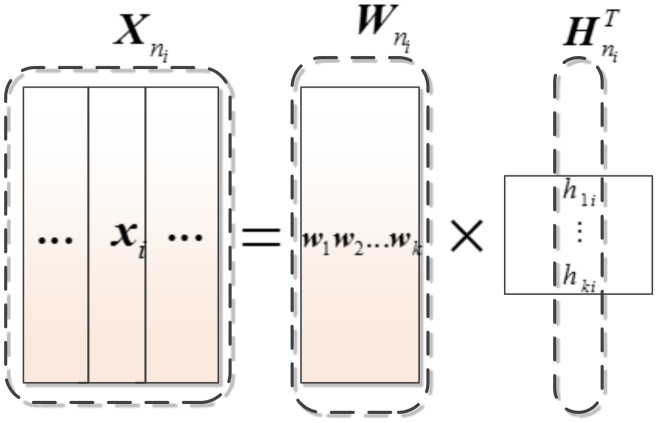
As illustrated in Figure 1, meta-samples can be regarded as basis samples that contain the essential information of the original data. A given testing sample can be represented by a linear combination of meta-samples from the same class. Concretely, suppose 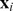 is associated with the
is associated with the 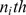 class, where
class, where 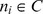 , and the
, and the 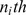 class samples in the training data have
class samples in the training data have 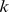 meta-samples, namely,
meta-samples, namely, 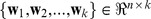 . Sample
. Sample 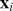 can be formulated as Eq. (1).
can be formulated as Eq. (1).
| (1) |
Figure 1. Illustration of meta-sample model: each column vector of 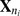 can be represented within a linear combination of meta-samples in
can be represented within a linear combination of meta-samples in 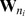 , and the column of
, and the column of 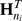 corresponds to the linear combination coefficients.
corresponds to the linear combination coefficients.
Mathematically, meta-samples extraction can be regarded as a type of matrix decomposition, including non-negative matrix factorization [15], singular value decomposition (SVD) [16], and principal component analysis [17], where matrix 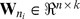 , and
, and 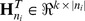 denote the meta-sample and meta-gene, respectively. In singular value decomposition,
denote the meta-sample and meta-gene, respectively. In singular value decomposition, 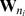 is a maximum linearly independent group of
is a maximum linearly independent group of 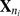 column vectors.
column vectors.
Biologically, meta-samples are also called eigenarray [18] or basis snapshot for gene expression data. Han et al. [17] used meta-samples to identify tumors from microarray data and found that meta-sample-based classification can effectively avoid over-fitting. Zheng et al. [10], [11], [18] proposed a novel cluster method based on meta-samples, which meta-samples can be regarded as cluster indictors.
Prior works revealed that meta-samples preserve some desired discriminant information of samples from the same class.
Sparse representation classification problem revisited
In this subsection, we revisit the sparse representation problem briefly. Sparse representation is one of the most important components of machine learning and data mining community that has wide applications in such fields as text mining, image classification, and bioinformatics. In this work, we interpret the sparse representation problem from the view of linear algebra.
From the standpoint of linear equations system 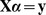 , the solution of
, the solution of 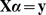 has three possible states:
has three possible states:
Linear equation systems have infinitely many solutions if they are underdetermined (i.e.,
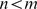 ).
).Linear equation systems have a unique solution if they are well posed.
Linear equation systems have no solution if overdetermined (i.e.,
 ).
).
In the first scenario, one can pursue the sparse solution by regularization [19]. The problem can be formulated as
| (2) |
However, 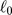 norm is an NP-hard combinational optimization problem, and difficult to solve, fortunately,
norm is an NP-hard combinational optimization problem, and difficult to solve, fortunately, 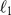 norm is an appropriate convex approximate to
norm is an appropriate convex approximate to 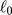 [20]. If the solution is sparse enough,
[20]. If the solution is sparse enough, 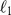 minimization is equivalent to
minimization is equivalent to 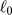 minimization [21], such that we can reformulate Eq. (2) as
minimization [21], such that we can reformulate Eq. (2) as
| (3) |
For the other two scenarios, the sparsity of  cannot be guaranteed. However, one can still obtain a sparse solution by adding a penalty term that shares the same formulation as LASSO [22]
cannot be guaranteed. However, one can still obtain a sparse solution by adding a penalty term that shares the same formulation as LASSO [22]
| (4) |
Compared with Eq. (3), Eq. (4) is an unconstrained convex problem. Notably, 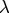 makes a tradeoff between sparsity and regression error and should be empirically chosen. A larger
makes a tradeoff between sparsity and regression error and should be empirically chosen. A larger 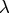 yields a sparser
yields a sparser  . However, one might run the risk of increasing regression error term
. However, one might run the risk of increasing regression error term 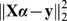 .
.
Sparse representation assumes that a signal can be reconstructed by a small number of basis signals within a linear combination. Thus, Eq (3) can be named as basis pursuit [23]. In bioinformatics applications, one can suppose that a testing sample can be well reconstructed by the training data from the same class within a linear combination, which is a very useful assumption for our later work.
Meta-sample based sparse representation
Zheng et al. [8] proposed MSRC method to predict tumor subtypes. In such situations,  classes of meta-samples are extracted, denoting as
classes of meta-samples are extracted, denoting as 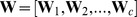 with the same classes being conjoined together, where meta-samples are column vectors (two kinds of meta-sample are proposed in [8]). Given a test sample
with the same classes being conjoined together, where meta-samples are column vectors (two kinds of meta-sample are proposed in [8]). Given a test sample 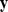 associated with class
associated with class  , MSRC tries to find sparse reconstruct coefficients in terms of all meta-samples using Eq. (4). In particular, [8] tries to solve the sparse representation problem using
, MSRC tries to find sparse reconstruct coefficients in terms of all meta-samples using Eq. (4). In particular, [8] tries to solve the sparse representation problem using 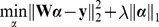 . In ideal cases, the nonzero entries in
. In ideal cases, the nonzero entries in  will only be associated with the
will only be associated with the 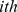 class meta-samples of
class meta-samples of 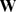 , as shown in Eq. (5).
, as shown in Eq. (5).
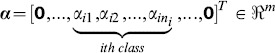 |
(5) |
Notably, the gene expression profile contains data with high dimensionality and small sample size (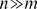 ). The sparsity can only be achieved by adding a penalty term. However, the optimal number of meta-samples and penalty factor
). The sparsity can only be achieved by adding a penalty term. However, the optimal number of meta-samples and penalty factor 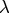 are essentially important in classification applications. Figure 2 illustrates that if the meta-samples are improperly set, the prediction accuracy of MSRC drops seriously on COLON dataset. Specifically, in the left part of Figure 2 shows that the 10-fold stratified cross validation classification accuracy is achieved by varying the number of meta-samples from 3 to 12 for each subclass. We can observe that the performance is less sensitive to various regularization parameters within the scope of
are essentially important in classification applications. Figure 2 illustrates that if the meta-samples are improperly set, the prediction accuracy of MSRC drops seriously on COLON dataset. Specifically, in the left part of Figure 2 shows that the 10-fold stratified cross validation classification accuracy is achieved by varying the number of meta-samples from 3 to 12 for each subclass. We can observe that the performance is less sensitive to various regularization parameters within the scope of 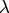 from the right part of Figure 2. Thus, model selection is essential and laborious work on different data sets.
from the right part of Figure 2. Thus, model selection is essential and laborious work on different data sets.
Figure 2. Optimal classification accuracy of MSRC achieved on COLON; the  -axis represents the number of meta-samples (left) and the regularization parameter (right).
-axis represents the number of meta-samples (left) and the regularization parameter (right).
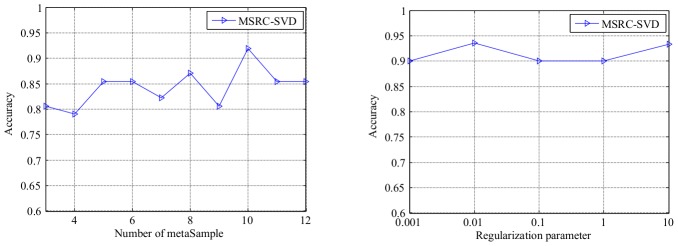
Classification accuracy is more sensitive to the number of meta-samples rather than to the regularization parameter.
To overcome this weakness, this study proposed a novel parameter free meta-sample based sparse representation classification (PFMSRC) method.
Parameter free meta-sample sparse representation (PFMSRC)
In this subsection, we first propose a heuristic weighted strategy, the reasonableness of which is theoretically proven. We then construct an underdetermined linear equation system, in which the data-dependent sparsity can be self-adaptively tuned by 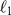 norm regularizer.
norm regularizer.
Let 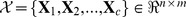 be gene expression profile data, with the same classes being conjoined together, that is,
be gene expression profile data, with the same classes being conjoined together, that is, 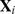 contains all samples associated with the
contains all samples associated with the 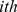 class. We factorize
class. We factorize 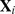 by performing SVD. The singular values are sorted in descending order
by performing SVD. The singular values are sorted in descending order 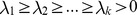 , where
, where 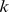 is the column rank of
is the column rank of 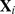 , and
, and 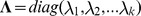 denotes diagonal matrix with singular values being diagonal elements. One can extract weighted meta-samples associated with class
denotes diagonal matrix with singular values being diagonal elements. One can extract weighted meta-samples associated with class  as
as 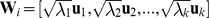 , where
, where 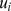 is a column vector in
is a column vector in 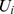 , and
, and 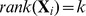 .
.
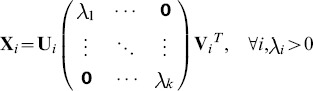 |
(6) |
Alternatively, Eq. (6) can be compactly reformulated as 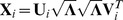 . This weighting scheme can enhance the influence of main singular vector in
. This weighting scheme can enhance the influence of main singular vector in 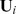 . That is, larger
. That is, larger 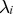 makes the associated meta-sample more important. Moreover, the weighting scheme works well in the following experiments. Compared with [8], Zheng et al. extracted meta-samples by performing SVD as well. However, in their algorithm framework, the number of meta-samples used for classification is determined during the cross-validation step. On the contrary, PFMSRC tries to avoid the cross-validation part by weighting the all meta-samples and weakening the influence of minor eigenvectors rather than using several of them for classification. Proposition 1 theoretically proves the reasonableness of the weighting strategy in measuring the importance of each metasample.
makes the associated meta-sample more important. Moreover, the weighting scheme works well in the following experiments. Compared with [8], Zheng et al. extracted meta-samples by performing SVD as well. However, in their algorithm framework, the number of meta-samples used for classification is determined during the cross-validation step. On the contrary, PFMSRC tries to avoid the cross-validation part by weighting the all meta-samples and weakening the influence of minor eigenvectors rather than using several of them for classification. Proposition 1 theoretically proves the reasonableness of the weighting strategy in measuring the importance of each metasample.
Proposition 1. Singular value is a reasonable weighting factor for measuring the importance of meta-samples.
Proof. Let 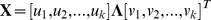 , where
, where 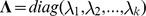 and
and 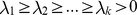 ,
, 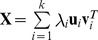 , considering evaluation metric function
, considering evaluation metric function 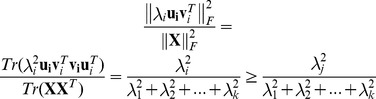 , one can conclude that
, one can conclude that
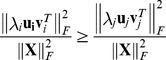 |
This completes the proof. □
The evaluation metric function is used to measure the meta-sample's contribution of the meta-sample to the raw data reconstruction in terms of 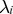 .
. 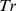 denotes matrix trace. Note that, functions
denotes matrix trace. Note that, functions 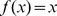 and
and 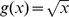 have the same monotonicity, which makes the weighting strategy reasonable.
have the same monotonicity, which makes the weighting strategy reasonable.
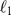 graph was proposed by Cheng et al. [24] to measure the similarity among samples. Inspired by their work, sparsity can be obtained by
graph was proposed by Cheng et al. [24] to measure the similarity among samples. Inspired by their work, sparsity can be obtained by 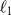 regularizer on underdetermined linear equation systems. Concretely, a testing sample can be recovered by weighted meta-samples within a linear combination with a noise term added, formulated as Eq. (7)
regularizer on underdetermined linear equation systems. Concretely, a testing sample can be recovered by weighted meta-samples within a linear combination with a noise term added, formulated as Eq. (7)
| (7) |
Let 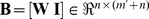 and
and 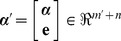 , where
, where 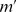 represents the number of meta-samples corresponding to
represents the number of meta-samples corresponding to  classes,
classes, 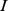 is an identity matrix, and
is an identity matrix, and  is the noise term. Alternatively, one can solve the following minimization problem:
is the noise term. Alternatively, one can solve the following minimization problem:
| (8) |
Theorem 1 proves that Eq. (8) is a underdetermined linear system. As stated in Subsection 2.2 the sparsity of underdetermined linear system can be automatically tuned by 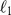 regularization (the first scenario). Moreover, (8) is a canonical convex problem with equality constraints, which can optimize sparse representation coefficients and noise term simultaneously. The globally optimal solution can be efficiently solved by CVX package [25] in polynomial time. Notably, the package solves the optimization problem by dualization rather than interior point method because the former is significantly faster than the latter.
regularization (the first scenario). Moreover, (8) is a canonical convex problem with equality constraints, which can optimize sparse representation coefficients and noise term simultaneously. The globally optimal solution can be efficiently solved by CVX package [25] in polynomial time. Notably, the package solves the optimization problem by dualization rather than interior point method because the former is significantly faster than the latter.
Theorem 1.
Linear equation system (8) is underdetermined, and
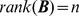 .
.
Proof. We can find a sub matrix in 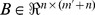 , such as
, such as 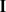 and
and 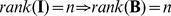 . This completes the proof. □
. This completes the proof. □
Note that 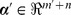 is a sparse vector with
is a sparse vector with 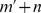 entries. The first
entries. The first 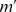 components correspond to linear representation coefficients, whereas the last
components correspond to linear representation coefficients, whereas the last  components characterize model noise or regression error. However, the test sample
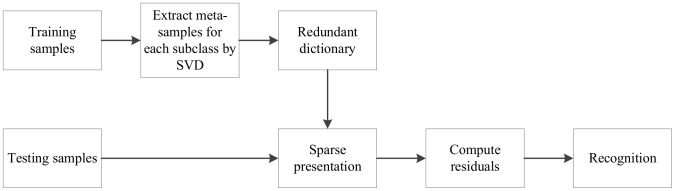
components characterize model noise or regression error. However, the test sample 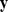 from one of the classes in training data cannot be well reconstructed by meta-samples associated with the same class in most instances because of the existence of noises. Figure 3 illustrates the flowchart of our PFMSCR scheme, the redundant dictionary is constructed by combining meta-samples and noise term.
from one of the classes in training data cannot be well reconstructed by meta-samples associated with the same class in most instances because of the existence of noises. Figure 3 illustrates the flowchart of our PFMSCR scheme, the redundant dictionary is constructed by combining meta-samples and noise term.
Figure 3. The flowchart of PFMSRC scheme.
We define a projection function 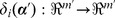 for each class
for each class  , which selects the coefficients associated with the
, which selects the coefficients associated with the 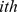 class from the first
class from the first 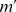 components in
components in 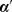 , whereas the other entries are appropriately padded with zeros in
, whereas the other entries are appropriately padded with zeros in 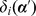 . The reconstruction relationship
. The reconstruction relationship 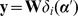 is not always holden. However, the minimized reconstruction error criterion
is not always holden. However, the minimized reconstruction error criterion 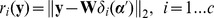 is a good approximation to classify testing samples. We summarize the proposed classification method as follows.
is a good approximation to classify testing samples. We summarize the proposed classification method as follows.
Step 1. Input training sets 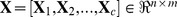 , class number
, class number  , and testing sample
, and testing sample 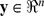 ;
;
Step 2. Normalize training set samples and testing sample to obtain unit 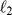 -norm;
-norm;
Step 3. Extract weighted meta-samples 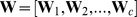 for each class (meta-samples with the same class are conjoint);
for each class (meta-samples with the same class are conjoint);
Step 4. Solve non-parametric sparse representation problem by Eq. (8);
Step 5. Compute residuals for each class 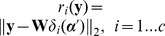 ;
;
Step 6. Return class label of 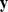 as
as 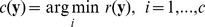 ;
;
PFMSRC can be considered as a non-parametric version of MSRC, compared with the former having the following merits:
The weighted meta-samples are orthogonal with one another. That is, no redundancy exists among meta-samples, and the weight enhances the influence of the main singular vector, such that discriminant information can be well retained.
The data-dependent sparsity can be automatically tuned without human intervention. Thus, PFMSRC has better scalability and robustness.
The time complexity of PFMSRC is lower than that of MSRC, since computationally expensive model selection work need not be accomplished for parameter optimization. Time complexity can be estimated as: weighted meta-sample extraction step needs time complexity
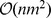 ,
, 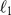 minimization needs time complexity
minimization needs time complexity 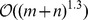 , the total complexity for PFMSRC is
, the total complexity for PFMSRC is  .
.
In the following section, we will conduct extensive experiments on micoarray data to evaluate the effectiveness of our scheme, and microarray data repository information as well as the accession number is given by Table 2.
Table 2. Descriptions of microarray data repository and the accession number.
| Datasets | Repository | Accession number |
| Colon | Gene Expression Omnibus | GDS4379 |
| Acute leukemia data | Gene Expression Omnibus | GSE19475 |
| DLBCL | Gene Expression Omnibus | GSE15177 |
| Gliomas | Gene Expression Omnibus | GSE54792 |
| SRBCT | Gene Expression Omnibus | GSE1825,GSE31186,GSE31217 |
| ALL | Gene Expression Omnibus | GSE23024 |
| MLLLeukemia | Gene Expression Omnibus | GSE11038 |
| LukemiaGloub | Gene Expression Omnibus | GSE10283 |
Experiments
In this section, we will evaluate the performance of the proposed PFMSRC algorithm against four state-of-the-art algorithms, namely, linear discriminant analysis (LDA+SVM), independent component analysis (ICA+SVM), SRC, and meta-sample sparse representation (SVD-MSRC). The former two are model based and accompanied by feature extraction. These two algorithms are regarded as baseline. For the model-based method, support vector machine [26], [27] with radial basis function kernel is employed as a classifier. The experiments are performed on four binary-class classification data sets and four multiclass classification data sets. All experiments are implemented in Matlab environment and run on a personal computer with intel Pentium4 dual core CPU 2.4 GHZ and 4 G RAM. The summarized descriptions of the eight gene expression profile datasets are provided by Table 3.
Table 3. Data set descriptions.
| Datasets | Samples | Genes | Subclass number |
| Colon | 62 | 2000 | 2 |
| Acute leukemia data | 72 | 5000 | 2 |
| DLBC | 77 | 7129 | 2 |
| Gliomas | 50 | 12625 | 2 |
| SRBCT | 83 | 2308 | 4 |
| ALL | 248 | 12626 | 6 |
| MLLLeukemia | 72 | 12582 | 3 |
| LukemiaGloub | 72 | 7129 | 3 |
Colon [28] consists of 62 samples with two subclasses including 40 tumor and 22 normal samples. The highest 2000 genes with minimal intensity in the tissues are retained from the original of more than 6500 genes. This dataset can be downloaded from [29].
Acute leukemia data [30], consist of 72 samples with two subclasses, including 47 acute lymphoblastic leukemia patients and 25 acute myelogenous leukemia patients. Each sample contains 7129 genes. This dataset can be downloaded from [29].
DLBCL [1] consists of 77 samples with two subclasses, including 58 diffuse large b-cell lymphoma samples and 19 follicular lymphoma samples. Each sample contains 7129 genes. This dataset can be downloaded from [31].
Gliomas [32] consist of 50 samples with two subclasses (Glioblastomas and Anaplastic Oligodendrogliomas), and each sample contains 2308 genes. This dataset are available at [31].
SRBCT [33] consist of 83 samples with four subclasses (Ewings sarcoma, Burkitts, Neuroblastoma and rhabdomyosarcoma). Each sample contains 2308 genes. The datasets are available at [31]
ALL [34] consists of 248 samples with six subclasses. Each sample contains 12626 genes. The datasets are available at [31].
MLLLeukemia [35] consists of 72 samples with three subclasses. Each sample contains 12582 genes. The datasets are available at [29].
LukemiaGloub [30] consists of 72 samples with three subclasses. Each sample contains 7129 genes. The datasets are available at [31].
Dataset preprocessing and experiment setup
Gene expression profiling involves data with high dimensionality and small sample size. The exclusion of redundant and irrelevant data is critical for classification. As suggested by [36], restaining only the top 400 genes makes a good tradeoff between computational complexity and biological significance. In our experiment, the top 400 genes are selected from each dataset by applying the Relieff [14] algorithm to the training set.
For LDA+SVM algorithm, we simply extract 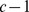 new features to train the classifier, as LDA can find at most
new features to train the classifier, as LDA can find at most 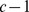 meaningful projection vectors in the subspace, where
meaningful projection vectors in the subspace, where  denotes the number of classes. SVM kernel parameters are determined by 10-fold cross-validation. In fact, the determination of the number of independent components is also an empirically dependent work. Here, we use the same method as suggested by [18].
denotes the number of classes. SVM kernel parameters are determined by 10-fold cross-validation. In fact, the determination of the number of independent components is also an empirically dependent work. Here, we use the same method as suggested by [18].
SRC and MSRC methods need parameter 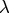 to control sparsity. MSRC also needs the number of meta-samples of each class as a key parameter. Each dataset
to control sparsity. MSRC also needs the number of meta-samples of each class as a key parameter. Each dataset 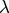 is searched from
is searched from 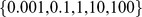 by 10-fold CV on training data, and the number of meta-samples for each class is set as recommended by [8].
by 10-fold CV on training data, and the number of meta-samples for each class is set as recommended by [8].
Experiments on binary classification problem
To evaluate the performance of five methods on a balanced split data set, we randomly select 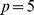 to
to 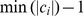 samples per subclass as training set and use the rest for testing to guarantee that at least one sample in each category can be used for test, 20 times training/testing are randomly split, and the average classification accuracies are presented. The best prediction accuracy is in boldface for each gene expression profile dataset.
samples per subclass as training set and use the rest for testing to guarantee that at least one sample in each category can be used for test, 20 times training/testing are randomly split, and the average classification accuracies are presented. The best prediction accuracy is in boldface for each gene expression profile dataset.
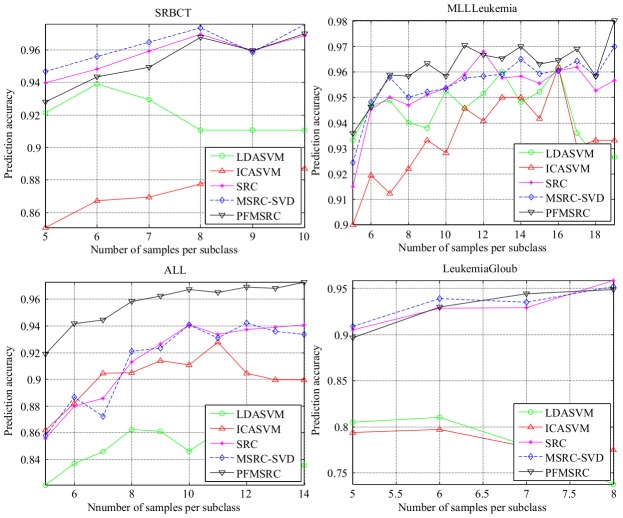
We show the average performance comparison on four binary classification tasks in Figure 4. PFMSRC exhibited encouraging performance. Although Gliomas was difficult for classification, the proposed approach can still achieve 85% classification accuracy via 20 samples per subclass used for training. Notably, the classification accuracy of LDA+SVM and ICA+SVM dropped quickly as more samples are taken for training; the same observations can be found in [36]. This fluctuation phenomenon can be interpreted as follows: (1) For the binary classification case, the feature extracted by LDA has only one dimension that is insufficient to capture the intrinsic discriminating information. Thus, model-based classification methods have difficulty in preventing the over-fitting phenomenon. (2) When evaluating the performance on the testing set the number of samples changes as more samples are used for training.
Figure 4. Comparison of prediction accuracy on four binary classification datasets by varying the number of samples from per subclass; when 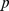 is larger than 10 the model based method prediction accuracy decreases as
is larger than 10 the model based method prediction accuracy decreases as 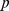 increases.
increases.
Classification accuracy, specificity, and sensitivity are some popular evaluation metrics. In this work, we use all three to evaluate performance, and the results are reported in Table 4, 5, and 6, respectively. The three methods can achieve satisfactory performance not only on the specificity metric but also on the sensitivity metric. Compared with SRC and MSCR, PFMSRC outperforms its competitors in most cases. A comprehensive consideration is that PFMSRC achieves the best performance, followed by MSRC and SRC.
Table 4. Comparison on four binary classification tumor data sets; for each data set, 10 samples per class are randomly selected for training and the rest are used for testing.
| Dataset name | LDA+SVM | ICA+SVM | SRC | MSRC-SVD | PFMSRC |
| colon | 74( 7.85) 7.85) |
64.55( 7.39) 7.39) |
84.20( 3.65) 3.65) |
84.20( 4.81) 4.81) |
85.45(
 3.33)
3.33)
|
| DLBC | 66.76( 6.67) 6.67) |
68.33( 4.78) 4.78) |
86.49(
 3.39)
3.39)
|
85.35( 4.91) 4.91) |
86.40( 5.69) 5.69) |
| Gliomas | 65.83( 8.08) 8.08) |
69.83( 9.52) 9.52) |
75.00( 6.35) 6.35) |
75.83( 7.24) 7.24) |
77.00(
 6.48)
6.48)
|
| Acute leukemia | 89.71( 3.14) 3.14) |
89.13( 4.96) 4.96) |
93.46( 3.82) 3.82) |
94.52( 3.65) 3.65) |
96.25(
 2.20)
2.20)
|
We report the standard deviations in parentheses.
Table 5. Comparison of specificity by different methods on four binary classification data sets.
| Dataset name | SRC | MSRC-SVD | PFMSRC |
| colon | 90.00 | 92.50 | 92.50 |
| DLBC | 96.55 | 94.83 | 96.55 |
| Gliomas | 72.73 | 77.27 | 77.27 |
| Acute leukemia | 100 | 100 | 100 |
Table 6. Comparison of sensitivity by different methods on four binary classification data sets.
| Dataset name | SRC | MSRC-SVD | PFMSRC |
| colon | 81.82 | 86.36 | 86.36 |
| DLBC | 1 | 1 | 94.74 |
| Gliomas | 82.14 | 78.57 | 89.29 |
| Acute leukemia | 88.00 | 92.00 | 84.00 |
Experiments on multiclass classification problem
We investigate multiclass classification performance on four publicly available data sets. The experimental setup is the same as that for the binary classification case. On one hand from Figure 5 and Table 7 it can be seen that (1) the classification accuracies of SRC, MSRC, and PFMSRC are increased on all multiclass classification datasets as more samples per subclass are taken for training. (2) ALL has six subclasses, and the proposed PFMSRC achieves the highest classification accuracy, which indicates that we have potential superiority on multiclass classification task. (3) LDA can capture more discriminating information on the multiclass classification task, and the over-fitting phenomenon is reduced compared with the binary classification task.
Figure 5. Comparison of prediction accuracy on four multiclass classification datasets by varying the number of samples from per subclass; when 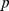 is larger than 10 the performance degradation of model based methods is less significant than that of binary classification.
is larger than 10 the performance degradation of model based methods is less significant than that of binary classification.
Table 7. Comparison on four multiclass tumor data sets; for each data set, 10 (8 for LeukemiaGloub) samples per class are randomly selected for training the rest are used for testing.
| Dataset name | LDA+SVM | ICA+SVM | SRC | MSRC-SVD | PFMSRC |
| SRBCT | 91.05( 4.61) 4.61) |
88.72( 5.56) 5.56) |
96.86( 2.64) 2.64) |
97.56(
 3.06)
3.06)
|
96.98( 2.51) 2.51) |
| ALL | 86.12( 3.81) 3.81) |
91.38( 3.28) 3.28) |
94.07( 2.38) 2.38) |
94.07( 2.93) 2.93) |
96.73(
 1.68)
1.68)
|
| MLLLeukemia | 93.81( 3.74) 3.74) |
93.33( 5.16) 5.16) |
95.36( 3.04) 3.04) |
95.36( 2.84) 2.84) |
95.83(
 2.88)
2.88)
|
| LukemiaGloub | 73.75( 5.25) 5.25) |
77.50( 6.98) 6.98) |
95.83(
 2.14)
2.14)
|
95.21( 2.35) 2.35) |
94.90( 2.74) 2.74) |
The average accuracy and corresponding standard deviations are reported.
On the other hand, sparse representation based classification methods are less sensitive to the number of samples used for training model-based classification methods, which suggests a natural approach to select a classifier when the training sample size is small. Table 7 provides the performance description of the five classification methods. The proposed PFMSRC method performs consistently well with small standard deviations. On the SRBCT and ALL datasets, PFMSRC achieved 96.98% and 96.73%, respectively.
Experiments with different number of genes
In this subsection, we evaluate the performance of the five methods with different feature dimensions on eight tumor data sets. For the training data, 10 samples per subclass are randomly selected, whereas the remaining samples are used for test. We perform the test with various numbers of genes, starting from 50 to 400 genes in steps of 20. The comparison experiment was performed 20 times, and the average prediction accuracy of our experiments on eight gene expression profile datasets was recorded for evaluation.
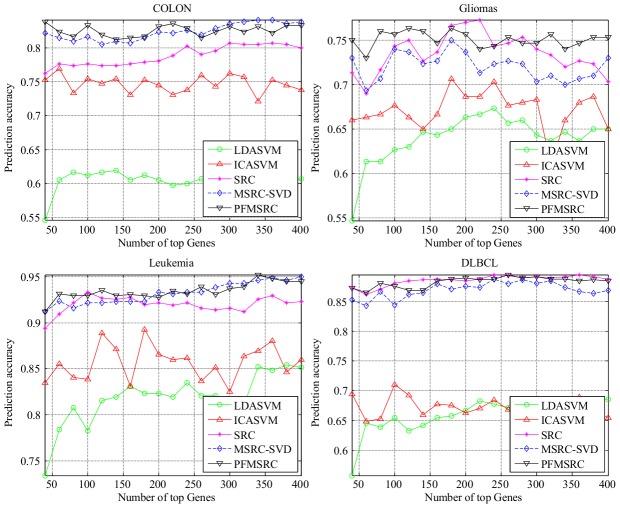
The balanced training sets for each dataset ensure fair evaluation as stated by [36]. The experimental result in Figure 6 shows that the proposed PFMRSC performs well when only 100 genes are used. We can observe the similar results in the multi-classification case as well.
Figure 6. Comparison of prediction accuracy on four binary classification datasets by varying the number of top selected genes.
In binary classification case, SRC, MSRC, and PFMSRC share the same curve trend. Compared with SRC and MSRC, PFMSRC performs well by using a smaller number of genes, SRC and MSRC can achieve comparable accuracy by using more genes. Evidently, SRC, MSRC, and PFMSRC consistently outperform LDA+SVM and ICA+SVM in all datasets.
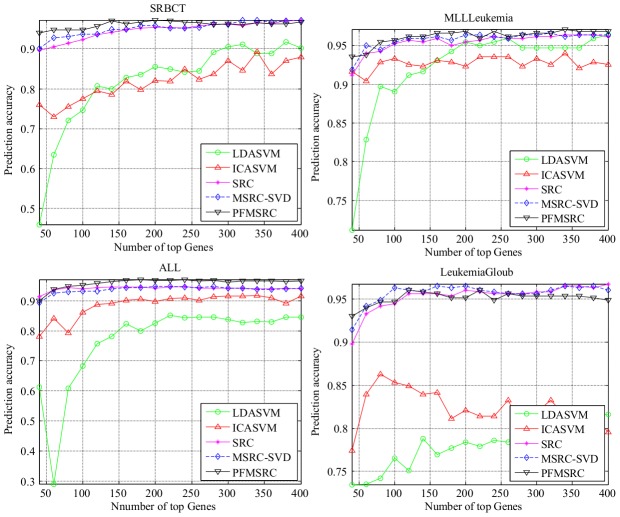
In the multiclass classification case, the performance of MSRC, SRC, and PFMSRC is very stable with respect to the number of genes, and all these methods converge fast to the optimal classification rate point. Figure 7 shows that compared with their performance in the binary classification case, SRC, MSRC, and PFMSRC are less influenced by gene dimension. Note that ALL is a multiclass dataset with six subclasses, but PFMSRC can still achieve a higher classification rate of 97% accuracy compared with SRC and MSRC. The same conclusion can be drawn for the SRBCT dataset.
Figure 7. Comparison of prediction accuracy on four multiclass classification datasets by varying the number of top selected genes.
In Table 8, we report the detailed classification accuracy. PFMSRC outperforms its competitors on most gene expression profile datasets, whereas SRC and MSRC-SVD perform the second best.
Table 8. The maximal average prediction accuracy of LDA+SVM, ICA+SVM, SRC, MSRC-SVD and PFMSRC on eight tumor microarray datasets.
| Dataset name | LDA+SVM | ICA+SVM | SRC | MSRC-SVD | PFMSRC |
| colon | 61.67 | 76.90 | 80.48 | 84.05 | 83.81 |
| DLBC | 68.07 | 71.05 | 89.47 | 88.42 | 89.47 |
| Gliomas | 67.33 | 70.67 | 75.33 | 75.00 | 76.00 |
| Acute leukemia | 85.38 | 88.85 | 93.27 | 95.00 | 95.19 |
| SRBCT | 91.16 | 89.30 | 97.21 | 97.21 | 97.21 |
| ALL | 85.16 | 91.44 | 96.46 | 93.59 | 97.02 |
| MLLLeukemia | 96.43 | 94.05 | 96.43 | 96.67 | 97.14 |
| LukemiaGloub | 81.63 | 91.81 | 94.79 | 94.68 | 96.05 |
Comparsion of CV performance
To evaluate the classification performance on imbalanced split training/testing sets, we perform 10-fold stratified CV on tumor subtype dataset. All samples are randomly divided into 10 subsets based on stratified sampling: nine subsets are used for training, and the remaining samples are used for testing. This evaluation process is repeated 10 times, and the average result is presented. The 10-fold CV results are summarized in Table 9.
Table 9. 10-fold CV prediction accuracy of eight tumor microarray datasets using different classification methods.
| Dataset name | LDA+SVM | ICA+SVM | SRC | MSRC-SVD | PFMSRC |
| colon | 81.67 | 90.00 | 87.14 | 90.24 | 90.24 |
| DLBCL | 92.14 | 97.14 | 97.14 | 91.96 | 95.89 |
| Gliomas | 86.50 | 86.50 | 78.33 | 78.33 | 84.00 |
| Acute leukemia | 96.50 | 95.57 | 96.07 | 97.50 | 95.00 |
| SRBCT | 96.64 | 95.75 | 1 | 1 | 1 |
| ALL | 97.61 | 94.83 | 96.46 | 93.59 | 97.63 |
| MLLLeukemia | 95.65 | 95.89 | 98.75 | 98.75 | 97.32 |
| LukemiaGloub | 97.32 | 96.32 | 98.57 | 98.57 | 96.07 |
Table 9 shows that as the training sample size increases, the performance of these five classification methods is significantly improved. Model based methods LDA+SVM and ICA+SVM perform very well, with the classification accuracy increased significantly. In particular, the prediction accuracy of ICA+SVM ranges from 86.5% to 96.57% in all tumor expression profile datasets, which is comparable with those of SRC, MSRC and PFMSRC.
We can conclude that model-based approaches are more vulnerable to the small sample size problem, over-fitting should be resolved properly.
Discussion
Based on the above experiments, we can draw the following observations:
Sparse representation based methods (SRC, MSRC, PFMSRC) consistently outperform the model-based methods (LDA+SVM, ICA+SVM) on all experiments. Especially, in balance splited datasets the prediction accuracy of model-based methods is significantly lower than that of sparse representation methods which may be attributed to the small sample size problem. However, SRC, MSRC, and PFMSRC perform well even when we take 5 samples per subclass for training and the rest for testing.
SRC, MSRC and PFMSRC are robust to various sample sizes and feature dimensions, as well as converge fast to the optimal classification rate. The experiments verify the results in [7], which favors the application of those methods. Note that, model-based methods (LDA+SVM, ICA+SVM) exhibit improved 10-fold CV classification accuracy. A reasonable explanation is that the over-fitting phenomena are dramatically reduced when 90% of original samples are used for training and the remaining 10% are used for evaluation in our experiments.
PFMSRC outperforms SRC and MSRC in most cases, which implies that the parameter free sparse representation and weighting strategies can capture more discriminating information, especially in multiclass classification. See Figure 5.
PFMSRC is a parameter-free method, in which the data dependent sparsity can be self-adaptively tuned, compared with SRC and MSRC in which search for a regularization parameter is laborious work. Moreover, the number of meta-samples is a key parameter for MSRC, as shown in Figure 2, which makes model selection more difficult.
Conclusions
In this study, we proposed a novel non-parametric meta-sample-based sparse representation. The algorithm assumes that test samples can be well reconstructed within a linear combination of weighed meta-samples in the same class. We theoretically proved the rationality of the weighting strategy. A simple but efficient projection function is constructed by the sparse representation coefficients to complete the classification work. We also compare the performance of PFMSRC with that of two model-based methods and two sparse representation-based methods on eight tumor expression datasets. Experimental results have shown the superiority of the proposed method. We then drew some conclusions on the effects of both balanced split and imbalanced split testing/training sets on tumor classification problems.
PFMSRC exhibits stable performance with respect to different training sample sizes and feature dimensions compared with the other four algorithms. Thus, the extension of the sparse representation with dimensionality reduction (feature selection or feature extraction) in a unified framework is one of our future works.
Funding Statement
This work is supported by the Program for New Century Excellent Talents in University (Grant NCET-10-0365), National Nature Science Foundation of China (Grant 60973082, 11171369, 61272395, 61370171, 61300128), the National Nature Science Foundation of Hunan province (Grant 12JJ2041), the Planned Science and Technology Project of Hunan Province (Grant 2009FJ3195, 2012FJ2012) and supported by the Fundamental Research Funds for the Central Universities, Hunan university, Graduate research and innovation projects in Hunan Province (Grant CX2012B144). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Alizadeh AA, Eisen MB, Davis RE, Ma C, Lossos IS, et al. (2000) Distinct types of diffuse large b-cell lymphoma identified by gene expression profiling. Nature 403: 503–511. [DOI] [PubMed] [Google Scholar]
- 2. West M (2003) Bayesian factor regression models in the large p, small n paradigm. Bayesian statistics 7: 723–732. [Google Scholar]
- 3.Liu B, Fang B, Liu X, Chen J, Huang Z (2013) Large margin subspace learning for feature selection. Pattern Recognition.
- 4.Cai D, He X, Zhou K, Han J, Bao H (2007) Locality sensitive discriminant analysis. In: IJCAI. pp. 708–713.
- 5. Sugiyama M (2006) Local fisher discriminant analysis for supervised dimensionality reduction. In: Proceedings of the 23rd international conference on Machine learning ACM, pp. 905–912. [Google Scholar]
- 6. Lazar C, Taminau J, Meganck S, Steenhoff D, Coletta A, et al. (2012) A survey on filter tech-niques for feature selection in gene expression microarray analysis. IEEE/ACM Transactions on Computational Biology and Bioinformatics (TCBB) 9: 1106–1119. [DOI] [PubMed] [Google Scholar]
- 7. Wright J, Yang AY, Ganesh A, Sastry SS, Ma Y (2009) Robust face recognition via sparse representation. Pattern Analysis and Machine Intelligence, IEEE Transactions on 31: 210–227. [DOI] [PubMed] [Google Scholar]
- 8. Zheng CH, Zhang L, Ng TY, Shiu CK, Huang DS (2011) Metasample-based sparse representation for tumor classification. Computational Biology and Bioinformatics, IEEE/ACM Transactions on 8: 1273–1282. [DOI] [PubMed] [Google Scholar]
- 9. West M, Blanchette C, Dressman H, Huang E, Ishida S, et al. (2001) Predicting the clinical status of human breast cancer by using gene expression profiles. Proceedings of the National Academy of Sciences 98: 11462–11467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Zheng CH, Ng TY, Zhang L, Shiu CK, Wang HQ (2011) Tumor classification based on non-negative matrix factorization using gene expression data. NanoBioscience, IEEE Transactions on 10: 86–93. [DOI] [PubMed] [Google Scholar]
- 11. Zheng CH, Zhang L, Ng V, Shiu CK, Huang DS (2011) Molecular pattern discovery based on penalized matrix decomposition. Computational Biology and Bioinformatics, IEEE/ACM Transactions on 8: 1592–1603. [DOI] [PubMed] [Google Scholar]
- 12. Statnikov A, Aliferis CF, Tsamardinos I, Hardin D, Levy S (2005) A comprehensive evaluation of multicategory classification methods for microarray gene expression cancer diagnosis. Bioinformatics 21: 631–643. [DOI] [PubMed] [Google Scholar]
- 13. Wright GW, Simon RM (2003) A random variance model for detection of differential gene expression in small microarray experiments. Bioinformatics 19: 2448–2455. [DOI] [PubMed] [Google Scholar]
- 14. Robnik-Šikonja M, Kononenko I (2003) Theoretical and empirical analysis of relieff and rrelieff. Machine learning 53: 23–69. [Google Scholar]
- 15. Seung D, Lee L (2001) Algorithms for non-negative matrix factorization. Advances in neural information processing systems 13: 556–562. [Google Scholar]
- 16. Alter O, Brown PO, Botstein D (2000) Singular value decomposition for genome-wide expression data processing and modeling. Proceedings of the National Academy of Sciences 97: 10101–10106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Han X (2010) Nonnegative principal component analysis for cancer molecular pattern discovery. Computational Biology and Bioinformatics, IEEE/ACM Transactions on 7: 537–549. [DOI] [PubMed] [Google Scholar]
- 18. Zheng CH, Huang DS, Zhang L, Kong XZ (2009) Tumor clustering using nonnegative matrix factorization with gene selection. Information Technology in Biomedicine, IEEE Transactions on 13: 599–607. [DOI] [PubMed] [Google Scholar]
- 19.Chen S, Donoho D (1994) Basis pursuit. In: Signals, Systems and Computers, 1994. 1994 Confer-ence Record of the Twenty-Eighth Asilomar Conference on. IEEE, volume 1 , pp. 41–44. [Google Scholar]
- 20. Donoho DL (2006) Compressed sensing. Information Theory, IEEE Transactions on 52: 1289–1306. [Google Scholar]
- 21.Sharon Y, Wright J, Ma Y (2007) Computation and relaxation of conditions for equivalence between l1 and l0 minimization. submitted to IEEE Transactions on Information Theory 5.
- 22.Tibshirani R (1996) Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society Series B (Methodological): 267–288.
- 23. Chen SS, Donoho DL, Saunders MA (1998) Atomic decomposition by basis pursuit. SIAM journal on scientific computing 20: 33–61. [Google Scholar]
- 24. Cheng B, Yang J, Yan S, Fu Y, Huang TS (2010) Learning with l1-graph for image analysis. Trans Img Proc 19: 858–866. [DOI] [PubMed] [Google Scholar]
- 25.Grant M, Boyd S, Ye Y (2008). Cvx: Matlab software for disciplined convex programming.
- 26. Chang CC, Lin CJ (2011) Libsvm: a library for support vector machines. ACM Transactions on Intelligent Systems and Technology (TIST) 2: 27. [Google Scholar]
- 27. Vapnik VN (1999) An overview of statistical learning theory. Neural Networks, IEEE Transactions on 10: 988–999. [DOI] [PubMed] [Google Scholar]
- 28. Alon U, Barkai N, Notterman DA, Gish K, Ybarra S, et al. (1999) Broad patterns of gene expression revealed by clustering analysis of tumor and normal colon tissues probed by oligonucleotide arrays. Proceedings of the National Academy of Sciences 96: 6745–6750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kent ridge bio-medical dataset. Available: http://datam.i2r.a-star.edu.sg/datasets/krbd/. Accessed: 2014 Feb 1.
- 30. Golub TR, Slonim DK, Tamayo P, Huard C, Gaasenbeek M, et al. (1999) Molecular classification of cancer: class discovery and class prediction by gene expression monitoring. science 286: 531–537. [DOI] [PubMed] [Google Scholar]
- 31.Gems database. Available: http://www.gems-system.org/. Accessed: 2014 Feb 1.
- 32. Nutt CL, Mani D, Betensky RA, Tamayo P, Cairncross JG, et al. (2003) Gene expression-based classification of malignant gliomas correlates better with survival than histological classification. Cancer research 63: 1602–1607. [PubMed] [Google Scholar]
- 33. Khan J, Wei JS, Ringner M, Saal LH, Ladanyi M, et al. (2001) Classification and diagnostic prediction of cancers using gene expression profiling and artificial neural networks. Nature medicine 7: 673–679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Yeoh EJ, Ross ME, Shurtleff SA, Williams WK, Patel D, et al. (2002) Classification, subtype discovery, and prediction of outcome in pediatric acute lymphoblastic leukemia by gene expression profiling. Cancer cell 1: 133–143. [DOI] [PubMed] [Google Scholar]
- 35. Armstrong SA, Staunton JE, Silverman LB, Pieters R, den Boer ML, et al. (2001) Mll translocations specify a distinct gene expression profile that distinguishes a unique leukemia. Nature genetics 30: 41–47. [DOI] [PubMed] [Google Scholar]
- 36. Wang SL, Zhu YH, Jia W, Huang DS (2012) Robust classification method of tumor subtype by using correlation filters. IEEE/ACM Transactions on Computational Biology and Bioinformatics (TCBB) 9: 580–591. [DOI] [PubMed] [Google Scholar]