The impact of covariance misspecification in multivariate Gaussian mixtures on estimation and inference: an application to longitudinal modeling

Abstract

Multivariate Gaussian mixtures are a class of models that provide a flexible parametric approach for the representation of heterogeneous multivariate outcomes. When the outcome is a vector of repeated measurements taken on the same subject, there is often inherent dependence between observations. However, a common covariance assumption is conditional independence—that is, given the mixture component label, the outcomes for subjects are independent. In this paper, we study, through asymptotic bias calculations and simulation, the impact of covariance misspecification in multivariate Gaussian mixtures. Although maximum likelihood estimators of regression and mixing probability parameters are not consistent under misspecification, they have little asymptotic bias when mixture components are well-separated or if the assumed correlation is close to the truth even when the covariance is misspecified. We also present a robust standard error estimator and show that it outperforms conventional estimators in simulations and can indicate the model is misspecified. Body mass index data from a national longitudinal study is used to demonstrate the effects of misspecification on potential inferences made in practice.

1. Introduction

Multivariate Gaussian mixtures are a class of models that provide a flexible parametric approach for the representation of heterogeneous multivariate outcomes potentially originating from distinct subgroups in the population. An overview of finite mixture models is available in many texts [1, 2, 3, 4, 5]. We can estimate covariate effects on the outcome as well as group membership probabilities by extending mixture models to include a regression structure for both the mean and mixing proportions. See De la Cruz-Mesía et al. [6] for a review of finite mixture models with a regression mean structure and Wedel [7] for the history of concomitant variable models that use baseline variables to explain variation in subgroups. These extensions are used in several medical applications [8] including epidemiology, genomics, and pharmacology in addition to other fields including astronomy, biology, economics, and speech recognition. When the multivariate outcome is a vector of repeated measures taken over time, these methods are identified as group-based trajectory modeling [9, 10] or latent-class growth analysis [11, 12]. See Pickles and Croudace [13] and references within for a review of mixture methods applied to longitudinal data. The use of mixture models for multivariate data is increasing due to computational advances that have made maximum likelihood (ML) parameter estimation possible, via the Expectation Maximization (EM) algorithm, through model-specific packages such as Proc Traj in SAS [14], Flexmix [15] and mclust [16] in R, and software such as Mplus [17] and Latent Gold [18].

Despite the increased use of these models, the sensitivity of estimated regression coefficients to model assumptions has only been explored to a limited degree. In a multivariate mixture model, one must specify the component distribution, the form of the mean, the structure of the covariance matrix, and the number of components; therefore, there are many ways to misspecify the model. For example, in practice, the number of components is unknown and model selection procedures based on the Bayesian information criterion are often employed. However, if the specified covariance structure is too restrictive relative to the truth, the estimated number of components will typically be greater than the true number because more components are needed to model the extra variability. The literature in estimating the number of components is vast [19] and continues to debate this unresolved issue. Due to the potential complexity of mixture models, simplifying assumptions are made to reduce the dimension of the parameter space, to make estimation possible, and for computational convenience. In particular, many researchers assume Gaussian components and/or restrict the components to have equal variance, both of which are known to result in asymptotic bias if the assumptions are not met [20, 21]. In this paper, we assume that the number of components, mean structure, and distribution are known and focus on other indeterminacies such as the covariance matrix.

In terms of the covariance matrix, eigenvalue and Cholesky decompositions [22, 23], as well as mixed effects structures [24], are used to impose structure and parsimony. Additionally, one common assumption is conditional independence—given the mixture component label, the outcomes for a subject are assumed independent [25, 26]. Of the available software that estimate regression effects for the mean and mixing probabilities, most of them make this simplifying assumption. This restriction is convenient when the data are unbalanced or if the sample size is small to make estimation of the covariance parameters more stable. Despite the wealth of proposed covariance models, there has been little work done in the area of mixture models with misspecified covariance structures, and the conditional independence assumption is unlikely to hold in many multivariate data settings, specifically in longitudinal applications. If the mixture consists of one component, work done by Liang, Zeger [27] and others suggest that regression estimates are asymptotically unbiased. However, these properties do not hold with additional components since estimation includes mixing proportions as well as component parameters.

Here, we investigate the impact of covariance misspecification on ML estimation of parameters and standard errors in multivariate Gaussian mixture models. In particular, our focus is on the assumption of conditional independence for the covariance structure; therefore, we assume the number of components, the distribution, and the mean structure is known. This paper is organized as follows. Section 2 presents the model specification. Section 3 describes the estimation procedure, issues, and asymptotic properties of the parameter estimators based on the seminal results of White [28]. In Section 4, we present a series of simulations of a simple misspecified example to compare asymptotic and finite-sample bias of parameter and standard error estimates under varying levels of dependence and separation between components. In Section 5, we apply these ideas to body mass index data from a national longitudinal study to demonstrate the effects of misspecification on potential inferences made in practice.

2. Model Specification

In a finite multivariate mixture, the density of a random vector y takes the form

$$f(\mathbf{y})={\pi }_1{f}_1(\mathbf{y})+\cdots +{\pi }_K{f}_K(\mathbf{y})$$

where π_k > 0 for k = 1, …, K and ${{\displaystyle \sum }}_k^K{\pi }_k=1$. The parameters π_k are mixing proportions and the functions f₁, …, f_K are component densities, assumed multivariate Gaussian here.

We extend the general model to allow other factors to affect the mean as well as the mixing proportions. Let $\mathbf{y}\in {\mathbb{R}}^m$ be a random vector whose distribution, conditional on regression covariates, x, and concomitant variables, z, is a mixture of K Gaussian densities with mixing proportions: π₁(z,γ),…., π_K(z,γ). That is, the conditional mixture density for y is defined by

$$f(\mathbf{y}|\mathbf{x},\mathbf{z},\mathit{\theta })={\displaystyle \sum }_{k=1}^K{\pi }_k(\mathbf{z},\mathit{\gamma })f_k(\mathbf{y}|\mathbf{x},{\mathit{\theta }}_k)$$ (1)

where f_k(y|x, θ_k) denotes the m-variate Gaussian probability density function with mean xβ_k and covariance matrix Σ_k (k = 1, …, K), θ_k includes both β_k and Σ_k, x is a m × p matrix, and z is a vector of length q. The regression covariates include measures that affect the mean while the concomitant variables influence the mixing proportions. This general structure allows the possibility that some baseline variables could be in both x and z.

We parameterize the mixing proportions using the multinomial logit with the form

$${\pi }_k(\mathbf{z},\mathit{\gamma })=\frac{\exp ({\mathbf{z}}^T{\mathit{\gamma }}_k)}{{\displaystyle {\sum }_{j=1}^K\exp ({\mathbf{z}}^T{\mathit{\gamma }}_j)}}$$

for k = 1, …, K where ${\mathit{\gamma }}_k\in {\mathbb{R}}^q,\mathit{\gamma }=({\mathit{\gamma }}_1^T,\dots ,{\mathit{\gamma }}_K^T)$ where γ_K = 0.

Throughout this paper, we generally assume conditional independence with constant variance within a component where ${\sum }_k={\sigma }_k^2{I}_m$ as the proposed estimation model, but it is straightforward to extend the covariance model to include other correlation structures such as exchangeable or exponential. Therefore, the vector of all unknown parameters, θ, consists of the mixing proportion parameters, γ_k, and the component regression and variance parameters, ${\mathit{\theta }}_k^T=({\mathit{\beta }}_k^T,{\sigma }_k^2)$, for k = 1,…, K and could include correlation parameters.

3. Estimation

3.1. EM Algorithm

Under the assumption that y₁,…,y_n are independent realizations from the mixture distribution, f(y|x, z, θ), defined in 1, the log likelihood function for the parameter vector, θ is given by

$$\log L(\mathit{\theta })={\displaystyle \sum }_{i=1}^n\log f({\mathbf{y}}_i|{\mathbf{x}}_i,{\mathbf{z}}_i,\mathit{\theta }).$$

The ML estimate of θ is obtained by finding an appropriate root of the score equation, ∂ log L(θ)/∂θ = 0. Solutions of this equation corresponding to local maxima can be found iteratively through the Expectation-Maximization (EM) algorithm [29]. This algorithm is applied in the framework where given (x_i,z_i) each y_i is assumed to have stemmed from one of the components and the indicator denoting its originating component is missing. The complete-data log likelihood is based on these indicator variables as well as the observed data {(y_i, x_i, z_i)}. The Expectation step (E-step) involves replacing the indicators by current values of the conditional expectation, which is the posterior probability of component membership, written as

$${\alpha }_{\mathit{ik}}={\pi }_k({\mathbf{z}}_i,\mathit{\gamma })f_k({\mathbf{y}}_i|{\mathbf{x}}_i)/{\displaystyle \sum }_{j=1}^K{\pi }_j({\mathbf{z}}_i,\mathit{\gamma })f_j({\mathbf{y}}_i|{\mathbf{x}}_i,{\mathit{\theta }}_j)$$

for i = 1, …,n and k = 1, …, K using current estimates of the parameters. In the Maximization step (M-step), the parameter estimates for the mixing proportions, regression effects, and covariance matrices are updated by maximizing the complete-data log likelihood using the posterior probabilities from the E-step in place of the indicator variables using numerical optimization. The E- and M-steps are alternated repeatedly until convergence. The EM algorithm guarantees convergence to a local maximum; global convergence may be attained through initializing the algorithm by randomly assigning individuals to initial components, running the algorithm multiple times and using the estimates associated with the highest log likelihood.

3.2. Issues

Although an estimation tool exists, there are potential issues of parameter identifiability with mixture models. Frühwirth-Schnatter [5] distinguishes between three types of nonidentifiability: invariance to relabeling of components, potential overfitting, and nonidentifiability due to the family of component distribution and the covariate design matrix. The first two issues are resolved through constraints such as θ_k ≠ θ_k′ for all k, k′ = 1, …,K, k ≠ k′. The last concern is solved by assuming Gaussian components since finite mixtures of multivariate Gaussians are identifiable [30, 31]. However, Hennig [32] suggests that the introduction of a regression structure to a Gaussian mixture requires a full rank design matrix as well as a rich covariate domain for regression parameters to be identifiable. On the other hand, mixing proportions parameters from a multinomial logit based on concomitant variables are identifiable by setting the parameters of one component to zero such as γ_K = 0 [33].

Besides identifiability, there are other known issues with finite mixture models. McLachlan and Peel [4] note that the sample size must be quite large for asymptotic theory to accurately describe the finite sampling properties of the estimator. Also, when component variances are allowed to vary between components, the mixture likelihood function is unbounded and each observation gives rise to a singularity on the boundary of the parameter space [34, 35]. However, Kiefer [36] outlines theory that guarantees that there exists a particular local maximizer of the mixture likelihood function that is consistent, efficient, and asymptotically normal if the mixture is not overfit. To avoid issues of singularities and spurious local modes in the EM algorithm, Hathaway [37] considers constrained maximum likelihood estimation for multivariate Gaussian mixtures based on the following constraint on the smallest eigenvalue of the matrix ${\sum }_h{\sum }_j^{-1}$, denoted as ${\lambda }_{\min }({\sum }_h{\sum }_j^{-1})$,

$$\underset{1\le h\ne j\le K}{\min }{\lambda }_{\min }({\sum }_h{\sum }_j^{-1})\ge c>0$$

for some positive constant c ∈ [0, 1] to ensure a global maximizer.

3.3. Asymptotic Properties

If the true underlying data-generating distribution is a member of the specified model class, then maximum likelihood estimation via the EM algorithm gives parameter estimates that are consistent [38, 39]. However, if the model specified does not contain the true underlying mixture, then the ML estimators potentially have asymptotic bias [20, 21]. Here, we are interested in the impact of misspecifying the covariance matrix structure on parameter estimation and inference.

General theoretical results for ML estimators are given by White [28]. Our investigation is a special case where the covariance matrices of mixture components are incorrectly specified but the mean structure and distribution are known. Let f(y|θ) be the assumed estimation model, g(y) be the true density, and C be a compact subset of the parameter space. It follows that the ML estimator, ${\widehat{\mathit{\theta }}}_n$, is consistent for the parameter vector, θ^*, that minimizes the Kullback-Leibler (KL) divergence, $\int \log [g(\mathbf{y})/f(\mathbf{y}|\mathit{\theta })]g(\mathbf{y})d\mathbf{y}=\int \log [g(\mathbf{y})]g(\mathbf{y})d\mathbf{y}-\int \log [f(\mathbf{y}|\mathit{\theta })]g(\mathbf{y})d\mathbf{y}$, under some regularity conditions [28], which is equivalent to maximizing $\int \log [f(\mathbf{y}|\mathit{\theta })]g(\mathbf{y})d\mathbf{y}$ with respect to θ.

In the case of mixture densities, this integral is mathematically intractable. Lo [21] used a modified EM algorithm for univariate data that maximized $\int \log [f(\mathbf{y}|\mathit{\theta })]g(\mathbf{y})d\mathbf{y}$ with respect to θ in order to estimate θ^*. This procedure could be adapted to bivariate data, but for outcome vectors of larger dimension, this procedure is not as useful. We know that for {y_i}_i=1,…n generated from the true density, under suitable regularity conditions [40],

$$\underset{\mathit{\theta }\in C}{\sup }\frac{1}{n}{\displaystyle \sum }_{i=1}^n\log f({\mathbf{y}}_i|\mathit{\theta })\stackrel{a.s.}{\to }\underset{\mathit{\theta }\in C}{\sup }{\displaystyle {\int }_{-\infty }^{\infty }\log f(\mathbf{y}|\mathit{\theta })g(\mathbf{y})d\mathbf{y}}\text{as}n\to \infty$$

Therefore, to investigate asymptotic bias under a misspecified covariance structure when g(y) is known, we numerically approximate θs using the EM algorithm on a large sample from g(y) of size n = 100, 000.

In addition to consistency, White [28] also showed that $\sqrt{n}({\widehat{\mathit{\theta }}}_n-{\mathit{\theta }}^{\ast })\to N(0,C({\mathit{\theta }}^{\ast }))$ where the asymptotic covariance matrix is C(θ^*)= A(θ^*)⁻¹B(θ^*)A(θ^*)⁻¹, with

$$A({\mathit{\theta }}^{\ast })=\left\{E\left(\frac{{\partial }^2\log f({\mathbf{y}}_i|{\mathit{\theta }}^{\ast })}{\partial {\theta }_j\partial {\theta }_l}\right)\right\},B({\mathit{\theta }}^{\ast })=\left\{E\left(\frac{\partial \log f({\mathbf{y}}_i|{\mathit{\theta }}^{\ast })}{\partial {\theta }_j}·\frac{\partial \log f({\mathbf{y}}_i|{\mathit{\theta }}^{\ast })}{\partial {\theta }_l}\right)\right\}.$$

Moreover, $C_n({\widehat{\mathit{\theta }}}_n)=A_n{({\widehat{\mathit{\theta }}}_n)}^{-1}{B}_n({\widehat{\mathit{\theta }}}_n)A_n{({\widehat{\mathit{\theta }}}_n)}^{-1}\stackrel{a.s.}{\to }C({\mathit{\theta }}^{\ast })$, with

$$\begin{array}{cc}{A}_n({\widehat{\mathit{\theta }}}_n)=\left\{\frac{1}{n}{\displaystyle \sum _{i=1}^n\frac{{\partial }^2\log f({\mathbf{y}}_i|{\widehat{\mathit{\theta }}}_n)}{\partial {\theta }_j\partial {\theta }_l}}\right\},& B_n\left({\widehat{\mathit{\theta }}}_n\right)=\left\{\frac{1}{n}{\displaystyle \sum _{i=1}^n\frac{\partial \log f({\mathbf{y}}_i|{\widehat{\mathit{\theta }}}_n)}{\partial {\theta }_j}\cdot \frac{\partial \log f({\mathbf{y}}_i|{\widehat{\mathit{\theta }}}_n)}{\partial {\theta }_l}}\right\}\end{array}$$

Following a similar procedure as Boldea and Magnus [41], we derive the score vector and Hessian needed to calculate A_n and B_n for a multivariate Gaussian mixture model. Derivations are available from the first author.

If the model is correctly specified, then both $-A_n{({\widehat{\mathit{\theta }}}_n)}^{-1}$ and $B_n{({\widehat{\mathit{\theta }}}_n)}^{-1}$ are consistent estimators of C(θ^*) [28], and two possible variance-covariance estimates for the parameter estimator are

$$\begin{array}{c}{\widehat{\text{Cov}}}_1({\widehat{\mathit{\theta }}}_n)={\widehat{\mathbf{W}}}_1=-{(n{A}_n({\widehat{\mathit{\theta }}}_n))}^{-1}\\ \text{and}\\ {\widehat{\text{Cov}}}_2({\widehat{\mathit{\theta }}}_n)={\widehat{\mathbf{W}}}_2=-{(n{B}_n({\widehat{\mathit{\theta }}}_n))}^{-1}\end{array}$$

On the other hand, $A_n{({\widehat{\mathit{\theta }}}_n)}^{-1}{B}_n({\widehat{\mathit{\theta }}}_n)A_n{({\widehat{\mathit{\theta }}}_n)}^{-1}$ provides a consistent estimator of C(θ^*) despite any misspecification. Therefore, a third and robust variance estimate of the parameter estimator is given by

$${\widehat{\text{Cov}}}_3({\widehat{\mathit{\theta }}}_n)={\widehat{\mathbf{W}}}_3=n^{-1}{A}_n{({\widehat{\mathit{\theta }}}_n)}^{-1}{B}_n({\widehat{\mathit{\theta }}}_n)A_n{({\widehat{\mathit{\theta }}}_n)}^{-1}$$

We refer to calculated standard error estimates corresponding to these three indexed variance-covariance estimates throughout the rest of the paper.

4. Simulations

We carry out two series of simulations to examine the behavior of the maximum likelihood estimators in terms of bias under misspecification of the covariance structure for finite samples from a multivariate mixture. Specifically, we are mainly interested in the impact of dependence in the true error structure on bias in parameter and standard error estimates when the conditional independence is assumed incorrectly and how this is affected by the (i) level of dependence and (ii) the separation between mixture components. Secondly, we investigate the behavior of the bias when the estimation structure gets closer to the true correlation structure by comparing the bias under three correlation structures.

In all of the simulations, the data with sample size n are generated from an m-variate Gaussian mixture model with parameters $({\mathit{\gamma }}_k,{\mathit{\beta }}_k,{\sigma }_k^2,{\mathbf{V}}_k)$ for k = 1,…,K where V_k is the true correlation structure as follows:

• Fix K.

• For each subject, i = 1,…, n,

  • – Fix x_i = 1_m and z_i = 1.

  • – Construct matrices A_k such that ${\mathbf{A}}_k{\mathbf{A}}_k^T={\mathbf{V}}_k$ for k = 1, …, K using the Cholesky decomposition.

  • – Randomly assign group membership, h_i, by drawing a value from the categorical distribution defined by P(h = k)= π_k(z_i, γ) for k = 1,…,K.

  • – Draw m standard normal random values e_i and let

$${\mathbf{y}}_i={\mathbf{x}}_i^T{\mathit{\beta }}_{h_i}+{\sigma }_{h_i}{\mathbf{A}}_{h_i}{\mathbf{e}}_i$$

Thus, ${\mathbf{y}}_i\sim N({\mathbf{x}}_i^T{\mathit{\beta }}_{h_i},{\sigma }_{h_i}^2{\mathbf{V}}_{h_i})$ We then estimate the parameters and standard errors, ${\widehat{\mathit{SE}}}_1$, ${\widehat{\mathit{SE}}}_2$, ${\widehat{\mathit{SE}}}_3$, using constrained maximum likelihood via the EM algorithm [37] doing five random initializations, based on a multivariate mixture model with a specified correlation structure and known design matrix.

For simplicity, we focus on a example of two Gaussian components (K =2) with constant mean vectors (i.e. no relationship between covariates and y), one component with independent errors, the other with some level of dependency in the errors. For the first series, the latter dependence is based on an exchangeable correlation structure where all outcomes in an observational unit are equally correlated, which is mathematically equivalent to a random intercept model.

To investigate the influence of the level of dependence, we set the vector length to m =5, equal mixing proportions (γ₁ =0 and baseline variables have no effect), mean of the components to β₁ = 1 and β₂ = 3, and the variance of the components to ${\sigma }_1^2=0.25$ and ${\sigma }_2^2=1$. The errors are independent (V₁ = I_m) in component one and we let the level of dependence vary with ρ = 0,0.5, 0.99 within the exchangeable structure (V₂= ρ(J_m − I_m) + I_m where J_m is a m × m matrix of 1’s) for component two. We present the bias of parameter estimates and the three standard error estimates under these conditions.

Then, we consider the separation between two component distributions using the concept of c-separation [42]. Two Gaussian distributions, N(μ₁,Σ₁) and N(μ₂,Σ₂), in ${\mathbb{R}}^m$ are c-separated if $\Vert {\mathit{\mu }}_1-{\mathit{\mu }}_2\Vert \ge c\sqrt{m\cdot \max ({\lambda }_{\max }({\sum }_1),{\lambda }_{\mathit{max}}({\sum }_2))}$where λ_max(Σ) is the largest eigenvalue of Σ. Dasgupta [42] notes that two Gaussians are almost completely non-overlapping when c = 2. This inequality can be rearranged to establish a measure of separation,

$$S=\Vert {\mathit{\mu }}_1-{\mathit{\mu }}_2\Vert /\sqrt{m\cdot \max ({\lambda }_{\mathit{max}}({\sum }_1),{\lambda }_{\mathit{max}}({\sum }_2))}$$

which is a standardized Euclidean distance between mean vectors. In this simulation, we calculate the value of S for data-generating component densities as a measure of the separation between the two components and if S > 2, the components do not overlap and are well-separated. For this series of simulations, we again use a strong level of dependence (ρ = 0.99) in the exchangeable structure, a vector length of m = 5, but vary the mean and variance of the second component (β₂ = 3, 5 and ${\sigma }_2^2=0.25,1,4$) to invoke different degrees of separation between components.

We perform 1000 replications of each simulation for sample sizes n = 100,500,1000. We approximate the true standard error with the standard deviation of the replicates. To estimate the asymptotic bias of the model parameters (n = ∞), we complete one replication with n = 100,000.

The two prong simulation described above focuses on the impact of using a conditional independence estimation model under different levels of dependence and separation in the data-generating components. In practice, we can choose correlation structures other than conditional independence. To explore the bias under difference covariance assumptions, we run a short simulation adjusting the data-generating model from above to use an exponential correlation structure, such that the dependence decreases as the time lag increases, rather than the constant dependence from the exchangeable structure. Therefore, for component two, the correlation between two measurements within a subject that are observed d time units apart is exp(−d/r) where r, the range parameter, determines how quickly the correlation decays to zero. This structure is general enough so that if r is close to zero, the correlation matrix is close to conditional independence and if r is very large, the structure is close to exchangeable correlation.

For this simulation, we continue using the two Gaussian components (K =2) with constant mean vectors (β₁ = 1 and β₂ = 3) of length m = 5 with observations at times t=1,2, 3,4 and 5, one component with independent errors, and the second component with a moderate level of dependence that decays exponentially (r =3). We estimate the mixing proportion, mean, and variance parameters assuming different correlation structures: conditional independence, exchangeable, and exponential correlation. We estimate and compare the finite-sample bias of parameters and standard errors by letting n = 500 with 1000 replications. Additionally, we compare the conventional estimate ${\widehat{\mathbf{W}}}_1$ of the covariance matrix of $\widehat{\mathit{\theta }}$ and the robust estimate ${\widehat{\mathbf{W}}}_3$ since if the estimation model is close to the true structure, the matrices should be similar and $\mathbf{Q}={\widehat{\mathbf{W}}}_1^{-1}{\widehat{\mathbf{W}}}_3$ should be close to the identity matrix. We calculate RJ = tr(Q)/ν where ν is the length of $\widehat{\mathit{\theta }}$, which has been termed the RJ criteria and should be close to 1 if the estimation model is close to the truth [43, 44].

4.1. Results

Table 1 lists bias estimates for the dependence-varying simulation study. The estimates range from close to zero when ρ = 0 to magnitudes of upwards of 0.3 when ρ = 0.99. It is clear from this table that stronger dependence in the errors results in greater finite-sample and asymptotic bias when estimating under the conditional independence assumption. Additionally, the magnitude of bias seems to reach the level of asymptopia at sample sizes of n = 500, but it is important to note that the estimates for the asymptotic bias, based on one replication with n = 100,000, are only numerically accurate to two decimal places for γ₁, ${\sigma }_1^2$, and ${\sigma }_2^2$ even when using computationally large sample sizes. We see this numerical inaccuracy when ρ =0 since the asymptotic bias should be zero when the conditional independence assumption is met. In terms of standard error estimates, the bias increases with increased dependence with values ranging from 0.001 when ρ = 0 to 0.111 when ρ = 0.99. We see a divergence between the three variance estimators with ${\widehat{\mathit{SE}}}_3$, the robust estimator, consistently having the least bias (Table 2). When the model is correctly specified with ρ=0, the three estimators are similar as supported by asymptotic theory.

Table 1.

Bias estimates (SE) of maximum likelihood parameter estimators when the covariance structure of a 2-component Gaussian mixture is assumed to be conditionally independent based on 1000 replications under each mixture distribution with m = 5, γ₁ = γ₂ = 0, β₁ = 1, V₁ = I_m, ${\sigma }_1^2=0.25$, β₂ = 3, V₂ = V (ρ) and ${\sigma }_2^2=1$ where V (ρ) is the exchangeable correlation matrix. Asymptotic estimates (n = ∞) are based on one replication with n = 100,000. Values equal to zero represent values less than 0.001.

Bias Estimates
ρ	n	${\widehat{\gamma }}_1$	${\widehat{\beta }}_1$	${\widehat{\sigma }}_1^2$	${\widehat{\beta }}_2$	${\widehat{\sigma }}_2^2$
0.00	100	−0.004 (0.006)	0.000 (0.001)	−0.000 (0.001)	−0.002 (0.002)	−0.006 (0.003)
	500	0.005 (0.003)	−0.000 (0.000)	−0.000 (0.000)	0.001 (0.001)	−0.000 (0.001)
	1000	0.004 (0.002)	−0.000 (0.000)	−0.000 (0.000)	0.001 (0.001)	−0.000 (0.001)
	∞	−0.001	0.000	0.001	−0.000	0.002
0.50	100	0.125 (0.006)	0.031 (0.001)	0.024 (0.001)	0.106 (0.003)	−0.136 (0.003)
	500	0.125 (0.003)	0.028 (0.001)	0.024 (0.000)	0.101 (0.002)	−0.124 (0.001)
	1000	0.125 (0.002)	0.028 (0.000)	0.024 (0.000)	0.098 (0.001)	−0.125 (0.001)
	∞	0.115	0.027	0.024	0.095	−0.125
0.99	100	0.370 (0.007)	0.087 (0.002)	0.033 (0.001)	0.327 (0.005)	−0.410 (0.005)
	500	0.346 (0.003)	0.078 (0.001)	0.030 (0.001)	0.310 (0.002)	−0.388 (0.002)
	1000	0.350 (0.002)	0.079 (0.001)	0.030 (0.000)	0.309 (0.001)	−0.385 (0.001)
	∞	0.353	0.082	0.031	0.315	−0.383

Table 2.

Bias estimates of the three standard error estimators (SE₁, SE₂, SE₃) when the covariance structure of a 2-component Gaussian mixture is assumed to be conditionally independent based on 1000 replications under each mixture distribution with m = 5, γ₁ = γ₂ = 0, β₁ = 1, V₁ = I_m, ${\sigma }_1^2=0.25$, β₂ = 3, V₂ = V (ρ) and ${\sigma }_2^2=1$ where V (ρ) is the exchangeable correlation matrix. Approximate standard error is based on the estimated standard deviation of the simulation distribution. Values equal to zero represent values less than 0.001.

Bias Estimates
ρ	n	${\widehat{\mathit{SE}}}_1({\widehat{\gamma }}_1)$	${\widehat{\mathit{SE}}}_2({\widehat{\gamma }}_1)$	${\widehat{\mathit{SE}}}_3({\widehat{\gamma }}_1)$	${\widehat{\mathit{SE}}}_1({\widehat{\beta }}_1)$	${\widehat{\mathit{SE}}}_2({\widehat{\beta }}_1)$	${\widehat{\mathit{SE}}}_3({\widehat{\beta }}_1)$	${\widehat{\mathit{SE}}}_1({\widehat{\sigma }}_1^2)$	${\widehat{\mathit{SE}}}_2({\widehat{\sigma }}_1^2)$	${\widehat{\mathit{SE}}}_3({\widehat{\sigma }}_1^2)$
0.00	100	0.007	0.007	0.007	0.000	0.001	−0.000	−0.001	0.001	−0.001
	500	0.002	0.002	0.002	−0.000	0.000	−0.000	0.000	0.000	0.000
	1000	0.001	0.001	0.001	0.000	0.000	0.000	0.000	0.000	0.000
0.50	100	0.004	0.004	0.004	−0.006	−0.008	−0.002	−0.007	−0.009	−0.004
	500	0.002	0.002	0.002	−0.003	−0.004	−0.001	−0.002	−0.004	−0.001
	1000	−0.001	−0.001	−0.001	−0.002	−0.002	−0.000	−0.001	−0.002	−0.000
0.99	100	−0.003	−0.003	−0.002	−0.026	−0.035	−0.010	−0.013	−0.016	−0.008
	500	−0.005	−0.005	−0.004	−0.011	−0.015	−0.003	−0.005	−0.007	−0.002
	1000	−0.003	−0.003	−0.002	−0.007	−0.010	−0.001	−0.003	−0.005	−0.002
ρ	n				${\widehat{\mathit{SE}}}_1({\widehat{\beta }}_2)$	${\widehat{\mathit{SE}}}_2({\widehat{\beta }}_2)$	${\widehat{\mathit{SE}}}_3({\widehat{\beta }}_2)$	${\widehat{\mathit{SE}}}_1({\widehat{\sigma }}_2^2)$	${\widehat{\mathit{SE}}}_2({\widehat{\sigma }}_2^2)$	${\widehat{\mathit{SE}}}_3({\widehat{\sigma }}_2^2)$
0.00	100				0.001	0.003	0.001	−0.008	−0.004	−0.010
	500				0.001	0.001	0.001	0.001	0.001	0.000
	1000				0.000	0.000	0.000	0.001	0.001	0.001
0.50	100				−0.046	−0.070	−0.005	−0.019	−0.028	−0.004
	500				−0.021	−0.032	−0.002	−0.010	−0.016	−0.001
	1000				−0.014	−0.021	−0.000	−0.009	−0.013	−0.002
0.99	100				−0.092	−0.122	−0.017	−0.085	−0.111	−0.022
	500				−0.040	−0.054	−0.006	−0.035	−0.049	−0.003
	1000				−0.027	−0.037	−0.002	−0.026	−0.036	−0.004

Figure 1 shows that the relationship between the level of component separation and the magnitude of bias is complex. As in the previous simulation, sample sizes of n = 500 and larger produce similar bias estimates so we only present the asymptotic results. When the level of separation is high, S > 2, then the magnitude of the bias is small, but when there is some overlap, S < 2, there is not a clear, consistent relationship between the value of S and the magnitude of the estimated bias for all parameters. That is, for two sets of parameter values, such as (β₂ = 3, ${\sigma }_2^2=0.25$) and (β₂= 5, ${\sigma }_2^2=1$), that have the same level of separation, S = 2.836, the magnitude of the bias for all parameter estimates is drastically different for the two settings. However, in general, the bias decreases as the level of separation increases for a fixed mean parameter. The only exception is that the estimator for the first component mean ( ${\widehat{\beta }}_1$) has increased bias when S= 1.418 as compared to S = 0.709, but the bias then decreases when S = 2.836. It appears that when there is high overlap between two components, there is a point at which the bias peaks and then starts to decrease as σ₂ increases even though the amount of overlap continues to increase. Lastly, similar to the parameter estimates, the greater amount of separation results in less bias in the standard errors with biases as large as 1.0 unit in the situation with the most overlap and as little as less than 0.001 when components are well-separated. Again, the robust estimator again has the lowest bias. Tables available upon request.

Figure 1.

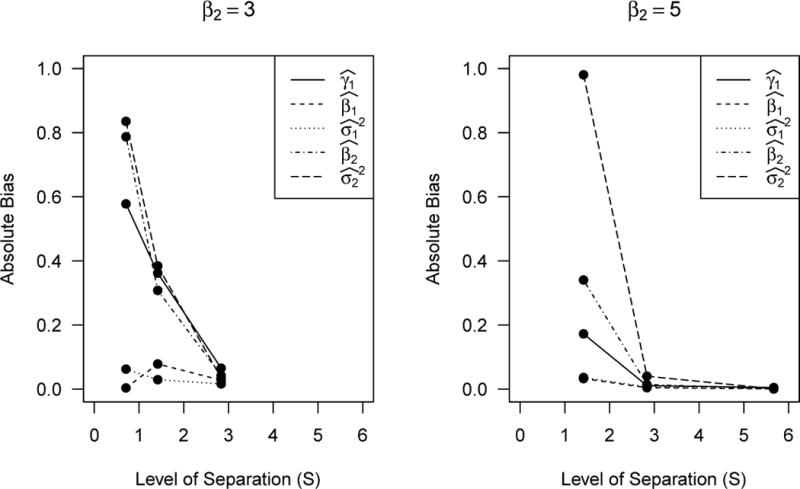
Asymptotic bias estimates of maximum likelihood parameter estimators when the covariance structure of a 2-component Gaussian mixture is assumed to be conditionally independent based on 1 replication with n=100,000 under each mixture distribution with m=5, γ₁=γ₂=0, β₁=1, V₁=I_m, σ₁

₂=0.25, V₂=V(ρ), and

ρ=0.99 where V(ρ) is the exchangeable correlation matrix. The level of separation (S) is calculated using the true mixture distribution. For β₂ = 3, variance parameters, σ₂

₂=0.25, 1, 4 result in S=2.836, 1.418, 0.709,

respectively. For β₂ = 5, variance parameters, σ₂

₂=0.25, 1, 4 result in S=5.671, 2.836, 1.418, respectively.

Values of S≥2 indicate almost completely separated components.

The simulations based on dependence and separation demonstrate the finite-sample and asymptotic bias in the ML estimators when the covariance structure is misspecified as conditional independence and the mixture components overlap. However, if two components are well-separated, the misspecification of the dependence in the errors does not result in large biases and thus any finite-sample bias could be removed potentially conventional techniques such as bootstrapping with careful tracking of component labels [45]. Additionally, when there is no covariance misspecification or when components are well-separated, all of the standard error estimates are similar and have little bias. However, when there is misspecification in the dependence structure, the estimates basely solely on the Hessian matrix or the score vector understate the true variability while the robust estimate has little bias. In cases where the true level of dependence is high, the bias in the Hessian estimator, ${\widehat{\mathit{SE}}}_1$, and the robust version, ${\widehat{\mathit{SE}}}_3$, can differ by as much as a relative factor of 2. In simulations not shown, using unequal mixing proportions result in similar conclusions. When the component proportions are unbalanced, the magnitude of bias increases when a majority of observations units originate from the misspecified component (here component two).

Figure 2 shows the absolute bias of parameter estimates under the three different covariance assumptions when the data was generating with the exponential correlation structure for component two. As expected, when the model is correctly specified, there is very little bias. We note that assuming the exchangeable structure, while incorrect, results in less bias than assuming conditional independence. As the RJ criteria gets closer to 1 from 1.97 to 1.02 to 0.99 using independence, exchangeable, and then exponential, the estimation correlation structure gets closer to the true structure resulting in little bias in the parameter estimates.

Figure 2.

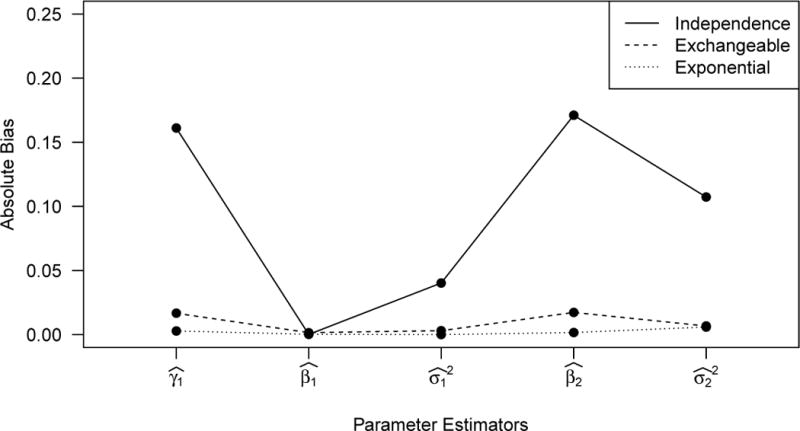
Bias estimates of maximum likelihood parameter estimators when the covariance structure of a 2-component Gaussian mixture is assumed to be conditionally independent, exchangeable, and exponential structure based on 1000 replications under each mixture distribution with n=500, m=5, γ₁=γ₂=0, β₁=1, V₁=I_m, σ₁

₂=0.25, β₂=3, V₂=V(r) and σ₂

₂=2 where V(r) is the exponential correlation matrix and r=3. Mean

values of the RJ criteria are RJ = 1.97, 1.02, 0.99 for the three covariance assumptions, respectively.

5. Data Example

To look at the behavior of the parameter and standard error estimates in practice, we use data from the 1979 National Longitudinal Survey of Youth (NLSY79). The NLSY79 is a nationally representative sample of 12,686 young American men and women aged 14–22 years in 1979, that oversampled Hispanic, Black, and economically disadvantaged non-Black/non-Hispanics. The cohort, interviewed annually from 1979 to 1994 and biennially thereafter, provide health and economic data for a total of 23 interviews (until 2008). In particular, the available body weight data for the 1979 cohort span a twenty-five year period [25]. We study body mass index (BMI) over time as it is an important longitudinal measure for public health and elucidating obesity development. Self-reported weight was collected in 17 interviews and height in five of those. BMI [weight (kg)/height (m²)] was calculated for each interview based on the weight and the average height.

For the purposes of this paper, the complex sampling structure is ignored and we randomly sample 500 subjects who were at least 18 years of age in 1981 and reported all 17 weight measurements. Of this sample, 51% are female, 54% are non-Hispanic/non-Black, 29.2% Black and 16.8% Hispanic. To model the BMI outcomes, we allow a quadratic relationship between mean BMI and age and include sex as a baseline concomitant variable. Therefore, for i = 1,…, 500, we assume that the observed data were generated according to

$$\mathit{BMI}={\beta }_{k0}+{\beta }_{k1}\cdot (\mathit{\text{AGE}}-18)+{\beta }_{k2}\cdot {\left(\mathit{\text{AGE}}-18\right)}^2+{\mathit{∊}}_k$$

with probability

$${\pi }_k(\mathbf{z},\mathit{\gamma })=\frac{e^{{\gamma }_{k0}+I_{(\mathit{\text{male}})}{\gamma }_{k1}}}{{{\displaystyle \sum }}_j{e}^{{\gamma }_{j0}+I_{(\mathit{\text{male}})}{\gamma }_{j1}}}$$

where ${\mathit{∊}}_k\sim N(0,{\sigma }_k^2{\mathbf{V}}_k)$ for k = 1,…, 4. The choice of four groups is based on previous research [25]. Using the EM algorithm with five random initializations, we estimate parameters and standard errors and present the estimates that produced the highest log likelihood. For the sake of comparison, we complete the estimation assuming conditional independence (V_k = I_m), and under an exchangeable (V_k = p_k(J_m − I_m) + I_m) and exponential (V_k = exp(−D/r_k) where D is the Euclidean distance matrix of the ages at interviews for a subject) correlation model.

5.1. Results

Parameter and standard errors are estimated for a four component multivariate Gaussian mixture model assuming conditional independence, exchangeable, and exponential correlation (Table 3). The regression parameter estimates are used to calculate the mean curves for the four groups under all three covariance assumptions and we see that the mean curves differ between the models mainly in terms of the innermost curves (Figure 3). Under exchangeable correlation, one of the middle curves represents little BMI increase over time in contrast to the other groups. Under the exponential correlation assumption, the two lowest groups have a similar pattern over time, but the dependence differs between these groups with the range parameters estimated as r₁ = 2.973 and r₂ = 23.579 indicating that component 2 has more long range dependence between the BMI outcomes than component 1. Our simulation results suggest the magnitude of bias in the parameter estimator depends on how close the estimation correlation structure is to the truth and the overlap between components. We note there are no well-separated components and we see bias in the mean estimates by comparing the three covariance assumptions.

Table 3.

Parameter and standard error estimates $({\widehat{\mathit{SE}}}_1,{\widehat{\mathit{SE}}}_3)$ for a random sample of 500 from NLSY79 assuming a four component mixture model with quadratic mean and the following correlation structures: conditional independence, exchangeable, and exponential correlation. Values equal to zero represent values less than 0.001. Additionally, the RJ criteria was calculated each covariance assumption: RJ = 7.34, 3.02, 2.22 under conditional independence, exchangeable, and exponential, respectively.

		Conditional Independence			Exchangeable			Exponential
		Estimate	${\widehat{\mathit{SE}}}_1$	${\widehat{\mathit{SE}}}_3$	Estimate	${\widehat{\mathit{SE}}}_1$	${\widehat{\mathit{SE}}}_3$	Estimate	${\widehat{\mathit{SE}}}_1$	${\widehat{\mathit{SE}}}_3$
Component 1	γ10	0.827	0.201	0.461	0.122	0.182	0.261	0.420	0.235	0.442
	γ11	−1.800	0.380	0.570	0.966	0.300	0.430	−0.888	0.734	2.275
	β10	19.315	0.140	0.178	20.994	0.208	0.225	19.984	0.358	0.467
	β11	0.104	0.020	0.027	0.155	0.010	0.017	0.217	0.049	0.056
	β12	0.001	0.001	0.001	−0.001	0.000	0.001	−0.002	0.001	0.001
	${\sigma }_1^2$	2.969	0.110	0.277	6.331	0.721	1.002	5.718	0.427	0.976
	ρ1	–	–	–	0.855	0.017	0.023	–	–	–
	r1	–	–	–	–	–	–	2.973	0.207	0.280
Component 2	γ20	0.599	0.206	0.435	−0.450	0.216	0.275	0.716	0.221	0.523
	γ21	0.435	0.280	0.385	0.851	0.344	0.464	1.424	0.511	1.687
	β20	20.979	0.120	0.312	24.041	0.520	0.689	20.910	0.241	0.389
	β21	0.238	0.016	0.023	0.198	0.032	0.070	0.187	0.024	0.029
	β22	−0.002	0.000	0.001	−0.005	0.001	0.002	−0.001	0.001	0.001
	${\sigma }_2^2$	3.150	0.104	0.365	21.113	2.926	4.716	8.147	0.788	2.458
	ρ2	–	–	–	0.805	0.027	0.022	–	–	–
	r2	–	–	–	–	–	–	23.579	2.016	4.213
Component 3	γ30	0.279	0.221	0.482	0.129	0.186	0.282	0.174	0.247	0.526
	γ31	0.534	0.296	0.402	1.066	0.304	0.424	1.739	0.514	1.575
	β30	22.818	0.207	0.721	21.165	0.275	0.372	23.516	0.385	0.563
	β31	0.449	0.027	0.051	0.366	0.016	0.031	0.464	0.049	0.085
	β32	−0.006	0.001	0.002	−0.002	0.000	0.001	−0.006	0.001	0.002
	${\sigma }_3^2$	6.416	0.260	1.162	11.241	1.225	2.230	13.049	1.004	2.851
	ρ3	–	–	–	0.822	0.018	0.019	–	–	–
	r3	–	–	–	–	–	–	10.215	0.675	0.826
Component 4	γ41	0	–	–	0	–	–	0	–	–
	γ40	0	–	–	0	–	–	0	–	–
	β40	25.713	0.480	0.672	22.473	0.573	0.480	24.356	1.054	0.833
	β41	0.679	0.069	0.108	0.725	0.042	0.080	0.636	0.138	0.099
	β42	−0.008	0.002	0.003	−0.008	0.001	0.003	−0.006	0.004	0.004
	${\sigma }_4^2$	26.864	1.154	7.891	32.982	3.484	6.928	44.788	4.093	13.757
	ρ4	–	–	–	0.681	0.034	0.044	–	–	–
	r4	–	–	–	–	–	–	8.058	0.654	0.850

Figure 3.

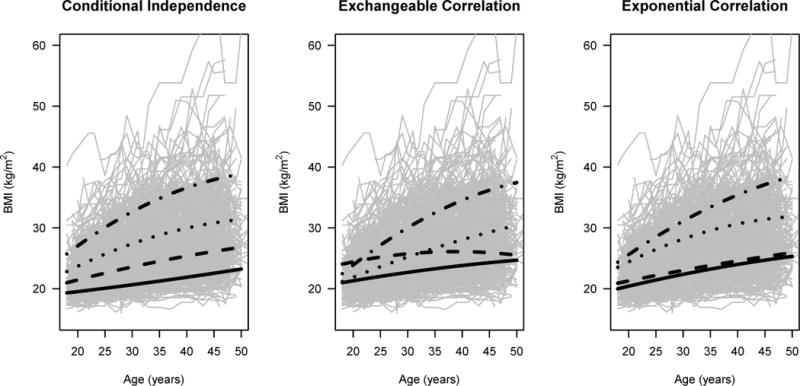
Random sample of 500 BMI trajectories from NLSY and mean curves for the four components estimated using a Gaussian mixture model specified with a quadratic mean under the covariance assumptions: conditional independence, exchangeable, and exponential correlation. The labeled are consistent with the tables in the text: component 1 (solid), component 2 (dashed), component 3 (dotted), and component 4 (dashed-dot). Additionally, the RJ criteria was calculated each covariance assumption: RJ=7.34, 3.02, 2.22 under conditional independence, exchangeable, and exponential, respectively.

Given that the repeated outcome is BMI, we expect some dependence in the error structure within individuals. We consider the level of dependence in errors by plotting the estimated autocorrelation function by calculating the empirical variogram of the residuals from the conditional independence model [46] for each estimated component by randomly assigned each individual to a component using posterior probabilities [47]. The estimated autocorrelation function of the residuals shows strong dependence between residuals within 5 to 10 years and the correlation decreases with increasing time lags (Figure 4). This correlation structure is therefore neither consistent with conditional independence nor exchangeable correlation, but rather decreases to zero which is more consistent with the exponential correlation structure. We see that the robust standard estimators are almost twice those of estimates using the standard estimators under conditional independence, and the RJ criteria, which compares the naive and robust estimates of the covariance matrix the parameters, suggests that the exponential correlation structure is the one closest to the truth.

Figure 4.

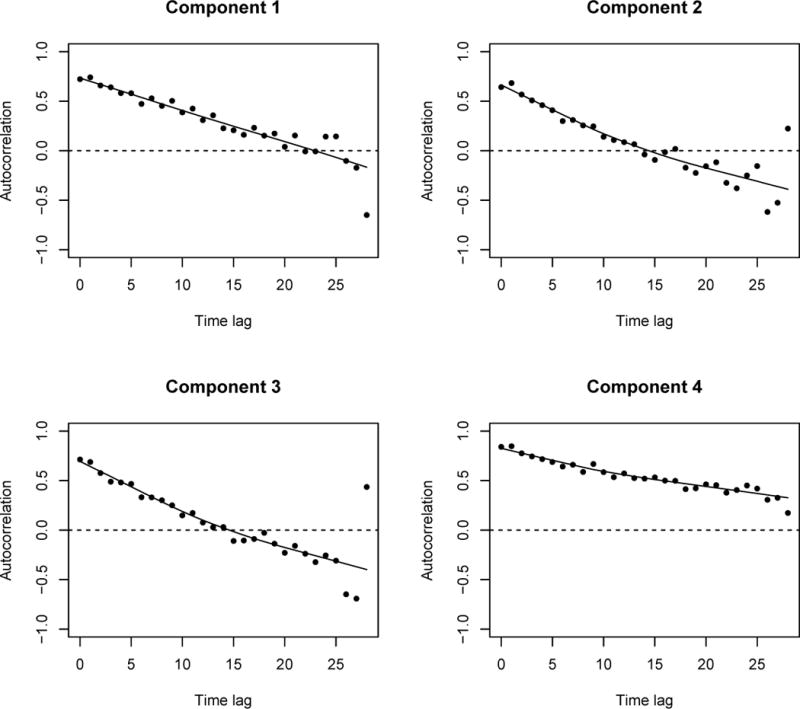
Smoothed sample autocorrelation of component residuals of estimated Gaussian mixture model specified with a quadratic mean and conditional independence with a random sample of 500 BMI trajectories from NLSY randomly assigned to components based on estimated posterior probabilities. The dashed line represents the estimated variance for each component.

In this data example, we see the influence of the covariance structure on the estimates, especially in terms of the regression parameters. Based on the simulation results and the RJ criteria, we expect the exponential correlation model fits the data the best out of the three structures. However, we note that we fixed the number of components to be four for the sake of consistency and this may not be the optimal number of components. In practice, this value is estimated from the data as mentioned earlier. This data application highlights the impact of covariance misspecification as well as the fact that the mean structure may not be the only aspect differing between individuals; the level of dependence and variability also distinguish groups of individuals.

6. Discussion

We have shown that covariance misspecification of a two-component Gaussian mixture may produce very little bias in regression and mixing probability parameter estimates when the components are well-separated. This is well-aligned with Lo’s univariate findings [21]. However, when there is some overlap in the component distributions, assuming the wrong correlation structure can produce asymptotically biased parameter estimates, the magnitude dependent on the level of separation and how close the structure is to the truth. With misspecified mixture models, the potential for biased mixing and regression parameters estimates differs from the one component models for which general estimating equations [27] produce unbiased estimates despite dependence present in the errors. Depending on the context and precision of the estimates, the bias may or may not have practical significance, but it is important to note that the ML estimators are inconsistent under covariance misspecification and there may be substantial bias when the components are not well-separated.

In addition to potential biases in the parameter estimates, the simulations provide evidence that conventional standard errors estimates which are based solely on the score equation, or the Hessian, can be extremely biased and underestimate the true variability of the estimators when the covariance structure is misspecified. Therefore, standard errors should be robustly estimated using White’s estimator that sandwiches the two conventional estimators. We use the exact formula for this estimator since the numerical approximations to the Hessian matrix and score vector are not by-products produced by the EM algorithm. To the authors’ knowledge, very few software programs currently have implemented a robust standard error estimator, but it should be implemented in every mixture model software as the default variance estimator and presented along with standard estimators to allow for comparisons, calculation of the RJ criteria, and the detection of misspecification bias.

Given our results, we recommend three things when estimating parameters in a mixture model. First, count the number of subjects whose maximum posterior probability is less than 0.95. If this count is non-zero, this indirectly indicates that the component distribution are not well-separated, suggesting that specifying the correct correlation structure is important. Second, if the components are not well-separated, fit the mixture model using several correlation structures such as conditional independence, exchangeable, and exponential correlation. For each model, calculate the RJ criteria based on the conventional and robust estimated variance-covariance matrix. Compare the parameter estimates to see if they change under the different assumptions and assess the RJ criteria values to see which structure results in a value closest to one. Choose the most parsimonious model that has an RJ criteria value close to one. Third, if none of these three structure fulfills this requirement, consider a more complex, potentially non-stationary covariance matrix as well as other sources of misspecification such as an incorrect number of components, assumed distribution, or an inflexible mean structure.

Our simulation study is limited, but the results likely apply to more complex mean structures and a larger number of components. In future studies, the impact of bias should be explored for more than two components with all components potentially having a misspecified covariance structure and for non-stationary covariance structures. Additionally, mixture models as specified in this paper group individuals with similar trajectories over time; we are currently investigating methods that distinguish between the shape of the trajectory and the vertical level of the curve when grouping individuals together.