Abstract
Surrogate measures are needed when recumbent length or height is unobtainable or unreliable. Arm span has been used as a surrogate but is not feasible in children with shoulder or arm contractures. Ulnar length is not usually impaired by joint deformities, yet its utility as a surrogate has not been adequately studied. In this cross-sectional study, we aimed to examine the accuracy and reliability of ulnar length measured by different tools as a surrogate measure of recumbent length and height. Anthropometrics [recumbent length, height, arm span, and ulnar length by caliper (ULC), ruler (ULR), and grid (ULG)] were measured in 1479 healthy infants and children aged <6 y across 8 study centers in the United States. Multivariate mixed-effects linear regression models for recumbent length and height were developed by using ulnar length and arm span as surrogate measures. The agreement between the measured length or height and the predicted values by ULC, ULR, ULG, and arm span were examined by Bland-Altman plots. All 3 measures of ulnar length and arm span were highly correlated with length and height. The degree of precision of prediction equations for length by ULC, ULR, and ULG (R2 = 0.95, 0.95, and 0.92, respectively) was comparable with that by arm span (R2 = 0.97) using age, sex, and ethnicity as covariates; however, height prediction by ULC (R2 = 0.87), ULR (R2 = 0.85), and ULG (R2 = 0.88) was less comparable with arm span (R2 = 0.94). Our study demonstrates that arm span and ULC, ULR, or ULG can serve as accurate and reliable surrogate measures of recumbent length and height in healthy children; however, ULC, ULR, and ULG tend to slightly overestimate length and height in young infants and children. Further testing of ulnar length as a surrogate is warranted in physically impaired or nonambulatory children.
Introduction
Recumbent length or standing height is an essential measure in the assessment and management of nutrition and growth in children (1, 2). Length or height is fundamental in calculating BMI and body surface area (3) and in estimating medication dosage (4), blood pressure (5), renal function (6), and pulmonary function (7, 8). Length and height also are important surveillance tools for public health monitoring (9, 10) and in chronic disease research (11–13). Despite the importance of length and height in assessing nutritional and growth status, length and height are usually unobtainable or unreliable in children who are temporarily hospitalized or who have long-term mobility impairment due to neuromuscular diseases or joint deformities (14, 15). Thus, a surrogate measure of length or height is needed, whether at a single point in time to estimate length or height for acute care management, or at consecutive clinic visits to monitor linear growth over time.
Linear growth of the body and its segments undergoes transformations from birth to adulthood (16, 17). Understanding these anthropometric changes offers insight into the possible effects of genetics, environment, and pathologic states. Surrogate measures of length and height are thus desirable for the following reasons: 1) they serve as clinical substitutes; 2) they permit an estimate of length or height through a formula calculation; 3) they provide in some cases greater accuracy than traditional length or height measurements; and 4) they offer insight into the differential growth of body segments as a function of age, sex, ethnicity, and pathologic conditions. Moreover, difficulties and problems in linear measurement can be encountered in field studies compared with clinical settings because of the portability, accessibility, and expense of specialized equipment. Therefore, surrogate measures of length and height that can be obtained via simple and portable tools are desirable.
Examples of surrogate measures of length or height include arm span (18–20), lower leg length or knee height (21, 22), and segmental lengths of long bones (humerus, radius, ulnar, femur, tibia, and fibula) (23–25), the majority of which have only been evaluated in adults. Of particular note, researchers have documented difficulties in measuring arm span in children with arm spasticity or contractures, which resulted in a considerable amount of missing data (26). In addition, researchers have reported difficulties in measuring lower leg length in children with lower-extremity cerebral palsy (27) and in the acutely ill elderly population (28). In contrast, ulnar length is a potential surrogate measure of length and height because its measurement is not usually impeded by joint deformity in these special populations.
Ulnar length was first described by Valk (29) by using a special device called the condylograph to assess children’s short-term growth. Two studies have subsequently assessed ulnar length as a surrogate measure of height in children by using the Harpenden anthropometer (i.e., a counter-type anthropometric caliper), which is less bulky and easier to use than the condylograph. Ulnar length was demonstrated as an accurate and reproducible surrogate measure of height in healthy Chinese children aged 3–18 y (r = 0.98) (30) and in healthy Australian children aged 5–19 y (males: R2 = 0.96, females: R2 = 0.94) (31). To date, no studies have investigated the relation between ulnar length and recumbent length in children <3 y of age, nor has the relation with height been assessed in children aged 2–5.9 y across different ethnicities in the United States.
As part of formative research for the National Children’s Study, a cross-sectional study of healthy infants and children aged <6 y was conducted to determine whether ulnar length can serve as a surrogate measure of recumbent length and height and whether 1 of 3 simple and portable tools (i.e., the caliper, ruler, or paper grid) for measuring ulnar length is a more optimal method. In particular, we developed a paper and pencil grid to measure ulnar length and considered whether a simple straight steel ruler would be a feasible surrogate for ulnar length as measured by caliper when length or height could not be measured (e.g., children with cerebral palsy or those temporarily injured).
Participants and Methods
Participants.
This research was a cross-sectional study of the anthropometric status of infants and children aged <6 y across 8 study centers (Supplemental Table 1) in the United States between 2011 and 2012. Mother-offspring dyads were recruited at daycare centers, churches, clinics, and community centers by study coordinators, word of mouth, and referral (n = 1634). Eligibility criteria included the following: mothers aged 18–49 y and noninstitutionalized, and offspring who were aged 0–5.9 y, healthy, of the same ethnicity [categorized as nonHispanic white (NHW),14 Hispanic, nonHispanic black (NHB), or other based on the mothers’ responses] and living with the mother, had not suffered from any illness associated with weight loss or been acutely ill within the past week, and were afebrile at the time of study visit. The analysis was restricted to infants and children (n = 1479) with at least 1 anthropometric measurement and 1 infant or child per mother to avoid cluster effects from shared sociodemographic characteristics and genetics of children in the same household. The study was approved by the institutional review board at the Eunice Kennedy Shriver National Institute of Child Health and Human Development and by those at each study center. Written informed consent was obtained from the mothers.
Anthropometric measurements.
A team of 2 trained researchers (1 measurer and 1 recorder) obtained anthropometric measurements in the home, community center, church, or clinic. Quality control and data collection standardization procedures were reported previously (32). Recumbent length and standing height were measured by using standard anthropometric protocols (33). Recumbent length was measured to the nearest 0.1 cm by using an infantometer (Ellard Instrumentation) for infants and children aged <3 y in the supine position with the body extended, head held steady facing upward, and knees held down. Height was measured to the nearest 0.1 cm in children aged 2–5.9 y by using a portable stadiometer (SECA) while the child was standing in bare feet with head (after removal of a hair piece when applicable), shoulders, buttocks, and heels touching the vertical plate and head in the Frankfort plane.
Ulnar length was measured on the right arm by using different tools to compare as surrogate measures of recumbent length and height. The measurer palpated and marked with ink a line of ∼1 cm at the distal end of the ulna (i.e., the styloid process) while the infant or child was in the sitting position with the right elbow flexed ∼90° (touching the table with the arm and hand pointing upward), the wrist straight, and the fingers extended. The proximal end of the ulna, the olecranon, was identified by palpation with the elbow flexed 90°. Ulnar length in centimeters was measured to the nearest 0.1 cm with the elbow flexed ∼90° by using 3 methods: 1) caliper (Rosscraft Innovations): placed the tips of the caliper against both end points of the forearm (i.e., the olecranon and styloid processes) with the arm placed in a horizontal plane (Supplemental Fig. 1A); 2) ruler: measured the distance between the 2 end points of the forearm by using a steel or hard plastic ruler with the elbow touching the table and the arm pointing upward in a vertical plane (Supplemental Fig. 1B); and 3) grid: marked the location of the 2 end points of the ulna parallel to the lines on the grid, which was secured on a rigid board or on the table (Supplemental Fig. 1C). The grid was developed on graph paper that has uniform dimensions to directly and precisely mark the measurements and read values. The grid was colored across rows/units of 10 boxes to facilitate reading the measurements. The colorful nature of the grid facilitated its use because the children enjoyed its rainbow effect. The grid method was performed in infants and children aged ≥3 mo.
Arm span was measured while the participant lay supine on a piece of paper on the floor, with shoulders flat against the surface and body extended. Both arms were stretched laterally outward and perpendicular to the long axis of the body with palms facing upward. The measurer and observer worked synchronously and gently pressed their hands against the participant’s elbow at the same time to maximize arm extension and to extend the fingers maximally on each side. Each simultaneously marked the most distal points of the middle finger of each hand on the paper by pencil or pen. The distance between the 2 points was measured to the nearest 0.1 cm by a steel or plastic (nonstretch) measuring tape.
Each measurement was taken in duplicate. The mean value of each anthropometric measurement was calculated if the 2 initial measurements agreed within 0.2 cm for length, height, ulnar length, and arm span. Otherwise, an additional measurement was taken and the mean of the 2 closest recordings was used. To determine the inter-observer measurement reliability, replicate measures were taken by reversing the researchers’ positions as measurer and recorder in an ∼10% random subsample (n = 119).
Statistical analyses.
Data preprocessing approaches applied in this study were reported previously (32). Descriptive statistics of anthropometrics were presented as means ± SDs or frequencies as appropriate by age, sex, and ethnicity. Shapiro-Wilk tests showed that all anthropometrics were normally distributed. Differences in anthropometrics were assessed by using the Student’s t test by sex, ANOVA across age groups, or ANCOVA among sex and ethnicity groups with age as the covariate and study center as a random effect. Post hoc tests were adjusted by Bonferroni correction. Inter-observer and intra-observer variability were analyzed by calculating the CVs for each anthropometric measure in the random subsample of repeated measurements in 119 infants and children, respectively. In addition, the intraclass correlation coefficients (ICCs) using a 1-way random model and absolute agreement type were calculated to assess the inter-observer and intra-observer reliability. Paired t tests with Bonferroni adjustment were computed to assess significant differences between ulnar length by caliper (ULC), ulnar length by ruler (ULR), and ulnar length by grid (ULG) in the total population and by age, sex, and ethnicity. Pearson’s correlation coefficients were calculated to assess the bivariate associations between length/height and surrogate anthropometrics (i.e., ULC, ULR, ULG, and arm span) by age, sex, and ethnicity.
Prediction equations for length and height by surrogate measures and covariates (age, sex, and ethnicity) were derived by using multivariate mixed-effects linear regression with study center as a random effect. We included ln (age + 1) [ln-transformed (age in mo + 1)] as a predictor in each equation to account for rapid growth in infancy and early childhood (34). To quantify the goodness-of-fit of the prediction models, the marginal R2 proposed by Nakagawa and Schielzeth (35) was calculated to represent the proportion of variance explained by fixed effects. The SEE was computed for each equation. According to the validation criteria recommended by Lohman et al. (33), the SEE of valid prediction equations should be <3.5 and R2 should be >0.7. To assess the agreement between the measured length/height and the predicted values by each prediction equation, we plotted the difference between the 2 measurements (i.e., predicted and measured length/height) against the mean of the 2 measurements as described by Bland and Altman (36). Linear regression analysis was used to calculate the unstandardized regression coefficient (b) of the difference between the predicted and measured length/height on their respective means. The limits of agreement were defined as the mean difference ± 1.96 SD. The Bland-Altman plots can identify whether the tools/methods can be used interchangeably by visually examining the relation between the differences of measurements from 2 tools/methods and the magnitude of the measurements.
All analyses were conducted with IBM SPSS 20 (IBM Corporation) and R Statistical Software (Foundation for Statistical Computing). Records with missing values for ≥1 of the predictors were excluded from each analysis and noted in the tables. Statistical significance was set at a 2-tailed P value of <0.05.
Results
Of the 1479 mother-offspring dyads, the mean ± SD age of the offspring was 23.7 ± 20.0 mo and 51.8% were boys (Table 1). The ethnic distribution of the study population was 45% Hispanic (largely Mexican American), 26% NHB, 20% NHW, and 8.7% other ethnic groups. Among the others, 55.8% were Chinese American and the remainder were largely other Asians (data not shown). As expected, all anthropometric values increased with increasing age. All anthropometric values were consistently smaller in girls than boys after age adjustment. Ethnic variation was observed for many anthropometrics after age adjustment. The other ethnic groups had shorter linear growth parameters (i.e., length, height, and ulnar length by the 3 tools, and arm span) than their NHB counterparts. The Hispanic participants compared with the NHW participants did not differ in length, ULC, ULR, and arm span, but were shorter in height and ULG.
TABLE 1.
Length, height, ULC, ULR, ULG, and arm span of infants and children by age, sex, and ethnicity1
| n (%)2 | Length | Height | ULC | ULR | ULG | Arm span | |
| cm | cm | cm | cm | cm | cm | ||
| Overall | 1479 (100) | 71.1 ± 12.0 | 100.7 ± 8.7 | 12.8 ± 2.9 | 12.7 ± 2.9 | 13.3 ± 2.6 | 82.5 ± 19.6 |
| Age (mo) | |||||||
| 0–11.9 | 574 (38.8) | 65.3 ± 0.5a | NA | 10.1 ± 0.08a | 9.8 ± 0.08a | 10.5 ± 0.08a | 62.8 ± 0.4a |
| 12–23.9 | 299 (20.2) | 79.8 ± 0.5b | NA | 12.4 ± 0.09b | 12.0 ± 0.10b | 12.3 ± 0.09b | 78.0 ± 0.5b |
| 24–35.9 | 193 (13.0) | 91.9 ± 0.7c | 91.3 ± 0.5a | 14.2 ± 0.11c | 13.8 ± 0.11c | 14.0 ± 0.10c | 91.6 ± 0.6c |
| 36–71.9 | 413 (27.9) | NA | 104.4 ± 0.4b | 16.3 ± 0.08d | 16.0 ± 0.08d | 16.1 ± 0.08d | 105.8 ± 0.4d |
| P3 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | |
| Sex | |||||||
| Boys | 766 (51.8) | 71.6 ± 0.3a | 101.4 ± 0.3a | 13.0 ± 0.06a | 12.9 ± 0.06a | 13.4 ± 0.06a | 84.3 ± 0.3a |
| Girls | 713 (48.2) | 69.9 ± 0.3b | 100.5 ± 0.3b | 12.7 ± 0.06b | 12.5 ± 0.06b | 13.1 ± 0.06b | 82.7 ± 0.3b |
| P4 | <0.001 | 0.007 | <0.001 | <0.001 | <0.001 | <0.001 | |
| Ethnicity | |||||||
| NHW | 296 (20.0) | 70.6 ± 0.4 | 101.4 ± 0.4a | 12.7 ± 0.09a | 12.5 ± 0.09a | 13.3 ± 0.09a | 83.2 ± 0.5a |
| Hispanic | 665 (45.0) | 70.6 ± 0.4 | 99.9 ± 0.5b | 12.7 ± 0.09a | 12.5 ± 0.10a | 13.0 ± 0.09b | 82.8 ± 0.5a,b |
| NHB | 385 (26.0) | 71.5 ± 0.4a | 102.5 ± 0.4a | 13.3 ± 0.08b | 13.2 ± 0.09b | 13.7 ± 0.08c | 86.3 ± 0.4c |
| Other | 129 (8.7) | 70.1 ± 0.6b | 98.9 ± 0.6b | 12.5 ± 0.13a | 12.3 ± 0.13a | 12.8 ± 0.13b | 81.1 ± 0.6b |
| P5 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 |
Values are means ± SEs unless otherwise indicated. Length was measured in children aged ≤3 y (n = 941). Height was measured in children aged 2–5.9 y (n = 578). ULG was measured in children ≥3 mo (n = 1262). Values with different superscript letters in a column are significantly different, P < 0.05 (Bonferroni post hoc test). NA, not available; NHB, nonHispanic black; NHW, nonHispanic white; ULC, ulnar length by caliper; ULG, ulnar length by grid; ULR, ulnar length by ruler.
Totals may be <1479 because of missing values.
ANOVA or Student’s t test with study center as a random effect.
Student’s t test with study center as a random effect, adjusting for age.
ANCOVA with study center as a random effect, adjusting for age.
The CVs for interobserver variability were consistently higher than the CVs for intraobserver variability for all measures in a random subsample of 119 participants (Table 2). Among surrogate measures, arm span had the least inter- and intraobserver variability, whereas ulnar length measured by different tools had the highest inter- and intraobserver variability. Intraobserver reliability evaluated by ICCs was consistently higher than interobserver ICCs for all measures except for arm span. Among the ulnar length measurements by the 3 tools, ULG had the lowest inter- and intraobserver reliability evaluated by ICCs.
TABLE 2.
Intraobserver and interobserver reliability of anthropometric measurements in a subsample of infants and children1
| Intraobserver reliability |
Interobserver reliability |
|||||
| n2 | CV | ICC (95% CI) | n2 | CV | ICC (95% CI) | |
| % | % | |||||
| Length | 58 | 0.20 | 1.000 (0.999, 1.000) | 56 | 0.53 | 0.999 (0.998, 0.999) |
| Height | 66 | 0.12 | 0.999 (0.999, 1.000) | 64 | 0.29 | 0.999 (0.998, 0.999) |
| ULC | 119 | 0.62 | 0.999 (0.998, 0.999) | 117 | 1.48 | 0.996 (0.984, 0.997) |
| ULR | 113 | 0.49 | 0.999 (0.998, 0.999) | 112 | 1.78 | 0.993 (0.990, 0.995) |
| ULG | 108 | 0.90 | 0.997 (0.995, 0.998) | 105 | 2.33 | 0.989 (0.983, 0.992) |
| Arm span | 109 | 0.26 | 1.000 (1.000, 1.000) | 105 | 0.34 | 1.000 (1.000, 1.000) |
ICC, intraclass correlation coefficient; ULC, ulnar length by caliper; ULG, ulnar length by grid; ULR, ulnar length by ruler.
n may be <119 because of missing values.
We calculated the mean paired differences between ULC and ULR or ULG by sex, age, and ethnicity with Bonferroni adjustment for multiple comparisons (Supplemental Table 2). Overall, ULC measurements were consistently longer than ULR and ULG measurements (except for NHW participants) with mean paired differences of 0.16 ± 1.04 and 0.07 ± 0.65 cm, respectively. Values of ULG were intermediate among the 3 measures but closer to ULC. In summary, among the 3 tools measuring ulnar length, the caliper and the grid were more comparable than the ruler.
Correlation coefficients between surrogate measures and length/height were always highest in arm span (Table 3). Among other surrogate measures than arm span, correlation coefficients between ULC and recumbent length were always higher than ULR or ULG, whereas the coefficients between height and ULC were similar to ULG and higher than ULR.
TABLE 3.
Pearson’s correlation coefficients between ULC, ULR, ULG, arm span, and recumbent length and height of infants and children by age, sex, and ethnicity1
| n | ULC | ULR | ULG | Arm span | |
| Recumbent length | 941 | 0.90* | 0.85* | 0.86* | 0.98* |
| Age (mo) | |||||
| 0–11.9 | 567 | 0.81* | 0.75* | 0.65* | 0.95* |
| 12–23.9 | 272 | 0.77* | 0.68* | 0.77* | 0.95* |
| 24–35.9 | 102 | 0.74* | 0.71* | 0.73* | 0.86* |
| Sex | |||||
| Boys | 497 | 0.89* | 0.87* | 0.85* | 0.98* |
| Girls | 444 | 0.91* | 0.84* | 0.87* | 0.99* |
| Ethnicity | |||||
| NHW | 172 | 0.91* | 0.88* | 0.86* | 0.99* |
| Hispanic | 458 | 0.87* | 0.90* | 0.83* | 0.98* |
| NHB | 242 | 0.94* | 0.74* | 0.89* | 0.98* |
| Other | 66 | 0.97* | 0.94* | 0.91* | 0.99* |
| Height | 578 | 0.87* | 0.82* | 0.87* | 0.96* |
| Age (mo) | |||||
| 24–35.9 | 166 | 0.75* | 0.57* | 0.73* | 0.92* |
| 36–71.9 | 412 | 0.82* | 0.75* | 0.82* | 0.94* |
| Sex | |||||
| Boys | 286 | 0.87* | 0.79* | 0.87* | 0.96* |
| Girls | 292 | 0.87* | 0.85* | 0.87* | 0.96* |
| Ethnicity | |||||
| NHW | 142 | 0.90* | 0.83* | 0.88* | 0.96* |
| Hispanic | 194 | 0.82* | 0.77* | 0.86* | 0.97* |
| NHB | 165 | 0.91* | 0.86* | 0.88* | 0.97* |
| Other | 77 | 0.88* | 0.89* | 0.86* | 0.94* |
Length was measured in children aged ≤3 y. Height was measured in children aged 2–5.9 y. *P < 0.001. NHB, nonHispanic black; NHW, nonHispanic white; ULC, ulnar length by caliper; ULG, ulnar length by grid; ULR, ulnar length by ruler.
In predictive equations developed from multivariate mixed-effects linear regression analysis (Table 4), surrogate measures (ULC, ULR, ULG, and arm span) and age were consistently significant in all models. The term ln (age + 1) was significant in all models for length (models 1–4) and in models for height predicted by ulnar length (models 5–7). Despite the substantial sex and ethnic differences in length and height observed in this study (Table 1) and previously (37–40), sex and ethnicity were only significant in some equations after inclusion of other predictive terms (models 1–3 for sex and models 4–8 for ethnicity). The proportions of variation in length accounted for by fixed effects in models 1–3 (95%, 95%, and 92%, respectively) were comparable with that in model 4 (97%). In contrast, the proportions of variation in height accounted for by fixed effects in models 5–7 (87%, 85%, and 87%, respectively) were less than that in model 8 (95%).
TABLE 4.
Regression equations to estimate recumbent length in children aged 0–3 y and height in children aged 2–5.9 y by using ULC, ULR, ULG, or arm span1
| Surrogate measures (cm) |
Ethnicity |
||||||||||||
| n | Intercept | ULC | ULR | ULG | Arm span | Age (mo) | ln (t) | Boy | NHW | NHB | R2marginal | SEE | |
| Length (cm) | |||||||||||||
| Model 1 | 918 | 36.83 | 1.48* | — | — | — | 0.51* | 5.42* | 0.91* | — | — | 0.95 | 2.62 |
| Model 2 | 864 | 39.84 | — | 1.09* | — | — | 0.55* | 5.90* | 1.09* | — | — | 0.95 | 2.75 |
| Model 3 | 741 | 38.15 | — | — | 1.44* | — | 0.53* | 5.01* | 0.99* | — | — | 0.92 | 2.73 |
| Model 4 | 784 | 16.30 | — | — | — | 0.67* | 0.16* | 2.64* | — | — | −0.80* | 0.97 | 1.99 |
| Height (cm) | |||||||||||||
| Model 5 | 577 | 14.25 | 2.71* | — | — | — | 0.10† | 10.7† | — | 1.17* | — | 0.87 | 3.18 |
| Model 6 | 571 | 28.80 | — | 2.29* | — | — | 0.21† | 7.34* | — | 1.22* | — | 0.85 | 3.43 |
| Model 7 | 573 | 13.93 | — | — | 2.64* | — | 0.10* | 11.0† | — | 0.89† | — | 0.88 | 3.11 |
| Model 8 | 551 | 21.39 | — | — | — | 0.71* | 0.16* | — | — | 0.98* | −0.87* | 0.94 | 2.07 |
Mixed-effects linear regression analysis using study center as a random effect. *P < 0.001, †P < 0.01. ln (t), natural log-transformed (age in mo + 1); NHB, nonHispanic black; NHW, nonHispanic white; R2marginal, coefficient of determination for fixed effects; ULC, ulnar length by caliper; ULG, ulnar length by grid; ULR, ulnar length by ruler.
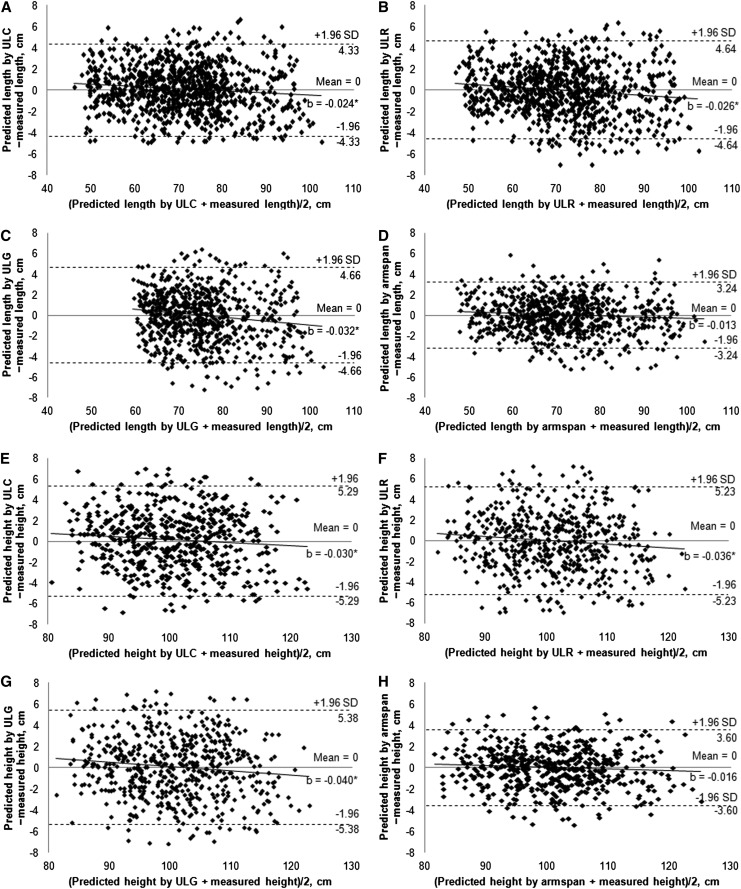
In the Bland-Altman plots, linear regression analysis revealed a weak but significant downward trend of the difference between the predicted and measured length/height as their means increased when ULC, ULR, or ULG served as a surrogate measure ( for length and E–G for height). Specifically, ulnar length tended to slightly overestimate length by using predictive models 1–3 (b = −0.024, −0.026, and −0.032, respectively) and height by using models 5–7 (b = −0.030, −0.036, and −0.040, respectively) in young infants and children (noted as the small mean values on the x-axis). In contrast, no significant trend was detected for arm span as a surrogate measure of recumbent length (Fig. 1D) and standing height (Fig. 1H) (b = −0.013 and −0.016, respectively; both P > 0.05). The 95% limits of agreement were smaller for the difference between predicted and measured length or height when arm span served as a surrogate measure (±3.24 and ±3.60 cm for length and height, respectively) compared with ULC, ULR, and ULG (range: ±4.33 to ±5.38 cm).
FIGURE 1.
Bland-Altman plots: the difference between the predicted and measured length in children aged 0–3 y (A–D) or height in children aged 2–5.9 y (E–H) plotted against the mean of the predicted and measured length or height. Solid lines represent the mean difference. Dashed lines represent the 95% limits of agreement (i.e., mean difference ± 1.96 SD). *P < 0.05. b, unstandardized regression coefficient; ULC, ulnar length by caliper; ULG, ulnar length by grid; ULR, ulnar length by ruler.
Discussion
In this study, surrogate measures of recumbent length and standing height in children using different methods were accurate and reproducible in healthy neonates, infants, and children aged <6 y. The CV and ICC values were comparable with or better than those reported previously (31, 41, 42). Thus, obtaining these surrogate measures in a variety of clinical settings is feasible and reliable by using trained personnel. Ulnar length and arm span were highly correlated with length in infants and children aged 0–3 y and with height in children aged 2–5.9 y. Multivariate mixed-effects linear regression analyses demonstrated that both ulnar length and arm span were significant predictors of recumbent length and standing height. Therefore, ulnar length and arm span can be used to estimate length and height by using the prediction models in Table 4 when actual length and height cannot be obtained accurately or reliably.
To our knowledge, this study is the first to report correlation coefficients between ulnar length measured by different tools and length/height in infants and children <6 y of age in the United States. Pearson’s correlation coefficients between length/height and arm span (r = 0.98 for length; r = 0.96 for height) were higher compared with ulnar length. Similarly, Miller and Koreska (43) reported that the correlation coefficient of arm span with standing height (r = 0.97) was higher than the coefficient of ulnar length (r = 0.91) in normal children, based on the anthropometric data of children aged 8–14 y in the United States (44). However, in children with Duchenne muscular dystrophy with contractures who could not fully extend their arms or fingers, arm span did not correlate well with height (r = 0.47), whereas ulnar length measurement was not impeded by wrist or finger contractures and its accuracy was thus not impaired (43).
Several studies have developed prediction equations for height from arm span. Arm span is an accurate and strong predictor of height in healthy Chinese children aged 4–16 y (males: R2 = 0.965, females: R2 = 0.972; SEE not reported) (45), in Malawian children aged 6–15 y without any physical deformities (R2 = 0.988 with age as a covariate; SEE = 0.76 cm) (19), and in nondisabled children aged 2–6 y in India (R2 = 0.93; SEE = 3.2 cm) (26). Fewer data are available for the ability of ulnar length to predict length/height. Agnihotri et al. (46) developed a prediction model of height from ULC in college students in Mauritius (R2 = 0.74; SEE not reported). In a sample of healthy Australian children aged 5–19 y (31), ulnar length (measured by a Harpenden anthropometer) and age explained 96% (SEE = 3.896 cm) and 94% (SEE = 3.785 cm) of variation in height, respectively. In contrast, the SEEs of length and height prediction by using ULC, ULR, and ULG as surrogates ranged from 2.62 to 3.43 cm in our study, all below the recommended validation criteria of <3.5 cm by Lohman et al. (33).
To our knowledge, this is the first study to date that developed prediction equations for length and height from ulnar length in infants and children aged <6 y in the United States. Results demonstrated that the accuracy of length prediction by ULC, ULR, and ULG was comparable with that by arm span, whereas height prediction by ULC, ULR, and ULG was less accurate than that by arm span in terms of the proportion of variation in length/height explained by these surrogate measures and covariates (age, sex, and ethnicity). However, the accuracy and reliability of arm span as a length/height proxy may be impaired in children with shoulder/arm spasticity or contractures because of the difficulty in establishing an outstretched position of both arms (47, 48). Under these circumstances, ulnar length is probably the best measure available that can provide a reasonably high prediction of accuracy. In addition, each of the 3 tools for ulnar length measurement may be used interchangeably because their respective values of marginal R2 in predicting length/height varied little in terms of prediction accuracy.
In Bland-Altman plots examining the agreement between the predicted and measured length/height, length/height predicted by ULC, ULR, or ULG had zero bias but some heteroscedasticity. Specifically, ULC, ULR, and ULG tend to slightly overestimate length in newborns and young infants. The trend of overestimation was more marked for height predicted by ulnar length in young children. Position issues related to ulnar length measurements might lead to measurement errors. For example, measurement accuracy can be compromised if the caliper is not held steady or parallel to the floor, if the ruler is not touching against the arm in a vertical plane, or if the arm rolls during the grid measurement. Indeed, a challenge in the use of the grid was the ability to mark the grid as proximally as possible to the marks for the olecranon and styloid processes of the ulna. These challenges were encountered more frequently in young infants and children whose arms were difficult to keep still in an appropriate position during measurement. Therefore, measurement errors inherent in ulnar length might subsequently affect the prediction accuracy in these young infants and children. In contrast, no trend or bias was detected when arm span served as a surrogate measure of length or height. However, whichever surrogate measure was used, the magnitude of the 95% limits of agreement in this study is considerably smaller than reported previously (49–51). For instance, the 95% limits of agreement of the difference between the predicted height by ulnar length (measured by using an anthropometric tape) and measured height were −10.0, 13.8 cm and −9.0, 9.8 cm in white men and women aged 21–62 y in the United Kingdom, respectively (50). Despite the high accuracy of length/height prediction by these surrogate measures at the group level, caution should be exercised when using surrogate measures for estimation of length/height in individuals because a 3- or 5-cm difference could potentially alter clinical assessment or management based on the calculation of BMI or estimation of renal or pulmonary function via length/height.
Certain limitations of this study need to be noted. To enrich the limited anthropometric data in nonwhite infants and children, we oversampled Hispanic, NHB, and other ethnic groups (mostly Asian American). Thus, the study population was not sampled to be nationally representative of the U.S. population, which would limit the generalizability of our findings. In addition, the Bland-Altman plots indicated there might be some heteroscedasticity in anthropometrics at different ages. Because of the limited sample size, we included age as a continuous variable in the prediction models. Future studies with an adequate sample size developing individual prediction equations of length and height by surrogate measures in stratified age groups are warranted to reduce variability and heteroscedasticity.
In conclusion, we report that ulnar length measurements by 3 different tools (i.e., caliper, ruler, and paper grid) and arm span can serve as accurate and reliable surrogate measures of recumbent length and standing height in healthy neonates, infants, and children aged <6 y across 8 study centers in the United States. Prediction equations developed from these surrogate measures by using age, sex, and ethnicity as covariates might be used to estimate length or height when actual length or height is not measured or cannot be obtained accurately or reliably because of postural problems or participants’ noncompliance. Arm span exhibited a higher level of accuracy in predicting height compared with ulnar length, whereas ulnar length may serve as a better surrogate in children with postural problems (e.g., joint deformities or chondrodysplasia). However, it is worth noting that the accuracy of length or height prediction by these surrogate measures might be compromised in individuals, especially by ulnar length because of challenges in palpating styloid and olecranon processes in newborns and young infants. The prediction equations developed in this sample of healthy neonates, infants, and children aged <6 y require further testing in children who are physically impaired or nonambulatory. Moreover, ulnar length measured by caliper, ruler, or grid provides an alternative option for estimating length or height in field settings where the use of an infantometer or a stadiometer could be limited because of portability, accessibility, and/or expense issues.
Supplementary Material
Acknowledgments
M.R.F., L.M.H., J.H.H., R.K.D., and S.H. designed the research; M.R.F., Y.Z., L.M.H., J.H.H., R.K.D., K.E.J., L.E.C., J.M.K., L.A., P.V., D.E.H., and N.K. conducted the research; M.R.F., Y.Z., L.M.H., J.H.H., and Y.D. analyzed the data; M.R.F., Y.Z., L.M.H., and J.H.H. wrote the paper; and M.R.F. had primary responsibility for the final content of the manuscript. All authors read and approved the final manuscript.
Footnotes
Abbreviations used: ICC, intraclass correlation coefficient; NHB, nonHispanic black; NHW, nonHispanic white; ULC, ulnar length by caliper; ULG, ulnar length by grid; ULR, ulnar length by ruler.
References
- 1.Walker SP, Grantham-McGregor SM, Himes JH, Powell CA. Relationships between wasting and linear growth in stunted children. Acta Paediatr 1996;85:666–9. [DOI] [PubMed] [Google Scholar]
- 2.Flegal KM, Wei R, Ogden C. Weight-for-stature compared with body mass index-for-age growth charts for the United States from the Centers for Disease Control and Prevention. Am J Clin Nutr 2002;75:761–6. [DOI] [PubMed] [Google Scholar]
- 3.Haycock GB, Schwartz GJ, Wisotsky DH. Geometric method for measuring body surface area: a height-weight formula validated in infants, children, and adults. J Pediatr 1978;93:62–6. [DOI] [PubMed] [Google Scholar]
- 4.Pinkel D. The use of body surface area as a criterion of drug dosage in cancer chemotherapy. Cancer Res 1958;18:853–6. [PubMed] [Google Scholar]
- 5.Rosner B, Prineas RJ, Loggie JM, Daniels SR. Blood pressure nomograms for children and adolescents, by height, sex, and age, in the United States. J Pediatr 1993;123:871–86. [DOI] [PubMed] [Google Scholar]
- 6.Schwartz GJ, Haycock GB, Edelmann CM, Jr, Spitzer A. A simple estimate of glomerular filtration rate in children derived from body length and plasma creatinine. Pediatrics 1976;58:259–63. [PubMed] [Google Scholar]
- 7.Zapletal A, Motoyama EK, Van De Woestijne KP, Hunt VR, Bouhuys A. Maximum expiratory flow-volume curves and airway conductance in children and adolescents. J Appl Physiol 1969;26:308–16. [DOI] [PubMed] [Google Scholar]
- 8.Wang X, Dockery DW, Wypij D, Gold DR, Speizer FE, Ware JH, Ferris BG., Jr Pulmonary function growth velocity in children 6 to 18 years of age. Am Rev Respir Dis 1993;148:1502–8. [DOI] [PubMed] [Google Scholar]
- 9.Eveleth PB, Tanner JM. Worldwide variation in human growth. 2nd ed. Cambridge, United Kingdom: Cambridge University Press; 1990. [Google Scholar]
- 10.Launer LJ, Harris T. Weight, height and body mass index distributions in geographically and ethnically diverse samples of older persons. Ad Hoc Committee on the Statistics of Anthropometry and Aging. Age Ageing 1996;25:300–6. [DOI] [PubMed] [Google Scholar]
- 11.Strandberg TE. Inverse relation between height and cardiovascular mortality in men during 30-year follow-up. Am J Cardiol 1997;80:349–50. [DOI] [PubMed] [Google Scholar]
- 12.Hart CL, Hole DJ, Smith GD. Risk factors and 20-year stroke mortality in men and women in the Renfrew/Paisley study in Scotland. Stroke 1999;30:1999–2007. [DOI] [PubMed] [Google Scholar]
- 13.Whitley E, Martin RM, Smith GD, Holly JM, Gunnell D. Childhood stature and adult cancer risk: the Boyd Orr cohort. Cancer Causes Control 2009;20:243–51. [DOI] [PubMed] [Google Scholar]
- 14.Dahl M, Thommessen M, Rasmussen M, Selberg T. Feeding and nutritional characteristics in children with moderate or severe cerebral palsy. Acta Paediatr 1996;85:697–701. [DOI] [PubMed] [Google Scholar]
- 15.Spender QW, Cronk CE, Charney EB, Stallings VA. Assessment of linear growth of children with cerebral palsy: use of alternative measures to height or length. Dev Med Child Neurol 1989;31:206–14. [DOI] [PubMed] [Google Scholar]
- 16.Parsons TJ, Power C, Manor O. Fetal and early life growth and body mass index from birth to early adulthood in 1958 British cohort: longitudinal study. BMJ 2001;323:1331–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Harvey NC, Mahon PA, Kim M, Cole ZA, Robinson SM, Javaid K, Inskip HM, Godfrey KM, Dennison EM, Cooper C. Intrauterine growth and postnatal skeletal development: findings from the Southampton Women's Survey. Paediatr Perinat Epidemiol 2012;26:34–44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.de Lucia E, Lemma F, Tesfaye F, Demisse T, Ismail S. The use of armspan measurement to assess the nutritional status of adults in four Ethiopian ethnic groups. Eur J Clin Nutr 2002;56:91–5. [DOI] [PubMed] [Google Scholar]
- 19.Zverev Y, Chisi J. Estimating height from arm span measurement in Malawian children. Coll Antropol 2005;29:469–73. [PubMed] [Google Scholar]
- 20.Torres LA, Martinez FE, Manco JC. Correlation between standing height, sitting height, and arm span as an index of pulmonary function in 6–10-year-old children. Pediatr Pulmonol 2003;36:202–8. [DOI] [PubMed] [Google Scholar]
- 21.Chumlea WC, Guo SS, Wholihan K, Cockram D, Kuczmarski RJ, Johnson CL. Stature prediction equations for elderly non-Hispanic white, non-Hispanic black, and Mexican-American persons developed from NHANES III data. J Am Diet Assoc 1998;98:137–42. [DOI] [PubMed] [Google Scholar]
- 22.Han TS, Lean ME. Lower leg length as an index of stature in adults. Int J Obes Relat Metab Disord 1996;20:21–7. [PubMed] [Google Scholar]
- 23.Duyar I, Pelin C. Body height estimation based on tibia length in different stature groups. Am J Phys Anthropol 2003;122:23–7. [DOI] [PubMed] [Google Scholar]
- 24.Pelin IC, Duyar I. Estimating stature from tibia length: a comparison of methods. J Forensic Sci 2003;48:708–12. [PubMed] [Google Scholar]
- 25.Lal CS, Lala JK. Estimation of height from tibial and ulnar lengths in North Bihar. J Indian Med Assoc 1972;58:120–1. [PubMed] [Google Scholar]
- 26.Yousafzai AK, Filteau SM, Wirz SL, Cole TJ. Comparison of armspan, arm length and tibia length as predictors of actual height of disabled and nondisabled children in Dharavi, Mumbai, India. Eur J Clin Nutr 2003;57:1230–4. [DOI] [PubMed] [Google Scholar]
- 27.Hogan SE. Knee height as a predictor of recumbent length for individuals with mobility-impaired cerebral palsy. J Am Coll Nutr 1999;18:201–5. [DOI] [PubMed] [Google Scholar]
- 28.Hickson M, Frost G. A comparison of three methods for estimating height in the acutely ill elderly population. J Hum Nutr Diet 2003;16:13–20. [DOI] [PubMed] [Google Scholar]
- 29.Valk IM. Accurate measurement of the length of the ulna and its application in growth measurement. Growth 1971;35:297–310. [PubMed] [Google Scholar]
- 30.Cheng JC, Leung SS, Chiu BS, Tse PW, Lee CW, Chan AK, Xia G, Leung AK, Xu YY. Can we predict body height from segmental bone length measurements? A study of 3,647 children. J Pediatr Orthop 1998;18:387–93. [PubMed] [Google Scholar]
- 31.Gauld LM, Kappers J, Carlin JB, Robertson CF. Height prediction from ulna length. Dev Med Child Neurol 2004;46:475–80. [DOI] [PubMed] [Google Scholar]
- 32.Zhu Y, Hernandez LM, Mueller P, Dong Y, Forman MR. Data acquisition and preprocessing in studies on humans: what is not taught in statistics classes? Am Stat 2013;67:235–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Lohman TG, Roche AF, Martorell R. Anthropometric standardization reference manual. Champaign, IL: Human Kinetic Books; 1988. [Google Scholar]
- 34.Livshits G, Peter I, Vainder M, Hauspie R. Genetic analysis of growth curve parameters of body weight, height and head circumference. Ann Hum Biol 2000;27:299–312. [DOI] [PubMed] [Google Scholar]
- 35.Nakagawa S, Schielzeth H. A general and simple method for obtaining R2 from generalized linear mixed-effects models. Methods in Ecology and Evolution. 2013;4:133–42. [Google Scholar]
- 36.Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986;1:307–10. [PubMed] [Google Scholar]
- 37.Jung E, Czajka-Narins D. Comparison of growth of black and white infants during their first two years of life. J Natl Med Assoc 1986;78:1157–60. [PMC free article] [PubMed] [Google Scholar]
- 38.Komlos J, Breitfelder A. Differences in the physical growth of US-born black and white children and adolescents ages 2–19, born 1942–2002. Ann Hum Biol 2008;35:11–21. [DOI] [PubMed] [Google Scholar]
- 39.Deurenberg P, Bhaskaran K, Lian PL. Singaporean Chinese adolescents have more subcutaneous adipose tissue than Dutch Caucasians of the same age and body mass index. Asia Pac J Clin Nutr 2003;12:261–5. [PubMed] [Google Scholar]
- 40.Nyati LH, Norris SA, Cameron N, Pettifor JM. Effect of ethnicity and sex on the growth of the axial and appendicular skeleton of children living in a developing country. Am J Phys Anthropol 2006;130:135–41. [DOI] [PubMed] [Google Scholar]
- 41.Klipstein-Grobusch K, Georg T, Boeing H. Interviewer variability in anthropometric measurements and estimates of body composition. Int J Epidemiol 1997;26(Suppl 1):S174–80. [DOI] [PubMed] [Google Scholar]
- 42.Ulijaszek SJ, Kerr DA. Anthropometric measurement error and the assessment of nutritional status. Br J Nutr 1999;82:165–77. [DOI] [PubMed] [Google Scholar]
- 43.Miller F, Koreska J. Height measurement of patients with neuromuscular disease and contractures. Dev Med Child Neurol 1992;34:55–60. [DOI] [PubMed] [Google Scholar]
- 44.Snyder RG, Spencen ML, Owings CL, Schneider LW. Anthropometry of U.S. infants and children. Automotive Engineering Congress and Exposition; 1975 Feb 24–28; Detroit, MI. Warrendale, PA: Society of Automotive Engineers; 1975. [Google Scholar]
- 45.Cheng JC, Leung SS, Lau J. Anthropometric measurements and body proportions among Chinese children. Clin Orthop Relat Res 1996;22–30. [DOI] [PubMed] [Google Scholar]
- 46.Agnihotri AK, Kachhwaha S, Jowaheer V, Singh AP. Estimating stature from percutaneous length of tibia and ulna in Indo-Mauritian population. Forensic Sci Int 2009;187:e1–3. [DOI] [PubMed] [Google Scholar]
- 47.Tompsett J, Yousafzai AK, Filteau SM. The nutritional status of disabled children in Nigeria: a cross-sectional survey. Eur J Clin Nutr 1999;53:915–9. [DOI] [PubMed] [Google Scholar]
- 48.Socrates C, Grantham-McGregor SM, Harknett SG, Seal AJ. Poor nutrition is a serious problem in children with cerebral palsy in Palawan, the Philippines. Int J Rehabil Res 2000;23:177–84. [DOI] [PubMed] [Google Scholar]
- 49.Beghetto MG, Fink J, Luft VC, de Mello ED. Estimates of body height in adult inpatients. Clin Nutr 2006;25:438–43. [DOI] [PubMed] [Google Scholar]
- 50.Madden AM, Tsikoura T, Stott DJ. The estimation of body height from ulna length in healthy adults from different ethnic groups. J Hum Nutr Diet 2012;25:121–8. [DOI] [PubMed] [Google Scholar]
- 51.Kwok T, Lau E, Woo J. The prediction of height by armspan in older Chinese people. Ann Hum Biol 2002;29:649–56. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.