Abstract
Purpose
MRI relaxation measurements are performed in the presence of a fictitious magnetic field in the recently described technique known as RAFF (Relaxation Along a Fictitious Field). This method operates in the 2nd rotating frame (rank n = 2) by utilizing a non-adiabatic sweep of the radiofrequency effective field to generate the fictitious magnetic field. In the present study, the RAFF method is extended for generating MRI contrasts in rotating frames of ranks 1 ≤ n ≤ 5. The developed method is entitled RAFF in rotating frame of rank n (RAFFn).
Methods
RAFFn pulses were designed to generate fictitious fields that allow locking of magnetization in rotating frames of rank n. Contrast generated with RAFFn was studied using Bloch-McConnell formalism together with experiments on human and rat brains.
Results
Tolerance to B0 and B1 inhomogeneities and reduced specific absorption rate with increasing n in RAFFn were demonstrated. Simulations of exchange-induced relaxations revealed enhanced sensitivity of RAFFn to slow exchange. Consistent with such feature, an increased grey/white matter contrast was observed in human and rat brain as n increased.
Conclusion
RAFFn is a robust and safe rotating frame relaxation method to access slow molecular motions in vivo.
Keywords: MRI, contrast, rotating frames, brain, white matter, grey matter
Introduction
The study of slow and ultra-slow motional regimes is an important area of MRI research. Ultra-slow motion has been assessed in single CaF2 crystal by conducting relaxation measurements in the rotating frames of ranks n = 2 and 3 using the application of separate radiofrequency (RF) fields (1). In these experiments, the magic angle was reduced from 54.5° to 39° and a significant reduction of dipolar line broadening occurred when the rank n was increased from 2 to 3. Fictitious magnetic fields were originally detected in NMR experiments on a paramagnetic solid, diphenyl pycril hydrazil, where changes in the longitudinal magnetization Mz were generated by a circularly polarized RF field in the xy plane in the pioneering work of Whitfield and Redfield (2). Fictitious fields which are produced during frequency-modulated (FM) pulses operating in the non-adiabatic regime were later on documented by Bendall and Pegg (3) and by Garwood and DelaBarre (4). Recently, we have shown that FM pulses operating in the non-adiabatic regime in the 1st rotating frame, and thus producing a large fictitious magnetic field in a 2nd rotating frame, can be used for generating novel MRI contrast in living samples (5, 6). This method entitled RAFF (Relaxation Along a Fictitious Field) provides the possibility to generate relaxation dispersion in MRI by altering the amplitude and orientation of the effective field H2(t) in the 2nd rotating frame. A high correlation between the relaxation time constant (TRAFF) and the histologic-derived cell density in a rat glioma gene therapy model was observed (7). Because relaxation occurs in the 2nd rotating frame in this case, the RAFF method is here entitled RAFF2. The relaxation time measured with RAFF2 (TRAFF2) is minimally affected by changes in frequency-offset and B1 inhomogeneity, although more so than adiabatic longitudinal and transverse rotating frame relaxation times, T1ρ and T2ρ respectively (5). An important feature of RAFF2 is that the practical implementation is less restricted by specific absorption rate (SAR) as compared to the continuous wave (CW) spin-lock (SL) relaxation method, T1ρ,CW.
Based on our earlier work with the RAFF2 method, in this paper we embarked on the study of MRI relaxation occurring in higher frames of rank n > 2. The technique developed here is entitled RAFFn. With the goal of characterizing the sensitivity of RAFFn to B0 and B1 inhomogeneities, we conducted phantom experiments and Bloch simulations. To evaluate the sensitivity of RAFFn to different regimes of 1H chemical exchange, we applied theoretical analyses using Bloch-McConnell formalism (6). We then obtained experimental data from the human brain in vivo to evaluate the relative relaxation time difference (RRTD) between grey/white matter (GM/WM) generated with RAFFn. Since RAFFn operates as a rotating frame rotary echo technique which refocuses magnetization (5, 8, 9), we anticipated that, as n increased, RAFFn would become more tolerant of B0 and B1 inhomogeneity and would have improved bandwidth profile. Given the theoretical and experimental evidence provided by the study of Mefed (1), and based on our previous work with RAFF2, we also hypothesized that high rank rotating frame relaxation measurements with RAFFn could probe slow motion and provide flexibility to alter image contrast. In the present study, we exploit these features of RAFFn to enhance GM/WM RRTD in brain MRI. Based on Bloch simulations and phantom studies we show that the bandwidth of RAFFn pulses increases as n increases. Finally, we evaluate SAR as a function of n and present a SAR comparison between conventional T1ρ,CW and RAFF2 techniques. In the following, the theoretical background that leads to the design of the RAFFn pulses will first be provided.
Theory
Rotating frames
Conventionally, precession of the net magnetization (M) around the external static magnetic field B0 is described in a first rotating coordinate system, in which the rotating frame evolves around the laboratory z axis with Larmor precession frequency ω0 = γB0, where γ is the gyromagnetic ratio. For convenience, herein magnetic field vectors are expressed in angular frequency units (i.e., ω0 = γB0z⃗). By convention, the RF field (B1) is applied along the x axis (x′) of the rotating frame and the RF field vector is ω1 = γB1x⃗′. In the case where the RF frequency varies during the pulse, the direction of ω1 remains stationary only when the rotation of the reference frame around the z axis has the same time-dependent angular frequency as the pulse. In this case, a time-dependent field component arises, Δω0(t)z⃗. This frame is defined as the first rotating frame (x′, y′, z′).
For the following description of rotating frames of increasing rank n, we adapt the nomenclature of Deschamps et. al (10), however with different indexes for H and α. Accordingly, in the first rotating frame, the effective field H1 is the vector sum of ω1(t)x⃗′ and Δω(t)z⃗′, with an amplitude in dimensions of angular frequency given by:
| (1) |
and the angle between H1 and z′ given by:
| (2) |
If ω1 and Δω are time invariant and M is initially collinear with H1, then α1 will also be time invariant and M will remain locked along H1. Conversely, if M is initially perpendicular to H1, it will precess in the plane perpendicular to H1.
When performing a frequency sweep, the effective field in the second rotating frame (H2) is the vector sum of D1 (≡H1) and a fictitious field component C1 (≡dα1/dt y⃗′) that results from the sweeping H1. In RAFF2, for example, the amplitude and orientation of H2 can be varied by changing the relationship between the C1 and D1 (6). M closely follows H1(t) when ω1(t) and Δω(t) are time dependent and the rate of change is small,
| (3) |
(i.e., when the adiabatic condition is well satisfied) (4). When the adiabatic condition is violated due to a rapid sweep of H1(t) through the angle α1(t) around y⃗′, a large fictitious field component C1 is generated. Transformation to a new coordinate system, (x″, y″, z″), with y″ = y′, simplifies the analysis since all field components remain stationary in time (Fig. 1). The effective field in this second rotating frame H2 is the vector sum of C1 and D1, with the amplitude given by:
| (4) |
and the angle between H2 and z″ defined as:
| (5) |
Fig 1.
Rotating frames of rank n = 1 to 5 used to describe RAFFn. The 1st-frame (n=1) describes conventional off-resonance spin lock T1ρ experiment. The 1st-frame rotates around laboratory z-axis at the angular velocity the RF field (ωRF), and therefore the RF field vector (ω1, in rad/s) is stationary in this frame. A frequency offset (i.e., a finite difference between ωRF and the Larmor frequency ω0) is equivalent to having a field component along the z′-axis equal to this frequency difference, Δω. The resulting effective field H1 is the vector sum of ω1x⃗′ and the fictitious component Δωz⃗′, and the orientation between H1 and the z′-axis is described by an angle α1 which is time invariant. To create the 2nd-frame, α1 is allowed to be linearly time-dependent. As the consequence of the time-dependence of α1, the first rotating frame undergoes rotation around the y′-axis leading to the 2nd-frame (n=2). In the 2nd-frame (denoted by double-primed axis labels), the new effective field H2 is the vector sum of two stationary field components: one of these components D1 is same as effective field in the 1st-frame (i.e., D1 = H1). The other component C1 is the fictitious component that arises from the time-dependence of α1 in the 1st-frame and thus has amplitude equal to dα1/dt along the y″ axis. This transformation can be continued to create rotating frames and RAFFn pulses of higher ranks. The 3rd, 4th, and 5th rotating frames correspond to ranks n = 3, 4, and 5, respectively.
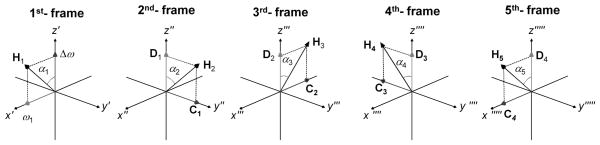
Note, the nomenclature in this work has been changed from our previous publications (5–7). Now α corresponds to α1, ε corresponds to α2, Beff corresponds to H1, and E corresponds to H2. Transformation to the next coordinate system of higher rank is performed around x″, and then the subsequent transformation takes place around y‴, and so forth (Fig. 1). The effective field amplitude in the nth rotating frame is determined by the equation:
| (6) |
and the angle between Hn and z⃗n is given by:
| (7) |
The modulation functions
To obtain time-invariant and equal amplitudes of the first frame field components, we define:
| (8) |
where is the peak RF amplitude in rad s−1. In the absence of frequency modulation, these field components create the effective field (in rotating frame of rank n = 1) in the classical T1ρ,CW experiment. To generate a fictitious field in rotating frames of rank n > 1 using frequency modulation, the recursive equations used are:
| (9) |
for n = 2, 4, 6, … and
| (10) |
for n = 3, 5, 7, … Equations (9,10) lead to the waveforms in which the final effective field Hn remains time invariant in the nth rotating frame (Fig. 1) (see Appendix for proof). In this work the amplitude of Hn is specifically chosen to be the same value for all RAFFn with n=1 to 5, which results in a decrease in the amplitude of ω1(t) as n increases (Fig. 2). The recursive nature of RAFFn pulses is illustrated in Fig. 3 where the components of the RAFF5 pulse are displayed in consecutive frames. RAFF5 generates a time invariant effective field in the 5th rotating frame, with field components of equal amplitude. The locking property of the RAFFn pulse in the 5th frame can be verified using Bloch simulations following previously described formalism in (5).
Fig. 2.
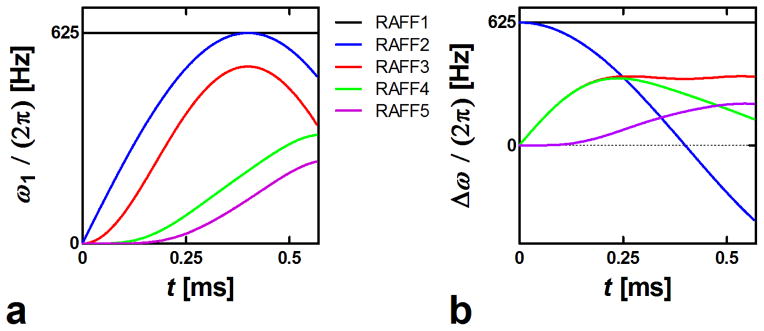
First P segment of the different RAFF1-5. (a) Amplitude modulation function, ω1(t); (b) Frequency-offset modulation function, Δω(t).
Fig. 3.
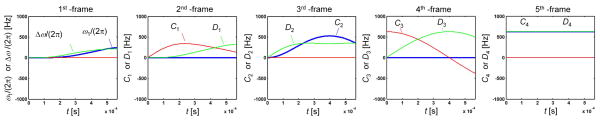
Field components of RAFF5 in different rotating frames. In the 1st-frame, relatively small amplitude ω1 and Δω components are applied. The amplitude of the field components for RAFF5 are calculated iteratively using Eqs. 8–10. When comparing the field components of RAFF5 in different rotating frames, it can be noticed that RAFF4 amplitude and frequency modulations can be found in the 2nd -frame, RAFF3 in 3rd -frame, RAFF2 in 4th –frame, and finally RAFF1 in 5th – frame suggesting stationary C4 and D4 in the 5th frame.
Methods
RAFFn pulses
With the definitions given in Equations (8–10), the amplitude of Hn remains constant for RAFFn pulses. All measurements used and pulse duration , as in previous works (5, 6). To create rotary echoes, four pulse elements were assembled into a P-packet according to the scheme PP−1PπPπ−1, as was previously used in adiabatic BIR4 and RAFF2 pulses (5, 11). The signal intensity decay was measured by incrementing pulse trains of P-packets of total duration between 0 and 144 ms and the experiments were repeated with an inversion pulse to account for the steady state, as described previously (5).
Simulations of exchange
To investigate the exchange-induced relaxation during RAFFn pulses, we carried out Bloch-McConnell simulations (6). The simulations were performed for two-site anisochronous exchange (2SX) between sites a and b using relationships: ka/pb = kb/pa, where pa and pb are the normalized equilibrium populations (pa + pb = 1.0) and ka and kb (kex = ka + kb) are the direct and backwards exchange rate constants, respectively. The calculations were performed as a function of chemical-shift difference δω using exchange rate constant kex equal to either 100 Hz or 10000 Hz, pa =0.9, and 0–64 PP−1PπPπ−1-packets.
Human in vivo experiments
Five healthy volunteers were scanned using a 4-T magnet (OMT, Inc., Oxon, UK) interfaced to an Agilent DirectDrive console (Agilent, Santa Clara, CA, United States). The subjects were scanned after obtaining informed consent. A volume coil was used for RF transmission and reception (12). The fast spin echo sequence was used as an imaging readout (TR=5 s, effective TE=74 ms s, echo train length =16, in-plane resolution 1×1 mm2 and slice thickness 4 mm). Human experiments were performed according to procedures approved by the Institutional Review Board of the University of the Minnesota Medical School.
Rat ex vivo experiments
Five female Wistar rats (weight 226 ± 6 g, age 93 ± 2 days, n=5) were euthanized using CO2 followed by a transcardial perfusion with 0.9% sodium chloride for 10 min (30 mL/min), and by 4% paraformaldehyde in 0.1 M phosphate buffer, pH 7.4, for 10 min (30 mL/min). Fixed brains were removed from the skull, rinsed in phosphate-buffered saline, and cryoprotected (24 h in 20% glycerol and 0.02 M potassium phosphate-buffered saline). For ex vivo MRI measurements, the brains were carefully wiped with tissue paper, and immersed in Galden. The brains were fastened in glass tubes with minimal effects to morphology, maintaining their position during overnight measurement. MRI measurements were carried out using a 9.4-T magnet (Oxford instruments) equipped with Agilent console (Agilent Corp., Palo Alto, CA, USA). A quadrature volume coil with an inner diameter of 19 mm (Rapid Biomed, Rimpar, Germany) was used as transceiver. The imaging slice was selected with extra care from fast spin echo images with slice thickness of 0.35 mm. The final slice thickness for relaxation measurements was 0.7 mm with 256×256 matrix size in 15 × 15 mm2 FOV (effective TE/TR 7/5000 ms). RAFFn pulse trains of 0–144 ms length were used to obtain RAFF weighting with and without adiabatic inversion pulse (hyperbolic secant (HS), Tp = 6 ms, ).
Rat in vivo experiments
For in vivo experiments, male Wistar rats (weight 311–356 g, age 86 days, n = 3) were anesthetized with 4% isoflurane (Baxter Oy, Helsinki, Finland), and during the imaging anesthesia was maintained at 1.4% isoflurane in NO2/O2 (75:25). Rat core temperatures were maintained close to 37°C using a water-heated pad. All rat measurements were carried out using same equipment and imaging parameters as for ex vivo measurements. Studies were performed according to the guidelines approved by the University’s Institutional Animal Care and Use Committee and Provincial government.
Data analysis
All relaxation time constant maps and B1 maps were calculated on a pixel-by-pixel basis using the Aedes software package (http://aedes.uef.fi/) on a Matlab platform (Mathworks, Natick, CA). Regions of interest were hand drawn based on T2 weighted images. Steady state formation was taken into account in RAFFn fitting as described previously (5). The relaxation time difference between GM and WM was calculated based on relaxation times by: RRTD = (T(GM)−T(WM))/T(WM) × 100%. The average RF power of RAFFn delivered to the coil was estimated by integration of the square of preparation RF pulses ∫B1(t)2 dt without taking into account the readout portion of the sequence. In calculation, pulse trains (0, 36, 72, 108 and 144 ms) were separately integrated and power distributed over TR = 5 s. The final SAR was obtained as an average of SARs calculated from each pulse train. For the calculations we used the maximum output power of our amplifier at 4T, which was ~ 3.3 kW. The 4T scanner is equipped with a SAR monitoring system and subject safety was ensured by keeping SAR well below the U.S. Food and Drug Administration limitations.
Results
One advantage of RAFFn (n > 2) as compared to RAFF2 is an increase of the bandwidth of the pulses when n increases, as demonstrated by Bloch simulations and in experiments (Fig. 4ab). Increased bandwidth originates from differences in magnetization paths during P segments of RAFFn (Fig. 4c). With RAFF1 (i.e., T1ρ,CW experiment) and RAFF2, magnetization is tipped 90° from z′ axis to the x′ y′ plane, with time averaged angles of 54° and 38°, respectively, while the tip angle produced by RAFF3-5 gradually decreases with the increase of n and approaches a time-averaged angle of ~3.6° for RAFF5 (Tab. 1). The decrease of tip angle with the increase of n is due to lower RF power delivered to the sample, resulting in a significantly decreased SAR (Tab. 1). The increase in bandwidth with n originates from the lower tip angle and an efficient refocusing of magnetization upon utilization of the PP−1PπPπ−1 packets.
Fig. 4.
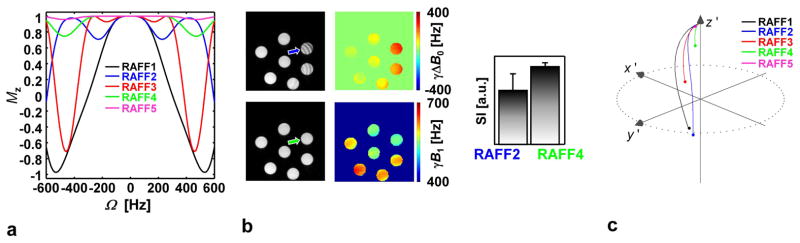
a) Bloch simulations with no relaxations, i.e. T1 = T2 = ∞, demonstrate offset dependence of the RAFFn pulses. The plots show normalized longitudinal magnetization (Mz) as a function of offset frequency (Ω) after one double rotary echo packet, PP−1PπPπ−1, which allows for an efficient refocusing of the off-resonance imperfections. Pulse peak powers were the same as in Fig. 2. The simulations show how the sensitivity to resonance offset decreases with the increase of n, if the limit 0.9·M0 is considered. b) Effect of increased bandwidth in experiments performed on a set of saline containing syringes measured with RAFF2 and RAFF4 pulses (pulse train length 54 ms) together with B0 and B1 field maps. The bar plot demonstrates a comparison of the signal intensities ± std for RAFF2 and RAFF4 from the center of the tube (arrows). In these experiments, the B0 standard deviation was 68 Hz and γ−1B1/(2π) was 581 ± 35 Hz (mean ± std) within the slice. c) Magnetization trajectories during double rotary echo packet of RAFF1-5, showing first portion P of the P-packet in the first rotating frame (n=1).
The enhanced sensitivity of RAFF4 and RAFF5 to slow exchange as compared to RAFF1-3 was demonstrated in simulations of exchange. Plotted in Fig. 5 are the exchange rate constant (Rex) and the Rex ratio for two exchange rates, kex = 100 Hz and kex = 10000 Hz, as a function of δω. The simulations show that Rex decreases with increase of n for both kex values investigated. However, the n dependence is substantially less significant for kex = 100 Hz (i.e., slow rate; Fig. 5a) versus kex = 10000 Hz (i.e., fast rate, Fig. 5b). This difference is easily seen in the relative ratio of the relaxation rates (Fig. 5c). Using product operator simulations of the exchange-induced relaxations during the RAFFn pulses (14), similar results were obtained (data not shown). Although these simulations do not represent a rigorous characterization of RAFFn relaxation in vivo, they could provide a possible mechanism for the increase in tissue contrast observed with increasing n.
Fig. 5.
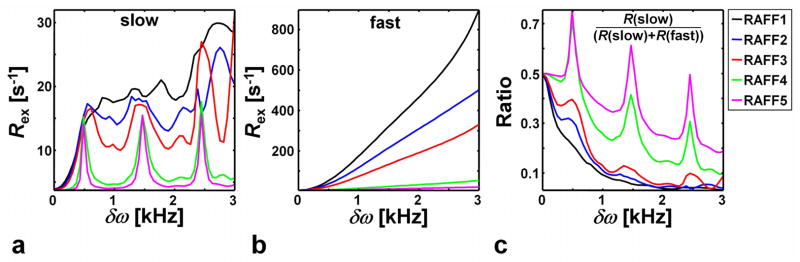
Bloch-McConnell simulations (6) of the chemical exchange-induced relaxation rate constant Rex for RAFF1, RAFF2, RAFF3, RAFF4 and RAFF5 as a function of chemical-shift difference δω for two-site chemical exchange (2SX), using exchange rate constant kex equal to a) 100 Hz and b) 10000 Hz. c) The fraction of slow motion induced relaxation from panel a compared to fast exchange induced relaxation from panel b. The fractional population of sites a and b used in the calculations were pa=0.9 and pb=0.1.
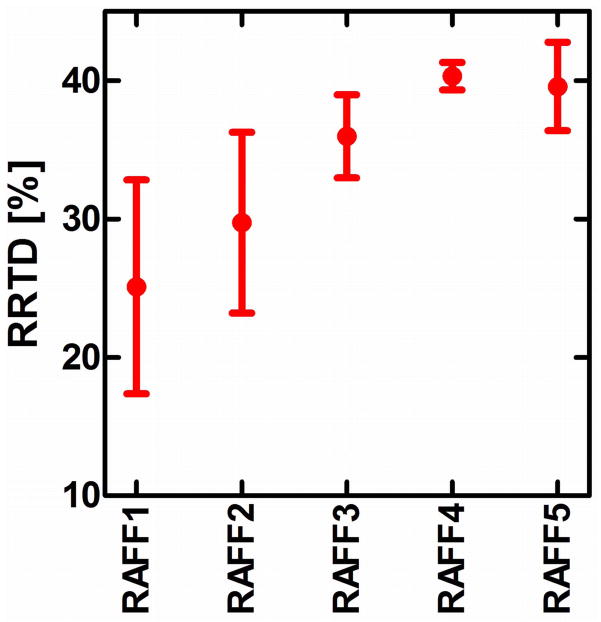
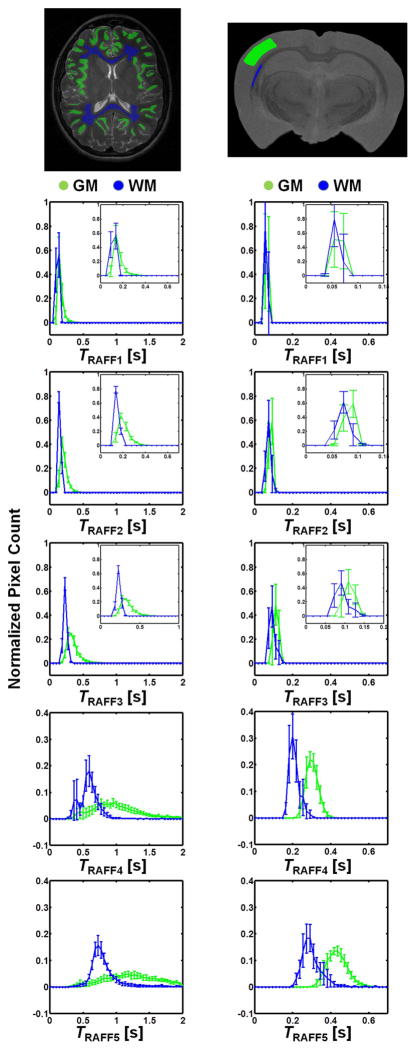
Maps of the relaxation time constants obtained in the human in vivo and rat ex vivo brains with RAFFn revealed an increase in the time constants with increasing n (Fig. 6). The TRAFFn values were longer in the human brains at 4-T than in the rat brains in vivo and ex vivo at 9.4-T. The increase in TRAFFn as a function of n was similar between human and rat measurements (Figs. 6 and 7). In addition, an increase between GM/WM RRTD in human brain was observed, reaching a maximal value with RAFF4 (Fig. 8). The relaxograms shown in Fig. 9 demonstrate that in GM TRAFF4 and TRAFF5 values varied more than in WM. The TRAFFn values in GM of rats have narrower peaks as compared with GM in the human brain (Fig. 9). Finally, the RAFFn experiments were repeated with varying pulse power (±3 dB). The relative relaxation time difference (TRAFFn (±3dB)/TRAFFn) from WM and GM decreased by 10–15% from RAFF1 to RAFF5, although the decrease was not monotonic.
Fig. 6.
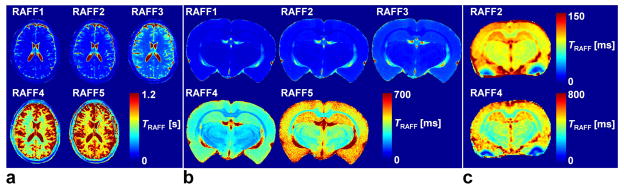
Representative relaxation time constant’s maps TRAFFn generated from human and rat brains using RAFFn technique. The maps depict a) normal human brain, b) ex vivo rat brain, and c) in vivo rat brain. Measurements were performed at 4-T human and 9.4-T animal systems.
Fig. 7.
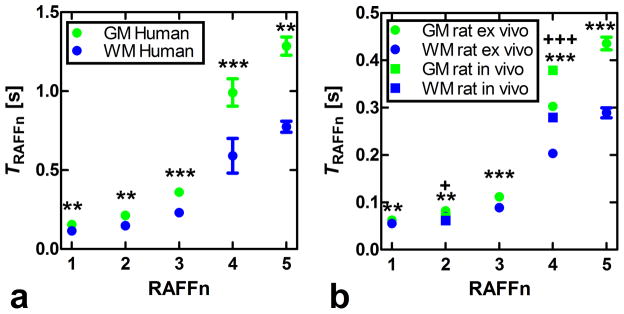
Plots of relaxation time constants TRAFFn as a function of n. Data were obtained from a) the healthy human brains and b) ex vivo and in vivo rat brains. Values are mean ± SEM [s]. Statistical analyses using a Student’s t-test were performed for differentiating grey matter (GM) from white matter (WM). For human brain and ex vivo rat brain measurements the ** p<0.01 and *** p<0.001, respectively, were obtained; for in vivo rat brain: + p<0.05 and +++ p<0.001).
Fig. 8.
RRTD = (T(GM)−T(WM))/T(WM) × 100% obtained from relaxation time maps in the human brain at 4T. Here T (mean ± std) is the relaxation time constant.
Fig. 9.
Relaxograms of TRAFFn (mean ± std.) obtained from manually drawn region of interests in GM (green) and WM (blue), measured in a) human brain at 4-T and b) ex vivo rat brain at 9.4-T. The insets in RAFF1-3 show more clearly the difference between WM and GM relaxograms.
Discussion
In this work the concept of iterative transformations of frequency-modulated RF pulses to the rotating frames of rank n is introduced. The particular example of the effective field H5 which is stationary in the rotating frame of rank 5 is described. A similar iterative concept can be used in the general case when Hn is not stationary in the nth rotating frame. However, these situations require separate analytical treatments and are out of the scope of this paper.
The minor differences between rat ex vivo and in vivo relaxation times (Fig. 7) are likely explained by the absence of blood in the ex vivo brain, and by the narrower line width in the ex vivo brain measurement. The lengthening of TRAFFn when n was increased is due to the evolution of M closer to the z axis. Here, we demonstrate an example of the tissue RRTDs generated in the rotating frames of ranks n in the human brain using a 4-T magnet. The pronounced increase of GM/WM RRTD was obtained with the increase of n reaching maximal value with RAFF4 (Fig. 8). Noticeably, because averaged angle between M and z′ decreases with the increase of n, the longitudinal relaxation contribution becomes significant with higher n. The Bloch-McConnell simulations presented in Fig. 5 suggest that slow exchange could be responsible for the increased GM/WM RRTD as detected by RAFF4 and RAFF5. The relaxograms of TRAFFn from human brain show greater variation than in rat brain, especially in GM. In both humans and rats the relaxograms exhibit greater separation between GM and WM with the increase of n (Fig. 9). This demonstrates the utility of RAFFn for generating in vivo contrast using high rotating frames. Although we present here the application of RAFFn to the brain, RAFFn can be also useful for the studying of other in vivo samples.
RAFFn is conceptually different from rotating frame T1ρ and T2ρ techniques and chemical exchange saturation transfer (CEST). With CW-SL and adiabatic T1ρ and T2ρ methods, relaxation is governed by longitudinal or transverse relaxation exclusively. On the other hand, RAFF2 has contributions from both T1ρ and T2ρ relaxations (5), and similarly RAFFn comprises both T1ρ(n) and T2ρ(n) relaxations. Moreover, RAFFn is also conceptually different from CEST since RAFFn is simultaneously sensitive to dipolar interactions, diffusion, and/or exchange which can all contribute in the in vivo case. CEST, on the other hand, directly measures saturation transfer between off-resonance spins and water. It is worth noting that saturation of off-resonance spins might occur also during rotating frame relaxation measurements that employ frequency-modulated pulses (such as RAFFn and in adiabatic T1ρ and T2ρ methods). For adiabatic T1ρ the contribution of the saturation transfer from off-resonance spins within the bandwidth of the adiabatic pulse is minor (up to 10%) (16). However, the contribution of off-resonance saturation to RAFFn relaxation was not quantified in this work and is the subject of future investigation. Yet, it is interesting to note that the RAFFn pulse produces side bands at frequencies defined by the duration of the RAFFn pulses, Tp (Fig. 5). These frequencies are determined by the assembling of the RAFFn pulses into P-packets, which refocuses the magnetization in the form of rotary echoes (4). It is possible that the side bands of the RAFFn pulses selectively saturate multiple exchanging sites (e.g., functional groups or residues) simultaneously.
In the present work, we simulated the RAFFn relaxations only in the presence of anisochronous exchange (Fig. 5), while leaving other relaxation processes (such as dipolar auto- and cross relaxations, or isochronous exchange) for future studies. Therefore, the current simulations are not comprehensive for describing relaxation contrast in tissue. In addition, as for any other relaxation method, the exchange rate that contributes to RAFFn is an “apparent” combination of the various exchange processes that unavoidably occur in vivo. Yet, those simulations demonstrate the sensitivity of RAFFn to slow exchange. In fact, with increase of the rank of the rotating frame the sensitivity of RAFFn to slow exchange increases, which provides a possible reason for the increased GM/WM contrast observed with RAFF4 and 5. Intriguingly, the increased difference in relaxation time constants between GM and WM of RAFF4 and 5 as compared to RAFF1-3 occurs despite a significant reduction in SAR.
For in vivo applications, the frequency-domain profile of the pulse is important because the frequency distribution in the inhomogeneous sample is often broad, especially at high magnetic fields (3-T and above). Broad frequency distribution is often due to magnetic susceptibility variations which increase when B0 field increases. The bandwidth of the RAFF2 pulse is in the range of ±100Hz (5). However, in several applications such as imaging the abdominal region, larger bandwidths are beneficial for compensating for B0 inhomogeneity. With RAFFn, the bandwidth of the pulses significantly increases when n increases, which is in part a consequence of the lower tip angle of RAFF5 as compared to RAFF2. Lower RF power requirements and therefore decreased SAR along with larger bandwidth promise broader applications of RAFFn (n>2) methods as compared to the previously developed RAFF2 and spin lock T1ρ techniques.
In conclusion, a series of high rotating frame MRI RRTDs in the rotating frames of ranks 3–5 were introduced and the MRI RRTDs in brain were characterized. Bloch-McConnell calculations as well as measurements in the human and rat brains reveal sensitivity of RAFF3-5 to slow motion. The highest RRTDs obtained with RAFF4 and 5 and the property of RAFFn as a rotating frame rotary echo technique are advantageous for rotating frame relaxation studies when the linewidth is broad and B0 and B1 inhomogeneities are significant.
Table 1.
Specific absorption rates for RAFFn and continuous wave irradiation in human experiment, and average magnetization flip angles during the pulse for RAFF1-5. Note that RAFF1 equals to continuous wave irradiation with the same amplitude. Average specific absorption rates for pulse lengths of 0, 36, 72, 108 and 144 ms are tabulated.
| RAFFn | SAR [W/kg] | Flip angle |
|---|---|---|
| 1 | 2.8 | 55.1 |
| 2 | 1.7 | 35.8 |
| 3 | 1.0 | 24.1 |
| 4 | 0.2 | 6.8 |
| 5 | 0.1 | 3.6 |
Acknowledgments
Authors thank Ms. Maarit Pulkkinen for technical assistance and following institutions for financial support: Academy of Finland, Sigrid Juselius Foundation, Instrumentarium Science Foundation, and NIH Grants which are P41 RR008079, P41 EB015894, P30 NS057091, R01 NS061866, S10 RR023730, and S10 RR027290.
List of abbreviations
- FT
Fourier transform
- GM
grey matter
- WM
white matter
- HS
hyperbolic secant
- RAFF
Relaxation Along Fictitious Field
- RAFFn
RAFF in nth frame
- RF
radio frequency
- ROI
region of interest
- SAR
specific absorption rate
Appendix
In the first rotating frame, the effective field with amplitude in dimensions of angular frequency is given by:
| (A1) |
and the angle between H1 and z⃗′ is
| (A2) |
For higher ranked rotating frames (for n = 2, 3, …), the effective frequency and the angle between the effective frequency and the fictitious frequency component are given by
| (A3) |
| (A4) |
The RAFFn pulse is given recursively as follows. For n = 1, the pulse components are defined as:
| (A5) |
where ω1 is the pulse amplitude. For n > 1, with even n = 2, 4, …, the recursion relation is
| (A6) |
and for odd n = 3, 5, …, the recursion relation is
| (A7) |
We will show that, if we choose the initial pulse amplitude modulation ω1 and the frequency modulation Δω to be and Δω(n), respectively, the final effective frequency (Hn) is constant in the nth rotating frame. The claim holds for n = 1, and the proof for even n begins with calculation of the effective frequency for n = 2 using Eqs. A3, A5, A6, and A7:
| (A8) |
where we assumed that Δω(n−1) is positive. Similarly, one expands
| (A9) |
Thus
| (A10) |
for some constant m (which is independent of t due to the requirement that α2 (t) is differentiable). Therefore, . For H2 we get
| (A11) |
and the relationship is satisfied
| (A12) |
Therefore, . By continuing this procedure for subsequent k, we can see that, Hk and dαk/dt are either or Δω(n−k) with alternating order, until finally for k = n,
| (A13) |
which are time independent. The proof for odd n = 3, 5, … can be completed in a similar manner.
References
- 1.Mefed A. Nuclear spin-lattice relaxation in the triply rotating frame and ultraslow molecular motions in solids. Appl Magn Reson. 2001;21:127–45. [Google Scholar]
- 2.Whitfield G, Redfield AG. Paramagnetic resonance detection along the polarizing field direction. Phys Rev. 1957;106:918–920. [Google Scholar]
- 3.Bendall MR, Pegg DT. Uniform sample excitation with surface coils for in vivo spectroscopy by adiabatic rapid half passage. J Mag Reson. 1986;67:376–381. [Google Scholar]
- 4.Garwood M, DelaBarre L. The return of the frequency sweep: Designing adiabatic pulses for contemporary NMR. J Magn Reson. 2001;153:155–77. doi: 10.1006/jmre.2001.2340. [DOI] [PubMed] [Google Scholar]
- 5.Liimatainen T, Sorce DJ, Connell R, Garwood M, Michaeli S. MRI contrast from relaxation along a fictitious field (RAFF) Magn Reson Med. 2010;64:983–94. doi: 10.1002/mrm.22372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Liimatainen T, Mangia S, Ling W, Ellermann J, Sorce D, Garwood M, Michaeli S. Relaxation dispersion in MRI induced by fictitious magnetic fields. J Magn Reson. 2011;209:269–76. doi: 10.1016/j.jmr.2011.01.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Liimatainen T, Sierra A, Hanson T, Sorce DJ, Ylä-Herttuala S, Garwood M, Michaeli S, Gröhn O. Glioma cell density in a rat gene therapy model gauged by water relaxation rate along a fictitious magnetic field. Magn Reson Med. 2012;67(1):269–77. doi: 10.1002/mrm.22997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Liimatainen T, Nissi M, Nieminen MT, Michaeli S, Garwood M, Gröhn O. Relaxation along Fictitious Field (RAFF) Contrast in Bovine Articular Cartilage. Proceedings of the 18th Annual Meeting of ISMRM; Stockholm, Sweden. 2010. p. abstract 836. [Google Scholar]
- 9.Solomon I. Rotary spin echoes. Phys Rev Lett. 1959;2:301–5. [Google Scholar]
- 10.Deschamps M, Kervern G, Massiot D, Pintacuda G, Emsley L, Grandinetti PJ. Superadiabaticity in magnetic resonance. J Chem Phys. 2008;129:204110. doi: 10.1063/1.3012356. [DOI] [PubMed] [Google Scholar]
- 11.Garwood M, Nease B, Ke Y, deGraaf R, Merkle H. Simultaneous compensation for B1 inhomogeneity and resonance offsets by a multiple-quantum NMR sequence using adiabatic pulses. J Magn Reson A. 1995;112:272–4. [Google Scholar]
- 12.Vaughan JT, Adriany G, Garwood M, Yacoub E, Duong T, DelaBarre L, Andersen P, Ugurbil K. Detunable transverse electromagnetic (TEM) volume coil for high-field NMR. Magn Reson Med. 2002;47:990–1000. doi: 10.1002/mrm.10141. [DOI] [PubMed] [Google Scholar]
- 13.Närväinen J, Hubbard PL, Kauppinen RA, Morris GA. Z-spectroscopy with alternating-phase irradiation. J Magn Reson. 2010;207:242–50. doi: 10.1016/j.jmr.2010.09.004. [DOI] [PubMed] [Google Scholar]
- 14.Idiyatullin D, Michaeli S, Garwood M. Product operator analysis of the influence of chemical exchange on relaxation rates. J Magn Reson. 2004;171:330–7. doi: 10.1016/j.jmr.2004.09.008. [DOI] [PubMed] [Google Scholar]
- 15.Rooney WD, Johnson G, Li X, Cohen ER, Kim SG, Ugurbil KSSC., Jr Magnetic field and tissue dependencies of human brain longitudinal 1H2O relaxation in vivo. Magn Reson Med. 2007;57:308–18. doi: 10.1002/mrm.21122. [DOI] [PubMed] [Google Scholar]
- 16.Michaeli S, Sorce DJ, Garwood M. T2ρ and T1ρ Adiabatic Relaxations and Contrasts. Curr Anal Chem. 2008;4:8–25. [Google Scholar]