Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Aug 13;4:6054. doi: 10.1038/srep06054

Pressure-Induced Magnetic Crossover Driven by Hydrogen Bonding in CuF2(H2O)2(3-chloropyridine)

Kenneth R O'Neal 1, Tatiana V Brinzari 1,7, Joshua B Wright 1, Chunli Ma 2,3, Santanab Giri 4, John A Schlueter 5,6, Qian Wang 4,8, Puru Jena 4, Zhenxian Liu 2, Janice L Musfeldt 1,a
PMCID: PMC4131223  PMID: 25116701

Abstract

Hydrogen bonding plays a foundational role in the life, earth, and chemical sciences, with its richness and strength depending on the situation. In molecular materials, these interactions determine assembly mechanisms, control superconductivity, and even permit magnetic exchange. In spite of its long-standing importance, exquisite control of hydrogen bonding in molecule-based magnets has only been realized in limited form and remains as one of the major challenges. Here, we report the discovery that pressure can tune the dimensionality of hydrogen bonding networks in CuF2(H2O)2(3-chloropyridine) to induce magnetic switching. Specifically, we reveal how the development of 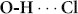Inline graphic exchange pathways under compression combined with an enhanced ab-plane hydrogen bonding network yields a three dimensional superexchange web between copper centers that triggers a reversible magnetic crossover. Similar pressure- and strain-driven crossover mechanisms involving coordinated motion of hydrogen bond networks may play out in other quantum magnets.

The interplay between charge, structure, and magnetism leads to rich phase diagrams and highly tunable properties in multifunctional materials1,2. This is because exotic properties tend to emerge when phases compete. Molecule-based materials are particularly revealing in this regard due to their low energy scales and sensitivity to various external stimuli like temperature, pressure, and magnetic field3,4,5,6,7,8,9,10,11,12. Another characteristic of molecule-based materials is their tendency to develop hydrogen bonding networks13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28. Pressure and strain are especially attractive tuning parameters in this case because they act directly on bond lengths and angles as well as the hydrogen bonding pattern.

While magnetic exchange interactions are traditionally established through direct and superexchange mechanisms between metal centers or metal centers and various ligands29, exchange can also occur through intermolecular hydrogen bonding14,15,16,17,18,19,20,21,22,23,24,25,26,27,28. Physical examples include coordination polymers and low-dimensional systems like Cu(pyz)(NO3)2, Cu(pyz)F2(H2O)2, and CuX2(pyrazine-N,N′-dioxide) (H2O)2 (X = Cl, Br), all of which display transitions that involve hydrogen bonding networks. Changes in bond lengths and angles along the magnetic exchange pathway affect the hopping integrals between magnetic centers, thereby altering the magnetic exchange J29,30. One might suspect that pressure-driven local lattice distortions modify the hydrogen bonds and thus the magnetism, although direct evidence for this mechanism is rare. CuF2(H2O)2(3-chloropyridine) attracted our attention due to its pentacoordinate copper environment, two-dimensional hydrogen bonding network, and pressure-induced magnetic transition that allows us to test this supposition31 (Schlueter, J. A. Unpublished work). This system differs from the prior examples in that the structure is fully molecular rather than being covalently bound (Fig. 1(a)). Moreover, it displays a buckled network of intermolecular hydrogen bonds between the H2O ligands and fluoride centers that act as superexchange linkages between the copper centers within the ab plane. This network facilitates antiferromagnetic ordering below 2.1 K31. There is evidence that the system displays ferromagnetic behavior under pressure (0.8 GPa)(Schlueter, J. A. Unpublished work).

Figure 1.

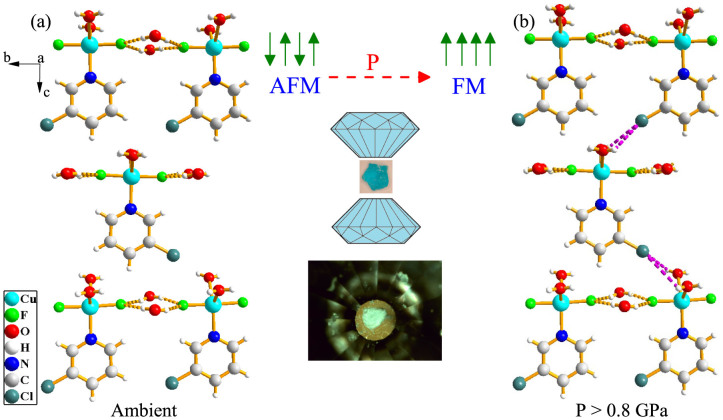
Figure 1

Open in a new tab

(a) Crystal structure of CuF2(H2O)2(3-chloropyridine) at 10 K showing the buckled two-dimensional hydrogen bonded layers31. Parts of neighboring CuF2(H2O)2(3-chloropyridine) molecules have been omitted to emphasize the hydrogen bonding. (b) Schematic rendering of the structure above 0.8 GPa illustrating the three dimensional network that is formed under compression. The connection in the third direction consists of intermolecular 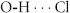Inline graphic hydrogen bonds, as indicated by the purple dashed lines. Also included are drawings of the pressure-induced magnetic crossover and diamond anvil cell as well as a photo of CuF2(H2O)2(3-chloropyridine) on the diamond culet.

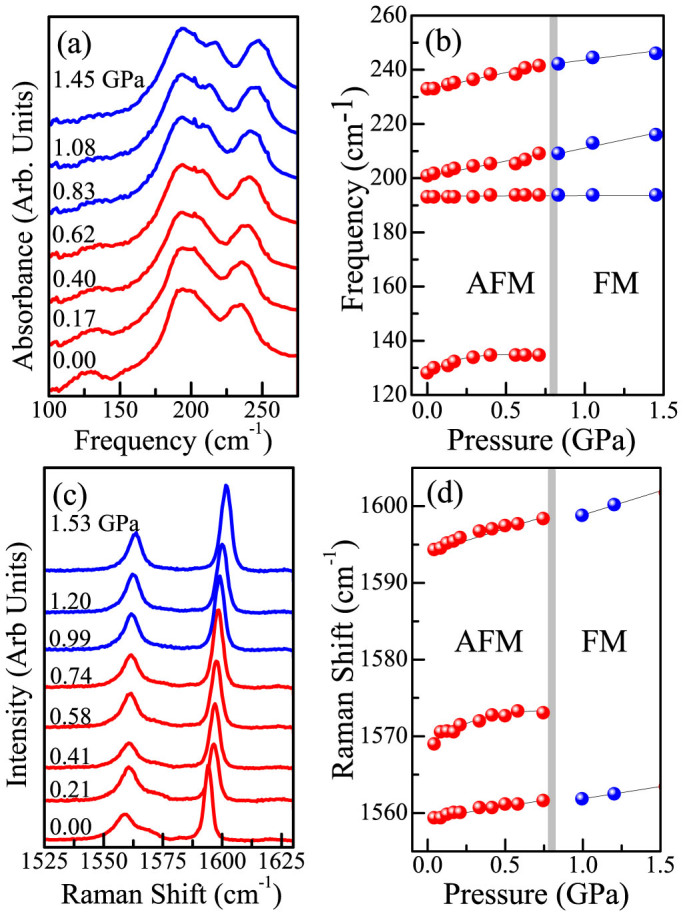
By combining diamond anvil cell techniques, high pressure infrared and Raman spectroscopies, and complimentary calculations of energy, local structure trends, and lattice dynamics, we uncover the ability of hydrogen bond formation to trigger the antiferromagnetic to ferromagnetic crossover in CuF2(H2O)2(3-chloropyridine). Our analysis reveals that compression enhances the in-plane 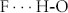Inline graphic exchange and creates new intermolecular hydrogen bonds between chlorine on the pyridine ring and the hydrogen centers on the water ligands. The latter pathway forms because compression reduces interatomic distances, aligns the Cl-containing ring, and widens the H2O ligands, leading to a three dimensional hydrogen bonding network between copper centers. This increased superexchange network dimensionality drives the 0.8 GPa magnetic crossover. This process is reversible, meaning that when pressure is released, the extra exchange pathway is eliminated. We conclude that magnetic tunability in CuF2(H2O)2(3-chloropyridine) derives from and depends upon the presence of flexible intermolecular hydrogen bonding networks. Further compression reveals another distortion between 4 and 5.5 GPa involving the bipyramidal copper environment although, at this time, it is not known whether there is a magnetic component. In addition to establishing how pressure-induced changes in bond lengths and angles control magnetism in hydrogen bonded quantum magnets like CuF2(H2O)2(3-chloropyridine), these findings are important for unraveling spin crossover processes and energy transfer mechanisms in other functional materials like multiferroics.

Results

Figure 2 (a,c) displays close-up views of the infrared and Raman spectra of CuF2(H2O)2(3-chloropyridine) between ambient pressure and 1.5 GPa. Both sets of spectra show signatures of the 0.8 GPa transition. With increasing pressure, the 125 cm−1 infrared active lattice mode diminishes and then disappears. The displacement pattern for this mode is highly collective and involves the F-Cu-F symmetric stretch, the O-Cu-O asymmetric bend, and libration of the 3-chloropyridine ring around the C-Cl bond. Turning to the Raman response, a shoulder around 1575 cm−1, which we assign as a combination of C = C and C-N in-phase, in-plane stretches and C-Cl rocking motion, also diminishes and then disappears. Figure 2 (b,d) shows frequency versus pressure plots for these structures. Their disappearance through the 0.8 GPa transition indicates that the lattice is sensitive to the magnetic crossover, a sign of magnetoelastic coupling32,33,34,35. Note that we employ room temperature, high pressure data to understand the low temperature response because the spectra are nearly insensitive to temperature. Although the magnetic crossover is observed at low temperatures, our variable temperature measurements show minimal spectral changes down to 4 K (see Supplemental Material), even through the orthorhombic (Pmma) to monoclinic (P21/c) transition takes place between 200 and 100 K. This allows the use of room temperature, high pressure data to understand the low temperature magnetic crossover..

Figure 2.

Figure 2

Open in a new tab

(a) Infrared spectra of CuF2(H2O)2(3-chloropyridine) at 300 K and various pressures demonstrating the disappearance of the 125 cm−1 lattice mode through the 0.8 GPa transition. (b) Frequency versus pressure for the infrared active modes in panel (a). (c) Room temperature Raman spectra at the indicated pressures showing the disappearance of a shoulder around 1565 cm−1. (d) Frequency versus pressure for the Raman active modes in panel (c). The vertical grey line marks the critical pressure for the 0.8 GPa magnetic crossover.

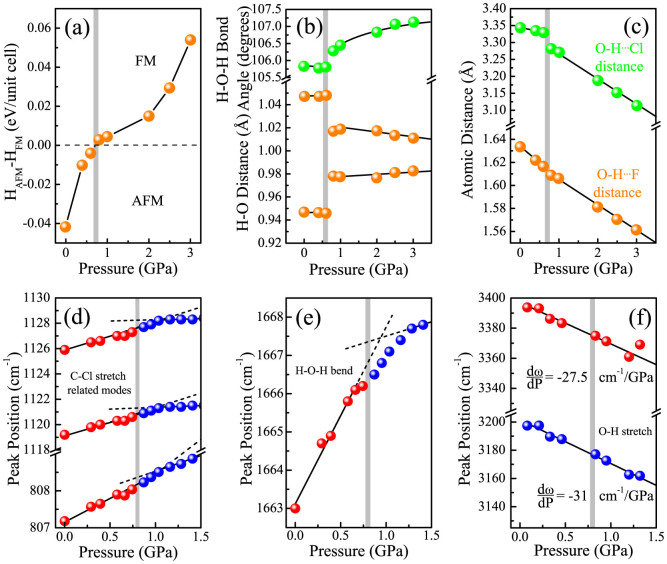
We carried out lattice dynamics calculations in order to assign the vibrational modes of CuF2(H2O)2(3-chloropyridine) and relaxations to model structural changes between the low-pressure antiferromagnetic and high-pressure ferromagnetic states (Fig. 3 (a–c)) (Schlueter, J. A. Unpublished work). Our calculations predict that the ferromagnetic state becomes energetically favorable above 0.75 GPa, in excellent agreement with the 0.8 GPa crossover found experimentally. As anticipated, most interatomic distances decrease under compression. The drastic decrease in the 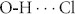Inline graphic distance with pressure is particularly striking. A small discontinuity also appears at the critical pressure. Moreover, one O-H bond length is predicted to increase while the other decreases (such that they become more similar), and the H-O-H bond angle widens dramatically. Taken together, our simulations suggest that changes in the 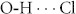Inline graphic distance and shape of the H2O ligands are the most important local lattice distortions through the 0.8 GPa transition.

Figure 3.

Figure 3

Open in a new tab

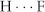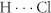(a) Relative enthalpy of the CuF2(H2O)2(3-chloropyridine) unit cell, predicting that the ferromagnetic state becomes energetically favored. (b) Calculated H-O bond distances and H-O-H bond angle and (c) Inline graphic and Inline graphic distances all indicate sharp changes at the critical pressure. The grey lines indicate the transition pressure which is in excellent agreement with the experimental pressure (0.75 vs. 0.8 GPa). (d) Experimental frequency versus pressure at 300 K for three modes involving the C-Cl bond, (e) H-O-H bend, and (f) O-H stretches. All modes involving the C-Cl bond show slight increases in dω/dP around the transition. The H-O-H bend hardens significantly with pressure. The difference in dω/dP (−27.5 ± 2 vs. −31 ± 1 cm−1/GPa) for the two O-H stretches results in increased splitting between the features. Lines are drawn to guide the eye and help visualize different mode behaviors through the transition.

Figure 3 (d–f) displays frequency versus pressure trends for three different vibrational modes: the C-Cl stretches, the H-O-H bend, and the O-H stretches. As our calculations predict, these features are sensitive to the transition. For instance, on approach to the 0.8 GPa transition, the C-Cl stretching modes blue shift with increasing pressure. Above the critical pressure, these same vibrational modes display a much smaller dω/dP, indicating the stabilization of a less compressible phase. At the same time, the H-O-H bend hardens significantly over the entire pressure range, consistent with the prediction of increasing angle36. There is also a notable change in slope through the transition regime. Finally, both O-H stretching features soften under pressure, although at different rates. Softening is characteristic of improved hydrogen bonding interactions15,37, and the divergent rates imply that the two O-H stretching modes in the water ligand are becoming more inequivalent. The latter trend is in apparent contradiction to the aforementioned prediction of one O-H bond lengthening and the other shortening. As discussed below, this observation has its origin in the breakdown of simple frequency-bond length correlations34,38,39.

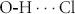Taken together, we find that hydrogen bonds are established between the H2O ligands and the Cl center through the 0.8 GPa magnetic transition (Fig. 1 (b)). The shortened Inline graphic distance falls within the range of a “long” hydrogen bond with chlorine40, which explains the hardening of the C-Cl stretching modes as the motion is dampened by the new interaction and increased stability beyond 1 GPa. This interaction also accounts for the disappearance of the 125 cm−1 infrared mode seen in Figure 2 (a,b) since the Inline graphic hydrogen bonds prevent the 3-chloropyridine ring from librating. Since the chlorine center is closer to one hydrogen than the other, the hydrogen bond forces the H-O-H angle to open, dampening the bending motion. This process hardens the H-O-H bending mode. What is formed in the end is essentially an asymmetric pair of O-H bonds (from the point of view of a single H2O ligand), in excellent agreement with our calculations (Fig. 3). The establishment of new hydrogen bonding also accounts for the prediction of one O-H bond lengthening and the other shortening (Fig. 3(b)). As the hydrogen closer to the chlorine is pulled away from the oxygen center, the bond length of the second O-H linkage ought to be reduced as the electrostatic repulsion is lessened. The intermolecular 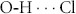Inline graphic hydrogen bond also shifts the electron density of the oxygen towards chlorine, effectively reducing bond order between the oxygen and the hydrogen center that is not interacting with the chlorine. This is evidenced in our spectra by increased splitting between the two O-H stretching modes as pressure is applied (−27.5 ± 2 vs. −31 ± 1 cm−1/GPa).

We propose that intermolecular hydrogen bonding between the water ligand and chlorine acts as an additional superexchange pathway between copper centers along the c axis, adding a third dimension to the hydrogen bonding network in CuF2(H2O)2(3-chloropyridine) above 0.8 GPa (Fig. 1 (b)). Once established, this supplemental linkage, combined with improved in-plane superexchange (due to shorter distances between F centers and 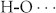Inline graphic), facilitates the pressure-induced antiferromagnetic to ferromagnetic crossover. The newly formed 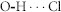Inline graphic hydrogen bond decreases the angle of the 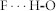Inline graphic exchange pathway, making it even further away from the ideal 180° angle to support ferromagnetism. This means that the new hydrogen bond pathway must be the driving mechanism of the magnetic crossover. Since the 0.8 GPa magnetic crossover is driven by these local lattice distortions, the transition should be considered magnetoelastic rather than purely magnetic41,42,43. Moreover, the crossover is an excellent illustration of how pressure-induced changes in bond lengths and angles modify the transfer integral t which in turn modifies the exchange interaction J12,33. In this case, the mechanism even changes the sign of J.

While the 0.8 GPa magnetic crossover in CuF2(H2O)2(3-chloropyridine) was previously identified (Schlueter, J. A. Unpublished work), there has been no investigation of structure at higher pressures. We extended our work up to 8 GPa and discovered an additional rather sluggish structural transition between 4 and 5.5 GPa. (Fig. 4) The low frequency Raman spectra are the most revealing in this regard. The appearance of five new modes, along with mode splitting at 120 cm−1 and the disappearance of the 85 cm−1 mode, signal the transition. The infrared-active modes show similar behavior in this pressure range (Supplemental Material). While we cannot precisely assign the new modes that appear, our dynamics calculations show that, in general, modes below 500 cm−1 are related to motion around the copper center, and those above 500 cm−1 are related to the 3-chloropyridine ring. Therefore, we conclude that this higher pressure distortion involves mostly the bipyrimidal copper environment, not the 3-chloropyridine ring. The increase in the number of vibrational modes through the transition indicates an overall reduction in symmetry around the copper center. It is clearly a lower symmetry subgroup of Pnma at 300 K and P21/c below the structural phase transition temperature31. X-ray diffraction will be needed to identify the space group of the high pressure phases.

Figure 4.

Figure 4

Open in a new tab

(a) Raman spectra as a function of pressure. The change in line color denotes a new phase (or coexistence of phases). (b) Raman shift versus pressure over the full pressure range investigated. The critical pressures are marked with grey vertical bands. The orthorhombic to high pressure phase I transition is at 0.8 GPa, and the broad transition with the coexistence of high pressure phases I and II is between 4 and 5.5 GPa. Here, Orth is Pmna orthorhombic (although at low temperature, the material is P21/c monoclinic in this regime)31, HP-I is the first high pressure phase, HP-II is the second high pressure phase, AFM is antiferromagnetic, and FM is ferromagnetic. The magnetic phases are present at low temperature.

Discussion

Having established the primary role of pressure-induced local lattice distortions in creating new hydrogen bonding pathways which in turn drive the antiferromagnetic to ferromagnetic crossover in CuF2(H2O)2(3-chloropyridine), we turn our attention toward prospects for control. One of the most important criteria in this regard is reversibility. As revealed by Fig. S4, the process is indeed reversible. Hydrogen bond networks form, diminish, and repeatedly reform under pressure. This implies that magnetism, which is determined by the dimensionality of the hydrogen bonding network that provides for superexchange between copper centers, is equally switchable. Whether this process can be demonstrated in thin film form and under lattice strain is an open question, but similar mechanisms involving coordinated motion of hydrogen bond networks that function as exchange pathways between magnetic centers are likely to play out in other quantum magnets. A secondary criteria is room temperature operation. The 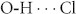Inline graphic connections in CuF2(H2O)2(3-chloropyridine) are robust at 300 K. However, these connections only function as superexchange linkages at low temperature. We therefore anticipate that pressure- or strain-controllable exchange interactions44 can be realized only below the ordering temperature, although short range interactions might increase the operating temperature by a few degrees. Materials like V(TCNE)x·y(CH2Cl2) and (Et4N)0.5Mn1.25[V(CN)5]·2H2O may offer pressure- and/or strain-driven switchability at high temperatures45,46. Spin-crossover materials may be good candidates as well. Finally, this kind of cooperative functionality is not limited to piezomagnetism. Low power piezoelectric devices may also be possible if magnetoelectric coupling can be made strong enough25.

Methods

CuF2(H2O)2(3-chloropyridine) was grown by slowly diffusing a vapor of 3-chloropyridine into an aqueous solution of CuF2(H2O)x as described previously31. Sample quality was confirmed by x-ray diffraction and magnetic susceptibility. A polycrystalline sample was loaded into diamond anvil cells either neat or with a pressure medium (vacuum grease for far and KBr for middle infrared) in order to apply quasi-hydrostatic pressure. The ruby fluorescence technique was used to measure the sample pressure inside the cell47. Raman measurements were performed with a 532 nm diode pumped solid state laser, with power below 1 mW to prevent sample degradation. Raman spectra were taken with a resolution of 0.5 cm−1, integrated between 60 and 120 seconds, and averaged three times. Infrared measurements were taken with a resolution of 1 cm−1 for all spectra. Due to the small sample size and 300 μm diamond culets, the National Synchrotron Light Source at Brookhaven National Laboratory was used for its high brightness infrared light48. Standard peak fitting procedures were employed as appropriate. We also measured the variable temperature infrared response at ambient pressure and found no signatures of the orthorhombic to monoclinic transition between 200 and 100 K (Supplemental Material)31. Thus, we can connect our 300 K, high pressure measurements to the low temperature magnetic crossover. To understand the spectral results as well as the magnetic properties of CuF2(H2O)2(3-chloropyridine), we carried out multi-scale calculations in which both the molecular unit was modeled using molecular orbital theory and the magnetic properties under pressure were calculated via super cell techniques and band structure methods. Using density functional theory with the generalized gradient approximation, we calculated lattice dynamics of a single unit of CuF2(H2O)2(3-chloropyridine) as well as an isolated 3-chloropyridine ring and water molecule to assign the vibrational modes. The relative enthalpy of the antiferromagnetic and ferromagnetic states was calculated at various pressures using spin-polarized density functional theory. See Supplemental Materials for additional details.

Author Contributions

J.L.M. conceived the project, developed the plan, and gathered the team. J.A.S. synthesized the material. K.R.O., T.V.B., J.B.W., C.M., Z.L. and J.L.M. performed the spectroscopic measurements. K.R.O. and J.B.W. analyzed the findings and discussed the data with J.L.M., Z.L., T.V.B., S.G., Q.W. and P.J. The theoretical calculations were performed by S.G., Q.W. and P.J. The paper was written by K.R.O., J.L.M. and P.J. with input from all coauthors.

Supplementary Material

Supplementary Information

Supplemental Material

srep06054-s1.pdf (910.2KB, pdf)

Acknowledgments

Research at the University of Tennessee was supported by the Petroleum Research Fund (52052-ND10) and the National Science Foundation (DMR-1063880). Work at Virginia Commonwealth University, the National Energy Research Scientific Computing Center, the National Synchrotron Light Source at Brookhaven National Laboratory, and Argonne National Laboratory were supported by the U.S. Department of Energy under contracts DE-FG02-96ER45579, DE-AC02-05CH11231, DE-AC02-98CH10886, and DE-AC02-06CH11357 respectively. The use of U2A beamline was supported by COMPRES under NSF Cooperative Agreement EAR 11-57758 and CDAC (DE-FC03-03N00144). JAS acknowledges support from the Independent Research/Development program while serving at the National Science Foundation.

References

  1. Dagotto E. Complexity in Strongly Correlated Electronic Systems. Science 309, 257–262 (2006). [DOI] [PubMed] [Google Scholar]
  2. Kimura T., Lawes G., Goto T., Tokura Y. & Ramirez A. P. Magnetoelectric Phase Diagrams of Orthorhombic RMnO3 (R = Gd, Tb, and Dy). Phys. Rev. B 71, 224425 (2005). [Google Scholar]
  3. Verdaguer M. et al. Molecules to Build Solids: High TC Molecule-Based Magnets by Design and Recent Revival of Cyano Complexes Chemistry. Coord. Chem. Rev. 190–192, 1023–1047 (1999). [Google Scholar]
  4. Sushkov A. B. et al. Magnetic Field Effects on the Far-Infrared Absorption in Mn12-Acetate. Phys. Rev. B 63, 214408 (2001). [Google Scholar]
  5. Liu C. et al. Preparation, Crystal Structure and Magnetic Properties of Ni2(dpa)2(pyz)(H2O)4. Polyhedron 30, 1420–1424 (2011). [Google Scholar]
  6. Zapf V. S. et al. Magnetoelectric Effects in an Organometallic Quantum Magnet. Phys. Rev. B 83, 140150 (2011). [Google Scholar]
  7. Landee C. P. & Turnbull M. M. Recent Developments in Low-Dimensional Copper(II) Molecular Magnets. Eur. J. Inorg. Chem. 13, 2266–2285 (2013). [Google Scholar]
  8. Martínez V. et al. Thermal-, Pressure- and Light-Induced Spin-Crossover Behaviour in the Two-Dimensional Hofmann-Like Coordination Polymer [Fe(3-Clpy)2Pd(CN)4]. Eur. J. Inorg. Chem. 2013, 813–818 (2013). [Google Scholar]
  9. Ghannadzadeh S. et al. Evolution of magnetic interactions in a pressure-induced Jahn-Teller driven magnetic dimensionality switch. Phys. Rev. B. 87, 241102 (2013). [Google Scholar]
  10. Wöhlert S., Jess I. & Näther C. [Co(NCS)2(1,2-bis(2-pyridyl)ethylene)]n: A New 1D Coordination Polymer that Shows a Metamagnetic Transition. Polyhedron 63, 21–27 (2013). [Google Scholar]
  11. Yoneyama S. et al. Large Structural Transformation and Ferromagnetic Ordering in a Coordination Polymer with a Two-Dimensional Square-Planar Lattice, Bis(glycolato)copper(II). Cryst. Eng. Comm. 15, 10193 (2013). [Google Scholar]
  12. Brinzari T. V. et al. Quantum Critical Transition Amplifies Magnetoelastic Coupling in Mn[N(CN)2]2. Phys. Rev. Lett. 110, 237202 (2013). [DOI] [PubMed] [Google Scholar]
  13. Jones B. R. et al. Optical Properties of β″(ET)2SF5RSO3 (R = CH2CF2, CHFCF2, and CHF): Changing Electronic Properties via Chemical Tuning of the Counterion. Chem. Mater 12, 2490–2496 (2000). [Google Scholar]
  14. Woodward F. M. et al. Two-Dimensional Heisenberg Antiferromagnets: Syntheses, X-ray Structures, and Magnetic Behavior of [Cu(pz)2](ClO4)2, [Cu(pz)2](BF4)2, and [Cu(pz)2(NO3)](PF6). Inorg. Chem. 46, 4256–4266 (2007). [DOI] [PubMed] [Google Scholar]
  15. Brown S. et al. Hydrogen Bonding and Multiphonon Structure in Copper Pyrazine Coordination Polymers. Inorg. Chem. 46, 8577–8583 (2007). [DOI] [PubMed] [Google Scholar]
  16. Manson J. L. et al. Experimental and Theoretical Characterization of the Magnetic Properties of CuF2(H2O)2(pyz) (pyz = pyrazine): A Two-Dimensional Quantum Magnet Arising from Supersuperexchange Interactions through Hydrogen Bonded Paths. Chem. Mater. 20, 7408–7416 (2008). [Google Scholar]
  17. Manson J. L. et al. Structural, Electronic, and Magnetic Properties of Quasi-1D Quantum Magnets [Ni(HF2)(pyz)2]X (pyz = pyrazine; X = PF6, SbF6) Exhibiting Ni-FHF-Ni and Ni-pyz-Ni Spin Interactions. Inorg. Chem. 50, 5990–6009 (2011). [DOI] [PubMed] [Google Scholar]
  18. Korabik M. et al. Hydrogen-Bond-Based Magnetic Exchange Between μ-Diethylnicotinamide(aqua)bis(X-salicylato)copper(II) Polymeric Chains. Z. Anorg. Allg. Chem. 637, 224–231 (2011). [Google Scholar]
  19. Halder G. J., Chapman K. W., Schlueter J. A. & Manson J. L. Pressure-Induced Sequential Orbital Reorientation in a Magnetic Framework Material. Angew. Chem. Int. Ed. 50, 419–421 (2011). [DOI] [PubMed] [Google Scholar]
  20. Seber G., Halder G. J., Schlueter J. A. & Lahti P. M. Pressure Effects n the Quasi-1-D Molecular Ferromagnet 2-(4,5,6,7-Tetrafluorobenzimidazol-2-yl)-4,4,5,5,-tetramethyl-4,5-dihydro-1H-imidazole-3-oxide-1-oxyl. Cryst Growth Des. 11, 4261–4266 (2011). [Google Scholar]
  21. Prescimone A. et al. Pressure-Driven Orbital Reorientations and Coordination-Sphere Reconstructions in [CuF2(H2O)2(pyz)]. Angew. Chem. Int. Ed. 51, 7490–7494 (2012). [DOI] [PubMed] [Google Scholar]
  22. Schlueter J. A. et al. Importance of Inline graphic Contacts for the Structural and Magnetic Properties of CuX2(pyrazine-N,N-dioxide)(H2O)2 (X = Cl and Br). Inorg. Chem. 51, 2121–2129 (2012). [DOI] [PubMed] [Google Scholar]
  23. Li S. et al. Pressure-Induced Phase Transitions in Ammonium Squarate: A Supramolecular Structure Based on Hydrogen-Bonding and π-Stacking Interactions. J. Phys. Chem. B 115, 8981–8988 (2012). [DOI] [PubMed] [Google Scholar]
  24. Levchenkov S. I. et al. The magnetic exchange interaction via NH-O-bonding in copper(II) complex with 1-phenyl-3-methyl-4-formylpyrazol-5-one 2-quinolylhydrazone. Inorg. Chim. Acta 405, 169–175 (2013). [Google Scholar]
  25. Horiuchi S., Kumai R. & Tokura Y. High-Temperature and Pressure-Induced Ferroelectricity in Hydrogen-Bonded Supramolecular Crystals of Anilic Acids and 2,3-Di(2-pyridinyl)pyrazine. J. Am. Chem. Soc. 135, 4492–4500 (2013). [DOI] [PubMed] [Google Scholar]
  26. Validov A. A. et al. ESR of Coupled Spin-1/2 Chains in Copper Pyrazine Dinitrate: Unveiling Geometrical Frustration. J. Phys. Condens. Matter 26, 026003 (2014). [DOI] [PubMed] [Google Scholar]
  27. Landee C. P. & Turnbull M. M. Review: A Gentle Introduction to Magnetism: Units, Fields, Theory, and Experiment. J. Coord. Chem. 67, 375–439 (2014). [Google Scholar]
  28. Malrieu J. P., Caballol R., Calzado C. J., de Graaf C. & Guihéry N. Magnetic Interactions in Molecules and Highly Correlated Materials: Physical Content, Analytical Derivation, and Rigorous Extraction of Magnetic Hamiltonians. Chem. Rev. 114, 429–492 (2014). [DOI] [PubMed] [Google Scholar]
  29. Goodenough J. B. Magnetism and the Chemical Bond, Interscience Publishers: New York-London, 1963. [Google Scholar]
  30. Anderson P. W. Theory of Magnetic Exchange Interactions: Exchange in Insulators and Semiconductors. Sol. State Phys. 14, 99–214 (1963). [Google Scholar]
  31. Lapidus S. H. et al. Antiferromagnetic ordering through a hydrogen-bonded network in the molecular solid CuF2(H2O)2(3-chloropyridine). Chem. Comm. 49, 499–501 (2013). [DOI] [PubMed] [Google Scholar]
  32. Popova M. N., Sushkov A. B., Golubchik S. A., Isobe M. & Ueda Y. High-Resolution Infrared Spectroscopy of α′-NaV2O5. Phys. B 284–288, 1617–1618 (2001). [Google Scholar]
  33. Musfeldt J. L. et al. Magnetoelastic Coupling through the Antiferromagnet-to-Ferromagnet Transition of Quasi-Two-Dimensional [Cu(HF2)(pyz)2]BF4 Using Infrared Spectroscopy. Phys. Rev. Lett. 103, 157401 (2009). [DOI] [PubMed] [Google Scholar]
  34. Brinzari T. V. et al. Magnetoelastic Coupling in [Ru2(O2CMe)4]3[Cr(CN)6] Molecule-Based Magnet. Phys. Rev. B 86, 214411 (2012). [Google Scholar]
  35. Krylov A. S., Sofronova S. N., Gudim I. A. & Vtyurin A. N. Magnetoelastic Interactions in Raman Spectra of Ho1−xNdxFe3(BO3)4 Crystals. Solid State Commun. 174, 26–29 (2013). [Google Scholar]
  36. Knittle E., Phillips W. & Williams Q. An Infrared and Raman Spectroscopic Study of Gypsum at High Pressures. Phys. Chem. Miner. 28, 630–640 (2001). [Google Scholar]
  37. Naidu P. R. Infrared Spectroscopic Study of Hydrogen Bonding: Hydrogen Bond Association of Phenols with Dioxan. Aust. J. Chem. 19, 2392–2395 (1966). [Google Scholar]
  38. Hardcastle F. D. & Wachs I. E. Determination of Molybdenum-Oxygen Bond Distances and Bond Orders by Raman Spectroscopy. J. Raman Spec. 21, 683–691 (1990). [Google Scholar]
  39. Cremer D., Wu A., Larsson A. & Kraka E. Some Thoughts about Bond Energies, Bond Lengths, and Force Constants. J. Mol. Model. 6, 396–412 (2000). [Google Scholar]
  40. Aullón G., Bellamy D., Brammer L., Brutonb E. A. & Orpen A. G. Metal-bound chlorine often accepts hydrogen bonds. Chem. Commun. 6, 653–654 (1988). [Google Scholar]
  41. Schrobinger-Papamantellos P., Buschow K. H. J. & Rodríguez-Carvajal J. Magnetoelastic Phase Transitions in the LuFe4Ge2 and YFe4Si2 Compounds: A Neutron Diffraction Study. J. Mag. Mag. Mater. 324, 3709–3715 (2012). [Google Scholar]
  42. Roy S. B. First Order Magneto-Structural Phase Transition and Associated Multi-Functional Properties in Magnetic Solids. J. Phys.: Condens. Matter 25, 183201 (2013). [DOI] [PubMed] [Google Scholar]
  43. Wang J. L. et al. Driving Magnetostructural Transitions in Layered Intermetallic Compounds. Phys. Rev. Lett. 110, 217211 (2013). [DOI] [PubMed] [Google Scholar]
  44. Bousseksou A., Molnár G. & Matouzenko G. Switching of Molecular Spin States in Inorganic Complexes by Temperature, Pressure, Magnetic Field and Light: Towards Molecular Devices. Eur. J. Inorg. Chem. 22, 4353–4369 (2004). [Google Scholar]
  45. Manriquez J. M., Yee G. T., McLean R. S., Epstein A. J. & Miller J. S. A Room Temperature Molecular/Organic-Based Magnet. Science 252, 1415–1417 (1991). [DOI] [PubMed] [Google Scholar]
  46. Entley W. R. & Girolami G. S. High-Temperature Molecular Magnets Based on Cyanobanadate Building Blocks: Spontaneous Magnetization at 230 K. Science 268, 397–400 (1995). [DOI] [PubMed] [Google Scholar]
  47. Mao H. K., Bell P. M., Shaner J. W. & Steinberg D. J. Specific Volume Measurements of Cu, Mo, Pd, and Ag and Calibration of the Ruby R1 Fluorescence Pressure Gauge from 0.06 to 1 Mbar. J. Appl. Phys. 49, 3276–3283 (1976). [Google Scholar]
  48. Carr G. L. et al. High-Power Terahertz Radiation from Relativistic Electrons. Nature 420, 153–156 (2002). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplemental Material

srep06054-s1.pdf (910.2KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES