The desorption of ribonuclease A from charge density gradient surfaces studied by spatially-resolved total internal reflection fluorescence

Abstract

A quaternary amine surface gradient was prepared on fused silica by a three-step surface modification process. The gradient surface displayed a transition of surface charges along the gradient dimension from a net negative surface charge of silica to a net positive surface charge at the quaternary amine end. The gradient surface was characterized by X-ray photoelectron spectroscopy, ellipsometry, colloidal gold decoration, and dynamic contact angle measurements. It displayed an increased adhesion of negatively charged gold particles towards the quaternary amine end. The water contact angles also increased with the increased surface density of aminopropylsilyl groups.

The desorption of ribonuclease A labeled with fluorescein-5-isothiocyanate (FITC–RNase) from the quaternary amine gradient surface was measured using spatially resolved total internal reflection fluorescence (TIRF) spectroscopy. The experimental FITC–RNase desorption results fitted exceptionally well to a two adsorbed protein populations model. A tentative assignment of the two adsorbed protein populations is proposed based on the effect of the ionic strength of the desorbing buffer. The faster desorption population interacted primarily with the quaternary amine gradient surface sites through electrostatic interactions. The slower desorption population interacted with the surface sites via hydrophobic and possibly some electrostatic interactions.

1. Introduction

The interaction of proteins with solid/liquid interfaces can be governed by a combination of hydrophobic and electrostatic effects [1]. Protein separation and purification techniques utilize electrostatic and hydrophobic interactions between the protein and the solid surface to achieve the desired performance [2]. In ion-exchange chromatography, a balance between these two types of interactions controls the selectivity and the resolution of a given chromatographic column [3,4].

An aminated silica surface is a very popular ion-exchange chromatography support for protein separation despite some uncertainties about the nature of the interactions of the amine groups with the silica surface. Chiang et al. [5] used FT-IR spectroscopy to study the structure of aminopropylsilane (APS) on glass surfaces. It was found that the amino groups are hydrogen bonded to the surface. An NMR study of molecular motion of the adsorbed APS on silica showed that the molecular motion of APS at approximately monolayer coverage was slower than the molecular motion of APS below monolayer coverage [6]. Horner et al. [7] concluded from X-ray photoelectron spectroscopy (XPS) of aminopropylsilyl silica (APS silica) that the amino groups are protonated by interaction with silica hydroxyl groups. Moses et al. [8] assigned the two peaks in the XPS nitrogen spectrum of the APS surface (400.3 eV and 401.9 eV) to two components: free and protonated amino groups, respectively. Only a fraction of the free and protonated amines could be interconverted by rinsing the surface with acidic or basic solutions, indicating that some amino groups were irreversibly protonated while others were irreversibly free.

We have previously studied protein adsorption onto the so-called “wettability gradient” surfaces [9–12]. Originally described by Elwing [13], the “wettability gradient” surface is characterized by an increase of the surface density of hydrophobic groups along one of the surface linear dimensions. In this study, we demonstrate how to prepare a surface density gradient of quaternary amine groups on a flat silica surface. Furthermore, we show that this surface can be used to rapidly screen protein–surface interactions. The surface density gradient of quaternary amine groups is prepared in three steps using a two-phase silanization approach [13]. In the third step, methyl iodide was used to modify free surface amino groups into quaternary amines [14,15]. The final result of the three surface modification steps is a negative-to-positive charge change on the silica surface. We call this surface a charge density gradient surface: on one end of the gradient is pure silica with negatively charged silanol groups and on the other end are positively charged quaternary amine groups.

We have tested the protein–surface interactions of the charge density gradient surface using a model protein, ribonuclease A (RNase), labeled with fluorescein-5-isothiocyanate (FITC–RNase). A small globular protein with several intramolecular disulfide bonds like RNase possesses good structural stability and behaves like a “hard” particle at solid/liquid interfaces interacting with surfaces through electrostatic and hydrophobic interactions [16,17]. The separation of RNase from other proteins by ion-exchange chromatography has been reported by a number of groups [18–20]. High-performance ion-exchange chromatography on a tertiary amine agarose column showed excellent resolution in separating RNase from other proteins in the mixture [19]. In this study, the desorption of FITC–RNase from the charge density gradient surface was studied using the spatially resolved total internal reflection fluorescence (TIRF) technique [9]. In order to understand the relative contributions of electrostatic and hydrophobic interactions in RNase desorption, two pH 7.0 phosphate buffers with different ionic strengths (0.0185 M vs. 0.1185 M) were used.

2. Materials and methods

2.1. Preparation and characterization of charge density gradient surface

The first step in the preparation of the charge density gradient silica surface was to prepare a gradient of isocyanatopropyldimethylsilyl groups (IPS gradient) on a flat silica surface and then to convert it into the aminopropyldimethylsilyl–silica (APDMS gradient) by acidic hydrolysis. The IPS gradient was prepared by the two-phase diffusion method [13]. The upper phase was p-xylene (Merck) and the lower phase was a solution of 0.1% (v/v) isocyanatopropyldimethylsilane (Petrarch Systems Inc.) in trichloroethylene (TCE; Merck). After a 90 min diffusion time, the silica plate was rinsed with TCE, ethanol and deionized water and then dried under nitrogen. The APDMS gradient was then prepared from the IPS gradient by hydrolysis at pH 3.8 (pH adjusted by means of HC1) at 50°C for 0.5 h.

The last step was the conversion of the surface amines into the quaternary amines. The APDMS gradient was immersed into the 5% (v/v) solution of methyl iodide in ethanol for 18 h [15]. Inagaki et al. [14] had used a similar method to quaternize amines in plasma-polymerized thin films. The summary of the reactions used for the preparation of the surface charge density gradient is shown in Fig. 1.

Fig. 1.

Schematics of the surface reactions used for the preparation of quaternary amine silica.

The surfaces were characterized by XPS spectroscopy, ellipsometry, contact angle measurement and colloidal gold adsorption. The XPS analysis was performed only on the quaternary end of the charge density gradient surfaces using a Hewlett Packard 5950B XPS spectrometer. The binding energy of nitrogen (N 1s) was used to deduce the relative population of reactive free amines on the APDMS silica surface. The surface density of aminopropyldimethylsilyl groups was determined indirectly using ellipsometry. All ellipsometric measurements were performed in air using the ellipsometer (Rudolf Research AR2000). The non-gradient APDMS surface, used in the ellipsometric measurements, was prepared on a 150 nm thick SiO₂ layer grown on the silicon wafer. Control experiments were performed using the clean Si/SiO₂ surface. Once the refractive index, n, and the thickness, d, of each layer were determined by ellipsometry, the composition of the APDMS surface layer was calculated using the Lorentz–Lorenz equation as described elsewhere [21]. The dynamic advancing and receding water contact angles on the gradient surfaces were measured by the Wilhelmy plate technique as previously described [10].

2.2. Colloidal gold adsorption onto quaternary gradient

The spatial distribution of quaternary amine groups on the gradient surface was analyzed using colloidal gold particle as a probe. These negatively charged particles adhere onto the positively charged surfaces via electrostatic interactions. The colloidal gold particles (Polysciences, Inc.), with an average particle diameter of 20 nm, were stored in a buffer solution (0.01 wt.% of gold particles in potassium carbonate/sodium citrate buffer pH 6.5). Under these conditions the colloidal gold was stable and did not coagulate. The quaternary amine gradient prepared on the Si/SiO₂ surface was incubated in the colloidal gold solution for 1 h. After the incubation, the surface was washed with deionized water to remove any residual buffer which would otherwise evaporate and crystallize in the scanning electron microscope vacuum and thus prevent the observation of adhered particles. Finally the sample was dried in air and imaged by a Hitachi S-450 scanning electron microscope using a magnification of 40000 × and an acceleration voltage of 30 kV. The scanning electron microscopy (SEM) observations were made as a function of distance along the surface gradient. The surface distribution of gold particles in the digitized SEM images was analyzed using image analysis software (Image 1.37, NIH).

2.3. RNase desorption

Ribonuclease A (bovine pancreas) (RNase; Sigma) was labeled with fluorescein-5-isothiocyanate (FITC; Aldrich). The RNase concentration in phosphate buffer was determined using the extinction coefficient: 0.73 mg⁻¹ ml cm⁻¹ at 280 nm [22]. The ratio of the 280 nm/494 adsorption bands of FITC (in solution) was determined to be 0.285. Using the same ratio for the FITC–RNase conjugate, the degree of labeling, FITC/RNase, was calculated to be 0.75. The RNase adsorption was performed using a spatially-resolved TIRF apparatus [9]. A two rectangular flow channels TIRF cell was used so that two parallel experiments could be performed on an identical gradient surface. The FITC–RNase was adsorbed to the surface from the flowing buffer solution (0.01 mg ml⁻¹; flow rate, 1 ml min⁻¹) for 11 min. The desorption segment of the experiment was initiated by replacing the flow of protein solution with the flow of buffer solution through the TIRF cell. An Ar⁺ ion laser (Lexel; Model 92; 10 mW at 488 nm) was used to excite the fluorescence of adsorbed FITC–RNase. Any fluorescence contribution from desorbed FITC–RNase was found to be negligible. The FITC–RNase desorption was studied at the same pH of 7.0 from two phosphate buffers of different ionic strengths: 0.0185 M and 0.1185 M, respectively. The higher ionic strength buffer was prepared by adding 0.1 M NaCl 0.0185 M ionic strength phosphate buffer.

3. Results

3.1. Characterization of the charge density gradient surface

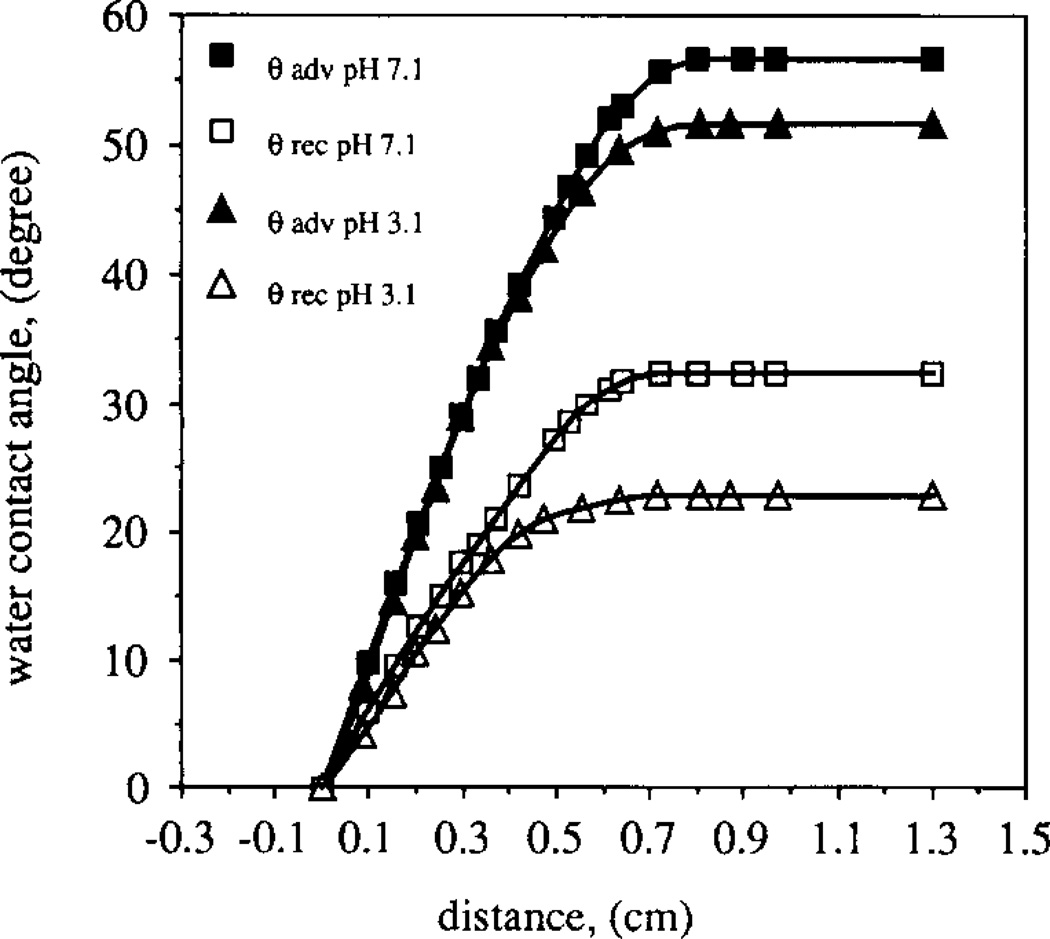
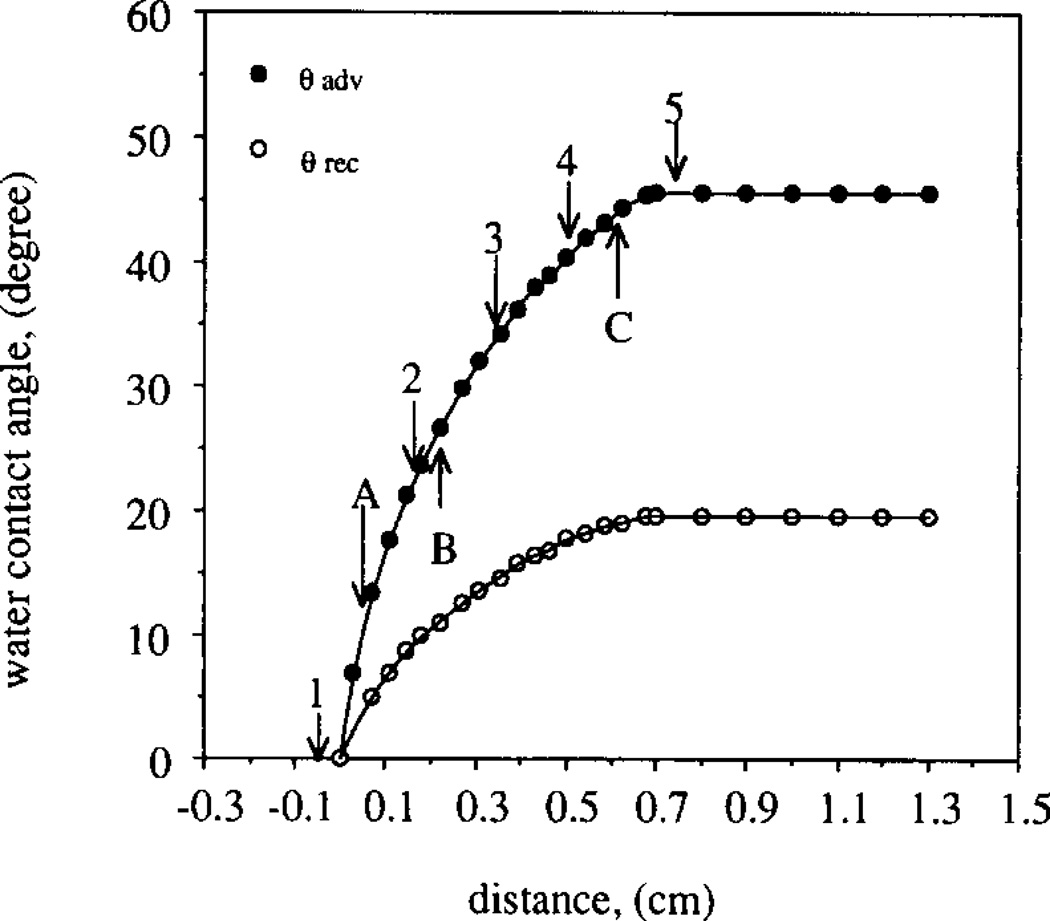
The wettability of a typical APDMS gradient surface, i.e. water contact angles, θ, as a function of position, is shown in Fig. 2. The water contact angles changed with the change in pH of the aqueous solution, indicating that chargeable groups exist along the gradient. After the quaternization step, the wettability of the gradient surface became insensitive to pH changes. Fig. 3 shows the water contact angles of the quaternary amine gradient as a function of gradient position at pH 7.0. The advancing contact angle, θ_adv, of the quaternary amine end of the gradient surface was 45° and the receding contact angle, θ_rec, was 20°. The gradient length was approximately 0.7 cm; the same length as in the case of the APDMS gradient shown in Fig. 2. On the silica end of the gradient surface, the contact angles decreased to zero.

Fig. 2.

Dynamic water contact angles of the APDMS gradient surface shown as a function of gradient position. The silica end of the gradient surface showed θ_adv = 0° and θ_rec = 0°. The gradient region and the amine end of the gradient surface showed that the contact angles depend on pH.

Fig. 3.

Dynamic water contact angles of the quaternary amine gradient surface. Advancing/receding contact angles θ_adv = θ_rec = 0° were recorded on the silica end of the gradient surface. The quaternary amine end of the gradient surface showed θ_adv = 46° and θ_rec = 20°. The angles were not dependent on pH. A, B and C indicate the positions along the gradient at which the adhered colloidal gold particles were imaged by SEM (Fig. 4). 1–5 indicate the positions along the gradient used in the fitting of the experimental results to the two adsorbed protein populations model (Eq. (4)).

The surface density of the aminopropyldimethylsilyl (APDMS) groups was calculated from the ellipsometric measurements using the Lorentz–Lorenz equation [21]. It was found that on average 1.4 APDMS groups exist on an area of 1 nm². Based on the geometric packing argument this density of APDMS groups translates into approximately half-monolayer coverage.

XPS analysis of the binding energy of the N 1s doublet peak of the uniform, non-gradient APDMS silica before and after quaternization was used to determine which fraction of amines was converted into the quaternary amines. The XPS N 1s results are listed in Table 1. The lower energy XPS peak of the N 1s doublet is often interpreted as originating from free amines and the higher energy XPS peak is thought to be due to protonated and hydrogen bonded amines [23]. However, according to Moses et al. [8], the amine groups on the silica surface exist in three forms:

1. free amines that resist protonation in acid (designated N);

2. amines that resist deprotonation (designated NH);

3. reversibly protonated amines (designated N/NH).

Table 1.

The relative area of two deconvoluted XPS peaks in the N 1s spectra

System		Higher binding energy N 1s peak		Lower binding energy N 1s peak
		Area (%)	Max. energy (eV)	Area (%)	Max. energy (eV)
(a)	APDMS; pH 3	45	400.5	55	398.5
(b)	APDMS; pH 7	35	400.8	65	398.7
(c)a	PEG5000 + APDMS; pH 7.0	28	400.8	72	399.3
(d)a	PEG2000 + APDMS; pH 7.0	25	400.8	75	399.3
(e)	Quaternary amine; pH 3	45	400.7	55	398.7
(f)	Quaternary amine; ethanol	45	400.6	55	398.5

^aTaken from Ref. [24].

While the N form contributes only to the lower energy XPS peak and the NH form contributes only to the higher energy XPS peak, the N/NH form of the amines will contribute to both depending on the acidity of the environment. Both the N and the NH forms of the amines can participate in hydrogen bonding. The test for the presence of the free base amines is to compare the XPS spectrum of N 1s before and after incubation in acid, since only the N/NH form will become protonated under acidic conditions. In the case of the APDMS surface (before quaternization), there was a 10% change in the higher and lower binding energy peak area after exposure of the surface to acidic conditions, suggesting that only a small fraction (0.1) of all surface amines was in the N/NH form (Table 1, systems (a) and (b)). Furthermore, after the reaction of the APDMS sample with aldehyde-terminated poly(ethyleneglycol) (PEG2000), the difference in peak area increased further by an additional 8–10% (Table 1, systems (c) and (d)) [24]. After the quaternization of the APDMS surface no change in the peak area was recorded, indicating that on this modified surface there were no more amines in the N/NH form that could be protonated (Table 1, systems (e) and (f)). From the difference between the peak areas one finds that only a small fraction of total surface amines (between 0.1 and 0.2) was quaternized.

The letters A, B, C in Fig. 3 indicate three positions along the quaternary amine gradient surface at which the adhered colloidal gold particles were imaged by SEM. Figs. 4a–4c show the respective scanning electron micrographs. Fig. 4b displays some gold particle dimers and a few smaller aggregates. Fig. 4c shows some gold particles in the form of aggregates implying that the distribution of the surface amines is not entirely random: the size of the aggregates ranged from 20 nm (single particle) to several hundreds of nanometers, but was seldom over 300 nm. The surface coverage of the adhered gold particles in Figs. 4a–4c was 1.5%, 15.3% and 46.2%, respectively. The respective advancing contact angles were 10°, 26° and 44°.

Fig. 4.

SEM image of colloidal gold particles adhered at three different positions along the quaternary amine gradient surface. The advancing contact angles at these three positions were (a) θ_adv = 10°; (b) θ_adv = 26°; (c) θ_adv = 44°, respectively.

The contact angle of a hypothetical surface fully covered with quaternary amines, θ_quat.amine, can be calculated by using the Cassie equation [25]

$$\text{cos }{\theta }_{\text{exp}}=f\text{ cos }{\theta }_{\text{quat}.\text{amine}}+(1-f)\text{ cos }{\theta }_{\text{silica}}$$ (1)

where f is the fraction of surface covered by quaternary amines, (1 − f) is the fraction of silica surface, θ_exp is the experimentally observed advancing water contact angle and θ_silica, is the contact angle of the clean silica surface (θ_silica = 0).

By assuming that the surface coverage of gold particles in Figs. 4b–4c is identical to the fraction of surface covered by quaternary amines, f, the value of θ_quat.amine is estimated as 68.5 ± 1.5°. While the absolute value of θ_quat.amine could not be confirmed by another method, a very small deviation (± 1.5°) indicated that colloidal gold decoration is a suitable method for the visualization of the spatial distribution of positively charged surface groups at intermediate surface coverages.

3.2. Desorption kinetics of ribonuclease A from the charge density gradient surface

The desorption kinetics of FITC–RNase have been analyzed for the five positions along the charge density gradient. The positions were located at −0.05, 0.17, 0.34, 0.51 and 0.73 cm in Fig. 3, (as indicated by the numbers of 1–5) corresponding to advancing contact angles of 0°, 23°, 34°, 41° and 46°, respectively. A typical example of the desorption kinetics of RNase from the quaternary amine end of the gradient surface (θ_exp = 46°) is shown in Figs. 5a and 5b: the desorption segment of the TIRF experiment was carried out in phosphate buffer solutions of 0.0185 M and 0.1185 M ionic strength, respectively.

Fig. 5.

Comparison between the TIRF-measured desorption kinetics and the fits to the two adsorbed protein populations model. (a) Desorption of FITC–RNase in 0.0185 M ionic strength phosphate buffer. (b) Desorption of FITC–RNase in the 0.1185 M ionic strength phosphate buffer. The experimental curves were measured at position 5, θ_adv = 46°; the time is counted from the start of the adsorption–desorption experiment.

The FITC–RNase desorption kinetics were first modeled by considering the desorption of a single adsorbed protein population [26]

$$\mathrm{d}\Gamma (t)/\mathrm{d}t=-k_{\text{off}}\Gamma (t)$$ (2)

or in the integral form as

$$k_{\text{off}}t=\text{ln }[{\Gamma }_0/\Gamma (t)]$$ (3)

where Γ₀ and Γ_(t) are the adsorbed amounts at the beginning of the desorption process and at the time, t, respectively, and k_off is the desorption rate. In order to determine the desorption rate, k_off, the actual adsorbed amounts, Γ_(t) and Γ₀, do not need to be known. The fluorescence intensity as a function of desorption time can be used instead, as long as it remains proportional to the adsorbed amounts of FITC–RNase. This assumption has not been rigorously tested for FITC–RNase; however, comparisons between the adsorbed amounts of FITC-labeled proteins along the gradient surfaces, as determined by autoradiography and by the TIRF technique, have generally been in excellent agreement [27]. Fitting of the observed FITC–RNase desorption kinetics to the one surface population model resulted in very poor correlation coefficients (below 0.7). Because of such a poor fit, the next simplest model was examined: the desorption of two adsorbed protein populations, a and b.

$$\Gamma {(t)}_{\text{tot}}={\Gamma }_0^{\mathrm{a}}{[\text{exp}(t\times k_{\text{off}}^{\mathrm{a}})]}^{-1}+{\Gamma }_0^b{[\text{exp}(t\times k_{\text{off}}^{\mathrm{b}})]}^{-1}$$ (4)

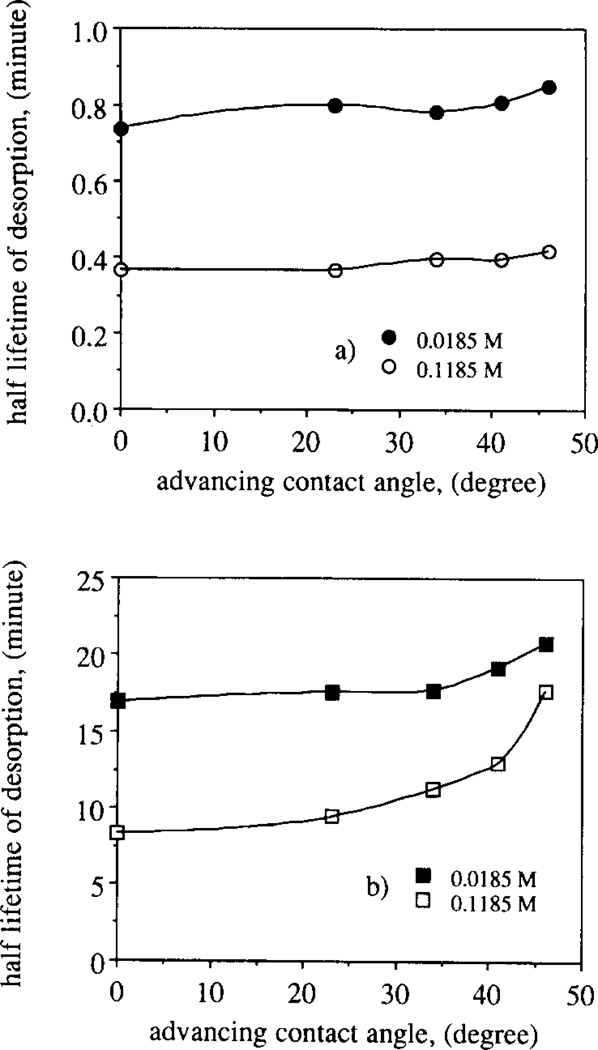
where the superscripts a and b denote the parameters associated with each adsorbed protein population. Table 2 summarizes the desorption parameters obtained by fitting the experimental desorption TIRF results to the two adsorbed protein populations model represented by Eq. (4). The fit improved significantly: the correlation coefficient, R, was higher than 0.99 except in one case where it amounted to 0.96. Figs. 6a and 6b show the half lifetimes of desorption, defined as (1/k_off) × ln 2, as a function of the advancing contact angle along the charge density gradient for each of the two surface adsorbed protein populations. One adsorbed protein population shows relatively fast desorption (Fig. 6a) while the FITC–RNase desorption from the other site is much slower (Fig. 6b) along the charge density gradient. The increase of the buffer ionic strength decreases the half lifetimes of desorption by approximately 50% in the case of the faster desorption process (i.e. increases the desorption rate, $k_{\text{off}}^{\mathrm{a}}$) (Fig. 6a). In the case of the slower desorption process, the higher ionic strength reduces the half lifetimes of desorption by 50% at the silica end of the gradient surface. At the quaternary amine end, the half lifetimes of desorption, $(1/k_{\text{off}}^{\mathrm{b}})\times \text{ ln }2$, decrease only by 15% (Fig. 6b). Comparison between Figs. 6a and 6b shows that the surface density of the quaternary amines has a larger influence on the slower desorption process than on the faster desorption process.

Table 2.

Summary of parameters obtained by fitting the experimental FITC–RNase desorption kinetics to the two adsorbed protein populations model (Eq. (4))^a

Parameter	1	2	3	4	5	1	2	3	4	5
θ	0°	23°	34°	41°	46°	0°	23°	34°	41°	46°
	Ionic strength, 0.0185 M; pH 7.0					Ionic strength, 0.1185 M; pH 7.0
$k_{\text{off}}^{\mathrm{a}}({\mathrm{s}}^{-1})$	0.0157	0.0144	0.0147	0.0143	0.0136	0.0314	0.0299	0.0291	0.0294	0.0277
$k_{\text{off}}^{\mathrm{b}}({\mathrm{s}}^{-1})$	0.000684	0.000658	0.000655	0.000602	0.000558	0.00127	0.00111	0.00093	0.00081	0.00064
${\Gamma }_0^{\mathrm{a}}(\text{counts }{\mathrm{s}}^{-1})$ b	2036	1840	1832	1786	1969	3596	3121	2865	2668	2637
${\Gamma }_0^{\mathrm{b}}(\text{counts }{\mathrm{s}}^{-1})$ b	2547	2210	2299	2324	2591	1227	1126	1238	1381	1724
$\text{ln }2/k_{\text{off}}^{\mathrm{a}}(\text{min})$	0.7364	0.8010	0.7847	0.8070	0.8515	0.368	0.386	0.397	0.394	0.417
$\text{ln }2/k_{\text{off}}^{\mathrm{b}}(\text{min})$	16.88	17.55	17.65	19.19	20.71	8.26	9.45	11.28	12.94	17.66
${\Gamma }_0^{\mathrm{a}}/({\Gamma }_0^{\mathrm{a}}+{\Gamma }_0^{\mathrm{b}})$ c	0.444	0.454	0.444	0.435	0.432	0.746	0.735	0.698	0.659	0.605
${\Gamma }_0^{\mathrm{b}}/({\Gamma }_0^{\mathrm{a}}+{\Gamma }_0^{\mathrm{b}})$ d	0.556	0.546	0.557	0.566	0.568	0.254	0.265	0.302	0.341	0.395
R	0.9946	0.9945	0.9945	0.9933	0.9905	0.9945	0.9943	0.9929	0.9921	0.9557

^aWater contact angles are given for positions 1–5 indicated in Fig. 3.

^bFluorescence intensity at the onset of the desorption process.

^cFraction of total RNase population that will desorb with the faster rate.

^dFraction of total RNase population that will desorb with the slower rate.

Fig. 6.

Half lifetime of desorption (in minutes) shown as a function of advancing contact angle of the quaternary amine gradient surface: faster (circles, Fig. 6a) and slower (squares, Fig. 6b) desorption of the two adsorbed protein populations in two buffers of ionic strengths 0.0185 M (filled symbols) and 0.1185 M (empty symbols) respectively.

The fractions of total FITC–RNase population at the onset of the desorption, ${\Gamma }_0^{\mathrm{a}}/({\Gamma }_0^{\mathrm{b}}+{\Gamma }_0^{\mathrm{a}})\text{ and }{\Gamma }_0^{\mathrm{b}}/({\Gamma }_0^{\mathrm{b}}+{\Gamma }_0^{\mathrm{a}})$, assumed to be identical to the fractions of total fluorescence calculated by the desorption model, are shown in Fig. 7 as a function of the advancing contact angle. The initial fractions were almost identical in the case of 0.0185 M buffer along the gradient (Fig. 7; filled symbols). The increase is the ionic strength of the desorption buffer makes the fractions different in magnitude as well as dependent on the surface density of the amines (Fig. 7; empty symbols). The faster desorbing fraction became larger than the slower desorbing fraction. The difference between the two initial fractions decreased towards the quaternary amine end of the gradient surface.

Fig. 7.

The fractions of total FITC–RNase population at the onset of the desorption, ${\Gamma }_0^{\mathrm{a}}/({\Gamma }_0^{\mathrm{b}}+{\Gamma }_0^{\mathrm{a}})\text{ and }{\Gamma }_0^{\mathrm{b}}/({\Gamma }_0^{\mathrm{b}}+{\Gamma }_0^{\mathrm{a}})$, shown as a function of the advancing contact angles of the quaternary amine gradient surface: faster (circles) and slower (squares) desorbing populations in two buffers of ionic strengths 0.0185 M (filled symbols) and 0.1185 M (empty symbols) respectively.

4. Discussion

A controllable change of a macroscopic surface parameter occurring on a single surface is very attractive because a single experiment can provide a multitude of experimental results. The interpretation of the results, however, requires a careful consideration of the microscopic distribution of important surface groups along the gradient. In the present study, one needs to consider both the net surface charge along the gradient and the microscopic distribution of the surface quaternary amine groups.

One expects to find two types of positively charged amines: quaternary amines and protonated amines, on the quaternary amine surface. The XPS analysis (Table 1, systems (c) and (d)) indicated that at least one-quarter of the total surface amines are protonated. An additional fraction, between 0.1 and 0.2, of the total surface amines were successfully converted into fully charged quaternary amines. With a total surface density of amines of 1.4 amine groups per square nanometer, as found by ellipsometry, one finds approximately 0.35 protonated amines and 0.14–0.28 quaternary amines per square nanometer. Assuming that the contribution from the silica surface charge remains constant along the gradient at the level of 0.3–0.4 negative electron charges per square nanometer [28], the net surface charge on the quaternary amine end of the gradient surface can be anywhere between 0.14 and 0.28 positive electron charges per square nanometer. It is important to recognize that these are the lower limits of net surface charge: the charge contribution from the silica surface may be smaller due to the reaction between the surface silanol groups and the silane reagent. The existence of an increasingly more positive charge on the charge density gradient surface was confirmed by the adsorption of negatively charged colloidal gold particles (Fig. 4).

The charge density gradient surface should display an interesting macroscopic effect: “a region of net zero charge” somewhere in the middle of the gradient. The FITC–RNase adsorption (not shown) and desorption results did not display any extraordinary effect that could confirm the existence of such an overall neutral surface region. This may be due to the electrostatic nature of the RNase molecule. The RNase molecule, although carrying an overall positive charge at neutral pH, is surrounded by two distinct lobes of positive and negative potentials [29,30]. This quasi-dipolar nature of RNase will allow the molecule to adsorb efficiently to both negatively and positively charged surfaces.

According to the results of the dynamic contact angle measurements, a large hysteresis of the contact angles exists at the quaternary amine end of the gradient surface (Fig. 3), suggesting the existence of patches of aminopropyldimethylsilyl surface groups. Some of these patches may be positively charged. Indeed, the SEM observations corroborate this conclusion (Fig. 4). The importance of microscopic distribution of the surface groups is inversely proportional to the size of the adsorbate molecule. The influence of the surface patchiness has recently been treated theoretically in a polymer adsorption theory [31]. To the best of our knowledge, the effect of the surface patchiness on protein adsorption has not been considered, perhaps because of the difficulties in controlling the surface patchiness experimentally. Protein adsorption onto the partially covered C18 silica surfaces showed a linear dependence of the adsorption rate on the C18 surface coverage in the case of low-density lipoproteins (LDL) [27]. Since the size of RNase is relatively small compared to LDL, one can expect that the surface patches may influence the RNase adsorption/desorption behaviour.

In modeling the RNase desorption, we have selected the two adsorbed protein populations model (Eq. (4)). The experimental desorption results fit this model expectionally well (R, Table 2). Two different adsorbed protein populations of RNase showed distinctly different desorption rates (Fig. 6). A tentative assignment of the two types of adsorbed FITC–RNase populations can be proposed based on the effect of the buffer ionic strength. The faster desorption (Table 2, sites a) is assigned to the adsorbed protein populations that primarily interact with the surface via electrostatic interactions. It was found that the higher ionic strength buffer influenced the rates of the slower desorption process; however, the effect diminished as the surface becomes more hydrophobic, i.e. towards the quaternary amine end. Hence, the slower desorption is assigned to the adsorbed protein population that interacts with the surface through a combination of hydrophobic and possibly some electrostatic interactions (sites b). Such an assignment is in agreement with a general notion that protein desorption from hydrophobic surfaces usually occurs very slowly or not at all, whereas proteins can desorb quite fast from hydrophilic, charged surfaces [32].

The most important conclusion from the present study is that the nature of each adsorbed protein population is not exclusive to a single type of protein–surface interaction. The FITC–RNase surface population interacts with surface sites via a multiplicity of interactions, including both hydrophobic and electrostatic interactions. This multiplicity of protein–surface interactions is the reason why two buffers of different ionic strength can “sample” different fractions of the RNase surface populations (Fig. 7). Ion-exchange chromatography uses the “sampling” effect by linearly increasing the salt concentration during the elution of protein from the column.

The two adsorbed protein populations model used in the present study neglects any lateral protein–protein interactions. Various forms of lateral interactions were included in the two adsorbed protein populations model and tested on the RNase experimental desorption results (not shown here). No improvements were found in the goodness of fit, indicating that the quality of the present experimental data is not sufficient to discriminate between these models. The lateral interactions are expected to play a significant role when a mixture of two or more proteins is interacting with a surface. We are currently examining the role of lateral interactions in the FITC–RNase + α-lactalbumin surface adsorption/desorption.

5. Conclusion

The quaternary amine surface gradient was prepared on fused silica by a three-step surface modification process. The gradient surface displayed a transition of surface charges along the gradient dimension from a net negative surface charge of silica to a net positive surface charge at the quaternary amine end. The gradient surface displayed an increased adhesion of negatively charged gold particles towards the quaternary amine end. The water contact angles also increased with the increased surface density of aminopropylsilyl groups.

The experimental FITC–RNase desorption results fitted exceptionally well to a two adsorbed protein populations model. A tentative assignment of the two adsorbed protein populations is proposed based on the effect of the ionic strength of the desorbing buffer. The faster desorption population primarily interacts with the surface sites through electrostatic interactions. The slower desorption population interacts with the surface sites via hydrophobic and possibly some electrostatic interactions.