Abstract
Aim:
To evaluate and compare the predictive capacity of four intraocular lens (IOL) power calculation formulas (SRK/T, Hoffer Q, Holladay 1, and Haigis) in eyes shorter than 22.0 mm.
Setting and Design:
Observational study.
Materials and Methods:
Participants in our study were 69 consecutive patients with a preoperative axial length (AL) of less than 22.0 mm in one or both eyes. All patients underwent phacoemulsification with IOL implantation and postoperative target of refraction was analyzed. Specifically, the differences in the mean absolute estimation error (AE) for the four formulas were analyzed. Furthermore, the percentage of eyes with AE within ±0.5 and ±1.0 D for each formula was estimated, as well as the correlation coefficient (r) between the AL and estimation error (E) for each formula. The Mann-Whitney U test was used to compare differences in the AEs of the formulas. A statistically significant difference was defined as P < 0.05.
Results:
The Haigis formula had statistically significant smaller mean AE in comparison to Holladay 1, Hoffer Q, and SRK/T. The Haigis formula predicted more eyes with E within ±0.5 and ±1.0 D of predicted spherical equivalent compared to other formulas. Correlation between AL and AE revealed a negative r value and P < 0.05 for all formulas.
Conclusions:
Haigis formula provides more accurate results concerning the postoperative target of refraction in eyes with AL less than 22.0 mm. Hoffer Q could be also used as an alternative.
Keywords: Axial length, formulas, lens, power, short eyes
Accurate intraocular lens (IOL) power calculation in cataract surgery is very important to achieve the postoperative target refraction and high patient satisfaction, as patients’ expectations have been progressively increased.[1,2] Therefore, there has been an ongoing effort to predict the postoperative refractive outcome with accuracy and consistency. The refractive power of the human eye depends on the power of the cornea, the lens and the axial length (AL) of the eye and the axial position of the lens.[1] The aforementioned factors are crucial to obtain the optimal postoperative refractive results.
IOL power is predicted preoperatively by means of several formulas.[1,2,3,4,5,6,7,8,9] Third generation formulas; such as Holladay 1, Hoffer Q, and SRK/T; attempt to predict the estimated lens power using AL, corneal curvature (K), and a constant, as the only variables. Fourth generation formulas, like Haigis, take into account the preoperative anterior chamber depth (ACD) and use three constants (a0, a1, and a2), which are analogous to surgeon factor (SF), ACD and AL respectively.[3] Of note, inaccuracy in measurement of ACD, AL, and K can contribute to 42, 36, and 22% of errors, respectively.[4]
It has been considered that IOL calculation formulas were more accurate for eyes with normal AL, but do not have the same level of postoperative refraction outcome for eyes with short AL.[1] In light of the above, the purpose of our study was to evaluate and compare the predictive capacity of four IOL power calculation formulas (SRK/T, Hoffer Q, Holladay 1, and Haigis) in eyes shorter than 22.0 mm.
Materials and Methods
Participants in our study were 69 consecutive patients, recruited from February to July 2012, with a preoperative AL of less than 22.0 mm in the eye candidate for cataract surgery. All patients underwent phacoemulsification with IOL implantation in one eye and postoperative target of refraction was analyzed. Preoperatively, all patients had manifest refraction and a complete ophthalmological examination, that is, measurement of best corrected visual acuity (BCVA) by means of Snellen charts, intraocular pressure (IOP) evaluation by Goldmann tonometry, slit lamp examination, and fundus examination. Additionally, corneal power (k) was measured by automated keratometry (Speedy-K, Righton, Right Mfg. Co, Ltd) and A-scan ultrasonography using the Ocuscan® RxP (Alcon®) was performed for each patient, to measure AL and ACD. In all cases, the immersion ultrasound A-scan technique was used. The appropriate IOL power was measured for each formula, using the software of Ocuscan, having optimized the lens constant. Indeed, “optimization” included “customization” of constants for a specific IOL (i.e. SN60WF by Alcon) by means of the OcuScan software. Specifically, the lens constants are shown on a table for 10 IOLs for each setting. Each entry can be edited to match to user's preferred IOL values. The factory defaults used for A constant is from the lens manufacturer's specifications. Additionally, there is the “lens constant update screen”, providing the user the ability to customize the A, ACD, and SF constants using the patient's preoperative and postoperative data for any of the 10 stored lenses on the selected doctor settings screen. Although the system will compute the constants based on a single patient case, a minimum of 20 patient cases was used in order to achieve higher statistical significance in the prediction of new constants.
Inclusion criteria were AL < 22.0 mm, presence of cataract, age more than 40 years, and postoperative BCVA of 20/40 or better. Exclusion criteria were factors likely to confound biometry readings, affect IOL positioning in the capsular bag or decrease the accuracy of measured refraction, that is, preoperative BCVA of 20/200 or worse, corneal abnormalities, previous intraocular or corneal surgery (including keratorefractive surgery), history of ocular injury or uveitis, and intraoperative complications, such as posterior capsule rupture, vitreous loss, lost nucleus, zonule dehiscence, and wound leak. The study was in accordance with the tenets of the Declaration of Helsinki. Written informed consent was obtained from all patients.
Surgeon's goal in IOL power selection was a lens power that would yield a postoperative refraction nearest to plano, erring on the side of myopia. The IOL formula that predicted a lens power with the above postoperative refraction was selected. All patients underwent uneventful phacoemulsification cataract surgery with a standard technique by the same surgeon. Proparacaine hydrochloride 0.5% drops (Alcaine®, Alcon laboratories, Fort Worth, Texas) were used as topical anesthetic and were administered 10 min prior to the beginning of surgery. A clear corneal 2.75 mm incision and side-port paracentesis were made. Ophthalmic viscoelastic device (OVD) was injected into the anterior segment and a continuous curvilinear capsulorrhexis was created. The lens nucleus and cortex were hydrodissected with balanced salt solution (BSS). This was followed by phacoemulsification, irrigation, and aspiration of cortical remnants via phacochops methods by using Infinity™ Vision System (Alcon, Fort Worth, Texas). OVD infusion and implantation of the foldable posterior chamber IOL were performed using the recommended injector system. Alcon lenses (SN60WF, Alcon, Fort Worth, Texas) were implanted to all patients. The viscoelastic material was subsequently removed and surgical wounds were hydrated with BSS. No sutures were applied. All wounds were checked for leakage and found to be watertight.
Postoperatively, patients were examined the 1st day and 1 month postoperatively. Estimation error (E) was defined as the difference between the actual postoperative spherical equivalent (SE) at the 1-month follow-up and the predicted postoperative SE. The absolute error (AE) was defined as the absolute values of E. Mean AE was calculated for each formula. The differences in the mean AE for the four formulas were analyzed. Furthermore, the percentage of eyes with AEs within ±0.5 and ±1.0 D for each formula was estimated. In addition, the correlation coefficient (r) between the AL and AE for each formula was calculated.
The Mann-Whitney U test was used to compare differences in the AEs of the formulas. A statistically significant difference was defined as P < 0.05. Statistical analysis was performed using Statistical Package for Social Sciences (SPSS) 17.0 (SPSS Inc, Chicago, IL, USA).
Results
A total of 69 eyes were included in the study, with a male to female ratio 3:4. The mean age was 73.5 ± 7.2 years. All patients reached 6/6 BCVA postoperatively. The mean AL was 21.5 ± 0.4 mm (range: 20.2-21.99), the mean ACD was 2.43 mm (range: 2.28-2.97), while the mean average K was 43.7 ± 1.5 D (range: 40.31-47.88). The mean preoperative SE was +2.25 ± 2.6 D. The mean E (± standard deviation (SD)) for Holladay 1, Hoffer Q, SRK/T and Haigis was 0.32 ± 0.17, −0.09 ± 0.10, 0.41 ± 0.23, and −0.02 ± 0.06, respectively.
The overall results concerning the AE and the range of E for the four formulas are shown in Table 1. The Haigis formula had statistically significant smaller mean AE in comparison to Holladay 1 (P < 0.001), Hoffer Q (P = 0.01), and SRK/T (P < 0.001).
Table 1.
Mean absolute estimation error and range of estimation error for each formula

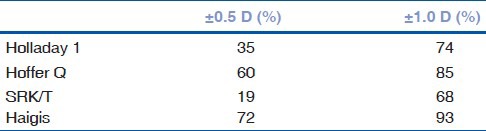
The Haigis formula predicted more eyes with E within ± 0.5 and ± 1.0 D of predicted SE compared to other formulas, as it is shown on Table 2.
Table 2.
Percentage of eyes within specified target refraction for each formula
Correlation between AL and AE revealed a negative r value and P < 0.05 for all formulas, indicating statistically negative correlation. Practically, as AL decreased, AE increased in all formulas [Fig. 1].
Figure 1.
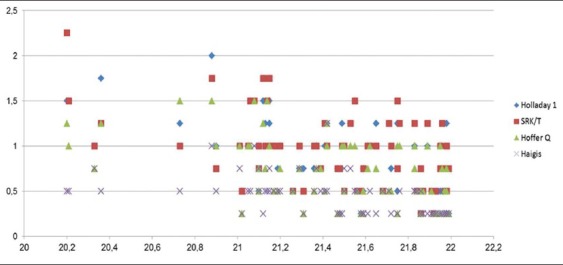
Correlation between axial length and absolute error
Discussion
The principal message of our study is that Haigis formula is more accurate than Hoffer Q, Holladay 1, and SRK/T in predicting the postoperative refraction after cataract surgery in eyes with AL less than 22.0 mm. It also predicted the greatest percentage of eyes that fell within ±0.5 and ±1.0 D of estimated error. In addition, the rate of decrease, as shown by the respective r values, was greater for the Haigis formula followed by Holladay 1, Hoffer Q, and SRK/T. In clinical terms, it means that Haigis formula is more accurate and seems to predict more closely the postoperative refractive error.
Previous studies examined the predictive accuracy of various IOL power calculation formulas in eyes with short AL. Narvaez et al., employed immersion ultrasonography and manual keratometry to evaluate 25 eyes with AL less than 22.0 mm, suggesting no statistically significant difference between Holladay 1, Holladay 2, Hoffer Q, and SRK/T.[5] Gavin and Hammond investigated 41 eyes with AL less than 22 mm, measured by IOLMaster, concluding that the Hoffer Q formula was more accurate than the SRK/T.[6] In line with our findings, MacLaren et al., reviewed 72 eyes with mean AL of 20.79 mm, reporting that in both IOLMaster and ultrasonography group, the Haigis formula was the most accurate followed by the Hoffer Q, while Holladay 1 and SRK/T were the least accurate.[7] Accordingly, Roh et al., suggested that Haigis formula provided the best results as far as the postoperative power prediction is concerned in 25 eyes with AL less than 22.0 mm.[1]
The mean E of each formula is significant to indicate the overall direction and magnitude of refractive error.[1,2,4] A mean E value close to zero indicated an optimized formula. A negative value indicated a tendency for myopic outcomes, whereas a positive value indicated a tendency for hyperopic outcomes. As a result, the Haigis (mean E = −0.02) and the Hoffer Q (mean E = −0.09) formulas were optimized for the parameters used in this study. On the other hand, the Holladay 1 (mean E = 0.32) and SRK/T (mean E = 0.41) formulas had a strong tendency for hyperopic results.
A potential limitation of our study pertains to the fact that partial coherent interferometry method (IOLMaster) was not used, although it has been thought to be more accurate than immersion ultrasonography method in IOL power calculation for patients eligible for cataract surgery. Nevertheless, our study had a relatively large study sample, taking into account that short AL is not very common. Additionally, we have used the customization of IOL constants by means of “Ocuscan software”, in order to obtain more accurate results and higher predictability of postoperative target refraction.
In conclusion, our study suggests that Haigis formula provides more accurate results concerning the postoperative target of refraction in eyes with AL less than 22.0 mm. Hoffer Q could be used as an alternative, if specific constants for the Haigis formula are not available.
Footnotes
Source of Support: Nil
Conflict of Interest: None declared
References
- 1.Roh YR, Lee SM, Han YK, Kim MK, Wee WR, Lee JH. Intraocular lens power calculation using IOLMaster and various formulas in short eyes. Korean J Ophthalmol. 2011;25:151–5. doi: 10.3341/kjo.2011.25.3.151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Olsen T, Thim K, Corydon L. Accuracy of the newer generation intraocular lens power calculation formulas in long and short eyes. J Cataract Refract Surg. 1991;17:187–93. doi: 10.1016/s0886-3350(13)80249-0. [DOI] [PubMed] [Google Scholar]
- 3.Wang L, Shirayama M, Ma XJ, Kohnen T, Koch DD. Optimizing intraocular lens power calculations in eyes with axial lengths above 25.0 mm. J Cataract Refract Surg. 2011;37:2018–27. doi: 10.1016/j.jcrs.2011.05.042. [DOI] [PubMed] [Google Scholar]
- 4.Lee AC, Qazi MA, Pepose JS. Biometry and intraocular lens power calculation. Curr Opin Ophthalmol. 2008;19:13–7. doi: 10.1097/ICU.0b013e3282f1c5ad. [DOI] [PubMed] [Google Scholar]
- 5.Narváez J, Zimmerman G, Stulting RD, Chang DH. Accuracy of intraocular lens power prediction using the Hoffer Q, Holladay 1, Holladay 2, and SRK/T formulas. J Cataract Refract Surg. 2006;32:2050–3. doi: 10.1016/j.jcrs.2006.09.009. [DOI] [PubMed] [Google Scholar]
- 6.Gavin EA, Hammond CJ. Intraocular lens power calculation in short eyes. Eye. 2008;22:935–8. doi: 10.1038/sj.eye.6702774. [DOI] [PubMed] [Google Scholar]
- 7.MacLaren RE, Natkunarajah M, Riaz Y, Bourne RR, Restori M, Allan BD. Biometry and formula accuracy with intraocular lenses used for cataract surgery in extreme hyperopia. Am J Ophthalmol. 2007;143:920–31. doi: 10.1016/j.ajo.2007.02.043. [DOI] [PubMed] [Google Scholar]
- 8.Fenzl RE, Gills JP, Cherchio M. Refractive and visual outcome of hyperopic cataract cases operated on before and after implementation of the Holladay II formula. Ophthalmology. 1998;105:1759–64. doi: 10.1016/S0161-6420(98)99050-9. [DOI] [PubMed] [Google Scholar]
- 9.Preussner PR, Olsen T, Hoffmann P, Findl O. Intraocular lens calculation accuracy limits in normal eyes. J Cataract Refract Surg. 2008;34:802–8. doi: 10.1016/j.jcrs.2008.01.015. [DOI] [PubMed] [Google Scholar]


