Gene pair signatures in cell type transcriptomes reveal lineage control

Abstract

The distinct cell types of multicellular organisms arise due to constraints imposed by gene regulatory networks on the collective change of gene expression across the genome, creating self-stabilizing expression states, or attractors. We compiled a resource of curated human expression data comprising 166 cell types and 2,602 transcription regulating genes and developed a data driven method built around the concept of expression reversal defined at the level of gene pairs, such as those participating in toggle switch circuits. This approach allows us to organize the cell types into their ontogenetic lineage-relationships and to reflect regulatory relationships among genes that explain their ability to function as determinants of cell fate. We show that this method identifies genes belonging to regulatory circuits that control neuronal fate, pluripotency and blood cell differentiation, thus offering a novel large-scale perspective on lineage specification.

INTRODUCTION

Mammalian organisms contain at least 250 cell types¹, each specified by a characteristic gene expression profile. Despite increasing availability of expression data, comprehensive characterization of cell type–specific expression profiles remains challenging due to inconsistencies in annotations and technical issues such as data normalization. Moreover, common differential expression analyses alone are insufficient to recover ontogenetic cell lineage relationships or to reflect regulatory relationships among transcription factors (TFs) that lead some to function as fate determinants.

We describe a data-driven method that addresses these problems in the context of the very mechanisms by which the gene regulatory networks govern lineage development. Our analysis is motivated by a two-gene circuit motif known to control binary developmental decisions². This motif, first hypothesized to control developmental switches in Drosophila^3,4, contains a pair of mutually-repressive TFs and effectively constitutes a toggle switch. These circuits allow a bipotent progenitor cell to simultaneously co-express two opposing TFs at low levels, the poised state {TF1 ≈ TF2},² but force it to choose between either of two stable configurations in which one TF dominates the other, {TF1 ≫ TF2} or {TF2 ≫ TF1}.

Such pairs of antagonistic TFs can govern the development of “sister” lineages. In addition to cross-inhibiting each other, these TFs also act as lineage-specifying master regulators of target genes that are reciprocally expressed in the two sister lineages, thus establishing lineage-specific gene expression profiles². The pair {SPI1, GATA1} is a well-studied example in the hematopoietic system⁵. SPI1 (PU.1) specifies the myeloid lineage characterized by SPI1 ≫ GATA1 whereas GATA1 specifies the erythroid lineage in which GATA1 ≫ SPI1⁶. The lineage split manifests as the establishment of a mutual exclusion, resulting in reversed expression between the two TFs, which can be exploited to identify master regulators. We score genes for potential participation in such expression reversals. We expect gene pairs that function as lineage determinants to exhibit consistent relative expression across samples from the same cell type (and lineage) and consistent reversal of relative expression between cell types from sister lineages, a property that has been exploited in expression-based classifiers^7–9.

By applying this method to curated gene expression data from 166 cell types and 2,602 transcription regulating genes, we show that experimentally verified master regulators of cell type fate are indeed revealed through quantification of their participation in expression reversals. Focusing on hematopoiesis, our method reveals known and novel candidate fate-specifying genes that exhibit the signature of participation in antagonistic circuits, results which were confirmed by genome-wide ChIP-seq data. Finally, we derived a cell type similarity measure from expression reversals with which we could recover known ontogenetic lineage-relationships reminiscent of the branching valleys of the epigenetic landscape envisioned by Waddington¹⁰.

RESULTS

Gene expression reversal analysis

We curated a dataset comprising 2,919 microarrays and representing 166 normal human cell types (described in Supplementary Results, Supplementary Tables 1–3 and Supplementary Fig. 1) and selected genes with functional annotation related to transcription regulation (Supplementary Results, Supplementary Tables 4 and 5 and Supplementary Fig. 2). A subset formed from strictly-defined TFs will be referred to as the TF set (844 genes). The term TF will be used to refer to all transcription regulating genes for simplicity.

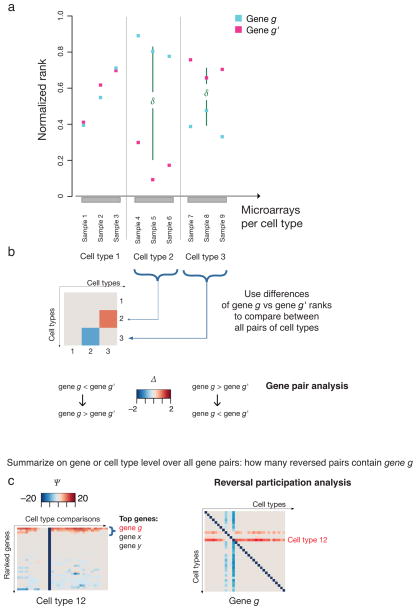
For every pair of genes and every pair of cell types, we define the reversal score Δ to be the difference between cell types of the mean rank difference (within each cell type) between genes (Eq. 1–3 in Methods, Fig. 1). Use of rank data rather than absolute expression obviates the need for sample normalization, typically needed due to sample distribution differences (Supplementary Fig. 3), because all direct comparisons between genes happen within samples, and conventional normalization methods are rank-preserving(Supplementary Results). Thus, large absolute values of Δ identify gene pairs that reverse expression between cell types. Δ is clamped to 0 for pairs of genes that do not change relative expression (the difference in their mean ranks does not change sign) between cell types. Fixing the gene pair in Δ and letting the cell types vary produces gene pair reversal plots which visualize the potential for a gene pair to participate in a lineage split between any pair of cell types (Fig. 1b). Finally, we define the participation score Ψ for a fixed gene (Eqs. 4,5 in Methods) to be an aggregate measure of the number and strength of reversals in which the gene participates (Fig. 1c).

Fig. 1. Gene pair expression reversal analysis exemplified by schematic data.

A schematic example to illustrate the principle of the expression reversal method is shown. (a) The ranks of two hypothetical genes g and g′ are plotted from microarray samples assigned to three hypothetical cell types. (b) Gene pair reversal plot. The reversal behavior of the {gene g, gene g′} gene pair quantified for all pair-wise comparisons of N = 3 cell types is shown as an N x N symmetric matrix. The value, indicating the extent of reversal behavior is represented by the color in the heat map. Red tones indicate that the pair configuration changes from gene g ≫ gene g′ in the first cell type of a comparison pair (“row-to-column comparison”) to gene g ≪ gene g′ in the second cell type. A reversal in the opposite direction in cell type comparisons are indicated in blue shades. (c) Reversal participation. The Ψ value for gene g quantifies its reversal participation from all gene pairs displayed across each pair-wise comparisons of (here N = 32) cell types. A specific gene pair configuration in multiple gene pairs involving g, will be reflected by a high score (dark red or blue). Alternatively, the gene reversal participation can be assessed at the cell type level by extracting from the gene portraits the cell type (row) of interest, and subsequently sorting by maximal Ψ value.

Revealing critical factors for induced pluripotency

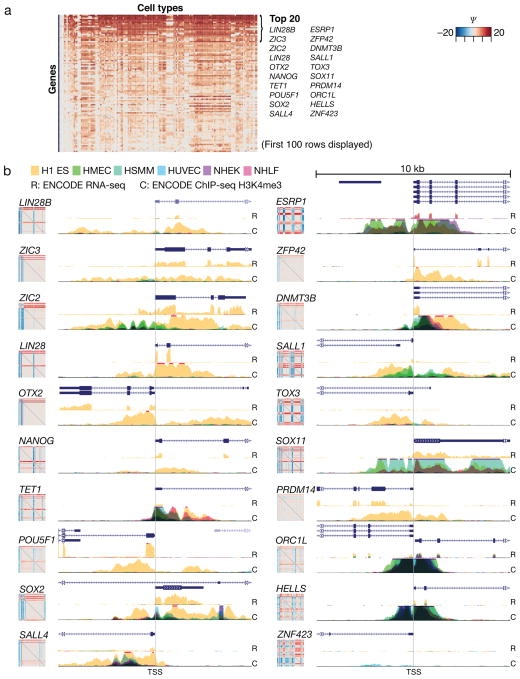
We hypothesized that participation of a gene in reversals involving a given cell type is indicative of the specificity of the gene for that cell type as well as its potential to participate in lineage determination. We sorted genes by their participation scores in comparisons of embryonic stem cells (ESC) with other cell types (Fig. 2a). Interestingly, the genes NANOG, POU5F1 (OCT3 or 4), SOX2 and LIN28 that appear on this top list are precisely those that jointly are capable of inducing the pluripotent state from differentiated cells¹¹ (see also Supplementary Fig. 4). A critical role in regulation of stem cell transcription has been reported for 17 of the top 20 genes (Supplementary Table 6). These results are very robust to noise and sample size differences (Supplementary Figs 5–7 and Supplementary Results).

Fig. 2. Cell type-level analysis of reversal participation in the ESC highlights genes used to induce pluripotency.

Reversal participation analysis for ESCs compared to all other cell types reveals genes that are important in determining ESC (refer to Supplementary Table 3 for the order of cell types in columns). (a) The first 100 rows (of 2,602 TFs evaluated) of the ESC cell portrait are displayed and the names of top 20 most specific ESC-high transcription regulating genes are indicated, including those used to induce pluripotency in human cells¹¹: LIN28, NANOG, POU5F1 and SOX2. (b) Active ESC transcription and promoter state was evaluated from ENCODE¹² RNA-seq (R) and ChIP-seq (C) of histone methylation datasets. The level of the H3K4me3 marker for active promoters around 5 kb up- or downstream from the gene transcription start site (TSS) is shown from six normal ENCODE cell types H1 ES: human ESC line H1, HMEC: breast epithelial cell, HSMM: skeletal muscle myoblast, HUVEC: umbilical vein endothelial cell, NHEK: epithelial keratinocyte, NHLF: lung fibroblast. RNA-seq data is available from H1 ES, HUVEC and NHEK cells. The high ESC expression and its specificity can be compared against the gene reversal portraits shown adjacent to the ChIP tracks.

We validated the cell type-restricted reversal patterns of the top 20 gene portraits using sequencing data¹² for chromatin markers (ChIP-seq) and for RNA (RNA-seq) from normal human cell types (including H1 ESCs in yellow) (Fig. 2b). Genes with a highly ESC-restricted gene portrait appear ESC-specific in both ChIP-seq and RNA-seq results. Furthermore, TF ChIP-seq data also suggest that the pluripotency inducing TFs NANOG, OCT4 and SOX2 co-occupy regulatory regions of genes that, with respect to our reversal participation score Ψ, are among the top 20 genes associated with ESCs¹³ (Supplementary Fig. 8). Therefore, our analysis highlights genes that are not only maximally restricted to the respective cell type but may also operate in a lineage-determining switch.

Reversals expose genes with lineage-determining potential

Our data shows that reversal participation captures cell type–restricted expression. We chose the ESC for the analysis since the discovery of induced pluripotency factors paved the way toward exploiting cell type plasticity to actuate direct lineage-conversions. The ability of our analysis to highlight the core ESC network suggested that such reversals may identify TFs with lineage-specifying power which could be used to induce differentiation towards a particular cell type. We investigated this possibility in a published reprogramming experiment¹⁴.

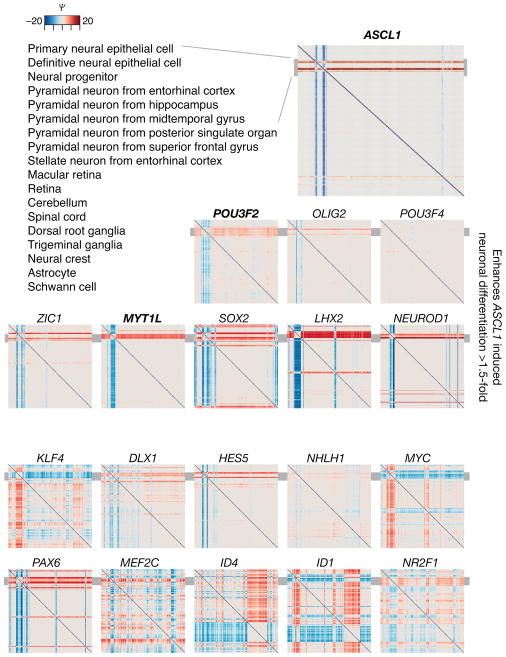
ASCL1 is a critical TF that alone and in combination with other factors was discovered to induce fibroblast to neuron conversion¹⁴. We sorted the reversal participation (Ψ) portraits of 19 candidate genes initially evaluated in the published reprogramming experiment by their potency¹⁴ in enhancing ASCL1-induced neuronal differentiation (as reflected by strong color bands localized to few cell type pairs) (Fig. 3). The diffuse patterns in the plots of the two bottom rows are in agreement with experimental results¹⁴ in which these genes showed no effect. Therefore, gene reversal participation also identifies potential fate-determining roles of a TF in a given lineage.

Fig. 3. Reversal participation analysis of a candidate gene set for the induction of neuronal differentiation reflects success in a functional assay.

A set of 19 candidate transcription regulating genes was characterized experimentally for their neuronal differentiation induction potential¹⁴. The reversal participation gene portraits of these genes are shown. The ordering of the portraits reflects the experimental success to induce neuronal fate in combination with ASCL1 that was found¹⁴ most potent on its own to induce the conversion of fibroblasts to neuronal cells. The grey bar indicates the location (rows) of neuronal cells in the figures.

Expression reversals in the hematopoietic lineage splits

To demonstrate how gene pair reversal analysis (Fig. 1b) can shed light on toggle switch circuits, we selected three characterized mutual repression circuits involved in blood cell lineage control: {GATA1, SPI1}, {GATA1, GATA2} and {GFI1, EGR2}. These pairs govern the lineage splits between erythroid vs. myeloid, erythroid vs. megakaryocyte and granulocyte vs. macrophage, respectively^5,15,16. The first lineage split occurs via the mutual repression of the {GATA1, SPI1} TF pair⁵. Here the {SPI1 ≈ GATA1} configuration is observed in the progenitor cells, consistent with the characteristic promiscuous expression pattern of multipotent cells¹⁷, whereas a pronounced reversal of their relative expression levels occurs between the pro-erythroid and pro-myeloid cells: GATA1 ≫ SPI1 in all pro-erythroid arrays and GATA1 ≪ SPI1 in all pro-myeloid arrays (Supplementary Fig. 9a). Thus, the behavior of this gene pair across all cell types in the comparison set highlights the erythroid-myeloid lineage split as a distinct pattern (Supplementary Fig. 9b). Similarly, the {GATA1, GATA2} TF pair is reversed between pro-erythroid cells and platelets that segregate in a downstream lineage split¹⁵ (Supplementary Fig. 9c). Finally, the {GFI1, EGR2} pair is strongly reversed between the granulocyte-lineage progenitors and the differentiated macrophages. Interestingly, this pair exhibits a signal in the lymphoid lineage, suggesting a broader role in the blood system, i.e. the reuse of circuits for different decisions² (Supplementary Fig. 9d).

Lineage branching is often controlled not just by one toggle switch circuit but rather the integrated action of many interconnected¹⁸ mutually repressing gene pairs. We demonstrate that using reversal scores and a priori knowledge of the lineage branching, we can identify TF pairs that exhibit an expression reversal associated specifically with the erythroid-myeloid lineage split or the B- vs T- lymphoid lineage split (Methods). We evaluated the reversal behavior of all gene pairs in the TF set in the context of an extended set of hematopoietic cell types. To increase specificity, we required that the TF pairs separating erythroid and myeloid cells are disjoint with the pairs separating lymphoid cells. For comparison, we performed a similar analysis using two rank-based methods to detect candidate genes based on differential expression (Supplementary Results).

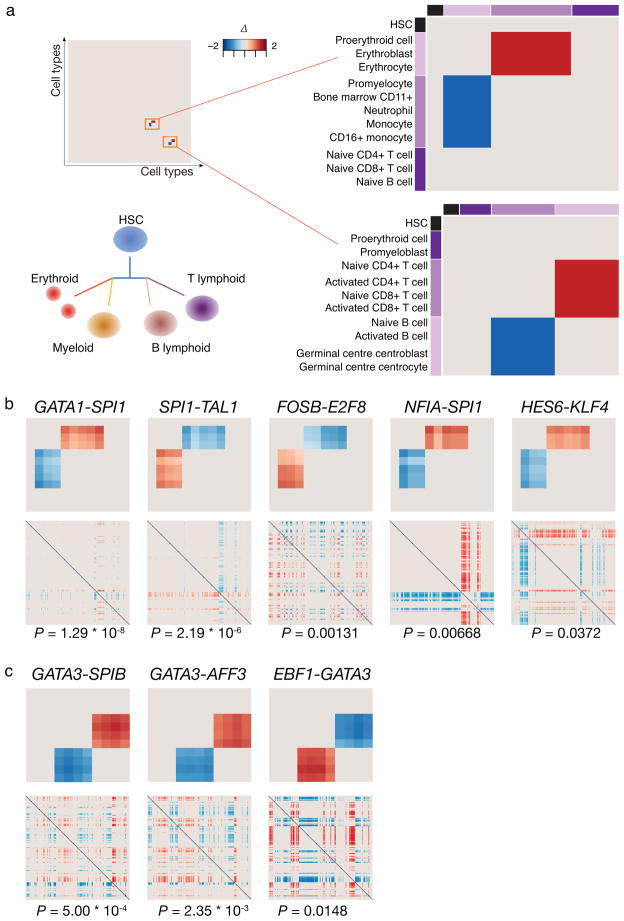
We matched the expression reversal pattern expected in these lineage splits (Fig. 4a) against the gene pair data to extract specific pairs {TF1, TF2} that are maximally lineage-restricted for either the common erythroid-myeloid or lymphoid progenitors and exhibit minimal reversal outside these cell types. To distinguish from reversals obtained by chance in comparisons between irrelevant cell types, we ordered the results of our reversal analysis by the probability of obtaining reversals in the entire 166x166 cell type comparison matrix using the hypergeometric distribution. Five pairs {TFi, TFj} that fulfill the erythroid-myeloid reversal pattern (exhibiting at least one reversal with |Δ| > 1) were found (Fig. 4b), including {GATA1, SPI1}. The complete (166x166 cell types) gene pair reversal plots used for the statistical significance calculation are shown below the pattern matched (exact p-values are indicated below the plots). The lymphoid pattern was matched to three TF pairs (Fig. 4c), each containing GATA3. Interestingly, many of the TFs found, including the validated GATA1-PU1 toggle switch, are known to be part of the core network that controls erythropoiesis, myelopoiesis or lymphopoiesis^19–27 and have been shown in some cases to engage in mutual interaction^5,28–30. For comparison, we also used standard rank-based differential expression to identify relevant genes (see Supplementary Results). In doing so, we also obtain several of the same genes but fail to capture the lineage differentiating property, as this is not attributable to single genes but pairs of genes (Supplementary Results, Supplementary Tables 7–9).

Fig. 4. Identification of reversal pairs in lineage splits of the blood system.

The HSC is the common precursor of all blood cells. Lymphoid cells branch off separately to give rise to the B and T cell lineages, wheras the myelo-erythroid lineage gives rise to the later binary split between the erythroid and myeloid cells. Lineage-determining TF pairs of the binary splits are expected to follow the reversal pattern shown in the idealized gene pair reversal plots for the subset of relevant lineages used as a query criterion. An ideal pair will also show no reversals for other cell type pairs in the full 166x166 cell type comparison matrix (a). Pairs of TFs that satisfy such properties and show a statistically significant restricted reversal in the 166x166 cell type data are shown with their p-values (hypergeometric test) for the erythroid-myeloid (in (b)) and B-T lymphoid (in (c)) splits. The heat maps represent gene pair reversal plots as in Fig. 1b, color corresponds to the mean normalized rank difference.

A number of independent experiments support the involvement in lineage determination of several of the genes identified by expression reversal scoring. Gata3 binding was observed in mouse ChIP-seq data³¹ near the TSS of Ebf1 but not Spib or Aff3. In support of an antagonistic pair interaction, Gata3 is among the Ebf1-repressed genes in a gain of function study³². In addition, human ChIP-seq data from the GM12878 lymphoblastoid cells¹² indicates EBF1 binding nearby GATA3 TSS. ChIP-seq data also confirmed the possibility of cross-inhibitory interactions at the DNA-level for all three putative toggle switch circuits from the erythroid-myeloid analysis (Supplementary Figs 10 and 11). Moreover, the observed binding of the regulatory factors to their own promoter indicated possible auto-regulation, proposed to be important for genes that participate in lineage-regulatory toggle circuits for stabilizing the poised progenitor state^2,6.

Here, we studied whether the binding of the TFs GATA1, TAL1, PU1, EBF1 and GATA3, that show evidence of cross-inhibitory interactions among the specific TF pair, maps on a genome-wide scale into the mutually exclusive phenotypes. Based on multiple independent ChIP-seq datasets (Supplementary Table 10) we performed genomic region enrichment analyses (Methods) to test whether their binding preferentially occurs in the vicinity of genes associated with the specific hematopoietic lineages. Indeed, we found that GATA1 and TAL1 binding is clearly associated with the erythrocyte phenotype and differentiation, SPI1 with the myeloid-macrophage, EBF1 with B cells and GATA3 with T cells (Supplementary Tables 11–15), matching the TF knockout phenotype (Supplementary Table 16). Furthermore, each member of the antagonistic pairs was associated with phenotype terms of the respective sister lineage. Such binding to the genes of the reciprocal fate is indicative of wide-spread repressive regulation, beyond the antagonistic pair.

The gene pair reversals reflect lineage relationships

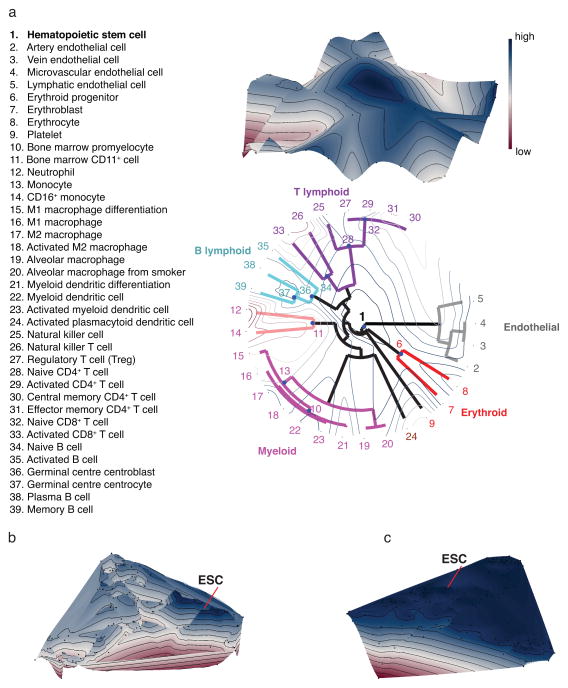
Lineage relationships are often illustrated as a tree because of the developmental genealogy of cell types, although the detailed structure of the actual “tree of development” (“cell fate map”)¹⁰ of all cell types in higher metazoa remains unknown. We hypothesized that the number of gene pairs with reversed expression between a pair of cell types is indicative of the relatedness of the cell types. Formalizing this, we define a similarity measure Φ(X,Y) between two cell types, X and Y, as the count of gene pairs for which |Δ| > 1. We selected well-studied sets of hematopoietic cells and the developmentally related endothelial cells to test whether the similarity measure Φ was able to capture the hierarchical lineage relationships, which are well studied in this system. Moreover, several precursor cells of these lineages were present in the transcriptome dataset, permitting the study of branch points. Although traditional hierarchical clustering methods generate dendrograms, they cannot reflect the biological lineage tree since all precursors (which exhibit promiscuous gene expression profiles) would necessarily be placed on terminal branches (leaves). To build this biological intuition into our analysis, we first performed a hierarchical clustering of differentiated cell types using Φ similarity, followed by a separate placement of precursor cell types onto the tree branch points, taking Φ into consideration (see Methods). The resulting dendrogram (Fig. 5a) reflects the well-known hierarchical lineage relationships among these cell types. To facilitate interpretation, the similarity Φ of each cell profile to that of the embryonic stem cell (ESC) is used to superimpose an elevation onto the dendrogram (Fig. 5a). Interestingly, this exposed a key feature of the cell fate map in that the HSC and other precursor cell types are more proximal to the ESC than terminally differentiated cells. The third dimension therefore captured properties of a true differentiation landscape reminiscent of Waddington’s metaphoric epigenetic landscape¹⁰. We obtained a very similar landscape for blood cell types using an independent dataset (see Supplementary Fig. 12 and Supplementary Table 17).

Fig. 5. Lineage relationships among hematopoietic and endothelial cell types revealed measuring similarity based on gene pair expression reversals.

An evaluation of utility of the similarity Φ to reflect lineage separation is shown. (a) Hierarchical clustering of differentiated cell types with the new feature of placement of precursor cell types to three branch points using the Hungarian algorithm and mapping of the tree to a landscape is visualized. The circular dendrogram in the x-y plane arranges cells to branching lineages identified by different colors. To represent all cell types and their similarity Φ, multidimensional scaling is shown with (b) TFs or (c) metabolic genes⁴³. The landscape elevation (z-dimension) represents the Φ similarity to the ESC giving rise to a potential-like landscape in which development follows the downhill gradient as in Waddington’s epigenetic landscape¹⁰. Blue color and high altitude on the landscape corresponds to large similarity to the pluripotent state.

To challenge this concept, we first extended the clustering to include all 166 cell types (Fig. 5b) and then compared to a result we obtained using metabolic genes³³ instead of TFs (Fig. 5c and Supplementary Fig. 13). Since the precursors of many cell types are not present in the dataset used, multidimensional scaling was used to visualize cell type dissimilarities on a plane. We used the similarity Φ from the ESC similarly to superimpose an elevation of the landscape. In the TF landscape, we found precursor cell types at elevated locations and a distinct peak for the pluripotent cells. In contrast, metabolic genes that are not expected to drive lineage-determination failed to discriminate the precursor cells that now resided in a large basin that connects cell types from multiple lineages and differentiation stages.

DISCUSSION

Here we show a unique way to analyze cell type gene expression profiles that is connected to the very principles by which gene circuits govern cell type diversification. Using the information in the reversal of gene expression levels between pairs of TFs in pairs of cell types, we generated “participation portraits” of cell types that identified TFs known to play a role in fate determination. Furthermore, our curated sets of TFs that operate at the core of cell fate switch circuits now pave the way towards investigating how TFs, chromatin modification and RNA processing act together in cell lineage control³⁴ and within regulatory networks. For instance, two genes, DNMT3B and TET1 that were highly ranked in ESCs by our analysis regulate DNA methylation: DNMT3B had been described as an epigenetic regulator of pluripotency genes^35–37. Upon its discovery, TET1 lacked annotation of its cellular function³⁸. Our analysis suggests a developmental function and links uncharacterized genes to specific cell types (a key role for TET1 in pluripotent cells was indeed subsequently found³⁹). Knowing the mechanistic interactions of transcriptional regulatory networks in different cell types⁴⁰ will enable cell type specific modeling of genetic networks and understanding how mutually repressive pairs of TFs that act as bistable lineage determining toggle switches affect other TFs and ultimately the global state of the network.

By exploiting the concept of bidirectional regulation epitomized by the toggle switch circuits that we show is manifested in expression reversal behavior, we ground our method on proposed mechanisms in developmental biology^2–4 to successfully identify highly lineage-specific profiles and TFs involved in core fate-determining circuits. Since the identified genes are not only reporters correlated with cell lineages, but possibly involved in regulatory circuits that carry out cell fate decisions, the interactive tool we provide to explore this dataset could also inform the choice of potential candidate genes used in cell fate reprogramming.

We identify with high significance eight relevant gene pairs for the developmental circuitry of the common progenitors in the blood system that allowed us to explore further how inherent properties of antagonistic pairs may manifest in other types of large scale datasets. Their active participation in developmental regulatory networks was confirmed by the high degree of inter-connectivity via co-occupied genomic sites and overlap in target genes found in ChIP-seq datasets. Finally, we utilize the reversal analysis to design a new cell type similarity measure that integrates regulatory information, affording a first opportunity to capture the “epigenetic landscape” of the cell differentiation tree directly from expression profile data. In conclusion, we present a global analysis of published cell type transcriptomes using the reversal of expression levels as a key quantity that captures the underlying regulatory dynamics in static gene expression profiles.

METHODS

Dataset collection and preprocessing of expression values

We analyzed 2,919 microarrays comprising 166 different cell types (in some cases tissues) that represent each cell type in its normal state. The dataset was collected from the GEO microarray repository from the hgu133Plus2 array type with each cell type represented by at least two arrays. Further details on the selection of the samples can be found in the Supplementary Results.

Gene expression for the transcription regulating gene set was summarized using the GC-RMA algorithm⁴¹ (no quantile normalization) and custom probe mappings. In total, the 2,602 genes are included in the analysis of which 844 represent TFs with high confidence (TF set). Details on gene set curation and probe mapping can be found in the Supplementary Results.

Representing gene expression data as gene pair data

To derive a normalization-independent quantity, we first convert the gene expression values to ranks r within each sample. The quantity that represents the gene pair configuration on a cell type level, the normalized mean rank difference of two genes, δ, is calculated as the mean rank difference of the two genes from each sample that represents this cell type with the requirement that the relative ranking between the pair members must be consistent (always r_g > r_g′ or r_g < r_g′).

Towards this end, let T be an ordered set of cell type labels, G be an ordered set of genes and n_t be the number of samples for t ∈ T (n_t ≥ 2 always). Let R_t = [r^(t) _gi] be the matrix of normalized expression ranks for gene g∈ G, and sample i for cell type t. By averaging over all samples n_t for a given cell type t, we construct the matrix R = [r_gt] of mean normalized expression ranks.

Normalized here means that simple rank values (integers in 1,…,|G|) are scaled by |G|⁻¹ so that r^(t)_gi ∈ [|G|⁻¹,1]. Clearly r_gt∈ [|G|⁻¹,1] as well. In the sequel, we will use “ranks” with the understanding that we are speaking of normalized ranks.

To detect a gene pair expression reversal, we are interested in how the two genes’ ranks differ between cell types. To this end, we define the mean normalized rank difference of two genes in a given cell type:

$$\delta (g,g^{\prime },t)=\{\begin{array}{c}{r}_{g^{\prime }t}-r_{gt}\forall i\in 1,\dots ,n_t:r_{gi}^{(t)}<r_{g^{\prime }i}^{(t)}\text{or}\forall i\in 1,\dots ,n_t:r_{gi}^{(t)}>r_{g^{\prime }i}^{(t)}\\ 0\text{otherwise}\end{array}$$ (1)

Notice that δ(g, g′, t) is non-zero if and only if the genes’ ranks manifest the same strict inequality across all samples associated with cell type t. Clearly, δ(g, g′, t) ∈ (−1, 1). In the text we denote this by δ for short.

Comparison of gene pair data across cell types: gene pair reversal analysis

Because we are interested in reversals of the genes’ relationship between cell types we similarly define the difference of differences as:

$$\mathrm{\Delta }(g,g^{\prime },t,t^{\prime })=\{\begin{array}{c}\delta (g,g^{\prime },t^{\prime })-\delta (g,g^{\prime },t)\text{if}sgn(\delta (g,g^{\prime },t^{\prime }))·sgn(\delta (g,g^{\prime },t))=-1\\ 0,\text{otherwise}\end{array}$$ (2)

Clearly, Δ (g, g′, t, t′) ∈ (−2, 2), and non-zero only if calculated from non-zero values. Those pairs with Δ ≠ 0 are referred to as reversal pairs. In order to extract only results where both members of a gene pair change their mean rank between the cell types, |Δ| ≥ 1 must hold. In the text we use the notation Δ for Δ (g, g′, t, t′).

A simple result to justify thresholds: |Δ| ≥ 1 is possible only when both genes’ mean ranks change between cell types. Assume without loss of generality the mean rank of g does not change between cell types, so r_gt = r_gt′. Then,

$$\begin{array}{l}\mathrm{\Delta }(g,g^{\prime },t,t^{\prime })=\delta (g,g^{\prime },t^{\prime })-\delta (g,g^{\prime },t)=(r_{g^{\prime }{t}^{\prime }}-r_{{gt}^{\prime }})-(r_{g^{\prime }t}-r_{gt})\\ =r_{g^{\prime }{t}^{\prime }}-r_{g^{\prime }t}\end{array}$$ (3)

and −1 < r_g′t′ −1 ≤ r_g′t′ − r_g′t < r_g′t′ ≤ 1 with each inequality by virtue of positivity of [r_gt].

To identify candidate toggle pairs we consider the ternary states Δ < 0, Δ > 0 or Δ = 0 and compare the expected configuration for the lineage split to the observed one within a particular cell type set (with representative cell types of a lineage split). To account for the possibility of obtaining a match by chance, the list is sorted based on the hypergeometric probability of obtaining the given number of reversals across cell type comparisons that include all 166 cell types.

Reversal participation

We define the reversal participation score Ψ to quantify the strength of participation of gene g in (potentially bistable) expression reversals in all pairs of cell types, t and t′. That is, g is fixed for the entire plot displayed, and t and t′ correspond to cell types. This measure of strength is the product of: (the log of) the number of reversals above a given threshold in which the gene participates and the actual magnitude of the strongest (positive or negative) reversal in which it participates.

First, we identify the gene ĝ with respect to which g exhibits the strongest reversal Δ for a given pair of cell types, t and t′ as:

$$\widehat{g}=\underset{\begin{array}{l}{g}^{\prime }\ne g\\ \mid \mathrm{\Delta }\mid >H\end{array}}{argmax}\left|\mathrm{\Delta }(g,g^{\prime },t,t^{\prime })\right|$$ (4)

and then define the reversal participation score as:

$$\mathrm{\Psi }=\mathrm{\Delta }(g,\widehat{g},t,t^{\prime })·{log}_2\sum _{g^{\prime }\ne g}I\left[|\mathrm{\Delta }(g,g^{\prime },t,t^{\prime })|>H\right],$$ (5)

where H is the |Δ | value above which we deem a reversal to have occurred, and I is the indicator function. We use H = 1 in our analysis. As t and t′ range over all 166 cell types, this yields square, skew-symmetric plots. Note that genes ubiquitously high expressed do not show up as reversal pairs thus separating them from lineage-specific high expressed genes.

Finding the top reversal pairs for a specific lineage split

A supervised search for candidate toggle gene pairs was formulated by setting criteria based on biological knowledge of lineage relationships and expected reversal pattern of such a gene pair in the precursor (P), lineage 1 (L1) and lineage 2 (L2) cells. An external (E) group corresponds to cell types outside the lineage split. The search was performed to extract the top pairs of the erythroid-myeloid and B-T lymphoid splits.

Erythroid-myeloid

The hematopoetic stem cell was selected as the precursor cell type (P), L1 has three erythroid (proerythroid, erythroblast, erythrocyte), L2 five myeloid (promyeloid, CD11b+ bone marrow cell, monocyte, CD16+ monocyte and neutrophil) cell types included, and three cell types from the lymphoid lineage (naive CD4+ T cell, naive CD8+ T cell and naive B cell) were selected as an external (E) group.

B-T lymphoid

The hematopoetic stem cell served again as the precursor cell type (P), L1 has four B-lymphoid (naïve B cell, activated B cell, germinal center centrocyte and centroblast), L2 four T-lymphoid (naive CD4+ T cell, activated CD4+ T cell, naive CD8+ T cell and activated CD8+ T cell) cell types included, and the proerythroid and promyeloid cell types were selected as an external (E) group.

We expect no reversals (Δ = 0) in the P-L1, P-L2, P-E, L1-E and L2-E comparisons and always a reversal in all L1-L2 comparisons (Δ < 0 for each L1 vs L2 and Δ > 0 for each L2 vs L1, or Δ > 0 for each L1 vs L2 and Δ < 0 for each L2 vs L1). The exact match is the first filter to find candidate pairs. (The external group can be omitted, but is useful if pairs that do not exhibit expression reversals in neighboring lineages should be excluded.) Additionally, at least one reversal with |Δ | > 1 is required to accept a candidate gene pair to the final list shown. Supplementary Table 7 shows additional results when one or more of these criteria are relaxed. Invariantly, the top pairs presented are among the most promising candidates. Finally, the hypergeometric probability to obtain a defined set of reversals was calculated for each pair and used to sort the gene pairs. To calculate this distribution, the number of successes in the sample corresponds to the observed reversals within the specified cell type set, the number of successes in the population to the observed reversals across all cell type comparisons and the sample size to the number of cell types assigned to P, L1, L2 and E.

Clustering of cell types

We define a similarity measure based on gene pair expression reversals, Φ, as the number of reversal pairs with | Δ | ≥ 1 (as defined above) for a given cell type comparison. By examining all possible pairs of TFs in our dataset we can count the number of reversal pairs {g, g′} between two cell types (X, Y). Then, the greater the number of reversal pairs, the greater the similarity Φ(X,Y) between the two cell types.

The cell lineage was reconstructed using hierarchical clustering with average linkage for the endothelial and hematopoietic cell types. Clustering was applied to terminally differentiated cell types. The hematopoietic and endothelial cells are closely related in early development. A hemangioblast cell type is a progenitor for both hematopoietic and endothelial precursors⁴². In the clustering, we do not have the common precursor cell type present, nor a precursor for endothelial differentiation. Therefore, all endothelial cells are assigned as differentiated cell types. The hematopoietic cell is the common precursor of the blood cell types and placed to the center. There are three early precursor cell types for the erythroid-myeloid lineage: erythroblast, bone marrow promyelocyte and CD11+ cells. In addition, we chose to assign monocyte as a precursor cell type as the data set contains multiple monocyte-derived cell types (macrophages and dendritic cells). There is no early lymphoid precursor in the data set. We chose to assign the naive cell types as precursors. For the B-cell lineage a further maturation step occurs in the germinal centers⁴³. For this reason, the germinal center centrocyte and centroblast were assigned as precursors. The other cell types were considered to represent a differentiated state.

The placement of the progenitor cell types {B₁,…,B_M}, where M is the number of progenitor cell types was done using Hungarian algorithm (HA)⁴⁴ to solve an assignment problem: Let X_n = {Φ(a₁,B_i),…,Φ(a_k,B_i)} and Y_n = {Φ(b₁,B_i),…,Φ(b_l,B_i)} contain the similarities Φ from progenitor cell type B_i to the cell types on the left {a₁,…,a_k} and right {b₁,…,b_l} branch of the node n, n ∈ {1,…,N} respectively and where N is the number of branches in the clustering tree. Here, k and l is the number of cell types in the left and right branches, respectively. Similarity D(n, B_i) of cell type B_i from node n is defined as D(n,B_i) = |mean {X_n} − mean{Y_n}|, where |.| denotes absolute value and mean{.} denotes the mean value from a set of similarities. The obtained similarity matrix D^N,M, containing D(n, B_i) for all the node and cell type pairs is then scaled by the similarity to the ESC from each progenitor cell type type D_s = D·d_esc, where d_esc = [Φ(A_esc,B₁),…, Φ(A_esc, B_M)] and A_esc is the ESC. d_esc is normalized to the [0,1] interval. This makes the ESC a reference point. HA is then applied on D_s to obtain the optimal assignment for each progenitor cell type.

It should be noted that there are more nodes in the clustering tree than there are progenitor cell types with measurement data. Thus, a progenitor cell type is assigned only to best fitting nodes according to HA optimization. For a representation containing all 166 cell types, multidimensional scaling was used to obtain a two-dimensional representation of the full reversal similarity matrix. A landscape is interpolated over the 2D representation of cell types using the similarity Φ to the ESC as elevation.

ChIP-seq data

The ChIP-seq datasets used are listed in Supplementary Table 10 and their use is further described in Supplementary Results. The peak lists as published by the authors were assembled for each TF. The peak sizes were equalized to +/− 250 bp around the peak centre. For the ESC data, overlapping intervals representing the binding of the same protein were merged into one. The intersection of peak lists between pairs of TFs was defined as a minimum 1 bp overlapping region. The genomic region enrichment analysis was performed using the GREAT⁴⁵ tool (binomial test, FDR 1%).

Online resource

The online data resource and interactive tool (http://trel.systemsbiology.net/) encompassing pair-wise comparisons of the genes and cell types presented in this article is available to explore transcriptome diversity in metazoa, accompanied by a user guide and video tutorial. The TF landscape is also available as an interactive browsable format online. The source code to perform the analysis is available upon request.