Sensitivity functions in the estimation of parameters of cellular exchange

Abstract

The analysis of multiple-indicator dilution curves to estimate the rates of transport of ions and substrates across the sarcolemma of myocardial cells requires the formulation of models for the blood-interstitial fluid-cell exchanges. The fitting of models to the sets of experimental data is dependent on acquiring a large enough data set, in one physiological state, that there is at least as much information in the data as there are unknown model parameters to be determined. Inasmuch as data are necessarily noisy, redundancy of data and overdetermination of the unknowns are highly desirable. Sensitivity functions are useful in demonstrating which portions of the data relate to which unknown parameters. They are also useful in adjusting model parameters to fit the model to the data, and therefore in parameter evaluation.

The estimation of unidirectional rates of transport into the cells of intact organs is complex. The transport process cannot be isolated so that its kinetics can be assessed only as a part of a larger system that includes the flow (and its heterogeneity), transport across capillary membranes, diffusion and distribution throughout the interstitial and cellular spaces, and perhaps intracellular consumption. The analysis therefore depends on defining a mathematical analog of the system, acquiring as much data on the system as is possible within a short time while the system is stable, and then analyzing the data by fitting the mathematical model to all of the data at once. The formulation of the model that best fits the data is considered then to provide estimates of the kinetic parameters governing each of the processes involved. In the presence of some variability in the data, and some imperfections or inadequacies in the model compared to reality, one has to question the reliability and accuracy of the parameter estimates. The answer depends on a number of features of experimentation, data collection, and model design as well as model fitting. Sensitivity analysis plays a role in experiment design as well as in analysis, but its contribution depends on accurate data collection and good model design, to neither of which can sensitivity analysis contribute.

MORE DATA, BETTER ANALYSIS?

When one is analyzing a complex system, the fewer redundant data available, the better the analysis should be. In effect, one can say that the more that one measures directly, the less one has to glean from the subsequent analysis. The purpose of modeling in any form is to provide an integrated viewpoint whereby the unknown features of a system, those that cannot be explored directly, are most strongly inferred by the measurements available. Thus if one has a set of data on a four-parameter system and if two of the parameters are known, then the data must be used to infer the values of the missing two parameters; if three are known then all the weight of the data goes toward estimating the one missing parameter value so that, if the model is the correct one, the accuracy of its estimation is greater than if two had to be estimated. The logic of the statement follows on an implicit condition, namely, that the conformation of the model to the data requires the mixed influences of the two missing parameters. This is usually the case, but not necessarily; in some cases, the two different parameters may be determined quite independently from one another from unrelated portions of the data set. In this condition the reduction from two missing parameters to one does not improve the accuracy of estimation of the one.

INFORMATION CONTENT OF DATA

How many independent items of information are contained in a set of data? With respect to even something as simple as a set of multiple-indicator dilution curves such as those described by Bassingthwaighte (2) or Goresky (6), the question is not easy to answer specifically. Let us consider a typical set of outflow dilution curves obtained after the injection of a bolus containing several tracers into the arterial inflow. Such a set might contain an intravascular indicator, albumin, an extracellular indicator, sucrose or L-glucose or cobaltic EDTA (5), and the one of interest that enters cells, D-glucose for example. Of this set the albumin dilution curve has the simplest form and can be described very well by a three- or four-parameter equation such as a γ variate function or a lagged normal density curve (1). Although the curve may be composed of 60 data points, the information content of the intravascular reference curve is really only three or four independent items. (Why three or four? Three suffice when the albumin curve has a smoothly falling downslope close to monoexponential. Four are needed when the tail of the curve is more prolonged by having a relatively low late component, as tends to be the case after injection into left atrium or the apex of left ventricle (3).)

The dilution curves for solutes that penetrate the capillary wall differ in their shapes and therefore contain different information. Now the enumeration becomes more difficult. The initial parts of these curves contain some redundant information; the fraction of the solute that fails to escape from the capillary has the same form as the reference curve, although the amplitude is lower. The later portions contain new information. Looked at individually, the curves for the extracellular solute and the solute that enters and leaves cells probably have forms describable by about six parameters in their governing descriptive equations. There would be one or two more items of information in the latter than the former because of the longer tail of the curve. Again there would be some redundancy: the information contained in a sucrose dilution curve would also be contained in a curve for D-glucose. The total number of items of information for three simultaneous dilution curves might therefore be four plus six plus seven minus redundancy. Suppose the number of truly independent items of information is only 10 of these. Is this enough information to provide good estimates of cellular transport rates?

This question is the critical one. The enumeration above has emphasized the description of a data set by the minimum number of descriptors. Numerical description has value for efficient (if approximate) storage of data sets, for comparisons of sets of data, or for classifying them, but can provide little insight into the behavior of a system. Insight is better provided by defining as precisely as one can what one believes the system to be, and expressing this in comprehensive, integrated fashion, i.e., a model.

MODELING ANALYSIS

The model that we have chosen for myocardial blood-tissue exchange processes is one in which there is dispersive transport through ateries and veins without exchange, and transport through sets of capillary-tissue regions that have a range of flows. (The specific model is that defined by Bassingthwaighte [see ref 2]; the rationale for such models is provided in detail by Bassingthwaighte and Goresky [see ref 4].) The capillary-tissue exchange region is longitudinally distributed, not lumped, and so requires partial differential equations, as given, for example, by Rose et al. (9). The parameters are the capillary flows, the capillary volume, the capillary permeability-surface area product PS_C, the volume of distribution of the solute in the interstitial fluid V′_I, the permeability-surface area product of the sarcolemma of the myocardial cell PS_Cell, the intracellular volume of distribution or equilibrative volume of the entering solute V′_Cell, and a rate constant for intracellular consumption K_Seq. For the reference intravascular solute, two of these are relevant: capillary flow and volume. For the extracellular solute two more are needed: capillary PS_C and interstitial volume V′_I. For the cellular solute, yet two more are needed, PS_Cell and V′_Cell, and sometimes a third, consumption (for substrates but not ions). The capillary-tissue units therefore require a minimum of six items of information, seven if there is consumption. More are needed unless the flows and volumes are the same for all solutes and unless PS_C is the same for the extracellular and cellular solute, as is the case for D- and L-glucose.

Some of the information on the flows and volumes must in practice be obtained from other experiments. For example, if the permeating solutes do not enter red blood cells, the relevant flow of solute-containing mother fluid is not the capillary blood flow but is the plasma flow; the other experiment is therefore simply to measure the large-vessel hematocrit. Capillary volumes are estimated from morphometric estimations from vascular casting, but are limited in applicability because of variation in the number of functional capillaries from one physiological state to another. The volume of distribution within the capillary is governed by the intracapillary hematocrit, information that is more difficult to obtain; approximate values were obtained for the heart from steady-state tracer measurements of 60–70% of the large-vessel hematocrit. Similarly, the interstitial volume V′_I can be obtained from steady-state tracer measurements of the difference in tracer volume of distributions between an extracellular marker and a plasma volume marker. Of the minimum number of seven, enumerated above, such data contribute fragmentary but useful data on two items, capillary and interstitial volumes of distribution, thereby reducing the minimum number of information items needed to approximately five or six. This ignores any influences of heterogeneities in the capillary and interstitial volumes. Steady-state measurements give no information on transport rates PS_C and PS_cell.

The intracellular space V′_Cell may be estimable from steady-state volumes of distribution. When the intracellular distribution is uniform and consumption negligible, then V′_Cell equals the intracellular water space available to solute times the ratio of the conductance for influx to the conductance for efflux across the sarcolemma. When the bidirectional conductances are equal, V′_Cell is the steady-state volume of distribution of the cellular solute minus that for the extracellular solute. Because this situation for passively equilibrated solutes is not applicable to substrates or ions, this is not an information item to be subtracted from our remaining minimum of five or six. Moreover, if PS_C differs for the extracellular and cellular solutes, the minimum is six or seven. There may also be differences in the interstitial volumes of distribution. In the steady state, any binding of the cellular solute to interstitial matrix or the cell surface cannot be distinguished from intracellular retention. They are potentially separable via kinetic studies if the rates of trans-sarcolemmal transport differ substantially from the rates of binding and release from interstitial sites.

The heterogeneity of flows is another item or set of items of information needed. The above minimum, five or six, or six or seven, applied to a single capillary-tissue exchange unit. For an aggregate of such units, further information on the probability density function of flows is needed. The heterogeneity of flows in the hearts of awake intact baboons is large, the standard deviation in flows being about 30% of the mean, as measured in pieces of myocardium of 0.1–0.2 g (1a). Although these distributions are not Gaussian, they are of fairly simple form and are fairly symmetrical. Translated into items of information, this means another two at a minimum, the mean flow and the variance (or the relative dispersion, RD, which is the square root of the variance divided by the mean), and might require three if there is significant skewness or kurtosis. The mean flow is directly measurable in most cases; the use of the microsphere deposition technique allows one to obtain a measure of the whole distribution of flows. When this is done, the capillary flows in each element of the aggregate model are known and the number of needed items is reduced by one to four or five, or five or six.

When only the mean flow is known and the heterogeneity must be defined via the modeling, then the variance and shaping factors (equivalent to skewness and kurtosis) must be defined via the modeling. This brings the needed items back up to six or seven, or seven or eight (depending on whether estimates of PS_C differ for the cellular and extracellular solutes). When the mean flow is not measured, then the needed items number seven or eight, or eight or nine. In their studies of palmitate uptake Rose and Goresky (8) require the seven or eight items. In our studies of D- and L-glucose (7) we needed only four or five; the difference was because we had available measurements of the distribution of regional flows (two items), and because D- and L-glucose have the same PS_C (one item instead of two).

When only 4 or 5 items need to be determined from the modeling of the indicator distribution curves, and the set of curves themselves contain ~ 10 items of information, then on the face of it one should be able to estimate the model parameter values with some assurance. Such comparisons of information items needed with information items available suggest that there is some extra information available. This is surely the desired situation, for noise in the data and fluctuations in the physiological state create inconsistencies that the redundancy helps to offset. Confidence that parameters can be evaluated is reasonable, given the proviso that the data are adequate to allow their distinction, that is, if the experiment design was such that the data are influenced by each of the parameters requiring evaluation. Sensitivity analysis can help to discern if this is so.

SENSITIVITY FUNCTIONS

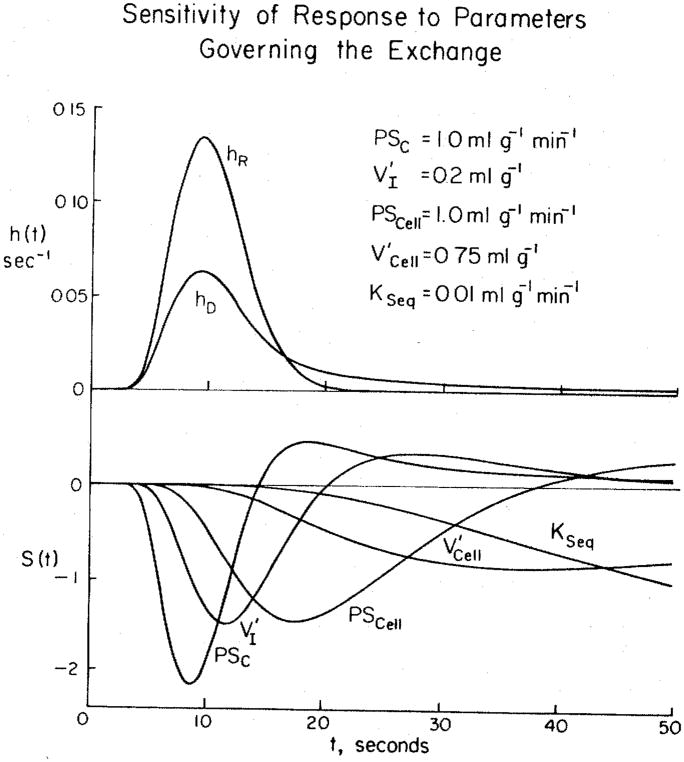
A set of sensitivity functions is shown in Fig. 1 for the model system described above. The sensitivity function of a parameter p is defined as

Figure 1.

Solutions and sensitivity functions for a model of blood-tissue exchange in the heart. Upper panel) Impulse responses for a system consisting of arteries and veins and a set of capillary-tissue units in parallel. The large-vessel transport functions are described by a unimodal density function with mean transit time 7.9 s, relative dispersion 0.34, and skewness 0.75 (3a). The curve for the intravascular reference h_R(t) is the large-vessel transport function convoluted with the weighted sum of 2, fifth-order Poisson operators representing the intracapillary transport and dispersion. The mean capillary transit time was 3.0 s. The curve h_D(t) for the permeating tracer has parameters suitable for D-glucose in the heart. The flow F_s was 1 ml · g⁻¹ · min⁻¹; the parameters governing the exchange and the intracellular sequestration K_Seq are listed. Lower panel) Sensitivity functions for each of the governing transport parameters. Note that all are different from the others, and that they are ordered in time in accordance with the sequence of solute transport from blood into the cells. The functions S(t) are for 1 % changes in parameter values and multiplied by scalars for display purposes: the scalars are 1 for PS_c, 160 for V′_I, 5 for PS_Cell, 500 for $V_{\text{Cell}}^{\prime }$, and 1500 for K_Seq.

$$S_p(t)=\frac{\partial {\widehat{h}}_D(t)}{\partial p}\doteq \frac{\mathrm{\Delta }{h}_D(t)}{\mathrm{\Delta }p}$$ (1)

In the figure, h_R(t) is the impulse response for the intravascular reference tracer and h_D(t) is the impulse response for a tracer that escapes (by diffusion or other process) across the capillary wall. For calculation of the curves, the parameter values were perturbed by 1%. The S_p(t)’s are the magnitude of the change of ĥ_D(t), the model solution for the permeating tracer, per unit change in parameter value around the current value; the units are therefore second⁻¹ divided by the units of the parameter. Sensitivity functions may be used in a dimensionless fashion, e.g., the fractional change in ĥ_D(t) per fractional change in the parameter value. How they should be calculated depends on both one’s point of view and the objective. For example, the fractional change in a parameter value around zero makes no sense whereas the absolute change gives clear information on the influence of turning a process on or off.

The simplest question that sensitivity analysis can answer is whether or not the parameters are mathematically independent. (Although this sounds like a trivial question, dependence is not always so obvious from the formulation of the equations for a complex system.) If two parameters appear inseparably as a product in the equation, as do the permeability P and surface area S of the barriers, then their sensitivity functions are identical. If two parameters occur inseparably as a quotient, then their sensitivity functions will be mirror images of one another. It is clear from Fig. 1 that neither of these simple dependencies occur. In this case this result could easily be anticipated because the partial differential equations are simple, but in more complex systems dependencies or similarities in sensitivities can be demonstrated that are not so obvious from the form of the equations.

The marked differences in positions and shapes of the sensitivity functions in Fig. 1 illustrate the separability of the influences of these parameters. The sequence of peak influences is just what one would expect: the ordering is the same as for the processes involved, permeation of the capillary wall, dilution in the interstitial fluid volume, permeation of the sarcolemma, dilution in the intracellular space, and finally, removal or sequestration by an intracellular reaction, e.g., the irreversible hexokinase reaction for D-glucose. All these five processes influence the curves in different ways and have their peak influence at different times, and each has an influence at some time that is opposite in sign to each of the others. Such a plot demonstrates the possibility of obtaining estimates of parameter values from the observed curves. Sensitivity functions are shown here only for the permeant solute. Nevertheless, the reference curve is critically important; not even the most accessible parameter PS_C can be calculated without the h_R(t) data because it provides the required information on the form of the concentration-time curve passing by the capillary exchange region.

The sensitivity functions are dependent on the values of other parameters. For example, if PS_Cell is close to zero, so little tracer enters the cell and leaves again that $V_{\text{Cell}}^{\prime }$ and K_Seq would remain unknown. A subtler situation is the influence of PS_C on the sensitivity to PS_Cell the higher the value of PS_C the less sensitive h_D(t) is to changes in PS_C and the more it is sensitive to PS_Cell and the other processes beyond the capillary barrier. The extreme case is obvious: if capillary PS_C is infinitely high then it has no influence at all; all remaining sensitivities result from processes in the interstitial fluid and the cell. In this sense the parameters have interacting influences on the importance of the others, but they nevertheless remain separable, and each remains identifiable so long as there is significant sensitivity to it.

SENSITIVITY FUNCTIONS IN EXPERIMENTAL DESIGN

The form of the sensitivity functions and their magnitudes give some hint as to the design of the experiment. For example, with reference to Fig. 1, if the goals were to estimate only PS_C and V′_I and PS_Cell were zero, then the data could be collected over only the first 20 s. This would be economically sensible. A more general criterion would be to collect the data until h_R(t) has diminished from its peak value to about 10% of the peak. Using an on-line detector, for example, indocyanine green detection through a densitometer, one can simply stop the outflow sample collection when the reference curve of indocyanine green bound to albumin diminishes to 10% of peak.

However, if estimates of cell volume or consumption are required, then data at long times are required. This is particularly so for these two parameters because their influences overlap so much. The data should be collected for 1.5–3 min—it is only at such late times that the influence of $V_{\text{Cell}}^{\prime }$ becomes positive and therefore opposite in sign to that of K_Seq. K_Seq always has a negative influence on h_D(t) because it represents a unidirectional process of removal, and therefore inhibits return flux to the outflow.

SENSITIVITY FUNCTIONS IN PARAMETER OPTIMIZATION

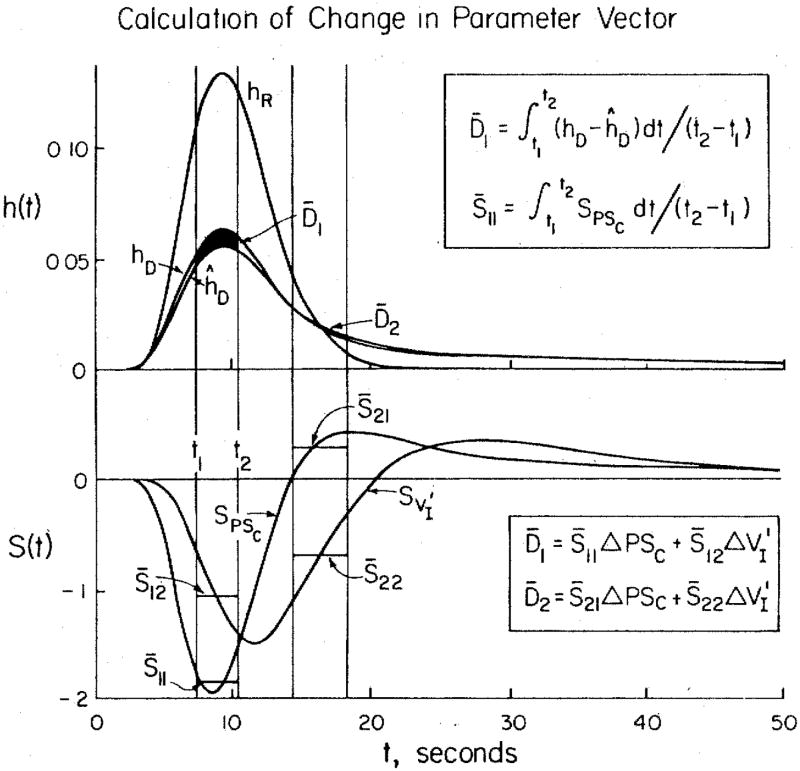
This is a new application of sensitivity functions that is in the process of development (7). The goal is to use local values of the sensitivity functions and estimates of the local distances between the model function and the data curve to adjust all the model’s free parameter values at once. An example is shown in Fig. 2 for a case in which there are only two unknowns, the capillary permeability-surface area product PS_C and the interstitial volume of distribution V′_I.

Figure 2.

Calculation of adjustment in parameter vector for fitting a model to data. There are two unknowns, PS_C and V′₁. The intravascular reference data curve is h_R(t). The model curve ĥ_D(t) differs from the data curve h_D(t): the differences in each of the two time windows are given by the average differences D̄₁ and D̄₂, the area divided by the window width. The average values of the sensitivity functions in the two time windows are given by the S̄’s. These give the coefficients defining the influences of the two parameters in each of the two regions along h_D(t).

The two data curves (actually model solutions) are h_R(t) and h_D(t). A model solution ĥ_D(t) is shown for only the permeating tracer; h_R(t) is fitted exactly by the model. Proper adjustment of the two parameters of ĥ_D(t) would give a perfect fit to h_D(t). The approach is the same as is used for the average differences D̄₁ and D̄₂ in each time window that are explainable in terms of the average sensitivities, the S̄’s, to each of the parameters in each window. The system is not linear, but the form of these influences can be considered to be a Taylor series, of which we use only the first term. The linear approximation can then be written simply:

$$\begin{array}{l}{\overline{D}}_1={\overline{S}}_{11}\mathrm{\Delta }{p}_1+{\overline{S}}_{12}\mathrm{\Delta }{p}_2\\ {\overline{D}}_2={\overline{S}}_{21}\mathrm{\Delta }{p}_1+{\overline{S}}_{22}\mathrm{\Delta }{p}_2\end{array}$$ (2)

where Δp₁ and Δp₂ are the steps in PS_C and V′₁ required to reduce D̄₁ and D̄₂ toward zero. Then the matrix is inverted to solve for the Δp’s:

$$\begin{array}{l}\mathrm{\Delta }{p}_1=({\overline{S}}_{22}{\overline{D}}_1-{\overline{S}}_{12}{\overline{D}}_2)/detS\\ \mathrm{\Delta }{p}_2=({\overline{S}}_{11}{\overline{D}}_2-{\overline{S}}_{21}{\overline{D}}_1)/detS\end{array}$$ (3)

where detS is the determinant S̄₁₁S̄₂₂ − S̄₁₂S̄₂₁.

The vector p in parameter space is adjusted so that p_new is p_old + Δp, and new solutions are obtained. The process can be repeated until the fit is satisfactory: the criterion for stopping the iterations may be some measure of goodness of fit, locally or globally. A least-squares assessment of the goodness of fit may be made even though it is not used in the algorithm for parameter adjustment.

For each iteration, new sensitivity functions are computed, and new window positions are chosen in accordance with the shifts in peak sensitivities, the maximal separability of the influences, and the regions of major difference between h_D(t) and ĥ_D(t). The method of Levin et al. (7) used only the distance function at the points of peak sensitivity. This simplification allowed oscillations to occur sometimes in the parameter vector p as a good fit was approached. Smoothing of the data and using finite window widths help prevent such instabilities. There are therefore a number of improvements to be made in the interests of gaining further efficiency.

CONCLUSION

Sensitivity functions are useful in giving an investigator a semiquantitative feeling for the influences of changes of parameter values on the behavior of a system of equations. When the biological system is complex but still describable, even though imperfectly, by sets of equations then the sensitivity functions may be useful in the design of optimal experiments that will elucidate the parts of the system least well known. As a corollary to this, the sensitivity functions can be used directly to adjust parameters of models of the system to fit experimental data.