Computing the Free Energy Barriers for Less by Sampling with a Coarse Reference Potential while Retaining Accuracy of the Target Fine Model

Abstract

Proposed in this contribution is a protocol for calculating fine-physics (e.g., ab initio QM/MM) free-energy surfaces at a high level of accuracy locally (e.g., only at reactants and at the transition state for computing the activation barrier) from targeted fine-physics sampling and extensive exploratory coarse-physics sampling. The full free-energy surface is still computed but at a lower level of accuracy from coarse-physics sampling. The method is analytically derived in terms of the umbrella sampling and the free-energy perturbation methods which are combined with the thermodynamic cycle and the targeted sampling strategy of the paradynamics approach. The algorithm starts by computing low-accuracy fine-physics free-energy surfaces from the coarse-physics sampling in order to identify the reaction path and to select regions for targeted sampling. Thus, the algorithm does not rely on the coarse-physics minimum free-energy reaction path. Next, segments of high-accuracy free-energy surface are computed locally at selected regions from the targeted fine-physics sampling and are positioned relative to the coarse-physics free-energy shifts. The positioning is done by averaging the free-energy perturbations computed with multistep linear response approximation method. This method is analytically shown to provide results of the thermodynamic integration and the free-energy interpolation methods, while being extremely simple in implementation. Incorporating the metadynamics sampling to the algorithm is also briefly outlined. The application is demonstrated by calculating the B3LYP//6-31G*/MM free-energy barrier for an enzymatic reaction using a semiempirical PM6/MM reference potential. These modifications allow computing the activation free energies at a significantly reduced computational cost but at the same level of accuracy compared to computing full potential of mean force.

Introduction

A valuable theoretical insight on mechanisms and rates of chemical reactions can be obtained from ab initio QM/MM free-energy surfaces. One of the main challenges in computing the free-energy surfaces is high computational cost due to multiple evaluations of electronic structures during configurational sampling. To overcome this limitation, a class of computational methods has emerged, which shares the idea of using a coarse-physics reference potential¹ (RP) to compute the minimum free-energy reaction path, to which a correction is added to approximate the ab initio QM/MM free-energy surface and(or) the corresponding activation barrier. While the computational cost can be reduced, by up to two orders² with one-dimensional (1D) reaction coordinate, obtaining reliable estimates for the ab initio QM/MM activation free-energy with these approaches still remains challenging.³ Perhaps, one of the main reasons is approximating the fine-physics reaction path with the coarse-physics counterpart. The coarse-physics free-energy surface can be substantially different from the ab initio QM/MM free-energy surface. A possible solution to this problem is to reweight the distribution of the reaction coordinate, using, for instance, the umbrella sampling⁴ or some alternative⁵ approach. Reweighting in fact was an early implementation of the method.^1a,1c However, it was found that obtaining convergent free energies is problematic due to a poor overlap between the RP and the ab initio QM/MM target potential (TP), what leads to the regime where the umbrella sampling becomes inefficient.⁴ The second reason is obtaining convergent estimates for the free-energy perturbation (FEP), which is often used to estimate the ab initio QM/MM free-energy correction to the coarse-physics reaction path. A popular solution to latter problem involves fixing the reacting fragments in a configuration from a predetermined reaction path, which essentially boils down to evaluation of a higher level-of-theory solvation free energy for a given solute configuration.^1f,1g,6 An alternative approach involves refinement of the RP,^1b which, however, can be a relatively time-consuming operation, since, in general, it is not a trivial automatic procedure. The third approach involves performing a limited sampling with the TP,^1d thus improving the FEP estimates by the multistep transformation (it is important not to confuse the efficiency of a method with the efficiency of the multistep perturbation, involving sampling from, at least, both the fine-physics and the coarse-physics ensembles). Two latter strategies have been gradually introduced and realized in the paradynamics model^2,3b which relies on refined empirical valence bond RP⁷ and evaluates the ab initio QM/MM correction using a two-step linear response approximation (LRA).⁸

Described in this work is a protocol which is based on the dual sampling (from both ensembles) and on the thermodynamic cycle of the paradynamics approach but is novel conceptually and algorithmically. The main idea of this method is to exactly compute the ab initio QM/MM free-energy surface locally, without relying on (and even computing) the reference free-energy surface. In other words, the coarse-physics solution is used as the initial guess for the fine-physics solution. Here these solutions are not the actual free-energy surfaces but the free-energy penalties of introducing the bias at reactants and at the transition state to the coarse-physics potential and to the fine-physics potential. Once the free-energy penalty of biasing the ab initio QM/MM is known, the umbrella sampling is used to provide a reliable estimate of the free-energy surface locally using the biased potential. While computing potential of mean force (PMF) with the umbrella sampling method, one has to calculate these penalties with the fine-physics potential in a multistep transformation. Here instead, it is computed using a thermodynamic cycle with the coarse-physics potential by introducing the bias to the coarse-physics potential and then switching the force law to the fine-physics potential. Another modification is that the actual fine-physic reaction path is located using a low-accuracy fine-physics free-energy surface obtained from the coarse-physics sampling.

The paper is organized as follows: in Methods, the techniques used in this work for computing the free change of altering the potential are reviewed: the exponential configurational average,⁹ the linear response approximation, and the thermodynamic integration. Furthermore, the equivalence of the LRA method to the TDI method for considered applications is demonstrated analytically and relation to the free-energy interpolation is shown. Next, the umbrella sampling method and the weighted-histogram analysis method¹⁰ (WHAM) are reviewed in the section dedicated to computing PMF. Finally, these methods are applied to derive the main equations of the presented approach, which is also shown to yield other formulations of the RP-based strategies as private cases while approximating the umbrella sampling equation. The algorithm for solving is formulated as an iterative strategy for improving accuracy of the target free-energy surface at selected regions to the level achieved in computing PMF. In Examples, the application of the considered method is provided with a comparison to the PMF results.

Methods

Computing Free-Energy Change of Altering the Potential

FEP: Free-Energy Perturbation

The free-energy change of moving from one potential to another (altering the force law) is calculated using the FEP method.^9,11 It involves evaluating the exponential average of the energy gap between two potentials. For instance, the free-energy of moving from a reference state described with a coarse-physics RP to the state defined by a fine-physics TP, E_REF → E_TGT, is

1

Here β^–1 = kT (Boltzmann constant multiplied by absolute temperature); ΔE(x) = E_TGT – E_REF is the energy gap; x is the coordinate vector; and N is the number of particles

The configurational average can be computed over time or over ensemble using molecular dynamics or Monte Carlo simulations, respectively:

2

Here and further on ⟨...⟩_Ei indicates that sampling is performed with the potential E_i, while obtaining the Helmholtz free energy for the canonical (NVT) ensemble. This formulation can be easily generalized to the Gibbs free energy (NPT) and other thermodynamic ensembles.^5,12

The free-energy change can be computed for the reverse process by taking the configurational average with the TP:

3

Ideally (in the limit of infinite sampling or infinitesimal perturbation):

4

However, in practice the forward FEP and the backward FEP of eqs 2 and 3 can show a hysteresis, and the corresponding average is a way to obtain a more reliable estimate.¹³

LRA: Linear Response Approximation

The perturbation in eqs 2 or 3 can be expanded in the power series and truncated¹⁴ to the linear free-energy expansion. While such an expansion can be done for both eqs 2 and 3, what would lead to the linear response approximation (LRA), the computational power of LRA was revealed from inspecting free-energy functions of the energy gap:⁸

5

Multistep Free-Energy Transformation

It was demonstrated in the context of the various free-energy calculations^8,15 and for the RP approach in particular^3b that a more reliable estimate of the corresponding free-energy change is obtained from averaging on both end-point potentials (RP and TP). Similar conclusion was made in derivation of the acceptance ratio method by Bennett, who also noted that this can be seen from the Gibbs–Bogolyubov inequality:¹⁶

6

To further improve the free-energy convergence, the perturbation is computed in a multistep manner by creating a series of n intermediate mapping potentials between the end points potentials E_REF and E_TGT:

7

This is achieved by changing the perturbation parameter λ_m from 0 to 1 with an increment of δλ. The multistep implementation of eq 7 involves sequentially applying the FEP scheme for adjacent simulation windows, so that the average of the forward FEP and the backward FEP is given by

8

TDI: Thermodynamic Integration

Alternatively, the same free-energy change can also be estimated by the thermodynamic integration (TDI) approach, which, however, requires analytical partial derivative of the free energy with respect to some perturbation parameter λ.

9

Here, the integral in eq 9 is computed numerically using a trapezoidal numerical integration. Substitution of the corresponding derivative of eq 7 with respect to the perturbation parameter to eq 9 yields

10

Multistep LRA, its Equivalence to TDI, and Relation to Free-Energy Interpolation

Finally, the multistep FEP of eq 7 can be computed with the multistep LRA approach,^3b which is just the generalization of the LRA to the multistep transformation:

11

Note that E_m+1 – E_m = Δλ·ΔE, and therefore, the multistep LRA and the multistep TDI eqs 10 and 11 are, in fact, identical.

In the limit of a big n, all the approaches give the same result; however, to minimize the computational cost, a small value of n is desired. The questions of statistical efficiency of analyzing data in free-energy calculations with aforementioned and the acceptance-ratio based schemes (as well as its relation with aforementioned methods) are discussed in great detail elsewhere.^16,17 In ref (16), it is mathematically shown that in the case of overlapping distribution (histograms) of the energy gap the acceptance ratio method (which is not covered here) is statistically very efficient, while in the case of a poor overlap between two energy gap distributions, the free-energy interpolation (the curve-fitting method) has an advantage. In Appendix 1, the relation of the LRA scheme to the curve-fitting method is analytically demonstrated. Thus, this relation provides theoretical support for using the LRA to compute the free-energy change while moving from RP to TP (when one expects a poor overlap of distributions) and additionally provides a possible recipe for improving the LRA estimate. The choice of the LRA and multistep LRA techniques was already validated by comparing to the average FEP with the multistep transformation^3b in the study which also showed that the most important part in computing the free-energy perturbation is to include sampling from both ensembles.

Computing High-Accuracy Free-Energy Surface

Mapping Free-Energy Surface by Sampling with Biased Potential

In order to efficiently sample the elevated regions of the reaction free-energy surface, the potential is modified by introducing a harmonic bias, centered at a particular value of reaction coordinate:

12

Here ξ designates a chosen reaction coordinate; ξ_m⁰ is the center of the harmonic bias, and the original potential is E_QM. In order to sample along the whole range of the reaction coordinate values, a set of harmonic biases is created by changing the mapping (coupling) parameter λ_m incrementally from 0 to 1:

13

Here ξ_LB⁰ and ξ_UB correspond to the values of the selected ξ at the lower and the upper boundaries. Since the convergence of FEP depends on the energy gap between the two potentials, implementation of eq 7 might give a faster convergence when there is a large energy gap between the two potentials.¹³ But the multistep approach of eq 13 provides more control in sampling the free-energy surface along the RC.

When reaction coordinate is represented by a two-dimensional vector, with ξ₁ and ξ₂ components, the corresponding mapping potentials include two harmonic biases, E_m = E_m(ξ₁,ξ₂):

14

The choice of the RC is problem-dependent, common examples include the energy gap RC (for empirical valence bond⁷ and similar potentials¹⁸) and nuclear RC (for molecular-orbital-based potentials).

Free-Energy Penalty of Introducing Bias to Potential

The reference state for the FEP methods is defined as the original potential, while the target state can be defined as the biased potential. This formulation is used for the mapping potentials E_m given by eq 12 in eqs 8, 10, and 11 to evaluate the relevant free-energy changes of introducing the bias. While applying FEP and LRA approaches to estimate the free-energy perturbation is similar to the previously considered case, the TDI approach requires calculation of a new partial derivative, since the perturbation parameter now is given by eq 13. The corresponding derivative for eq 9 (with the fixed force constant) is given by

15

By expanding the LRA eq 11 using eq 12 and eq 13 one arrives at

16

In Appendix 2, it is shown that with the perturbation parameter given by eq 13, the multistep LRA formulation is equivalent to the result of numerical thermodynamic integration using a trapezoidal rule with the derivative given by eq 15.

As was already mentioned, the multistep formulation of eq 13 provides an effective way of improving the efficiency of sampling along the reaction coordinate, which is crucial in PMF calculations. The efficiency of sampling can be monitored by creating a distribution function (histograms). For the best sampling efficiency, one should try to achieve a uniform distribution, which can be done by adjusting the force constants. However, increasing the force constant will require increasing the number of simulation windows to ensure the even sampling distribution (histogram overlap) along the whole range of the reaction coordinate. Special care should be taken when the initial system configuration is far from the minimum on the mapping potential, since it might create strong biasing forces. One way to solve this is to gradually increase the force constant while monitoring, in parallel, the deviation of the reaction coordinate from the center of bias.

Umbrella Sampling Method

The ultimate goal in the free-energy simulation, however, is to obtain the probability distribution (and the corresponding PMF) with unbiased potentials. Therefore, it is necessary to recover the corresponding Boltzmann probability distribution from the sampling obtained with mapping potentials. The target PMF obtained with a TP is given by

17

where the probability distribution function of the reaction coordinate is

18

In order to improve the sampling efficiency, a bias is introduced to the original potential (e.g., see eqs 12 and 14). The unbiased probability distribution of eq 18 is related to the configurational averages computed with the modified (biased) target potential given by eqs 12 or 14, which is further called T_m, through the umbrella sampling formula:⁴

19

Rewriting this equation in terms of the free-energy¹⁹ changes gives two terms:

20

The first right-hand side (rhs) term (the denominator of eq 19) is the free-energy penalty for introducing a bias (cf. eq 2), which can be calculated by any FEP method with a multistep scheme. The second rhs term is the numerator of eq 19, and it arises from the probability distribution of the reaction coordinate.

Combining the result of several mapping potentials when calculating the PMF can be done by overlaying points²⁰ generated with all mapping potentials using eq 20. Also, the free-energy functions can be obtained by calculating the weight-average among different mapping potentials, which is called the weighted PMF (w-PMF):²¹

21

Within the umbrella sampling formulation of eq 19, the bias to the original potentials can also be represented by Gaussians, EVB mapping potential, etc.^3b Once the free-energy levels, corresponding to denominators of eq 19, are known, one can immediately evaluate multiple distributions [e.g., two-dimensional (2D) projections from 1D mapping].

Weighted Histograms Method

Another tool, employed to combine results of simulations is weighted histograms analysis method, WHAM:^10a,22

22

23

WHAM equations provide both the PMF and the free-energy penalties of introducing the bias.

Reducing Computational Cost of Computing Free-Energy Surfaces

Low-Accuracy PMF from Reweighting

The methodology described in the previous section is a conventional way of calculating the PMF. However, mapping the reaction free-energy surface with a fine-physics TP is extremely computationally expensive, particularly in a many dimensional reaction coordinate space, since one has to perform a long configurational sampling with multiple mapping potentials. While using the coarse-physics sampling significantly reduces the computational cost, the main question becomes how to use this sampling to obtain reliable estimates for the fine-physics model.

A straightforward implementation of the RP approach involves performing sampling exclusively with the RP, followed by applying a reweighting strategy such as umbrella sampling^1a or WHAM-based reweighting strategy.⁵

From sampling performed with a biased reference potential given by eq 12 (which is further called R_m), the fine-physics distributions are recovered with eq 19, which becomes

24

With the use of the free-energy representation eq 20, the denominator of eq 24 can be represented as two free-energy terms:

25

But ΔF(E_TGT → E_REF) does not depend on the bias ξ_m⁰ and the dependence on the reaction coordinate is integrated out, it is a constant free-energy shift, which can be subtracted from the free-energy shifts for all mapping potentials R_m, whereas the second term is accurately evaluated from sampling with the RP using the multistep FEP.

Thus, evaluation of the numerator in this approach is the most problematic step due to a poor overlap in the configurational space (the regime in which the umbrella sampling is inefficient). In other words, configurations generated with the RP are, mostly, unlikely configurations for the TP. The corresponding sampling is not representative for the TP, and the PMF convergence is slow, thus providing a low-accuracy estimate.

Low-Accuracy PMF from FEP

An alternative to computing the low-accuracy target free-energy surface with the reweighting approach of eq 24 is based on computing the vertical free-energy perturbation from the high-accuracy coarse-physics PMF. The free-energy perturbation is calculated with the RP averages only, that is using eq 1 or its linear expansion. This method of computing the perturbation is very similar to a number of other reference-potential based strategies.^1h,23 The reaction coordinate distribution is evaluated with the RP only. Mathematically it is equivalent to the approximation:

26

Note that E_TGT – T_m = E_TGT – T_m = −K(ξ – ξ_m⁰)². Then the denominator of eq 19 which is the free-energy of introducing the bias to the target potential is computed via the thermodynamic cycle ΔF(E_TGT → T_m) = ΔF(E_TGT → E_REF) + ΔF(E_REF → R_m) + ΔF(R_m → T_m), where the first two terms are discussed in the previous section and the last term is computed using the linear expansion, thus

27

While the convergence of eq 27 is limited by convergence of the denominator, the accuracy of evaluating the activation free-energy is also limited by the assumption of eq 26, which with 1D representation of the reaction coordinate is additionally equivalent to the assumption of the same reaction paths.

Paradynamics

In certain cases, the assumption of similarity of reaction paths can be justified, but it is hard to quantify the error: it might work in some cases and fail in others. The issue is addressed using a parametric or functional fitting of the RP to the TP, what was proposed and implemented in the paradynamics approach for empirical valence bond method² (for semiempirical methods, such refinement can be adapted from other works²⁴). However, performing parametric refinement of the RP is a nontrivial task and requires a good knowledge of the potential. An alternative strategy^3b involves functional refinement of the RP by adding the difference between the RP and the TP along the reaction coordinate approximated by Gaussian functions. In recent works,^1h,23a an implicit refinement strategy is used by choosing a suitable semiempirical RP, what requires a detailed knowledge on the parameterization of the potential.

The paradynamics approach assumes that after refinement the reaction paths on the reference and on the target free-energy surfaces are very close, and the error is limited by the denominator in eq 27. To address this issue, the perturbation is computed using the two-step LRA eq 5. The LRA approach is applied to compute the free-energy perturbation while switching from the RP biased at reactants and the TS, ξ_m⁰ ≈ ξ_REF, to the TP^3b with the same bias, assuming that ξ_TGT^≠ ≈ ξ_REF. Then by virtue of eq 26, the free-energy perturbation reproduces the difference between two free-energy functions: ΔF(R_m → T_m) = F_TGT (ξ_TGT^≠) – F_REF (ξ_REF).

In the case when the transition paths (transition states) are dissimilar, ξ_REF^≠ ≈ ξ_TGT, reliably computing the activation free-energy [even if the free-energy perturbation ΔF(R_m → T_m) converges] would generally represent significant challenges, since it might not provide the necessary estimate of moving to the fine-physics path.

In this work, another strategy for improving reliability and accuracy of the free-energy estimates, alternative to refining the reference potential, is proposed. It is based on computing the low-accuracy target free-energy surface using eqs 24 and 27 (both schemes are realized simultaneously). These surfaces are used only for the purposes of locating the reactants and the transition state for the subsequent limited sampling with the TP. Once the reaction path on the target free-energy surface is located, the fine-physics targeted sampling is performed at those regions. This is the main difference between the presented approach and other reference potential-based approaches, which compute the correction to the reference PMF, thus relying on relevance of the coarse-physics reaction path.

It is essential that the coarse-physics sampling is not restricted along the narrow coarse-physics reaction path (in order to cover the fine-physics path). This can be generally achieved by calculating the free-energy surface for the reaction coordinate representation, which dimensionality is capable of capturing both paths. One can see the problem of using a 1D reaction coordinate in movies provided as additional external files (https://www.dropbox.com/sh/53a4coext3i3ywq/0f9jxzTruI): the coarse-physics sampling is confined to the coarse-physics path and the fine-physics path being poorly sampled. This difference can be even more extreme when the corresponding reaction paths are more associative and dissociative. In that case, using a 2D representation of the reaction coordinate (and mapping the free-energy surface in two dimensions using eq 14 instead of eq 12) is rather necessary and would result in a better sampling along the fine-physics path and a more reliable estimate of the low-accuracy free-energy surface but at a greater computational cost.

High-Accuracy Local PMF Regions from Targeted Sampling

In the proposed approach, the accuracy in evaluating the numerator of eq 19 ⟨δ(ξ′ – ξ)exp[− β(E_TGT – T_m)]⟩_Tm is not reduced compared to PMF calculations by taking advantage of the limited fine-physics sampling targeted at the selected regions of the low-accuracy free-energy surface (computing the low-accuracy free-energy target surface allows identifying the local PMF regions for the targeted sampling). However, computing the reaction coordinate distribution from this sampling provides the full accuracy PMF regions only locally.

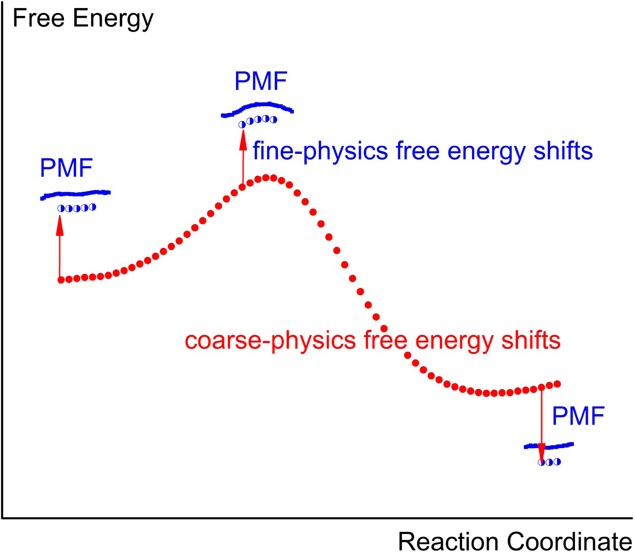
To compute the reaction barrier accurately in PMF calculations, the denominator in eq 19 is computed using a multistep FEP procedure (in other words, using many overlapping histograms in WHAM). This perturbation is associated with the free-energy penalty of introducing the bias to the original TP (see Figure 1). Alternatively, this penalty is computed with the thermodynamic cycle identical to the paradynamics model:

28

Figure 1.

Calculating the activation free-energy by positioning local PMF regions relative to the coarse-physics free-energy shifts instead of computing full PMF from fine-physics sampling. PMF calculations involve sampling with a series of biased fine-physics potentials T₁..T_M.. along the reaction coordinate (cyan circles). These mapping points are sequentially connected using the multistep free-energy perturbation ΔF(T₁ → T_M), what is depicted by cyan arrows. An alternative approach involves computing PMF locally (blue dots) using fewer fine-physics potentials (blue stars). The free-energy difference ΔF(T₁ → T_M) is instead computed from the thermodynamic cycle, shown by blue and red arrows. Red arrows show connecting a sequence of biased coarse-physics potentials R₁..R_M.. using the multistep free-energy perturbation ΔF(R₁ → R_M). Blue arrows show the free-energy perturbation of switching from the coarse-physics potential to the fine-physics potential (both having the same bias) at reactants and at the transition state, ΔF(R_i → T_i). This allows for the positioning of two local PMF regions (blue dots) and to determine the activation free-energy (shown with a black arrow).

The first rhs term of eq 28 does not depend on the reaction coordinate and is just a constant shift (same at the reactants and at the TS), the second term is accurately calculated while mapping the free-energy surface with the RP. While ξ_m⁰ ≈ ξ_TGT can be different from the bias, close to the ξ_REF^≠, the corresponding free-energy penalties ΔF(E_REF → R_m) are computed and well-converged for all biases from mapping with the RP. The last term can be calculated by any FEP methods presented above, but the actual estimate is taken from LRA (which as shown in Appendix 1 is closely related to the free-energy interpolation approach which provides a more reliable estimate when two distributions of the energy gap poorly overlap¹⁶):

29

Note, however, that if the biases are different in R_m and T_m (e.g., different force constants), the equation should be

30

In practice, better estimates of the TS and RS regions of the target free-energy surface are obtained with several mapping potentials favoring sampling of the respective regions (see Figure 1), those estimates can be averaged using the procedure described below for even more accurate estimates. The overall efficiency of this approach therefore is determined by convergence of eq 29. For a RP retaining adequate physical description of changes in electron density of reacting fragments, the corresponding structural changes in the system upon moving to the TP biased at the same region of the free-energy surface are smaller than changes caused by moving the system on the TP from the reactants to the transition state. In other words, the perturbation of eq 30 should converge in less simulation windows than the perturbation associated with changing the reaction coordinate according to eq 13. Furthermore, the method computational cost relative to the conventional PMF approaches will increase as the reaction coordinate dimensionality increases.

Improving Accuracy of Positioning Local PMF Regions

To further improve accuracy of positioning the local PMF regions, the multistep transformation of eq 7 is used^3b until the left-hand side of eq 29 convergence. In practice, the multistep LRA eq 11 is used since it involves only computing the energy gap. The difference between three-steps and two-steps LRA estimates are added to the rhs of eq 28. Once ΔF(R_m → T_m) is converged by virtue of eqs 28 and 20 the estimate of the activation free-energy barrier is of the same accuracy as computing eq 20 with the PMF approach.

The main steps of the proposed algorithm are summarized in Figure 2.

Figure 2.

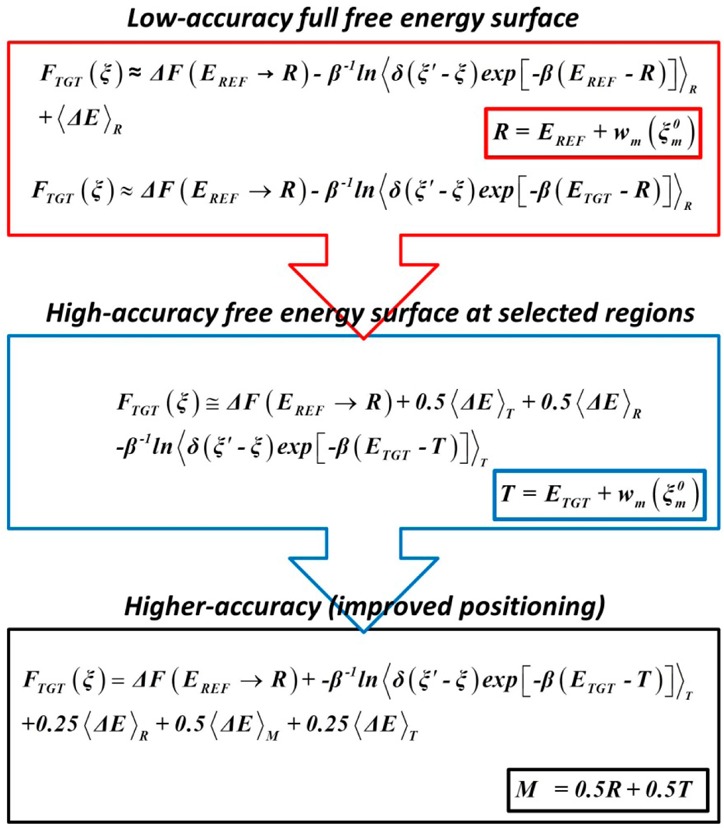
Iterative accuracy improvement of the fine-physics free-energy surface computed from coarse-physics sampling. The first step involves computing a low-accuracy free-energy surface from the coarse-physics sampling by reweighting and by free-energy perturbation approaches (red upper block). All ensemble averages are computed with the coarse-physics reference potential, <···>R. Once the surface is constructed, the regions of interest (reactants and the transition state) are identified. In the next step, a limited fine-physics sampling is performed at those regions. This allows computing the ensemble averages with fine-physics target potential <···>T, which are used to calculate a high-accuracy free-energy surface at those regions (blue medium block). After the second step, the accuracy becomes limited by positioning the local regions. In the third step, a limited sampling is performed in the same regions with a linear combination of the two potentials. With the use of the generated data, the free-energy perturbation is further improved by including the corresponding average for the intermediate ensemble.

All methods, reviewed above, are implemented in the PD-M program. It is currently available from the author upon request.

Examples

To demonstrate application of this method, a computational study is performed on an enzymatic reaction, which is shown in Figure 3. The system consists of an enzyme, haloalkane dehalogenase, with a substrate, 1,2-dichloroethane. The reaction scheme, which describes nucleophilic substitution, the S_N2 mechanism, is given in Figure 4. The QM region includes atoms shown in Figure 4, where one of the hydrogen is a link-atom. A semiempirical PM6/MM²⁵ potential was taken as a reference potential and a hybrid density functional theory B3LYP²⁶//6-31G*/MM as a target potential. To demonstrate that the proposed approach is capable of delivering the activation free-energy estimate of the same accuracy as the full PMF scheme, the target PMF was computed. Next, the activation free-energy was computed using the developed algorithm, outlined in Figure 2.

Figure 3.

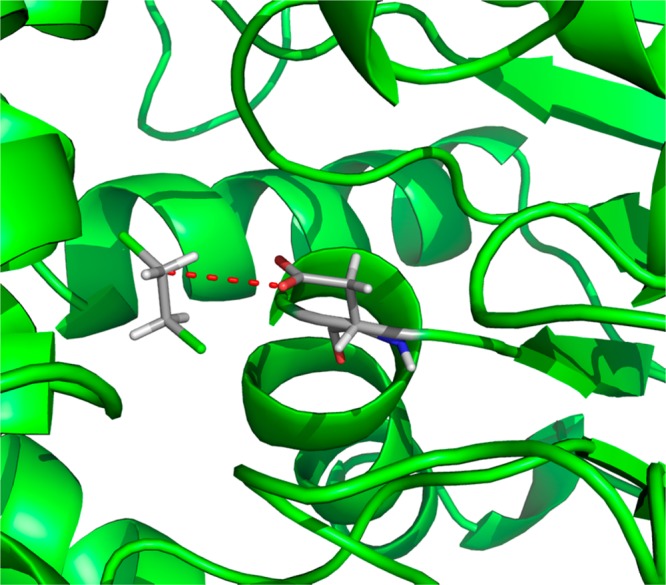
Active center of haloalkane dehalogenase. The protein backbone is shown in green; the catalytic residue, aspartate, and the substrate are shown as sticks. The dotted red line depicts the direction of the nucleophilic attack on the substrate, 1, 2-dichloroethane.

Figure 4.

Reaction scheme for the studied reaction.

Calculating the Activation Free-Energy from PMF

The reaction free-energy surface was defined with a 1D reaction coordinate, represented as a difference between the breaking (C–Cl) and the forming (C–O) bond lengths: ξ = d(C – Cl) – d(C – O). The sampling along the reaction coordinate was performed with a harmonically based PM6/MM potential. This was also repeated with a hybrid DFT B3LYP//6-31G*/MM potential. Totally 64 equidistant mapping potential were used with biases centered at −1.125 ≤ ξ_m⁰ ≤ 2.025, the force constant value was K = 125 kcal/(mol Ų). The electronic embedding QM/MM²⁷ protocol implemented in MOLARIS-XG²⁸ with a file-based interface to MOPAC2012²⁹ (for PM6) and to Gaussian09³⁰ (for B3LYP). The MM part was represented with a SCAAS³¹ sphere of solvent (protein and water) described with ENZYMIX³² force-field of 22 Å radius. The ionizable protein residues were represented by their neutral states. All free energies were computed using an in house PD-M program, which simultaneously process data using all free-energy perturbation and PMF methods reviewed in corresponding Methods. The free-energy changes reported below were computed using the corresponding multistep LRA method described above. PMFs were computed using the umbrella sampling approach of eq 19 combined with the multistep LRA method and compared with the WHAM estimates.

Calculating the Activation Free-Energy from Coarse-Physics Sampling

Identifying Target Regions from Low-Accuracy PMF

While carrying out configurational sampling with the RP, the energy gap with the TP (B3LYP//6-31G*/MM) was computed for 13000 configurations each 2 fs. The number of configurations for which the energy gap is evaluated can be significantly reduced in real simulations (by at least ten times), and this number was taken to obtain the methods’ best possible estimate. From the generated data the low-accuracy target free-energy surfaces were computed using eqs 24 and 27 in combination with the w-PMF, eq 21. The resulting low-accuracy target PMFs are shown in Figure 5. From these surfaces, the region of interest (reactants, transition state, and products) were located (shown with gray-shaded areas).

Figure 5.

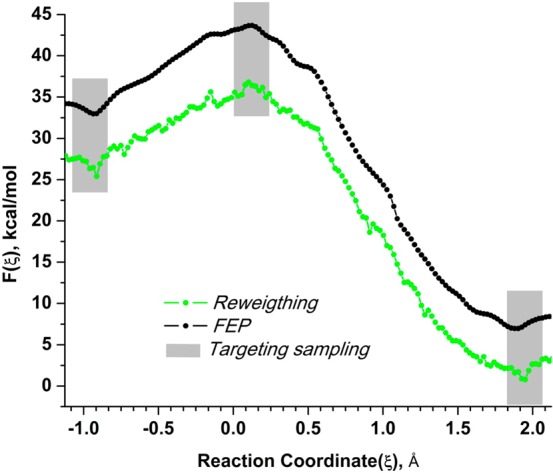
Selecting regions for targeted fine-physics sampling from low-accuracy B3LYP/MM free-energy surfaces computed from sampling with PM6/MM reference potential for the benchmark enzymatic reaction. These surfaces are used for detecting reactants and the transition state (shown by shaded gray areas). The first surface (shown in green) is computed by reweighting the reaction coordinate distribution from PM6/MM sampling using the umbrella sampling method. Another low-accuracy surface (shown in black) is calculated by adding the linear expansion of the free-energy perturbation to the PM6/MM high-accuracy PMF.

Computing High-Accuracy PMF Locally

At the identified regions, a limited sampling using the target potential with the same biases (see Table 1) was performed for 10000 2 fs MD steps; simultaneously the energy gap was evaluated. The reaction coordinate distribution for the obtained sampling is shown at the bottom in Figure 6. The data was used to compute the local PMFs (using 3–5 mapping potentials). The local PMFs are shown at the top in Figure 6. Then the corresponding free-energy perturbations were computed at each bias, LRA estimates and the corresponding averaged energy gaps are reported in Table 1. Also the difference between the linear expansion and the (2-step) LRA are given in the last column.

Table 1. Averages of the Energy Gap Computed from Biased B3LYP (T) Sampling and from Biased PM6 (R) Sampling, the Corresponding Free-Energy Perturbation Computed with LRA and the Difference between Two-Step LRA and One-Step LRA^a.

ξm0	⟨ΔE⟩T	⟨ΔE⟩R	ΔFLRA(Rm → Tm)	ΔFLRA – ⟨ΔE⟩Rb
Reactants
–1.125	20.25	33.11	26.68	0.22
–1.075	19.31	33.64	26.47	–0.51
–1.025	19.30	32.36	25.83	0.12
–0.975	19.85	32.66	26.26	0.25
–0.925	19.86	30.37	25.11	1.39
Transition State
0.025	17.71	34.02	25.86	–1.51
0.075	17.31	32.35	24.83	–0.87
0.125	17.19	33.46	25.32	–1.49
0.175	16.61	32.80	24.70	–1.44
0.225	16.87	30.13	23.50	0.02
Products
1.925	4.84	15.93	10.38	1.11
1.975	6.95	17.28	12.11	1.49
2.025	6.58	17.44	12.01	1.22

^aThe bias is in Angstroms, energies are in kcal/mol.

^bΔF_LRA – ⟨ΔE⟩_R –

Figure 6.

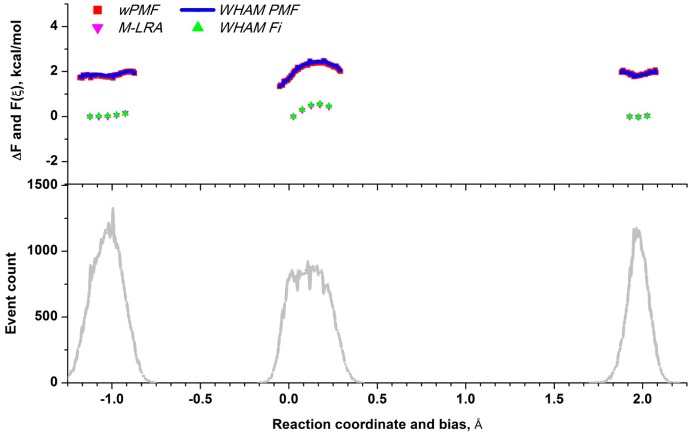
Improving the accuracy of probability distributions of the reaction coordinate at selected regions of the reaction path by performing local sampling with B3LYP/MM potential for the benchmark system. The upper plot shows local regions of the free-energy surface computed from the targeted sampling: green and magenta triangles show free-energy penalties of incrementally moving along the reaction coordinate relative to the first (leftmost) bias at each region. They are generated with multistep linear response approximation (M-LRA) and with WHAM, respectively. Red and blue lines are the local PMF computed using the weight-averaged umbrella sampling approach (red) and WHAM (blue), respectively. The lower plot shows biased distributions of the reaction coordinate for the data points used in calculations.

These estimates added to the corresponding free-energy penalties computed with the reference potential are also shown in Figure 7. By comparing them to the one-step LRA estimates, one can see that the two-step LRA estimate improved the accuracy of eq 28. However, the error with respect to the exact solution varies among different LRA estimates, therefore, the average estimate is computed as described below.

Figure 7.

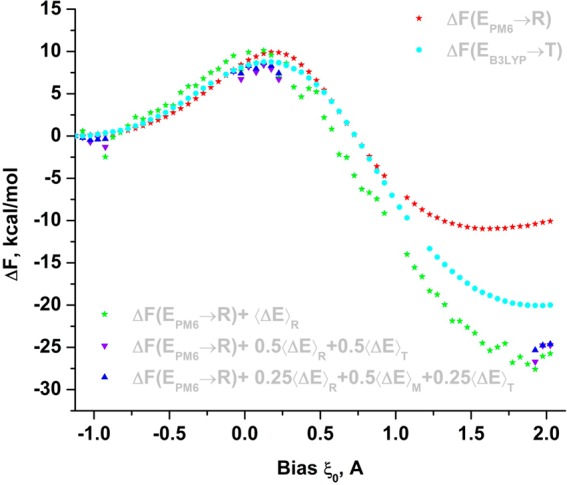
Improving accuracy of the free-energy shifts associated with changing the center of bias ξ_m⁰ while moving along the reaction coordinate. All changes are computed relative to the leftmost (first) bias. Red stars correspond to free energies computed from sampling with biased PM6/MM reference potential (R) using a multistep free-energy perturbation. The cyan circles represent the exact searched solution and correspond to free energies computed from sampling with a biased B3LYP/MM target potential (T) using a multistep free-energy perturbation. Green stars correspond to the PM6/MM free-energy shifts to which the linear expansion of the free-energy perturbation to B3LYP/MM potential is added (at corresponding biases). This perturbation is computed as PM6 ensemble average of the energy gap between B3LYP and PM6, ΔE. These shifts are used in constructing the low-accuracy B3LYP free-energy surface. After performing a limited fine-physics sampling with B3LYP target potential (T), a more-accuracte estimate for these shifts is computed (purple ▲) using two-step linear response approximation. These estimates are used for positioning the local PMF regions (see the main text). Next, the estimates are improved further with a three-step perturbation (blue ▲), which involves computing the average energy gap with intermediate potentials M = 0.5R + 0.5T.

From local (targeted) sampling with n biased target potentials at each identified region, the algorithm computes PMF locally and connects these windows using the multistep LRA eq 11 ΔF(T_m → T_m+i). On the other hand LRA provides an estimate of ΔF(R_i → T_i) at each ξ_m+i⁰. The LRA and local free-energy shifts are however related:

31

Therefore, one can compute the average free-energy perturbation over n simulation windows at each local region:

32

and use this estimate to position the local PMF region. This will further improve the accuracy of eq 29. Computed values are reported in Table 2.

Table 2. Positioning Local PMF Regions Using Averaged LRA Estimates by Eq 32^a.

ξm0	ΔF(T1LOC → Tm)	ΔF(R1LOC → Rm)	ΔFLRA(Rm → Tm)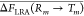
Reactants
–1.125	0.00	0.00	26.68	26.17 (0.00)b
–1.075	–0.01	0.05	26.54
–1.025	0.00	0.13	25.96
–0.975	0.06	0.23	26.43
–0.925	0.15	0.27	25.23
Transition State
0.025	0.00	0.00	25.86	25.11 (−1.06)b
0.075	0.29	0.45	24.99
0.125	0.47	0.75	25.60
0.175	0.52	0.93	25.11
0.225	0.44	0.90	23.97
Products
1.925	0.00	0.00	10.38	11.66 (−14.51)b
1.975	–0.01	0.16	12.29
2.025	0.04	0.33	12.30

^aThe first column (in Angstroms) is the bias center. The second and third columns are free energies of changing the bias, relative to the smallest (the most negative) bias in the group. The third column shows LRA estimates. All energies are given in kcal/mol.

^bRelative to the reactants region.

Estimates computed with eq 32 were used to position the transition state and products regions relative to the reactants, as shown in Figure 8.

Figure 8.

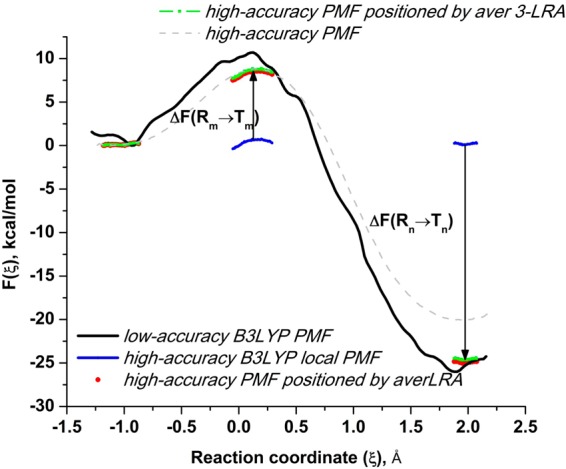
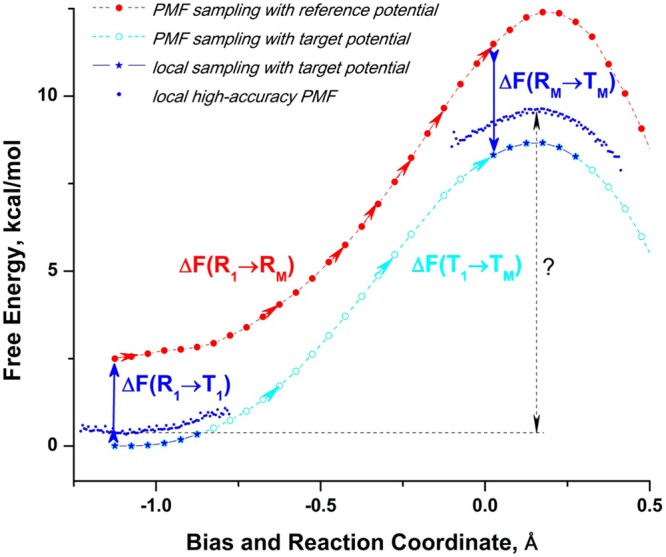
Increasing accuracy of the B3LYP activation free-energy barrier computed by positioning the local PMF regions from the targeted sampling and its comparison to the full PMF. Full B3LYP/MM PMF (dashed gray line) is computed from 64 molecular dynamics B3LYP trajectories. Black line is a low-accuracy PMF computed from 64 PM6 trajectories using the averaged energy gap with the B3LYP potential. It is used to identify regions for targeted sampling with B3LYP. Local B3LYP PMFs are computed from this targeted sampling, which includes 5 trajectories at reactants, 5 trajectories at the transition state, and 3 trajectories at products (blue line), but the relative positions of these regions is not known. They are found by computing the free-energy perturbations of switching from PM6 reference potential (R) to B3LYP target potential (T), shown by black arrows. The local PMF regions, positioned using a two-step linear response approximation, are shown in red. Three-step free-energy perturbation slightly further improves the positioning, and the activation free-energy estimate (shown in green). The three-step estimate involves additional targeted sampling at the same regions with 0.5R + 0.5T potential.

Improving Accuracy of Positioning High-Accuracy PMF Segments

In the next step, a limited sampling at the same regions (and using the same biases as in the previous part) was performed with a linear combination of the reference and of the target potential, M_m = 0.5R_m + 0.5T_m. From eq 11, it follows that to increase the accuracy of the free-energy perturbation, one has to compute the energy gap between the target and the reference potential. Thus, this step constitutes a three-step perturbation approach (Δλ = 0.5), which is estimated using

33

Now by estimating the average difference between two-step LRA and three-step LRA, and their average over the simulation potentials at corresponding local regions, a higher accuracy estimate is obtained (see Table 3). The 3-step LRA correction for positioning the transition state PMF region (relative to the reactants) is only 0.19 kcal/mol. The updated positioning is shown in Figure 8, from which one can see that the positioned local PMFs essentially coincide with the full PMF.

Table 3. Positioning Local PMF Regions using Averaged 3-Step LRA Estimate of eq 33^a.

ξm0	⟨ΔE⟩M	ΔF3–LRA (Rm → Tm)	ΔF3–LRA – ΔFLRAb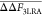
Reactants
–1.125	24.20	25.44	–0.33	–0.15 (0.00)c
–1.075	23.88	25.18	–0.39
–1.025	23.79	24.81	–0.11
–0.975	23.34	24.80	–0.55
–0.925	24.56	24.83	0.63
Transition State
0.025	23.61	24.74	–0.22	0.04 (0.19)c
0.075	23.19	24.01	0.09
0.125	23.34	24.33	–0.08
0.175	22.98	23.84	0.05
0.225	22.45	22.97	0.38
Products
1.925	10.66	10.52	1.04	0.18 (0.33)c
1.975	9.68	10.90	–0.31
2.025	9.78	10.90	–0.21

^aAll energies are given in kilocalories/mol.

^bΔF_3–LRA – ΔF_LRA –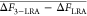

^cRelative to the reactants region.

Analysis

While the barrier for the forward reaction in Figure 8 is in excellent agreement with the estimate drawn from the conventional PMF, the reverse reaction barrier is about 3 kcal/mol higher than the PMF estimate. This is believed to be the result of an insufficient amount of simulation windows in PMF calculations for the high reverse barrier (big spacing in eq 13). To understand the methodological advantage of positioning locally computed PMF regions over computing the fine-physics correction to the coarse-physics reaction path, it is instructive to inspect movies provided as additional external files. File movie1.mov shows two high-accuracy free-energy surfaces, PM6 and B3LYP, and the minimum free-energy reaction paths computed from 1D PMF and projected on a 2D representation of the reaction coordinate. One can easily note the difference in the corresponding reaction paths. The other two files, movie2.mov and movie3.mov, show low-accuracy B3LYP free-energy surfaces computed from PM6 sampling using the umbrella sampling reweighting of eq 24 and one-step LRA correction of eq 27, correspondingly, for 2D representation of the reaction coordinate. From comparison of these surfaces with the high-accuracy B3LYP surface, one can see that the minimum free-energy reaction path on the low-accuracy surfaces is not the one on the high-accuracy surface. File movie4.mov shows high-accuracy local regions of B3LYP computed from limited B3LYP sampling and positioned using 2-step free-energy perturbation. The reaction paths are identical.

While the goal of this work is to provide a proof of the proposed concept, and not to study dehalogenase, it is important to make sure the calculations are consistent. This system was studied earlier with other reference potential approaches,^1d,3a and the authors of those works came to different conclusions on the applicability (due to the accuracy limitation) of the approach. The B3LYP//6-31G*/MM free-energy barrier calculated for the catalyzed reaction in protein with full PMF and with the proposed approach are 8.8 and 8.7 kcal/mol, which are drastically lower than the experimental estimate of 15.3 kcal/mol.^1d However, it is important to analyze the source of the error. The applied computational protocol was earlier verified by calculating the reference reaction in water, and the corresponding catalytic effect with PM3/MM, PM6/MM, and B3LYP//6-31G*/MM models.³³ The PMF protocol employed here fairly closely reproduced the experimental catalytic effect of 11.7 kcal/mol using PM6/MM activation free energies computed from PMF in the reference reaction in water (19.0 kcal/mol + the solvent cage effect³⁴) and in the protein (10 kcal/mol). Both potentials (PM6/MM and B3LYP//6-31G*) are known to underestimate the activation free-energy barrier in the gas phase, with B3LYP//6-31G* reportedly underestimating by as much as 8 kcal/mol compared to the MP2//6-311G** results.³⁵ Additional source of error can be in the way charges for QM atoms are derived; for instance, for a similar type of reaction in water between methyl chloride and chloride, using Mulliken charges with PM3/MM potential leads to about 3 kcal/mol lower barrier than using the charges fitted to the electrostatic potential.^3b While reproducing the absolute energetics for the reaction barriers is challenging, the relative catalytic effect leads to the error cancellation and, therefore, is considered to be a reliable tool for checking the consistency of calculations for enzymatic reactions.³⁴

While analyzing the computational cost of elevating the PMF regions compared to building the full PMF, one should note that for the second and third steps of the algorithm, sampling can be performed with a single mapping potential at each region (even though it would decrease reliability of the estimates). Thus, in the case of the 1D reaction coordinate, the second iteration (for two-step LRA) requires propagating a minimum of two (three if the products region is included) simulations with the TP, the third (and subsequent) iterations add one extra simulation for each region. Considering that the full PMF for the 1D case required more than 60 simulations, local PMF elevated with the paradynamics’ LRA approach requires 60/3, 60/6, and 60/12 times less fine-physics sampling simulations (trajectories) for the two-, three-, and five- multistep FEP correction, respectively. When the mapping of the reaction free-energy surface is performed with a two-dimensional reaction coordinate, the number of simulation windows with the conventional PMF approach increases quadratically, and the local PMF with positioning using the multistep LRA approach becomes almost 2 orders of magnitude less expensive than the full PMF in terms of the number of required trajectories. Thus, the proposed scheme will be particularly computationally efficient for calculating the free-energy surfaces with 2D representation of the reaction coordinate).

Concluding Discussion

The focus of the current contribution is to improve accuracy of calculating the fine-physics activation free-energy from coarse-physics sampling, up to the level achieved in computing PMF from the fine-physics sampling. The proposed solution is to compute and to position the fine-physics local PMFs using the fine-physics sampling targeted to selected regions identified on the low-accuracy free energy surface computed from extensive exploratory coarse-physics sampling.

Limited sampling with the target potentials has been used earlier in the paradynamics model^2,3b and with other LRA-based models^1d for improving accuracy of the free-energy perturbation. Here the sampling is targeted more precisely using the low-accuracy fine-physics free-energy surface and is also used for computing the distribution of the reaction coordinate. Further modifications and improvements introduced in this contribution include the following. (1) Instead of computing the free-energy perturbation correction to the coarse-physics minimum free-energy reaction path, the proposed method computes the fine-physics free-energy surface locally, and positions these segments relative to the free-energy shifts computed with the coarse-physics potential. (2) The segments of the fine-physics reaction path are found from a low-accuracy fine-physics free-energy surface. This surface is obtained from sampling with the coarse-physics potential using the umbrella sampling reweighting of eq 24 and the free-energy perturbation approximation of eq 27. (3) No explicit parametric or functional refinement of the reference potential (along the reaction path) to the target potential is performed. (4) The distribution of the reaction coordinate is computed with the target potential from the local targeted sampling, which is analogous to computing PMF locally. (5) Locally computed PMF regions are positioned using the averaged LRA eq 32 to minimize the error, which limits the accuracy of the approach. (6) The accuracy of positioning of the local PMF regions is further improved by computing three-step free-energy perturbation. (Which also can be done over several simulation windows locally, see eq 33).

These advances allow for reaching accuracy of the full PMF, what is demonstrated analytically from the umbrella sampling equation and is showed numerically on a benchmark reaction by computing the B3LYP PMF locally (using the sampling with the PM6 potential).

These advances can be viewed as a recipe for computing the fine-physics solution from the initial conditions generated with the coarse-physics model. The searched solution in fact is not the free-energy surface, but the free-energy penalty of introducing a bias to the target potential. Unlike in the PMF calculations, where this penalty is computed in a multistep transformation of eq 13, this approach computes the penalty through the free-energy perturbation by switching the reference potential to the target potential at the same bias location. The convergence of the perturbation will be reached in fewer multistep transformations than in PMF mapping along the reaction coordinate if the corresponding structural changes are less extensive. This might require a more careful choice of the reaction coordinate. A particularly common and illustrative case in chemistry is the associative versus concerted versus dissociative pathways. The constraint on the 1D representation of the reaction coordinate (similar to one used for the numerical example) can satisfy both the associative and the dissociative pathways. Thus, if the reference potential and the target potentials favor two different pathways, the perturbation of eq 30 would involve extensive structural changes while switching from the RP to the target potential at the same bias location. In the case of the 2D representation, this problem will not be encountered. The same argument applies to the structural changes caused by different coordination numbers, if the metal center is included, or by structural deformations by mechanical stimuli unaccounted for in the reaction coordinate and not fixed by the bias.

Successful and efficient use of sampling with the RP in calculating the activation free-energy involves overcoming three key challenges: (1) choosing a good RP, (2) choosing an efficient strategy for sampling rare events, and (3) choosing a good reaction coordinate and an efficient scheme for relevant free-energy calculations.

Choosing a Good RP

The choice of the RP is, perhaps, the most important factor, which determines the overall method computational cost and therefore its efficiency. First, the proximity of the RP to the TP, or their overlap, determine how representative (efficient) sampling with the RP for the fine-physics minimum free-energy reaction path, that is how often the most probable configurations of the TP are generated while sampling with the RP. This, in turn, influences the decision for the third problem, since convergence of the free-energy change while moving to the TP greatly depends on its overlap with the RP. Second, the difference in computational cost between the TP and the RP is what essentially determines efficiency of the RP approach. Thus, the RP should be orders of magnitude less expensive to compute, and yet it should capture enough physics to roughly approximate the TP. There is no single universal recipe on how to choose the RP. The choice is system dependent and is affected both by the simulation system and by the TP. The choice of semiempirical potential as a RP is motivated by their abundance, popularity of the free-energy based studies of chemical reactions in the condensed phase with semiempirical potentials,^3a,23,36 and with recently emerged SCC-DFTB potentials.^1h,37

While the choice of the RP is problem-dependent, it should be noted that the method described in this work is problem independent, still the strategies considered above can be applied for two models of the same dimensionality. Trivially, the number of degrees of freedom for a higher level of theory model is higher, thus the number of degrees of freedom should be normalized to the coarser model. Here the number of degrees of freedom is reduced at each molecular dynamics steps to 3N for the expense of the electronic degrees of freedom which are condensed in the Born–Oppenheimer approximation to the atomic degrees of freedom via energy gradients acting on nuclei in a particular configuration. Another example of reduction of dimensionality is the centroid³⁸ molecular dynamics approach which reduces dimensionality of the ring polymer to its central distribution.³⁹ An alternative approach to the normalization is the centroid-based quantized classical particle approach,⁴⁰ which increases dimensionality of a classical molecular dynamics trajectory to the ring-polymer type approach in order to describe the nuclear quantum tunneling effect. At least in principle, similar approaches can be extended to normalize dimensionality of atomistic simulations to supra-atomistic coarse grained models,⁴¹ what allows for application of the methods presented in the paper to a wide spectrum of problems in addition to chemical reactions.

This approach can also be used to improve accuracy of the activation free-energy by moving from a lower level of theory ab initio QM (e.g., HF, DFT) to a higher level of theory QM [e.g., CCS(D), hybrid DFT] what is routinely done in the energy minimization studies. Furthermore, it can be used to increase the QM region in QM/MM, up to moving to a full ab initio QM description.

While the presented method removes the need of having the same minimum free-energy reaction path, and therefore of careful refinement, the reference potential still must be physically appropriate for modeling a particular chemical reaction.

Choosing an Efficient Strategy for Sampling Rare Events

The choice of the sampling strategy to construct the free-energy surface is identical to choosing the rare event sampling method. The proposed approach is currently formulated for a common strategy of mapping the free-energy surface with a grid of harmonically biased potentials and combining data from multiple ensembles using free-energy perturbation and umbrella sampling approaches. One thing that needs to be considered in this aspect is the force constant for the harmonic bias. In general, the problem can be that the force constant used to keep the reference potential might not be optimal for the target potential. This issue can be resolved by adjusting the force constant on the fly to make sure that the deviation from the bias center is small. This would improve the umbrella sampling efficiency by reducing the gap between the mapping and the target potentials. Then the free-energy penalties would almost exactly reproduce the PMF. This idea in fact is used in the metadynamics model,⁴² where the free-energy surface is not computed from the probability distribution but is approximated by the cumulative bias. The proposed algorithm can be generalized to include other sampling schemes, for instance the metadynamics approach. The basic strategy is outlined in Appendix 3.

Choosing a Good Reaction Coordinate and an Efficient Scheme for Relevant Free-Energy Calculations

Generally, the choice of the reaction coordinate should ensure that the perturbation depends approximately equally on all degrees of freedom, that is, that other degrees of freedom (on which the perturbation depends strongly) are included in the reaction coordinate, which is kept fixed by the same bias in eq 30. This condition also ensures good convergence of the free-energy interpolation¹⁶ and of LRA (see Appendix 1).

The presented algorithm for computing the activation free-energy is formulated in order to construct a high-accuracy fine-physics free-energy surface locally at selected regions of the reaction path. It is derived and is shown to reproduce the full PMF computed with fine-physics sampling. These regions are positioned using the multistep LRA approach, which is chosen based on the analysis in Appendices 1 and 2.

The presented algorithm is conceptually similar to another multistage method⁴³ of computing the target free-energy surface (and improving its accuracy), which computes a low-accuracy (high-dimensional) free-energy surface with the TP using the metadynamics⁴² approach and then refines the surface to a high-accuracy (low-dimensional) free-energy surface using the metadynamics potential as a bias in the umbrella sampling. In this approach, however, both the metadynamics and the umbrella sampling steps require sampling with the target (fine-physics) potential, and the improvement of accuracy is achieved by reducing the dimensionality and by increasing the sampling accuracy (and computing the reaction coordinate distribution) with the umbrella sampling. A similar idea was also proposed in the paradynamics-based model^3b in the sense that both the reference and the target low-accuracy free-energy surfaces were computed using the energy minimization approach and fitted with Gaussians. The difference was additionally used to refine the original reference potential, which was used in the umbrella sampling method (thus avoiding sampling with the target potential), while computing a higher-accuracy free-energy surface estimate.

The ideology of this work is to use a coarse-physics sampling to construct a low-accuracy fine-physics free-energy surface, which is used for targeting the fine-physics sampling, computing the fine-physics free-energy surface regions locally and positioning them relative to the coarse-physics free-energy shifts. The use of the coarse-physics reference potential sampling is thus the key to reducing the computational cost of calculating the fine-physics activation barrier or the reaction path (in many dimensions). Obtaining accurate fine-physics activation free energies is achieved by, first, identifying the actual fine-physics minimum free-energy path on a low-accuracy fine-physics free-energy surface (which is computed from the coarse-physics sampling) and by, second, refining accuracy of selected regions of the reaction path (rather than by correcting the coarse-physics path) using targeted fine-physics sampling at those regions.

Appendix 1. Connection between LRA and Free-Energy Interpolation

The umbrella sampling equation written for the probability distribution of the energy gap between the target potential and the reference potential is

A1.1

where ΔE = E_TGT(r) – E_REF(r) and x = E_TGT – E_REF is a particular value of the energy gap.

Since ⟨f(x)δ(x – x₀)⟩ = f(x₀)⟨δ(x – x₀)⟩, eq A1.1 becomes

A1.2

which is eq 19 in ref (16). Taking the log:

A1.3

where p_i(x) = ⟨δ(ΔE − x)⟩_Ei.

A1.4

Ref (16) suggests that the free-energy change can be determined graphically from the vertical distance between two functions:

A1.5

and

A1.6

Further it suggested fitting ln p with a polynomial, which can be extrapolated to the region between two distributions. Another approach is to fit the distributions with Gaussians instead p(x) = exp[−α(x – μ)²], where μ_i = ⟨ΔE⟩_i. Then ln p would be two parabolas:

A1.7

and

A1.8

The vertical distance between these two parabolas can be estimated most accurately at the centers of two distributions:

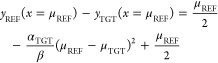A1.9

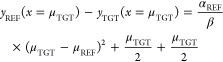A1.10

The average of eqs A1.9 and A1.10 yields the best estimate of the free-energy:

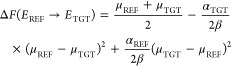A1.11

The first right-hand side term is the LRA equation and the last two terms are the correction for the unequal curvature of parabolas.

If the width of two distributions is similar (α_REF ≈ α_TGT) then eq A1.11 becomes the LRA equation. If the width is not similar, then the LRA error gets larger with the separation between two energy gap distributions.

Appendix 2. Relationship between Multistep LRA and Thermodynamic Integration

Below the equivalence between two multistep FEP techniques is shown using the mapping potential and its analytical derivative:

A2.1

A2.2

That is

A2.3

A2.4

The free-energy change computed with the multistep LRA

A2.5

A2.6

The only difference is in the bias location:

A2.7

A2.8

Now

A2.9

A2.10

but from eqs A2.7 and A2.8:

A2.11

Substitution of eq A2.11 into eq A2.10 yields

A2.12

Similar is true for the average over the ensemble described with the potential A2.6:

A2.13

On the other hand, computing the average free-energy derivatives given by eq A2.2:

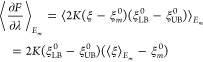A2.14

A2.15

Substitution of eqs A2.12 and A2.13 into A2.4 gives the same result as substitution of eqs A2.14 and A2.15 into eq A2.3.

Appendix 3. On Adapting the Metadynamics Sampling

The idea of this paper on using the coarse-physics potential for computing the low-level of accuracy fine-physics free-energy surface can be extended to other rare events sampling strategies (e.g., to the metadynamics approach).⁴² Metadynamics can be initially used to compute the potential w_MTD, which flattens the reference free-energy surface. The negative of this potential provides a good approximation for the reference free-energy surface:

A3.1

Next it can be used for sampling with the flat reference potential, E_REF – Γ_REF, from which the energy gap with the target potential is evaluated, and by using eqs 24 and 27 with R_m = Γ_REF, the low-quality target free-energy surface is computed. The surface can be fitted with Gaussians^3b

A3.2

and used as bias T_m = Γ_TGT in eq 19, with the umbrella sampling approach as suggested in ref (43) (and also localizing sampling with the target potential at selected regions of the free-energy surface).

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States