Hamiltonian Switch Metropolis Monte Carlo Simulations for Improved Conformational Sampling of Intrinsically Disordered Regions Tethered to Ordered Domains of Proteins

Abstract

There is growing interest in the topic of intrinsically disordered proteins (IDPs). Atomistic Metropolis Monte Carlo (MMC) simulations based on novel implicit solvation models have yielded useful insights regarding sequence-ensemble relationships for IDPs modeled as autonomous units. However, a majority of naturally occurring IDPs are tethered to ordered domains. Tethering introduces additional energy scales and this creates the challenge of broken ergodicity for standard MMC sampling or molecular dynamics that cannot be readily alleviated by using generalized tempering methods. We have designed, deployed, and tested our adaptation of the Nested Markov Chain Monte Carlo sampling algorithm. We refer to our adaptation as Hamiltonian Switch Metropolis Monte Carlo (HS-MMC) sampling. In this method, transitions out of energetic traps are enabled by the introduction of an auxiliary Markov chain that draws conformations for the disordered region from a Boltzmann distribution that is governed by an alternative potential function that only includes short-range steric repulsions and conformational restraints on the ordered domain. We show using multiple, independent runs that the HS-MMC method yields conformational distributions that have similar and reproducible statistical properties, which is in direct contrast to standard MMC for equivalent amounts of sampling. The method is efficient and can be deployed for simulations of a range of biologically relevant disordered regions that are tethered to ordered domains.

Introduction

A significant percentage of eukaryotic proteins are classified as being intrinsically disordered¹. They are referred to as intrinsically disordered proteins or IDPs because, as autonomous units, they fail to fold into well-defined three-dimensional structures. Importantly, IDPs challenge the conventional structure–function paradigm given that they feature prominently in protein–protein and protein-nucleic acid interactions. Many IDPs can adopt ordered structures in specific bound complexes.² The intrinsic heterogeneity in their unbound forms is reflected in their ability to adopt different folds in the context of different complexes.³ An additional area of interest is the ability of IDPs to mediate the formation of nonmembrane bound liquid-like or gel-like supramolecular assemblies via microscale phase transitions.⁴

Within the sequence-structure–function paradigm, functional annotation is enabled by the ability to assign a fold to an amino acid sequence.⁵ IDPs challenge this paradigm because they adopt heterogeneous ensembles of conformations in aqueous solutions for which no single structure or collection of structures provides an adequate description. This does not imply that the sequences of IDPs encode random conformational preferences. In fact, coarse grained⁶ and atomistic simulations⁷ in conjunction with single molecule,⁸ ensemble,⁹ and other¹⁰ experiments have provided synergistic descriptions of the conformational ensembles sampled by different categories of IDP sequences. These efforts have yielded a predictive “diagram of states”,^7c which provides a framework for quantitative coarse grain polymeric descriptions of the type of conformational ensemble, such as rod, coil, globule, or chimera, that an IDP sequence will most likely access for given solution conditions.¹¹ Additionally, the degree of heterogeneity in conformational ensembles of IDPs can also be quantified.¹² Accordingly, descriptions of sequence-ensemble relationships and comparative assessments of conformational heterogeneity have enabled the use of de novo design approaches to modulate the conformational properties of IDPs. In reality, a majority of IDPs are in fact intrinsically disordered regions (IDRs) that are tethered to ordered domains (ODs).¹³ While the study of IDRs as autonomous units yields useful insights regarding their sequence-ensemble relationships, it is imperative that the biophysical properties of these regions be studied in their naturally occurring contexts, that is, tethered to ODs. Figure 1 shows schematics for three categories of IDRs. Based on the tethering mode IDRs are either bristles or linkers. If the number of bristles is greater than one, then the collection of tethered IDRs make up a polymer brush (see Figure 1).¹⁴

Figure 1.

Schematic representations of different modes that are expected for IDRs. These include the bristle (panel A), linker (panel B), and brush (panel C) modes. In each panel, the IDRs are sketched in black and the ordered domains are shown in green. Short Linear Motifs or SLiMs⁴⁵ are shown as red triangles and those SLiMs that can be the target of post-translational modifications are depicted as blue triangles. In the bristle mode, a single IDR is tethered to an ordered domain. Panel B depicts the linker mode where the IDR connects two ordered domains. Panel C shows the polymer brush mode whereby multiple bristles are either tethered to a single ordered domain (left), a single filament (middle) as in intermediate filaments⁴⁶/microtubules,⁴⁷ or grafted onto the surface lining the interior of a pore (right) as is the case with nuclear pore complexes.⁴⁸

Simulation Challenge for Tethered Systems

The amplitudes of conformational fluctuations of a disordered region are likely to be larger than the relatively rigid OD. Further, the energy landscapes of IDRs are expected to be “weakly funneled”,¹⁵ whereby conformational heterogeneity results from equivalent thermodynamic preferences of disordered regions for multiple, albeit conformationally distinct minima. In standard Metropolis Monte Carlo (S-MMC) simulations, we deploy a series of moves that are designed to be ergodic to enable the sampling of a broad range of conformations that are thermodynamically relevant for IDPs.¹⁶ Tethering an IDP to an OD introduces a new set of interactions viz., those between the IDR and the OD. Interactions within the IDR and between the IDR and OD can create deep energy traps. These traps can severely limit the range of thermodynamically relevant conformations that are sampled in a typical S-MMC simulation.

A predictive “diagram of states” for IDPs^7c,7e that connects sequence compositional biases to conformational classes has emerged from high-throughput investigations whereby atomistic simulations were carried out for O(10²) archetypal sequences drawn from databases such as DisProt.¹⁷ These ensembles of simulations, spanning multiple investigations, were enabled by the combination of a fast and accurate implicit solvation model,¹⁸ improved methods for Monte Carlo sampling that leverage the advantages of implicit solvation models,¹⁶ refinements to force field parameters,¹⁹ the deployment of thermal replica exchange (TREx)²⁰ simulations to obtain conformational characterization for each of the archetypal sequences,^7c−7e,21 and advanced weighted histogram analysis methods²² for analyzing the collection of simulation results. A similar high throughput approach is required for IDRs whereby all relevant combinations of archetypal IDRs and frequently occurring ODs are investigated in order to unmask the degree to which different modes of tethering affect the intrinsic conformational properties of tethered IDRs. These systems pose unique challenges because an IDR tethered to an OD is an archetype of a “hot” region tethered to a “cold” domain.

Naïve deployments of TREx^20b,23 are not particularly useful because several conceptual and logistical issues confound the design of TREx simulations. These are as follows: (i) At higher simulation temperatures the ordered domains will unfold and the feature of a hot IDR and cold OD will be lost at higher temperatures. This is not ideal because our interest is in the range of conformations accessible to the IDR in the context of the OD rather than its unfolded counterpart. (ii) Of course, one could work around the difficulty of ODs unfolding at higher temperatures by adding suitable conformational restraints to maintain foldedness. However, this can only make sense for the temperatures where the OD should remain folded. Therefore, the design of TREx will have to incorporate replicas where the OD thermally unfolds, which creates a biphasic problem whereby some replicas involve the IDR tethered to a folded OD whereas higher temperatures involve replicas tethered to an unfolded OD. (iii) In order to ensure significant overlap of energy distributions between replicas corresponding to the two phases, we would need to incorporate a nonlinear increase in the number of replicas used for each TREx simulation. From a logistical standpoint, much of the sampling for a finite amount of computational resources will be invested in communication between replicas. Previous work has demonstrated the importance of performing multiple independent TREx or S-MMC simulations in order to minimize the statistical uncertainty on estimates of different moments of conformational distributions.^7c−7e,16 This is difficult to obtain by dedicating large numbers of compute nodes to single TREx runs. (iv) Finally, the growth in system size further slows down the time taken per TREx simulation and together these constraints severely limit our ability to carry out high throughput assessments of sequence-ensemble relationships for a spectrum of tethered IDRs.

Here, we pursue a strategy to circumvent the logistical barriers posed by tempering methods such as TREx. Our design requirement is that we should be able to gather and analyze information from multiple, independent, “embarrassingly parallel” runs in order to obtain a robust description of the conformational ensembles for tethered systems. For such an approach to be reliable it is imperative that we obtain similar statistical distributions for a range of conformational properties from each independent simulation. Standard sampling methods cannot solve the problem of broken ergodicity and hence a naïve deployment of a large number of multiple, independent simulations will fail to meet the design specifications. We therefore pursue an alternative route that meets our design specifications while leveraging the intrinsic “hot” and “cold” nature of the IDR and OD, respectively.

New Sampling Method for Tethered IDRs

We have adapted a method based on the algorithm proposed by Gelb.²⁴ Monte Carlo sampling on complex, multidimensional energy landscapes can be improved by the introduction of an auxiliary Markov chain that draws conformations from a Boltzmann distribution governed by an approximate potential energy function. Gelb’s proposal, referred to in the literature as Nested Markov Chain Monte Carlo or NMCMC,²⁵ was motivated by the need to reduce computational costs associated with Markov Chain Monte Carlo sampling when using quantum mechanical and polarizable Hamiltonians that are expensive even for single point energy calculations. The formalism developed by Gelb satisfies detailed balance and can be adapted to any pair of Hamiltonians, where only one of the Hamiltonians is of interest. The other can, in theory, be any conceivable approximation, as long as it is useful and helps achieve efficient sampling. We refer to our adaptation of Gelb’s formalism as Hamiltonian Switch Metropolis Monte Carlo or HS-MMC. This terminology highlights the fact that we engineer a switch between distinct Hamiltonians (potential functions) and uses the Metropolis criterion for Markov Chain Monte Carlo simulations. In the following sections, we describe the details of this method and show three examples of realistic sampling problems that are overcome by its use.

Methods

Force Field, Degrees of Freedom, a Parameters

All simulations were performed using the ABSINTH implicit solvation model¹⁸ and force field paradigm as implemented in the CAMPARI software package (http://campari.sourceforge.net). The general functional form of the potential function is shown in eq 1. The simulations use atomistic descriptions of polypeptides, explicit representations of solution ions (Na⁺ and Cl^–), and the ABSINTH implicit solvation model to capture solvent-mediated interactions. For any system that includes polypeptides and mobile ions, the backbone ϕ, ψ, ω, and side chain χ dihedral angles as well as the rigid-body coordinates for the polypeptide chains and solution ions constitute the degrees of freedom. For a specific configuration of polypeptide and solution ions, the energy function takes the form

1

Here, W_solv is a multibody, direct mean field interaction term that captures the energetics of transferring a solute (polypeptide plus ions) in a specific configuration from the gas phase into the continuum solvent with dielectric constant of ε = 78; W_el denotes the mean field electrostatic term that accounts for dielectric inhomogeneities in the screening/descreening of interatomic electrostatic interactions; U_LJ models van der Waals interactions between nonbonded pairs of atoms and U_other denotes the collection of terms used to model specific torsions, coupling between bond angles and torsions, the puckering of flexible rings, the coupling between ring puckering and backbone torsion angles, and any additional restraint terms that are included in the simulation.^18,19

All of the force field parameters were taken from the abs_3.2_opls.prm file that is part of version 1 of the CAMPARI distribution. These parameters are based on the charges derived from the OPLS-AA/L force field.²⁶ They include the default Lennard-Jones parameters from preceding versions and the modified parameters that were designed for simulations of sequences that include prolyl residues. In addition, the parameters used here replace the default Lennard-Jones parameters for alkali and halide ions with those developed by Mao and Pappu.^19b

Choice of Ordered Domain

We selected the Src Homology domain (SH3) from the sequence of the multidomain human cytoplasmic noncatalytic region of the tyrosine kinase adaptor protein also known as NCK1 (Uniprot ID P16333, http://uniprot.org/). For simplicity, we refer to this domain as SH3. Panel A in Figure 2 shows a model for the structure of the SH3 domain that was derived from coordinates deposited in the protein data bank (http://rcsb.org), PDB code 2JS0.

Figure 2.

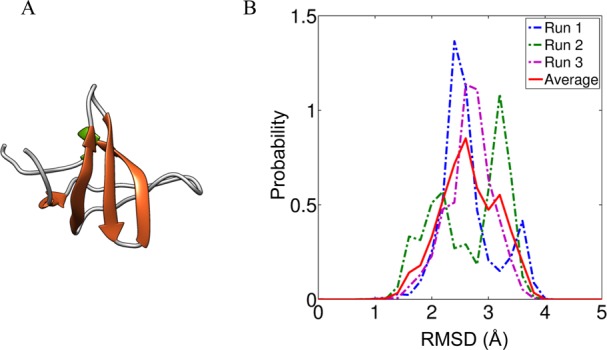
Structure (PDB code 2JS0) of the SH3(2) domain (panel A) from human cytoplasmic NCK1 (showing residues 107–165 from the sequence with UniProt ID P16333) drawn using the VMD package.⁴⁹ The color-coding is based on secondary structures. Panel B quantifies the reliability of the force field and sampling paradigm for simulations of the folded protein. Here, we show histograms of root-mean-square deviations (RMSDs) from the folded structure that were observed for three different independent S-MMC simulations that start from the folded state of SH3, depicted as Runs 1–3. The curve in red is the histogram obtained by averaging across the three runs. Histograms were generated using bin widths of 0.2 Å.

Choice of IDRs

Sequence details of the IDRs used in this work are summarized in Figure 3. Two of the IDRs were extracted from the NCK1 protein. The third IDR, designated as IDR3 was derived from sequence shuffling of IDR2 based on the recent observation of Das and Pappu,^7c who showed that the conformational properties of polyampholytic sequences can be modulated by altering the linear sequence distribution of oppositely charged residues. This linear sequence patterning is quantified using the parameter κ that is shown in Figure 3. Based on its amino acid composition, IDR1 is designated as a weak polyampholyte and is expected to prefer compact, globular conformations as an autonomous unit. Conversely, IDRs 2 and 3 are strong polyampholytes and their conformational properties are likely to correspond to semicompact hairpins and random-coils, respectively. These expectations are based on the combination of amino acid composition and κ values for IDR2 and IDR3.^7c

Figure 3.

Sequence details of two naturally occurring IDRs excised from the sequence of human cytoplasmic NCK1. IDR1 and IDR2 span residues 166–192 and 62–106, respectively for the NCK1 sequence with UniProt ID P16333. The sequence depicted as IDR3 is a variant of IDR2 obtained by a redistribution of the residues along the linear sequence while keeping the amino acid composition fixed. The table summarizes various composition and sequence-specific parameters for each sequence including N, the chain length; f₊ and f_– the fraction of positive and negatively charged residues, respectively; NCPR = | f₊ – f_– |, the net charge per residue; FCR = (f₊ + f_–), the fraction of charged residues; and κ, the parameter that quantifies the segregation/mixing of oppositely charged residues within the linear sequence. Higher the value of κ, the more segregated the oppositely charged residues within the sequence—compare the sequence of IDR2 to IDR3. The bottom panel shows a snapshot of IDR2 tethered to the SH3 domain depicted using a surface electrostatic representation that was generated using the APBS tool⁵⁰ that is built into the UCSF Chimera package.⁵¹ The calculated isopotential contour surfaces are plotted at ±2 kT/e where kT denotes thermal energy calculated using the Boltzmann constant k at temperature T, and e is electronic unit of charge. In the figure, red denotes a negative potential while blue denotes a positive potential. All the simulations described in this work were performed in bristle mode with each IDR tethered to the N-terminal end of the SH3 domain.

Simulation Setup

IDRs modeled as autonomous units or tethered to the N-terminus of the SH3 domain were placed inside large spherical droplets along with explicitly represented Na⁺ and Cl^– ions to neutralize the net polypeptide charge and include excess ion pairs to mimic a 15 mM salt solution. All simulations were performed with a spherical droplet boundary condition. The droplet radius was 100 Å for tethered systems and 90 Å for IDRs modeled as autonomous units. The spatial cutoffs for the Lennard-Jones and electrostatic interactions between net-neutral charge groups were set at 10 and 14 Å, respectively. No cutoffs were employed for computing electrostatic interactions involving solution ions and side chain moieties that have a net charge. The N- and C-termini of all sequence constructs were N-acetylated and N′-methylamidated, respectively.

Standard Metropolis Monte Carlo (S-MMC) Protocol

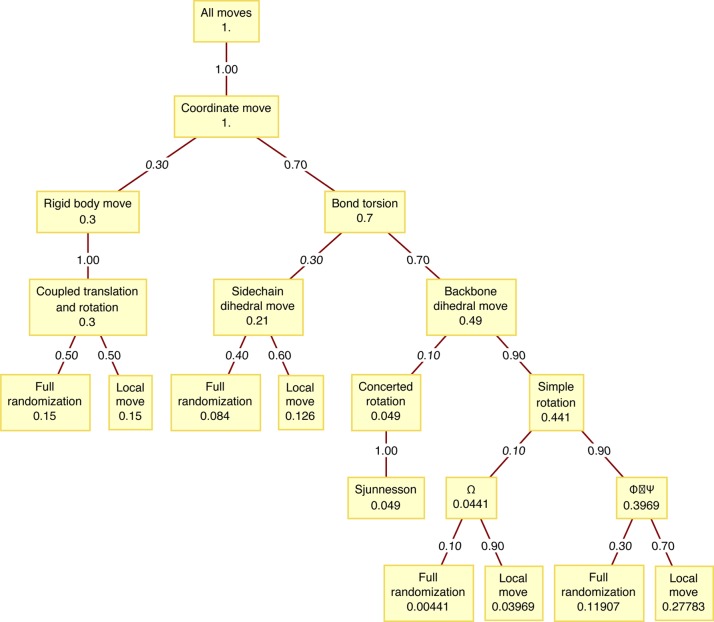
The main sampling strategy is based on S-MMC and includes a composite set of moves that have been designed to ensure efficient and ergodic sampling of conformational space.¹⁶ These move sets include backbone pivots, concerted rotations, randomization of side chain torsions, perturbing torsional coordinates, rigid body translations of mobile spherical ions, and rigid body translations and rotations of the polypeptide. The frequencies for different moves were chosen based on the decision tree shown in Figure 4. These were designed to achieve efficient sampling of conformational space while preserving detailed balance. In all simulations of tethered systems, the conformational degrees of freedom of the IDR are sampled preferentially over those of the ordered domain because we are interested in the conformations that the IDR adopts in the context of being tethered to the ordered domain. Moves designed to alter the IDR degrees of freedom are proposed three times as often as moves that are designed to alter the degrees of freedom within the ordered domain. This preferential sampling of the IDR is taken into account in a modified Metropolis criterion in order to ensure against biases and preserve detailed balance.²⁷ Each independent S-MMC simulation of a tethered system deploys a total of 8 × 10⁷ proposed moves. In order to ensure a fair comparison between the S-MMC and HS-MMC approaches, we used identical numbers of moves for independent runs of both approaches.

Figure 4.

Decision-tree utilized that is used for the selection of S-MMC moves based on the full Hamiltonian. Each nonleaf node corresponds to a class of moves; each node is annotated with the overall probability of that move or class of moves being selected. Each edge is annotated with the probability of the decision process branching toward the child once the parent has been reached. The decision is complete once a leaf node is reached.

Additionally, we performed reference simulations, the results of which are designated with the prefixes excluded volume (EV), Flory random coil (FRC),²⁸ and Lennard-Jones (LJ). In the EV simulations, the W_el, W_solv (see eq 1) and the r^–6 dispersive term of the Lennard-Jones potential are switched off; for the LJ simulations, the W_el and W_solv in eq 1 are switched off. Finally, for the FRC simulations, all terms in the potential function are switched off and we generate ensembles by drawing backbone and side chain dihedral angles from a presampled library for each residue.

TREx Simulations

We used TREx MMC sampling for simulations of IDRs modeled as autonomous units. For each sequence, we created 13 replicas according to the following temperature schedule [280 K, 285 K, 294 K, 298 K, 310, K, 320 K, 330 K, 340 K, 370 K, 400 K]. The schedule was chosen based on prior results for similar types of systems^7c,7d and quantification of the overlap statistics between pairs of neighboring replicas. The average swap probability for pairs of replicas was 0.4 for the prescribed schedule. For each of the IDRs shown in Figure 3, we performed three independent simulations using a total of 4.5 × 10⁷ overall proposed moves per TREx run.

Generation of Starting Conformations

In all simulations, the starting conformations for IDRs, that is, the initial values for backbone ϕ, ψ, ω, and side chain χ dihedral angles were drawn randomly from a pre-equilibrated distribution of atomistic self-avoiding random walks. The initial coordinates for the SH3 domain were based on the model in PDB file 2JS0. To generate a starting conformation that was usable in all simulations, the coordinates extracted from the PDB file were subjected to 10³ steps of standard Metropolis Monte Carlo (S-MMC) sampling at a simulation temperature of 260 K. These simulations incorporated harmonic restraints on the backbone and side chain torsion angles of the SH3 domain. The stiffness of each restraint was 0.2 kcal/(mol-deg²). After the initial 10³ steps, the restraints were removed and an additional 10³ steps of S-MMC sampling were performed at a simulation temperature of 298 K to converge on an equilibrated conformation for the SH3 domain that was subsequently used as the starting conformation in all simulations involving this domain. This structure had a root-mean-square deviation (RMSD) of 1.1 Å from the coordinates in the PDB file as calculated over all backbone atoms. In order to calibrate the stability of the SH3 domain with the force field of choice, we performed, multiple, long (4 × 10⁷ steps), independent S-MMC simulations of the SH3 domain in the presence of 15 mM NaCl and in the absence of any harmonic restraints at a simulation temperature of 298 K. The results, summarized in panel B of Figure 2, demonstrate that the folded state of the SH3 domain is maintained in lengthy S-MMC simulations.

For each simulation of a tethered system, the randomly chosen IDR conformation was tethered to the N-terminus of the structure of the pre-equilibrated SH3 domain. The starting conformations for simulations of tethered systems were obtained by 10³ of S-MMC simulations performed at 298 K in the presence of torsional restraints on the ordered SH3 domain. The starting conformations were further thermalized using 10⁷ S-MMC steps of sampling after the addition of suitable numbers of Na⁺ and Cl^– ion pairs to mimic a bulk salt concentration of 15 mM.

Introducing the HS-MMC Methodology

The Hamiltonian Switch Metropolis Monte Carlo (HS-MMC) Algorithm

The design of HS-MMC relies on the use of two Markov chains that sample conformations drawn from two distinct Boltzmann distributions. In the interest of completeness, we first introduce our notations for S-MMC sampling. We shall assume that the current coordinates of the system comprising of an IDR tethered to the OD are denoted as i. A random change is made to these coordinates and the nature of this change depends on the move set. We denote the new state proposed by virtue of the randomly chosen move to be j. The transition probability to go from state i to j is given by the Metropolis criterion²⁹ as

2

Here, α_ij denotes the elements of the transition matrix that determine the probability that the prescribed move set yields a transition from i to j; ΔU_ij = U_j – U_i is the difference in potential energies between states j and i; β = (RT)⁻¹ where R = 1.987 × 10^–3 kcal/(mol K) is the Boltzmann constant and T is the simulation temperature in degree Kelvin. The move sets we use ensure that α_ij = α_ji; that is, the transition matrix is symmetric. Accordingly, π_ij can be written in compact notation in terms of the equilibrium probabilities (normalized Boltzmann weights) p_i and p_j associated with states i and j, respectively as

3

In HS-MMC, a majority of the states are generated using S-MMC sampling that is based on the Boltzmann distribution governed by the full Hamiltonian (FH in Figure 5), which corresponds to eq 1 in the methods section. Each S-MMC step also includes an additional test. A uniformly distributed random number r_EV is drawn and compared to p_EV where 0 ≤ p_EV ≤ 1. If r_EV < p_EV, the Hamiltonian is switched for the next n_EV steps of the simulation, and S-MMC sampling based on a second Markov chain is used to draw states from the Boltzmann distribution for the excluded volume (EV) Hamiltonian. The EV Hamiltonian combines two terms viz., U_EV and U_restr. The term U_EV is the repulsive arm of the Lennard-Jones potential and models pairwise steric repulsions between atoms within the IDR and between atoms of the IDR and those of the OD. The term U_restr refers to a set of harmonic restraints with a force constant of 0.2 kcal/(mol-deg²) that are applied over all torsional degrees of freedom of the OD in order to maintain its current configuration while the EV Hamiltonian leads to new conformations for the IDR. The EV Hamiltonian has the form:

4

Here, U_EV denotes the repulsive arm of the standard 12–6 Lennard-Jones (LJ) potential and the parameters σ_ij and ε_ij for pairwise interactions are identical to those used for modeling LJ interactions in the full Hamiltonian.

Figure 5.

Schematic representation of the design of the HS-MMC simulation approach. Here, FH-MMC refers to a Markov chain generated using the standard Metropolis Monte Carlo simulations (MMC) based on the full Hamiltonian (FH). The simulation switches to an alternative Markov chain based on a Hamiltonian where intra-IDR interactions and those between the IDR and ordered domain are modeled using steric repulsions alone–the so-called excluded volume (EV) limit. During this EV-MMC part of the simulation, an additional term is included in the Hamiltonian that applies restraints to maintain the structure of the OD. In the schematic, the circles with letters depict distinct conformations sampled along the distinct Markov chains. The symbols p_j and p_i denote the Boltzmann weights associated with states j and i, respectively for the full Hamiltonian (FH) and conversely, p_n^′ and p_m represent the Boltzmann weights associated with the EV Hamiltonian for states n and m, respectively. The acceptance ratios for the sampling that is internal to the Markov chains for the FH and EV sections are the standard Metropolis criteria. The final state of the EV-MMC part of the simulation is accepted or rejected based on the acceptance ratio proposed by Gelb that satisfies detailed balance—see eq 5

Let m denote the conformation prior to the Hamiltonian switch and start of the S-MMC sampling based on the second Markov chain while p denotes the conformation that results after S-MMC sampling for n_EV steps along the second Markov chain. The conformation p is accepted or rejected according to the criterion:

5

Here, p_m^′ and p_p denote the equilibrium Boltzmann probabilities associated with conformations m and p, respectively for the EV Hamiltonian whereas the unprimed probabilities are those associated with the full Hamiltonian. Gelb has shown that the functional form in eq 5 satisfies detailed balance, which we further ensure by choosing moves based on symmetric transition matrices. Figures 5 shows a sketch of the design of the HS-MMC method.

Justifying the Choice of the EV Hamiltonian in HS-MMC

The design of HS-MMC is sufficiently general, and it can accommodate any approximation of the full Hamiltonian or an entirely different Hamiltonian. Our choice of the EV Hamiltonian is based on the observation that long S-MMC simulations based on this Hamiltonian generate converged distributions of thermodynamically relevant atomistic self-avoiding random walks. Importantly, the intra-IDR and IDR-OD interactions are purely short-range repulsions. Therefore, unlike other possible choices for the auxiliary Hamiltonian, the EV term ensures a systematic dilution of contacts and yields states, which if accepted, will depart from energy traps and hence improve the sampling on the rugged energy landscape encoded by the full Hamiltonian. Of course, one could just as easily apply a coupling parameter λ (0 ≤ λ ≤ 1) on the set of non-EV terms in the Hamiltonian in order to create a series of Hamiltonian replicas of the system and perform replica exchange simulations in λ-space.^20b,23,30 In such methods, the improved sampling comes with the additional cost of setting up communication between the different replicas. In switching, as opposed to exchange simulations, one can use each computational core for a single HS-MMC run and this allows us to carry out multiple independent simulations in order to assess the similarity of statistics obtained across each simulation.

Instead of the U_EV term, one could use the Weeks–Chandler–Andersen (WCA) potential,³¹ which excises a purely hard sphere term from the Lennard-Jones potential. As a result the spatial range for repulsions would be shorter for WCA when compared to the U_EV terms. This might improve the acceptance ratios and allow for longer auxiliary Markov chains with the switched Hamiltonian. We have not explored the WCA model as an auxiliary potential because previous work showed that the U_EV term, which belongs to the family of inverse power potentials,³² encodes significant fine structure into the energy landscape, which allows us to ensure that local conformational propensities such as the residue and context specific biases for polyproline II, α-helical, and β-strand ϕ, ψ values is preserved.^18,33 This feature does not obtain with the WCA model, which eliminates all such local preferences since all sterically allowed conformations have equal weights.

Parameterization of HS-MMC

The two parameters of HS-MMC that need optimization are p_EV and n_EV. As noted above, the Hamiltonian switch is attempted with a probability p_EV at every step along the first Markov chain. The parameter p_EV needs to be low enough to guard against frequent switches to ensure efficient sampling from the distribution governed by the full Hamiltonian. It should, however, be finite enough to ensure that a sufficient number of Hamiltonian switches are attempted in a single HS-MMC run. Through a series of trials, we converged on an optimal choice of p_EV = 5 × 10^–4 for the systems studied here. This choice yields a percent probability of 1–5% for the acceptance criterion shown in eq 5. We deem this to be acceptable given the extent of decorrelation that is achieved by the systematic dilution of contacts engendered by the use of the EV Hamiltonian. The optimal choice for n_EV can be made independently or it can be coupled to the optimization of p_EV. We converged on the optimal choice for n_EV by performing a series of simulations with different values for n_EV and monitoring the conformational dissimilarity and energy differences between the conformations depicted as m and p in Figure 5. The goal was to prescribe a range for n_EV that maximizes the conformational dissimilarity between m and p while minimizing the energy difference ΔU_pm (see Figure 5). This approach resulted in the choice of n_EV being in the range 25–75 steps.

It does not follow that the choices listed here can be transferred automatically to any tethered IDR-ordered domain system. The peculiarities of the system and the full Hamiltonian will mandate the necessary problem specific optimization in the choices for p_EV and n_EV although some level of automation seems reasonable if the problems belong to a specific category. The choices for p_EV and n_EV make HS-MMC fundamentally different from Gelb’s method and other variants of his NMCMC approach. In the latter, a bulk of the sampling is performed using the auxiliary Markov chain that uses the less expensive approximate Hamiltonian. This can create a severe shortage of distinct, uncorrelated conformations drawn from the ensemble for statistical analysis. Although this is not a major weakness when the application calls for a characterization of discrete points on a quantum mechanical energy surface, it becomes a major weakness for our applications because we require quantitative descriptions for a broad range of uncorrelated IDR conformations. As is inferred by the optimal choices for p_EV and n_EV the majority of the sampling in HS-MMC is performed using the full Hamiltonian, and the auxiliary Markov chain can be viewed as a random, unbiased interjection of an alternative set of moves that provide transitions out of energetic traps.

Results

Tests of HS-MMC for Sampling Conformational Ensembles of Tethered Systems

Figures 6–10 summarize the statistics gleaned from multiple, independent HS-MMC runs for IDRs 1–3 simulated as bristles that are tethered to the N-terminus of the SH3 domain (see Figure 3). These results are compared to those obtained from multiple, independent S-MMC simulations with identical amounts of sampling. As noted in panel B of Figure 2, the SH3 domain does not undergo large-scale conformational fluctuations under the simulation conditions used here. Accordingly, we focus our analysis on the conformational properties of the IDRs. In doing so, we obtain assessments of the improvements obtained using HS-MMC as compared to S-MMC runs. The latter, as noted above, tends to be confounded by problems of broken ergodicity. The lack of self-averaging is a classic signature of broken ergodicity and there are several approaches for diagnosing such problems.³⁴ Here, we employ a simple criterion that quantifies the degree to which sufficiently long independent simulations produce similar statistical distributions for different conformational properties.

Figure 6.

Assessing the sampling quality for S-MMC and HS-MMC. Results are shown for IDR1 simulated in bristle mode by tethering it to the N-terminal end of the SH3 domain. Column 1 summarizes the results from ten independent S-MMC runs and these are compared to results in column 2 that summarize the results from ten independent HS-MMC runs. The histograms along the top row show results for the distributions of R_g values (in Å) extracted from each independent simulation. The histograms along the bottom row show results for the distributions of asphericity values (δ*). The results show that HS-MMC produces distributions for polymer sizes and shapes that have greater similarity from one independent run to the next (see column 2) when compared to the independent S-MMC runs (see column 1). The histograms were generated using bin widths of 0.1 Å (top row) and asphericity units of 0.01 (bottom row).

Figure 10.

Comparison of the conformational properties of IDRs modeled as autonomous units to IDRs modeled as bristles that are tethered to the N-terminus of the SH3 domain. Here, we plot the scaling of ensemble averaged spatial separations between pairs of residues i and j versus the linear sequence separation |j–i| for each IDR. In each plot, the open squares, cross marks, and open diamonds denote the expected scaling of ⟨R_iij⟩ against |j–i| for a self-avoiding random walk (EV), a classic Flory random coil (FRC), and a random Lennard-Jones globule (LJ). IDR1 samples compact conformations as an autonomous unit and this feature is preserved in the bristle mode. IDR2 and IDR3, respectively sample semicompact, hairpin-like and Flory-random-coil-like conformations as autonomous units. For both sequences, their intrinsic conformational properties are maintained, although some degree of expansion is evident and is attributable to the excluded volume effect of the ordered SH3 domain.

Row A in Figure 6 shows the raw histograms obtained for the radius of gyration (R_g) values calculated over the IDR1 stretch from ten independent S-MMC and HS-MMC runs. Row B quantifies equivalent histograms for asphericity (δ*) values. We use these two parameters because R_g quantifies the overall size (density) of the IDR and δ* quantifies its shape. For each conformation, the asphericity is calculated from eigenvalues of the conformation specific gyration tensor. For spheres, δ* ≈ 0; for rods δ* ≈ 1; and for ellipsoids, δ* will have intermediate values. Visual inspection shows that the histograms obtained from the independent S-MMC runs show greater variability when compared to those obtained from HS-MMC runs (see Figure 6). We put this observation on a quantitative footing as shown in Figure 7. For each observable, viz., R_g and δ*, we calculated the overlaps between all unique pairs of histograms for S-MMC and HS-MMC runs. Panel A in Figure 7 shows the average pairwise overlap obtained for histograms of R_g values for each of the three tethered IDRs whereas panel B in Figure 7 shows equivalent results derived from histograms of δ* values. These results demonstrate that the overlap between histograms obtained from HS-MMC runs is systematically higher for equivalent amounts of sampling when compared to S-MMC runs. This is true irrespective of the observable viz., R_g or δ* and remains valid even for higher-order distributions such as the joint distributions of δ* and R_g values (Figure 8). Importantly, lengthening each of the independent simulations can increase the overlap of statistical distributions obtained among different runs. Further, the robustness of these statistical properties can be gleaned by increasing the number of independent runs by an order of magnitude because these simulations are “embarrassingly parallel” and do not require any communication between compute nodes. These simulations are efficient in that it takes ca. 250 h of wall clock time to complete a single HS-MMC run (∼10⁸ steps for the systems studied here) on a single core of an Intel-Xeon E5-2670 2.6 GHz node with eight cores.

Figure 7.

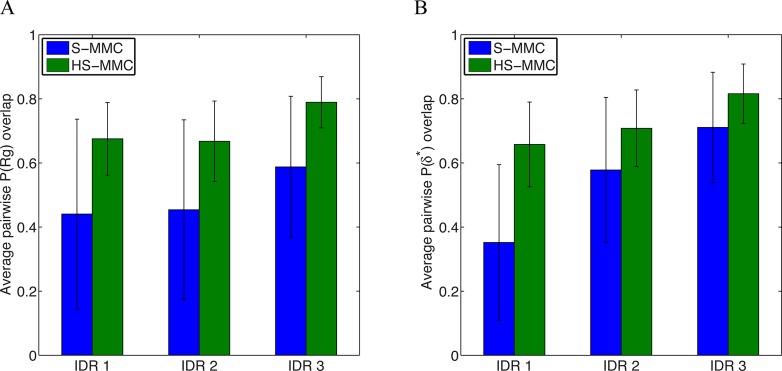
Panels A and B quantify the average overlap between pairs of distributions shown in rows 1 and 2 of Figure 6, respectively. In general, the pairwise overlap is higher for distributions generated using HS-MMC simulations (green bars in both panels) than the S-MMC simulations (blue bars). The error bars quantify the standard error in the estimate of the mean.

Figure 8.

Simulation results can also be analyzed to extract statistics for two-dimensional histograms viz., P(δ*,R_g). Panels A and B show histograms drawn from individual, independent S-MMC and HS-MMC runs, respectively, for IDR1 tethered to the SH3 domain. HS-MMC enables the sampling of a broader range of conformations for the tethered IDR. Panel C quantifies the average overlap between pairs of two-dimensional histograms P(δ*,R_g) which are extracted from pairs of independent S-MMC (blue) and HS-MMC (green) simulations, respectively. Again, the overlap between distributions obtained using HS-MMC is higher than for S-MMC runs.

HS-MMC Generates Ensembles of Increased Conformational Heterogeneity

Recently, Lyle et al.^12a introduced a measure to quantify the degree of heterogeneity within ensembles of thermodynamically relevant conformations that are extracted from converged simulations. This parameter, denoted as Φ, approaches unity for a homogeneous ensemble characterized by small-scale conformational fluctuations and approaches zero for ensembles characterized by a broad range of diverse conformations. For a chain of N residues, each conformation c is represented as an n_d × 1 conformational vector V_c where n_d = (N(N – 1)/2), V_c = {d₁₂,d₁₃,...,d_N–1,N}, and each element d_ij in V_c represents the spatial distance between a unique pair of residues, i and j. For each pair of residues i and j, we calculate d_ij = 1/Z_ij·Σ_m∈iΣ_n∈j|r_mⁱ – r_n|. Here, r_mⁱ and r_n^j denote the position vectors of atoms m and n within residues i and j, respectively, and Z_ij is the number of unique pairwise interatomic distances between the two residues. To compare a pair of conformations k and l, one calculates a pairwise dissimilarity measure where cos(Ω_kl) = V_k·V_l/|V_k||V_l|. An ensemble of n_c conformations produces an ensemble of conformational vectors, V₁, V₂,...,etc. These vectors are used to calculate a distribution 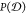of n_c(n_c – 1)/2 conformational dissimilarity values. 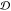For each ensemble we actually calculate two distributions of dissimilarities viz., the distribution of -values for pairs of conformations within an ensemble and a distribution of 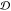-values comparing each conformation to an ensemble of conformations drawn from a Flory random coil model as described by Lyle et al.^12a Averaging over the former yields and averaging over the latter, which is an ensemble of ensembles yields . The values of and lead to an estimate of the degree of heterogeneity Φ within the ensemble. We first compute the ratio 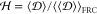and use it to calculate .

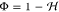Figure 9 plots the values for Φ obtained from S-MMC versus HS-MMC runs for each of the three tethered IDRs. We find a systematic trend whereby the heterogeneity within each conformational ensemble is higher (the values of Φ are lower) for HS-MMC runs compared to S-MMC runs. This suggests that we are able to sample a broader spectrum of thermodynamically relevant conformations using HS-MMC when compared to S-MMC.

Figure 9.

Quantification of the ensemble heterogeneity Φ from ten independent S-MMC and HS-MMC simulations of the three IDRs tethered to the SH3 domain. The trends in Φ are identical between the two simulation approaches. The quantitative assessments of heterogeneity are, however, different between the two approaches and the HS-MMC method yields ensembles of higher conformational heterogeneity.

Comparative Assessments of Conformational Properties of IDRs Modeled As Autonomous Units to Tethered IDRs

Finally, Figure 10 shows a comparison between the conformational properties of each IDR modeled as an autonomous unit to that obtained for the tethered IDRs. There is no a priori reason to expect significant distortion of the intrinsic properties of IDRs given that the measured conformational properties of the stable SH3 domain, in general, remain unperturbed by the tethering of IDRs. This suggests weak coupling between the IDR and the ordered domain. As shown in Figure 10, the HS-MMC simulations yield results that support the expectation of weak coupling. Here, we plot the so-called internal scaling profiles that provide a complete summary of conformational properties for each IDR. In each plot the ordinate refers to ⟨R_ij⟩, the ensemble-averaged inter-residue distances calculated for all pairs of residues that are |j–i| apart along the linear sequence. These internal scaling profiles quantify local concentrations of chain segments around each other. They are particularly useful for classifying conformational ensembles because the profiles show distinct limiting behaviors for self-avoiding random walks, Flory random coils, and random globules, respectively (see Figure 10).

In concordance with expectations based on previous reports,^7c,7e,35 IDR1 forms a heterogeneous ensemble of compact, globular conformations as an autonomous unit. Conversely, IDRs 2 and 3 are expected to form semicompact hairpin-like conformations and Flory random coil-like conformations,^7c respectively, and these features are reproduced for these sequences modeled as autonomous units. If the coupling between the IDRs and the SH3 domain is weak, then we expect that the intrinsic conformational properties of IDRs should be preserved even upon tethering, and Figure 10 shows that this is indeed the case. Perturbations about the intrinsic properties are attributable to the excluded volume effects of the OD. The results shown in Figure 10 are not realizable when internal scaling profiles are calculated using conformations drawn from S-MMC runs (data not shown). Instead, the results vary considerably from one run to the next as established in the analyses of Figures 6–8.

Discussion

In the preceding paragraphs, we summarized results that compare the similarities of statistics for a set of conformational properties that were obtained from multiple independent HS-MMC and S-MMC runs, respectively. These results highlight the improvements afforded by the HS-MMC algorithm in terms of (a) alleviating broken ergodicity as measured by the similarity of statistics among different runs; (b) yielding ensembles with systematically increased conformational heterogeneity; and (c) generating ensembles with conformational properties that are consistent with the expectation of weak interactions between the IDRs and the ordered SH3 domain.

The HS-MMC approach is a direct adaptation of the NMCMC method proposed by Gelb, which enables the use of approximate/alternative Hamiltonians for enhancing conformational sampling. This method bears conceptual resemblance to other Monte Carlo sampling methods such as J-walking³⁶ and smart darting.³⁷ One can also envisage the use of a suitable simulated tempering based approach such as Hamiltonian replica exchange,^23b,30 reservoir exchange,³⁸ general library based Monte Carlo methods,³⁹ resolution exchange,⁴⁰ or generalizations of simulated tempering that are based on Tsallis statistics.⁴¹ All of these methods offer distinct advantages. We selected a switching based method as opposed to tempering based methods in order to eliminate the need for communication between replicas and thereby leverage the use of multiple, independent “swarms” of simulations. By removing the need for interprocess communication, HS-MMC simulations can be run in a highly distributed manner, across heterogeneous hardware without the need for any form of message passing between compute nodes. A particular advantage is the ability to design direct probes for robustness by assessing the reproducibility of statistics from one run to the next. In fact, this class of approaches are well-suited to distributed computing applications, which have significant advantages such as the ability to unmask robust features of conformational landscapes as demonstrated by various investigations carried out under the auspices of the Folding@Home project.⁴²

It is worth emphasizing that, our preliminary results aside, it does not automatically follow that all IDRs will always interact weakly with the ordered domains to which they are tethered. There exists the possibility that ordered domains can modulate the conformational properties of IDRs, especially if the compositional biases within IDR sequences are not particularly strong. It is also possible that tethered IDRs will induce local unfolding of ordered domains or secondary structure motifs as has been documented in simulations⁴³ and experiments.⁴⁴ A general framework for quantifying the synergy between IDRs and ordered domains is likely to be accessible through deployment of the HS-MMC method in conjunction with the ABSINTH force field paradigm for studying the ensembles of a large number of archetypal tethered systems.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States