Inferring Microscopic Kinetic Rates from Stationary State Distributions

Abstract

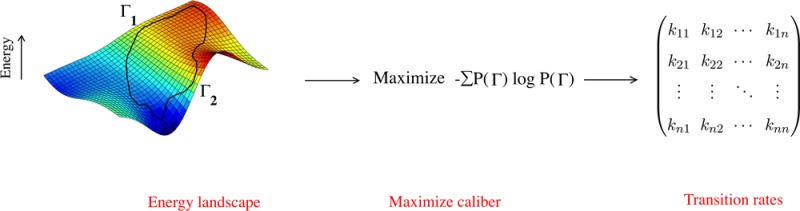
We present a principled approach for estimating the matrix of microscopic transition probabilities among states of a Markov process, given only its stationary state population distribution and a single average global kinetic observable. We adapt Maximum Caliber, a variational principle in which the path entropy is maximized over the distribution of all possible trajectories, subject to basic kinetic constraints and some average dynamical observables. We illustrate the method by computing the solvation dynamics of water molecules from molecular dynamics trajectories.

Introduction

We propose a method for inferring the kinetic rate matrix for stochastic systems for which the steady state popuations are known. The types of systems of interest include protein folding,¹⁻³ ion channels,⁴ molecular motors,⁵ the evolutionary dynamics of protein sequences,⁶ the collective firing patterns of neurons,⁷ or noisy gene expression.⁸ In such studies, stationary probabilities {p_i} of N stable states {i} are often known or estimated from experimental data,^6,7 detailed molecular mechanics calculations,³ coarse grained theories,^1,4 or from Maximum Entropy.^6,7,9−12 Moreover, suppose further that we know some average global dynamical quantity, such as the average mutation rate (number of amino acid changes per unit time), the average current through an ion channel, or the average number of neurons that change their state from spiking to resting (and vice versa) per unit time step. How can we infer the full distribution of microscopic state-to-state rates, given just the stationary-state populations and one or more average overall rate quantities?

More specifically, we are interested in a principled way to solve the following under-determined “inverse” kinetics problem. Consider a stationary and irreducible Markov process among i = 1,2,3,...,N states. Suppose you know the following: (a) the stationary state probability distribution, {p_i} of the occupancies of those states, and (b) the value ⟨w⟩ of some dynamical observable w averaged over the ensemble of stationary state trajectories. From these N + 1 quantities, we want to infer the N × N microscopic transition probabilities,

1

between those states.

While the stationary distribution indeed constrains the transition probability matrix, it does not uniquely determine it. Here, we develop a procedure based on the principle of Maximum Caliber, a variant of the principle of Maximum Entropy, that is applicable to dynamical processes.^13,14 This variational principle allows us to uniquely infer ∼N² transition probabilities that are consistent with ∼N imposed constraints.

First, we define the path entropy, S, over a given ensemble {Γ} of trajectories Γ ≡ ... → i → j → k → l... as

2

Maximum Caliber is a variational principle that chooses a unique probability distribution {P(Γ)} over trajectories from all possible candidate distributions as the one that maximizes the path entropy while otherwise satisfying the relevant stationary and dynamical constraints.¹³⁻¹⁶

Consider an ensemble of stationary state trajectories {Γ} (see above) having a total time duration T. Restricting our attention to first-order Markov trajectories allows us to greatly simplify the path entropy and carry out our analysis in terms of trajectories of single steps, i → j.^2,17−19 The Markov property implies that the probability of any particular trajectory Γ can be expressed in terms of the transition probabilities {k_ij},

3

The path entropy of the above ensemble is directly proportional to the total duration T of the trajectory. The path entropy per unit time is given by^20,21

4

The microscopic transition probabilities of any Markov process are subject to two types of constraints. First, from state i at time t, the system must land somewhere at time t + dt. Second, a system in state j at time t + dt must arrive from somewhere, so

5

Third, we require one additional constraint that is global, that is, averaged over the entire ensemble of trajectories. We fix the path ensemble average of some dynamical quantity w. The average ⟨w⟩_Γ over any given stationary trajectory Γ is given by

6

The path ensemble average ⟨w⟩ is

7

Since Γ is a stationary state trajectory, the path ensemble average ⟨w⟩ of eq 7 simplifies to

8

Maximization of the path entropy subject to these three constraints can be expressed equivalently in terms of maximization of a quantity called the Caliber 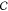:¹⁴

9

where γ is the Lagrange multiplier associated with the constraint ⟨w⟩ and {a_i} and {l_i} enforce the to-somewhere constraint and the from-somewhere constraint, respectively.

To solve for the matrix k_ij of transition probabilities, we take the derivative of the Caliber 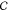with respect to k_ij and equate it to zero. This gives

10

where we have made the substitutions: e^a_i–1 = β_i/p_i and e^l_j = λ_j. The values k_ij^* are the transition probabilities that satisfy the constraints and otherwise maximize the caliber. For simplicity of notation, we drop the superscript * in the remainder of this paper, that is, k_ij ≡ k_ij.

In this problem, the values of p_i are given. To compute the k_ij values, we first must determine the values of the Lagrange multipliers β_i, λ_j, and γ. We do so by substituting the constraint relations mentioned above.

Determining the Lagrange Multipliers

For a given value of γ, the modified Lagrange multipliers β_i and λ_j are determined by satisfying the to-somewhere and from-somewhere conditions indicated above. From eqs 5

11

where e^–γw_ij = W_ij. Equation 11 can be simplified if we define a nonlinear operator D over column vectors x̅ = [x₁,x₂,...]^T as D[x̅]_i = p_i/x_i. We have

12

where λ̅ = [λ₁,λ₂,...]^T and β̅ = [β₁,β₂,...]^T are the column vectors of Lagrange multipliers.

For a particular value of the Lagrange multiplier γ, eqs 12 can be numerically and self-consistently solved for {β_i} and {λ_i}. In practice, we choose an appropriate γ by first constructing transition probabilities {k_ij} for multiple values of γ (see eq 10) and choosing the value of γ that satisfies

13

where ⟨w⟩ is the prescribed value of the ensemble average of the dynamical quantity w.

Detailed Balance

So far, the treatment above is generally applicable to nonequilibrium systems. However, if we are interested in restricting our attention to systems in thermodynamic equilbrium, we can impose an additional constraint that the system must satisfy detailed balance, p_ik_ij = p_jk_ji. In this case, the Caliber can be expressed as

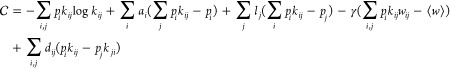14

Here, d_ij are Lagrange multipliers that impose the detailed balance condition. Differentiating with respect to k_ij and setting the derivative to zero, we find (see eq 10)

15

where δ_ij = e^d_ij–d_ji = 1/δ_ji.

Now we have to determine the modified Lagrange multipliers β_i, λ_j, δ_ij, and γ from the imposed constraints. Let us first impose detailed balance to determine δ_ij. We have

16

Since δ_ij = 1/δ_ji, we have

17

In eq 17, identifying ρ_i = (β_iλ_i)^1/2,

18

where e^{–γ/2(w_ij+w_ji)} = W_ij^sym is the symmetrized form of W_ij = e^–γw_ij (see above). It is easy to see that k_ij in eq 18 satisfies detailed balance. The Lagrange multipliers ρ̅ = [ρ₁,ρ₂,...,ρ_N] and γ are determined by the same procedure as described above. We have

19

In other words, ρ̅ is the solution of the nonlinear equation

20

and γ is determined by adjusting the path ensemble average

21

An Illustration: Computing the Dynamics of a Solvation Shell from Simulated Populations

We now illustrate how the present MaxCal method can be used to take a stationary-state distribution and a global dynamical constraint and to infer microscopic kinetics. Consider a shell of solvating water molecules surrounding a single water molecule. The number, n(t), of water molecules in the hydration shell is a quantity that fluctuates with time t (see Figure Figure 1). We want to compute how fast the water molecules enter or exit the solvation shell. If the time interval dt is small, n(t) and n(t + dt) will be statistically correlated. Here, we construct a Markov process to model the time series {n(t)}. We will require the Markov process to reproduce (a) the stationary distribution p(n) that is observed in molecular dynamics simulations, and (b) the average change in occupancy Δ per time step of duration dt, a path ensemble average (see Appendix for details of molecular simulation). While the choice of dynamical constraint(s) remains somewhat arbitrary, it is validated only a posteriori. In other words, the constrain(s) is a modeling aspect of any maximum entropy method.²² We have

22

where n(t) = i and n(t + dt) = j.

Figure 1.

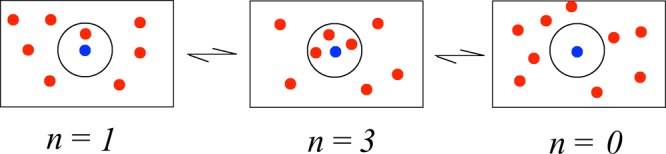
Hydration shell (black circle) around a central water molecule (blue disc) is dynamically populated by other water molecules in the bulk solvent medium (red discs). The probability, p(n) that the hydration shell has exactly n water molecules is a key quantity in determining the solvation free energy of liquid water.^23,24

Since the system should satisfy detailed balance, the transition probability k_ij for a transition n(t) = i → n(t + dt) = j is given by (see eq 18),

23

For a given value of γ, we determine the Lagrange multipliers ρ_i from eqs 20 above. In order to determine the Lagrange multiplier γ which dictates the rate of transition between states, we first construct Markov processes for different values of γ. Panel B of Figure Figure 2 shows that the path ensemble average of the change in occupation number per unit time step Δ is exponentially decreasing with γ. From trajectories sampled at every 5 fs from the MD simulation, we find that experimental trajectory average Δ_expt = 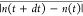≈ 0.0629 which corresponds to γ ≈ 3.29. From here onward, we use γ = 3.29 and construct the transition probabilities {k_ij} (see eq 23). Note that the path ensemble average Δ and consequently the Lagrange multiplier γ, depend on the time interval dt between two observation (dt = 5 fs here).

Figure 2.

Panel A: The stationary distribution p(n) of the number of water molecules in the hydration shell of radius r = 3.2 Å of a reference water molecule. Panel B: The dependence of the ensemble average of change in water occupancy number Δ = ⟨|n(t + dt) – n(t)|⟩ on the Lagrange multiplier γ. We see that Δ depends exponentially on γ. A higher γ implies slower dynamics and vice versa. We choose γ = 3.29 to match the observed Δ ≈ 0.0629 in the molecular dynamics simulation.

From the Markov process constructed with γ = 3.29 (see above), we now compute various dynamical quantities: (a) the probability P_d of jump size d, (b) the occupancy autocorrelation ⟨δ_n(0),n(τ)⟩, and (c) the transition probabilities k_ij, and we compare to those obtained directly from the MD simulation trajectory. In general, the MaxCal method will be of value when transitions are hard to simulate, such as for large kinetic barriers. Here, we are just illustrating with a toy problem for which we can determine the transition probabilities independently from the simulations.

From the long simulation trajectory, the probability P_d of jump size is estimated as the histogram of d = n(t + dt) – n(t). Here d could be both positive and negative. P_d is given by

24

The normalized occupancy autocorrelation is simply the joint probability that n(t) and n(t + τ) are equal. It is given by

25

where K(τ) = k^τ is the τ^th power of the matrix of transition probabilities {k_ij}.

In Figure 3 we plot P_d, ⟨δ_n(0),n(τ)⟩, and {k_ij} estimated from the molecular dynamics trajectory and compare them to our predictions from Markov modeling. Even though we constrained only the mean value Δ = ⟨|d|⟩ of P_d, the modeled Markov process captures the entire distribution P_d with high accuracy. Similarly the occupancy correlation ⟨δ_n(0),n(τ)⟩ is also reproduced with high accuracy even though we did not utilize any information about it when inferring the transition probabilities of the Markov process. Moreover, our modeling also accurately captures the individual transition probabilities {k_ij} over 4 orders of magnitude.

Figure 3.

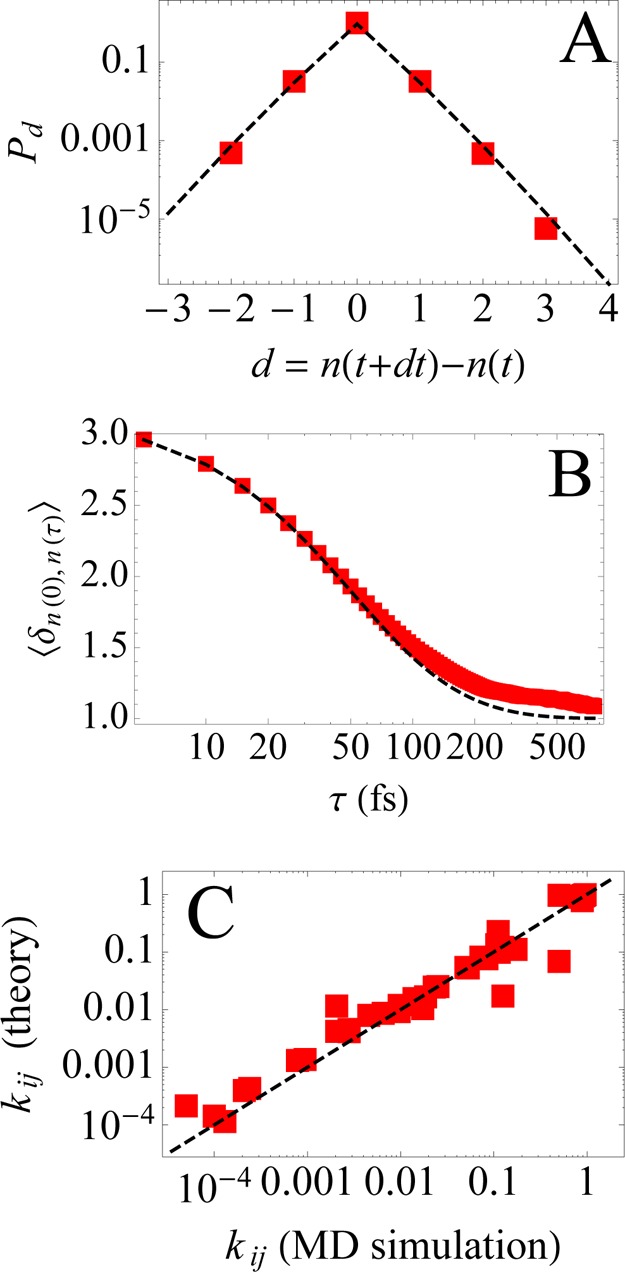
Panel A: The probability P_d of jump size estimated from the trajectory derived from MD simulation (red squares) is compared to the one predicted using the transition probabilities of the Markov process (dashed black line). Panel B: The normalized occupancy autocorrelation ⟨δ_n(0),n(τ)⟩ as estimated from the MD trajectory and as predicted from the transition probabilities of the Markov process. Panel C: We directly compare the transition probabilities k_ij for the probability of transition i → j empirically obtained from the MD trajectory to the ones predicted by using eq 23.

Discussion and Summary

We have presented here a variational approach that computes N × N microscopic transition probabilities of a Markov process, given only knowledge of a stationary state population distribution and one trajectory-averaged dynamical property. In this approach, we maximize the path entropy subject to constraints; that is, we maximize the Caliber. We show that this method gives correct values of dynamical quantities in an example of molecular dynamics simulations of a water solvation shell around a single water molecule. This method may be useful for analyzing single-molecule experiments such as on ion channels,⁴ dynamics of neuron firing,⁷ and the dynamics of protein-sequence evolution,⁶ for example.

Appendix I: MD Simulation

We performed a molecular dynamics simulation on 233 water molecules^25,26 at 300 K and at a constant volume using NAMD²⁷ with help of the Langevin thermostat. The oxygen atom of one of the water molecules was fixed at the origin. The time step of integration was 1 fs and the trajectory was stored every 5 fs. Sampling the trajectory every 5 fs ensures that correlations in n(t) have not vanished.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States