Electroosmosis in a Finite Cylindrical Pore: Simple Models of End Effects

Abstract

A theoretical model of electroosmosis through a circular pore of radius a that traverses a membrane of thickness h is investigated. Both the cylindrical surface of the pore and the outer surfaces of the membrane are charged. When h ≫ a, end effects are negligible, and the results of full numerical computations of electroosmosis in an infinite pore agree with theory. When h = 0, end effects dominate, and computations again agree with analysis. For intermediate values of h/a, an approximate analysis that combines these two limiting cases captures the main features of computational results when the Debye length κ^–1 is small compared with the pore radius a. However, the approximate analysis fails when κ^–1 ≫ a, when the charge cloud due to the charged cylindrical walls of the pore spills out of the ends of the pore, and the electroosmotic flow is reduced. When this spilling out is included in the analysis, agreement with computation is restored.

1. Introduction

Electroosmosis in a circular cylindrical pore of finite length h differs from that in an infinitely long pore due to end effects. If the cylinder length h = 0, then the pore consists of a hole in a charged membrane of zero thickness, and electroosmosis can be considered to be entirely due to end effects. This case was considered by us previously.¹ When the cylindrical pore is infinitely long, end effects are negligible, and the computation of the electroosmotic volumetric flow rate Q, for arbitrary Debye lengths and surface charge densities, is standard^2,3 (with similar results available for infinitely long planar channels⁴⁻⁷). Here, we are interested in intermediate values of h.

Full numerical computation of the Poisson–Nernst–Planck (PNP) equations for ionic motion is, of course, possible, and some typical results were reported by Mao et al.¹ Such numerical computations, however, do not identify the mechanisms underlying the qualitative features of the physical system. Here, we discuss how simple models, based on continuity of electric current and volumetric flow rate, can be combined in order to estimate end effects for pore lengths h > 0. We assume that the zeta potential on the surface of the membrane is small, so that the Poisson–Boltzmann equation governing the equilibrium charge cloud can be linearized, and the electroosmotic velocity can be determined by an analysis equivalent to that of Henry⁸ for electrophoresis, i.e., fluid motion is generated by the effect of the applied electric field acting on the equilibrium charge cloud (which is not deformed either by the applied electric field or by fluid motion). In this limit, the electroosmotic volumetric flow rate Q through the hole in the membrane can be determined by means of the reciprocal theorem.¹

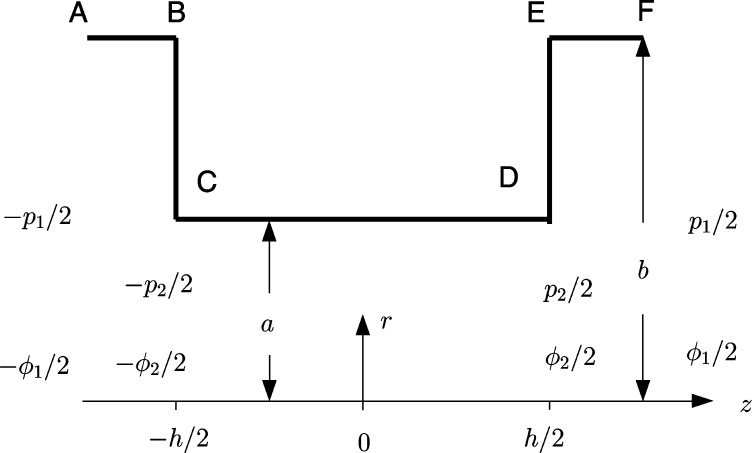
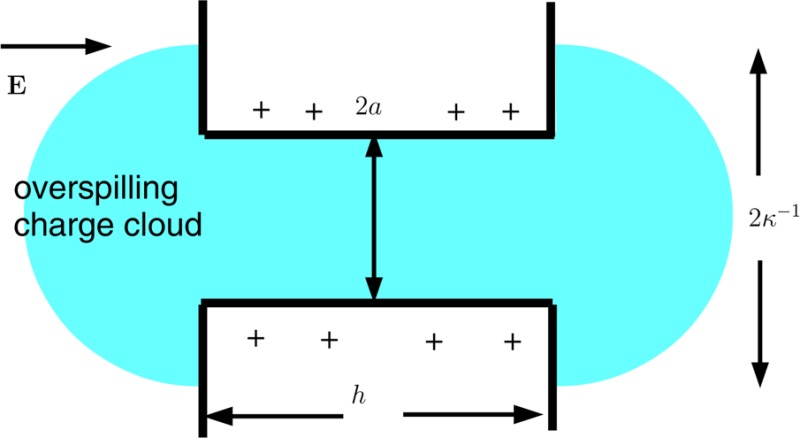
Figure 1 shows the axisymmetric geometry that we are considering. The cylindrical pore CD has radius a and length h. The cylindrical surface CD of the pore has surface charge density σ_c , and the membrane surfaces BC and DE have surface charge density σ_m. An electrical potential difference is applied between the fluid reservoirs at either side of the membrane, and electroosmotic flow is generated by the resulting electric field acting on the charge cloud adjacent to the charged surfaces. The analysis of Mao et al.¹ assumed that the external reservoirs on either side of the pore were unbounded, with radius b = ∞. For the numerical computations presented in section 3, the external reservoirs were bounded by uncharged cylinders of radius b ≫ a, sufficiently large that numerical results when h = 0 differed little from the analytic results for h = 0 and b infinite. There have been many studies in which flow is generated in cylinders of different dimensions, connected either in series⁹ or in networks intended to represent porous media.¹⁰ Here, however, we are interested in the effect of the surfaces BC and DE of the membrane on electroosmotic flow within the cylindrical pore, and any boundaries, AB and EF, of the external reservoirs are so far away that they can be neglected.

Figure 1.

Cylindrical pore CD, of length h and radius a with surface charge density σ_c , passing through the membrane with surface charge density σ_m on the two surfaces BC and DE. The reservoirs on either side of the membrane are large (b ≫ a). The pore and reservoirs are axisymmetric about the z axis.

We shall allow the surface charge density σ_m on the membrane to differ from the charge density σ_c on the wall of the cylindrical pore. There have been previous detailed studies of the effect of a discontinuity in surface charge density on electroosmosis.^11,12 The fine details of the charge cloud and fluid motion around such a discontinuity will be lost by the simple models presented here. They are, of course, fully taken into account in the numerical computations discussed in section 3.

In section 2.2, we set up the approximate analysis of end effects and compare results to those obtained from full numerical computations. The analysis is presented from first principles, but it can alternatively be set within the framework of the reciprocal theorem, as explained in section 2.6. The agreement between the approximate analysis and full computation is, in general, good, except for large Debye lengths κ^–1 ≫ a. In section 4, we consider this case in more detail in order to evaluate how much of the charge cloud due to the charged walls of the cylindrical pore lies within the pore and how much spills out beyond the ends of the pore. When this overspill is taken into account, the agreement between the computations and the approximate model is improved.

2. Composite Electroosmotic Coefficient

2.1. Pore Geometry

The axisymmetric geometry that we are considering is shown in Figure 1. We use cylindrical polar coordinates (r,z), with the z axis along the axis of symmetry and z = 0 at the midpoint of the cylindrical pore, the ends of which are at z = ±h/2. When h = 0, we shall also use oblate spherical coordinates (ξ,η), with

1

where −∞ < ξ < ∞ and 0 ≤ η < π/2.

The cylindrical pore and the reservoirs at either end are filled with liquid with electrical conductivity Σ and viscosity μ. The wall CD of the cylindrical pore is charged, with uniform surface charge density σ_c , and the surface charge density over the membrane surfaces, BC and DE, is σ_m. The electrical permittivity ϵ_s of the membrane will be typically much smaller than the permittivity ϵ of the liquid, and we assume ϵ_s = 0. We assume that the reservoir boundaries AB and EF are uncharged and at infinity. We shall occasionally refer to the surface potential ζ, which will not, in general, be uniform, but which is required to be small, with ζ ≪ kT/e, where e is the elementary charge and kT the Boltzmann temperature. The electrical potential ϕ₀ within the equilibrium charge cloud therefore satisfies the linearized Poisson–Boltzmann equation so that

2

where κ^–1 is the Debye length, and the charge density in the equilibrium charge cloud is

3

2.2. The Applied Electric Field

The applied electric field is E = −∇χ, where the potential χ satisfies the Laplace equation

4

with gradient

5

normal to the walls of the membrane and of the cylindrical pore. In z > 0, the electric potential far from the membrane is χ = ϕ₁/2, and the potential far from the membrane in z < 0 is χ = −ϕ₁/2.

When the membrane thickness h = 0, the potential can be expressed explicitly as¹³

6

On the plane of the membrane, within the circular opening,

7

The liquid within the pore has electrical conductivity Σ; we have assumed that surface charge density (and hence the density of charge in the cloud of counterions) is small, so that surface conductivity may be neglected. Indeed, if the mobilities of the various ionic species are identical, then the surface conductivity due to the mobile charge cloud given by the linearized model (2) at O(eζ/kT) is zero. The total electric current I_m flowing through the hole in the membrane is therefore

8

If h > 0, then we assume that the potential within the cylindrical pore varies linearly and approximate the potential within the pore as

9

as would be expected in the absence of any end effects. The potential in z > h/2 is approximated by that outside a membrane (with a hole) of zero thickness

10

with χ(r,z) = −χ(r,–z). This approximation (9) and (10) is continuous at z = ±h/2 where the potential is assumed to be ±ϕ₂/2 across the entire width of the opening (by eq 7). The as yet unspecified potential ϕ₂ is determined by requiring continuity of the electrical current at z = ±h/2. The current I_c through the cylindrical pore is

11

and the electrical current through the reservoir in z > h/2 is, by eq 8,

12

Equating I_c (11) and I_m (12), we find

13

This computation suggests that the system can be treated as two resistors in series, with composite resistance

14

However, this estimate assumes a uniform potential over the ends of the pore at z = ±h/2, and we have effectively inserted thin, perfectly conducting sheets over the pore ends. Removal of these sheets can only increase the resistance and hence R_comp is an underestimate for the true total resistance R_tot. Figure 2a shows R_tot/(aΣ) computed numerically by means of the Freefem++ finite element package,¹⁴ together with R_comp/(aΣ). The difference is small and is shown in Figure 2b.

Figure 2.

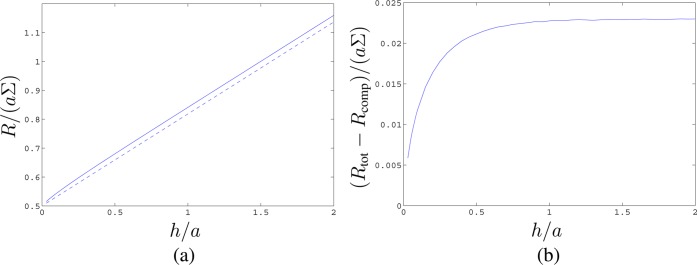
(a) Nondimensional Ohmic resisistance R/(aΣ) of a hole of radius a in a membrane of thickness h, as a function of h/a. Solid line, R_tot/(aΣ) computed numerically; dashed line, the approximation R_comp/(aΣ) (14). (b) The difference (R_tot – R_comp)/(aΣ).

2.3. Electroosmosis through an Infinite Cylindrical Pore

We assume throughout this article that the perturbation of the equilibrium charge cloud by the applied electric field and by fluid motion is negligibly small. The force acting on the ions in the charge cloud due to the applied electric field −∇χ is therefore −ρ₀∇χ.

The equilibrium potential within an infinite cylindrical pore is

15

In the absence of any end effects, if the electric field E₀ = −ϕ₂/h is applied along the length of the cylindrical pore, then the fluid velocity is¹⁵

16

and the total electroosmotic volumetric flow rate is²

17

where the electroosmotic coefficient

18a

18b

The total current through the cylindrical pore is I_c (11), so the ratio between volume flux and current is

19a

19b

2.4. Electroosmosis through a Membrane (h = 0)

It was shown by Mao et al.¹ that if the equilibrium charge density is ρ₀, the imposed electric field is E = −∇χ and the fluid velocity generated by a pressure difference p₁ across a pore (of arbitrary geometry) is

20

then the reciprocal theorem¹⁶ for Stokes flows can be used to show that electroosmotically generated volumetric flow rate through the pore is

21

where the integral is over all the fluid.

The fluid velocity generated by the pressure difference p₁ across a circular hole in a membrane of zero thickness is

22

An explicit expression for G^m(r,z) is available,^1,16 and the potential χ is given by eq 6. The charge density in the equilibrium charge cloud around a membrane of zero thickness is¹

23

which consists of the charge density adjacent to a uniform charged surface, from which has been subtracted the charge density around a uniformly charged disk. The integral (21) can be evaluated numerically,¹ and the electroosmotic flow rate through a hole in a membrane of zero thickness can be expressed in the form

24

where

25

with

26

The ratio of the electroosmotic volume flux Q_me to the electrical current I_m is

27

where

28

with

29

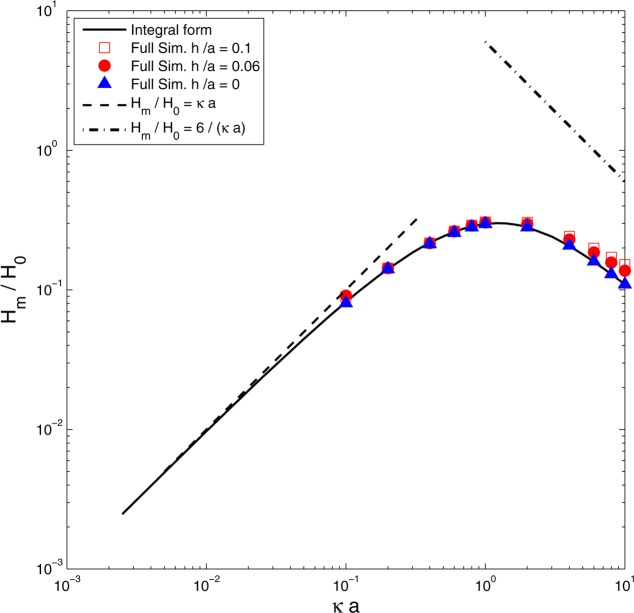
Figure 3 shows a log–log plot of results for H_m/H₀ obtained by Mao et al.¹ The continuous line shows the analytic result (21) obtained via the reciprocal theorem, and the asymptote (25) for aκ ≪ 1 is indicated.

Figure 3.

Electroosmotic coefficient H_m, scaled by H₀ (26), for a membrane of thickness h = 0, as a function of aκ. Solid line, analytic result (21); dashed line, asymptote (25) for aκ ≪ 1; triangles, full PNP numerical computation (h = 0). The dot–dashed line shows H_m/H₀ = 6/(aκ) with the expected slope for large aκ. Squares and circles show electroosmotic coefficients H/H₀ for nonzero membrane thickness h > 0, computed by numerical integration of the full PNP equations: solid circles, h/a = 0.06; open squares, h/a = 0.1.

The membrane has zero thickness, so there is always a region near the edge of the pore where the Debye length κ^–1 cannot be considered small compared with h; Smoluchowski’s analysis for thin charge clouds, which would predict H = 6H₀/(aκ) if ζ_m took the uniform value ϵκσ_m, therefore, cannot automatically be invoked when aκ ≫ 1. However, if we set up a local coordinate s indicating distance from the edge of the pore, then both the electric potential χ (6) and the fluid velocity G^m (22) vary as s^1/2 when s ≪ a (i.e., near the pore edge). The charge cloud density ρ₀ decays over a length scale κ^–1, and only counterions of membrane surface charge within a distance κ^–1 from the edge contribute to ρ₀ within the hole. The contribution of the edge to the integral (21) is therefore O((aκ)⁻¹), as was similarly found for the electrophoretic velocity of a charged disk.¹⁷ We therefore expect H_m ∼ H₀/(aκ) when aκ ≫ 1. The data in Figure 3 do not extend to sufficiently high values of aκ to allow us to estimate the asymptote with any accuracy, and for the figure, we simply indicate the line H_m/H₀ = 6/(aκ) suggested by the Smoluchowski analysis. A similar reduction in the broadside electrophoretic velocity of a disk below the value predicted by Smoluchowski was noted by Sherwood and Stone.¹⁷ Individual points in Figure 3 indicate results obtained from full numerical solutions of the Poisson–Nernst–Planck equations in a symmetric electrolyte at low applied potential and low surface charge. In the computations, the length of the reservoirs in the z direction was equal to their radius b, with b = max(10a,10κ^–1). Other details of the computations are reported in section 3.

2.5. Composite Electroosmotic Coefficient H_comp

When h > 0, it is natural to suppose that the electric field outside the membrane pumps fluid toward the cylindrical pore at a rate

30

and the electric field within the cylindrical pore pumps fluid through the pore at a rate

31

However, in general, Q_me (30) and Q_ce (31) differ, and a pressure ±p₂/2 builds up at z = ±h/2 (i.e., at the entrance and exit to the cylindrical pore) in order to ensure that the volumetric flow rate is continuous. We now determine this pressure p₂.

Consider a membrane of zero thickness (h = 0), with pressure p = p₁/2 (above the reference ambient pressure) at infinity on the side z > 0 and with p = −p₁/2 at infinity on the other side. The pressure within the hole in the membrane is

32

The fluid velocity generated by the pressure difference p₁ across the membrane is u = p₁G^m (22), and the corresponding volumetric flow rate is¹⁶

33

If h > 0, then we approximate the pressure field in the fluid in much the same way as we approximated the electrical potential within the fluid: we patch a linearly varying pressure p(z) within the cylindrical pore to the pressure field outside a membrane of zero thickness, and we take the pressure over the two ends z = ±h/2 of the cylindrical pore to be ±p₂/2. Thus, the pressure within the pore is approximated as

34

the fluid velocity within the pore is

35

and the volumetric flow rate within the pore is

36

Outside the cylindrical pore, the fluid velocity is now assumed to be

37

with u_r(r,z) = −u_r(r,–z) and u_z(r,z) = u_z(r,–z). The volumetric flow rate outside the membrane is now

38

We have ensured that the pressure (but not the fluid velocity or the volumetric flow rate) is continuous across the ends z = ±h/2 of the cylindrical pore.

When an electric field generates an electroosmotic velocity, the volumetric flow rates within the cylindrical pore and outside the membrane are identical if p₂ is such that Q_mh + Q_me = Q_ch + Q_ce , i.e., if

39

But the pressure at infinity is zero in the electroosmotic problem, so p₁ = 0, and ϕ₂ is given by eq 13. Hence

40

and the total electroosmotic flow is

41

An alternative derivation of this approximate composite H_comp (41) is given in the next section.

Inserting into eq 41 the various estimates for G_m (38), G_c (36), R_m (8), and R_c (11), we obtain

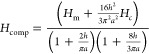42

For small h/a, the approximate composite H_comp is larger than H_m if

43

Experimental arrangements sometimes involve measurements at fixed current, and a coefficient K_comp that gives the electroosmotic flux per unit current is therefore useful. This quantity may be obtained readily from eqs 11, 13, and 41

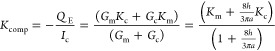44

which changes from K_m when h = 0 to K_c when h ≫ a.

2.6. Composite Electroosmotic Coefficient H_comp Derived via the Reciprocal Theorem

We now show that approximations to the electric potential χ and pressure-driven velocity G within a pore of nonzero length h > 0, when inserted into the integral expression (21) for the electroosmotic volume flux, lead to an approximate electroosmotic coefficient identical to H_comp (42) obtained in the previous section.

We have already shown that we may approximate the electric potential by a composite potential (9) and (10) of the form

45a

45b

45c

We now create a similar approximation for the fluid velocity for flow through a membrane of thickness h subjected only to a pressure drop p₁ but no applied potential drop. We suppose that in z > h/2 the fluid velocity is given by eq 37, corresponding to flow outside a membrane of zero thickness, and that within the cylindrical pore the fluid velocity is given by eq 35. Continuity of the volumetric flow rates (36) and (38) at the entrance to the cylindrical pore requires that the pressure ±p₂/2 at the two ends of the pore satisfies

46

so that

47

Hence, our approximation to the fluid velocity is u = Gp₁, with

48a

48b

The (small) errors involved in this approximation are discussed by Dagan et al.¹⁸

We now use approximations (45) and (48) in integral (21) in order to compute the electroosmotic volumetric flow rate. But the integration splits naturally into an integral over the cylindrical pore and an integral over the regions outside the membrane. The integral over the cylindrical pore is exactly the integral required to determine the electroosmotic flow rate H_c (17) in a cylinder, and the integral outside the membrane is exactly that required to determine H_m (24). Hence, the integral yields the composite electroosmotic flow rate

49

identical to (41), obtained in section 2.5 by elementary methods.

2.7. Predictions of the Composite Electroosmotic Coefficient

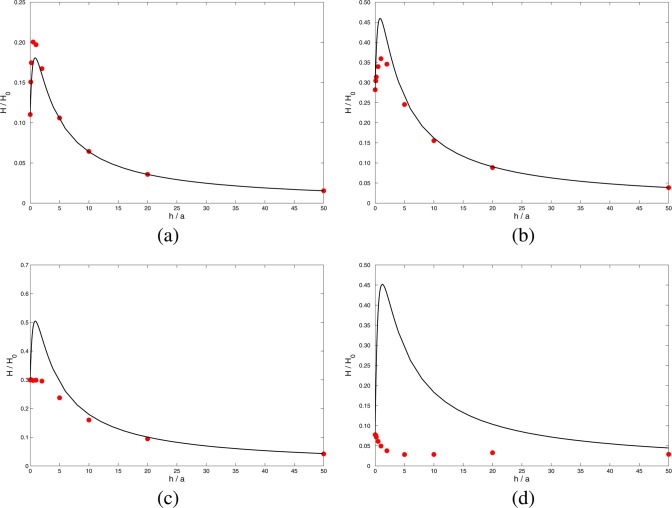
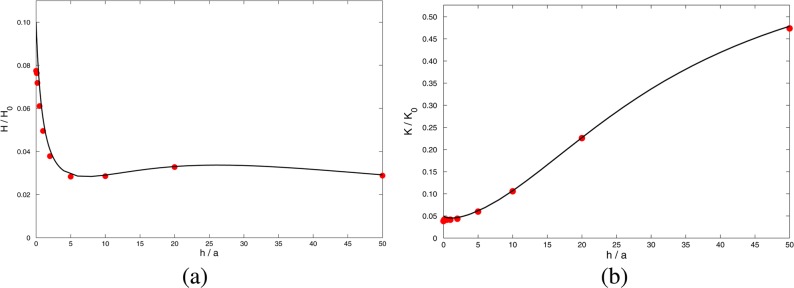
Figure 4 shows H_comp (42) as a function of h/a for four different values of aκ, with σ_m = σ_c. Also shown are the results of full numerical computations based on the Poisson–Nernst–Planck equations¹ and described in section 3. The coefficient H_c (17) is proportional to h^–1 and is very large when the pore length h is small, leading to a large electroosmotic coefficient H_comp. The action of the electric field acting on charge confined within the cylindrical pore is much more efficient at creating fluid motion than is the weaker electric field acting on charge outside the pore. We see that for aκ ≥ 1 the approximate analysis captures the main features of the full numerical results, and it is clear from (42) that it also has the correct limits as h/a → 0 and h/a → ∞. However, it is also evident from Figure 4d that the theory is unsatisfactory when aκ ≪ 1.

Figure 4.

Electroosmotic coefficient H scaled by H₀ (26) for σ_m = σ_c , as a function of h/a, for (a) aκ = 10, (b) aκ = 2, (c) aκ = 1, and (d) aκ = 0.1. Solid line, H_comp (42); solid circles, full PNP numerical computation.

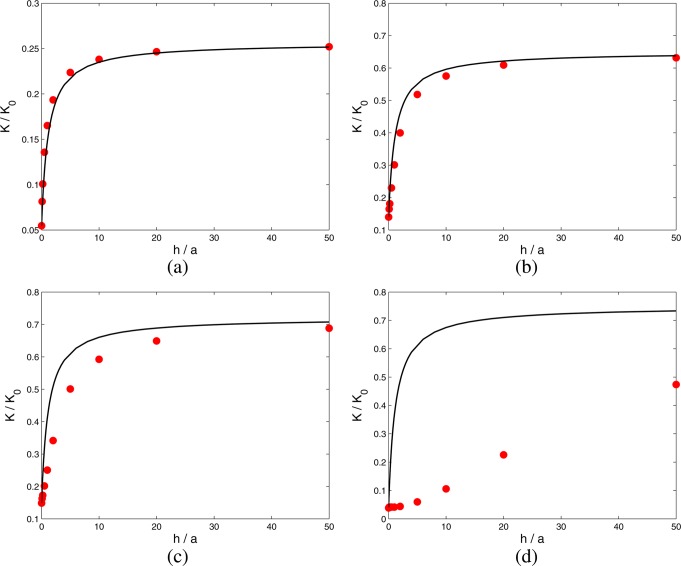
The results of Figure 4 are presented in terms of the coefficient K_comp (44) in Figure 5. Both K_comp and the full numerical results now increase monotonically with h, with a final end point K_comp = K_c that is independent of h when h ≫ a. Figure 5, like Figure 4, shows that the theory leading to K_comp is inadequate when aκ ≪ 1. We discuss this limit in section 4, where we shall show that when aκ ≪ 1 some of the charge cloud of ions that neutralizes the surface charge on the cylindrical wall of the pore spills out of the ends of the pore, where it is less effective at generating electroosmotic flow. The scenario is shown schematically in Figure 6.

Figure 5.

Results of Figure 4, presented in terms of the electroosmotic coefficient K = HR_tot scaled by K₀ (29) for σ_m = σ_c , as a function of h/a, for (a) aκ = 10, (b) aκ = 2, (c) aκ = 1, and (d) aκ = 0.1. Solid line, K_comp (44); solid circles, full PNP numerical computation.

Figure 6.

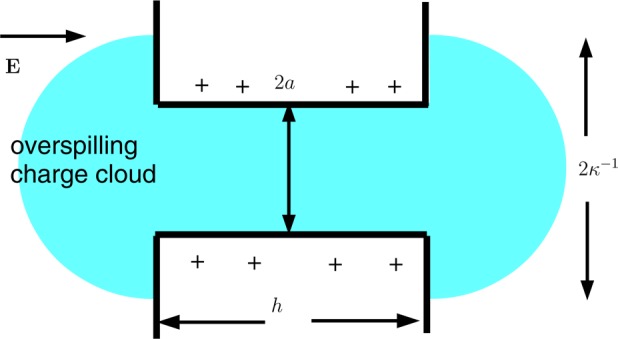
When the Debye length κ^–1 is large compared with the pore radius a, the cloud of counterions associated with the charged cylindrical wall of the pore spills out of the ends of the pore.

3. Numerical Simulation

The time-independent PNP–Stokes equations governing the electrical potential ϕ, the ionic number density of the ith ionic species nⁱ (i = 1, ..., N), the fluid velocity u and fluid pressure p are

50

51

52

53

where z_i is the valence of the ith ionic species and ωⁱ is its mobility. Here, we restrict our attention to the case N = 2, with z₁ = −z₂ = 1.

We used a finite volume numerical scheme to solve the system of coupled eqs 50–53 in the axisymmetric geometry depicted in Figure 1. Thus, we considered a cylindrical pore of radius a and length h connecting two large cylindrical reservoirs of radius b. The lengths of AB and EF in our simulation were also taken to be b, which was kept much larger than either a or the Debye length κ^–1 so that the reservoirs were effectively infinite.

3.1. Boundary Conditions

At A and F, the two ends of the reservoirs, ion concentrations were set equal to the concentration in the bulk electrolyte (i.e., nⁱ = n_∞ⁱ); a potential difference ΔV was applied across the system by setting ϕ to ±ΔV/2, respectively, at A and F, where the pressures were set equal to the bulk pressure, p = p_∞. At AB and EF, the side walls of the cylindrical reservoirs, the radial component of the electric field, ionic flux, and velocity were all set to zero, as was the tangential shear stress, in order to minimize the effect of these boundaries. The last condition was imposed as the cylindrical reservoirs merely represent a convenient computational domain; the walls of the real physical reservoir are far enough away from the pore to be essentially irrelevant. At the membrane and pore surfaces, BC, CD, and DE, a no-flux condition was used for (51), and a no-slip condition was used for the flow. At solid–fluid interfaces (with unit normal n̂), the electric potential is continuous, but the normal component of the electric field undergoes a jump, with [ϵE·n̂] = σ_m at BC and DE and [ϵE·n̂] = σ_c at CD.

An electrohydrodynamic solver was implemented to solve the system described above using the OpenFOAM CFD library,²⁰ a C++ library designed for computational mechanics. A structured mesh was constructed by means of the polyMesh meshing tool within OpenFOAM. The grid was refined near the membrane and pore surfaces to resolve the Debye layer. Grid independence was checked in all cases by refining the grid and verifying that the solution did not change within specified tolerances.

For the finite volume discretization of the governing equations, central differences were used for all diffusive terms in (51) and viscous terms in (52). A second-order upwind scheme was used for the convective terms in (51). The discretized linear system was solved using a preconditioned conjugate gradient solver if the matrix was symmetric or a preconditioned biconjugate gradient solver if the matrix was asymmetric.²¹

An iterative scheme was used to solve the PNP–Stokes equations. Initially, the flow velocity was set to zero. Equations 50 and 51 were then solved sequentially in a loop with under-relaxation (to ensure stability of the nonlinear PNP system) until the absolute residual was smaller than a specified tolerance, in our case, 10^–6. The electric force density −∇ϕ∑_iz_ienⁱ was then obtained from this solution and used as an explicit external forcing in the solution of the incompressible Stokes flow problem, (52) and (53), solved by means of the SIMPLE algorithm. The flow field so computed was then substituted into (51), and the PNP equations were solved again using the updated flow field. An outer loop was constructed to iterate over the PNP loop and Stokes flow module until the solution changed negligibly between two outer iterations.

Our main object of interest is the volumetric flux, Q. This was obtained by numerically integrating the axial velocity over the plane z = 0. At the low voltages employed, the linear relation found between Q and ΔV leads to the electroosmotic coefficient H = Q/ΔV, shown as discrete points in Figures 3–5 and 7. The amount of charge within the pore was determined by numerical integration and used to obtain the quantities h_lost and h_gained reported in Table 1.

Figure 7.

(a) Electroosmotic coefficient H scaled by H₀ (26) for σ_m = σ_c, as a function of h/a, for aκ = 0.1, including the effect of overspilling charge clouds. Solid line, H_comp (42), using H_c given by (96) and H_m given by (97); solid circles, full PNP numerical computation (cf. Figure 4d, in which overspill was neglected). (b) The same results, presented in terms of K = R_totH scaled by K₀ (29). Solid line, K_comp (44), using K_c = R_cH_c and K_m = R_mH_m; solid circles, full computation (cf. Figure 5d).

Table 1. Charge Lost^a,^c from the Ends of a Charged Pore when the Membrane Charge Density σ_m = 0, and the Charge Gained Inside an Uncharged Pore (σ_c = 0) from the Charge Cloud Adjacent to the Charged Membrane Surface^b,c.

		hlost/a		hgained/a
h/a	hκ	theory (73)	numerical	theory (86)	numerical
10.0	1.0	8.9186	8.9249	0.4081	0.4119
1.0	0.1	0.9953	0.9954	0.0455	0.0459
0.1	0.01	0.1000	0.1000	0.0046	0.0046

^aIn terms of an equivalent pore length h_lost (73).

^bIn terms of an equivalent pore length h_gained (86).

^caκ = 0.1.

4. Charge Overspill from the Ends of the Pore, aκ ≪ 1

4.1. Overspill of Charge from the End of a Semi-Infinite Pore

We consider a cylindrical pore of radius a, with surface charge density σ_c. When the Debye length κ^–1 ≫ a, the equilibrium potential ϕ₀ (15) in an infinitely long cylinder can be expanded as

54

where

55

Thus, the equilibrium potential ϕ₀ and charge density ρ₀ = −ϵκ²ϕ₀ within the charge cloud vary little over the cross-section of the pore. On the other hand, if the cylinder is not infinitely long and uniform, ϕ₀ and ρ₀ vary in the axial (z) direction with a length scale κ^–1. We can therefore consider the equilibrium potential ϕ₀ within the cylindrical pore to be a function only of z.¹⁹

We first consider a semi-infinite, charged cylindrical pore going from z = 0 to z = ∞. The equilibrium potential ϕ₀ satisfies a one-dimensional Poisson–Boltzmann equation

56

The solution that tends to the uniform potential ϕ_a within the pore as z → ∞ far from the pore end at z = 0, is

57

for some unknown constant A. The charge density within the charge cloud inside the pore is −ϵκ²ϕ₀, and when the cylindrical pore is infinite (and hence uniform) the charge per unit length in the charge cloud is −πa²ϵκ²ϕ_a = −2πσ_ca, equal and opposite to the charge per unit length on the pore walls. When the pore is semi-infinite, with a nonuniform charge cloud (57), the total charge that is lost from within the pore is

58

At the end of the pore (z = 0), the potential is ϕ = ϕ_a – A.

In z < 0, the charge cloud is no longer confined by the walls of the cylindrical pore and spreads out radially: it is no longer possible to assume that ϕ₀ is a function of z alone. We therefore need to solve the linearized Poisson–Boltzmann equation in the half-space z < 0, with ϕ₀ = ϕ_a – A over the region z = 0, r < a and ∂ϕ₀/∂z = 0 on z = 0, r > a. At large distances from the end of the pore, the potential decays as exp(−κR)/R, where R = (z² + r²)^1/2 is a spherical polar coordinate, but in the important region R = O(a), the potential can be approximated by the electrostatic potential corresponding to a solution of the Laplace equation (i.e., κ = 0). Hence, from (6),

59

To relate the potential (59) to the amount of charge in the overspilling charge cloud (in z < 0), we note that the charge on one side of a charged disk at uniform potential (ϕ_a – A) in unbounded space is q = 4aϵ(ϕ_a – A). Alternatively, one can argue that far from the plane z = 0, the spherical distance R ≈ a cosh ξ, so that the potential (59) is approximately

60

In a spherically symmetric geometry this field corresponds to the far field around a point charge of magnitude 8aϵ(ϕ_a – A), and the total surface charge on one side of the disk is q = 4aϵ(ϕ_a – A), in agreement with the charge obtained by considering the capacitance of the disk. The charge in the overspill charge cloud in z < 0 is equal and opposite to q and is therefore

61

But the total charge (61) in the overspill outside the end of the pore must be equal to the charge (58) that has been lost from within the pore. Hence

62

so that

63

and the potential at the end of the pore is

64

The charge that has been lost from the end of the pore is equivalent to the charge usually found in a pore of length

65

The loss of charge implies that the combined charge cloud and wall surface charge over a cross-section of constant z are no longer electrically neutral, as pointed out by Baldessari and Santiago.^4,6

4.2. Overspill from the Two Ends of a Finite Pore

We can now perform the same analysis for a pore that occupies the region −h/2 < z < h/2. The equilibrium potential within the pore has the form

66

where we have chosen the solution that is symmetric about the center of the pore at z = 0. The charge that has been lost from within the pore is

67

The total flux of electric field through the two ends of the pore is

68

Comparing (67) and (68), we conclude that C = ϕ_a. The potential over the ends of the pore is

69

The total charge in the two overspill charge clouds is therefore, by (61),

70

and this must be equal to the charge (67) lost from within the pore. Hence

71

and

72

The total charge that has been lost (from the two ends) is equivalent to a total lost length

73

74

75

We see from eqs 65 and 74 that when κh ≫ 1 the lost charge is twice that lost from a single end of a pore. We also note that h – h_lost > 0, and that when the pore is short (κh ≪ 1) the amount of charge remaining within the cloud within the pore is proportional to

76

4.3. Overspill from the Membrane Surface into the Pore

If the cylindrical pore itself is uncharged, but the membrane surfaces are charged, ions from the charge cloud adjacent to the membrane surface are able to move into the ends of the pore.

If the membrane has zero thickness, then the charge density ρ₀ in the equilibrium charge cloud is given by (23), and both ρ₀ and the potential ϕ₀ = −ρ₀/(ϵκ²) vary over the area of the pore. Nevertheless, we may work out the mean potential over the circular pore

77

where, when aκ ≪ 1

78

Thus, when the membrane has zero thickness (and there is no cylindrical pore into which ions can escape) the absence of surface charge over the area of the pore changes the average potential over the opening from the value ϕ₀ = σ_m/(ϵκ) due to a uniformly charged surface to βσ_m/(ϵκ), where

79

We now consider the charge that leaks into a pore of length h > 0 from the charge clouds on either side of the membrane. We suppose that the potential on the planes z = ±h/2 is perturbed by an amount D and becomes

80

Within the pore, the potential obeys the one-dimensional Poisson–Boltzmann equation (52), with solution

81

and the additional charge within the pore is

82

Outside the pore, the perturbed potential (80) is associated with a total additional charge (61)

83

on the two sides of the membrane. But the total change in charge caused by this redistribution must be zero, i.e., q_in + q_out = 0. Hence

84

i.e.

85

The total charge q_in = −q_out (83) that leaks into the pore at the two ends corresponds to the charge inside a uniformly charged cylinder with surface charge density σ_m, of length

86

87

88

Thus, h_gained (86) is smaller than h_lost (73) by a factor aκβ/2. We can compare predictions (73) and (86) against results obtained from full numerical solution of the nonlinear Poisson–Boltzmann equation with either σ_m = 0 and aeσ_c/(ϵkT) = aκeζ_c/(kT) = 0.00273 or σ_c = 0 and aeσ_m/(ϵkT) = 0.00273: results for aκ = 0.1 are given in Table 1. We see that there is excellent agreement between the numerical computations and the analysis presented above.

4.4. Composite Electroosmotic Coefficient

We first consider how the electroosmotic coefficients H_c and H_m are modified by the overspill of the charge cloud from inside the cylindrical pore to outside the membrane. If a uniform electric field of strength E = −ϕ₁/h is applied between the ends of the pore, then the Navier–Stokes equations for steady flow yield the axial velocity profile

89

so that the volumetric flow rate is

90

But Q is independent of z (by incompressibility), and the difference in pressure p between the two ends of the capillary is zero. Hence, integrating (90) along the length h of the cylindrical pore and noting that the total amount of charge in the charge cloud remaining within the pore is 2πaσ_c(h – h_lost), we find

91

which may be compared to the result (18b) which ignores overspill. The charge cloud outside the pore is enhanced by the overspill and becomes (in z > 0)

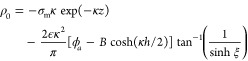92

with the final term [ϕ_a–B cosh (κh/2)], corresponding to the overspill charge cloud (72), being approximately valid in a volume O(a³) around the pore, but invalid at large distance O(κ^–1) from the pore, where the exponential decay of the charge density is not captured by the solution (59) of the Laplace equation. The volumetric flow rate through a pore of zero thickness created by a potential difference ϕ₁ is given by the integral (21) and was shown by Mao et al.¹ to be

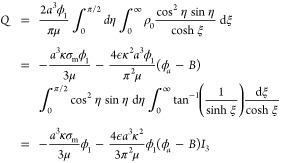93

where

94

Hence, the electroosmotic flow rate Q = H_mϕ₁ due to the charge cloud outside the membrane is modified, and H_m becomes

95

If σ_m is comparable to σ_c , then we saw in section 4.3 that the change in the charge within the pore due to the charge cloud outside the membrane entering the pore is O(aκ) smaller than the loss of charge from the charge cloud within the pore to the regions outside the membrane. However, this contribution can be included with very little effort and becomes important in the limit h → 0, when the gain (87) in charge within the pore from the outside surface charge density σ_m is proportional to h_gained ∝ h, whereas the charge cloud (due to σ_c within the pore) remaining within the pore is proportional to h – h_lost ∝ h², by (76). The electroosmotic coefficient H_c for the cylindrical pore (91) becomes

96

and the electroosmotic coefficient H_m for the charge cloud outside the membrane (95) becomes

97

Now that H_c (96) and H_m (97) have been corrected for the effects of overspill in the two directions, they can be inserted into expression (42) for the composite electroosmotic coefficient H_comp. Results are shown in Figure 7a, together with full numerical solutions of the Poisson–Nernst–Planck equations. We see that the agreement between theory and computation is much better than when overspill is ignored (Figure 4d). Charge overspill or underspill causes the total charge of mobile ions within the pore to differ from what might be expected on the basis of net electroneutrality of the pore. Thus, the driving force is modified, leading to deviations from the calculated result that ignores such effects. The “lost length” h_lost in (96) restores this effect. Figure 7b shows the results of Figure 7a expressed in terms of K, rather than H, and there is again good agreement between the theoretical K_comp and full numerical results.

Note that when h ≪ κ^–1 the effective length of the cylindrical pore h–h_lost ≈ πaκ²h/2, by (76). The approximation (96) for H_c is therefore dominated by the term h_gained and gives H_c ∼ πa⁴κβσ_m/(8hμ), with H_c/H_m ∼ 3πaβ/(8h). We conclude from (43) that H_comp is a decreasing function of h near h = 0, as seen in Figure 7a.

5. Concluding Remarks

The analysis presented here shows that it is possible to use simple analyses based on continuity of volumetric flow rate and electric current to estimate electroosmotic end effects in a charged cylindrical pore traversing a membrane of thickness h > 0. Note that we have made repeated use of the assumption that surface charge densities, and corresponding zeta potentials, are small. We have not only worked with the linearized Poisson–Boltzmann equation (2), but have also used superposition to combine various contributions to the charge clouds due to overspill of the clouds from one region (inside/outside the pore) to the other. At high potentials, it would also be necessary to keep track of the fluxes of individual ion species, rather than simply ensuring that the total electrical current is continuous.⁹

The assumption of small potentials also justifies our neglect of other nonlinear electrokinetic effects such as induced charge electroosmosis (ICEO),^22,23 which can produce vortices in the vicinity of sharp corners²⁴ or near rapid constrictions in channels²⁵ when the permittivity of the solid ϵ_s > 0. However, numerical solutions confirm the expectation that the flow rate is only weakly affected by such vortices, particularly under conditions of small potentials.²⁶

In recent experiments²⁷⁻³¹ on nanopores, potential differences Δϕ ∼ 0–200 mV were applied across the pore. Here, we have assumed that Δϕ ≪ ζ, where ζ itself is assumed small in comparison with the thermal voltage kT/e ∼ 25 mV. Thus, our results can only be expected to describe the initial linear part of the current–voltage and flow–voltage characteristics, even though numerical simulations seem to show²⁶ that this linear regime extends to applied voltages ∼100 mV.

Finally, we point out that the correction factor β (79) reminds us that the hole in the charged membrane removes a circular region of surface charge and reduces the equilibrium potential at the entrance to the pore. The introduction of β < 1 improved the agreement between theoretical and numerical results for h_gained in Table 1. However, the analysis is not rigorous, since the equilibrium potential across the hole is not uniform. The O(1 – β) correction to the equilibrium potential corresponds to an O(1 – β) correction to the charge density ρ₀. If we use this in the integral expression (93) in order to determine a correction to the electroosmotic flow rate through a membrane of zero thickness, then the analysis suggests that the correction to the leading order result (25) for aκ ≪ 1 should be O((aκ)²), whereas investigation of the difference (seen in Figure 3) between numerical results and the asymptote (25) indicates additional corrections O((aκ)² ln aκ).

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States