Joint iris boundary detection and fit: a real-time method for accurate pupil tracking

Abstract

A range of applications in visual science rely on accurate tracking of the human pupil’s movement and contraction in response to light. While the literature for independent contour detection and fitting of the iris-pupil boundary is vast, a joint approach, in which it is assumed that the pupil has a given geometric shape has been largely overlooked. We present here a global method for simultaneously finding and fitting of an elliptic or circular contour against a dark interior, which produces consistently accurate results even under non-ideal recording conditions, such as reflections near and over the boundary, droopy eye lids, or the sudden formation of tears. The specific form of the proposed optimization problem allows us to write down closed analytic formulae for the gradient and the Hessian of the objective function. Moreover, both the objective function and its derivatives can be cast into vectorized form, making the proposed algorithm significantly faster than its closest relative in the literature. We compare methods in multiple ways, both analytically and numerically, using real iris images as well as idealizations of the iris for which the ground truth boundary is precisely known. The method proposed here is illustrated under challenging recording conditions and it is shown to be robust.

1. Introduction

One approach to boundary localization in gray-level images to is to find a set of points that define the object by an edge-detecting mechanism and proceed to find a geometric curve that best fits that set, see for example [1–3] and [4]. In these approaches no prior assumption is made as to what shape the boundary might have, even if later one tries to fit a simple geometric curve to the set of points found to describe it. We refer to this approach hereafter as find and fit methods. In such methods, it is often assumed that the data points representing the geometric curve are uniformly sampled and this is hardly the case when an arc or section are missing. When part of a pupil image is uncertain, e.g. momentarily covered by eyelids or eyelashes, this uncertainty will propagate into the fit [5] often in a catastrophic way for tracking.

With the notable exception of the integro-differential operator method for circles [6] and for elliptical contours [7], global methods—which enforce a priori knowledge of the geometric curve describing the boundary—have been mostly overlooked. The integro-differential operator method leverages the fact that the pupil is generally darker than the iris. By taking the absolute value of the optimization function, the method can be extended to detect brighter than iris, in cases of abnormal lens opacity (cataract) or the occasional red-eye effect caused by coaxial illumination. However, for non-ideal, noisy images this method is very sensitive to artifacts, particularly reflections seen inside the pupil or at its border. In specific contexts this method can be successfully implemented [8] albeit with preprocessing (heuristics) to deal with artifacts which further degrades its computational performance. Preprocessing has the potential to increase the number of parameters in the procedure to a level similar to those in find and fit methods, eroding its attractiveness for simple shapes.

Application of these classical methods to image analysis and pattern recognition problems has been widespread and successful, particularly useful for complex contours [9–14]. Nevertheless for the type of sudden artifacts common to dichoptic multi-focal pupillography (see [15, 16]) where minute pupil contraction and dilation, in response to multi-focal stimuli are of main interest, these approaches carry intrinsic instabilities and some of these artifacts are hard to overcome consistently and in real time. Dynamic artifacts—such as the formation of tears or new reflections, that may sometimes cross the pupillary boundary–tends to derail tracking based on the local classical methods mentioned above. For the challenge presented by pupil tracking, new benchmarks are necessary—a single bad fit in a video frame, a consequence of any of these various artifacts, can jeopardize the accuracy of thousands of subsequent frames. While popular open databases for biometric devices such as in [10] provide a subjective ground truth for testing iris recognition algorithms, they give no figure of merit for the quality of the fit, only a binary flag for positive localization of the iris. Also, in having to localize the full iris, those procedures often make use of the limbic boundary to help localize the pupillary boundary, which is usually much less pronounced.

To overcome these problems we have developed a global method that assumes a priori that the pupil boundary has a certain geometrical (circular or elliptical) shape with a dark interior, so it can be found and fit simultaneously. Our method involves minimizing a sum of products functional which penalizes points of the image far away from the pupil border defined by the candidate curve parameters. This optimization problem has a special form that enables us to obtain analytic derivatives of the objective function. In fact, the objective function, its gradient, and Hessian can also be vectorized, making the implementation very efficient. We carefully compare the performance of the proposed method with the most closely related method in the literature [6]. In brief, the method proposed here, being global, has the same attractiveness of the integro-differential method, but improves significantly on its robustness and performance.

An analysis of the optimization problem for the proposed method and for the integro-differential operator method is carried out, including a stability analysis of their respective solutions. The performance of these methods is accessed using a numerically simulated pupil, where the true boundary is known beforehand. We also perform the same analysis using real images, where the true boundary is established (subjectively) by visual inspection. We illustrate the use of our method for tracking real recording data, highlighting a variety of dynamic artifacts that it can overcome.

2. Optimization methods

2.1. Integro-differential operators

At the core of the method proposed in [6], in the context of biometric identification, is the circle-finding integro-differential operator. This method consists of a search for the circle c(r, x₀, y₀) that maximizes the absolute value of the functional

$$G_{\sigma }(r)*\frac{\partial }{\partial r}\left\{\frac{{\oint }_c\frac{I(x,y)}{\pi r}ds}{{\oint }_{c^{\prime }}\frac{I(x,y)}{\pi r}ds}\right\}.$$ (1)

Where the path c is a circle of integration slightly larger than a concentric circle c′. The optimisation search is over a three-parameter space for the centre (x,y) and average radius r of these two concentric circles. When those three parameters happen to correspond closely to those of an actual pupil in an eye image, the blurred partial derivative of Eq 1 has a large maximum. This rationale can be easily appreciated by representing the image gray levels I(x, y) by a simple, rotationally invariant, step (Heaviside) function, H(r). Assuming the center of the image is correct, the image functional in Eq. (1) simplifies to

$$G_{\sigma }(r)*\frac{\partial }{\partial r}\left(\frac{H(r)}{H(r-a)}\right).$$ (2)

Note that

$$\frac{\partial }{\partial r}\left(\frac{H(r)}{H(r-a)}\right)=\frac{\delta (r)}{H(r-a)}-\frac{H(r)\delta (r-a)}{H{(r-a)}^2},$$ (3)

which, for r >> a i.e, a small, is just a δ(r) so the image functional in Eq. (1) has a gaussian profile G_σ(r − r′), with extremum at r = r′, the optimal radius. Similar analysis can be performed considering a mismatch between the coordinates for the origin on both integrals and the center of the image. Again the objective function simplifies to a gaussian profile centered at the correct origin.

2.2. Proposed method

Frequently, the pupil boundary can be approximated by a circle or sometimes an ellipse with similar axis lengths. In this section we focus on describing a method to jointly finding and fit an elliptical boundary to the pupil—a circular boundary extension of this method is a straightforward special case. Points (x, y) belonging to a quadric with generalized radius r_sq and center (a, b) satisfy the equation

$$r_{\mathit{sq}}=c{(x-a)}^2+d{(y-b)}^2+2e(x-a)(y-b).$$ (4)

With the change of variables,

$$z=\frac{1}{\delta }(r_{\mathit{sq}}-1),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}w=-z{\text{exp}}^{-\frac{1}{2}{z}^2},$$ (5)

where the contour is defined at z = 0 and the parameter δ serves as a scale (or range 1/δ), enforcing a gaussian decay profile on w, so values of r_sq away from unity (away from the contour) give a contribution to w exponentially smaller. We search for a set of parameters {a, b, c, d, e} which minimizes the functional

$$Z=-\sum _{x,y}w(z)I(x,y),$$ (6)

where I(x, y) is a gray-level image. This optimal set of parameters corresponds to the largest elliptical curve with a dark interior found in I(x, y). This can be readily seen, as the functional in Eq. (6) is the accumulation of the product of the exponential profile and the image: whenever this product moves away from the correct position it contributes more (as w(z) gets smaller) to the sum parcels, increasing the value of the objective function. Figure 1 shows an image of a reasonably circular pupil and the initial and final circle: the solution of the minimization problem proposed in this paper is the circle displayed using a dashed line, the circle in a continuous line is the, far off, initialization of the algorithm. Note that the solution is close to what would have been obtained by visual inspection, and showcases the potential of the proposed method, particulary in face of presence of strong reflections. The objective function in Eq. (6) has two very useful properties. Firstly, analytic derivatives are easily obtained,

$$\nabla Z(r_{\mathit{sq}})=\frac{1}{\delta }\sum _{xy}{w}^{\prime }(r_{\mathit{sq}})\nabla r_{\mathit{sq}}I(x,y),$$ (7)

with

$$\nabla r_{\mathit{sq}}=\left(\begin{array}{c}2e(b-y)+2c(a-x)\\ 2e(a-x)+2d(b-y)\\ {(a-x)}^2\\ {(b-y)}^2\\ 2(a-x)(b-y)\end{array}\right).$$ (8)

A similar expression for the second-order derivative of Z is straightforward. Secondly, both the objective function and its derivatives can be fully vectorized. The objective function Z itself is a simple scalar product w_(xx,yy)(:) * I_(x,y)(:), where aa is a matrix obtained by concatenating n copies of the column vector a and V_aa(:) stands for the linear expansion of V.

Fig. 1.

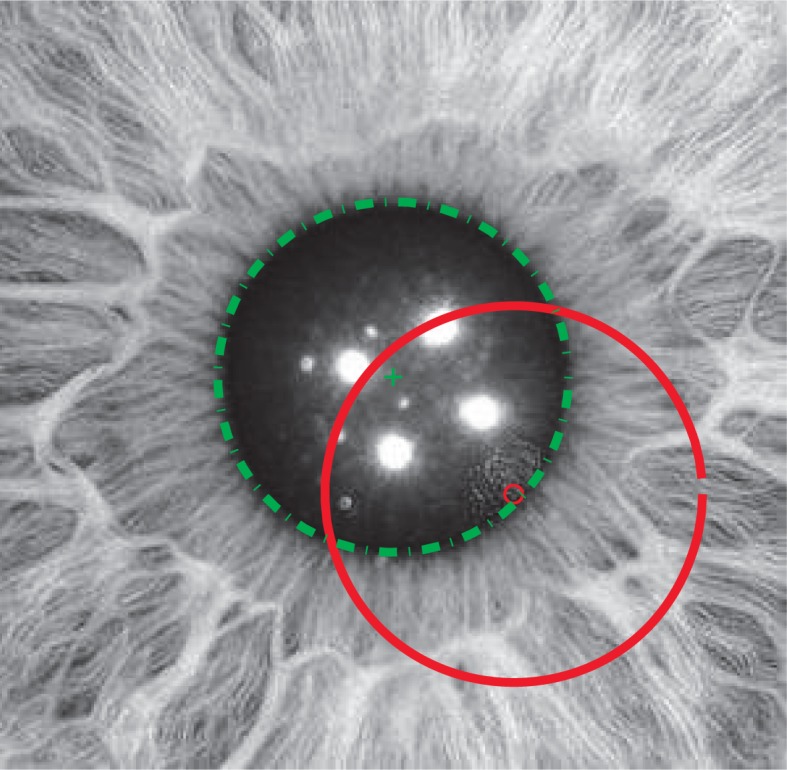
An example of a pupil image showing a candidate fit in dashed line and the (far off) initial circle using a solid line. The parameters for the pupil-iris boundary fit corresponds to the minimum of the proposed objective function in Eq. (6). Image from [17].

3. Optimization landscape

Because most segmentation tasks can be very subjective, we first turn to pupil simulations where we can control exactly where the center and boundary are located. We study in this section increasingly realistic pupil profiles, producing increasingly better approximations of the optimization landscape, giving a general outlook of the challenges the subsequent optimization algorithms will face.

3.1. Idealized pupil, analytic

In this section we examine in more detail the optimization problem in Eq. (6). An idealized boundary for the pupil border can be modeled by a smooth approximation to the Heaviside function such as

$$H(\delta z)=\underset{k\to \infty }{\text{lim}}\frac{(1+\text{erf}(k\delta z))}{2},$$ (9)

and Z becomes

$$\begin{array}{ll}Z\hfill & =\int w(z)H(\delta z)dzd\theta ,\hfill \\ \hfill & =-\pi {\text{exp}}^{-z^2/2}(1+\text{erf}(k\delta z)+\frac{\delta k\text{erf}(\alpha \text{z})}{\alpha },\hfill \end{array}$$ (10)

where α = (1/2 + kδ²)^1/2.

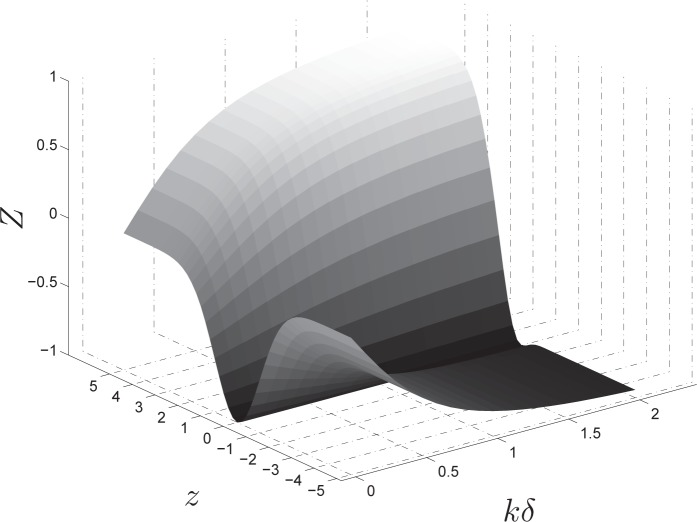
Thus, as is the case with the integro-differential operator method of Eq. (1), we can have a glimpse of objective function of in Eq. (6) by using an idealized pupil profile approximation such as in Eq. (9). Figure 2 shows this artificial minimization valley—a manageable gaussian-like profile with a clear minimum for a range of values of kδ.

Fig. 2.

An approximation of the objective function Z in Eq. (6), as a function of z and for various values of the product kδ. The pupil Heaviside approximation parameter is k while δ is the scale parameter in Eq. (5).

3.2. Idealized pupil, numeric

In the previous section we used a rough idealization of the pupil using the error function in Eq. (9) as a proxy for the step function. In this section, to access the performance of these global segmentation methods, we go one step further by numerically analyzing the optimization problem using a slightly more realistic pupil approximation with known center and radius. We produced a simple pupil prototype, based on the same error function approximation of the step function in Eq. (9), but with multiplicative Gaussian noise to mimic the iris texture.

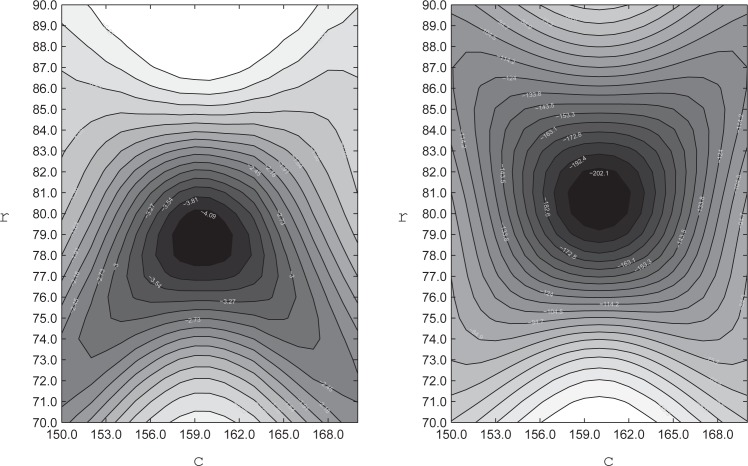
Figure 3 shows the contours of the optimization valley for both objective functions, assuming the center of the idealized pupil at c = (160, 160) and radius r = 80. On the left we have the objective function contours for the integro-differential method Eq. (1), while on the right we display the optimization landscape for the objective function of this paper Eq. (6). Note that although both pictures display well-defined global maxima, with a smooth profile near the true optimum, for the integro-differential method there are two routes towards the two lower corners that can either slow down the gradient ascent or derail the search for the maximum. Also note that there is an upper limit on the initial radius that would lead to local maxima. None of these features are present on the right side picture for the method presented in this paper, the landscape is a smooth gradient throughout the whole range of initial conditions shown. This is the first indication that our method should be robust regarding variations of the initial conditions, a very important feature for tracking, as we recycle the previous frame parameters as initial values for the next frame, and this can be in considerable error after a blink or a saccade.

Fig. 3.

The optimization landscape for the idealized pupil of Eq. (10). On the left is the landscape contours for the integro-differential operator method of Eq. (1), and on the right for the objective function of the method proposed in this paper in Eq. (6). Both the radius r and center c in pixels.

3.3. Real pupil

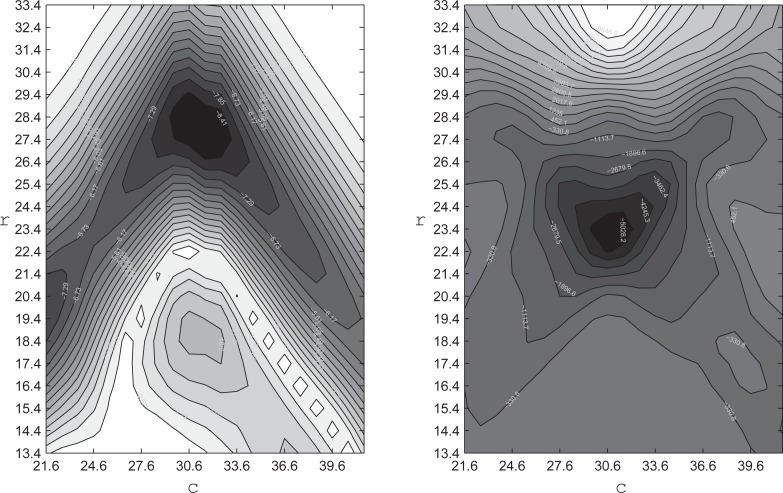
In this section visualize the actual objective function with a real pupil image containing typical artifacts, as in Fig. 1. Figure 4 shows the objective function values in the neighborhood of its extremum, at the left for the integro-differential operator method and at the right for the method proposed here. Comparing Figs. 3 and 4, we see how the extrema are still present for both methods. Nevertheless, the deterioration of the optimization landscape is much more pronounced for the integro-differential objective than it is for the method proposed here. This smoother optimization landscape indicates that our method has the potential to perform better during the solution of the optimization problem. In the next section we show how significant this difference in the optimization landscape smoothness is, by actually searching for the maximum from various different initial center positions and radii.

Fig. 4.

The optimization landscape for the real pupil image of Fig. 1. On the left is the landscape contours for the integro-differential operator method of Eq. (1) and on the right for the objective function of this paper, Eq. (6). Actual radius at r = 24 and center c = 31, in pixels.

4. Stability analysis

We saw in the previous section that the optimization landscape, although having a clear global extremum for both methods, can be quite complex for real images, particularly for the integro-differential method. Far away from the global extremum, local extrema can trap the optimization algorithm. In this section we solve both optimization problems with a range of starting conditions, again using a numeric pupil approximation and real pupil image with its many artifacts, as in Fig. 1. We vary the distance from the correct center, the offset, from 20px to 120px. We also vary the angle of the line connecting the correct center and the initial center, the offset angle, by 45 degrees to a full turn. The initial radius is varied from the correct radius plus minus a gap of 20px, every 5px. We start with the pupil simulation and then repeat the stability analysis for the real pupil image of Fig 1.

4.1. Ideal pupil

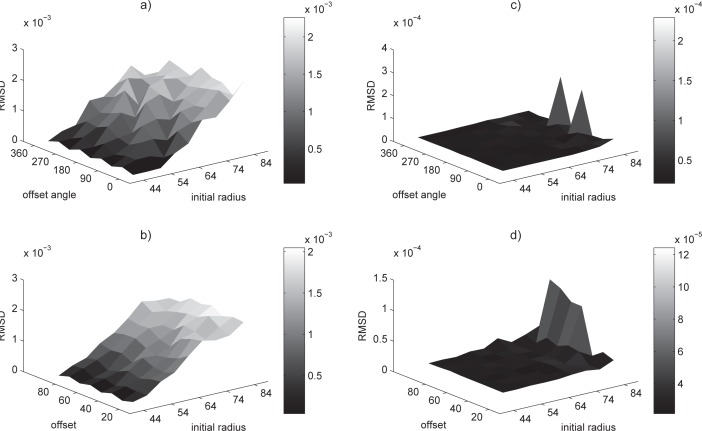
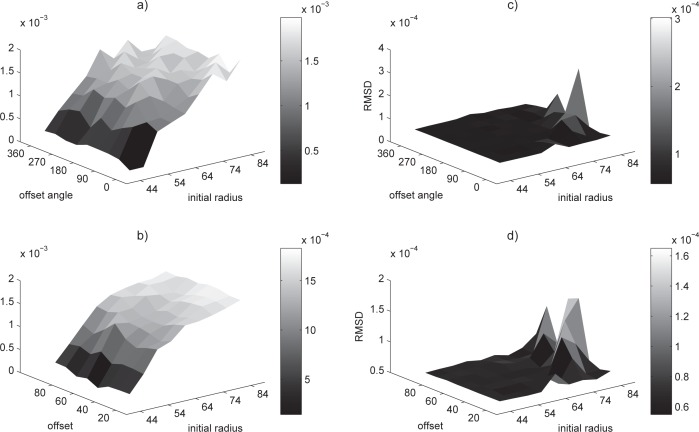
We first removed the effect of distracting artifacts, by using an iris simulation. We study the ability of the optimization algorithm, for both the method proposed here and the integro-differential operator method, to find the best solution from various initial positions and radii. For sake of comparison we used the same Nelder–Mead simplex algorithm (see [18,19]) for both optimization problems. Figure 5 shows the relative distance from the final output of the optimization solution to the known boundary of the pupil simulation, in terms of RMSD, as a function of the various initial conditions. It is clear from Fig. 5(a) that, for the integro-differential operator method, the error increases consistently with an increasing initial radius, while being not so sensitive about the offset angle and even less so about the offset, Fig. 5(b). For the method proposed here we can see in Fig. 5(c) and (d), that the error remains about an order of magnitude smaller, for the whole range of initial conditions—regardless of type. This is consistent with what one would expect from the smoother landscape seen in Fig. 3.

Fig. 5.

Stability analysis of integro-differential (left) and the method proposed here (right), using a simulated pupil and a range of initial radii. In the top row the deviation is shown as a function of the offset angle (averaged by offset), while in the bottom row it is displayed as function of the offset (averaged by offset angle).

4.2. Real pupil

Using the real pupil image of Fig. 1 again, we selected by visual inspection the center and radius that will serve as the ground truth. Figure 6 shows the relative deviation in RMSD terms, from the solution of the maximization problem to the subjectively collected ground-truth parameters. For the integro-differential operator method the error grows as the initial radius increases and is less sensitive to either the offset or its angle, Figs. 6(a) and (b). On the other hand—for the method proposed here and as it was for the artificial pupil—the fit error is still one order of magnitude smaller [see Figs. 6(c) and (d)] for the whole range of initial conditions. This is consistent with the more cluttered optimization landscape shown for a real iris and the fact that this landscape (see Fig. 4) deteriorates much less for the method proposed here.

Fig. 6.

Stability analysis of integro-differential (left) and the method proposed here (right), using a real pupil and a range of initial radii. In the top row the deviation is shown as a function of the offset angle (averaged by offset), while in the bottom row it is displayed as function of the offset (averaged by offset angle).

5. Tracking

5.1. Hardware

Dichoptic stimulation [16] was provided at 60Hz via a pair of stereoscopically arranged LCD displays. The individual stimulus regions of the visual field were spatially low pass filtered to contain no spatial frequencies above 1.5 cpd. This assisted in providing tolerance to mis-refraction of 2 to 3 D. Subjects were refracted to the nearest 1.5 D spherical equivalent. Each region received statistically independent stimulus presentations at a mean rate of 1/s/stimulus region. The aggregate presentation rate to the two eyes was thus 48 stimuli/s. The recording duration was 4 min for each test, divided into eight segments of 30s duration. Pupil responses were recorded by video cameras under infrared illumination. The video sampling was at 30 frames/s, made synchronous (via software) with the LCD displays.

5.2. Offline method

In this section we describe the tracking method used in conjunction with the global fit algorithm of Section (2). We implemented an automatic find and fit method, using the approach described in [20], to provide the initial contour for the minimization problem, which was suitable for the first frame whenever there was no blink or major artifact. We also implemented an interactive 6 point ellipse-fitting algorithm that essentially solves an over-determined linear system and always gives a solution. In our experimental design we ensured that there were no blinks at the first frame, so the automatic routine was successful on every occasion.

Our tracking method was designed to correlate the responses of the pupil to multifocal light stimuli. For this reason, whenever we encountered a large artifact, such as halfway drooping lid that interfered significantly with the amount of light passing through the pupil, those frames were flagged to be discarded, regardless of the fit quality. Nevertheless, simple image preprocessing can improve the quality of those fits considerably, by exploring the symmetry of the objective function. We describe this procedure with examples in the next section. In order to stabilize the fit during a blink or other significant artifact we used a circular buffer of good frames. Frames within a set threshold in dynamic range for the fit parameters entered this buffer. Whenever a frame failed to be within this range, the initial condition for the next frame was taken from the median of the buffer. In this way we avoided fitting spurious dark regions in the image during blinks.

5.3. Results

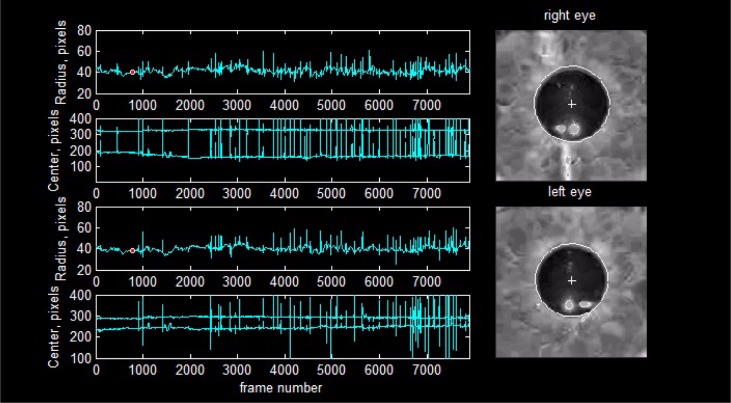
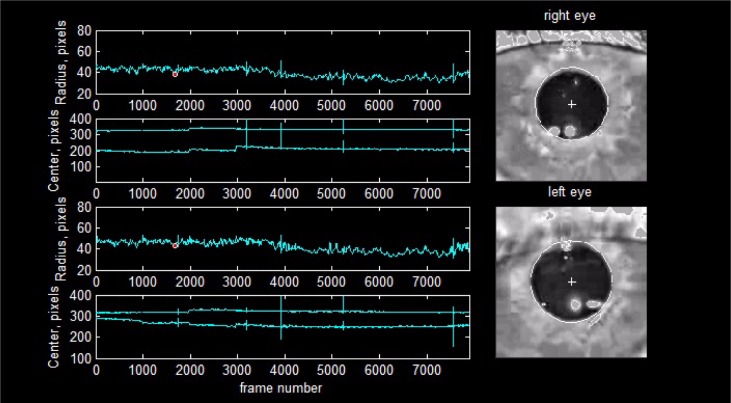
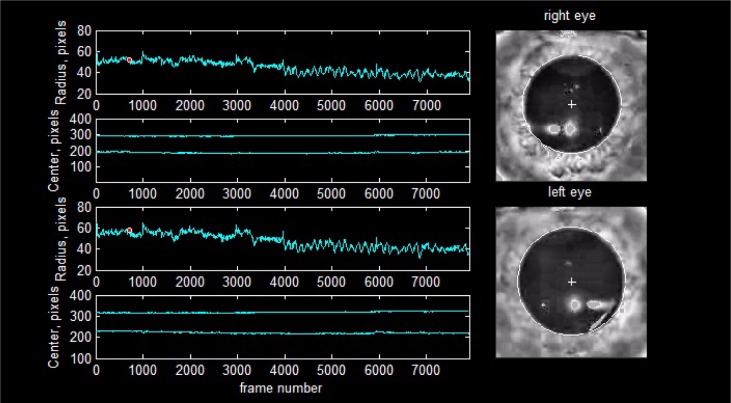
We show the tracking ability of our method under unfavourable recording conditions of the pupil response to multi-focal stimulation. We considered a favorable recording condition to be one in which the video shows only occasional blinks, no eyelids or eyelashes interference, no droopy eyelids (either constant or intermittent), no reflections at, near, or crossing the pupil boundary, no tears forming throughout the recording session and moving across the boundary, good focus, and steady centers. To overcome the disruptive influence of reflections we replace the high pixel values in these spots for the median value of pixels found just outside the pupil contour. This effectively makes those reflection points invisible to our minimization problem by making the terms of the objective function symmetric for points belonging to a highlight and near the pupil border. Our method tracking ability is apparent in Fig. 8 for a record with a busy blinking pattern and a typical pupil geometry. Figure 9 displays a droopy eyelid and a pupil whose shape departs notably from a circle. Not only is the shape non-circular, but the way this particular pupil dilates is uneven, approaching circularity at some radius and departing sharply from it at others. Figure 10 shows a high dynamic range recording together with the previous artifacts in which we have almost the maximum observed variation in pupil diameter in a single frame.

Fig. 8.

An example of tracking with lots of blinks and tear formation, see Media 1 ^{(9.1MB, AVI)} .

Fig. 9.

An example of tracking with prominent droopy eye-lid interference, see Media 2 ^{(7.6MB, AVI)} .

Fig. 10.

An example of tracking with large dynamic range and uneven shape during dilation, see Media 3 ^{(8.2MB, AVI)} .

6. Discussion

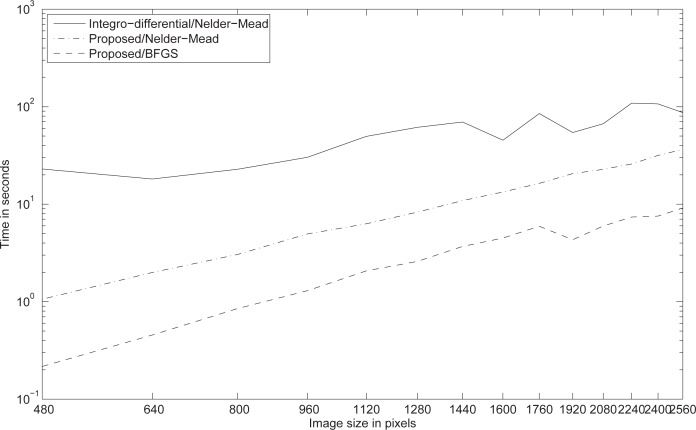
In order illustrate the scaling performance of our method, we deploy once more an artificial pupil (see Section 3.2), for which we have the knowledge of the true pupil center and boundary and can also conveniently scale the image size. We fix the tolerance to a tight margin of the real value, stressing equally the optimization algorithms in their search for the optimum value. Figure 7 reports this scaling performance for the fitting of a circular artificial pupil image varying in size from 160px to 1280px for both the integro-differential and the method presented in this paper. Although our algorithm scales quadratically with image size, it does so gently, and even for very large images our method is considerably faster. We use the same Nelder-Mead simplex algorithm (see [18, 19]) to solve the optimization problem for the integro-differential method and for the method proposed in this paper. Naturally, solving the optimization problem using the analytic gradient provided by our method, with a quasi-Newton solver (see [21–24]), it becomes significantly more competitive for large images.

Fig. 7.

The computational performance of our algorithm (dashed lines) compared to the integro-differential operator method (solid line). We fit a circle within a tight error margin of the artificial pupil center and radius, stressing both algorithms equally. While the proposed method scales quadratically with image size, it does so gently, and even for very large images it is still considerably faster.

We illustrate the quasi-real time tracking ability our method (see Figs. 8, 9, 10 and their associated Media 1 ^{(9.1MB, AVI)} , Media 2 ^{(7.6MB, AVI)} , Media 3 ^{(8.2MB, AVI)} ) on real pupils in unfavourable conditions with an offline algorithm running at 0.05s per frame in Matlab^®. We assume byreal time a value close to 1/24s per frame, thus real time performance is likely to be achieved by using a non-interpreted programming language. The Matlab^® implementation of our algorithm will be made openly available.

While the images from our current hardware are very small at 320px, it is worthwhile to mention some processing approaches to mitigate the impact of greater resolution cameras. One option is to sub-sample images while searching for the optimal value. Another, independent, way to reduce the computation load is to use an annular mask to eliminate about half of the image points for the minimization search or gradient methods. Both of these alternatives can be vectorized as a consequence of the simple form of our objective function.

7. Conclusion

The reason for using global methods, as shown in this paper, is more related to robustness than speed. Nevertheless, as we have shown, our method can still be implemented in real time. With clear images and fixed and controlled artifacts most of the alternative fitting methods cited in this paper should find the boundary without problems. But in our experience with tracking pupils for up to 4 minutes with moving artifacts (reflections, eyelashes and lids) crossing the dilating boundary, tear formation and sometimes very odd shapes during dilation, the alternative methods we tried misfit a frame at some point and derailed tracking, even with added heuristics. We show in this paper an approach for joint pupil boundary detection and fit that achieves reliable tracking results under adverse recording conditions, overcoming consistently these prevalent artifacts.