Abstract
The use of structured illumination in fluorescence microscopy allows the suppression of out of focus light and an increase in effective spatial resolution. In this paper we consider different approaches for reconstructing 2D structured illumination images in order to combine these two attributes, to allow fast, optically sectioned, superresolution imaging. We present a linear reconstruction method that maximizes the axial frequency extent of the combined 2D structured illumination passband along with an empirically optimized approximation to this scheme. These reconstruction methods are compared to other schemes using structured illumination images of fluorescent samples. For sinusoidal excitation at half the incoherent cutoff frequency we find that removing information in the zero order passband except for a small region close to the excitation frequency, where it replaces the complementary information from the displaced first order passband, enables optimal reconstruction of optically sectioned images with enhanced spatial resolution.
OCIS codes: (180.2520) Fluorescence microscopy, (180.6900) Three-dimensional microscopy, (100.6640) Superresolution
1. Introduction
Spatially structured illumination (SI) is used in fluorescence microscopy to remove out of focus light and create optically sectioned images [1]. For example, a sectioned image may be generated from the square root of the sum of squared differences between 3 images of the specimen, each obtained under sinusoidal excitation with a relative phase shift of [2]. However, excitation with patterned light also results in frequency mixing which shifts normally unobservable high spatial frequencies in the specimen inside the passband of the imaging system. By illuminating the specimen with sinusoidal excitation patterns of different phases and exploiting precise knowledge of the frequency and orientation of the excitation pattern, these aliased components can be weighted and shifted to their true location in Fourier space. By performing this operation for several (usually 3) orientations of the excitation pattern, the spatial frequency cutoff can be extended, approximately isotropically, up to twice that of an equivalent imaging system employing uniform illumination [3, 4]. These two attributes of SI are often exploited independently, to generate either optically sectioned or super-resolved fluorescence images. However, they may combined by modifying the linear Fourier space SI reconstruction algorithm to suppress out of focus light present in the various SI passbands [5, 6]. Such modifications exploit the fact that out of focus information is contained primarily with the ‘missing cone’ region close the center of each SI passband [7]. Attenuation of the passbands around their missing cone regions reduces the out of focus information in the reconstructed image. This removal of out of focus light also has the effect of reducing the optical transfer function (OTF) at the attenuated frequencies, decreasing the signal to noise ratio in the reconstructed images.
SI can also enable 3D imaging with improved axial resolution (3D-SIM) using a modified excitation pattern, typically formed by interfering three mutually coherent beams [7]. A drawback to this method is an increase to the number of raw image frames required to reconstruct a superresolution image. 3D-SIM requires both more image frames per focus plane and also the acquisition of images across multiple focal planes in order to reconstruct a single image plane. 2D-SIM thus offers advantages in terms of increased speed and reduced overall light exposure for imaging planes within an extended volume.
In this paper we compare several image reconstruction approaches for achieving simultaneous enhancement of spatial resolution and optical sectioning in 2D structured illumination microscopy (SIM). We begin by briefly reviewing established 2D-SIM image reconstruction methods for optical sectioning (OS-SIM) and resolution enhancement (SR-SIM) and how these concepts may be combined through the removal of the zero order passband in the linear Fourier space reconstruction method (LROS-SIM). We then consider a deterministic scheme for minimizing the out of focus light in the reconstructed image by including information from the first or zero order passband depending on which has the largest axial OTF support at each frequency (Max kz-SIM). For an excitation pattern at half the incoherent cutoff frequency, this latter approach can be approximated by removing information from the zero order passband apart from within a region close to the centre of the shifted first order passbands, where it replaces the complementary region of the first order passband (WLR-SIM). Empirical adjustment of the function used to attenuate the passbands allows a tradeoff between the optical sectioning and the signal-to-noise ratio at these frequencies. The effectiveness of these different reconstruction schemes is compared for SIM images of fluorescent microspheres and a fluorescently labelled cell sample.
2. Structured illumination theory
Optical sectioning using SI in fluorescence microscopy (OS-SIM) relies on the fact that a single spatial frequency in the focal plane decays rapidly in contrast along the optical axis. An OS-SIM image, , may be obtained by exciting the sample sequentially using three sinusoidal excitation patterns,
| (1) |
with three equally spaced phases across 2π and a pattern wavevector being equal in magnitude to half the incoherent cutoff frequency. The images of the sample obtained under illumination with these three excitation patterns, are then combined using the image arithmetic [2]
| (2) |
Equivalently, is given by the modulus of the first component of a discrete Fourier transform of the three images performed with respect to the phase variable. Out of focus light (caused by the so-called ‘missing cone’ in the diffraction limited OTF [7]) is largely contained within the zero-order component of the transform and is thus removed from the image. The non-linearity of this image reconstruction technique means that the imaging process can no longer be described using an OTF [8]. Small, isolated fluorescent objects are imaged with a diffraction limited OTF, whereas parts of the image containing closely packed objects can be resolved beyond the diffraction limit and with enhanced contrast. This effective contrast enhancement arises due to higher order harmonics resulting from the modulus operation.
2D superresolution structured illumination microscopy (SR-SIM) uses the same raw data as OS-SIM, but exploits precise knowledge of the phase, orientation and period of the excitation pattern to shift aliased high frequency image information back to its correct location in Fourier space. In practice, the various Fourier space image components, , are separated by solving a relevant set of linear equations. In the case of illumination using three phase stepped sinusoidal illumination patterns, these equations can be written
| (3) |
where is a 2-dimensional wave vector. If the phase steps are chosen to be equally spaced spanning the range , the image components may be obtained from a discrete Fourier transform with respect to the phase variable. This choice of illumination patterns also averages to give uniform illumination of the sample. In order to reconstruct a superresolution image, the high frequency image components are translated in Fourier space by , which increases the effective frequency cutoff by in the direction of the pattern wavevector. The extension of the passband cutoff can be made more isotropic by using 3 sinusoidal patterns rotated by 60° with respect to each other. For notational convenience we denote the recovered and shifted image components as and where is an index for the different orientations of . A Fourier space SR-SIM image, , is reconstructed by summing together the various images components
| (4) |
where is the number of pattern orientations. An inverse Fourier transform then yields the corresponding real space image, . In this simple approach, the value of each frequency component in the image is simply the sum of the recovered and shifted components. It is common to combine image components through a generalized Weiner filter to include deconvolution and apodisation [7]. This allows for a reduction in the anisotropy of the effective SIM OTF and a suppression of image components with a low signal-to-noise ratio. For simplicity, and to enable a direct comparison between reconstruction techniques, we do not perform any deconvolution or filtering steps in our later results.
The primary difference between the SR-SIM and OS-SIM reconstruction methods is that the former includes information from the zero order passband, , and reassigns the aliased high frequency information in the first order passbands, to the correct location in Fourier space. SR-SIM is an inherently linear imaging method described by an OTF with an extended cutoff, whereas the non-linearity of OS-SIM means the effective resolution at each point in the image is dependent upon the local spatial frequency spectrum. In addition, the choice of is usually different for these two methods; for OS-SIM, optimal sectioning is obtained when is equal to half the incoherent cutoff frequency [8]. In SR-SIM one usually seeks to maximize the extension of the OTF cutoff by illumination with a pattern of frequency close to the incoherent cutoff.
It is possible to combine the attributes of OS-SIM and SR-SIM by simply removing the zero order information component from the SR-SIM reconstruction [5]. This results in an optically sectioned image with increased lateral resolution given by
| (5) |
The exclusion of the zero order information component means that an acceptable signal-to-noise ratio at low spatial frequencies requires an appreciable overlap between the shifted first order passbands. In practice, for this method to be effective, a compromise must be made through the choice of in order to balance the extension of the passband cutoff against the signal-to-noise ratio at low spatial frequencies. We choose a value of equal to half the incoherent cutoff, which extends the passband cutoff to 1.5 times its diffraction limited value.
A limitation of the OS and LROS methods is that they do not remove the out of focus information contained within the missing cones of the first order passbands. As a result it is possible to devise alternative methods to combine information from the various passbands to further reduce the overall amount out of focus light in the reconstructed image. To achieve this we use the maximal axial extent of the 3D OTF as a switch to decide which passband contributes information at each position in Fourier space. The 3D OTF support, , for a high numerical aperture (NA) incoherent imaging system with a circular pupil is given by [9]
| (6) |
where , being equal to the refractive index of the objective immersion medium, and , where is the wavelength of the emitted light. Integrating this support over the axial direction results in the OTF extent as a function of the transverse wavevector ,
| (7) |
Using this function, and translated copies of it, we can generate a set, , in which each element corresponds to the extent of each passband, , for each pattern orientation, ,
| (8) |
Figure 1(a) shows the supports of the zero and first order passbands. The set can be queried to generate a function, , which returns a pair of indices that define which passband should be used to provide the signal at each ,
| (9) |
The way in which maps depends on the logic we apply to the set of 3D supports. We could choose an that maximizes for all ,
| (10) |
Although this choice of returns the theoretical optimally sectioned image, it has many segments formed by the different passbands (Fig. 1(e)) leading to a large number of discontinuities in . In order to simplify whilst retaining the essence of maximizing , we first identify which (the centre point of each passband) is closest to the under consideration and then calculate whether or has the largest extent. Through symmetry only the positive passbands need be considered as the mapping can be extended to the negative passbands by reflection about the origin. This time the function, , maps to an integer creating a binary mask for choosing between the information in the first or zero order passbands at each frequency.
| (11) |
| (12) |
| (13) |
This mapping is shown in Fig. 1(f).
Fig. 1.
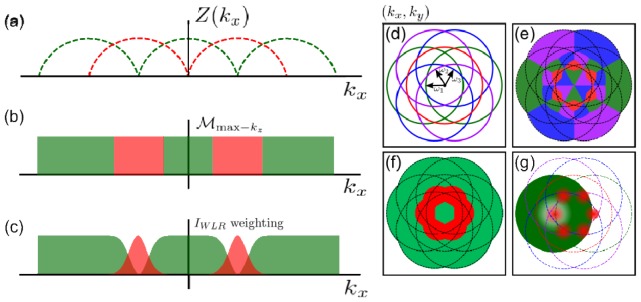
(a) Axial (Z) extent of 3D OTF support in the plane for (red) and (green). (b) 1D illustration showing the frequency range over which information is included from the zero (red) and first order (green) passbands in the Max kz reconstruction scheme. (c) Weighted combination of information from zero (red) and first order (green) passbands in the WLR method. (d) Boundary of OTF support with 3 orientations of when is equal to half the incoherent cutoff frequency. (e) Combination of the zero and first order passbands which maximises the axial support of the OTF for all spatial frequencies. (f) Combination of the zero and first order passbands in the Max kz method. (g) Weighted combination of zero and first order passbands in the WLR method. For clarity, only the weighting for each (red) and a single weighting for (green) are shown.
In practice the performance of this Max kz algorithm is degraded by noise due to the removal of areas with high absolute signal. Therefore we have developed a weighting scheme which approximates the Max kz approach while allowing empirical adjustment between gains in sectioning and the signal-to-noise ratio. This weighting scheme applies complimentary Gaussian and inverted Gaussian weights centred on to the zero and first order passbands,
| (14) |
where the standard deviation of the Gaussian, , is an empirically adjusted parameter. Using this weighting scheme we construct a weighted linear SIM image (WLR-SIM) according to
| (15) |
as shown in Fig. 1(g)
In practice there are many other possible choices for , the main requirement being that the function equals 1 at and tends to zero for large .
3. Experimental results
3.1 Structured illumination microscope system
In order to investigate the differences between the reconstructed images generated using these different algorithms, fluorescent samples were imaged using a custom built SIM system (Fig. 2). Sinusoidal excitation patterns were created using a liquid crystal on silicon spatial light modulator (SLM) configured as a binary phase grating as described in [10]. The SLM (SXGA-3DM, Forth Dimension Displays) was illuminated with collimated light from a fibre-coupled optically pumped semiconductor laser at 488 nm (Sapphire 488 LP, Coherent Inc.). The SLM was imaged, via a spatial filter, onto the sample by a pair of 4f relay systems; the first comprising a pair of achromatic doublets and the second a further achromatic doublet and the microscope objective lens (UPLSAPO 60x/1.3, Olympus). The spatial filter in the Fourier plane of the SLM, made by drilling 3 pairs of circular holes into a 1 mm thick aluminium disc (Fig. 2, inset III), blocked all but the positive and negative first-orders diffracted from the SLM. These two orders were imaged to diametrically opposed points in the pupil of the objective lens, creating a sinusoidal excitation pattern at half the incoherent cutoff frequency (Fig. 2, inset IIII). To obtain optimal pattern contrast, the polarization vector of the interfering beams should be co-rotated with the grating in order to maintain s-polarization [11]. In practice, as the first diffracted orders are incident only halfway across the pupil, the loss in contrast due to polarization rotation by the objective lens was not significant and for experimental simplicity a single fixed linear polarization state was used for all excitation patterns. Fluorescent images of the samples were acquired using a scientific CMOS camera (ORCA-Flash4.0, Hamamatsu Photonics), with the global exposure period of the camera’s rolling shutter synchronized with the pattern displayed on the SLM using hardware trigger signals between the devices.
Fig. 2.
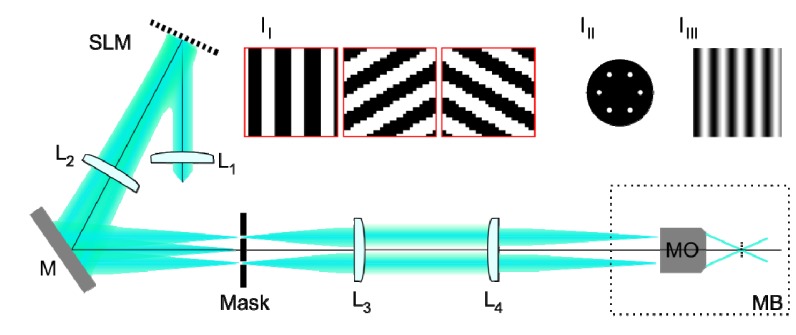
Schematic diagram of the SIM system used to acquire images for testing reconstruction algorithms. Lenses L1-L4 are achromatic doublets, SLM is a ferroelectric liquid crystal on silicon spatial light modulator, M is a plane mirror and MB is the microscope body. Inset I1 shows regions of the phase gratings displayed on SLM for 3 different excitation pattern orientations. Inset III shows the mask in the Fourier plane of the SLM used to select the positive and negative first diffracted orders. Inset IIII shows a sinusoidal intensity pattern at the focal plane of the microscope objective lens (MO).
Each raw image sequence was acquired under illumination of the sample with 9 sinusoidal illumination patterns; corresponding to 3 pattern orientations separated by 60° and 3 phase steps for each orientation. The image data for each orientation was processed separately and data for the three orientations was then combined to create the final image. The widefield image was calculated as a sum of the three phase stepped images. The OS-SIM image was calculated as the modulus of the first-order component of the Fourier transform with respect to the phase variable. The SR, LROS, Max kz and WLR images were reconstructed following a modified version of the procedure described in [7]. Briefly, the positive and negative first-order Fourier components were shifted by a vector corresponding to the frequency and orientation of the excitation pattern, and respectively. The shift vector, , was determined from the peak in the correlation of the first and zero-order Fourier space images to sub-pixel accuracy (by multiplication with cosines in real space). Phase offsets between the passbands were determined by complex linear regression in their areas of overlap after accounting for OTF differences. Information from the various passbands was combined, as described in the theory section, before an inverse Fourier transform was performed to yield the corresponding real space image. For both samples investigated here, the standard deviation of the Gaussian functions was set to as this was found to give a good balance between optical sectioning and signal to noise ratio. Zero padding was performed to accommodate the Fourier space shifts for the SR, LROS, Max kz and WLR reconstructions, the widefield and OS images were similarly padded to display them on the same sampling grid.
3.2 Comparison of reconstructed images
Figure 3(a) shows widefield and SI images of yellow-green fluorescent microspheres of nominal diameter 0.17 μm (PS-Speck green, Life Technologies). The sample was prepared by allowing a drop of solution containing the microspheres to dry on a coverslip before adding a drop of antifade solution and placing a microscope slide on top. For such a thin specimen there is no significant out of focus light, and the differences between the images reflect differences between the effective OTFs for the various reconstruction algorithms. Figure 3(b) shows a magnified image of a single isolated microsphere along with line profiles through its centre. The measured full width at half maximum (FWHM) from the widefield image is 0.30 μm, this is reduced to 0.21 μm in the conventional linear (SR) SIM reconstruction. As expected, the FWHM in the OS image (0.27 μm) is only slightly less than in the widefield image, as for sparse point-like objects OS-SIM does not significantly improve spatial resolution [8]. Individual microspheres in the Max kz reconstruction are surrounded by faint rings, caused by the discontinuities in the OTF. These rings are reduced in intensity in the WLR image due to the more gradual transition between the passbands. The FWHM is similar in the three linear optical sectioning SIM reconstructions and is slightly lower than the SR-SIM image due to the attenuation of low spatial frequency information. Figure 3(c) shows line profiles through two microspheres within a closely-packed monolayer. The close packing means that the two microspheres are not resolved in the widefield image, however they can be clearly identified from the line profiles in all the SIM images. As with the image of the single microsphere, the attenuation of low spatial frequencies in the sectioning SIM algorithms increases the effective contrast compared to SR-SIM. In this part of the image OS-SIM gives an effective spatial resolution similar to that obtained from the linear sectioned SIM algorithms.
Fig. 3.
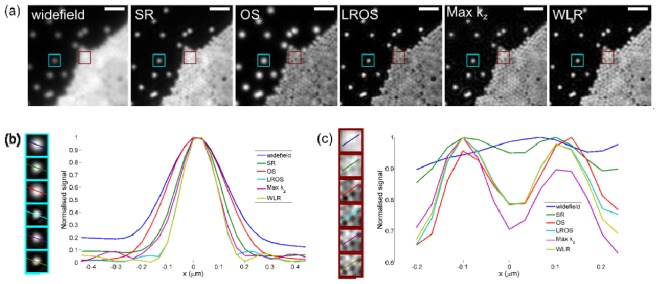
(a) Widefield and SI images of 0.17 μm diameter yellow-green fluorescent microspheres dried on a glass coverslip. Scale bar is 1 μm. (b) Line profiles drawn through a single isolated microsphere. Measured FWHM is 0.30 μm, 0.21 μm, 0.27 μm, 0.17 μm, 0.18 μm, 0.17 μm for widefield, SR, OS, LROS, Max kz and WLR reconstructions respectively. (c) Line profiles drawn through two fluorescent microspheres in a part of the image containing a densely packed monolayer of microspheres.
Figure 4(a) shows the axial response for the different algorithms obtained from a z stack of images of a single microsphere. The axial response was measured from the change in signal at the pixel in the transverse centre of the microsphere as the sample was translated axially in 0.2 μm steps. Figure 4(b) shows the mean FWHM of the axial response, which can be taken as a measure of optical section thickness [12], plotted against the FWHM of the transverse line profile in the in focus image slice, for 10 individual fluorescent microspheres. As expected, the sectioning algorithms all show an improved axial response over the widefield and SR methods. The OS and LROS methods have similar optical sectioning performance, since both are generated from the same image information. The Max kz and WLR methods further improve the axial response by attenuating out of focus light around the centres of the shifted first order passbands. Max kz results in the thinnest optical sections, however this comes at the expense of the ringing image artefacts caused by the discontinuities in the OTF (Fig. 1(f)). The relatively large standard deviation in the axial response for the SR method is due to image artefacts caused by out of focus light.
Fig. 4.
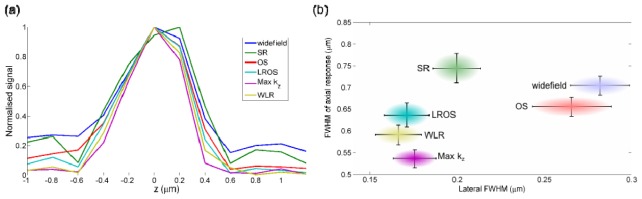
(a) Axial response from images of a single yellow-green fluorescent microsphere reconstructed using different SI algorithms. (b) FWHM of axial response versus lateral FWHM of each method averaged over 10 individual fluorescent microspheres. Horizontal and vertical axes of ellipses show standard deviation in the measured FWHMs. Mean measured lateral and axial FWHM values, in µm, are (0.28, 0.70), (0.20, 0.74), (0.27, 0.66), (0.17, 0.64), (0.18, 0.54) and (0.17, 0.59) for the widefield, SR, OS, LROS, Max kz and WLR reconstructions respectively.
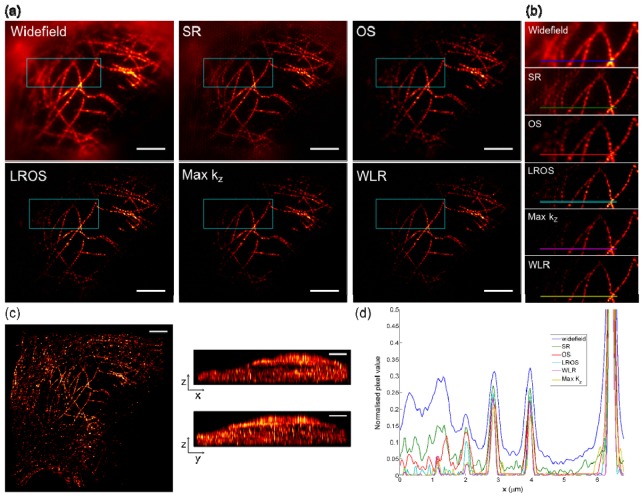
To test the performance of the different algorithms in the presence of out of focus light, raw image sequences were acquired of the microtubule network in a HeLa cell, labeled with rat anti-tubulin primary and anti-rat-Alexa 488 secondary antibodies (Fig. 5(a)). The well-resolved filaments in the centre of the image lie over the cell nucleus, while the diffuse haze at the edge of the widefield image is due to fluorescence signal originating away from the focal plane. Phase offsets in this out of focus light results in a periodic patterning artefact in the SR-SIM reconstruction, and is effectively removed by all four optical sectioning algorithms. The magnified views of the boxed regions in the main images shown in Fig. 5(b), give a qualitative indication of the optical sectioning provided by the different algorithms. In the Max kz and WLR images, attenuation of signal close the centres of the first-order passbands removes additional out of focus light originating from microtubules located towards the left hand side of the image. This is further emphasized by the line profiles shown in Fig. 5(d), where signal intensity in the left hand side of the profile is lowest for the WLR and Max kz reconstructions. As with the fluorescent microspheres, the hard edges in the Max kz OTF result in ringing around the filaments which is significantly reduced in the WLR image. We measured the axial response for the different algorithms by taking an image z-stack (with a 0.2 μm separation between image planes) and summing pixel values within a small region at the intersection of two microtubules close to the centre of main image. The FWHM of this axial response was 0.82 μm, 0.71 μm, 0.67 μm and 0.66 μm for the OS, LROS, Max kz and WLR methods respectively. As previously, the Max kz and WLR methods give improved optical sectioning performance due to attenuation of out of focus information near the centre of the first order passbands. Figure 5(c) shows image projections from a 3D rendering of the WLR image z stack.
Fig. 5.
(a) Images of microtubules in a HeLa cell. Staining for tubulin with rat anti-tubulin primary and anti-rat-Alexa 488 secondary antibodies. (b) Magnified images of boxed regions in main images. FWHM of the axial response for a small region close to the center of the image was 0.82 μm, 0.71 μm, 0.67 μm and 0.66 μm for OS, LROS, Max kz and WLR methods respectively. (c) Projections of a 3D rendering of the z-stack of images formed using the WLR reconstruction. Scale bars are 4 μm. (d) Line profiles along the coloured lines shown in (b).
4. Discussion and conclusions
Removal of out of focus light from 2D-SIM images requires a tradeoff between the effective optical section thickness and the signal-to-noise ratio in the reconstructed image. In general the optimal approach will depend on the properties of the sample; specifically it’s spatial frequency spectrum. Theoretically, optimal sectioning is achieved by maximizing the axial extent of the OTF support, which suggests including only image information from the passband with the largest extent at each location in Fourier space. In practice this implied binary logic may be approximated using an empirically adjusted function which allows tradeoff between the signal-to-noise and optical sectioning in the reconstructed image. For illumination with a sinusoidal pattern at half the incoherent cutoff frequency the logic can be reasonably well approximated by multiplying the zero order passband with a Gaussian function centred at the excitation frequency and the first order passband with a complementary inverted Gaussian function. Both the binary (Max kz) method and its empirically adjusted Gaussian approximation (WLR) presented here give improved optical sectioning performance over other non-linear [2] and linear SIM [5] reconstruction approaches by suppressing out of focus light around the centres of the first order passbands. Both these latter methods were found to give similar sectioning performance for images of fluorescent microspheres and the fluorescently labelled microtubule network in a HeLa cell. For other samples, in particular those which are weakly fluorescing, and hence result in raw images with a low signal-to-noise-ratio, or those containing large amounts of out of focus fluorescence, the flexibility of WLR approach may enable the reconstruction of superior SIM images.
The amount of overlap between the various passbands depends upon the frequency of the excitation pattern. As a result there is a compromise to be made between the increase in the OTF cutoff frequency and the signal-to-noise ratio obtained with sectioning SIM algorithms, particularly in those parts of the frequency spectrum where the one of the passbands is significantly attenuated. Computational SIM methods are particularly sensitive to noise [13] since both in focus and out of focus light are present at the detector. The noise in the sectioned image is determined by the total incident photon flux and not just the in focus component; unlike optical sectioning using a confocal pinhole where out of focus light is physically prevented from reaching the detector. In practice, we have tested the WLR algorithm for resolution enhanced, optically sectioned SI imaging with excitation patterns up to 0.7 times the incoherent cutoff frequency and found it performs well.
The principal advantage of the 2D-SIM reconstruction method described here over the 3D-SIM approach is a reduction in the required number of raw image frames. This enables increased imaging speed, and a corresponding reduction in sample light exposure, when imaging a plane, or planes, within an extended volume. However, for applications in which axial resolution is of greater importance than imaging speed 3D-SIM may yield better results. 3D-SIM reduces the extent of the 3D point spread function for all points within the measured volume, but does not remove light which originates from outside the measured volume. Depending on the sample, 3D-SIM may also benefit from suppression of the out of focus light by attenuation of the various passbands as considered here. Suppression of the zero order passband would be particularly effective as there is significant overlap, up to twice the Abbe limit, of the first and second orders used in 3D SIM patterns.
Acknowledgments
The authors thank Daniel Metcalf for preparation of HeLa cell samples and Alex Knight for supporting SIM development at the National Physical Laboratory. This work was partially funded by the Chemical and Biological Metrology Programme of the UK's National Measurement System. The identification of certain commercial equipment does not imply recommendation or endorsement by the authors or their institutions, nor does it imply that the equipment identified is the best available for the purpose.
References and links
- 1.Heintzmann R., “Structured Illumination Methods,” in Handbook Of Biological Confocal Microscopy, Pawley J. B., ed. (Springer US, 2006), pp. 265–279 [Google Scholar]
- 2.Neil M. A. A., Juskaitis R., Wilson T., “Method of obtaining optical sectioning by using structured light in a conventional microscope,” Opt. Lett. 22(24), 1905–1907 (1997). 10.1364/OL.22.001905 [DOI] [PubMed] [Google Scholar]
- 3.Gustafsson M. G. L., “Surpassing the lateral resolution limit by a factor of two using structured illumination microscopy,” J. Microsc. 198, 82–87 (2000). [DOI] [PubMed] [Google Scholar]
- 4.Heintzmann R., Cremer C., “Laterally modulated excitation microscopy: Improvement of resolution by using a diffraction grating,” Proc. SPIE 3568, 185–196 (1999). 10.1117/12.336833 [DOI] [Google Scholar]
- 5.Thomas B., Momany M., Kner P., “Optical sectioning structured illumination microscopy with enhanced sensitivity,” J. Opt. 15(9), 094004 (2013). 10.1088/2040-8978/15/9/094004 [DOI] [Google Scholar]
- 6.Wicker K., Mandula O., Best G., Fiolka R., Heintzmann R., “Phase optimisation for structured illumination microscopy,” Opt. Express 21(2), 2032–2049 (2013). 10.1364/OE.21.002032 [DOI] [PubMed] [Google Scholar]
- 7.Gustafsson M. G. L., Shao L., Carlton P. M., Wang C. J. R., Golubovskaya I. N., Cande W. Z., Agard D. A., Sedat J. W., “Three-dimensional resolution doubling in wide-field fluorescence microscopy by structured illumination,” Biophys. J. 94(12), 4957–4970 (2008). 10.1529/biophysj.107.120345 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Karadaglić D., Wilson T., “Image formation in structured illumination wide-field fluorescence microscopy,” Micron 39(7), 808–818 (2008). 10.1016/j.micron.2008.01.017 [DOI] [PubMed] [Google Scholar]
- 9.Philip J., “Optical transfer function in three dimensions for a large numerical aperture,” J. Mod. Opt. 46(6), 1031–1042 (1999). 10.1080/09500349908231324 [DOI] [Google Scholar]
- 10.Kner P., Chhun B. B., Griffis E. R., Winoto L., Gustafsson M. G. L., “Super-resolution video microscopy of live cells by structured illumination,” Nat. Methods 6(5), 339–342 (2009). 10.1038/nmeth.1324 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.O’Holleran K., Shaw M., “Polarization effects on contrast in structured illumination microscopy,” Opt. Lett. 37(22), 4603–4605 (2012). 10.1364/OL.37.004603 [DOI] [PubMed] [Google Scholar]
- 12.Wilson T., “Resolution and optical sectioning in the confocal microscope,” J. Microsc. 244(2), 113–121 (2011). 10.1111/j.1365-2818.2011.03549.x [DOI] [PubMed] [Google Scholar]
- 13.Somekh M. G., Hsu K., Pitter M. C., “Stochastic transfer function for structured illumination microscopy,” J. Opt. Soc. Am. A 26(7), 1630–1637 (2009). 10.1364/JOSAA.26.001630 [DOI] [PubMed] [Google Scholar]