High-resolution solid-state NMR structure of Alanyl-Prolyl-Glycine

Abstract

We present a de novo high-resolution structure of the peptide Alanyl-Prolyl-Glycine using a combination of sensitive solid-state NMR techniques that each yield precise structural constraints. High-quality ¹³C–¹³C distance constraints are extracted by fitting rotational resonance width (R²W) experiments using Multimode Multipole Floquet Theory and experimental chemical shift anisotropy (CSA) orientations. In this strategy, a structure is first calculated using DANTE-REDOR and torsion angle measurements and the resulting relative CSA orientations are used as an input parameter in the ¹³C–¹³C distance calculations. Finally, a refined structure is calculated using all the constraints. We investigate the effect of different structural constraints on structure quality, as determined by comparison to the crystal structure and also self-consistency of the calculated structures. Inclusion of all or subsets of these constraints into CNS calculations resulted in high-quality structures (0.02 Å backbone RMSD using all 11 constraints).

1. Introduction

Determining the high-resolution structures (backbone RMSD < 0.1 Å) of uniformly labeled polypeptides with solid-state NMR is often prohibitively difficult due to a lack of precision available with homonuclear broadbanded recoupling techniques such as RAD [1], DARR [2] and TSAR [3]. Although these experiments can define the secondary and tertiary structure and yield a clear global structure of the protein, the lack of high-precision measurements can leave detail of the active site and mechanisms that are of broader interest to the biological community still undefined. More precise techniques such as REDOR [4], RFDR [5], DRAWS [6], and local field correlations yield sub-angstrom precision, but are often limited to spin-pair labeled systems.

A previous study on the polypeptide, N-f-MLF-OH, demonstrated the use of FS-REDOR, and torsion angle constraints to determine a high-resolution de novo structure [7]. Since the publication of that structure, additional high-resolution techniques applicable to uniformly ¹³C, ¹⁵N labeled systems have been developed, such as rotational resonance width (R²W) [8,9] and DANTE-REDOR [10]. DANTE-REDOR can yield high-quality restrictions on torsion angles, in addition to heteronuclear distance constraints. R²W utilizes band-selective R² to recouple homonuclear spin pairs and can separate weaker dipolar oscillations (from long distance, structurally relevant spin pairs) from relaxation processes using a constant mixing time strategy and has been recently applied to measure distances in uniformly labeled proteins [11]. However, Ramachandran et al. [12] discussed the effect of the relative CSA orientation of the two spins in extracting accurate distances from R²W experiments. To make R²W a truly de novo, precise, and accurate technique for making homonuclear distance measurements, one must obtain the relative CSA orientation of the spin pair experimentally.

We demonstrate the utility of an iterative approach to structure determination of uniformly labeled polypeptides using various solid-state NMR methods. Namely, ψ torsion angle and ¹³C–¹⁵N distances from NCCN [13] and DANTE-REDOR measurements are first used to establish a structure from which approximate relative CSA orientations are available. Those orientations are then utilized into the fitting routines of R²W profiles to also obtain precise and accurate ¹³C–¹³C distances. Finally all experimentally determined homonuclear, heteronuclear, and torsion angles constraints are used in a final energy minimization that yields a high-quality de novo structure. We further discuss the effect of each sub-group of structural constraints on the structural quality as judged by self-consistent backbone RMSD and comparison to the known crystal structure.

2. Results and discussion

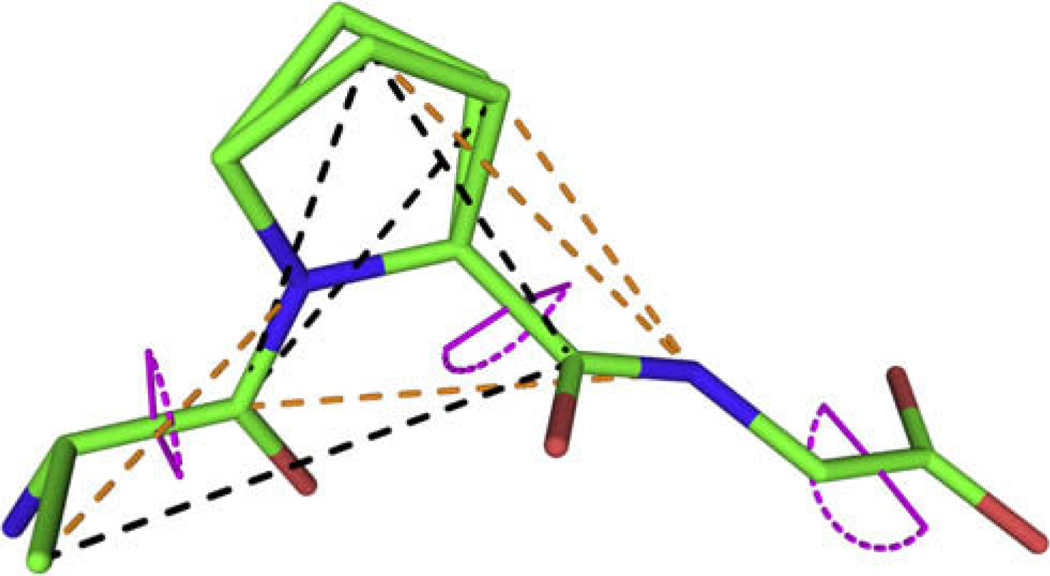
Fig. 1 shows the 11 constraints determined for APG listed in Table 1. Comparison with the X-ray crystal structure indicates the level of accuracy achieved in each measurement. Two of the restrictions on ψ dihedral angles were determined with a local field NCCN experiment [13]. DANTE-REDOR was used to determine the glycine ψ angle, and four ¹³C–¹⁵N internuclear distances. The four carbon internuclear distances were extracted using R²W.

Fig. 1.

Crystal structure of APG [14] showing the 11 SSNMR experimental constraints used in the structural refinement. Torsion angles are displayed in violet, REDOR distances in orange and R²W constraints in black. Note that the proline ring has a split occupancy between two conformers in the crystal structure. (For interpretation of colour mentioned in this figure, the reader is referred to the web version of this article.)

Table 1.

Experimental solid-state NMR constraints used in the structure calculation and corresponding values from the crystal structure from all NMR experiments; DANTE-REDOR (orange), NCCN torsion angles and R²W distances (black).

ψ Torsion Angles	X-ray (°)	SSNMR (°)
ψGly	178	180 ± 15
ψAla	153	152 ± 5
ψPro	157	162 ± 5
Distances	X-ray (Å)	SSNMR (Å)
Pro N–Ala Cβ	3.2	3.2 ± 0.1
Gly N–Pro Cβ	3.2	3.2 ± 0.15
Pro C′–Pro Cγ	3.3/3.6	3.9 ± 0.39
Ala C′–Pro Cβ	3.6	3.8 ± 0.38
Ala C′–Pro Cγ	3.6	3.9 ± 0.39
Gly N–Ala C′	4.1	4.1 +0.6/−0.3
Gly N–Pro Cγ	4.5/4.3	4.2 +0.6/−0.3
Pro C′–Ala Cβ	4.7	4.4 ± 0.44

2.1. CSA parameters for precise R²W fitting

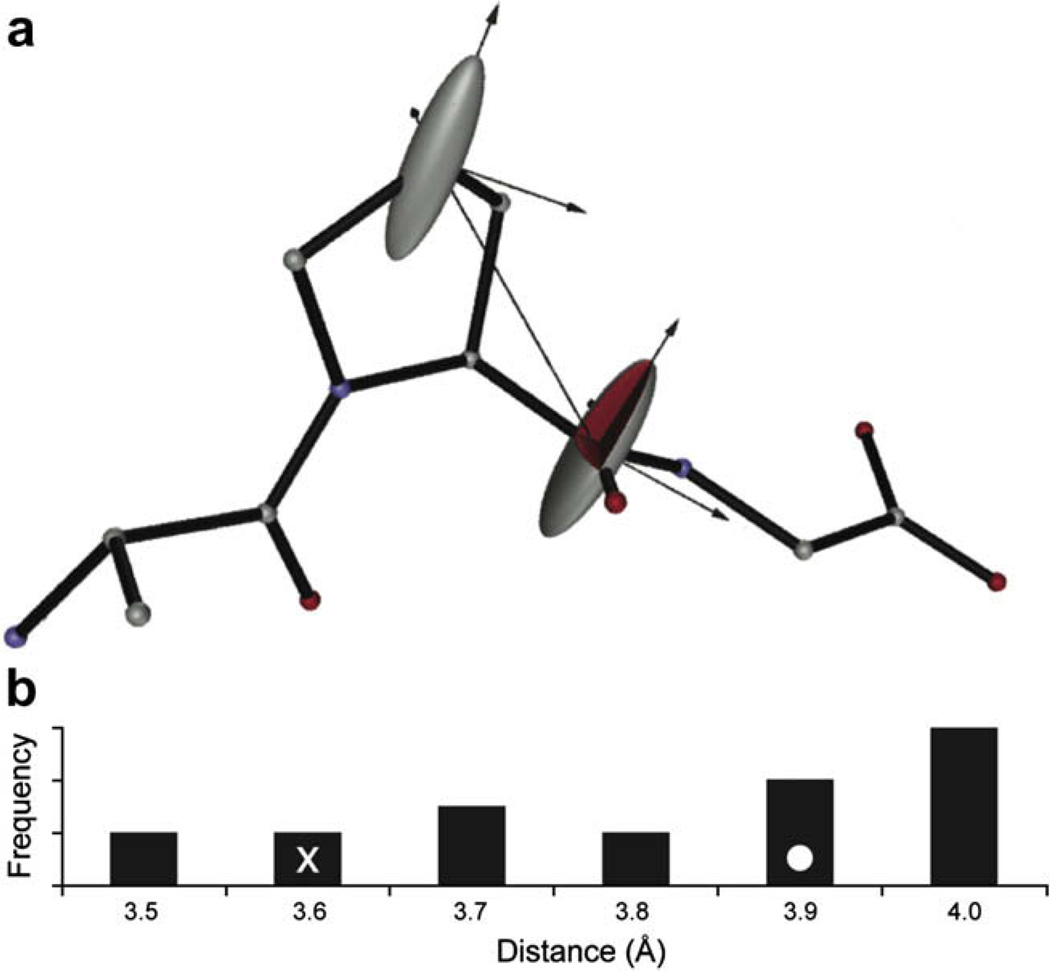
The CSA magnitude and relative orientation of the two spins being recoupled by R² has a profound impact on the spin dynamics [15] and accuracy of the distances extracted using R²W [12]. For example Fig. 2b shows the distribution of distances resulting using different CSA orientations taken from an ensemble of structures generated from simulated annealing without experimental constraints. The range of motion displayed in unconstrained simulated annealing is large enough even in this small molecule to cause substantial deviation in the final R² calculations, which demonstrates the importance of first calculating a lower resolution structure.

Fig. 2.

(a) Relative orientations of the Proline C′ and C^γ CSAs are shown superimposed on the initial structure calculated using REDOR and torsion angle constraints. (b) Histogram displaying the range of Pro C′-Pro C^γ distances calculated from an ensemble of accessible structures generated using simulated annealing (CNS) without any constraints. X-ray (x) and reported NMR (o) distances are indicated. This graphic was produced with SIMMOL [17].

As a starting point in the R²W fitting routine, an initial structure based on REDOR and torsion angle measurements was first calculated. The relative CSA orientation from this structure was then used as an input for the R²W fitting routine, which is derived from a Multimode Multipole Floquet Theory (MMFT) treatment of the two spins [16]. The ¹³C–¹³C distances from these R²W fits were then used together with the REDOR and torsion angle constraints to calculate a final structure. R²W fits generated with relative CSA orientations found in the final structure yielded the same distance as those generated from the initial REDOR-torsion angle structure. Thus we found it unnecessary to perform further iterations in which the structure generated with initial R²W distance constraints is used to refine these constraints.

The default values from SIMMOL were used for relative CSA – molecular orientations, the span and skew of carbonyl carbons were extracted from a 4 kHz CP-MAS spectrum according to Herzfeld and Berger [18], and aliphatic carbon span and skew values were taken from Ye et al. [19].

2.2. Carboxyl terminus

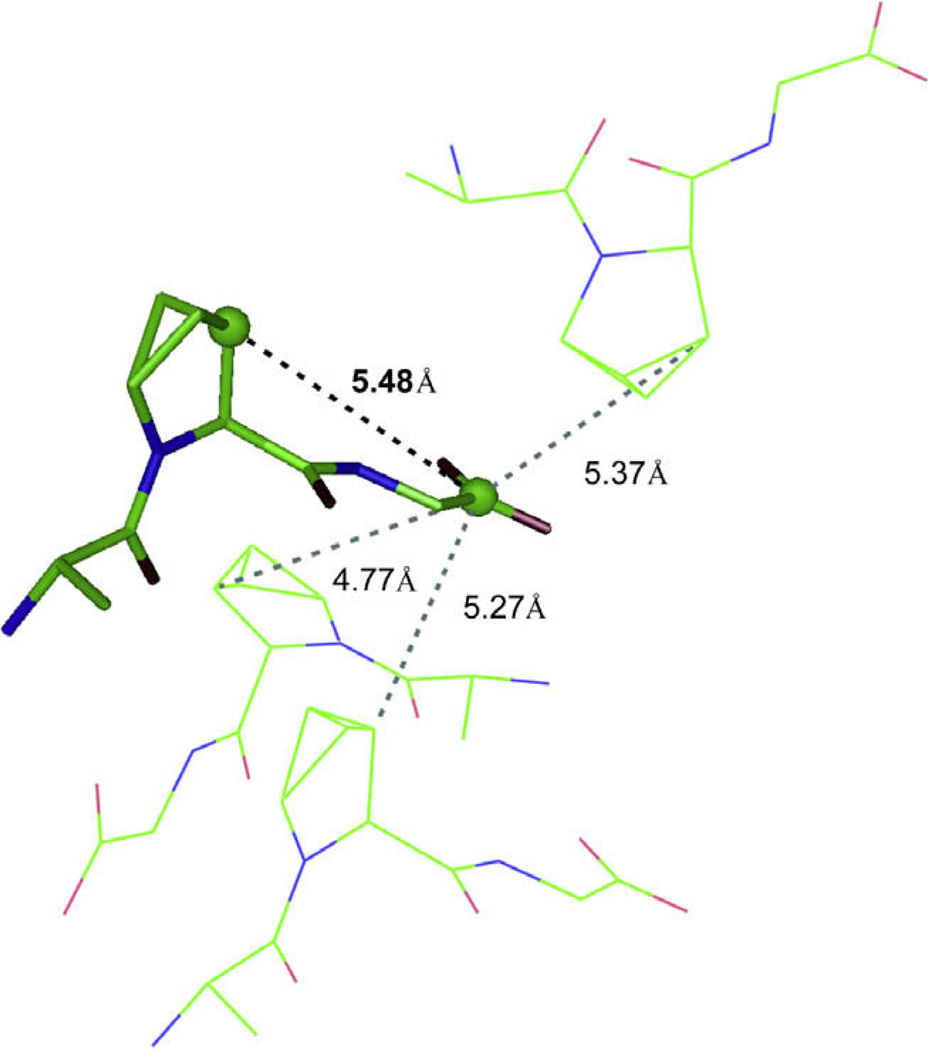
The carboxyl terminus is not well defined due to the absence of ¹³C–¹³C constraints to the Gly carboxyl carbon (see Fig. 1). This is predominantly due to intermolecular and dipolar truncation effects complicating any ¹³C–¹³C distance measurements between the Gly C′ and the Pro C^α and Pro C^β. The Pro C^β carbon to Gly C′ carbon intermolecular distance is 5.5 Å in the crystal structure, but there are three other intermolecular Pro C^β to Gly C′ separations that are less than 5.4 Å (see Fig. 3). The crystals consisted of 10% ¹³C–labeled peptide diluted with natural abundance APG to reduce the number of intermolecular contacts, however there still appears to be enough coupling between intermolecular Pro C^β–Gly C′ pairs to substantially effect the R²W profile and result in a fitting of the data to 4.7 Å rather than 5.5 Å seen in the crystal structure.

Fig. 3.

Crystal lattice of APG showing competing intermolecular distances to the long-range internuclear distance that could be used for structural refinement.

Furthermore, the one-bond Pro C′–Pro C^α dipolar coupling truncates the Pro C′–Gly C^α coupling which would also constrain the carboxyl terminus. Even though R²W is a band-selective recoupling technique and thus usually does not suffer from dipolar truncation [20], the single bond coupling is an order of magnitude stronger than the coupling of interest and is also recoupled when the spinning frequency is set to the N = 2 recoupling condition for the Pro C′ to Gly C^α interaction; the stronger coupling dominates and insufficient polarization is transferred to the Gly C^α. We note that the dipolar truncation should not be as pronounced at higher magnetic fields where the resonances are more separated and the recoupling condition is thus more selective.

2.3. Constraints effect on structural quality

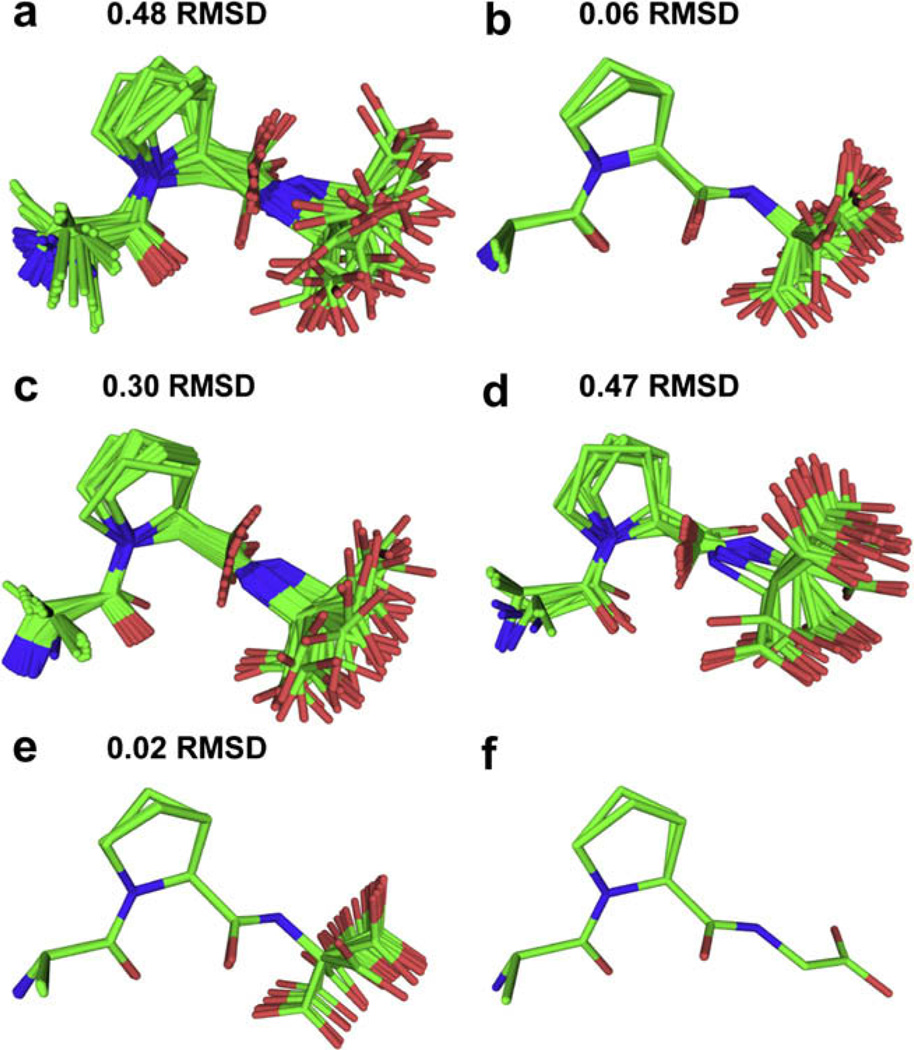
The standard annealing protocol in the program CNS [21,22] was used to generate 40 APG structures in order to generate an ensemble that shows both an average geometry and demonstrates the degree of conformational variability allowed by the geometrical constraints.

In order to compare the usefulness of different structural constraints, a backbone RMSD among the 40 structures of each ensemble was calculated. This shows the level of precision attained by the different NMR experiments, indicating their ability to define overall conformation in this peptide. The results are summarized in Fig. 4 and show excellent agreement with the crystal structure. Since we were not able to perform a measurement that constrains the ψ_Gly angle, the Gly carboxyl group was omitted from the RMSD calculations. The final NMR structure and the crystal structure agree to within an RMSD of 0.09 Å.

Fig. 4.

Twenty lowest energy structures of APG using simulated annealing (CNS) (a) no constraints (b) 2 ψ angles from NCCN measurements (c) 4 ¹³C–¹³C distance constraints (d) 4 ¹³C–¹⁵N heteronuclear constraints (e) all 11 constraints (f) crystal structure.

3. Conclusions

Precise ¹³C–¹³C, ¹³C–¹⁵N, and ψ torsion angles were measured in a uniformly ¹³C, ¹⁵N labeled peptide using R²W in a de novo manner, DANTE-REDOR and local field NCCN experiments. Using these sub-angstrom structural constraints we were able to determine a high-quality structure of APG. The 0.02 Å backbone RMSD structure was sufficient to observe the same conformational heterogeneity of the proline ring that is seen in the X-ray structure at 100 K. The ability to discriminate the two conformers by using structural constraints with sub-angstrom precision and CNS could be applied to address biological questions that require high-resolution structural detail. Furthermore, the short intramolecular contacts present in the tripeptide lattice studied here should not be present in larger proteins and should enable the extension of this de novo R²W strategy to distances up to 8 Å.

Finally, the NCCN torsion and many of the internuclear distances that were experimentally determined with SSNMR are indicative of trans-proline. Although proline is almost always in the trans-isomer, the isomerization to the cis can play an important role in mitotic regulation [23], and we emphasize the strategies for structure determination presented here could be used to further investigate the biological function of proline isomerization.

4. Experimental methods

4.1. Sample preparation

Experiments were performed on a sample of uniformly ¹³C and ¹⁵N labeled Alanyl-Prolyl-Glycine (APG) that was diluted to 10% in the corresponding natural abundance tripeptide to attenuate intermolecular dipolar couplings. The tripeptide was synthesized by CS Bio (CA) with labeled amino acids from Cambridge Isotopes (Andover, MA) and natural abundance material from BaChem (Switzerland). A 9:1 natural abundance to labeled APG mixture was dissolved in a minimal amount of water (solubility was approximately 45 mg/ml). The aqueous solution was placed in a desiccator next to a container of excess ethylene glycol. After a week, crystals were collected, crushed and packed into a rotor.

4.2. Assignments

To assign the ¹³C resonances, a 2D ¹³C–¹³C SPC-5 [24] spectrum was recorded spinning at ω_r/2π = 7.5 kHz using TPPM decoupling [25]. γB₁ for ¹³C was set to 37.5 kHz required by the recoupling condition. The mixing time was 1.07 ms corresponding to 16 rotor cycles, during which time a 120 kHz continuous wave γB₁ field was applied on the proton channel for decoupling. In the indirect dimension, 256 time points were recorded using 16 scans for each t₁ point. The overall measurement time was 7 h. The direct and indirect dimensions were linearly predicted forward to 1024 points, zero-filled to 2048 points and Fourier transformed using NMRPIPE [26].

4.3. NCCN local field correlations

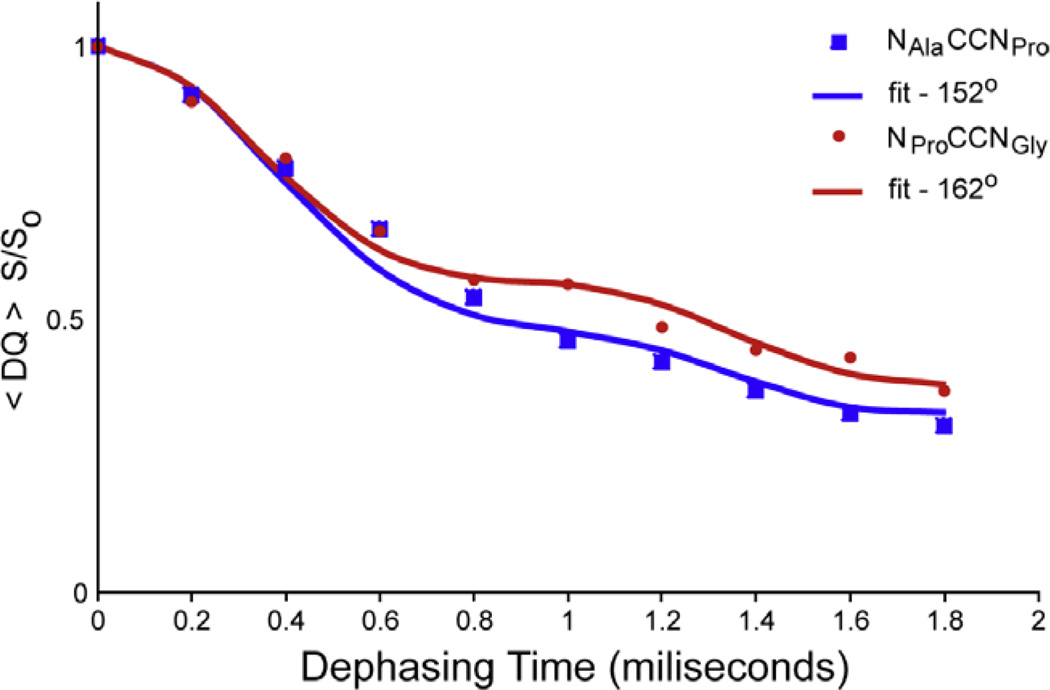
The torsion angles, ψ_Ala and ψ_Pro were determined with the double-quantum heteronuclear local field experiment previously described [13]. SPC-5 [24] was used to create the ¹³C–¹³C double-quantum coherence. The homonuclear mixing time was 800 µs, corresponding to eight rotor periods and the ¹³C carrier was set precisely between the two resonances targeted for recoupling. γB₁ equal to 50 kHz was used for both ¹³C and ¹⁵N during homonuclear mixing and the REDOR [4] dephasing pulses. The spinning frequency was 10 and 110 kHz continuous wave γB₁ decoupling field on protons was applied during SPC-5 mixing and REDOR periods; 136 kHz TPPM [25] decoupling was used during the acquisition period. About 512 scans were taken per dephasing time, and a 3 s recycle delay was used between scans. Each dephasing point was normalized to the intensity of the corresponding resonances absent of REDOR pulses during the dephasing period. The resonances were integrated and the intensities fit (see Fig. 8) to extract the torsion angle with SPINEVOLUTION [27].

Fig. 8.

Dephasing curves for extraction of Ψ torsion angle. An N_GlyCCN_Pro Ψ angle of 152° (blue) was extracted compared to 153° from the X-ray data and N_AlaCCN_Gly Y angle was found to be 162° (red) versus 157° from the X-ray data. SPINEVOLUTION [27] was used to fit the data. (For interpretation of colour mentioned in this figure, the reader is referred to the web version of this article.)

4.4. Rotational resonance width

NMR spectra were recorded on a 360 MHz Spectrometer (courtesy of Dr. D.J. Ruben) with a commercial Chemagnetics triple resonance MAS probe equipped with a 4.0 mm Chemagnetics spinning module. Spinning frequencies were regulated with a Bruker MAS controller.

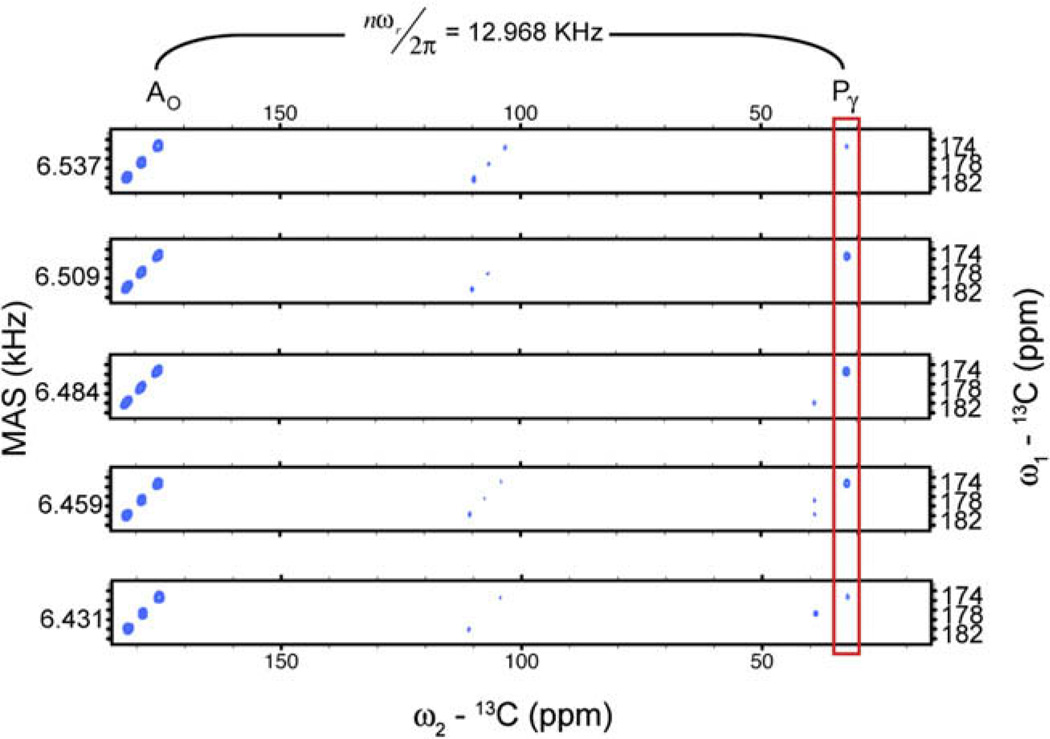
The crosspeak volumes (see Fig. 7) were extracted by automated fitting to two-dimensional Gaussians using NMRPIPE [26]. All data points in each 2D-slice were normalized to the carbonyl intensities of reference experiments conducted at identical spinning frequencies with zero mixing time.

Fig. 7.

R²W spectra at five spinning frequencies. The P_γ crosspeak intensifies as the spinning frequency is swept the R² condition between the spin pair.

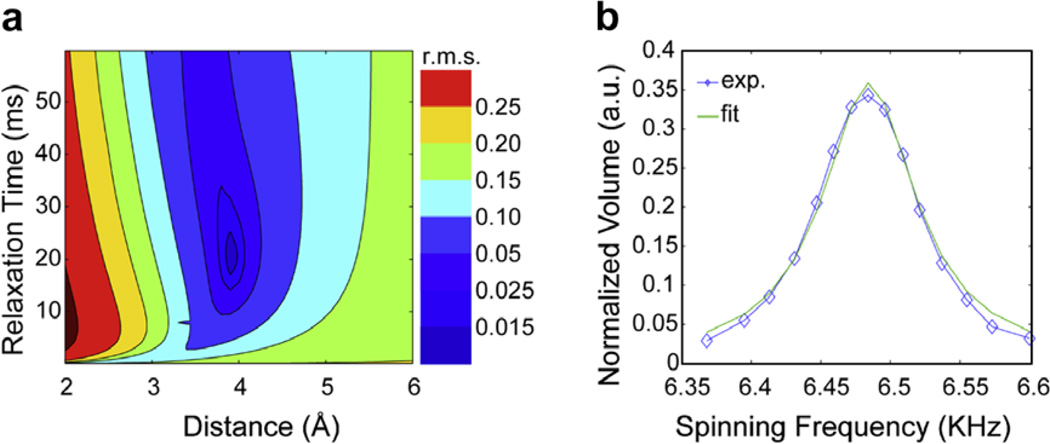
A Gaussian pulse of 250 µs duration was used, followed by a z-filter of 750 µs to select the carbonyl region of the spectrum. 32 t₁ points were recorded with an increment of 250 µs and 16 scans per point with a recycle delay of 3.1 s leading to a total experimental time of about 50 min per two-dimensional slice. A series of experiments were performed as a function of the sample spinning frequency under a constant mixing time of 30 ms (see Fig. 5).

Fig. 5.

(a) Contour plot of the root mean square deviation between experimental and simulated R²W profiles for P_O to P_γ as a function of distance and relaxation. (b) Magnetization transfer from P_o to P_γ in R²W as a function of spinning frequency. The experimental data is shown in blue, and the fit in green. (For interpretation of colour mentioned in this figure, the reader is referred to the web version of this article.)

4.5. DANTE-REDOR

DANTE-REDOR measurements were carried out on a custom assembled NMR spectrometer with a Discovery console (Tecmag; Houston, TX), 14.1 T magnet (Magnex; Oxford, England), and a 39-channel matrix shim system (Resonance Research, Inc.; Billerica, MA), operating at a proton frequency of 600.377 MHz (150.987 MHz for ¹³C). A doubly tuned 4 mm magic angle spinning probe (Doty Scientific; Columbia, South Carolina) was employed.

The DANTE-REDOR pulse sequence is described in [10] and follows after DANTE-REDOR based work of Kaustov [28] and Schaefer [29]. This sequence adapts the orientation information available in a specifically labeled sample to a uniformly labeled system. By employing a DANTE pulse train as the selective pulse in FS-REDOR, the orientation information in REDOR sidebands is retained. Thus at the end of the REDOR evolution time, the ¹³C spin-echo intensity is modulated only by dipolar couplings to the selected ¹⁵N and the resulting REDOR curve can be fit to the analytical expression for an isolated spin pair. The effects of proton couplings are attenuated with Small Phase Incremental Alternation (SPINAL-64) decoupling [25]. The proton decoupling field was 100 kHz, the ¹⁵N REDOR π-pulse width was 16 us and the DANTE π-pulse trains consisted of 33 2 µs rotor synchronized pulses.

Fourier transforms were applied with no apodization and zero filling to twice the acquisition time of 15.36 ms. Only zero order phase correction was used. Dephasing (S) and full-echo (S₀) peak areas were determined by integrating the center band and all observed sidebands. For distance determinations, the sum of all bands in the S and S₀ spectra were used. For extraction of orientation information, the dephasing of each individual band was compared.

Distances were determined by fitting the experimentally observed REDOR curve to the analytical expression, ΔS/S₀(τ) = λ[1 − 〈cos(ω_CNτ)〉]. ΔS/S₀ = 1 − S/S₀, where S and S₀ are the dipolar dephasing and reference intensities, respectively. The coupling ω_CN is a function of the dipolar coupling constant, b_CN, and 〈〉 indicates the powder average over a uniform distribution of crystallite orientations. The scaling factor λ accounts for ¹³C spins without a neighboring ¹⁵N spin, which is a result of imperfect labeling and dilution of the labeled compound in natural abundance material. In the DANTE-REDOR experiment, λ also accounts for imperfect inversion of the ¹⁵N spin magnetization by the selective pulse and decay of coherence due to insufficient decoupling.

For each distance measurement, the weighted χ², ${\chi }_{\nu }^2$, was minimized to fit the data. ${\chi }_{\nu }^2\propto {\sum }_i{w}_i{(S_{i,\text{exp}}-S_{i,\text{sim}})}^2$. In this expression, w_i is the inverse uncertainty in each point squared (σ⁻²). Since the noise in each data point is approximately constant, w_i was easily determined by propagation of error. In the minimization of ${\chi }_{\nu }^2$, the coupling constant, b_CN, was varied freely and the amplitude scaling factor λ was varied within the narrow range of values determined for strong couplings, for which this parameter can be easily determined. The reported uncertainties are at the 95% confidence level according to the following procedure [30]. First, b_CN and λ are varied to determine the best-fit dipolar coupling, ${\chi }_{\nu ,\text{min}}^2$. Next, several trial b_CN values are selected about the best-fit, and the data are re-fit by optimizing λ within the previously defined range. The uncertainties are represented by ${\chi }_{\nu }^2$ values that differ from ${\chi }_{\nu ,\text{min}}^2$ by $F{(\nu )}^{*}{\chi }_{\nu ,\text{min}}^2$ where F(ν) is a constant that depends on the number of degrees of freedom, ν, and the confidence level. For the case of 95% confidence, and 2 degrees of freedom, F(ν) = 19.

Each best-fit b_CN value was linearly scaled by dividing by 0.95 in order to account for thermal motion at 298 K. Internuclear C–N distances are related to the dipolar coupling constants by the equation $b_{\mathrm{C}\mathrm{N}}=-\frac{{\mu }_0{\gamma }_C{\gamma }_N\hslash }{4\pi r_{\mathrm{C}\mathrm{N}}^3}$ [31].

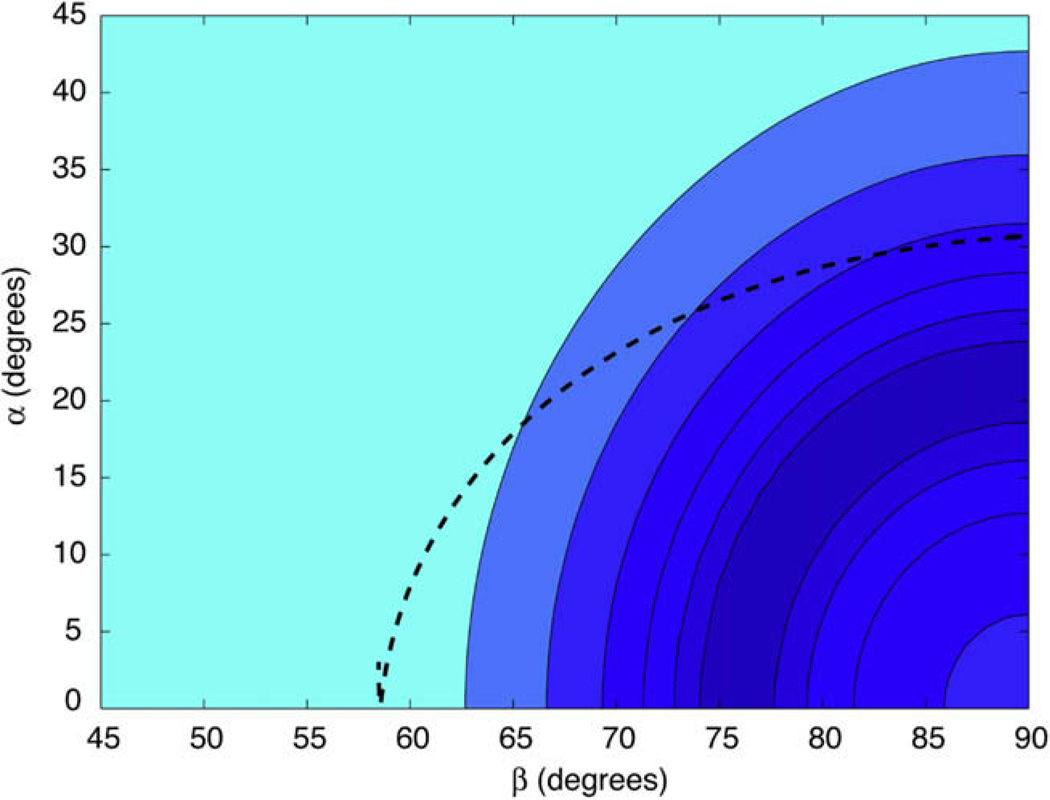
The orientation of the nitrogen in the CSA principle axis system was determined by fitting the experimentally observed REDOR curves (see Fig. 6) of each sideband to numerical simulations explained previously [32]. The weighted χ², ${\chi }_{\nu }^2$, was minimized to fit the data. ${\chi }_{\nu }^2\propto {\sum }_{i,N}w{(S_{\text{exp}}-S_{\mathit{\text{sim}}})}^2$, where the sum is taken over spectral bands N, and mixing times i. As before, w_i is the inverse uncertainty in each point squared (σ⁻²). The uncertainties in the dipolar and azimuthal angles alpha and beta are represented by ${\chi }_{\nu }^2$ values that differ from ${\chi }_{\nu ,\text{min}}^2$ by $F{(\nu )}^{*}{\chi }_{\nu ,\text{min}}^2$ where F(ν) is a constant that depends on the number of degrees of freedom, ν, and the confidence level. The best-fit dipolar coupling is used in this determination, so this is really a three-parameter fit. However, since the REDOR dephasing is approximately linear in the beginning of the curve (before the first extremum in the REDOR curve, where we fit the data) a small error in the dipolar coupling does not significantly alter the position of the best-fit orientation, and thus can be treated as a two parameter fit.

Fig. 6.

The χ² surface for azimuthal (α) and polar (β) angles of the CSA-dipole orientation with each contour level two times the previous level. Labeled APG was diluted to 10% in natural abundance APG and data were collected at 14.1 Tesla with an MAS spinning frequency of 8929 Hz. The superimposed dashed line shows the allowed azimuthal and polar angles corresponding to a rotation about the terminal ψ dihedral angle, with the best-fit at α = 31°, β = 90°.