Abstract
Objective
To assess the feasibility and appropriateness of magnetoencephalography (MEG) for both adult and pediatric studies, as well as for the developmental comparison of these factors across a wide range of ages.
Methods
For 45 subjects with ages from 1 to 24 years (infants, toddlers, school-age children and young adults), lead fields (LFs) of MEG sensors are computed using anatomically realistic boundary element models (BEMs) and individually-reconstructed cortical surfaces. Novel metrics are introduced to quantify MEG sensor focality.
Results
The variability of MEG focality is graphed as a function of brain volume and cortical area. Statistically significant differences in total cerebral volume, cortical area, MEG global sensitivity and LF focality are found between age groups.
Conclusions
Because MEG focality and sensitivity differ substantially across the age groups studied, the cortical LF maps explored here can provide important insights for the examination and interpretation of MEG signals from early childhood to young adulthood.
Significance
This is the first study to (1) investigate the relationship between MEG cortical LFs and brain volume as well as cortical area across development, and (2) compare LFs between subjects with different head sizes using detailed cortical reconstructions.
Keywords: magnetoencephalography, pediatrics, lead field, modeling, boundary element method
Introduction
Magnetoencephalography (MEG) is a neuroimaging technique for measuring the magnetic fields associated with the intracellular current flows within neurons. MEG is widely used to study brain activity at a millisecond resolution, which is currently unavailable to functional magnetic resonance imaging (fMRI) (Dale and Halgren, 2001). Although (1) MEG spatial resolution is indeterminate and (2) its generators can be modeled in different ways depending upon modeling assumptions, a minimum level of resolution certainty exists, as set by biological constraints upon possible generator parameters, and by physical constraints upon sensor sensitivity. Neural currents which give rise to MEG signals are caused by flows of ions involving both ligand-gated and active voltage-gated channels (Murakami et al., 2003, Murakami et al., 2002). Active trans-membrane currents generate intracellular currents as well as passive return currents across neuronal membranes with spatial profiles which are dependent upon neuron shape as well as upon the spatial distribution and type of ion channels on the membrane (Einevoll et al., 2007). Intracellular currents produce the MEG (Hamalainen et al., 1993) whenever the former are spatially aligned such that they can summate to generate measurable signals. In most cases, such configurations are restricted in the brain to the apical dendrites of neocortical pyramidal cells. Because MEG signals decrease by the square of the distance from the source and because nearly all of gray matter (GM) close to the sensors is cortical, possible generators of MEG can be modeled as cortical dipoles which are perpendicular to the local cortical surface (Dale and Sereno, 1993).
The inverse problem of bioelectromagnetism—which consists of localizing electric currents from measurements of magnetic fields—is ill-posed, i.e. an infinity of solutions exist unless specific constraints are imposed with regard to the nature of the sources, their number, locations, orientations, correlations, etc. The inverse solution is dependent upon the assumed conductivity distribution of the head as well as upon the assumed dipole locations and their orientations in the brain, which describe how MEG measurements are assumed to arise from cortical currents. Whereas the electric potentials measured by electroencephalography (EEG) are attenuated by conductive layers interposed between sources and sensors, magnetic fields are instead primarily dependent on tissue permeability, which in the case of biological matter is almost equal to that of free space (μ0).
Although a vast literature of MEG modeling studies exists, few of these studies investigate how MEG sensitivity varies with age, brain volume or cortical area. This relationship is of interest not only for the study of adult populations, but also for that of children, where head size is expected to correlate with MEG sensor sensitivity to underlying cortical sources. Thus, in children, MEG has been applied toward the mapping of electrical activity in pediatric brain tumor patients (Gaetz et al., 2010), language impairments (Rezaie et al., 2011), epilepsy (Brazzo et al., 2011), and bipolar disorder (Rich et al., 2011). However, the mapping of electrophysiological activity using MEG involves challenges which are particularly important when examined in the context of pediatric samples. The first of these factors is the possibly smaller and more variable head sizes of pediatric subjects, depending on age (Pang et al., 2003), which carries with it the possibility that the typical distance between cortex and MEG sensors is larger, on average, than in adults, thus resulting in poorer signal-to-noise ratios (SNRs). Nevertheless, head size variability and its relationship to MEG focality are also of interest for studies of adult populations, where head size is also an important quantity which may be correlated with MEG sensitivity. Because MEG instrumentation requires a fixed Dewar vessel size, the sensitivities of this technique in measuring and localizing brain function share an intimate relationship with subject characteristics such as head size and sensor array configuration. Although Dewar vessel architectures designed specifically for younger pediatric populations (i.e., infants) are available, such technology requires entirely separate, dedicated systems which cannot be used for adult MEG experiments; this limitation consequently implies the necessity for significant financial investment on the part of researchers whose experiments involve both populations. Additionally, because of such instrumentation differences, the use of distinct MEG systems for comparative studies of children and adults to assess developmental brain changes can, in itself, introduce undesirable confounds. Another important factor is the greater likelihood for head motion in young subjects and patients (Brown et al., 2010, Wehner et al., 2008), which can require motion correction using highly accurate modeling of signal sources over time and the assessment of cortical lead fields (LFs).
As MEG is employed more often with pediatric populations in both research and clinical care, it is increasingly important to (1) empirically establish the spatial relationship between MEG sensors and the specific locations of pediatric cortical activity generators, as well as to (2) quantify this relationship in comparison to adult measures from the same MEG system. Consequently, in this article, it is our aim to map and investigate the statistical relationship between age, brain volume and cortical area, on the one hand, and MEG cortical LFs, on the other hand. In this context, LFs are quantities specifying the portions of the cortex whose neuronal sources contribute to the signal recorded by a given MEG sensor. Because the relationship between LFs and cortical area as well as brain volume is of general relevance in studies which involve MEG, the investigation of the former is ideally suited for the assessment of MEG feasibility and appropriateness for both adult and child studies, as well as for the developmental comparison of these factors across a wide range of ages. For 45 subjects with ages ranging from 1 to 24 years, LFs of anatomically realistic Boundary Element Method (BEM) models involving individually-reconstructed cortical surfaces were employed here to (1) explore how focality and global sensitivity metrics vary with age, brain volume and cortical area, and also to (2) validate comparison of adult and pediatric populations using the same MEG system/Dewar vessel type. The cortical LF maps explored here can, therefore, provide important insights for the examination and interpretation of MEG signals from infancy to young adulthood.
Methods
Modeling of pediatric MEG LFs was performed based on the 306 MEG sensor design of the whole-head Elekta Neuromag® scanner at the University of California, San Diego, which is located in a magnetically shielded room (IMEDCO, Hägendorf, Switzerland). The SQUID (Superconducting QUantum Interference Device) sensors of the scanner are positioned as triplets at 102 locations containing one magnetometer (MAG) and two orthogonal planar gradiometers (GRAD1, GRAD2). Calculations were conducted for 45 healthy subjects (21 males and 24 females with ages between 1.1 and 23.6 years). This included three age groups: infants and toddlers (n = 7, 5 females, aged 1.1–3.8 years, mean age = 2.0 years); school-age children (n = 21, 12 females, aged 5.4–11.6 years, mean age = 9.2 years); and young adults (n = 17, 7 females, aged 18.2–23.6 years, mean age = 21.1 years). There was no statistically significant difference among the three groups in the proportion of males versus females (Pearson Chi-Square = 2.05, p = 0.36). Imaging data used in this study were obtained from the NIH Pediatric MRI Data Repository (Release 4) created by the NIH MRI Study of Normal Brain Development. This is a multisite, longitudinal study of typically developing children from ages newborn through young adulthood conducted by the Brain Development Cooperative Group and supported by the National Institute of Child Health and Human Development, the National Institute on Drug Abuse, the National Institute of Mental Health, and the National Institute of Neurological Disorders and Stroke (Contract #s N01-HD02-3343, N01-MH9-0002, and N01-NS-9-2314, -2315, -2316, -2317, -2319 and -2320). A listing of the participating sites and a complete listing of the study investigators can be found at: http://www.bic.mni.mcgill.ca/nihpd/info/participating_centers.html. 3D T1-weighted magnetic resonance image (MRI) volumes were acquired using the spoiled gradient recalled (3D SPGR) echo sequence, and images were segmented in Freesurfer (Dale et al., 1999). To reconstruct each cortical surface, an automatic deformable template algorithm involving three-stage flood-filling (Dale and Sereno, 1993) was used to identify the boundary between white matter (WM) and gray matter (GM) and to generate a connected volume representation of the WM volume. In the first step, an initial estimate of the WM volume was obtained by performing a volume fill as guided by the MRI volume. Then, the volume located outside the volume filled in the first step was also filled to eliminate internal holes. In the third step, the volume located inside the volume filled in the second step was itself filled to eliminate external islands and to generate a connected volume representation of the WM. A unique, closed tessellation of the WM surface was constructed from the faces of filled voxels bordering unfilled voxels, subject to the optimization criterion that the surface areas of all triangular faces in the tessellation should be equal. In all subjects, the tessellated border between WM and GM was chosen as the representative cortical surface being populated with electric dipole sources (Dale and Sereno, 1993). Within the tessellated surface of the GM-WM border, each vertex was assumed to denote the location of a cortical source with an effectively equidistant spacing of 1 mm between dipoles and with a tessellation composed of triangular faces with an area of ~1.73 mm2, resulting in 269,642 ± 4,677 (mean ± standard deviation over subjects) dipoles for the entire brain. This is accurate enough to capture cortical anatomy in regions with large curvature, such as gyral crowns or sulcal troughs.
The head was assumed to be positioned ideally under the scanner, so as to simulate the optimal scenario where the distance from each recording site to the scalp is comparable for as many sensors as possible. This assumption does not involve altering the relative location of sensors with respect to each other; in other words, the spatial arrangement of the sensors remains unaltered from their true arrangement. The constraint of ideal head positioning is necessary so as to avoid bias due to preferential focality of MEG to parts of the head which are closest to the scanner, as the latter can occur under conditions of suboptimal positioning. This constraint is also useful for the purpose of evaluating MEG sensitivity in experimental paradigms involving the activation of distributed sources located throughout the entire brain, as opposed to one or two focal areas. Furthermore, since many cognitive potentials are evoked by sources which are distributed over large cortical areas, this methodological constraint is reasonable.
Realistically shaped anatomical models are known to have higher accuracy for source localization compared to spherical shell models (Buchner et al., 1995, Meijs et al., 1987, Mosher, 1999a, b, Mosher et al., 1999a, Stok et al., 1986), and consequently a one-shell, realistically shaped boundary element method (BEM) model was used for the head, as constructed from tessellated surfaces of the inner-skull generated from MRI. A one-shell BEM was used because it is known to have adequate accuracy (Hamalainen, 1993, Meijs, 1987, Stok, 1986). From the BEM anatomical model of each subject the forward matrix A was generated, which is an array of dimensions M × N, where M is the number of sensors and N is the number of sources. For every source j, the column aj specifies the projection of that source onto the sensors, i.e. the relationship between the source and the physical quantity being measured at each sensor. The forward matrix thus provides the linear transformation from source space to sensor space. Calculations were performed using the linear collocation method (Mosher et al., 1999b) because it has been shown to provide adequate accuracy (Yvert et al., 1996, Yvert et al., 2001). A single (inner skull) shell with about 2,500 nodes was used for the boundary layer.
For the purpose of describing the forward matrix, we adopt a convention first introduced by Tripp et al. (1983) and reiterated in more detail, among others, by Ermer et al. (2001) and by Malmivuo & Plonsey (1995), which makes a formal distinction between forward fields (FFs) and LFs. In this convention, the FF is ‘the observed potential across all sensors due to an elemental dipole’, whereas the LF is ‘the flow of current for a given sensor through each of the dipole locations’ (Ermer, 2001, Tripp, 1983). Thus, FFs and LFs correspond to rows and columns of the forward matrix, respectively. The cortical LF of an MEG sensor can be defined as the strength and direction associated with the projection of each cortical source to that sensor (Liu et al., 1998, Malmivuo, 1980, Rush and Driscoll, 1969). For any sensor i, let ai denote the i-th row of A and aj denote the j-th column of A. The entries aii (where i = 1, …, M and j = 1, …, N) specify the cortical FF vectors (projections of each cortical dipole j onto sensor i). Thus, the vector length of each dipole as ‘viewed’ at the sensor can be visualized using a color map scaled to the magnitude of the largest dipole projection onto that sensor (Malmivuo et al., 1997). Because, as explained in the introduction, measurable MEG signals are mostly due to electric currents generated by spatially aligned apical dendrites of neocortical pyramidal cells, dipole orientation was assumed to be normal with respect to the cortical surface in all subjects. Dipole direction, i.e. toward or away from the local cortex, can be color-coded to yield cortical LF maps, examples of which are shown in the following section. Each dipole was constrained to be normally oriented with respect to the cortical surface and the matrix element aij was assumed to be positive (or negative, respectively) if the normal component of dipole j detectable by sensor i was oriented out of (or into, respectively) the cortex.
Combining the cortical LFs ai of all sensors i = 1, …, M allows one to create and visualize a ‘total’ FF aj. First, for each cortical dipole j, its average contribution to every sensor i is calculated as the global sensitivity index (IGS) given by
| (1) |
which is the root mean square (RMS) over all sensors i = 1, …, M of the cortical FF aj. Since this measure can also be written as
| (2) |
it results that IGS is the scaled L2 norm of the cortical FF, i.e.
| (3) |
The IGS measure allows one to quantify the ‘average’ sensitivity of MEG to the signal generated by each cortical dipole. One disadvantage of this measure is that it can only provide insight on the measurement modality as a whole, without allowing one to distinguish between the measurement capabilities of distinct sensors. The IGS was mapped across the entire cortex for subjects of all ages to investigate the capacity of MEG to record from various brain areas.
Quantification of the focality associated with the cortical LF of each sensor can be performed using the focality measure F(i) where, for some sensor i, F(i) is equal to one minus the sum from 1 to N (the number of sources) of all values in the cortical LF vector |ai|, normalized by the number of sources N and by the largest value in |ai|. That is,
| (4) |
Because the quantity in parantheses on the right hand side is the L1 norm |ai|1 of the LF vector ai, this can also be written as
| (5) |
It also follows that F(i) is equal to 1 minus the normalized average magnitude of the LF ai. F(i) varies from 0 to 1, with greater numbers indicating more focal cortical LFs.
Results
Total Cerebral Volume and Area
As expected, total cerebral volume differed significantly among the three age groups. An analysis of variance (ANOVA) showed a significant main effect of group (Fisher’s F statistic = 3.79, p < 0.03), and Tukey-Kramer post-hoc pairwise comparisons showed that the effect was driven by school-age children and young adults showing significantly larger cerebral volumes than infants and toddlers (p < 0.05). For young adults, the mean volume was 1220 mm3, for school-age children 1183 mm3, and for infants and toddlers 1083 mm3. Likewise, the total cortical surface area was significantly different among the three age groups. ANOVA yielded a significant main effect of group (Fisher’s F statistic = 19.31, p < 0.0001) driven by significantly greater cortical surface area among young adults and school-age children than in infants and toddlers (Tukey-Kramer honestly significant difference (HSD), p < 0.05). For young adults, the average total cortical surface area was 1831 mm2, 1815 mm2 for school-age children, and 1281 mm2 for the infant and toddler group.
Cortical LFs
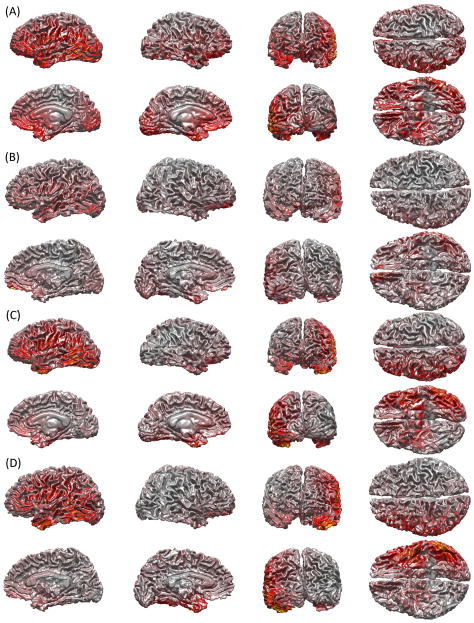
Figure 1 shows examples of sensor LFs for both magnetometers and gradiometers. In all insets (A through D), LFs are shown for sensors located directly above the junction between the Sylvian and Rolandic fissures. The values are plotted on the WM surface and they represent the absolute values of LF values for the sensor of choice. Because the forward matrix specifies the visibility of every source to the sensor, the cortical LF plots in Figure 1 are indications of how many sources can contribute to the signal recorded by the selected sensor. In inset A, the LF of the magnetometer located above that point is shown for the subject with the lowest total brain volume (TBV). By contrast, inset B displays the magnetometer LF for the subject with the highest total brain volume. Comparison of insets A and B easily reveals that the sensor in question records from a notably larger portion of cortex in Figure 1A compared to Figure 1B. In the case of the subject with the lowest TBV, the magnetometer whose LF is depicted records from essentially the entire dorsolateral portion of the left hemisphere, and additionally from frontal and occipital portions of the medial left and right hemispheres. By contrast, the magnetometer located above the junction of the rolandic and sylvian fissures in the subject with highest TBV (Figure 1B) records from a smaller portion of the cortex. Comparison of Figures 1C and 1D reveals that TBV (i.e. head size) has an important effect not only upon magnetometer focality, but also upon the focality of gradiometers. For example, comparison of the medial and posterior views of the two brains in Figures 1C and 1D illustrates the ability of the selected gradiometer to record from a larger proportion of the cortex in the case of the subject with the lowest TBV (Figure 1C). When comparing differences in focality between gradiometers and magnetometers based on LF illustrations of the same brain (e.g. comparison of Figure 1A to Figure 1C, or comparison of Figure 1B to figure 1D), one can confirm that the LFs of gradiometers are more focal than those of magnetometers. For example, whereas the selected magnetometer can record from frontal and occipital portions of the medial surface in Figure 1A, this is not the case to the same extent for the gradiometer (Figure 1C).
Figure 1.
Cortical LFs for sample sensors illustrating the dependence of MEG sensitivity upon brain size. LFs are shown for sensors located directly above the junction between the sylvian and rolandic fissures. The values are plotted on the WM surface and they represent the absolute values of LF values for the sensor of choice. LFs were normalized with respect to the maximum absolute value of the LF being displayed on each cortical surface. Since the LF specifies the visibility of every source to the sensor, these cortical LF plots indicate how many sources can contribute to the signal recorded by the selected sensor. (A–B) illustrate magnetometer LFs for the subjects with the lowest (A) and highest (B) TBVs, respectively. By contrast, (C–D) display gradiometer LFs for the same subjects as in (A) and (B), respectively. The distance between the sensor and the cortex is equal to 3.12 cm (A) and 4.96 cm (B).
Global Sensitivity
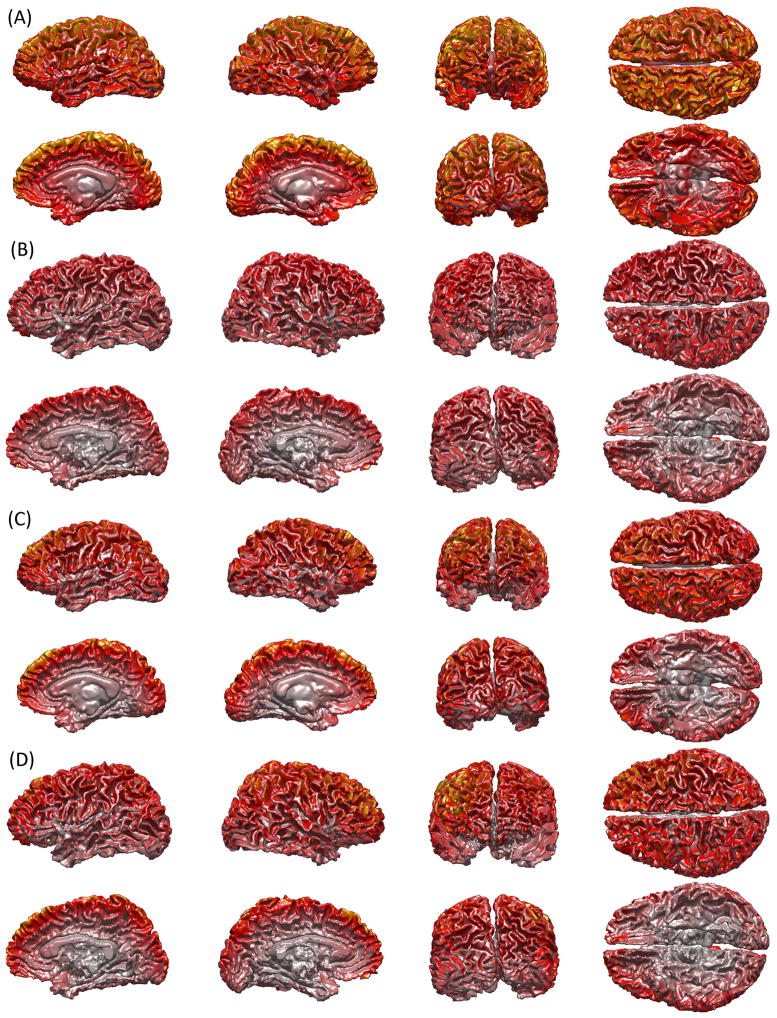
Figure 2 depicts the global sensitivities of MEG for the same two subjects as in Figure 1. Thus, whereas Figure 1 displays examples of cortical LFs for only one sensor per derivation, Figure 2 displays the overall sensitivity of all sensors, and thus shows the parts of the cortex accessible to different MEG derivations. Comparison of Figures 2A and 2B reveals that, in the case of the subject with the lowest TBV (Figure 2A), deep sources contribute to the overall global sensitivity of MEG to a greater extent than in the case of the subject with the highest TBV (Figure 2B). This finding is explained by the fact that, for subjects with comparatively larger heads, superficial cortex is located closer to the MEG sensor array, which makes its contribution to global sensitivity much higher than that of deep cortex. On the other hand, in the case of the subject with a smaller head (Figure 2A), the superficial portions of the cortex are located farther away from the set of sensors, which implies that the contribution of deep sources to the global sensitivity is larger than in Figure 2B. Another way to conceptualize this phenomenon is by noting that the distance between the surface and the center of the head is smaller in subjects with smaller heads, and larger in subjects with larger heads. Thus, given the rapid decrease in magnetic field amplitude with distance from the source, it results that sources which are closer together contribute to the recorded signal by a more appreciable amount (Figure 1A) than sources which are farther apart (Figure 1B). The discussion above applies equally well, for similar reasons, to the comparison of gradiometers, as presented in parts C and D of Figure 2. Finally, one can note from comparing Figure 2A to Figure 2C (or, alternatively, Figure 2B to Figure 2D) that the global sensitivity of magnetometers to deep sources is higher than that of gradiometers for a given head size.
Figure 2.
Global sensitivities of magnetometer (A, B) and gradiometer (C, D) MEG. Whereas Figure 1 displays examples of cortical LFs for only one sensor per derivation, this figure displays the overall sensitivity of all sensors, and thus shows the parts of the cortex accessible to different MEG derivations. (A) and (C) display global sensitivities for the subject with the lowest TBV, while (B) and (D) show the same quantity for the subject with the largest TBV. Global sensitivity is shown for both magnetometers and gradiometers so as to illustrate differences between them from the standpoint of their spatial sensitivity patterns.
Focality
Statistical fits of the linear relationship between the focality F, on the one hand, and age, TCA, and TBV on the other hand are presented in Table 1 by sensor type and age group. When including subjects of all ages, TCA was highly and most strongly correlated with F, accounting for up to 88% of the variance for gradiometers (mean F) and 76% of the variance for magnetometers (median F). Across the three different subject age groups, age in years showed the weakest statistical association with F, accounting for about half of the variance in school-age children for both types of sensors, and age showed no association with focality among young adults. These results are not surprising given the high individual differences variability in brain size across this age range and particularly after the childhood years of maximum annualized change. For each of the age groups computed separately, TCA was most strongly correlated with gradiometers’ F, with somewhat weaker correlations between TBV and magnetometers’ F. Corresponding p values for these statistical tests can be found in Table 2.
Table 1.
Coefficients of determination (R2) for the linear association between age, total cortical area (TCA), and total brain volume (TBV), on the one hand, and mean and median focality (F), on the other hand, for gradiometers (grad) and magnetometers (mag). Statistical fits were computed separately for all subjects and by age group. R2 equals the percentage of variance in one variable explained by the other.
| all subjects | mean F
|
median F
|
||
|---|---|---|---|---|
| grad | mag | grad | mag | |
| age | 0.33 | 0.27 | 0.29 | 0.24 |
| TCA | 0.88 | 0.72 | 0.82 | 0.76 |
| TBV | 0.69 | 0.59 | 0.66 | 0.65 |
| infant/toddler | ||||
| Age | 0.14 | 0.17 | 0.15 | 0.21 |
| TCA | 0.89 | 0.89 | 0.92 | 0.89 |
| TBV | 0.87 | 0.84 | 0.83 | 0.76 |
| school-age | ||||
| age | 0.55 | 0.47 | 0.53 | 0.44 |
| TCA | 0.83 | 0.65 | 0.73 | 0.69 |
| TBV | 0.75 | 0.59 | 0.66 | 0.67 |
| young adult | ||||
| age | <0.01 | <0.01 | 0.01 | <0.01 |
| TCA | 0.87 | 0.69 | 0.85 | 0.75 |
| TBV | 0.81 | 0.6 | 0.76 | 0.66 |
Table 2.
p-values for the linear bivariate fit between age, total cortical area (TCA), and total brain volume (TBV), on the one hand, and mean and median focality (F), on the other hand, for gradiometers (grad) and magnetometers (mag). Statistical fits were computed separately for all subjects and by age group.
| all subjects | mean F
|
median F
|
||
|---|---|---|---|---|
| grad | mag | grad | mag | |
| age | 0.0001 | 0.0003 | 0.0002 | 0.0006 |
| TCA | <0.0001 | <0.0001 | <0.0001 | <0.0001 |
| TBV | <0.0001 | <0.0001 | <0.0001 | <0.0001 |
| infant/toddler | ||||
| Age | 0.41 | 0.36 | 0.38 | 0.31 |
| TCA | 0.0014 | 0.0015 | 0.0007 | 0.0013 |
| TBV | 0.0022 | 0.0037 | 0.0046 | 0.011 |
| school-age | ||||
| age | 0.0001 | 0.0006 | 0.0002 | 0.0011 |
| TCA | <0.0001 | <0.0001 | <0.0001 | <0.0001 |
| TBV | <0.0001 | <0.0001 | <0.0001 | <0.0001 |
| young adult | ||||
| age | 0.85 | 0.87 | 0.73 | 0.82 |
| TCA | <0.0001 | <0.0001 | <0.0001 | <0.0001 |
| TBV | <0.0001 | 0.0003 | <0.0001 | <0.0001 |
Highly statistically significant differences were found when comparing the three age groups on measures of LF focality. ANOVAs of both the mean and median focality for gradiometers demonstrated significant main effects of age group (mean: Fisher’s F statistic = 12.84, p < 0.0001; median: Fisher’s F statistic = 9.8, p < 0.0003), driven by a significantly larger focality index for the infant and toddler group than for school-age children and young adults (Tukey-Kramer pairwise test, p < 0.05). Measures of magnetometer focality also showed significant age group differences for mean focality (Fisher’s F statistic = 7.3, p < 0.002) and median focality (Fisher’s F statistic = 7.2, p < 0.002), again showing a significantly higher focality index (i.e., larger and less focal) in the infant and toddler group as compared to both school-age children and young adults (Tukey-Kramer HSD, p < 0.05).
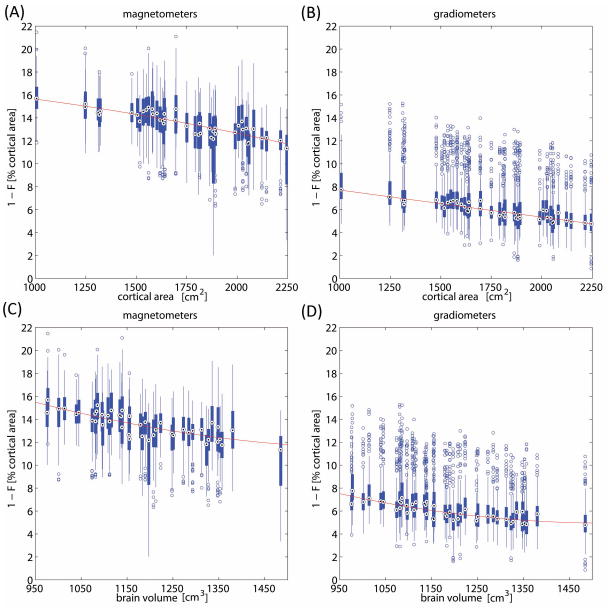
In Figure 3, we quantify the dependence of lead field focality upon brain volume and cortical area by displaying box-and-whisker diagrams of focality values for and within every subject. Because 1 – F roughly represents the proportion of total cortical area from which a sensor can record, the former quantity—rather than F itself—is displayed in Figure 3 so as to ease interpretation. Each displayed diagram corresponds to one subject, for a total of 45 diagrams or subjects. As customary, the diagrams quantify the most important statistics associated with the sensor focality values of a particular subject: the box (thick vertical blue line rectangle) reveals the interquartile range (IQR), the black dot represents the sample median, and the whiskers (thin blue lines extending above and below each box) are drawn from the ends of the IQR’s to the furthest observations within the whisker length. Observations beyond the whisker length are marked as outliers (blue circles), i.e. as values which are more than 1.5 times the IQR away from the top or bottom of the box. Shown in red is the line of best quadratic fit to the median values for the population.
Figure 3.
Dependence of 1 – F (i.e. the proportion of the cortical area from which an MEG sensor can record) upon cortical area (A, B) and brain volume (C, D). Box-and-whisker diagrams of focality values are displayed within and for every subject. Each displayed diagram corresponds to one subject, for a total of 45 diagrams or subjects. Diagrams quantify the most important statistics associated with the sensor focality values of a particular subject: the box (thick vertical blue line rectangle) reveals the interquartile range (IQR), the black dot represents the sample median, and the whiskers (thin blue lines extending above and below each box) are drawn from the ends of the IQR’s to the furthest observations within the whisker length. Observations beyond the whisker length are marked as outliers (blue circles), i.e as values which are more than 1.5 times the IQR away from the top or bottom of the box. Shown in red is the line of best quadratic fit to the median focalities of the population.
As already obviated in Figures 1 and 2, Figure 3 also confirms that, on average, magnetometers (A, C) have larger values of 1 - F (i.e. poorer focalities) than gradiometers (B, D). In fact, two notable differences between magnetometers and gradiometers which are apparent in Figure 3 are that (1) gradiometer samples have an appreciably larger number of outlier F values compared to magnetometers, and that (2) these outliers are typically values of 1 – F which are larger than the upper limit of the IQR. Investigation of this result revealed that this phenomenon is due to the fact that a large number of sensors located around the lower posterior rim of the Elekta Neuromag Dewar vessel are typically located much farther from the cortex than most other sensors if the head is assumed to be optimally positioned in the scanner. Consequently, because focality decreases as the source-to-sensor separation increases, it is expectable for such sensors to have smaller values of F, and larger values of 1 - F (hence lower focality). In the case of magnetometers, whose lead fields are more diffuse than those of gradiometers, the additional increase in distance between sensors and the brain does not produce an appreciable effect. In the case of gradiometers, however, which are typically more focal as already stated, the additional separation between sensor and sources leads to the presence of outliers in their distribution of F values, as made clear in the figure.
Figure 3A shows that, as cortical area decreases from ~2,250 cm2 to ~1,000 cm2, the value of 1 - F for magnetometers increases from ~12% to ~16% of the total cortical area. In the case of gradiometers (Figure 3B), 1 - F similarly increases from ~5% at ~2,250 cm2 to ~8% at ~1,000 cm2. Consequently, decreases in cortical area affect gradiometer focality to a much greater extent than it affects magnetometers, although both derivations are appreciably affected. This type of analysis can also be performed by quantifying the dependence of 1 - F upon brain volume, as opposed to cortical area. This reveals how, as brain volume decreases from ~1,480 cm3 to ~970 cm3, 1 - F increases from ~12% to ~15% of the total brain volume for magnetometers (Figure 3C), and from ~5% to ~7% for gradiometers (Figure 3D).
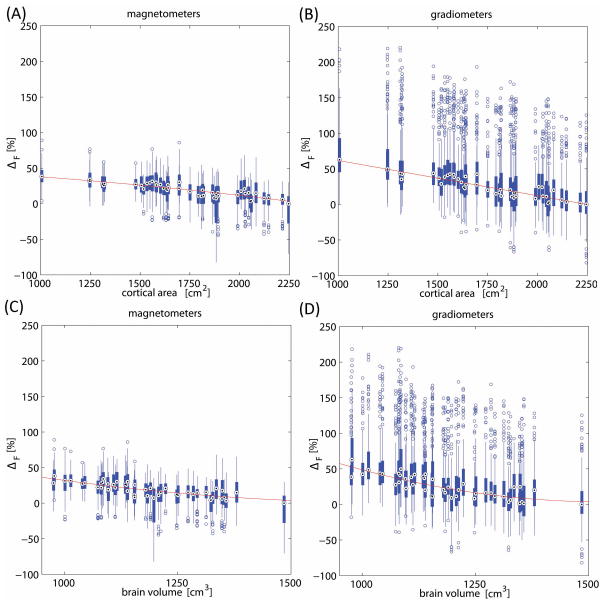
Whereas Figure 3 conveys the dependence of 1 – F upon cortical area and brain volume, Figure 4 explores the relative changes in focality which occur with changes in each of the former two measures. As the definition of F reveals, a sensor with an F value equal to 0 would be a sensor which can record from the entire cortex, whereas a sensor with an F value of 1 would be one which can only record from a single cortical location. Consequently, because the focality measure is defined to accommodate this entire range of conceivable focalities, one of its drawbacks is that it can be inconvenient or misleading to compare the focalities of two sensor types only by examining the absolute difference in their F values. For example, the fact that the changes in 1 – F shown in Figure 3 (e.g. ~4% and ~3% for magnetometers and gradiometers, respectively, as a function of cortical area) are relatively small compared to unity may lead one to draw the inappropriate conclusion that the cortical area from which MEG sensors can record varies little with brain size. This shortcoming of the focality measure, however, can be overcome by investigating relative differences in focality which are computed with respect to some reference value. The results of such a calculation are presented in Figure 4, where relative changes in the quantity 1 – F are illustrated. In that figure, the largest median value of 1 – F over any subject (where 1 – F roughly represents, as previously stated, the cortical area from which a sensor can record) is selected as the reference value, and all other values are plotted as percentage differences with respect to the reference. Thus, Figure 4 indicates that, as cortical area decreases from ~2,250 to ~1,000 cm2, the cortical area from which the typical magnetometer and gradiometer can record increases by ~50% (Figure 4A) and ~60% (Figure 4B), respectively. Similarly, as brain volume decreases from ~1,500 to ~1,000 cm3, the cortical area from which the typical MEG sensor can record increases by ~40% for magnetometers (Figure 4C) and by ~50% for gradiometers (Figure 4B). Thus, our results strongly indicate that large differences in brain size and cortical area do translate into appreciable differences in relative sensor focality, and that the cortical area from which the average MEG sensor records can be as much as one and a half times as large in children as it is in adults.
Figure 4.
Relative dependence of 1 – F (i.e. the proportion of the cortical area from which an MEG sensor can record) computed as a percentage of the maximum median value of 1 – F across subjects. First, the largest median value of 1 – F over subjects was selected as the reference value, and then all other values were plotted as percentage differences Δ with respect to the reference. The behavior of Δ is explored as a function of cortical area (A, B) and brain volume (C, D), for both magnetometers (A, C) and gradiometers (B, D).
Discussion
Novelty and significance
This is the first study to (1) investigate the relationship between MEG cortical LFs and brain volume as well as cortical area across development and (2) specifically compare LFs between subjects with different head sizes using detailed cortical reconstructions in order to address an important methodological issue for studying cross-sectional and longitudinal development, where a direct comparison of child, adolescent, and adult populations is required. In this study, cortical LFs of MEG were computed using realistic BEM forward models as well as detailed cortical reconstructions whose orientations were perpendicular to the cortical surface. Two measures–the global sensitivity index (IGS) and focality (F)—were used to quantify and compare LFs between subjects of various head sizes, and two MEG modalities (magnetometer and planar gradiometer) were investigated. As expected, sensitivity and focality were found to vary as a function of brain volume and cortical area. Not surprisingly, individual variability in head size was more strongly associated with IGS and F than age per se. This characterization of the cortex-to-sensor relationship across different ages (and head sizes) provides a quantitative guide for the use of the same MEG Dewar vessel in making cross-sectional and longitudinal age comparisons. Individuals with the smallest brains, regardless of age, showed lower sensitivity and focality profiles, as expected. Infants and toddlers showed consistently lower focality than school-age children and young adults, linked to their significantly smaller head and brain sizes.
Two findings with regard to LF size are important. Specifically, (1) gradiometer MEG LFs were confirmed to be more focal than magnetometers across all ages and head sizes, and (2) magnetometers were confirmed not to be sensitive to dipoles located directly underneath the sensor, which is where gradiometer sensitivity is, by contrast, maximal. Finally, MEG was confirmed to be relatively insensitive to radial sources positioned on gyral crowns, as well as to deep sources. In subjects with comparatively larger heads, gradiometer LF are localized to a relatively small region directly beneath the sensor, and it can therefore be practical to select pairs of sensors with non-overlapping LFs whenever the effect of such overlap upon sensor-space synchronization measures is sought to be minimal. Thus, for such subjects, coherence between two planar gradiometer signals can be interpreted as being dominated by coherence between the underlying cortical areas provided that both of these areas are active.
As MEG techniques are rapidly being applied with greater frequency toward questions about human functional brain development—comparing brain recordings across a wide range of ages—it becomes increasingly important to validate methods and to evaluate potential confounding factors which may drive spurious age differences in brain activity characteristics. It is well established that total brain volume and total cortical surface area undergo significant and non-monotonic developmental changes even from preschool age into young adulthood (Brown and Jernigan, 2012, Brown et al., 2012, Jernigan and Tallal, 1990, Jernigan et al., 1991). Since the vast majority of developmental MEG studies which compare children and adults employ the same MEG system and Dewar vessel type, there is the strong assumption that these systematic differences in brain anatomy do not themselves affect activity characteristics derived from source modeling. Because differences in brain ‘size’ straightforwardly would be predicted to affect MEG measures, it is critical that the nature of the relationships among these variables be empirically disentangled. This issue is particularly important with regard to making inferences about the focality of brain activity sources, since it has been suggested by many researchers that human functional brain organization itself progresses from a relatively more diffuse to a relatively more focal organization between early school-age and young adulthood (Brown et al., 2006).
Here, we quantify the magnitude of the correlative relationship involving brain size, which both validates the use of the same MEG Dewar system across certain ages and offers a guide for which ages and brain sizes might begin to be problematic for drawing conclusions about the location, focality, and amplitude of brain activity. In general, our results suggest that the same MEG system and Dewar vessel type can be reasonably used to make cross-sectional and longitudinal comparisons between young adults and school-age children down to about the age of five with a fairly high degree of confidence for the purpose of studying developmental changes in localized brain activity sources and cerebral functional organization. Across infant and toddler age ranges, there begin to be some differences in brain activity sensitivity and focality which could affect inferences made about developmental changes in functional brain organization.
Researchers using MEG to directly compare localized brain activity patterns in subjects among the smallest in head and brain size (i.e., infants) with older individuals will need to exercise caution. If the spatial extent of the developmental changes that are found are sub-lobar, for example, they may be at least partly driven by changes in head and brain size. On the other hand, if brain activity differences which appear to be age-related are found at greater distances (e.g., across lobes, hemispheres), our findings would suggest that there is less chance for such effects to be driven solely by differences in the gross size characteristics of the growing neural substrate. However, it should be noted that any age-based rules of thumb such as this remain quite coarse, because of the high variability in brain and head size among individuals of the same age. The best method for determining the appropriateness of any across-age comparisons will be to use measures such as cortical area and cerebral volume and to ensure comparability across different phases of development. In the present context, the use of the term “sub-lobar” is an attempt to give a rough but reasonably conservative rule of thumb for developmental studies which employ MEG. In our intended definition, multiple focal activations within right frontal cortex would be sub-lobar and thus more susceptible to subject age and to localization ambiguities driven by brain/head-size than, say, activations spanning the left and right frontal lobes. Obviously, the most posterior aspects of left temporal lobe, for further example, are far enough from the most anterior aspects of the left temporal lobe to be safer from these potential problems than when the regions of activation in question come from the posterior left temporal lobe and the left anterior occipital lobe. These characterizations should hold for both activation and coherence studies. However, they convey only a general sense of these potential effects and would be subject to the quantitative aspects of many relevant factors including registration precision, source modeling, and the magnitude of the head/brain size differences being compared.
Methodological considerations
For the purposes of this study, the type of positioning being used is referred to as ‘ideal’ because it reflects our interest in studying MEG as a measurement technique without a priori knowledge concerning the locations of cortical generators which are of interest in a particular study. In other words, one of our modeling assumptions is that all areas of the cortex are of equal interest to the MEG researcher in the context of our results. Naturally, asymmetrical head placement in the MEG helmet can and often should be attempted in studies which target a very specific region of the brain (such as somatotopic cortex), and the investigation of MEG sensitivity in such scenarios can be of appreciable interest in the context of such studies. However, it remains the case that a substantial number of MEG research studies are concerned with sources of electrical activation which are distributed throughout the entire brain rather than focal, in which case ideal positioning as described here is often preferable to asymmetrical head placement in the MEG scanner. In addition, the concept of ideal positioning as understood in the present context is justifiable here because our primary concern is with the focality of MEG as a recording technique, rather than with the preferential focality of certain MEG sensors relatively to others. Consequently, the results of our study should be interpreted in this limited context, as further research is necessary in order to extend our modeling perspective to the case of asymmetric head placement in the MEG scanner. The assumption of idealized head positioning was also made due to the need to select a suitable modeling context when investigating the effects of total area and volume upon focality. Holding the sensor-to-head distance as constant as possible across sensors was useful to isolate the main variables of interest (global sensitivity and focality), without the added complexity of the scalp-to-sensor distance varying greatly across sensors, as in the scenario of aligning the sensor array to the back of the head or as in other scenarios involving asymmetric head positioning. The latter could create a more complicated relationship between area, volume, and our measures of sensitivity and focality, making our analysis considerably less tractable due to the large variety of possible head placements. Nevertheless, it should be acknowledged that the modeling assumption of a certain head positioning and the inherent choice of a certain scalp-to-sensor distance profile is an additional modeling variable which is independent of development. Thus, our decision to implement this study under the assumption of ideal head positioning may admittedly confine some of our conclusions to this context and should consequently be acknowledged as a limitation of this study.
Comparison with previous studies
As used in this study, the focality measure F is similar in spirit to the concept of half sensitivity volume (HSV), in that both metrics aim to quantify the spatial extent of the region populated with electrical sources from which a sensor can record. The HSV was introduced by Malmivuo and Plonsey (1995) and is defined by these authors as the volume of the source region in which the magnitude of the detector’s sensitivity is more than one half of its maximum value in the source region. The first important difference between the HSV and F is that, whereas the HSV is defined over the volume of the head, F is defined over the cortical surface. This feature of the F measure makes it a more appropriate metric in the present study because our source model assumes that the MEG is produced only by sources distributed uniformly across the cortical sheet, and because the focus of the study involves the sensitivity of MEG to such sources. If the source model, however, were to account for non-cortical dipoles distributed throughout the volume of the head, the HSV measure would be preferable because the F measure is a surface (rather than a volume) sensitivity measure. The second important difference between the HSV and F involves the fact that the HSV quantifies the volume of the source region in which the sensor sensitivity magnitude is greater than half of the latter’s maximum. By contrast, F conveys how much of the cortical surface is covered with sources where sensor sensitivity is greater than the average sensitivity of the sensor to any source. One implication of this difference between the two measures is that, in addition to the maximum LF magnitude (upon which both metrics are dependent), F is also explicitly dependent upon the mean LF value over the cortex. For this reason, the use of the F measure may be preferable in cases where sensor sensitivity should be explicitly quantified based on the expected value associated with its distribution.
Limitations and caveats
In this study, the dependence of LF measures upon age and head size was investigated in the context of the Elekta Neuromag® MEG scanner. Because our investigation does not discuss these measures as pertaining to other hardware systems which are in current use, it is necessary to acknowledge this as an important limitation of our study. Specifically, two parameters which can be expected to affect substantially the extent to which the conclusions of our analysis may be applied to other systems are the size of the Dewar vessel and the type of MEG sensors used. In the first case, an increase in the size of the Dewar vessel can be expected to have an undesired effect upon sensor focality because, as the average distance from any given sensor to the cortex decreases, the preferential sensitivity of that sensor to cortical sources which are directly beneath it goes down. Conversely, a smaller Dewar vessel size can be expected to translate into an increase in average sensor focality because the average sensor is closer to the scalp than in our case, and the sensor is therefore more preferentially sensitive to cortical sources directly below it. When considering MEG arrays which (1) have planar gradiometers and/or magnetometers and which (2) differ from the Neuromag® scanner in their number of sensors or in their spatial configuration, one can reasonably expect that their sensitivity to the head size of the subject would be comparable to ours provided that the size of the Dewar vessel is similar to that of the Elekta Neuromag® system. Nevertheless, it is possible that the hardware configuration of the device of interest could include other sensor types of which many exist, including vector magnetometers, axial gradiometers, second-order or even third-order gradiometers, etc. (Seki and Kandori, 2007, Uzunbajakau et al., 2005). The latter two types of sensors may be based on an appreciable variety of coil arrangements, and therefore many varieties of MEG systems are used in neuroimaging (Lima et al., 2004). Modeling studies involving these and other systems requires familiarity with their hardware design specifications, including relative sensor positioning and physical coil parameters (baseline, diameter, etc.), which can vary greatly across systems. Quite often, because such hardware specifications are not made public by their manufacturers, the task of including them in studies such as ours can pose substantial challenges. For these reasons, modeling MEG sensor sensitivity for other types of sensors and systems was not attempted here, though the present framework can be applied to other sensor configurations as well. Because the two types of sensors examined here are very commonly used by the MEG community, our results remain relevant to an appreciable cross section of MEG researchers.
It should be noted that, in recent years, MEG recording systems which are intended specifically for use with infants and small children have become more widely available (Johnson et al., 2010, Kikuchi et al., 2011, Yoshimura et al., 2013). Typically, these systems employ smaller Dewar vessels, contain fewer sensors, and will consequently impose a limit upon the range of ages and head sizes of the subjects whose MEG recordings can be measured using these devices. However, their better fit to smaller heads offers improved sensitivity for measuring and localizing brain activity in the very young. Using a custom child-sized MEG system, He et al. (2013), for example, recently demonstrated a robust face-sensitive M170 magnetic component in a four-year-old child despite the failure to find such an effect in several studies using conventional adult-size systems. These results help to underscore the importance of taking careful consideration of the factors which are examined in the current study.
Implications for clinical research
In addition to the emerging popularity of MEG in autism and language research, this technique has increasingly been used to identify epileptogenic foci for the purpose of surgical resection in pediatric patients with intractable epilepsy (RamachandranNair et al., 2007). Most pediatric MEG studies of this condition have suffered from the drawbacks associated with inverse localization based on single dipole forward models. Wolff et al. (2005) used MEG to perform single dipole source estimation for epileptic focus localization in pediatric patients and additionally investigated the correlation between epileptogenic spike location and selective cognitive deficits due to focal interictal epileptic pathology. The regions which were most closely associated with epileptic spiking in this study were the left inferior central sulcus, parieto-occipital sulcus, and calcarine sulcus. Whereas the central sulcus and the lateral aspect of the parieto-occipital sulcus are superficial structures with cortical sources oriented tangentially with respect to the scalp, the medial parieto-occipital sulcus and the calcarine fissure have not only shallow but also deep sources, to which MEG can be less sensitive. Due to this factor as well as to the low focality of MEG LFs in subjects with small heads, these experimental studies highlight the appeal of using distributed source forward models in this population.
It is important to note that the focality of MEG is strongly dependent upon the distance of the MEG sensor to the cortical source. This is a significant factor which is intimately related to the effect of head size especially in subjects with small heads, where achieving optimal head position is difficult to accomplish. In a study involving pediatric patients, Pang et al. (2003) suggested that MEG recordings from patients whose heads are smaller than those of adults can be subject to bilateral temporal source interference, particularly in binaural auditory tasks. Our present findings provide a solid biophysical and methodological basis for the observations of such studies, and additionally offer quantitative assessments of pediatric LFs, which can be taken into account when designing pediatric MEG experiments, selecting inverse models and analyzing inverse solutions. In conclusion, highly accurate, anatomically correct forward modeling of pediatric LFs—as in our paper—can be crucial for the design of experiments and analysis of MEG data acquired from infants, children, and adolescents. In conclusion, the foregoing discussion indicates that, collectively, the results reported in this paper should be informative for the interpretation of MEG recordings from pediatric subjects across a wide age range.
Highlights.
MEG sensor sensitivity and focality vary appreciably with age, head size and brain size
Findings provide a solid biophysical and methodological basis for the interpretation of MEG pediatric studies
Our quantitative assessments of pediatric MEG lead fields should be taken into account when designing and interpreting pediatric MEG experiments
Acknowledgments
Support was provided by a Fellowship from the UCSD Institute for Neural Computation and by an Innovative Research Award from the Kavli Institute for Brain and Mind. We gratefully acknowledge Anders M. Dale, Donald J. Hagler, Eric Halgren, Matthew K. Leonard, Jason S. Sherfey, Katherine E. Travis and John D. Van Horn for useful discussions and contributions on the topic of this paper.
Footnotes
The authors declare no conflict of interest.
References
- Brazzo D, Di Lorenzo G, Bill P, Fasce M, Papalia G, Veggiotti P, et al. Abnormal visual habituation in pediatric photosensitive epilepsy. Clin Neurophysiol. 2011;122:16–20. doi: 10.1016/j.clinph.2010.06.002. [DOI] [PubMed] [Google Scholar]
- Brown TT, Jernigan TL. Brain development during the preschool years. Neuropsychol Rev. 2012;22:313–33. doi: 10.1007/s11065-012-9214-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown TT, Kuperman JM, Chung Y, Erhart M, McCabe C, Hagler DJ, Jr, et al. Neuroanatomical assessment of biological maturity. Curr Biol. 2012;22:1693–8. doi: 10.1016/j.cub.2012.07.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown TT, Kuperman JM, Erhart M, White NS, Roddey JC, Shankaranarayanan A, et al. Prospective motion correction of high-resolution magnetic resonance imaging data in children. Neuroimage. 2010;53:139–45. doi: 10.1016/j.neuroimage.2010.06.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown TT, Petersen SE, Schlaggar BL. Does human functional brain organization shift from diffuse to focal with development? Dev Sci. 2006;9:9–11. doi: 10.1111/j.1467-7687.2005.00455.x. [DOI] [PubMed] [Google Scholar]
- Buchner H, Waberski TD, Fuchs M, Wischmann HA, Wagner M, Drenckhahn R. Comparison of realistically shaped boundary-element and spherical head models in source localization of early somatosensory evoked potentials. Brain Topogr. 1995;8:137–43. doi: 10.1007/BF01199777. [DOI] [PubMed] [Google Scholar]
- Dale AM, Fischl B, Sereno MI. Cortical surface-based analysis - I. Segmentation and surface reconstruction. Neuroimage. 1999;9:179–94. doi: 10.1006/nimg.1998.0395. [DOI] [PubMed] [Google Scholar]
- Dale AM, Halgren E. Spatiotemporal mapping of brain activity by integration of multiple imaging modalities. Curr Opin Neurobiol. 2001;11:202–8. doi: 10.1016/s0959-4388(00)00197-5. [DOI] [PubMed] [Google Scholar]
- Dale AM, Sereno MI. Improved Localization of Cortical Activity by Combining EEG and MEG with MRI Cortical Surface Reconstruction - a Linear-Approach. J Cogn Neurosci. 1993;5:162–76. doi: 10.1162/jocn.1993.5.2.162. [DOI] [PubMed] [Google Scholar]
- Einevoll GT, Pettersen KH, Devor A, Ulbert I, Halgren E, Dale AM. Laminar population analysis: estimating firing rates and evoked synaptic activity from multielectrode recordings in rat barrel cortex. J Neurophysiol. 2007;97:2174–90. doi: 10.1152/jn.00845.2006. [DOI] [PubMed] [Google Scholar]
- Ermer JJ, Mosher JC, Baillet S, Leah RM. Rapidly recomputable EEG forward models for realistic head shapes. Phys Med Biol. 2001;46:1265–81. doi: 10.1088/0031-9155/46/4/324. [DOI] [PubMed] [Google Scholar]
- Gaetz W, Scantlebury N, Widjaja E, Rutka J, Bouffet E, Rockel C, et al. Mapping of the cortical spinal tracts using magnetoencephalography and diffusion tensor tractography in pediatric brain tumor patients. Childs Nerv Syst. 2010;26:1639–45. doi: 10.1007/s00381-010-1189-8. [DOI] [PubMed] [Google Scholar]
- Hamalainen MS, Hari R, Ilmoniemi RJ, Knuutila J, Lounasmaa OV. Magnetoencephalography - Theory, Instrumentation, and Applications to Noninvasive Studies of the Working Human Brain. Rev Mod Phys. 1993;65:413–97. [Google Scholar]
- He W, Brock J, Johnson BW. Face-sensitive brain responses measured from a four year old child with a custom-sized child MEG system. J Neurosci Meth. 2014;222:213–7. doi: 10.1016/j.jneumeth.2013.11.020. [DOI] [PubMed] [Google Scholar]
- Jernigan TL, Tallal P. Late childhood changes in brain morphology observable with MRI. Dev Med Child Neurol. 1990;32:379–85. doi: 10.1111/j.1469-8749.1990.tb16956.x. [DOI] [PubMed] [Google Scholar]
- Jernigan TL, Trauner DA, Hesselink JR, Tallal PA. Maturation of human cerebrum observed in vivo during adolescence. Brain. 1991;114 ( Pt 5):2037–49. doi: 10.1093/brain/114.5.2037. [DOI] [PubMed] [Google Scholar]
- Johnson BW, Crain S, Thornton R, Tesan G, Reid M. Measurement of brain function in pre-school children using a custom sized whole-head MEG sensor array. Clin Neurophysiol. 2010;121:340–9. doi: 10.1016/j.clinph.2009.10.017. [DOI] [PubMed] [Google Scholar]
- Kikuchi M, Shitamichi K, Yoshimura Y, Ueno S, Remijn GB, Hirosawa T, et al. Lateralized theta wave connectivity and language performance in 2- to 5-year-old children. J Neurosci. 2011;31:14984–8. doi: 10.1523/JNEUROSCI.2785-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lima EA, Irimia A, Wikswo JP. The magnetic inverse problem. In: Clarke J, Braginski AI, editors. The SQUID Handbook: Fundamentals and technology of SQUIDS and SQUID systems. Mannheim, Germany: Wiley-VCH; 2004. [Google Scholar]
- Liu LC, Ioannides AA, Muller-Gartner HW. Bi-hemispheric study of single trial MEG signals of the human auditory cortex. Electroencephalogr Clin Neurophysiol. 1998;106:64–78. doi: 10.1016/s0013-4694(97)00068-0. [DOI] [PubMed] [Google Scholar]
- Malmivuo JAV. Distribution of MEG detector sensitivity: an application of reciprocity. Med Biol Eng Comput. 1980;18:365–70. doi: 10.1007/BF02443394. [DOI] [PubMed] [Google Scholar]
- Malmivuo JAV, Plonsey R. Bioelectromagnetism--principles and applications of bioelectric and biomagnetic fields. New York: Oxford University Press; 1995. [Google Scholar]
- Malmivuo JAV, Suihko V, Eskola H. Sensitivity distributions of EEG and MEG measurements. IEEE Trans Biomed Eng. 1997;44:196–208. doi: 10.1109/10.554766. [DOI] [PubMed] [Google Scholar]
- Meijs JWH, Bosch FGC, Peters MJ, Dasilva FHL. On the Magnetic-Field Distribution Generated by a Dipolar Current Source Situated in a Realistically Shaped Compartment Model of the Head. Electroencephalogr Clin Neurophysiol. 1987;66:286–98. doi: 10.1016/0013-4694(87)90078-2. [DOI] [PubMed] [Google Scholar]
- Mosher JC. Efficiently solving the EEG/MEG forward model. Int J Psychophysiol. 1999a;33:39. [Google Scholar]
- Mosher JC. Solutions to EEG/MEG inverse models. Int J Psychophysiol. 1999b;33:39. [Google Scholar]
- Mosher JC, Leahy RM, Lewis PS. EEG and MEG: Forward solutions for inverse methods. IEEE Trans Biomed Eng. 1999a;46:245–59. doi: 10.1109/10.748978. [DOI] [PubMed] [Google Scholar]
- Mosher JC, Leahy RM, Lewis PS. EEG and MEG: forward solutions for inverse problems. IEEE Trans Biomed Eng. 1999b;46:1069–77. doi: 10.1109/10.748978. [DOI] [PubMed] [Google Scholar]
- Murakami S, Hirose A, Okada YC. Contribution of ionic currents to magnetoencephalography (MEG) and electroencephalography (EEG) signals generated by guinea-pig CA3 slices. J Physiol (Lond) 2003;553:975–85. doi: 10.1113/jphysiol.2003.051144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murakami S, Zhang T, Hirose A, Okada YC. Physiological origins of evoked magnetic fields and extra-cellular field potentials produced by guinea-pig CA3 hippocampal slices. J Physiol (Lond) 2002;544:237–51. doi: 10.1113/jphysiol.2002.027094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pang EW, Gaetz W, Otsubo H, Chuang S, Cheyne D. Localization of auditory N1 in children using MEG: source modeling issues. Int J Psychophysiol. 2003;51:27–35. doi: 10.1016/s0167-8760(03)00150-8. [DOI] [PubMed] [Google Scholar]
- RamachandranNair R, Otsubo H, Shroff MM, Ochi A, Weiss SK, Rutka JT, et al. MEG predicts outcome following surgery for intractable epilepsy in children with normal or nonfocal MRI findings. Epilepsia. 2007;48:149–57. doi: 10.1111/j.1528-1167.2006.00901.x. [DOI] [PubMed] [Google Scholar]
- Rezaie R, Simos PG, Fletcher JM, Juranek J, Cirino PT, Li Z, et al. The timing and strength of regional brain activation associated with word recognition in children with reading difficulties. Front Hum Neurosci. 2011;5:45. doi: 10.3389/fnhum.2011.00045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rich BA, Carver FW, Holroyd T, Rosen HR, Mendoza JK, Cornwell BR, et al. Different neural pathways to negative affect in youth with pediatric bipolar disorder and severe mood dysregulation. J Psychiatr Res. 2011;45:1283–1294. doi: 10.1016/j.jpsychires.2011.04.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rush S, Driscoll DA. EEG electrode sensitivity - an application of reciprocity. IEEE Trans Biomed Eng. 1969;16:15–22. doi: 10.1109/tbme.1969.4502598. [DOI] [PubMed] [Google Scholar]
- Seki Y, Kandori A. Two-dimensional gradiometer. Jpn J Appl Phys. 2007;46:3397–401. [Google Scholar]
- Stok CJ, Meijs JWH, Peters MJ, Rutten WLC. Model Evaluation Using Electroencephalography and Magnetoencephalography. Acta Otolaryngol (Stockh) 1986;102:5–10. doi: 10.3109/00016488609108878. [DOI] [PubMed] [Google Scholar]
- Tripp J. Physical concepts and mathematical models. In: Williamson SJ, Romani GL, Kaufman L, Modena I, editors. Biomagnetism: an interdisciplinary approach. New York: Plenum; 1983. pp. 101–39. [Google Scholar]
- Uzunbajakau SA, Rijpma AP, ter Brake HJM, Peters MJ. Optimization of a third-order gradiometer for operation in unshielded environments. Ieee Trans Appl Supercond. 2005;15:3879–85. [Google Scholar]
- Wehner DT, Hamalainen MS, Mody M, Ahlfors SP. Head movements of children in MEG: quantification, effects on source estimation, and compensation. Neuroimage. 2008;40:541–50. doi: 10.1016/j.neuroimage.2007.12.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolff M, Weiskopf N, Serra E, Preissl H, Birbaumer N, Kraegeloh-Mann I. Benign partial epilepsy in childhood: selective cognitive deficits are related to the location of focal spikes determined by combined EEG/MEG. Epilepsia. 2005;46:1661–7. doi: 10.1111/j.1528-1167.2005.00255.x. [DOI] [PubMed] [Google Scholar]
- Yoshimura Y, Kikuchi M, Shitamichi K, Ueno S, Munesue T, Ono Y, et al. Atypical brain lateralisation in the auditory cortex and language performance in 3- to 7-year-old children with high-functioning autism spectrum disorder: a child-customised magnetoencephalography (MEG) study. Mol Autism. 2013;4:38. doi: 10.1186/2040-2392-4-38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yvert B, Bertrand O, Echallier JF, Pernier J. Improved dipole localization using local mesh refinement of realistic head geometries: an EEG simulation study. Electroencephalogr Clin Neurophysiol. 1996:99. doi: 10.1016/0921-884x(96)95691-x. [DOI] [PubMed] [Google Scholar]
- Yvert B, Crouzeix-Cheylus A, Pernier J. Fast realistic modeling in bioelectromagnetism using lead-field interpolation. Hum Brain Mapp. 2001;14:48–63. doi: 10.1002/hbm.1041. [DOI] [PMC free article] [PubMed] [Google Scholar]