A model of social influence on body mass index

Abstract

In this paper, we develop an agent-based model of social influence on body weight. The model's assumptions are grounded in theory and evidence from physiology, social psychology, and behavioral science, and its outcomes are tested against longitudinal data from American youth. We discuss the implementation of the model, the insights it generates, and its implications for public health policy. By explicating a well-grounded dynamic mechanism, our analysis helps clarify important dependencies for both efforts to leverage social influence for obesity intervention and efforts to interpret clustering of BMI in networks.

Introduction

Obesity is a growing global epidemic and represents a pressing public health challenge. As of 2010, mean body mass index (BMI) in the United States was 28.7 among adult males and females. ¹ Age-adjusted prevalence of obesity was 35.5% for adult males and 35.8% for adult females, while obesity prevalence among American children and adolescents was 16.9%.² Globally, an estimated 1.46 billion adults were overweight in 2008, including 502 million who were obese.³ Health risks associated with overweight and obesity include heart disease, hypertension, type 2 diabetes, hypercholesterolemia, stroke, asthma, and arthritis, making the obesity epidemic a major contributor to rising healthcare costs.^4–6

The determinants of obesity are complex, with interaction between multiple pathways representing a challenge both for understanding the current epidemic and for preventing further increases in obesity.^7–8 Our focus here is on social influence, which substantial evidence now supports as one important pathway in the emergence and persistence of obesity,^9–14 potentially through multiple channels.¹⁵ This work suggests that social influence may not only help to explain the persistence of obesity, but could provide a critical policy lever to combat it. However, the identification of specific dynamic mechanisms underlying social influence on obesity remains an important gap in this literature, and is the focus of a growing body of research.^9,16–17 Our aim in this paper is to help address this gap by developing a better theoretical understanding of how one particular mechanism of social influence—body type norms—can independently support the development and persistence of obesity. The model offers guidance for future empirical work in this area, as well as the potential to facilitate policy and intervention design.

Earlier work¹⁸ developed an initial hypothesis for the mechanism underlying social influence through body weight norms, known as “follow the average” (FTA). This hypothesis built on literature from psychology¹⁹ and is consistent with empirical evidence regarding body image norms' effect on obesity.^20–22 The mathematical model developed in that paper demonstrated how a simple desire on the part of individual actors to conform to the average weight of their peers could in fact produce increases in BMI at the population level, given certain key assumptions. While recognizing the likelihood of multiple interacting drivers of obesity, the paper hypothesized that such a process could provide a partial explanation for upward trends in BMI observed empirically. This mechanism—individual conformity that produces upward shifts in population BMI—will be our point of departure here.

In this paper, we revisit the FTA hypothesis, re-examining each of its key assumptions one by one and replacing them where necessary with empirically informed assumptions. We test whether the central insight from the original model holds and explore what new insights can be gained from a more detailed model of social influence. We then apply the model to a large longitudinal dataset to test its potential explanatory power and, finally, we explore potential policy implications.

Initial model

Our methodological approach is agent-based modeling^8,23–25 a type of computational micro-simulation particularly effective for the study of dynamic interplay between individual behavior and population-level outcomes. In an agent-based model, each individual actor (or agent) is modeled individually with characteristics and adaptive rules that govern interaction with other actors and with the environment. These decentralized interactions generate population-level dynamics, which can in turn feed back to shape individual trajectories. We begin here by constructing an agent-based model of the FTA process. The agent-based model (ABM) approach will provide the flexibility needed to extend the model later, but we first ensure that it can replicate results from the analytical model given equivalent assumptions.

In this initial simulation, each individual agent possesses one property: BMI. For each time period (tick), every agent calculates the mean BMI of all other agents in the model. If an agent's own BMI differs from the mean, he/she adjusts it upward or downward by a discrete increment δ to approach the population mean. This process continues until the population mean reaches equilibrium.^a

As Figure 1 illustrates, this base case–simulation model replicates the central result from the analytical FTA model. All agents converge toward the population mean BMI, but in the process drive the mean BMI upward from its starting point (as long as the initial distribution is right skewed). This occurs because the initial population contains more agents with BMI below the mean than above the mean. Given a constant adjustment rate, the average BMI becomes a moving target, shifting upward even as all individuals converge toward it. One limitation of this initial model is that the same process which produces upward shift in mean BMI also collapses variance in BMI (e.g., all agents end with BMI at or very near the population mean).

Figure 1. Mean BMI over time produced by the follow the average (FTA) agent-based model.

The original FTA model (and our base case simulation) makes four key assumptions, which in the following sections we will revisit and modify as necessary: (1)individuals' ideal BMI is the mean BMI of peers, which can be both observed and precisely calculated by each individual; (2) agents are only satisfied when their BMI closely matches their ideal; (3) the entire population serves as each agent's peer comparison set; and (4) BMI can be directly manipulated by agents. Below, we take these assumptions in turn, refining the simulation model to better reflect empirical evidence (both in assumptions and output).

Body image ideals

The key conceptual assumption in the base model is that individuals desire to conform to (and are able to calculate) the mean observed BMI of their peers. Some general evidence in public health and psychology supports this assumption. For example, population-survey evidence from the United States finds that norms about appropriate body weight have trended upward over the past 25 years, concurrent with a similar shift in population body weight.²² A study of Canadian schoolchildren finds that subjects with more overweight parents or peers are more likely to perceive themselves as underweight.²⁶ Additionally, experimental studies at the individual level from cognitive science suggest that humans can indeed calculate the mean size of sets of physical objects with considerable speed and accuracy.^27–31

To build additional confidence in this assumption in the specific context of weight norms, we analyzed data from Quebec En Forme (QeF), an extensive survey of 13,746 students aged 10–17 from the Canadian province of Quebec.³² There are 181 schools in the dataset, and information was collected on students' actual body image, ideal body image, weight, nutrition, physical activity levels, and attempts to gain or lose weight in the previous year. Actual and ideal body images are assessed using a nine-point pictographic scale (one is severely underweight, nine severely overweight, and five a healthy weight).³³

For the purposes of our analysis, we define an individual's reference network as the set of children in the same school, grade, and gender as the individual. This definition is consistent with observed data on childhood friendship networks,^34–35 and may serve as an appropriate comparison group for children's development of body image norms. Table 1 reports the results from regressing the children's ideal body image on mean actual body image of other children within their network. The mean body image of children within one's network had a significant effect on self-reported ideal body image, controlling for one's own body image, age, and gender. These findings are consistent with our hypothesis that individuals calculate their ideal body image based on the mean BMI of their peers.

Table 1. Regression coefficients and standard deviations, estimating Ideal Body Image.

	(1)	(2)	(3)
	{School, sex, grade}	{School, sex}	{Sex, grade}
Network body image	0.053 (0.018)*	0.037 (0.029)	0.038 (0.082)
Actual body image	0.373 (0.006)*	0.373 (0.006)*	0.374 (0.006)*
Age	0.212 (0.060)*	0.226 (0.060)*	0.218 (0.065)*
Age-squared	−0.006 (0.002)*	−0.007 (0.002)*	−0.006 (0.002)*
Male	1.05 (0.024)*	1.07 (0.032)*	1.07 (0.080)*
Observations	13638	13638	13638
R-squared	0.494	0.494	0.494

Note: There are three specifications of peer networks: (1) children of the same grade and gender within one's school, (2) children of the same gender within one's school, and (3) children of the same grade and gender throughout Quebec. Only specification (1) yields a significant effect of network mean BMI on ideal body image, suggesting that these local networks have an effect on body type norms whereas more diffuse networks do not.

^*Coefficients marked with are statistically significant.

Although limited to self-reporting, these results add support to the assumption that individuals desire to conform to the mean BMI of their peers. Nevertheless, we would like the model to incorporate the possibility that individuals may calculate this mean with some error, or be satisfied with a BMI within some distance of their ideal. In the next section, we introduce this type of satisficing behavior into the model and explore its impact on dynamics of BMI change.

Satisficing rule

To remain consistent with the best available evidence, the model must account for some misperception of BMI and/or falloff in motivation to conform within a certain proximity of the true average. For instance, studies of dieting behavior among U.S. adults suggest some level of error in weight perception^26,36 and that likelihood of dieting increases with body weight.³⁷ Whether driven by cognitive bias, by information-processing limitations, or by indifference to small discrepancies, the implication is that smaller deviations from the average BMI of peers may not yield the same motivation to adjust weight status as larger deviations.

Examining the data from QeF we find that even when respondents report that their actual and ideal body images are unequal, this does not always translate into an effort to gain or lose weight.

To incorporate this more realistic behavior into the model, we initialize each agent with a satisficing rule. Under this rule, an agent j will attempt to gain or lose weight only if the difference between his or her actual BMI (BMI_j) and ideal BMI (I_j) is greater than some specified magnitude (ε). We then define agent j's satisfaction interval (SI) as any body weight in the interval [I_j − ε, I_j + ε]. Thus the agent's decision rule becomes: “If BMI_j > I_j + ε, lose weight; if BMI_j < I_j & minus; ε, gain weight. While BMI_j is within SI_j, make no adjustments to weight.”

Introducing satisficing behavior into agent decision making can have an important effect on the model's dynamics. As illustrated in Figures 3 and 4, increasing the size of the ideal interval dampens and can even reverse the trend towards increasing population BMI when the initial distribution is skewed. Figure 3 reports mean BMI generated by the model over time, and Figure 4 shows the range of equilibrium outcomes (mean BMI) that can be obtained by varying the parameter ε.

Figure 3.

Mean BMI over time produced by model with satisficing rule (ε = 0.5).

Figure 4.

Model dynamics with satisficing rule (initial skew = 10, initial mean BMI = 19.84). Each data point represents the equilibrium mean BMI produced from a single simulation run. Between-run variation (not shown) is extremely low for this configuration of the model.

The intuition behind these results depends on the interplay between individual behavior and population norms. Increasing the ideal interval makes it more likely that individual agents will be satisfied with their current state, and refrain from changing their BMI. As SI increases from zero, this shift in individual behavior dampens the increase in population BMI. If SI increases sufficiently, the lighter BMI agents become satisfied with their state before the heavier agents, resulting in an overall population decrease in BMI. The point at which this inflection occurs depends crucially on the comparison set that agents use for calculating their ideal BMI, a subject to which we turn in the next section.

In addition, the distribution of BMI at equilibrium generated with SI is bimodal—rather than agents converging to a single BMI as they do in the base case, they converge to one of two BMI values within 2ε of one another. Like complete convergence, this limiting distribution is not empirically plausible. In the next section, we will relax the assumption that agents compare themselves to all other agents in the population, and introduce localized networks—allowing for greater heterogeneity of BMI in equilibrium.

Networks

In the base case FTA model, each agent's comparison set consists of all the other agents in the population. This assumption may be appropriate in some contexts (like the population within each individual school in the QeF survey), but substantial literature in social science suggests that network structure is likely to shape social norm dynamics over larger populations.^38–41 In the context of obesity, another dynamic process may also be at work—agents may select their friends based on homophily,^10,42 shaping the resulting network reference set. In this section, we explore the impact of varying network topologies on the model's dynamics.

We begin by moving from a mean-field whole-population comparison set to a Moore neighborhood structure, defined as a network in which agents are located on a grid and use their eight neighbors on the grid as their comparison set. This simple form of clustered network structure yields some important differences in outcome, as shown in Figure 5. As opposed to the mean field variant of the model, the model with local social networks sustains heterogeneous BMI at equilibrium. We also see that the FTA mechanism itself can result in clustering of BMI among subpopulations—without needing to explicitly incorporate a homophily process.

Figure 5.

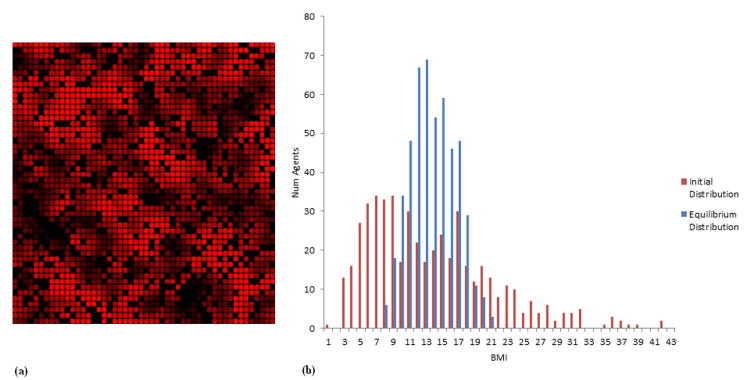
(a) Top-down view of agent population shaded by individual BMI at equilibrium (higher BMI a lighter red). Illustrates the spatial clustering that occurs when there is local network structure (each agent's comparison group consists of its immediate neighbors) in x–y space. (b) Histogram of initial and final distribution of BMI from the model with Moore space.

A random network structure (i.e., one in which each agent has a set number of friends, but has an equal probability of being friends with anyone in the network) results in outcomes similar to those with Moore neighborhoods, though clustering is less pronounced in equilibrium. Because peer connections in this network are random, there are no local clusters isolated from the rest of the population, which dampens clustering.

While network structure produces important variance in local outcomes, Figure 6 shows that neither Moore nor random network structure necessarily undermines the central qualitative results from the previous model variants: a secular increase in population BMI can result from a process of local conformity, and this increase can be dampened (or reversed) by changes in SI.

Figure 6.

Equilibrium BMI by network configuration and ideal interval. Each data point represents average of mean BMI across 11 simulation runs (with error bars representing standard deviation).

Closer examination of network structure also uncovers an important interaction effect between the assumed SI and the assumed network form. If the network is initially clustered by BMI, the population-level outcome generated by the simulation can vary significantly. To test the effect of such clustering, at the beginning of the simulation we allow agents to randomly rewire each friendship tie, choosing a new friend whose BMI is closer to their own. The results show that such clustering dampens the upward shift in population BMI, much like an increase in the size of the satisfaction interval (SI). The impact of clustering on equilibrium mean BMI depends in part on SI value (Fig. 6).

All of the models presented thus far assume that agents can directly manipulate their BMI, an assumption that is unrealistic in practice. In the next section, we refine the model by incorporating sophisticated metabolic models into our agents.

Physiology

Direct manipulation of BMI is not a realistic model of weight management. Individuals seeking to adjust their BMI in the real world do so by adjusting their caloric intake or energy expenditure. To replicate this in our agent-based simulation, we incorporate a well-validated model of physiology⁴³ into each agent, which translates caloric intake choices into weight change. Resting energy expenditure of an agent is calculated using the Mifflin-Jeor regression equations,⁴⁴ and the calorie surplus or deficit is then translated into weight change through a series of differential equations accounting for lean/fat mass composition, glycogen dynamics, and physical activity.^b We use the Runge–Kutta method to approximate discrete time solutions in the agent-based context.⁴⁵

Agents are assumed to be reasonably accurate at calculating the level of calorie consumption needed to maintain their body weight, and when they are not trying to gain or lose weight, will consume calories equal to that equilibrium rate. When attempting to gain or lose weight, agents add or subtract some amount (C) from their maintenance calories, and maintain that level of caloric intake until they reach a weight within their ideal interval. To gauge the effect of this parameter on BMI change, we simulate the model varying C between 50 and 500 calories in 50-calorie increments. This range of dieting rules is well supported by the literature on dieting and weight management.^46–49

Drawing direct comparisons between the physiological and non-physiological instances of the model is difficult because of the way physiology affects the adjustment increment. (Adjustment is non-constant in the physiological case. An agent attempting to gain weight, for instance, does so less effectively over time with a fixed calorie surplus, a consequence of increasing resting metabolic rate.) However, all four of the principal qualitative findings from the model with direct adjustment presented above are replicated in the model with physiology: local conformity can produce population BMI increases, increasing agents' SI dampens the mean BMI increase, changing network topology affects the shape and dispersion of the final distribution but not its mean, and an initially clustered network yields a dampened BMI increase with magnitude depending on SI.

Incorporating this type of physiological model allows us to concretely represent the time scales on which changes in BMI occur within the model. This addition is crucial for the empirical exercise in the following section, matching the dynamics of the model to longitudinal BMI data.

Empirical application

To test the extent to which the model can offer an explanatory mechanism for real-world BMI changes, we calibrated the simulation to fit longitudinal data from a survey of American youth. The NLSY97⁵⁰ is an nationally representative American sample of roughly 9,000 individuals, 12 to 16 years old as of December 1996. The data is longitudinal, collected on an annual basis over a four-year period, and includes data on BMI, census region (Northeast, South, Midwest, and West), sex, age, and desire to gain or lose weight.

Our aim in this section is to demonstrate that the mechanism outlined in this paper can generate, over plausible time scales, the increases in BMI observed in real-world data. We do not contend that this is the only such mechanism that can do so, or that other mechanisms are not at work, but rather that FTA exhibits “generative sufficiency.”²⁴ Additionally, though our empirical exercise is performed on data from American adolescents, the model itself is not tied to this specific demographic, so the results obtained here should be generalizable to any population that exhibits local conformity in BMI. We assume, as in the QeF exercise, that males compare themselves only to males, and females only to females. Both make comparisons only within their reported census region, and we model the network structure as a Moore neighborhood. Keeping SI fixed at 0.5, we then vary calorie surplus and calorie deficit in increments of 10 to determine which combination of parameters yields the best fit for the observed time-series data (by minimizing mean squared error between the mean BMI produced by the model and the data). Figure 7 illustrates the mean BMI trajectory produced by the model at given these best fit parameters.

Figure 7.

Empirically calibrated simulation results (compared to NLSY mean BMI by census region and gender). Simulation results represent best-fit individual runs (minimized sum of squared error in each year). Between-run variance (not shown) is low.

The results suggest that the social influence model developed here is sufficient to generate observed longitudinal changes in BMI with a plausible set of estimated parameters.

Discussion

Formal or computational models can contribute insights to a field in multiple ways. For example, models can leverage existing evidence to develop internally consistent hypotheses about mechanisms underlying an observed outcome, inform empirical inquiry by identifying concepts for which new or improved measures are needed, develop theory to shape appropriate inference from observation, or provide insights that inform policy and intervention design.

Here, we present a model of social influence on body weight that serves a number of these goals. We extend a previous theoretical model, using existing literature and new empirical analyses to explicate a well-grounded mechanism that offers explanatory insight into important features of the obesity epidemic (upward population BMI trend and clustering in networks). Our simulation analysis uncovers a conceptual construct (the satisfaction interval) that can strongly shape dynamics in the model, and for which better and more accurate empirical measurement is needed. We show that a commonly observed empirical pattern (BMI clustering in networks) need not be driven by a single linked dynamic process (homophily), but can be generated by a less obviously related process (local conformity). Our results also show how the impact of clustering (and thus interpretation of its significance) can depend on the conceptual construct of satisfaction interval. Finally, while our model is not aimed at exploring any specific policy or intervention regime, we show that the same dynamic co-evolution of individual behavior and social norms that produces an upward shift in population BMI can potentially be harnessed to instead yield downward pressure on BMI. However, the richness of the dynamic interplay we demonstrate in our model suggests that efforts to design interventions to shape obesity norms (or to evaluate such interventions) may require sufficient consideration of dependencies in the dynamics of social norm change.

Current evidence suggests that multiple distinct pathways of social influence can drive changes in obesity, but both empirical analysis and intervention design in this area have been hampered by a lack of sufficiently rich and explicit models of the underlying mechanisms of social influence. While in no way comprehensive, the model presented above addresses this gap by providing a clear explication of one mechanism, exploring the implications of the dynamics it produces, and testing its explanatory power. There is significant potential for future work to connect this mechanistic model with other factors influencing obesity, to gain a more complete understanding of the policy levers necessary to ameliorate the epidemic. Similar explication of other mechanisms of social influence is needed to allow more comprehensive insight into the role of social influence in obesity.

Figure 2.

Percent of respondents in QeF survey who reported an attempt to gain or lose weight over the previous year, by distance from ideal body image (1 through 9 from pictographic scale).