Abstract
Motivation: Disease progression is driven by dynamic changes in both the activity and connectivity of molecular pathways. Understanding these dynamic events is critical for disease prognosis and effective treatment. Compared with activity dynamics, connectivity dynamics is poorly explored.
Results: We describe the M-module algorithm to identify gene modules with common members but varied connectivity across multiple gene co-expression networks (aka M-modules). We introduce a novel metric to capture the connectivity dynamics of an entire M-module. We find that M-modules with dynamic connectivity have distinct topological and biochemical properties compared with static M-modules and hub genes. We demonstrate that incorporation of module connectivity dynamics significantly improves disease stage prediction. We identify different sets of M-modules that are important for specific disease stage transitions and offer new insights into the molecular events underlying disease progression. Besides modeling disease progression, the algorithm and metric introduced here are broadly applicable to modeling dynamics of molecular pathways.
Availability and implementation: M-module is implemented in R. The source code is freely available at http://www.healthcare.uiowa.edu/labs/tan/M-module.zip.
Contact: kai-tan@uiowa.edu
Supplementary information: Supplementary data are available at Bioinformatics online.
1 INTRODUCTION
Complex diseases like cancer involve a continuum of molecular events that starts with early initiation events through progression and catastrophic end-stage events. Analyzing and understanding disease-stage-specific molecular events are critical for understanding disease etiology and development of therapeutic interventions. Network biology has proven to be a powerful tool for representing and analyzing complex molecular networks. Previously, several lines of investigations have leveraged dynamic changes in molecular networks to predict disease outcomes. Focusing on hub genes in human protein interactome, several groups have shown that they can be categorized into different types based on topological measures such as degree and modularity (de Lichtenberg et al., 2005; Han et al., 2004). It was further demonstrated that such topological features of hub genes can be used to improve the prognosis of breast cancer patients (Taylor et al., 2009). Chuang et al. used a different strategy by examining the differentially expressed subnetworks (instead of hub genes) between two cohorts of breast cancer patients (Chuang et al., 2007). They demonstrated that subnetworks with differential expression levels are effective markers for breast cancer metastasis. Besides nodal changes in a molecular network, several studies have shown that gene/protein connectivity is also highly dynamic during disease development and stress response. Goh et al. (2007) showed that there is a higher degree of physical connectivity between proteins whose genes are mutated in the same disease state. Zhong et al. (2009) found a large fraction of cases in which a single gene is linked to multiple disorders via distinct interactions, which they call edgetic perturbations. Bandyopadhyay et al. (2010) discovered widespread changes in gene–gene interactions among yeast kinases, phosphatases and transcription factors as the cell responds to DNA damage.
A common theme in these pioneering studies is the dichotomization of the disease development, either for the onset or the severity of the disease. Those methods analyze each condition individually to determine which hub genes, subnetworks or edge sets are significantly associated with one of the two conditions, instead of collectively modeling and analyzing omics data from patient samples as a single continuum. This inability to account for dependence among pathways at different time points limits our ability to observe changes at a pathway level during disease progression.
Computational methods for joint analysis of multiple networks have been developed before. They fall into two categories in terms of their purposes: (i) studying conservation of multiple protein–protein interaction networks across species (Kelley et al., 2003; Koyuturk et al., 2004), and (ii) functional gene-interaction modules across multiple networks of the same species under various conditions (Hu et al., 2005; Huang et al., 2007; Li et al., 2011; Narayanan et al., 2010). Neither approach has been applied to study subnetwork dynamics during disease progression. To address this critical gap, we have developed a general framework to reveal subnetwork dynamics by joint analysis of multiple gene co-expression networks during disease progression. We introduce a novel measure to capture changes in the connectivity of a subnetwork. Using breast cancer as an example, we demonstrate that adding information about network connectivity dynamics significantly improves the classification accuracy of multiple stages of the disease.
2 METHODS
Mathematical model for M-module
Given M gene networks with the same node set but different edge sets, , they can be represented by a 3D matrix , where denotes the weight on the edge E(i,j) in network Gk. An M-module, C, is defined as a set of genes whose connectivity within them is stronger than random expectation across all M networks under consideration. We introduce a graph entropy-based measure to quantify the connectivity of an M-module in multiple networks. For a given vertex , let denote the total weight between vertex v and other vertices in the M-module C in the network Gk, i.e. . Similarly, let denote the weight between v and vertices outside of the M-module, C. We defined the connectivity of vertex v to C as follows:
| (1) |
where . The motivation for using graph entropy is that it quantifies the skewness of in-module connectivity versus out-module connectivity. However, unlike other measures such as modularity (Newman, 2006a), entropy makes full use of the probability distribution of a graph, which avoid the limitations of modularity or graph density including the resolution limit (Fortunato and Barthelemy, 2007). The connectivity between v and the M-module C across all networks is given as follows:
| (2) |
We expect that each component subnetwork of an M-module is well connected in each network. Thus, the overall connectivity of M-module C among all nodes and across all networks is as follows:
| (3) |
H(C) is used as the score of the candidate M-module. To search for an M-module C, we minimize the entropy value of C, i.e. . Given this objective function, we formulate the M-module identification problem as a combinatorial optimization problem. Denote as the group of M-modules being sought where τ is the number of M-modules. An index matrix is constructed to represent module membership such that columns correspond to M-modules and rows correspond to genes. Each element denotes the i-th gene that belongs to the j-th M-module and otherwise 0. The overall objective function for finding M-module is defined as follows:
| (4) |
It is NP-hard to minimize the scores of all component modules of an M-module across the networks. Relaxing the above objective, we obtain the final overall objective function as follows:
| (5) |
A heuristic algorithm for M-module search
The objective function in Equation (4) is an integer programming problem of finding a binary combinatorial for the index matrix. It is an NP-hard problem (Li et al., 2011). We introduce a heuristic algorithm to solve this problem. The algorithm consists of three major steps: seed selection; M-module search by seed expansion and entropy minimization; and refinement of M-modules.
Step 1: Seed selection
We first rank each gene in a single network and then combine ranks across multiple networks to obtain the final rank for each gene.
For each network with an adjacency matrix , we wish to construct a function such that g(v) denotes the importance of vertex v in the corresponding network. We first compute the degree-normalized weighted adjacency matrix where D is diagonal matrix with element . The importance of the vertex could be measured by two features: (i) its topological feature in the network and (ii) previous knowledge about its contribution to the phenotype under study. Many essential genes have been shown to have unique topological features such as high degree and centrality in gene networks (Goh et al., 2007; Taylor et al., 2009). Likewise, genetic mutations have been observed to concentrate on certain pathways for a given disease (Vogelstein et al., 2013), and this observation can be leveraged to identify disease genes (Masica and Karchin, 2011; Vanunu et al., 2010). Given these two considerations, we used the following function to rank genes. A similar approach was also used in (Vanunu et al., 2010):
| (6) |
where captures the topological importance of nodes and Y is a vector denoting the prior information for the nodes. The parameter α is a value between 0 and 1 that controls the relative contributions by topological importance and prior knowledge. The topological importance of node v is defined as , where is the set of neighbors in . This means the importance of a node depends on the number of its neighbors, strength of connection and importance of its neighbors. The exact solution to Equation (6) is , indicating that how the importance of nodes is associated with network topology and prior information. However, computing the matrix inversion is time-consuming. Here, we use the following fast iteration-based algorithm introduced by Zhou et al. (2004)
| (7) |
where t denotes the iteration, and .
To determine the prior information of vector Y, we use gene mutation information from the COSMIC database (Pleasance et al., 2010). For each gene, we calculate the number of independent biological samples in which the gene was mutated. Based on the mutation frequencies of all genes associated with breast cancer, we estimated the probability density function using a kernel density function. The fitted function is in the form
where x is the number of samples in which a gene was observed to be mutated, and a and b are breast cancer-specific parameters (Supplementary Fig. S1). Next, for each mutated gene u observed in k samples, the prior probability of mutation is calculated as follows:
For each gene, after obtaining its ranks in all individual networks, denoted as , we calculate a z-score for each rank . Then we obtain the rank for that gene across all networks by averaging the z-scores across all networks.
In this article, we selected the top 5% of the genes in the network as seeds because the number of significant M-modules does not change with higher number of seeds (Supplementary Fig. S1).
Step 2: M-module search by seed expansion and entropy minimization
For a given seed v ∈ V, we treat it as a M-module C = {v}. For each vertex u in its neighborhood in all networks, we define N(v) = UiNi(v) where Ni(v) is the neighbor set in Gi as the candidate for C. For each u ∈ N(v), we calculate the entropy decrease between the new M-module C′ = CU{u} and C, i.e. ΔH(C′,C) = H(C) − H(C′). ΔH(C′,C) > 0 indicates that addition of vertex u improves the connectivity of the former M-module C. The vertex u whose addition maximizes ΔH is added to C. If there is more than one vertex that can be included at each step, we randomly select one. The expansion step terminates until no additional vertex can reduce the entropy of the evolving M-module further.
Step 3: Refinement of M-modules
M-modules whose sizes are smaller than five are removed. If two M-modules have a Jaccard index of 0.5, they are merged.
Statistical significance of M-modules
The statistical significance of M-modules is computed based on the null score distribution of M-modules generated using randomized networks. Each network is completely randomized 100 times by degree-preserved edge shuffling. To construct the null distribution for M-module scores, we perform M-module search on the randomized networks. Using the null distribution, the empirical P-value of an M-module is calculated as the probability of the module having the observed score or smaller by chance. P-values are corrected for multiple testing using the method of Benjamini–Hochberg (Benjamini and Hochberg, 1995). An adjusted P-value of 0.05 is considered as significant.
Module connectivity dynamic score
To quantify the connectivity dynamics of an M-module, we compare adjacent component subnetworks of an M-module across disease stages. Specifically, given an M-module C whose weighted adjacency matrices of the corresponding induced subgraphs are , the change in connectivity between two adjacent component modules is defined as the l2 norm of the matrix subtraction normalized by the number of genes in the M-module,
| (8) |
where is the matrix l2 norm. The module connectivity dynamic score (MCDS) of an M-module is defined as the average of connectivity changes across all adjacent stages:
| (9) |
The statistical significance of dynamic M-modules is computed in a similar way as that for M-modules. Briefly, we first calculate the null distribution for M-module dynamic scores based on randomized networks. The empirical P-value of an M-module dynamic score is calculated using the null distribution. P-values are corrected for multiple testing using the method of Benjamini–Hochberg (Benjamini and Hochberg, 1995). An adjusted P-value of 0.05 is considered as significant.
Construction of features for Support Vector Machine classifier
Given a module identified by the different algorithms, following the strategy by Chuang et al. (2007), we normalize the expression level of each gene across patient samples and across genes in a sample using z-score transformation. The final z-score is denoted by Zij. For each patient sample J, the activity score of the Sth M-module CS is defined as follows:
| (10) |
where is the cardinality of CS. For each patient sample, a feature vector was constructed as where m is the number of modules used as features. For a given M-module CS, the weighted M-module feature value is defined as the product of its activity score and connectivity dynamics, i.e.
| (11) |
where denotes the connectivity dynamic of module CS, l is the number of samples. For differentially expressed genes and random genes, each gene is a feature and the number of genes in each set equals the total number of M-modules.
3 RESULTS
The M-module algorithm for identifying shared co-expression modules across multiple networks
To examine the dynamics of pathway connectivity, we developed a novel algorithm, M-module, to identify shared subnetworks present in multiple gene co-expression networks. Here we term these subnetworks M-modules. They have the same set of member genes but potentially different connectivity among the members. Using M-modules, we can quantify the dynamic changes in module connectivity. The core M-module algorithm consists of three major components: seed selection, M-module search by seed expansion and graph entropy minimization and refinement of M-modules (Fig. 1).
Fig. 1.
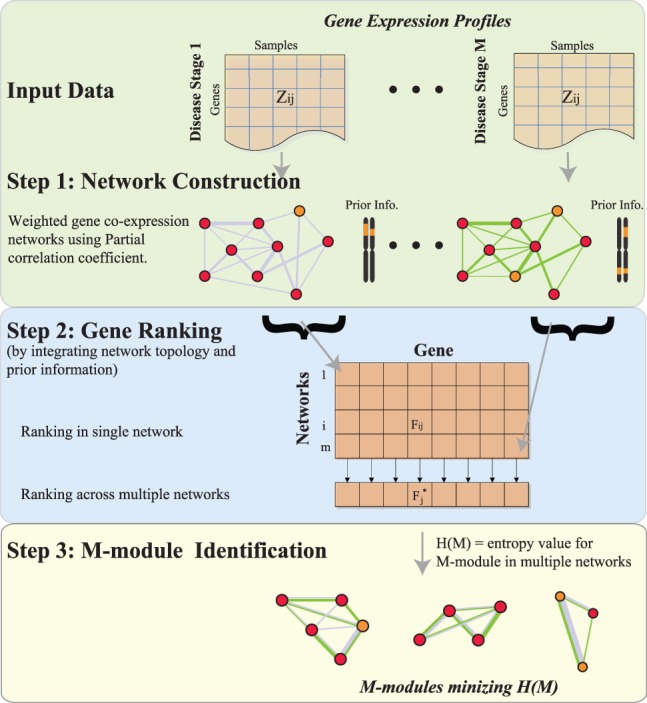
Overview of the M-module framework. The algorithm consists of three key components: construction of multiple co-expression networks, seed selection and M-module search. First-order partial Pearson correlation coefficient is used as edge weight to construct the gene co-expression network. For each network, we integrate topological and gene mutation information to rank genes via network propagation. The overall ranking of a gene across multiple networks is computed by considering rankings in all networks. The top genes are used as seeds and a graph-entropy–based function is used to guide the M-module search
M-module takes as inputs multiple edge-weighted co-expression networks and a set of prior probabilities representing the mutation probability of a gene based on experimental data. Along with network topological features, the prior probabilities are used to rank and select seeds (See Supplementary Methods). We transform the M-module search problem into a minimum entropy problem by introducing a graph-entropy–based objective function for M-modules. Finding M-modules whose entropy values are all minimal is an NP-hard problem (Li et al., 2011). We therefore developed a greedy algorithm for M-module search based on seed expansion. Empirical P-values of candidate M-modules are determined by using randomized networks. The software implementing the algorithm is freely available on request.
Performance benchmarking of M-module on simulated and real networks
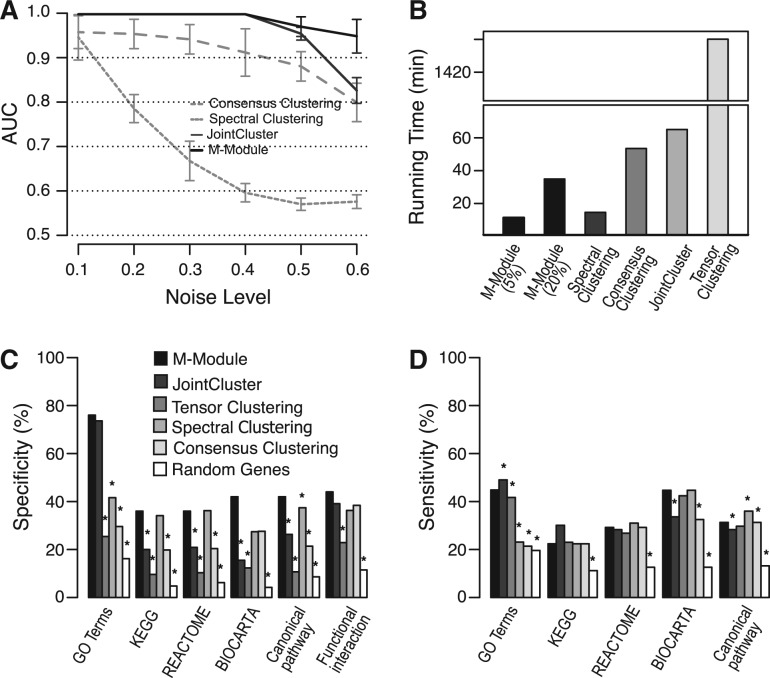
To characterize the performance of the M-module algorithm, we first used simulated networks in which the module membership for each node is known (see Supplementary Methods). We also introduced various levels of noise into the networks, which is controlled by the ratio of intra-module edges to inter-module edges for each node. We compared M-module with several state-of-the-art algorithms, including JointCluster (Narayanan et al., 2010), Tensor Clustering (Li et al., 2011), Consensus Clustering (Lancichinetti and Fortunato, 2012) and Spectral Clustering (Newman, 2006b). For brevity, we abbreviated these algorithms as JC, TC, CC and SC. We used the receiver operating characteristic (ROC) curve to evaluate the performance (see Supplementary Methods). When the noise level is <0.5, both JC and M-module have the best performance. However, unlike JC, M-module maintains its superior performance over other methods when network noise is >0.5 [P = 0.01, ROC test by (DeLong et al., 1988)]. Because of the low node coverage (<10%) and high overlap between discovered modules (>70%), performance of TC is not included in Figure 2A.
Fig. 2.
Performance assessment of M-module using simulated and real networks. (A) Performance as a function of the amount of noise in three simulated networks. AUC was used as the performance measure. Shown here are average AUC values of 50 runs of each method at each noise level. (B) Time complexity of different methods. Inputs are four gene co-expression networks constructed using breast cancer data. For M-module, two strategies were used to select seeds: top 5% genes as seeds and top 20% as seeds (in this case, >90% genes were covered by the discovered modules). (C) Specificity of the methods. Gene modules found by each method are evaluated by a set of gold-standard pathway annotations. Specificity is defined as the fraction of predicted modules that significantly overlaps with reference pathways. (D) Sensitivity of the methods. Sensitivity is defined as the fraction of reference pathways that significantly overlaps with predicted modules. Pathway overlap P-values were computed using hypergeometric distribution. P-values for the difference in specificity and sensitivity were computed using Fisher’s exact test. All P-values were corrected for multiple testing using the method of Benjamin–Hochberg. *P < 0.05
We next compared the performance of the five methods on real networks. We used a compendium of 531 gene expression profiles of breast cancer samples generated by the TCGA consortium. The patient samples were classified into four clinical stages using the latest American Joint Committee on Cancer staging system (Edge, 2010) (Supplementary Table S1). We constructed one co-expression network for each cancer stage. We identified 50, 110, 1573, 91 and 100 modules using M-module, JC, TC, SC and CC, respectively. The respective average sizes of the modules are 17, 70, 10, 85 and 77 genes and the respective gene coverages are 8.2, 99.4, 20.7, 100 and 100%. Note that because JC, SC and CC are partition-based algorithms, their gene coverage is essentially 100%. We evaluated the resulting sets of gene modules using multiple reference pathway annotations, including Gene Ontology (Ashburner et al., 2000), KEGG (Kanehisa et al., 2012), Biocarta (Nishimura, 2001), Canonical pathways (Subramanian et al., 2005) and functional gene interactions (Lee et al., 2011). M-module achieves significantly higher specificity when evaluated using all reference sets while maintaining comparable sensitivity (P < 0.05, one-sided Fisher’s exact test, Figure 2C and D).
We also benchmarked the time complexity of the algorithms. When tested on the same breast cancer co-expression networks (7737 genes and 10 970 386 edges), M-module has the fastest speed among the five algorithms. In particular, it is 5 and 120 times faster than JC and TC algorithms, designed for multiple network analysis (Fig. 2B).
M-modules reveal distinct properties of the dynamics of pathway connectivity
Pathway dynamics can be attributed to both changes in gene expression level and changes in the connectivity among genes (i.e. pathway rewiring). Although less studied, the latter type of dynamics has recently been shown to be critical for understanding disease progression and treatment, including the role of hub genes (Taylor et al., 2009) and rewiring of signaling pathways during cancer treatment (Lee et al., 2012). Because component subnetworks of an M-module share the same set of genes in multiple co-expression networks but can differ in their connectivity, M-module provides a natural way to capture pathway connectivity dynamics. To this end, we introduce a novel measure to quantify changes in the connectivity of an entire subnetwork across multiple networks. We term it the MCDS. As the co-expression networks are weighted based on gene expression correlation, MCDS quantifies not only the presence and absence of edges but also changes in edge weights that can be viewed as interaction strength among genes. By comparing the MCDS values of real 4-modules to a null distribution of MCDS values of random 4-modules, we found that 30 of the 50 discovered 4-modules have significant dynamic scores (P = 1.9E-10, one-sided t-test, Fig. 3B). An example of dynamic 4-modules involved in Errb2/Her2 signaling is shown in Figure 3A. As the tumor progresses, multiple interactions in this module are significantly changed (P < 0.05, see Supplementary Methods), suggesting a significant role of pathway rewiring during the disease progression.
Fig. 3.
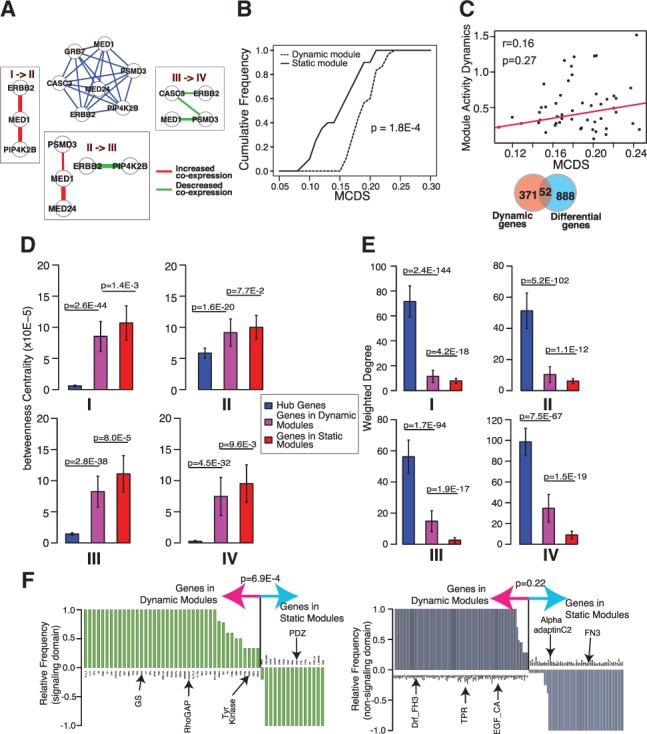
Evidence and properties of module connectivity dynamics across multiple networks. 4-modules were identified using co-expression networks representing four stages of breast cancer. (A) An example dynamic 4-module representing the Erbb2/Her2 signaling pathway. Middle subnetwork, composite 4-modules whose edges are the average co-expression correlations across four networks. Surrounding subnetworks, subnetworks induced by edges that show significant changes in values between two adjacent co-expression networks. (B) Cumulative distributions of connectivity dynamic scores of discovered 4-modules. MCDS, module connectivity dynamic score. (C) Module connectivity dynamics is not correlated with expression level dynamics of module members. Top, correlation between gene expression dynamics and gene connectivity dynamics of module members. Bottom, overlap between 4-module genes and differentially expressed genes. (D) Betweenness centrality of genes in 4-modules and hub genes. (E) Sum of edge weights of genes in 4-modules and hub genes. (F) Occurrence frequency of signaling (left) and non-signaling (right) protein domains encoded by 4-module genes
We confirmed that the dynamics captured by MCDS is because of changes in the connectivity among module members instead of changes in their expression levels. First, we found that gene expression changes and MCDS between adjacent cancer stages are not correlated (r = 0.16, P = 0.27, Fig. 3C top). Second, we found no significant overlap (P = 0.49, hypergeometric test) between genes of dynamic 4-modules and differentially expressed genes (P < 0.05, one-way ANOVA) (Fig. 3C).
Previously, connectivity dynamics of hub genes in protein interaction networks has been used to improve prognosis accuracy of breast cancer (Taylor et al., 2009). We next contrasted topological and biochemical properties of three groups of genes: hub genes and genes in dynamic and static 4-modules. For hub genes, we used the top 5% genes (387) with the highest degrees in the input networks. We found that genes in dynamic 4-modules exhibit distinct values with regard to these properties. We first examined two topological features, betweenness centrality and weighted degree. Betweenness centrality measures the relative importance of a node in the network, whereas weighted degree measures the interaction strength of a gene with other genes. We found that genes in dynamic 4-modules have significantly lower centrality than hub genes but significantly higher centrality than genes in static 4-modules (one-sided t-test, Fig. 3D). The lower centrality of genes in static 4-modules may be because of the higher fraction of protein complexes represented by these modules (Supplementary Fig. S2). Bandyopadhyay et al. (2010) have shown that interactions among members of protein complexes are generally stable in response to perturbation, whereas interactions in signaling pathways are more dynamic.
In terms of weighted degree, we found that genes in dynamic 4-modules have significantly lower degrees than hub genes, but higher degrees than genes in static 4-modules (one-sided t-test, Fig. 3E), suggesting that genes in dynamic 4-modules tend to have stronger interactions among themselves.
Next, we asked whether the proteins encoded by genes in dynamic and static 4-modules possess different biochemical properties. We found that cell signaling domains [based on the SMART database (Letunic et al., 2006)] were enriched in proteins encoded by genes of dynamic 4-modules (P = 4.8E-4, binomial test, Fig. 3F), whereas non-signaling domains were evenly distributed between the two groups of proteins (P = 0.22, binomial test).
Incorporation of module connectivity dynamics significantly improves disease stage classification
Given that dynamic M-modules are associated with breast cancer progression and they have unique topological and biochemical properties, we hypothesized that they can be used to improve breast cancer stage classification. To test this hypothesis, we built statistical classifiers using different feature sets for classifying multiple stages of breast cancer.
As a baseline comparison, we first compared the classification accuracy using the following feature sets: significant M-modules (both static and dynamic M-modules), modules generated by TC, SC, CC and JC, size-matched set of genes that are differentially expressed across stages (P < 0.05, one-way ANOVA) and size-matched set of randomly selected genes. We trained Support Vector Machine (SVM) classifiers to perform multi-class classification simultaneously (see Section 2). SVM classifier using M-modules as features achieved marked improvement over other feature sets in both accuracy and area under curve (AUC) based on 5-fold cross validation experiments (Fig. 4), suggesting that M-modules can capture discriminative information across the entire spectrum of breast cancer stages better than those identified by other methods.
Fig. 4.
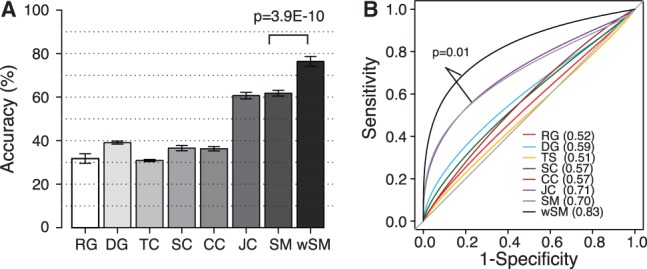
Module connectivity dynamics improves disease stage classification. Results are based on 50 independent 5-fold cross validations. (A) Classification accuracy of breast cancer stages using different feature sets, including randomly selected genes (RG, N = 50 features, 50 genes), differentially expressed genes (DG, N = 50 features, 50 genes), TC modules (N = 1573 features, 1601 genes), SC (91 features, 7737 genes), CC (100 features, 7737 genes), Jointclustering (JC, 110 features, 7690 genes), significant 4-modules (SM, 50 features, 635 genes) and weighted 4-modules (wSM, 50 features, 635 genes). Accuracy is defined as the number of patient samples correctly classified. Y-axis, mean accuracy. Error bar, standard deviation. (B) Receiver operating characteristic curves for SVM classifiers trained with different feature sets. AUC values are in parenthesis
Next, we asked whether information in module connectivity dynamics can be used to further improve classification accuracy. To this end, we weighted each M-module based on its MCDS and used the weighted feature to train a SVM classifier (see Supplementary Methods). We found that the MCDS-weighted classifier achieved significantly higher accuracy (76.4 versus 61.6%, P = 3.9 × 10−10, Wilcoxon test) and AUC (0.83 versus 0.70, P = 0.01, ROC test by DeLong et al., 1988) than classifier trained using M-modules without feature weighting (Fig. 4).
To rule out the possibilities that the above result is because of the choice of classifier, cross validation scheme and how unbalanced data are corrected, we performed additional analyses by varying each of these parameters. Collectively, our results demonstrate that the weighted M-modules consistently outperform other feature sets across different parameter settings (Supplementary Methods and Supplementary Figs S3–S5).
To rule out the possibility that confounding factors in the TCGA dataset contribute to the classification accuracy, we evaluated the performance of the SVM classifiers (trained on TCGA data) using two external microarray datasets, both of which cover all four stages of breast cancer. Our result shows that the observed performance is not because of hidden confounding factors in the TCGA dataset (Supplementary Fig. S6).
A meta-network of 4-modules associated with breast cancer progression
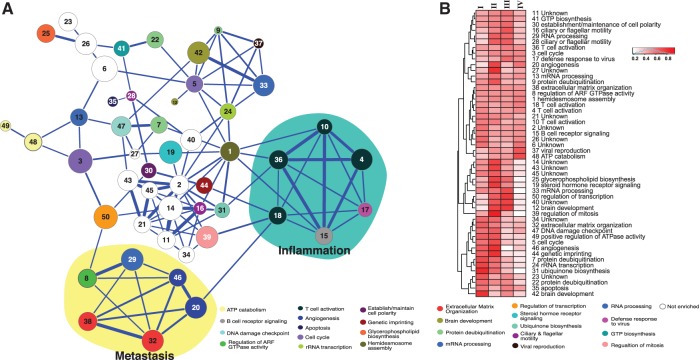
To obtain a systems view of the discovered 4-modules, we computed the Pearson correlation between the first principle components of the expression profiles of a pair of modules (Langfelder and Horvath, 2007). We then constructed a meta-network based on the Pearson correlation coefficients (see Supplementary Methods and Fig. 5A). Hierarchical clustering of the correlation matrix revealed five clusters, four of which are tightly clustered (Supplementary Fig. S7). This analysis highlights two groups of 4-modules that are known to be critical for cancer progression: inflammation (teal) (Andre et al., 2013) and metastasis (yellow) (Nguyen et al., 2009). The inflammation cluster consists of T-cell activation (modules 4, 10, 18, 36), B-cell receptor signaling (module 15) and innate immune response (module 17), indicating the induction of an adaptive immune response associated with tumor-infiltrating immune cells. The metastasis cluster captures genes involved in several critical steps during the development of metastasis, including extracellular matrix process (modules 32, 38), angiogenesis (modules 20, 46) and the Ras family of GTPases (modules 8, 29) (Hernandez-Alcoceba et al., 2000).
Relative importance of 4-modules for the classification of each stage of breast cancer
The multi-class SVM classifier consists of six subclassifiers, each of which classifies one of the six pairwise comparisons. To understand the importance of each 4-module to the classification of each disease stage, we determined their relative importance based on their normalized classifier weights over six sets of subclassifier weights (see Supplementary Methods). Hierarchical clustering of the feature importance matrix reveals distinctive sets of four-modules that are important for the classification of each cancer stage (Fig. 5B and Supplementary Table S2). For instance, ciliary mobility and establishment of cell polarity are more important for stage III classification than other stages. Inflammation involving immune cells is more important for stage four than previous three stages. In contrast, genetic imprinting, steroid hormone (Errb2/Her2) signaling, regulation of mitosis and protein deubiquitination pathways are more important for the first two stages. Knowing the relative importance of each 4-module enables us to gain new insights into the molecular mechanism of breast cancer progression.
Fig. 5.
Characteristics of discovered 4-modules. (A) Meta-network view of 4-modules across breast cancer stages. Edge thickness is proportional to the Pearson correlation of the first principle components between the expression profiles of two modules across all patient samples. Node size is proportional to the average connectivity dynamic score of a 4-module over three adjacent stage transitions. Node color, enriched GO biological process terms. (B) Feature importance for cancer stage classification. Each row represents a feature (4-modules) and each column represents a breast cancer stage. Feature importance values are clustered using hierarchical clustering. Feature ID and enriched GO biological process term are shown to the right of the dendragram
4 DISCUSSION
Our current knowledge about the dynamics of gene networks during disease progression is rather limited. Conceptually, the problem of understanding network dynamics can be divided into two subproblems: (i) identifying the subnetworks that exhibit structural changes in response to different growth or developmental events or different spatial location; and (ii) quantifying the dynamic changes in the subnetwork structure. Our framework addresses both subproblems. To identify subnetworks that change over multiple conditions, many previous approaches first perform all pairwise network comparisons and then identify a unified subnetwork that partially overlaps with pairwise comparisons (Doering et al., 2012; He et al., 2012; Palla et al., 2007; Tomlins et al., 2007; Zhang et al., 2013). In contrast, the JC, TC and the M-module algorithms analyze multiple gene networks simultaneously. By doing so, the latter approach can reduce noises as well as capture subtle but consistent changes in the subnetworks. The three latter methods use different objective functions to identify shared subnetworks. JC uses the modularity measure (Newman, 2006a), whereas TC uses frequent dense subgraphs. The modularity measure is known to have a resolution limit that prohibits the discovery of small modules (Fortunato and Barthelemy, 2007). On the other hand, strictly relying on network density prevents the discovery of subnetworks with sparser and linear topologies such as signaling pathways. M-module alleviates both problems by using graph-entropy–based objective function (Dehmer and Mowshowitz, 2011). In addition, M-module incorporates both network topological feature and prior knowledge about the mutational status of genes for the disease under investigation.
The second subproblem of network dynamics is how to quantify structural dynamics in the subnetwork. We introduced a novel measure (MCDS) based on the matrix norm of adjacency matrices that represent subnetworks. Unlike degree comparison, which was commonly used in previous studies, MCDS takes into account both the existence and strength of connectivity between genes in a subnetwork.
We compared both the quality and the classification accuracy of modules derived using individual networks separately and using M-modules. We found that M-modules have higher sensitivity and comparable specificity based on known pathway annotations. More importantly, we found that M-module–based features achieve significantly higher accuracy in predicting cancer stages (Supplementary Fig. S8). This result emphasizes the importance of joint analysis of multiple gene networks to more accurately capture the dynamics of gene pathways.
Much of previous studies on connectivity dynamics have been focused on the dynamics of hub genes. M-module enables analysis of entire pathway instead of hub genes only. Our result suggests that genes in dynamic modules have unique topological and biochemical properties that may contribute to their function in cancer progression. In particular, we found that genes encoding signaling domains are enriched in dynamic modules but not static modules. This finding is consistent with previous results that signaling domains are more frequently associated with oncogenesis and play critical roles in rewiring signaling networks and driving phenotypic alteration as disease progression (Lee et al., 2012) or during cellular stress responses (Bandyopadhyay et al., 2010).
We see ample opportunities to improve on the basic concept of M-module in future work. First, although this study uses breast cancer as a proof-of-principle, the M-module framework is broadly applicable to any cohort of patients for which disease-stage–specific transcriptome data are available. Second, integrating multiple types of molecular analytes beyond gene expression and somatic mutation (e.g. epigenome, miRNA, CNVs) might further expand our ability to identify dynamic molecular events that are associated with disease progression. Finally, comparing and contrasting dynamic events involving different molecular types may yield new mechanistic insights into their interactions in the context of disease progression.
Supplementary Material
ACKNOWLEDGEMENTS
The authors thank the members of the Tan lab for helpful discussion. The authors thank Lucas Van Tol and the University of Iowa’s Institute for Clinical and Translational Science for providing computing support.
Funding: This study was supported by the National Institutes of Health (grants HG006130 and HL110349 to K.T.).
Conflicts of Interest: none declared.
REFERENCES
- Andre F, et al. Molecular pathways: involvement of immune pathways in the therapeutic response and outcome in breast cancer. Clin. Cancer Res. 2013;19:28–33. doi: 10.1158/1078-0432.CCR-11-2701. [DOI] [PubMed] [Google Scholar]
- Ashburner M, et al. Gene ontology: tool for the unification of biology. The Gene Ontology Consortium. Nat. Genet. 2000;25:25–29. doi: 10.1038/75556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bandyopadhyay S, et al. Rewiring of genetic networks in response to DNA damage. Science. 2010;330:1385–1389. doi: 10.1126/science.1195618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benjamini Y, Hochberg Y. Controlling the false discovery rate–a practical and powerful approach to multiple testing. J. R. Stat. Soc. B Methadol. 1995;57:289–300. [Google Scholar]
- Chuang HY, et al. Network-based classification of breast cancer metastasis. Mol. Syst. Biol. 2007;3:140. doi: 10.1038/msb4100180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Lichtenberg U, et al. Dynamic complex formation during the yeast cell cycle. Science. 2005;307:724–727. doi: 10.1126/science.1105103. [DOI] [PubMed] [Google Scholar]
- Dehmer DM, Mowshowitz A. A history of graph entropy measures. Inf. Sci. 2011;181:57–78. [Google Scholar]
- DeLong ER, et al. Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach. Biometrics. 1988;44:837–845. [PubMed] [Google Scholar]
- Doering TA, et al. Network analysis reveals centrally connected genes and pathways involved in CD8+ T cell exhaustion versus memory. Immunity. 2012;37:1130–1144. doi: 10.1016/j.immuni.2012.08.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edge SB, et al. AJCC Cancer Staging Manual. Springer; 2010. [Google Scholar]
- Fortunato S, Barthelemy M. Resolution limit in community detection. Proc. Natl Acad. Sci. USA. 2007;104:36–41. doi: 10.1073/pnas.0605965104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goh KI, et al. The human disease network. Proc. Natl Acad. Sci. USA. 2007;104:8685–8690. doi: 10.1073/pnas.0701361104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han JD, et al. Evidence for dynamically organized modularity in the yeast protein-protein interaction network. Nature. 2004;430:88–93. doi: 10.1038/nature02555. [DOI] [PubMed] [Google Scholar]
- He D, et al. Coexpression network analysis in chronic hepatitis B and C hepatic lesions reveals distinct patterns of disease progression to hepatocellular carcinoma. J. Mol. Cell Biol. 2012;4:140–152. doi: 10.1093/jmcb/mjs011. [DOI] [PubMed] [Google Scholar]
- Hernandez-Alcoceba R, et al. The Ras family of GTPases in cancer cell invasion. Cell. Mol. Life Sci. 2000;57:65–76. doi: 10.1007/s000180050499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu HY, et al. Mining coherent dense subgraphs across massive biological networks for functional discovery. Bioinformatics. 2005;21:I213–I221. doi: 10.1093/bioinformatics/bti1049. [DOI] [PubMed] [Google Scholar]
- Huang Y, et al. Systematic discovery of functional modules and context-specific functional annotation of human genome. Bioinformatics. 2007;23:I222–I229. doi: 10.1093/bioinformatics/btm222. [DOI] [PubMed] [Google Scholar]
- Kanehisa M, et al. KEGG for integration and interpretation of large-scale molecular data sets. Nucleic Acids Res. 2012;40:D109–D114. doi: 10.1093/nar/gkr988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelley BP, et al. Conserved pathways within bacteria and yeast as revealed by global protein network alignment. Proc. Natl Acad. Sci. USA. 2003;100:11394–11399. doi: 10.1073/pnas.1534710100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koyuturk M, et al. An efficient algorithm for detecting frequent subgraphs in biological networks. Bioinformatics. 2004;20:200–207. doi: 10.1093/bioinformatics/bth919. [DOI] [PubMed] [Google Scholar]
- Lancichinetti A, Fortunato S. Consensus clustering in complex networks. Sci. Rep. 2012;2:336. doi: 10.1038/srep00336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langfelder P, Horvath S. Eigengene networks for studying the relationships between co-expression modules. BMC Syst. Biol. 2007;1:54. doi: 10.1186/1752-0509-1-54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee I, et al. Prioritizing candidate disease genes by network-based boosting of genome-wide association data. Genome Res. 2011;21:1109–1121. doi: 10.1101/gr.118992.110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee MJ, et al. Sequential application of anticancer drugs enhances cell death by rewiring apoptotic signaling networks. Cell. 2012;149:780–794. doi: 10.1016/j.cell.2012.03.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Letunic I, et al. SMART 5: domains in the context of genomes and networks. Nucleic Acids Res. 2006;34:D257–D260. doi: 10.1093/nar/gkj079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li W, et al. Integrative analysis of many weighted co-expression networks using tensor computation. PLoS Comput. Biol. 2011;7:e1001106. doi: 10.1371/journal.pcbi.1001106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Masica DL, Karchin R. Correlation of somatic mutation and expression identifies genes important in human glioblastoma progression and survival. Cancer Res. 2011;71:4550–4561. doi: 10.1158/0008-5472.CAN-11-0180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Narayanan M, et al. Simultaneous clustering of multiple gene expression and physical interaction datasets. PLoS Comput. Biol. 2010;6:e1000742. doi: 10.1371/journal.pcbi.1000742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newman ME. Modularity and community structure in networks. Proc. Natl Acad. Sci. USA. 2006a;103:8577–8582. doi: 10.1073/pnas.0601602103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newman MEJ. Finding community structure in networks using the eigenvectors of matrices. Phys. Rev. E. 2006b;74:036104. doi: 10.1103/PhysRevE.74.036104. [DOI] [PubMed] [Google Scholar]
- Nguyen DX, et al. Metastasis: from dissemination to organ-specific colonization. Nat. Rev. Cancer. 2009;9:274–284. doi: 10.1038/nrc2622. [DOI] [PubMed] [Google Scholar]
- Nishimura D. BioCarta. Biotech. Softw. Internet Rep. 2001;2:117–120. [Google Scholar]
- Palla G, et al. Quantifying social group evolution. Nature. 2007;446:664–667. doi: 10.1038/nature05670. [DOI] [PubMed] [Google Scholar]
- Pleasance ED, et al. A comprehensive catalogue of somatic mutations from a human cancer genome. Nature. 2010;463:191–196. doi: 10.1038/nature08658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Subramanian A, et al. Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles, Proc. Natl Acad. Sci. USA. 2005;102:15545–15550. doi: 10.1073/pnas.0506580102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor IW, et al. Dynamic modularity in protein interaction networks predicts breast cancer outcome. Nat. Biotechnol. 2009;27:199–204. doi: 10.1038/nbt.1522. [DOI] [PubMed] [Google Scholar]
- Tomlins SA, et al. Integrative molecular concept modeling of prostate cancer progression. Nat. Genet. 2007;39:41–51. doi: 10.1038/ng1935. [DOI] [PubMed] [Google Scholar]
- Vanunu O, et al. Associating genes and protein complexes with disease via network propagation. PLoS Comput. Biol. 2010;6:e1000641. doi: 10.1371/journal.pcbi.1000641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vogelstein B, et al. Cancer genome landscapes. Science. 2013;339:1546–1558. doi: 10.1126/science.1235122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang B, et al. Integrated systems approach identifies genetic nodes and networks in late-onset Alzheimer's disease. Cell. 2013;153:707–720. doi: 10.1016/j.cell.2013.03.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhong Q, et al. Edgetic perturbation models of human inherited disorders. Mol. Syst. Biol. 2009;5:321. doi: 10.1038/msb.2009.80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou D, et al. Learning with local and global consistency. Adv. Neural Inf. Proc. Syst. 2004;16:321–328. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.