Introductory Review of Computational Cell Cycle Modeling

Abstract

Recent advances in the modeling of the cell cycle through computer simulation demonstrate the power of systems biology. By definition, systems biology has the goal to connect a parts list, prioritized through experimental observation or high-throughput screens, by the topology of interactions defining intracellular networks to predict system function. Computer modeling of biological systems is often compared to a process of reverse engineering. Indeed, designed or engineered technical systems share many systems-level properties with biological systems; thus studying biological systems within an engineering framework has proven successful. Here we review some aspects of this process as it pertains to cell cycle modeling.

1 Introduction

The complexity of biological systems requires us to take a systems-level view in order to holistically understand the networks of cellular regulation. Such approaches involve in silico modeling of biological systems and have a remarkable similarity to reverse engineering. Indeed, designed or engineered technical systems share many systems-level properties with evolved biological systems [1]. The cell cycle, which consists of an orderly sequence of events, is an example of biological complexity and involves both positive and negative feedback regulations. Such regulations are also at the core of other major oscillating systems including circadian rhythms; thus computational systems biology has become an important area of cell cycle research [2– 4]. Here we describe an introductory overview of the main steps required to develop cell cycle models.

2 Steps of the Modeling Process

2.1 Scope and Goals

Model development is an iterative process, whereby graphical representations, mathematical implementations, simulations, predictions, and experimental validations are continuously refined until all project goals are reached. Modeling can also help to provide consistency between different experimental efforts as well as to generate and test new hypotheses. The first step in the modeling process is to define the scope and objectives of the model, and to identify all state variables such as genes or proteins, which change their state or activity through transcription, phosphorylation, or other mechanisms. The most difficult part of a modeling process is to accurately define all necessary rates and parameters and to make a decision on the most adequate level of complexity or comprehensiveness and scale. Most likely, the modeler is faced with a situation where some parameters are available, and some not. Parameters missing can be initially estimated, and experimental research can be guided to determine more precise values. This task is greatly enhanced by focusing on the most essential items required to build the model; it is essential to discern which components of a model are absolutely necessary and have to be prioritized. Obviously, it is also important to gauge which components can be omitted in the initial model and reintroduced in future extensions. In many areas, the development of models naturally follows a pattern from simple to more complex. For instance, an early model of the MAPK pathway originally contained only nine state variables [5], but subsequently grew to a network representation with 202 proteins, and additional ions, oligomers, and genes [6]. However, the qualitative behavior of the pathway in terms of a negative feedback had already been captured correctly by the initial model. Cell cycle models are no exception. The first models published by Tysen [7] and Goldbeter [8] in 1991 have grown steadily in complexity. The Goldbeter model is the most minimalistic model featuring three state variables; however, it captures the essential behavior of the core constituents of the cell cycle. While the examples of this model discussed below assume a continuous cycling, which is a suitable assumption for embryonic development, most cell cycles are different from a continuous oscillatory system, since they depend on and are regulated by external cues and internal cell cycle checkpoints.

2.2 Model Topology

The second major step is to lay out the topology of the connectivity or network wiring in a graphical fashion. While the interactions of proteins are typically defined by biochemical reactions rates, the topology can be defined in terms of control elements or regulatory network motifs, such as feedback loops [9, 10]. In combination, rates and network topologies determine the overall dynamic of the system. Both amplifying positive and inhibitory negative feedback motifs are relevant for cell cycle regulation, and their fine-tuned interaction gives rise to a cyclic behavior.

Using formal graphical notations, as compared to pathway cartoons, promotes model exchange and enhances the process of deriving mathematical formulations. Among the early schematic representations used in biology, specifically in ecology, are Forrester diagrams and Petri Nets with different level of abstraction [11]. Forrester diagrams make use of only one graphical element for state variables with sources and sinks limiting the representation of more complex diagrams in which state variables of different kinds have to be discerned. Another limitation is that these diagrammatic concepts were developed when computer graphics and user interfaces were still in initial development; thus no convenient computer programs were available to support the development of such diagrams, and the application was limited to simpler models.

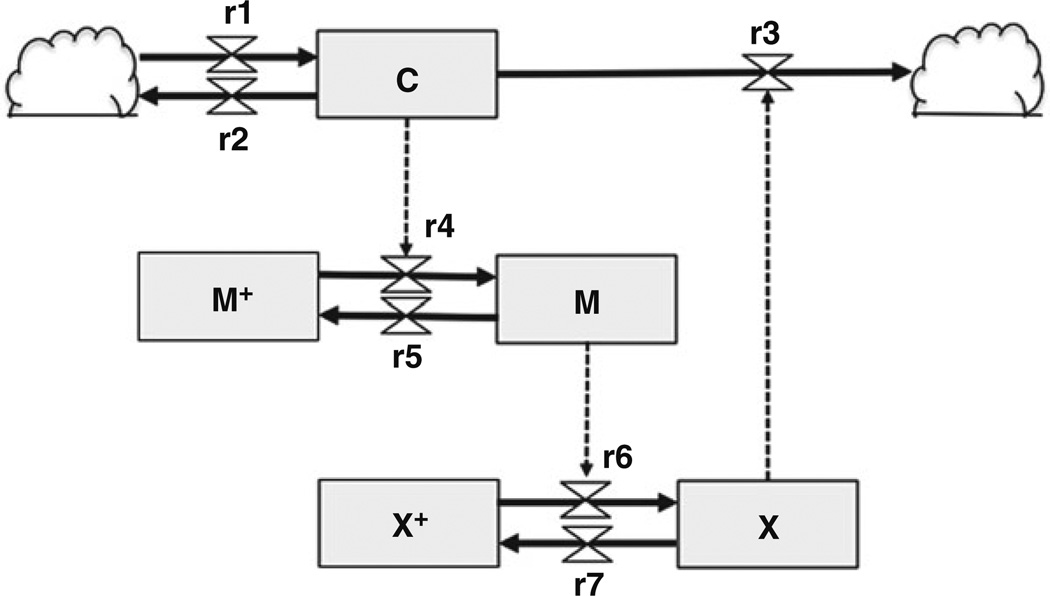
Figure 1 shows a diagram for a simple cell cycle model using Forrester Diagram notation. This model, which is proposed by Goldbeter, is a minimalistic model of a mitotic oscillator during the cell cycle [8]. In this model, the mathematical representation uses three state variables of interest: Cyclin (C), active dephosphorylated Cdc2 (also known as CDK1) kinase (M), and active phosphorylated protease (X). The Cyclin protein (C) is a key ingredient in the cell cycle, since its periodic buildup and breakdown drives cell cycle progression. When Cyclin exceeds a certain threshold, it begins to combine with and activate a protein kinase Cdc2 to form a complex called “maturation-promoting factor (or M-phase promoting factor, MPF: M),” which stimulates mitosis. The Cdc2 kinase stimulates degradation of Cyclin by activating a protease (X). Since Cyclin promotes its own degradation by a protease related to MPF, this constitutes a negative feedback. The biochemical reactions r1–r7 based on enzyme kinetics constitute the in- and outflows, which in combination determine the behavior of each state variable. The cloud symbols denote undefined sources and sinks; these are outside the scope of the Goldbeter model. In this circuit, Cyclin (C) is constantly synthesized (r1), while nonspecific degradation of Cyclin also occurs constantly (r2). When the concentration of Cyclin is below the threshold, Cyclin does not form a complex with Cdc2, keeping Cdc2 inactive (M⁺). In r4, when Cyclin (C) concentration rises over the threshold, Cyclin activates the Cdc2 kinase by increasing the velocity of the phosphatase that activates the kinase (M⁺ → M). In this reaction, the phosphatase (Cdc25 protein, not modeled) converts inactive Cdc2 (M⁺) to the active form (M), by removing the inhibitory phosphate groups (r4). In r5, although it is not explicitly modeled, the Wee1 kinase deactivates Cdc2 by adding the inhibitory phosphate group to Cdc2. Here, the amount of Wee1 is considered to be constant (r5). When the Cdc2 kinase is activated (M), it directly promotes r6 without other intervening factors. In this reaction, Cdc2 phosphorylates and activates Cyclin-specific protease (X⁺ → X), which promotes r3 that degrades Cyclin. Finally, in r7, Cyclin-specific protease is deactivated, and the amount of deactivating phosphatase (not modeled) for the cyclin protease (X) is considered to be constant. In this reaction, the activating phosphate groups are removed from the Cyclin-specific protease. Taken together, the total amounts of (M + M⁺) and (X + X⁺) are constant, thus completing the mitotic oscillator cycle, which is caused by negative feedback.

Fig. 1.

Schema for the mitotic oscillator from Goldbeter [8] using Forrester diagram notations. The state variables [Cyclin (C), maturation promotion factor (M), and protease (X)] are shown by boxes, with in- and outflows denoted by valves of defined molecular reaction rates. The cloud symbols represent sources or sinks, and dotted lines indicate regulatory connections

One instructional implementation and description of the Goldbeter model is available from Mathworks (http://www.mathworks. com). The model from Tyson [7] has also been available as an educational resource [12]. To handle the increasing complexity of molecular data several graphical modeling tools, such as CellDesigner [6], still based on the principles used in Forrester diagrams, are now available to conveniently design molecular networks graphically. Based on a Systems Biology Graphical Notation (SBGN) standard, such programs use different symbols for variables (genes, proteins, and phenotypes); they allow for entering functions and reaction rates to define the mathematical model, and subsequently support to execute the simulation. As part of these developments model sharing through using standardized formats such as Systems Biology Markup Language (SBML) and the use of model repositories (such as CellML or BioModels at EMBL-EBI) has become essential to advance the field.

2.3 Simulation and Prediction

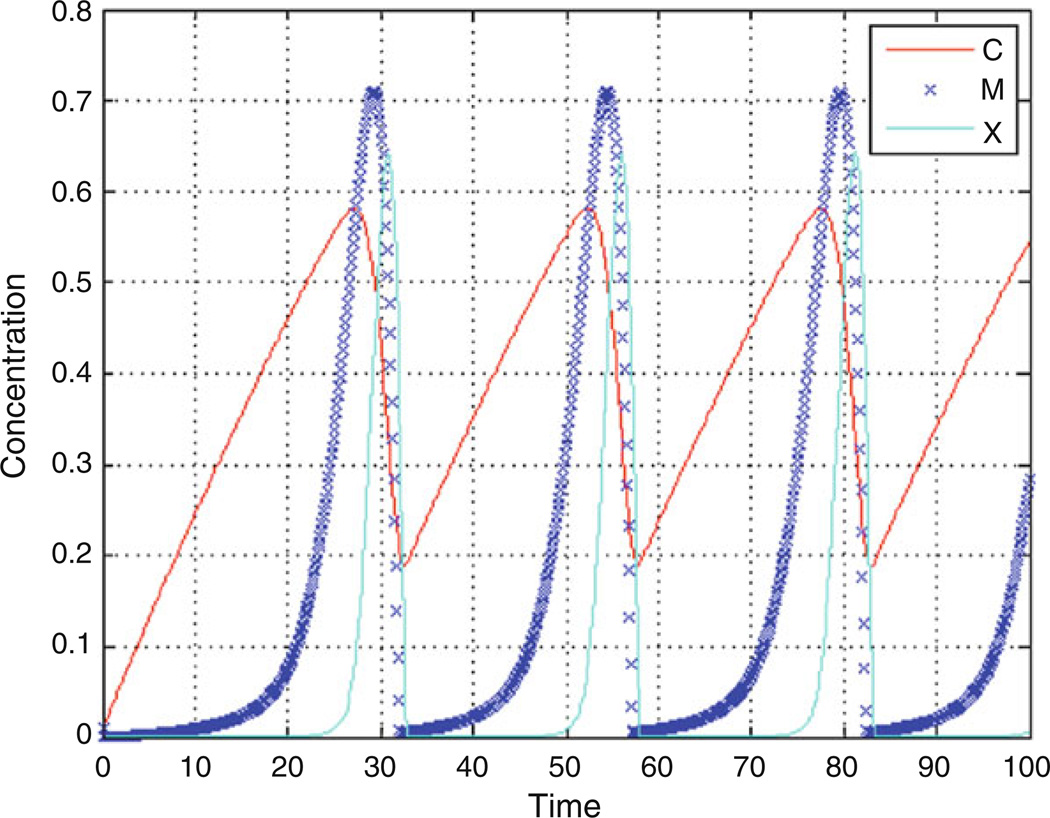
The mathematical equations resulting from graphical models are typically linear or nonlinear ordinary differential equations (ODE). Each ODE represents one state variable and its change during each time step, which means for most systems several ODEs have to be solved at each time step. The connection to other state variables is expressed in any of the terms defining either an increase or decrease of the state variable, or expressed in auxiliary equations. Rate equations are solved by ODE solvers such as Euler, Runga-Kutta, or Stiff solvers. Stiff solvers with variable time steps are most adequate and computationally efficient for systems that have a fluctuating dynamic consisting of regimes of smooth change with more rapid changes. User-defined error thresholds will force the computation to take small step sizes when the system changes, and will relax the step size when the change is more linear, as demonstrated in Fig. 2 for the parameter M.

Fig. 2.

Example of a cell cycle simulation using the Goldbeter model. Shown are the oscillations of Cyclin (C), the maturation promoting factor (M), and the activity of the protease (X). As C increases, it activates M and X, which subsequently degrades C. The simulation has been performed with a stiff solver of variable step size, as demonstrated for M

However, using classical mathematical modeling can pose limitations. Not all parameters might be available, specifically if there is an understanding about the role of other factors, external regulators, or interaction with other networks. The understanding of the topology of a network can grow more rapidly than the ability to quantify all required parameters. The two alternative approaches are Boolean logic [13] and Fuzzy-logic [14, 15]; both are used to develop rule-based representations. In these cases, the qualitative known regulatory mechanisms of interactions are implemented as defined rules into the model. Fuzzy-logic rule-based models can be adjusted to the granularity of available quantitative data; i.e., they can start with a low resolution (ON/OFF) but can be calibrated to a higher resolution if more discernable states are provided.

2.4 Model Analysis

An objective analysis of the relevance of components and properties can be made once the model is complete. A mathematical representation has the ability to identify how defined perturbations influence the overall behavior of the model. Such a computational task can be done repeatedly and iteratively in a manner not available in the wet laboratory. One goal could be to identify state variables most amenable to experimental perturbation for the purpose of experimental model validation. Another goal could be to identify targets most suitable for intervention and drug development. In addition, it may be useful to identify unnecessary components in the overall model to reduce model complexity. A sensitivity analysis, which allows a ranking of all model parameters, is the most commonly applied. In such an analysis, each parameter is changed by a defined degree, and compared to a defined output parameter. One definition is the Sensitivity Objective Function (SOF), a ration of % change in outcome and % change of rate. An example of a sensitivity analysis for the Goldbeter model is shown in Table 1. V2 is the parameter with the greatest sensitivity out of all the parameters when the initial value is perturbed by 10 %, using the amount of C at the end of the calculation as a reference. This is the case because the V2 parameter is involved in the enzyme kinetics of reaction r5 (see Fig. 1), which determines the outflow or conversion of the active into the inactive form of MPF. As long as M is active, it activates the protease (r6 in Fig. 1), and herewith influences the cyclic behavior. V4, which is involved in reaction r7 and represents degradation of the active protease, has the least effect on the simulation outcome, and requires a stronger perturbation to cause a noticeable effect.

Table 1.

Example of a sensitivity analysis using the mitotic oscillator model by Goldbeter

Perturbation target	End amount of cyclin	% Change in outcome	S.O.F
None	0.54	0	0
K1 (r4)	0.53	0.016	0.165
K2 (r5)	0.52	0.031	0.317
K3 (r6)	0.54	0.007	0.071
K4 (r7)	0.53	0.021	0.213
Kc (r4)	0.33	0.379	3.790
Kd (r3)	0.53	0.012	0.123
Kdd (r2)	0.53	0.011	0.113
V2 (r5)	0.06	0.880	8.800
V4 (r7)	0.54	0.006	0.058
Vd (r3)	0.56	0.043	0.428
VM1 (r4)	0.26	0.518	5.182
VM3 (r6)	0.51	0.050	0.496

Each parameter or constant involved in the molecular reactions is perturbed by 10 %. V2, part of the reaction r5 (see Fig. 1), is the most sensitive parameter, and V4, part of reaction r7, is the least sensitive.

The investigation of sensitivities can lead to broader questions such as robustness of the biological system. Robustness is a systems-level property, not determined by a single factor alone, but by the overall behavior of the system, its circuitry, and connectivity. Fluctuations can arise from stochastic effects in gene transcription and protein concentrations [16], as well as environmental perturbations. A high sensitivity in certain parameters can make the system fragile to specific perturbations, while the topology of a network can contribute to an enhancement of stability. It can be assumed that the evolved design of an essential process such as cell cycle regulation is stable and provides robustness against many common fluctuations [17]. Thus, mathematical modeling has become an important tool to conveniently study and compare responses to perturbations and noise [18 – 21].

3 Conclusions and Outlook

The reverse engineering of the cell cycle has been a successful enterprise in systems biology. The mathematical models can be executed conveniently and repeatedly to study the influence of specific or random perturbations. The model revisited here is minimalistic and had been chosen to demonstrate essential steps involved in the modeling process. The reader is referred to systems biology textbooks for an in-depth discussion of computational modeling and applications [22 – 25].

The growing complexity of cell cycle models is mostly driven from experimental insights, and panels of genetically engineered strains in model organisms allow validation of hundreds of model parameters [26]. Current model development strides are designed to integrate cell cycle models into a larger scope of cellular mechanisms and functions, which includes identifications of cell cycle regulators and checkpoints, which are hooks to connect other models representing signaling, transcriptional regulation, or metabolism [27, 28]. Functional and hierarchical modularity can keep the growing model complexity manageable [29]. Finally, such aggregated models will allow studying the involvement of the cell cycle regulation in development, aging, and disease.