Multi-parametric MRI characterization of inflammation in murine skeletal muscle

Abstract

Myopathies often display a common set of complex pathologies that include muscle weakness, inflammation, compromised membrane integrity, fat deposition, and fibrosis. Multi-parametric, quantitative, noninvasive imaging approaches may be able to resolve these individual pathological components. The goal of this study was to use multi-parametric MRI to investigate inflammation as an isolated pathological feature. Proton relaxation, diffusion tensor imaging (DTI), quantitative magnetization transfer (qMT-MRI), and dynamic contrast enhanced (DCE-MRI) parameters were calculated from data acquired in a single imaging session conducted 6 - 8 hours following the injection of λ-carrageenan, a local inflammatory agent. T₂ increased in the inflamed muscle and transitioned to bi-exponential behavior. In diffusion measurements, all three eigenvalues and the apparent diffusion coefficient increased, but λ₃ had the largest relative change. Analysis of the qMT data revealed that the T₁ of the free pool and the observed T₁ both increased in the inflamed tissue, while the ratio of exchanging spins in the solid pool to those in the free water pool (the pool size ratio) significantly decreased. DCE-MRI data also supported observations of an increase in extracellular volume. These findings enriched the understanding of the relation between multiple quantitative MRI parameters and an isolated inflammatory pathology, and may potentially be employed to other single or complex myopathy models.

Introduction

Chronic muscle diseases, such as the idiopathic inflammatory myopathies (IIM) and muscular dystrophies (MD), exhibit complex pathologies that include variable degrees of muscle weakness, inflammation, adipose infiltration, loss of membrane integrity, and fibrosis (1,2). Of these, muscle weakness is the most common clinical feature, and is often accompanied by inflammation (3). Muscle groups are often disproportionately affected by these pathological features and different regions of a single muscle can be found at any stage of progression at any time (2,4-6). Thus, in advanced disease, a spatially heterogeneous disease presentation occurs. In addition to these common aspects, each myopathy has unique metabolic, perfusion, and neurological signatures, which further confound the interpretation of clinical data (1,7-9).

Monitoring these pathological characteristics is needed for accurate diagnosis and effective treatment design for myopathy patients (10). Clinical serology and biopsy have been the traditional means of diagnosis and monitoring. Serology cannot localize pathology, and the existence of a heterogeneous pathology may cause affected regions to be missed with spatially limited biopsy approaches (11,12). Muscle functional assessments have clear relevance, but rely on patient compliance. In contrast, noninvasive imaging techniques have proven informative for managing chronic myopathy patients, by avoiding direct harm to the tissue and better assessing the spatial distribution of muscle damage. MRI is particularly well suited to detecting structural and physiologic changes in diseased soft tissue (13). Most routine clinical MRI sessions for chronic myopathy patients include collecting anatomical reference scans, T₁-weighted and T₂-weighted images, and short tau inversion recovery images (3,14). However, a direct correlation between MR-based observations and clinical presentation of IIM or MD are not always present; as noted by Park et al (15) ³¹P magnetic resonance spectroscopy (³¹P-MRS) reveals metabolic defects related to functional disabilities.

Several quantitative MRI-based techniques have emerged in recent years that are sensitive to the pathological characteristics of muscle diseases. For example, T₂ increases and becomes multi-exponential with edema and inflammation (16-18). While it has long been recognized in ¹H-MRS studies that healthy skeletal muscle has multi-exponential T₂ decay associated with anatomical compartmentalization of protons (19,20), where as MR imaging studies have typically assumed mono-exponential transverse relaxation (21,22). Diffusion indices, such as the apparent diffusion coefficient (ADC) and fractional anisotropy (FA), are affected with ADC increasing and FA decreasing in models of muscle injury (16,23,24). Park et al. observed a 24% increase in T₁ in affected vastus lateralis muscles in dermatomyositis patients (9). However, T₁-weighted images of IIM muscle may show no contrast in regions that are hyper-intense on T₂-weighted and short tau inversion recovery images (2,9,14). Quantitative models of magnetization transfer (qMT-MRI) techniques were used to estimate the relative population fractions of proton pools (free and bound) (25,26), their relaxation rates and exchange rates. The perfusion-permeability product and volume fraction of the extracellular space can be measured by dynamic contrast enhanced MRI (DCE-MRI) (27). But while each of these techniques has been previously employed to study muscle disease, each has its particular limitations. T₂ not only increases with inflammation, but also with exercise (28) and fat infiltration (29). Magnetization transfer may reflect inflammation-induced increase in the free proton pool, but may also be affected by changes in the macromolecular proton pool (30), such as those caused by fibrosis. Thus, while each of these tools individually provides non-invasive insights into one or more biophysical tissue characteristics, the complex and heterogeneous nature of the myopathic landscape complicates simple interpretations of any single parameter.

One solution is to build multi-parametric profiles of isolated pathological characteristic models. For example, detailed studies using pairs of these methods have been reported in models of both muscle disease and inflammation (16,22). The combined effects of T₂ and diffusion have been well characterized (16,22), and the relationship between T₂ and magnetization transfer has been explored in muscle (31,32) and in several studies of MT in brain imaging (33-35). However, understanding these issues in complex animal models of myopathy, and especially in human myopathy patients, is difficult. Because the first major convergence among many muscle diseases is inflammation, a simplified inflammation model provides a logical starting point for developing and understanding a multi-parametric approach. Therefore, the goal of this study was to elucidate relationships between these MR-based observations in a simplified animal model of muscle inflammation.

Methods

We used a multi-parametric MRI approach to investigate inflammation as an isolated pathological feature in the quadriceps muscles of mice 6 - 8 hours after an injection of λ-carrageenan. In a single imaging session, transverse and longitudinal relaxation parameters were measured and qMT-MRI, diffusion tensor imaging (DTI), and DCE-MRI data sets were collected.

Animals

The following procedures were approved by the Vanderbilt University Institutional Animal Care and Use Committee. Eight healthy, male C57BL/j6 mice (Jackson Laboratories, Bar Harbor, ME), between 12 and 14 weeks old were studied using MRI. The mice were housed in a light/dark regulated facility and were allowed food and water ad libitum. Between one and three days (mean = 2.0 ± 0.3 days) prior to the imaging experiment, the mice received a surgically implanted jugular vein catheter to be used in the DCE-MRI procedure. The mean weight of the mice on the day of catheter implantation was 28.0 ± 0.4 g. The catheters' ports were monitored and flushed daily prior to use in the imaging experiment. On the day of the imaging experiment, the mice were injected with 100 μl of 1% λ- carrageenan (in saline) in the superficial, lateral portion of the anterior compartment of the thigh, directly over the vastus lateralis muscle. The needle was used to breach the epimysium of the VL muscles to ensure that the muscle would be exposed to the subcutaneously injected λ-carrageenan. In 5 mice, the right thigh was injected and in the other 3 mice, the left thigh was injected. In addition, four animals were studied using histology (see below).

MRI Acquisition

General Imaging Methods

Between 6 and 8 hours after the injection (16,36), the mice were imaged on a 4.7T Agilent/Varian Direct Drive scanner (Agilent Technologies, Santa Clara, CA, USA), with a 38 mm inner diameter, 33 mm rung length, 8 element Litz quadrature coil, tuned to 200.25 MHz (Doty Scientific, Inc. Columbia, SC, USA). Mice were anesthetized and maintained with 1 - 2.5 % isoflurane/oxygen and placed prone in a custom mouse holder (Fig. 1). This assembly was placed into the volume coil. Respiration was monitored using a pneumatic pillow sensor, which was used as an external trigger when respiratory gating was utilized. The target respiration rate of 25 - 45 breaths per minute was maintained by adjusting the isoflurane percentage [Small Animal Instruments, Inc. (SAI), Stony Brook, NY, USA]. The animal's external temperature was monitored using a thermistor probe placed between the right forelimb and the torso (SAI). To keep core body temperature at approximately 37 °C, axillary temperature was maintained at 34 °C by a flow of heated air into the bore of the magnet, controlled using a feedback circuit. The RF coil was placed at the isocenter of the magnet inside of copper covered, fiberglass sleeve that added additional shielding inside the bore. The instrument was equipped with Agilent 205/120HD imaging gradients with a gradient sensitivity of 2 mT/m/A and a maximum gradient strength of 600 mT/m (Agilent Technologies, Santa Clara, CA, USA) and was controlled using the VNMRj software package (version 3.2, Agilent Technologies, Santa Clara, CA, USA).

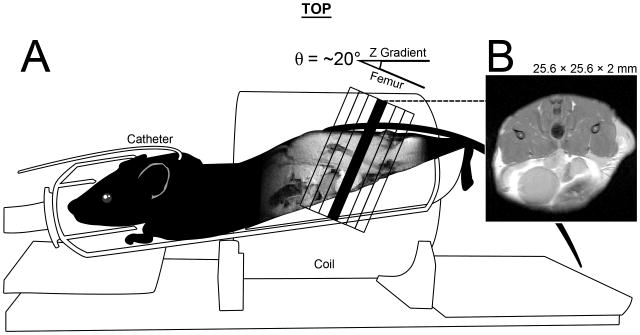
Figure 1.

An illustration of mouse positioning for MRI data acquisition. A) Mice were placed, prone and feet first, into a 38 mm inner-diameter, 33 mm long, 8 element, Doty-Litz coil. A custom mouse holder was built that elevated the hind limbs to minimize the angle θ between the laboratory z-axis and the angle of the femur. θ ranged from 12-25° and also served as the oblique angle for our axial images, which were perpendicular to the femur in the sagittal plane. The thigh muscle compartment rests above the lower abdomen, note the bladder in the ventral/anterior region of both sagittal and axial cross-sections. B) A representative image. All images were 25.6 × 25.6 × 2 mm. Multi-slice data (anatomical and DTI), had 7 slices that were centered on the femur (black outlined slices). Single slice data was acquired using the position of the center slice (black). Also shown is the placement of the jugular catheter used for DCE MRI.

The imaging protocol included high-resolution fast spin echo anatomical images, DTI, multiple-spin echo for T₂ calculations, selective inversion recovery (SIR) for T₁ and QMT parameter fitting, and a series of gradient echo images for DCE-MRI. The anatomical images were acquired by using a multiple-slice, fast spin-echo (FSE) sequence with TR/Effective TE = 2000/12 ms, matrix = 256 × 256, number of excitations (N_EX) = 4, 7 contiguous slices with slice thickness = 2 mm, frequency selective fat saturation, and echo train length (ETL) = 8. The 7 slices were positioned to cover the entire length of the femur, as shown in Fig. 1. For single slice data acquisition, the center slice (slice 4) position was used to define single slice geometry in 7 out of 8 mice; in one case slice 5 was used.

T₂ MRI Data Acquisition

T₂ data were collected using a multiple-echo, single slice sequence. Stimulated echo formation was minimized by using a Poon-Henkelman crushing scheme (37) (duration = 2 ms) and by using a composite 90x-180y-90x composite refocusing pulse (38). The imaging parameters were: TR = 2,000 ms, 40 total echoes with echoes 1 - 32 having 9 ms echo spacing [i.e. TE=(9, 18, 27,…, 288)] and echoes 33 - 40 having 50 ms echo spacing [i.e. TE = (338, 388, 438,…, 688)] ms, 128 × 128 sampling matrix, and slice geometry identical to the central anatomical slice.

Diffusion Tensor Imaging Data Acquisition

DTI data were acquired with a diffusion weighted multiple-slice FSE sequence. Imaging parameters included: TR/Effective TE = 1,200/25 ms, ETL = 2 with echo #1 corresponding to k-zero, 128 × 96 sampling matrix, 10 diffusion-weighted directions specified according to Jones et al. (39), and diffusion-encoding (b-) values of 12 s/mm² (imaging gradients only) and 500 s/mm² (imaging, diffusion sensitive, and cross terms). Frequency-selective fat saturation was applied using a single 10 ms Gaussian RF pulse to reduce the signal contribution from fat tissue. The offset frequency for the frequency-selective, fat-saturation-pulse was measured in non-localized 1-D spectra, acquired using a single-pulse sequence. The offset frequency ranged from − 684 Hz to - 616 Hz. Crushing gradients following the fat saturation pulse and before and after the refocusing pulse had a duration of 2 ms.

Quantitative Magnetization Transfer Data Acquisition

QMT data were collected using a single slice SIR imaging sequence with FSE readout using the methods of Li et al. (40). SIR imaging parameters included: TE = 10 ms, 64 × 64 sampling, inversion recovery time (TI)/pre-delay time(TD) = 1/3502, 290/4603, 330/1507, 222/3273, 767/10 ms. ETL = 8, with 8 more dummy echoes to ensure the saturation of both pools at the end of the echo train (26).

Dynamic Contrast Enhancement Data Acquisition

Finally, DCE data were collected by adapting procedures from Loveless et al. (41). A bolus of 120 μl of Magnevist® (0.1 mmol/kg Gd-DTPA) was auto-injected using a rapid infusion pump (Model PHD 2000 Programmable, Harvard Apparatus, Holliston, MA, USA) into each mouse through the jugular vein catheter at an infusion rate of 2.4 ml/min, over 3 seconds (41). A dynamic series of 250 single-slice gradient echo images was continuously acquired for 2.55 minutes prior to injection (30 images) and for 18.7 minutes afterwards (220 images). The DCE imaging parameters included: TR/TE = 10/3.1 ms, 128 × 128 sampling matrix, N_EX = 4, dynamic scan time of 5.1 s.

Except for DCE-MRI, which was always performed last, the quantitative imaging datasets were acquired in random order.

MRI Data Processing

General Imaging Analysis

All analyses were performed in MATLAB (The Mathworks, Inc., Natick MA). The anatomical images were used to define regions of interest (ROIs) in the VL muscles of the injected limb (“Inflamed”) and were compared to similar regions in the contra-lateral limb (“Control”). The same ROIs were used in all analyses described below and the mean signal magnitude in the ROIs were used for all image analyses. In addition, for visualization purposes only, parametric maps were formed by repeating all analyses on a pixel-wise basis. Signal to noise ratios (SNR) were calculated using the equation: SNR = mean ROI signal magnitude / (0.8 • standard deviation noise).

T₂ MRI Data Analysis

Mean signal magnitude data from ROIs of control and inflamed muscle were fit to both mono-exponential and bi-exponential transverse relaxation functions, shown respectively below in Equation 1:

$$S(\mathit{\text{TE}})=S_0{e}^{-\mathit{\text{TE}}/T_{2,\mathit{\text{mono}}}}+N$$ [1a]

$$S(\mathit{\text{TE}})=f_I{S}_0{e}^{-\mathit{\text{TE}}/T_{2,I}}+(1-f_I)S_0{e}^{-\mathit{\text{TE}}/T_{2,E}}+N$$ [1b]

where S(TE) is the observed signal, S₀ is the signal at TE = 0, N is the baseline noise, f is the volume fraction, and the subscripts I and E indicate the intracellular and extracellular spaces, respectively. Estimates of S₀, f, and T_2mono were obtained by using the fminsearch function in MATLAB to minimize the χ² statistic according to a Simplex algorithm. In addition, the appropriateness of the bi-exponential model was verified by conducting a non-negative least squares (NNLS) analysis. NNLS analysis was performed using the Multi-Exponential Relation Analysis (MERA) Toolbox Version 1.0 (http://www.vuiis.vanderbilt.edu/∼doesmd/MERA/MERA_Toolbox.html) running in the MATLAB environment.

Diffusion Tensor Imaging Data Analysis

The diffusion tensor, D, was formed using a weighted least squares algorithm, as described previously (42). D was diagonalized and the eigenvalues were magnitude-sorted. The mean apparent diffusion coefficient (ADC) was calculated as one-third of the trace of D and the FA was calculated using the standard equation (43).

Quantitative Magnetization Transfer Data Analysis

The mean signal intensity values in the ROIs were fitted as described by Li et al. (40), yielding the following parameter estimates: k_mf (the exchange rate between macromolecular bound pool to free pool), PSR (p_m/p_f, macromolecular-to-free water pool size ratio), M_f∞ (magnetization at full relaxation), S_f (inversion efficiency), R_1obs (R₁ observed) and R_1f (R₁ of the free pool). While the model fit for relaxation constants (R_1f and R_1obs) we discuss these parameters as the time constants T_1f and T_1obs. Due to the smaller matrix size of 64 × 64, qMT ROIs were resampled from those drawn for the other imaging contrast methods.

Dynamic Contrast Enhancement Data Analysis

Because of a skewed noise distribution, the signal intensity time courses were smoothed using a seven point sliding median filter. The data were fit to the standard and extended Tofts' models using the population-averaged arterial input function method described by Loveless et al. (41). T_1obs values, derived from the ROI analysis of the qMT data, were used to convert signal verses time to gadolinium concentration versus time for DCE analysis. This analysis yielded estimates of the interstitial volume fraction (v_e) and the contrast agent's transfer coefficient (K^trans, interpretable as the microvascular perfusion-wall permeability product). However, we were unable to obtain physiologically appropriate parameter estimates from this analysis consistently (vide infra). Therefore, we also conducted a simplified analysis in which we normalized the signal time course to a pre-injection mean signal of one. We then calculated the area under the curve (AUC) for the 1,000 s following injection (t = 0 s). Also, the mean normalized signal was measured for each ROI at ± 5 data points centered on t = 100 s, t = 400 s, and t = 1,000 s. Finally, we calculated the slopes between t = 100 s to t = 400 s (M_100,400) and t = 400 s to t = 1000 s (M_400,1000).

Statistical Analysis

Descriptive statistics include the mean and standard error (SE). For each variable of interest, a paired Student's t-test was used to compare the control and inflamed muscle data. In cases where we had a directional hypothesis, one-tailed t-tests were performed. Pearson correlations were calculated among all combinations of the following variables: T₁, T_2mono, λ₁, λ₂, λ₃, ADC, FA, PSR, AUC, M_100,400, M_400,1000. Statistical significance was accepted at p < 0.05.

Histology

Four additional mice were injected with λ-carrageenan and sacrificed 8 hours later, without MRI, and their VL muscles were excised for histology. Muscles were removed during a non-survival surgery and were pinned at resting length, coated in Tissue-Tek® optimum cutting temperature compound (Sakura, Torrance CA), and frozen in melting isopentane. Thin sections of 4 μm were cut using a Sakura cryostat. Slides were stained with hemotoxylin and eosin (H&E) and viewed with a light microscope.

Results

A representative high-resolution anatomical image is illustrated in Fig. 2 A. In the inflamed, λ-carrageenan injected limb, fluid pooled in the subcutaneous space and signal intensity increased in the affected region of muscle. In all animals, the VL was affected. In some animals, other quadriceps muscles were also affected; because of the inconsistent presentation of the effect, only data from the VL are presented. However, data from the other affected muscles generally matched those of the VL.

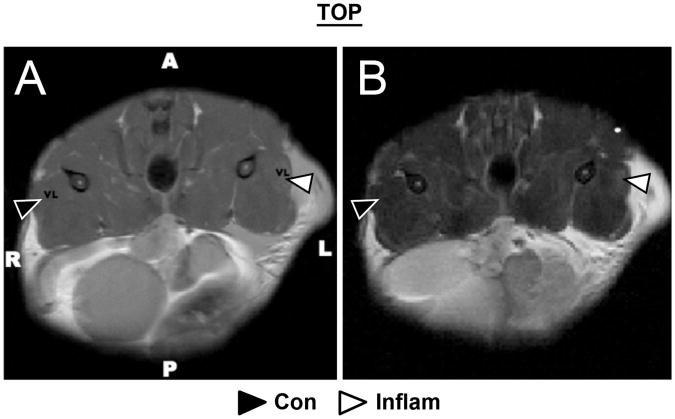
Figure 2.

Representative anatomical (A) and T₂-weighted (B) axial images of murine thigh muscles. The high resolution anatomical fast-spin-echo image (A) was used to define regions of interest in vastus lateralis (VL) muscle in the healthy-control tissue (black arrowhead) and the inflamed tissue (white arrowhead); near the site of the subcutaneous λ-Carrageenan injection. The edematous muscle has elevated signal on T₂-weighted (TR/TE = 2 s/54 ms) images (B). Pooling of fluid outside of the muscle compartment on the side of inflammation was commonly observed (A and B). The T₂ of this fluid was very high, and so this fluid presented with high signal in all images.

Transverse Relaxation in Inflamed Skeletal Muscle

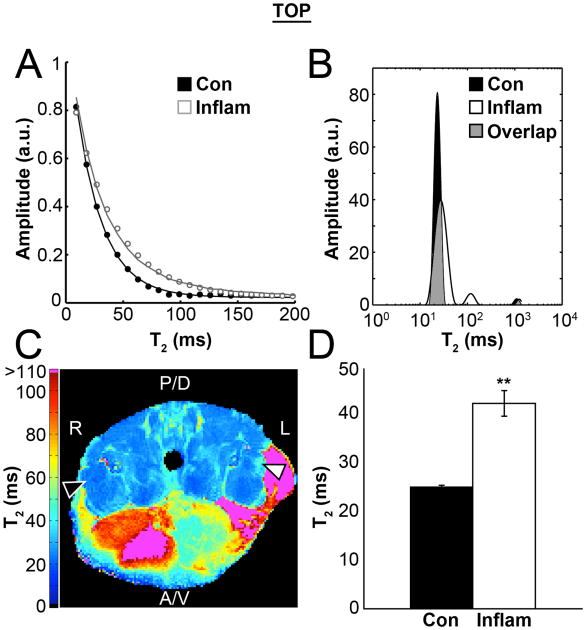
T₂-weighted images exhibited positive contrast in the inflamed regions. Control muscle had a mean SNR of 157.2 ± 4.9 in the TE = 9 ms images. Sample ROI signal decay data are shown in Fig. 3 A and demonstrate the results of the mono-exponential T_2mono curve fits. The NNLS T₂ spectra revealed two major components in the inflamed muscles and always a single distribution for the control data (Fig. 3 B). In the two cases of mild inflammation that did not clearly resolve into two peaks, the single peaks were broadened and shifted to higher T₂ values. A sample mono-exponential T₂ map is shown in Fig. 3 C. The T₂ value estimated by the mono-exponential fit was significantly greater in the inflamed muscles than in the control limb (Control 24.80 ± 0.38 ms vs. Inflamed 41.89 ± 2.59 ms; see Fig. 3 C – 3 D and Table 1). Fitting the data to bi-exponential T₂ models yielded a significant second component in 6 of 8 mice within the inflamed muscles (Table 1), but a second component having an apparent volume fraction greater than 0.05 and a T₂ value appropriate for interstitial water was never seen in the control limbs.

Figure 3.

A) Estimates of T₂ were calculated from the mean signal intensity in the control (Con) and inflamed (Inflam) muscle ROIs using 40 echo times, spaced by 9.1 ms. B) Non-negative least squares analysis suggests a second component appears in the T₂ spectrum when inflammation is present, as well as a broadening of the distribution of the faster components (> 100 ms); areas where there is overlap between the shorter components (∼25 - 40 ms) is shaded grey so that both curves can be visualized. C) A map of mono-exponential T₂ curve-fits shows regionally elevated T₂ values in the inflamed VL muscle (White arrowhead) as compared to the normal control limb (Black arrowhead). D) Finally, group means of the mono-exponential T₂ values were significantly longer than those of the healthy contralateral control tissue (n=8, p<0.001).

Table 1.

A multi-parametric comparison of control and inflamed muscle in the vastus lateralis of the quadriceps of C57BL6/j mice. Parameters were calculated from mean ROI signal from the original data. All parameters had an n = 8, unless otherwise noted. The last column provides the percent change (%Δ) and the absolute change (Δ) in mean values of each parameter. One tailed t-tests were applied when the hypothesis was directional. All t-test were paired, as the healthy contralateral limb served as the control.

	Parameter	Control	Inflammation	p (t-test)	%Δ (Δ)
T2	T2,mono(ms)	24.8 ± 0.4	41.9** ± 2.6	1.67 × 10−4	+69.2% (17.09)
	T2,I (ms)†	--	26.5 ± 0.9	--	--
	T2,E (ms)†	--	98.1 ± 3.9	--	--
	fI†	--	79.3 ± 2.7 %	--	--
	fe†	--	20.7 ± 2.7 %	--	--
DTI	λ1 (mm2/s)×10−3	1.63 ± 0.053	1.77** ± 0.042	6.69 × 10−3	+8.7% (+0.136)
	λ2 (mm2/s)×10−3	1.24 ± 0.067	1.39** ± 0.062	1.84 × 10−3	+12.3% (+0.152)
	λ3 (mm2/s)×10−3	0.91 ±0.086	1.06** ± 0.083	3.79 × 10−3	+19.3% (+0.157)
	ADC (mm2/)×10−3	1.26 ± 0.060	1.41** ± 0.055	1.14 × 10−3	+12.3% (+0.148)
	FA	0.20 ± 0.026	0.18 ± 0.022	0.0591	−9.37% (−0.023)
qMT	T1f(s−1)	1.67 ± 0.051	1.91* ± 0.037	0.0008	−12.6% (−0.242)
	PSR	0.10 ± 0.005	0.08** ± 0.003	7.19 × 10−3	−17.4% (−0.019)
	kmf	39.6 ± 4.581	34.3 ± 1.017	0.182	−5.55% (−5.230)
	Sf	−0.90 ± 0.028	−0.89 ± 0.011	0.411	−0.05% (+0.008)
	T1(s)	1.58 ± 0.043	1.78** ± 0.032	0.01	+12.9% (+0.20)
DCE	AUC	125.17 ± 13.80	237.32** ± 17.97	1.6 × 10−5	+95.9% (+112.1)
	Signal 100 s	1.13 ± 0.02	1.15 ± 0.02	0.17	+1.28% (+0.014)
	Signal 400 s	1.14 ± 0.02	1.27** ± 0.02	0.8 × 10−5	+11.6% (+0.132)
	Signal 1000 s	1.12 ± 0.02	1.28** ± 0.04	1.96 × 10−4	+14.1% (+0.159)
	M100,400	0.001 ± 0.002	0.025** ± 0.004	9.6 × 10−5	+2400% (+0.024)
	M400,1000	−0.002 ± −0.007	5×10−4± 0.002	0.055	−125% (+0.0027)
	Ktrans††	0.174 ± 0.031	0.156 ± 0.016	0.25	--
	ve††	0.427 ± 0.046	0.854** ± 0.119	6.35 × 10−3	--
	Ktrans (ET)††	0.147 ± 0.033	0.145 ± 0.015	0.47	--
	ve (ET)††	0.403± 0.048	0.844** ± 0.120	6.56 × 10−3	--
	vp (ET)††	0.031± 0.007	0.023 ± 0.009	0.28	--

Abbreviation not previously noted: ET, Extended Tofts model.

^**p < 0.01,

^*p < 0.05, 1-tailed t-test, paired

^†n = 6,

^††n = 4.

Diffusion in Inflamed Skeletal Muscle

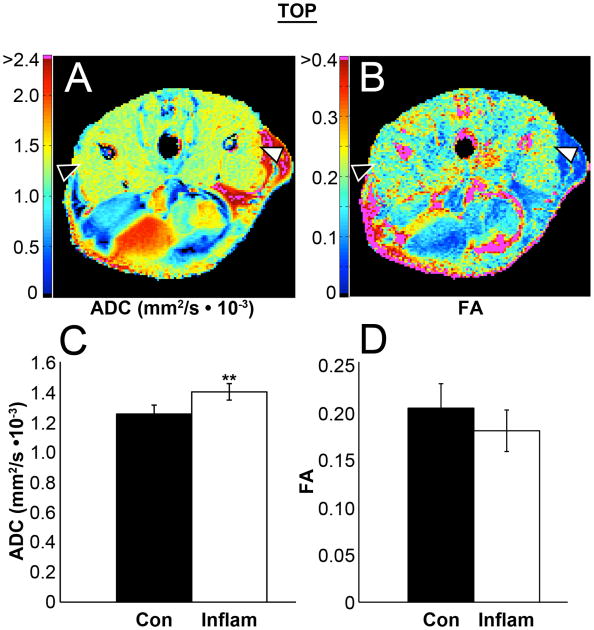
Raw diffusion-weighted images (DWI) had a signal-to-noise ratio (SNR) of 68.3 ± 2.8 (non-diffusion weighted image). All three eigenvalues (λ₁, λ₂, and λ₃) were increased significantly in inflamed muscle (by 8.7 %, 12.3 %, and 19.3 % respectively; Table 1). While the relative changes in the eigenvalues differed, the absolute changes among the eigenvalues were similar (mean change = 0.148 × 10³ mm²/s; Table 1). The ADC values in the control vs. inflamed muscle were 1.26 ± 0.06 vs. 1.41 ± 0.06 × 10³ mm²/s, respectively; p < 0.001 (Fig. 4 A,C, Table 1). Surprisingly, the FA did not change significantly, but trended toward a decrease in the inflamed muscle (p = 0.059; Fig. 4 B,D, Table 1); this lack of significance is likely due to FA not changing at all in two individuals or even slightly increasing in two other mice. In cases with large ADC increases in the inflamed limb, FA was always reduced. This inverse relationship was demonstrated further with correlation analysis (ADC vs. FA, r = -0.77; Table 2).

Figure 4.

Diffusion tensor imaging data was collected, using 10 directions of diffusion sensitive gradients. Tensors were calculated both per individual voxel for qualitative parameter maps of ADC (A) and FA (B), and from the ROI signal mean from each of the DW-images for group comparisons of the Eigen values and the ADC (C) and FA (D). All of the Eigen values and the ADC were significantly increased in the inflamed muscle. Note that regions of low SNR due to fat saturation can result in overestimated FA values (magenta regions in subcutaneous fat and bone; panel B).

Table 2.

Correlation coefficients for relationships between parameters in inflamed skeletal muscle. Parameters were calculated from mean ROI signal in all cases. T_2mono was calculated independently, while indices of diffusion (ADC and FA) were estimated in the same fitting process and are dependant on λ₁, λ₂, and λ₃. Similarly, T₁ and PSR are related, as they were estimated during the qMT data fitting.

	T1	T2mono	λ1	λ2	λ3	ADC	FA	PSR	AUC	M100,400	M400,1000
T1	1.00	0.83**	0.18	0.17	0.66*	0.44	−0.66*	−0.82*	0.06	0.31	0.34
T2mono		1.00	0.45	0.58	0.90**	0.79*	−0.86**	−0.51	0.14	0.63*	0.18
λ1			1.00	0.74*	0.55	0.81**	−0.28	0.20	−0.11	0.61	−0.37
λ2				1.00	0.69*	0.91**	−0.58	0.23	0.00	0.45	−0.32
λ3					1.00	0.90**	−0.95**	−0.44	0.05	0.66*	0.16
ADC						1.00	−0.77*	−0.08	0.00	0.65*	−0.14
FA							1.00	0.52	−0.10	−0.52	−0.29
PSR								1.00	−0.05	−0.06	−0.55
AUC									1.00	0.48	0.77*
M100,400										1.00	0.33
M400,1000											1.00

(Pearson's r, n=8,

^*p<0.05,

^**p<0.01)

Quantitative Magnetization Transfer in Inflamed Skeletal Muscle

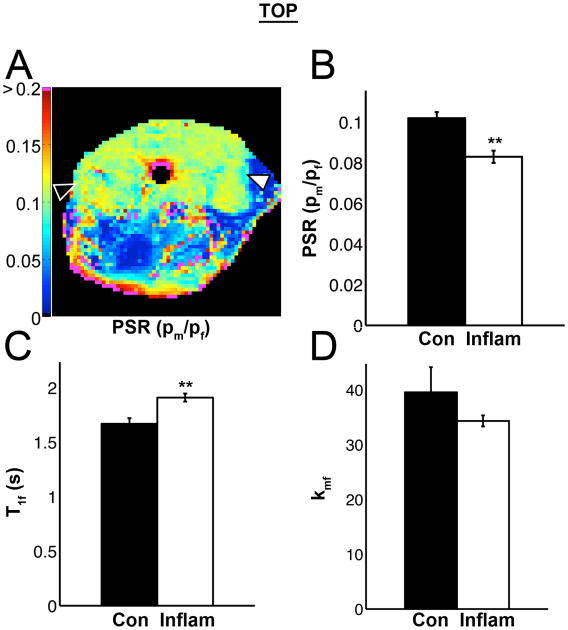
The SNR of the first inversion recovery time/pre-delay delay (1/3502) images was 555.0 ± 106.5. S_f was used as a quality control monitor and was not different between the two groups (Table 1): -0.90 ± 0.01 (Control) and -0.89 ± 0.01 (Inflammation). The pool-size-ratio (PSR) was significantly reduced (0.102 ± 0.003 vs. 0.083 ± 0.003; p < 0.001) in the inflamed muscle tissue (Fig. 5 A-B, Table 1). T_1obs increased significantly in the inflamed muscle tissue, as well as the T₁ of free water (T_1f) (Fig. 5 C, Table 1; p < 0.05). The fast macromolecular-to-free-pool exchange rate constant k_mf did not change significantly (Fig. 5 D).

Figure 5.

Quantitative magnetization transfer (qMT) imaging data were collected with 5 acquisition parameter combinations of [inversion recovery times (ms)/pre-delay times (s)]: 2.8/3.502, 30.8/4.603, 34.8/1.507, 223.8/3.27, and 768.8/0.01. 64 × 64 pixel parameter maps were calculated for R_1f, R₁, PSR, S_f, k_mf, and M_f∞. A PSR map is shown in panel A. B) In group data, PSR significantly decreased in inflamed muscle. C) The T₁ of the free water pool (T_1f) also significantly increased, as well as T₁ observed (T₁; Table 1). D) The fast exchange rate k_mf was not different and was sensitive to noise.

Dynamic Contrast Enhancement in Inflamed Skeletal Muscle

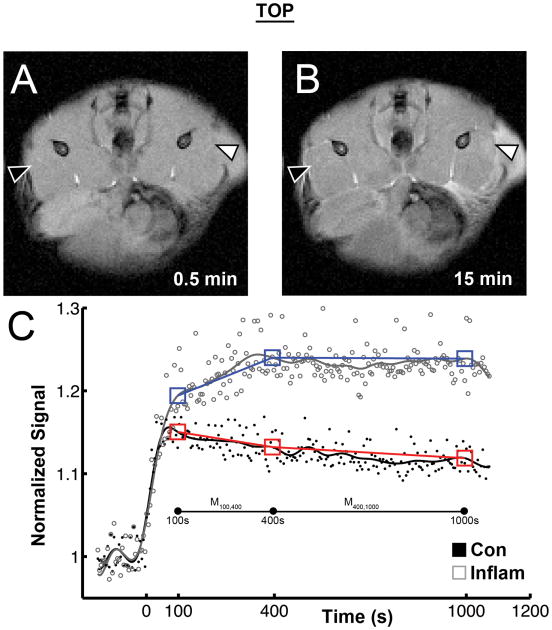
Fig. 6 shows sample images from the DCE experiment, prior to (panel A) and following (panel B) injection. The mean SNR in control tissue of the baseline images was 47.5 ± 1.4. As Fig. 6 B shows, the contrast agent injection caused the signal intensity to increase, peak, and then wane over time (Fig. 6 C). The AUC was significantly larger for the inflamed muscles than for the control muscles (Fig. 6 C, Table 1). The K^trans estimates from the standard and extended TOFTS models were physically and physiologically reasonable, but v_e was consistently overestimated. Furthermore, curve-fitting of the inflamed muscle ROIs often resulted in v_e values greater than 1, and thus were deemed to be unacceptable results. In the simplified analysis, the mean signal in the control and inflamed ROIs did not differ at t = 100 s. There were significant signal increases in the inflamed tissue ROI's (p < 0.01) at both t = 400 s and 1000 s (Table 1). The M_100,400 slope was significantly increased in the inflamed limb (p < 0.01).

Figure 6.

To investigate changes in perfusion and the extra-cellular space, 20 minutes of dynamic contrast enhancement MRI data were acquired. Before gadolinium contrast agent was injected, 2.5 minutes of baseline gradient echo images (5.1 s temporal resolution) were collected. Panel A shows a baseline GRE image. After the time of injection (t = 0), the signal in both control and inflamed muscle sharply increased, but this effect was consistently greater in the inflamed limb. This was reflected in the significant increase in the area under the curve (AUC) measurements. Panel C shows the signal time course of a typical animal. AUC was calculated from t = 0 to t = 1000 from a polygon fit of the raw data (Control: black circles, Inflamed: grey open circles). Since TOFTs model failed to fit the data well, a Butterworth filter was used to smooth signal noise (Control: black line, Inflamed: grey line). From this smoothed data, signal means were calculated for t = 100 s, t = 400 s, and t = 1,000 s, with a window of ± 5 data points (Control: red boxes, Inflamed: blue boxes). The slopes between these points were then calculated (M_100,400 and M_400,1000). The M_100,400 for the Inflamed muscle were significantly increased (p < 0.01).

Histology of healthy and inflamed muscle

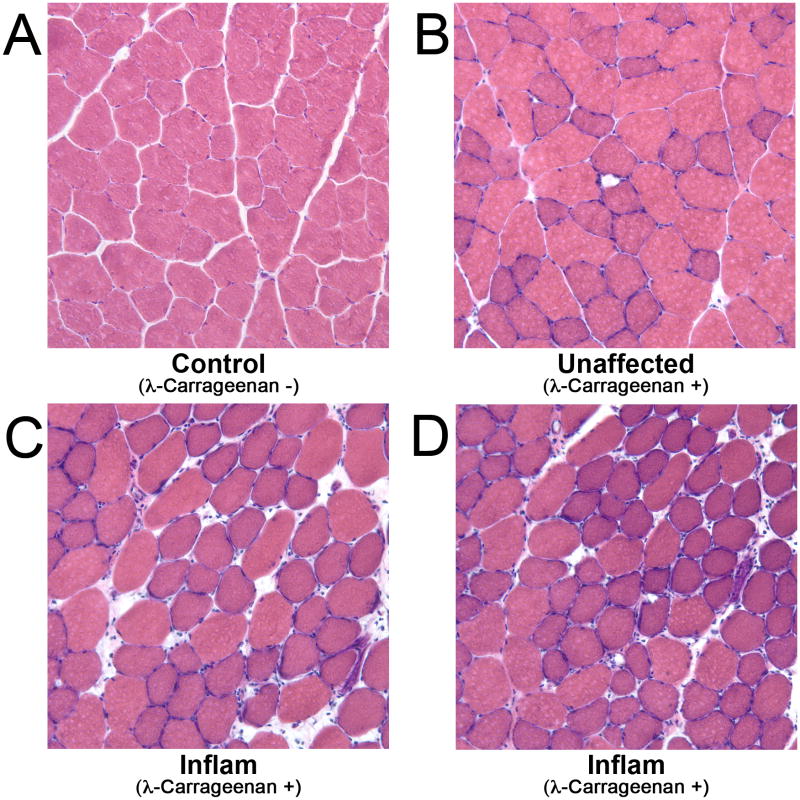
Figure 7 provides the histology data. All healthy control muscle had a similar appearance to the data presented in Fig. 7A, features of which included angular muscle fibers with minimal extracellular space and few leukocytes among the fibers. Like the distribution of elevated T₂ in the muscles of the injected limb, signs of inflammation in the histological data showed the inflamed regions to be focal, surrounded by un-affected regions of muscle (such as Fig. 7B). Local regions of acute inflammation, such as in Fig. 7C and 7D, displayed many infiltrating cells and large gaps between fibers. In addition, the fibers were swollen and have a round cross-sectional morphology.

Figure 7.

Hemotoxylin and Eosin stained healthy control muscle (A), apparently unaffected muscle from the λ-carrageenan injected limb (B), and inflamed skeletal muscle (C,D). The healthy muscle in panel A has angular fibers, minimal spacing between fibers, and a low number of infiltrating cells. Panel B shows muscle from the injected limb that does not appear to be inflamed. Panels C and D show regions of inflamed muscle tissue; note the swollen, round appearance of the fibers, the increased interstitial space, and the numerous leukocytes migrating into the region.

Discussion

The use of small animal models of chronic muscle disease has been a fruitful approach to developing MRI biomarkers for muscle health. Because of their complex pathology, however, they exhibit multiple pathological features that can complicate interpretation of the data. Therefore, we used a simplified model of inflammation to describe the changes in relaxation, diffusion, qMT, and DCE parameters due to inflammation alone. Inflammation was chosen as the isolated pathological feature for this initial study because of its early and central role in myopathy progression and because immuno-suppression is credited with both reducing chronic necrosis and prolonging skeletal muscle function in IIM and MD (44,45). These factors indicate the importance of monitoring and treating inflammation in muscle disease. The multi-parametric approach used in the present study produced an array of noninvasive measures that agree with reported physical attributes of inflamed muscle and that provide the basis for further study in more complex models of muscle pathology.

It has been widely reported that T₂ relaxation is elevated in inflamed skeletal muscle (16,17,46). The T₂ data in Fig. 2 and Fig. 3 and in Table 1 further demonstrate that this parameter is highly sensitive to inflammation. The MRI signal from control muscle was best fitted to a mono-exponential model (Table 1), in accord with other findings (16). However, the data from inflamed muscles were generally best described by a bi-exponential transverse relaxation model, including a long T₂ component that is consistent with the addition of a significant extracellular water fraction (Table 1) (16,19,22). Likewise, NNLS analysis also indicated a second T₂ component: in 6 out of 8 cases a second peak or a bimodal distribution of T₂ components appeared. Other studies have similarly shown that osmotically driven edema and λ-carrageenan induced inflammation in the rat paw (22) and in lower limb muscle of mice (16) have bi-exponential T₂ behavior similar to the data presented here. In addition, histology studies have shown that λ-carrageenan induces a local inflammatory response, driven by polymorphonuclear monocytes (PMNs), complement, and histamine, and causing immune cell invasion and increased vascular permeability (47). The increase in vascular permeability is traditionally held responsible for the accumulation of extracellular fluid (48). The histology results presented in Figure 7 are consistent with these previously reported data, as there were rounded fibers, an expanded interstitial space, and infiltrating cells in the injected limb only.

In the current study, the shorter T₂ component in the bi-exponential model of edema is very close to the mono-exponential T₂ of healthy tissue. The intracellular T₂ value (short component ∼25 ms) did not change. Because there is a linear relationship of T₂ and intracellular volume (49,50), this suggests that the change in intracellular volume corresponding to cell margin rounding (Fig. 7C-D) was not significant enough to change the intracellular T₂ value. Collectively, these data indicate that global increases in T₂ of inflamed muscle of this model are largely due to the expansion of the extracellular compartment.

Concerning the interpretation of the DCE data, we first note that we were unable to find a physiologically relevant and appropriate fit of the data using either the standard Tofts or extended Tofts models, for either the control or injected muscles. The K^trans values that we obtained were similar to other values in the literature (51), and did not differ significantly between the control and inflamed regions, suggesting similar levels of perfusion. However, the v_e estimates were inappropriately high, with the greatest difficulties having been encountered in the inflamed muscles when the late phase of Magnevist enhancement resulted in plateau or waxing signal behavior. These findings may suggest that these models were particularly inappropriate for inflamed skeletal muscle. This would occur if the rapid mixing assumption is not valid; or it may have been that the population-averaged AIF approach was not appropriate for these experimental conditions. In either case, caution is advised in employing these models in inflamed muscle tissue, at least during studies of low molecular weight contrast agents such as Magnevist; we note that Faranesh et al. observed physiologically appropriate v_e values in the DCE study using a gadolinium-linked macromolecule agent (52). Furthermore, the Faranesh et al. study illustrates the negative effects of noise on fitting to the TOFT's models and, at an SNR of 47.5, it is possible that our data were SNR limited in this respect.

As an alternative to model-based DCE analysis, we used the mean normalized signal values at times of 100 s, 400 s, and 1000 s following injection of contrast agent, and the slopes between these points, as indicators of the scale and rate of signal change. This is similar in principle to the approach described by Loerakker et al. (53), except that we used three time points rather than two. The 100, 400, and 1000 s time points were chosen because visual inspection showed them to reflect the approximate points of peak signal intensity from control tissue (100 s) and inflamed tissue (400 s) and to correspond approximately to a point at which late gadolinium enhancement is observed clinically (1000 s). The initial (up to 100 s) portions of the signal enhancement curves appeared similar in the control and inflamed regions and the mean signal values from the two regions did not differ significantly from each other at t = 100 s. However, the signal values from inflamed muscle regions were significantly increased at both the 400 s and 1000 s time points (Table 1). The M_100,400 slope was significantly greater in inflamed muscle regions than in control regions, and this slope was also significantly correlated with the monoexponential T₂ values (Table 2). The M_400,1000 slopes did not differ significantly; and although the AUC was greater for inflamed muscle than for control muscle, this value was not correlated with T₂. Given the appearance of the second T₂ component, the known restriction of Magnevist to the extracellular space of tissues whose cells have intact plasma membranes, and the previously reported histological findings, it is reasonable to interpret the changes in DCE parameters as reflecting contrast agent pooling in an enlarged extracellular space. Of all the DCE-derived parameters measured, the rate of signal enhancement during the time period from 100 s to 400 s post-injection was the most sensitive DCE index of inflammation.

This increase in extracellular water also affected the water diffusion properties of the inflamed muscle, as revealed by DTI. DTI has proven to be a useful method for characterizing normal and pathologically altered muscle tissue (54). The basis for these studies is that the protein and membranous structures in muscle provide barriers to diffusion, causing the self-diffusion coefficient of water to be lower in muscle than in free water. Moreover, these barriers to diffusion are less frequent along the fiber axis than orthogonal to it, causing diffusion anisotropy to exist. Microscopic changes in the cellular and molecular environments, such as Z-line streaming, increased membrane permeability to water, and inflammation, are expected in chronic myopathies. Because these structural changes affect the spacing of physical barriers to free diffusion, DTI-MRI provides an imaging method sensitive to those pathological characteristics of muscle disease that are structural in nature. In the present study, a significant increase in ADC occurred in the inflamed muscle, having been brought about by a general increase in diffusivity in all directions. This increase in general diffusivity is likely to be a direct effect of the expanded extracellular space, despite having used a short TE that (by virtue of T₂ effects) would tend to bias these measurements toward the diffusion properties of the intracellular space. Indeed, there was a significant correlation between ADC and T₂. In addition, λ₃ experienced a large relative increase and was strongly correlated with T₁, T_2,mono, and M_100,400 (Table 2). All of these observations are consistent with an increase in extracellular water (interstitial, and possibly, vascular fluid).

Unlike studies of muscle damage using ischemia/reperfusion protocols (23) or eccentric contraction-induced injury in dystrophic muscle (55) which cause significant sarcolemmal damage and necrosis, or a previous study of inflammation induced by an injection of λ-carrageenan (16), we did not observe a significant decrease in FA. The SNR of the DTI data, used as a quality control measure, was deemed adequate (42,56). While a significant change in FA was not detected, there was a significant correlation between ADC and FA (p < 0.05, Table 2). These parameters are intrinsically related, in that they are calculated from the same eigenvalues. Nonetheless, the association of FA with ADC, T₂, and other MRI parameters sensitive to inflammation suggests that the lack of significant change in the mean FA value may reflect the combined effects of low dynamic range, noise sensitivity, and biological variability in the responses. A second possible interpretation lies in the conclusion, made above, that the intracellular compartment experienced little if any expansion of volume. Also, we would anticipate that the cellular membrane permeability to water was not affected. It is thus possible to speculate that the decrease in FA previously reported in more complex muscle pathology models may have been influenced by intracellular or membrane changes, rather than by the expansion of the extracellular space. Finally, it may be that a longer TE would have provided greater sensitivity of the FA to diffusion changes in the extracellular space, as the FA of the extracellular water in this model of muscle inflammation is lower than that of the intracellular water (16). To understand muscle tissue diffusion more completely, a range of diffusion times and TE values should be further investigated.

Magnetization transfer MRI is sensitive to changes in the amount of protonated macromolecules in relation to the cellular water. Parameters associated with qMT may be valuable in early detection of tissue fibrosis, but this may be overshadowed by the effects of edema. To better understand the effects of inflammation alone, we also collected qMT data. There was a decrease in PSR as the free water pool increased in the inflamed tissue. We observed an increase in T_1f within the inflamed muscle. It is interesting that there was a negative correlation between PSR and T₁ (Table 2). The fast exchange rate, k_mf, is particularly sensitive to noise (40) and changes were small and not significant. These findings indicate the sensitivity of PSR and T₁ to inflammation.

It could reasonably be argued that more advanced implementations of some of the MRI approaches could have been used. For example, additional tissue microstructural characterization might have been possible by using multiple b-values to observe additional diffusion or pseudo-diffusion components and/or to measure diffusion kurtosis; or by obtaining additional diffusion directions to fit the data to a model such as high angular resolution diffusion imaging. Balancing the additional the additional information gained by approaches such as these are 1) a loss of potential translatability to human studies and 2) the potential benefits of the multi-parametric approach in producing a more specific interpretation of imaging findings by reducing the ambiguity that is present by measuring a smaller number of parameters.

Summary and Conclusions

The multi-parametric MRI approach to assessing skeletal muscle health implemented here is based on the observation that diseased muscles may experience a large variety of pathological processes simultaneously. This condition makes it difficult to attribute individual MR-based measures to a specific pathological feature. The current study of inflammation as an isolated pathological feature increases our understanding of how inflammation influences quantitative MRI parameters that are commonly used or proposed to characterize of muscle diseases. We aim to continue investigating this approach in increasingly complex mores of human muscle disease.

List of Abbreviations and Symbols

ADC

Apparent Diffusion Coefficient

AUC

Area Under the Curve

b-value

Diffusion Weighting Value

DCE

Dynamic Contrast Enhancement

DTI

Diffusion Tensor Imaging

DWI

Diffusion Weighted Imaging

ETL

Echo Train Length

f_I

Intracellular Fraction from the Bi-exponential model of T₂

f_E

Extracellular Fraction from the Bi-exponential model of T₂

FA

Fractional Anisotropy

FOV

Field Of View

FSE

Fast Spin Echo

IIM

Idiopathic Inflammatory Myopathies

k_mf

Exchange rate from the macromolecular pool to the free water pool

MD

Muscular Dystrophies

MRI

Magnetic Resonance Imaging

MRS

Magnetic Resonance Spectroscopy

MT

Magnetization Transfer

N_ex

Number of Excitations

NNLS

Non-Negative Least Squares

p

Probability of a Type I statistical error

PMN

Polymorphonuclear Monocytes

PSR

Pool Size Ratio

qMT

Quantitative Magnetization Transfer

ROI

Region Of Interest

SIR

Selective Inversion Recovery

SNR

Signal to Noise Ratio

STIR

Short Tau Inversion Recovery

T₁

Longitudinal Relaxation Time Constant

T_1f

Longitudinal Relaxation Time Constant of the Free Proton Pool

T₂

Transverse Relaxation Time Constant

T_2,mono

T₂ from the mono-exponential model

T_2,I

T₂ of the Intracellular Component from the Bi-exponential model

T_2,E

T₂ of the Extracellular Component from the Bi-exponential model

TD

Delay Time

TE

Echo Time

TI

Inversion Time

TR

Repetition Time

VL

Vastus Lateralis Muscle

λ₁

First eigenvalue of the diffusion tensor

λ₂

Second eigenvalue of the diffusion tensor

λ₃

Third eigenvalue of the diffusion tensor