Estimate of the uncertainties in the relative risk of secondary malignant neoplasms following proton therapy and intensity-modulated photon therapy

Abstract

Theoretical calculations have shown that proton therapy can reduce the incidence of radiation-induced secondary malignant neoplasms (SMN) compared with photon therapy for patients with prostate cancer. However, the uncertainties associated with calculations of SMN risk had not been assessed. The objective of this study was to quantify the uncertainties in projected risks of secondary cancer following contemporary proton and photon radiotherapies for prostate cancer. We performed a rigorous propagation of errors and several sensitivity tests to estimate the uncertainty in the ratio of relative risk (RRR) due to the largest contributors to the uncertainty: the radiation weighting factor for neutrons, the dose-response model for radiation carcinogenesis and interpatient variations in absorbed dose. The interval of values for the radiation weighting factor for neutrons and the dose-response model were derived from the literature, while interpatient variations in absorbed dose were taken from actual patient data. The influence of each parameter on a baseline RRR value was quantified. Our analysis revealed that the calculated RRR was insensitive to the largest contributors to the uncertainty. Uncertainties in the radiation weighting factor for neutrons, the shape of the dose-risk model and interpatient variations in therapeutic and stray doses introduced a total uncertainty of 33% to the baseline RRR calculation.

1. Introduction

The advancement of technologies in radiation therapy has accelerated rapidly in recent decades. Newer treatment planning and beam delivery technologies have enabled clinicians to escalate and conform doses to tumor volumes while simultaneously reducing radiation exposures to normal tissues. Normal tissue sparing is of increasing importance because cancers are being diagnosed at earlier ages and survival rates for primary cancers are increasing. For example, 5 year disease-specific survival rates for patients with prostate cancer are greater than 99% (SEER 2007). However, epidemiological studies have established that radiation therapy is risk factor for secondary malignant neoplasms (SMN) (Brenner et al 2000). The combination of these factors suggests that increasing numbers of patients treated for cancer will live long enough following treatment for a SMN to develop.

Ideally, the controversy surrounding the risk for developing a SMN following contemporary external-beam radiotherapies would be resolved with randomized patient outcome studies that include high-quality dose reconstructions and a 10 year or longer mean follow-up time. However, the inherent length of such studies limits their feasibility as well as their relevance to the latest treatment technologies. To overcome this problem, several investigations have instead focused on predicting the risk of SMN (Fontenot et al 2009b, Newhauser et al 2009c, Taddei et al 2008, 2009, Schneider et al 2006, 2007, 2008, Zacharatou Jarlskog et al 2008). In this approach, dose-response models from the literature have been combined with new dosimetric data to predict the risk of SMN incidence and mortality. The uncertainties of the risk projections calculated in this manner depend on many factors, including the endpoint (cancer incidence versus mortality), the type of risk (relative risk versus absolute risk), the accuracy of the therapeutic and stray radiation dose distributions, the relative biological effectiveness (RBE) of the radiation for carcinogenesis, the radiation type (e.g. photons versus protons), details of the beam delivery (e.g. scanned versus scattered proton beams), and the age and gender of the patient. For example, Newhauser et al (2009c) recently estimated the risk of SMN incidence for a pediatric patient receiving proton therapy for craniospinal irradiation, examining the impact of neutron RBE, scanned versus scattered proton beams and other factors on the risk analysis. More recently, Fontenot et al (2009b) reported on relative risk projections for patients receiving proton versus photon radiation therapies for cancer of the prostate. Although that work included a limited discussion of the corresponding uncertainties, the influence of the largest sources of uncertainty on the risk calculations was not examined. Namely, itwas unknown how the results of that studywould be affected by uncertainties in the dose-responsemodel for radiation carcinogenesis, uncertainties in the radiation weighting factor for neutrons, and interpatient variations in absorbed dose.

The objective of this study was to quantify the uncertainties in projected risks of SMN following contemporary proton and photon radiotherapies for cancer of the prostate. In particular, we performed a rigorous propagation of errors and several sensitivity tests to estimate the uncertainty in the ratio of relative risk (RRR) following passively scattered proton therapy to that of intensity-modulated photon radiotherapy (IMRT).

2. Methods and materials

2.1. Baseline RRR calculation

Our previously reported methods for determining SMN risk in patients undergoing radiation therapy for early-stage prostate cancer (Fontenot et al 2009b) are summarized here. In brief, a two-field, parallel-opposed proton therapy plan and a seven-field 6 MV photon IMRT plan were developed in accordance with clinical protocol at our institution. Normal tissue doses from the therapeutic beam were calculated by the treatment planning software (Eclipse, Varian Medical Systems, Palo Alto, CA). Stray doses from proton therapy treatments (e.g. neutrons) were determined fromMonte Carlo simulations (Newhauser et al 2009b, Fontenot et al 2008), while stray doses from IMRT (e.g. leakage) were determined from available data (Howell et al 2006, Kry et al 2005). Neutron doses emanating from proton treatment were weighted using mean radiation weighting factor, $\overline{w_R}$, values determined from International Commission on Radiological Protection (ICRP) Publication 92 (2003) and the calculated neutron spectral fluence in each organ. Risk of SMN was determined by calculating the excess relative risk (ERR) in each organ using the linear no-threshold (LNT) model and organ-specific coefficients from the Biological Effects of Ionizing Radiation (BEIR) VII Committee (2006). For organs exposed to non-uniform doses, ERR was calculated voxel by voxel and the total ERR for developing a SMN was computed as the sum of the ERR values over all sensitive tissues (designated by T). This approach is mathematically equivalent to the formalism of Schneider et al (2007), who calculated absolute risk for organs irradiation with an inhomogeneous dose distribution. The RRR value was then calculated as the ratio of the ERR from proton therapy to the ERR from photon therapy:

$$RRR=\frac{ER{R}_{\text{proton}}}{ER{R}_{\mathrm{I}\mathrm{M}\mathrm{R}\mathrm{T}}},$$ (1)

where the ERR for each modality m is given by

$$ER{R}_{\mathrm{m}}=\sum _{\mathrm{T}}ER{R}_{\mathrm{T}},$$ (2)

where ERR_T is the ERR of developing a second cancer in tissue T, and is given by

$$ER{R}_{\mathrm{T}}=ER{R}_1+ER{R}_2=(D_{1,\mathrm{T}}{w}_{1,R}+D_{2,\mathrm{T}}{w}_{2,R})\times R_{\mathrm{T}},$$ (3)

where ERR₁ and ERR₂ are the ERR of developing a second cancer in tissue T from therapeutic and stray radiation, respectively; D_1,T and D_2,T are the absorbed doses to tissue T from therapeutic and stray radiation, respectively; $\overline{w_{1,R}}$ and $\overline{w_{2,R}}$ are the mean radiation weighting factors of the therapeutic and stray radiation fields, respectively; and R_T is a tissue-specific risk coefficient. The calculated RRR value for the ‘medium’ patient in our previous study was 0.66 (Fontenot et al 2009b), indicating that proton therapy confers a significantly lower risk of a SMN than IMRT. For the purpose of the present uncertainty analysis, the ‘medium’ patient, taken from a sample of ten consecutive patients from our clinic, is assumed to be representative of the patient population treated at our institution for low-risk prostate cancer.

2.2. Uncertainties

Using standard error propagation techniques, the uncertainty in RRR can be expressed as

$${\left(\frac{{\sigma }_{RRR}}{RRR}\right)}^2=\sum _{\mathrm{m}}{\left(\frac{{\sum }_{\mathrm{T}}{\sigma }_{ER{R}_{\mathrm{T}}}^2}{{({\sum }_{\mathrm{T}}ER{R}_{\mathrm{T}})}^2}\right)}_{\mathrm{m}}-2\frac{{\sigma }_{ER{R}_{\mathrm{h}}ER{R}_{\mathrm{p}}}^2}{ER{R}_{\text{proton}}ER{R}_{\mathrm{I}\mathrm{M}\mathrm{R}\mathrm{T}}},$$ (4)

where the final term is the covariance. Expanding terms, the uncertainty in the RRR (not including the covariance term) is

$${\left(\frac{{\sigma }_{RRR}}{RRR}\right)}^2=\dots \sum _{\mathrm{m}}{\left(\frac{{\sum }_{\mathrm{T}}{(ER{R}_1)}^2{\left(\frac{{\sigma }_{D_{1,\mathrm{T}}}}{D_{1,\mathrm{T}}}\right)}^2+{(ER{R}_1)}^2{\left(\frac{{\sigma }_{\overline{w_{1,R}}}}{\overline{w_{1,R}}}\right)}^2+{(ER{R}_2)}^2{\left(\frac{{\sigma }_{D_{2,\mathrm{T}}}}{D_{2,\mathrm{T}}}\right)}^2+{(ER{R}_2)}^2{\left(\frac{{\sigma }_{\overline{w_{2,R}}}}{\overline{w_{2,R}}}\right)}^2+{(ER{R}_{\mathrm{T}})}^2{\left(\frac{{\sigma }_{R_{\mathrm{T}}}}{R_{\mathrm{T}}}\right)}^2}{{({\sum }_{\mathrm{T}}ER{R}_{\mathrm{T}})}^2}\right)}_{\mathrm{m}}.$$ (5)

The uncertainties associated with radiation weighting factors and risk models used in our previous work (Fontenot et al 2009b) are large and difficult to estimate from first principles. Therefore, we approximated ${\sigma }_{\overline{w_R}}$ and σ_RT as zero for both modalities for the baseline RRR calculations. The present analysis extends that work by taking into account plausible interval of values of ${\sigma }_{\overline{w_R}}$ and σ_RT. Additionally, we sought to characterize the uncertainty in the RRR value arising from interpatient variations in organ doses, particularly to the rectum and bladder. This approach allowed for comprehensive testing of the sensitivity of the RRR to changes in these key variables, with the advantage of obviating the need for a detailed mechanistic understanding of the underlying processes of radiation carcinogenesis. Our approach to examining each of these variables is described below.

2.2.1. Mean radiation weighting factor

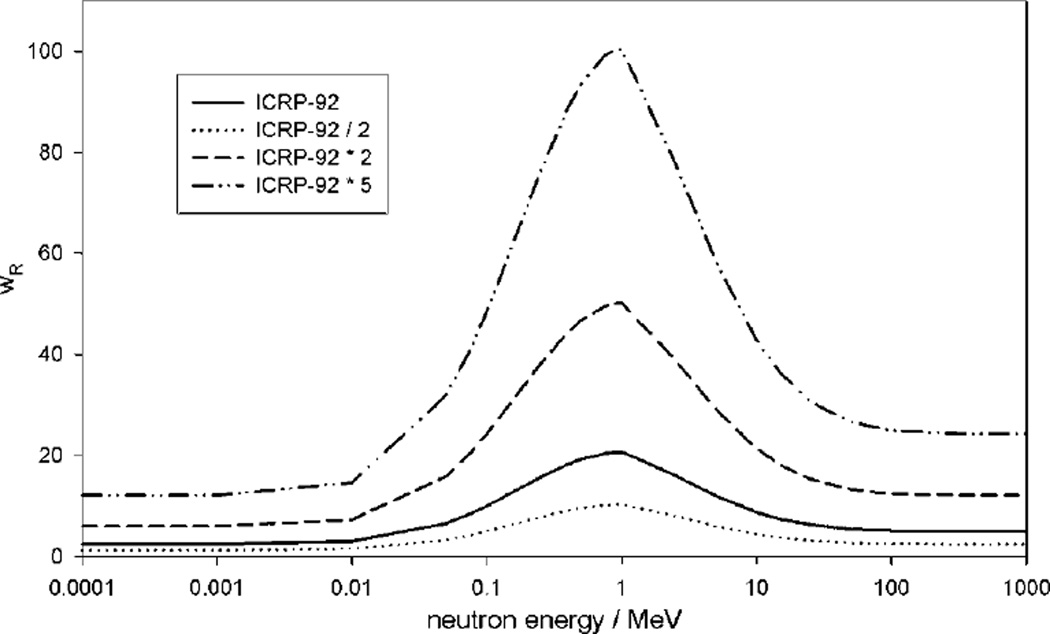
For the baseline RRR calculation, we determined the $\overline{w_R}$ value used to convert absorbed dose, D, from neutrons to equivalent dose, H, using values recommended in ICRP Publication 92 and the calculated neutron spectral fluence. However, there is substantial uncertainty in $\overline{w_R}$ values. For example, the ICRP recommended a maximum neutron radiation weighting factor of 20 for low-energy neutrons, but a recent reanalysis of atomic bomb survivor data has suggested that the neutron RBE for carcinogenesis could be as high as 100 (Kellerer et al 2006). Therefore, we estimated the sensitivity of RRR to uncertainties in the neutron radiation weighting factor by recalculating the RRR value (using the LNT model) for the ‘medium’ patient using baseline $\overline{w_R}$ values that were scaled linearly by factors of 0.5 and 2 (see figure 1). These values were chosen because they bound the plausible interval of the true $\overline{w_R}$ value (Hall 2007). Additionally, we re-computed with a larger scaling factor of 5 to determine the value of $\overline{w_R}$ at which RRR exceeded unity (i.e. the point at which the risk of SMN from proton therapy was greater than that from photon therapy). Because neutrons are not generated from 6MV photon beams, we considered neutrons only in the case of proton therapy. The interval of RRR values returned by different radiation weighting factors was used to estimate the 95% confidence interval of the RRR value resulting from ${\sigma }_{\overline{w_R}}$.

Figure 1.

Functions of the various radiation weighting factors (w_R) for neutrons used to convert absorbed dose to equivalent dose from neutrons examined in this work.

2.2.2. Shape of the dose-risk model

During radiotherapy, patients are exposed to very low doses in some tissues and high doses in others. Risk data on SMN incidence in humans have been drawn mainly from studies of low-dose radiation, namely, exposures in survivors of atomic bombs (Preston et al 2003, 2004, Pierce et al 1996), radiation accidents (Hall 2006) and medical radiation procedures (Suit et al 2007). These data were also supplemented with results from animal and in vitro cell studies (Suit et al 2007). The consensus is that the dose-response curve is probably best estimated with the LNT model for exposures up to a few sieverts for most organs and tissues. As a result, the baseline RRR value was computed on the assumption of an LNT relationship between exposure to radiation and risk of a SMN. However, at higher equivalent doses, available evidence suggests that significant deviations from the widely used LNT model are possible in some organs (Hall 2004).

Some studies of radiation-induced thyroid cancer in children have suggested a linear relationship between radiation exposure and carcinogenic risk up to approximately 20 Sieverts (Sv), with a decline in risk at doses higher than 15–20 Sv (Ronckers et al 2006, Sigurdson et al 2005). Meanwhile, studies of radiation-induced bladder cancer have indicated a linearly increasing relationship between exposure and carcinogenic risk at doses up to 10 Sv, with a constant risk at higher doses (Brenner et al 2000, Boice et al 1988, Neugut et al 1997). Hence, two principal models have been derived that are believed to describe the shape of the dose-response curve at high equivalent doses: the linear-exponential model (in which cancer risk increases linearly at low equivalent doses and then decreases exponentially at higher equivalent doses) and the linear-plateau model (in which the increase in risk is also linear at low equivalent doses and then levels off at higher equivalent doses) (Hall 2006).

We tested the sensitivity of the baseline RRR values to uncertainties in the risk model by recalculating the RRR using both the linear-exponential and linear-plateau models. Because we were modeling irradiation of the prostate, we needed to apply the linear-plateau and linear-exponential models only to the colon/rectum and bladder (because equivalent doses in all other tissues met the low-equivalent dose criterion of less than 2.5 Sv (Fontenot et al 2009a). Using the LNT risk models recommended in the BEIR-VII report, we added inflection doses to the risk model of each organ. Above each inflection dose, the two possible response curves (plateau and exponential decay) were modeled. The inflection doses were set at 10 and 40 Sv, representing the extrema of plausible value reported in the literature. Thus, a total of four dose-response curves (two linear-plateau and two linear-exponential curves) were tested for the ‘medium’ patient RRR calculation.

The form of the risk models was similar to those suggested by Schneider et al (2007, 2006). The model describing a linear-exponential behavior of an organ-specific risk model, R_T, is given by

$$R_{\mathrm{T}}=R_{\mathrm{T}}^0{H}_{\mathrm{T}}{\mathrm{e}}^{-{\alpha }_{\mathrm{T}}{H}_{\mathrm{T}}},$$ (6)

where $R_{\mathrm{T}}^0$ is the low-equivalent dose, organ-specific risk model from the BEIR-VII report, H_T is the equivalent dose to organ T and α_T is an organ-specific cell sterilization parameter. Similarly, the form of the linear-plateau model is given by

$$R_{\mathrm{T}}=\frac{R_{\mathrm{T}}^0}{{\delta }_{\mathrm{T}}}(1-{\mathrm{e}}^{-{\delta }_{\mathrm{T}}{H}_{\mathrm{T}}}),$$ (7)

where $R_{\mathrm{T}}^0$ and H_T are as previously defined and δ_T is an organ-specific cell sterilization parameter. Numerical values for α_T and δ_T for the colon/rectum and bladder were determined empirically. Additionally, we varied the $R_{\mathrm{T}}^0$ values slightly for each model so that the ERR value at 1 Sv would be consistent with the BEIR-VII value. Those parameters are listed in table 1.

Table 1.

Organ-specific parameters of the linear-exponential and linear-plateau risk models at low (10 Sv) and high (40 Sv) equivalent dose inflection points.

		Bladder		Colon/rectum
Risk model	Roll-off dose (Sv)	${\left(\frac{ERR}{H}\right)}_{\mathrm{T}}^0$	αT	${\left(\frac{ERR}{H}\right)}_{\mathrm{T}}^0$	δT
Linear	n/a	0.45	–	0.56	–
Linear-exponential	10	0.49	0.090	0.61	0.090
Linear-exponential	40	0.46	0.025	0.57	0.025
Linear-plateau	10	0.51	0.25	0.65	0.25
Linear-plateau	40	0.47	0.068	0.58	0.068

2.2.3. Interpatient variations

We calculated the baseline RRR value for a ‘typical’ patient. The machine settings required to deliver a prostate treatment to a particular patient are unique to the patient’s anatomy. Therefore, we also examined the effects of anatomical and treatment variations that could influence the calculated RRR value.

The effects of variations in therapeutic absorbed dose in the rectum and bladder across a population were assessed by determining the standard deviation of the absorbed dose in those organs in ten consecutively sampled patients who were treated for prostate cancer with proton therapy at our institution. For IMRT, the variation in stray absorbed dose was estimated from surveying monitor unit (MU) settings in treatment plans, following the method described by Fontenot et al (2008). For 6 MV photon IMRT, exposure to leakage radiation scaled directly with the MU setting. Thus, the predominant variable determining the amount of stray exposure in different patients was the number of delivered MUs.

The variation in stray absorbed dose from proton therapy was determined from Monte Carlo data previously reported by Fontenot et al (2008). In that study, proton beam range, spread-out Bragg peak width, collimated field size and air gap were varied over the interval of values used for prostate irradiation so that the sensitivity of stray absorbed dose to various clinical variables could be quantified.

3. Results

The results of the uncertainty analysis of each of the variables examined in this work are described below.

3.1. Radiation weighting factor for neutrons

The baseline RRR calculation was somewhat sensitive to changes in $\overline{w_R}$, as can be seen in table 2. ERR_IMRT was not influenced by $\overline{w_R}$ because no neutrons are produced by 6 MV photon beams. However, ERR_proton did vary with $\overline{w_R}$. As $\overline{w_R}$ increased, the ERR of organs out of the therapeutic field (for which stray equivalent dose was the only contributor to risk) increased linearly. Although neutron absorbed doses in the in-field organs (e.g. the rectum and bladder) were small, a large $\overline{w_R}$ for neutrons did significantly increase the ERR in those organs. For example, the ERR in the bladder increased from 3.99 to 5.47 (40%) when the $\overline{w_R}$ scaling factor was increased from 1 to 5. Overall, RRR values for the scaling factors of 0.5, 1 and 2 were 0.61, 0.66 and 0.75, respectively, suggesting that proton therapy can reduce the risk of SMN in patients undergoing radiation therapy for prostate cancer for plausible values of $\overline{w_R}$. When the scaling factor was set to 5, the RRR became greater than 1, indicating an elevated risk of SMN from proton therapy compared to photon therapy. However, a scaling factor of 5 would correspond to maximum $\overline{w_R}$ values of 100 for neutrons, which is not supported by the preponderance of current evidence (BEIR 2006, Newhauser et al 2009c).

Table 2.

Excess relative risk (ERR) in each tissue (ERR_T), sum of ERR_T values over all tissues (ERR_modality) and the ratio of ERR_proton to ERR_IMRT (RRR) for various scaling factors of the radiation Weighting factor (w_R).

	ERRT
	Nominal wR		wR × 0.5		wR × 2		wR × 5
Organ	Protons	IMRT	Protons	IMRT	Protons	IMRT	Protons	IMRT
Colon	2.25	2.73	2.11	2.73	2.52	2.73	3.33	2.73
Lung	0.05	0.02	0.02	0.02	0.10	0.02	0.24	0.02
Stomach	0.04	0.02	0.02	0.02	0.09	0.02	0.22	0.02
Bladder	3.99	6.92	3.80	6.92	4.36	6.92	5.47	6.92
Liver	0.07	0.03	0.03	0.03	0.13	0.03	0.33	0.03
Thyroid	0.01	0.00	0.00	0.00	0.01	0.00	0.03	0.00
Remainder	0.11	0.18	0.06	0.18	0.23	0.18	0.57	0.18
ERRmodality	6.50	9.90	6.10	9.90	7.40	9.90	10.20	9.90
RRR	0.66		0.61		0.75		1.03
95% CI	0.63–0.69		0.59–0.63		0.72–0.78		0.99–1.07

IMRT = intensity-modulated photon therapy; CI = confidence interval.

3.2. Shape of the dose-risk model

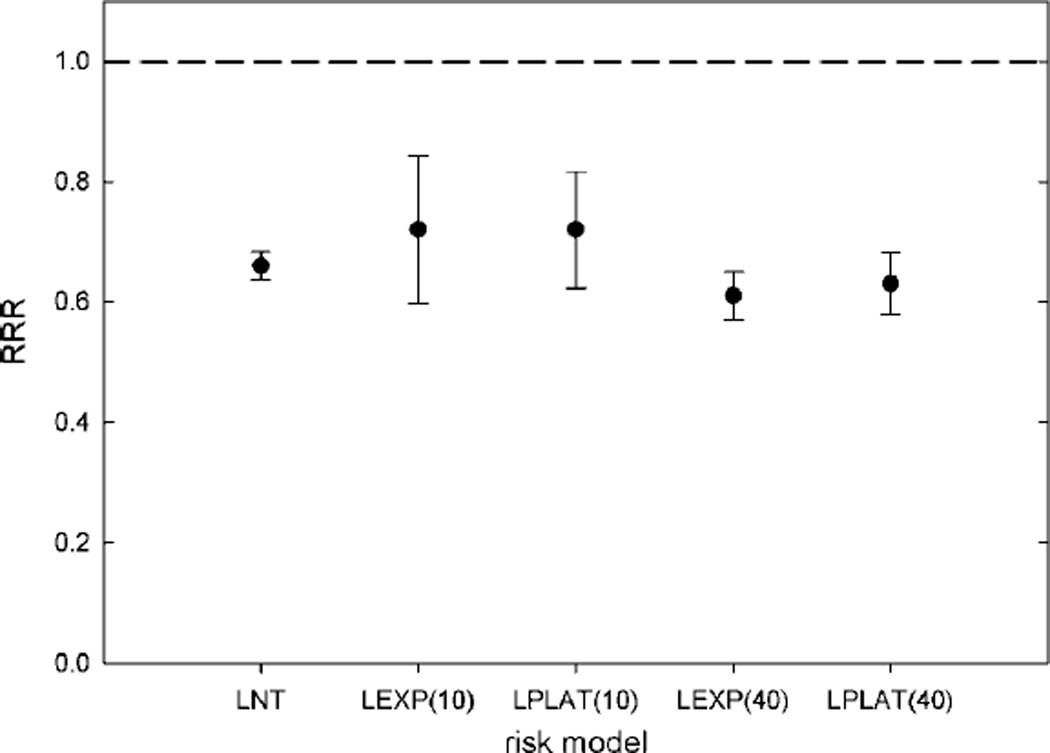
The baseline RRR value showed only a small sensitivity to the shape of the dose-risk model. The calculated RRR varied from 0.66 to 0.72 over all risk models examined (see figure 2). As expected, the ERR_T values in organs far from the therapeutic field were independent of the differences in the risk models since doses in those organs were below the roll-off doses. However, the ERR_T values in the bladder and colon/rectum showed substantial sensitivity to the selected risk model for both modalities. For the linear-exponential model with a 10 Sv roll-off, the in-field organs accounted for 26% and 76% of the total ERR for proton and photon therapies, respectively. For the linear-plateau model with a 40 Sv roll-off, the in-field organs accounted for 66% and 90% of the ERR for proton and photon therapies, respectively. In other words, when the risk from high equivalent doses was suppressed, the majority of the risk from the proton plans resulted from stray radiation. Conversely, the majority of the risk from the photon plans resulted from the therapeutic beam, independent of the risk model.

Figure 2.

The ratio of relative risk (RRR), defined as the ratio of ERR for protons (ERR_proton) to that for intensity-modulated photon therapy (ERR_IMRT), of the medium patient for various dose-response models. Error bars represent the uncertainty in RRR due to variations in stray radiation exposures from proton therapy and IMRT in a population of ten prostate cancer patients. The response models were LNT, linear no-threshold; LEXP(10), linear-exponential rolling off at 10 Sv; LPLAT(10), linear-plateau rolling off at 10 Sv; LEXP(40), linear-exponential rolling off at 40 Sv; and LPLAT(40), linear-plateau rolling off at 40 Sv.

3.3. Interpatient variations in anatomy and dose

3.3.1. Therapeutic dose

The RRR value was somewhat sensitive to anatomically related variations in exposure to the therapeutic beam. Based on an evaluation of ten patients (table 3), the mean therapeutic proton dose to the bladder and rectum varied by ±62% and ±23%, respectively (95% CI). For photon therapy, the mean equivalent dose to the bladder and rectum varied from the mean by ±67% and ±15%, respectively (95% CI). Because exposure to the therapeutic radiation was the predominant contributor to ERR in the baseline calculations, these variations in dose introduced enormous variations into the calculated ERR values. However, for a given patient, dosimetric variations were highly correlated between the two modalities. Because variations in the mean dose to organs can principally be attributed to anatomical variations, if the anatomy of a given patient resulted in a large mean dose to an organ in a photon plan, then the same was true in the proton plan in nearly equal proportion. Thus, for any given prostate patient, there was strong positive covariance between the uncertainties in mean dose to the bladder and rectum. The dosimetric correlation coefficient (r_xy) is used to characterize the strength and relationship of two variables (x and y) such that

$$r_{xy}=\frac{\sum (x-\mathrm{x̅})(y-\mathrm{y̅})}{\sqrt{\sum {(x-\mathrm{x̅})}^2\sum {(y-\mathrm{y̅})}^2}}.$$ (8)

Based on the data from this study, the value of r between the mean bladder dose from proton and photon therapies was 0.95. Similarly, the value of r between the mean rectal dose from proton and photon therapies was 0.70. Including these coefficients in the covariance term of equation (4) resulted in an uncertainty of ±30% in the RRR value resulting from interpatient variations in absorbed dose.

Table 3.

Mean equivalent doses to the rectum and bladder from proton therapy and intensity-modulated radiation therapy (IMRT) of the prostate in ten patients.

	Mean bladder absorbed dose (Gy)		Mean rectal absorbed dose (Gy)
Patient number	Protons	IMRT	Protons	IMRT
1	9.1	33.3	19.4	34.9
2	11.7	27.4	22.7	38.9
3	18.8	33.7	20.4	35.4
4	16.8	29.7	21.7	31.6
5	13.2	19.7	21.4	33.8
6	6.5	29.3	26.9	34.2
7	12.4	20.0	24.1	37.6
8	9.6	13.1	22.5	35.3
9	15.0	13.5	22.0	33.5
10	17.1	16.8	27.1	40.0
Mean	13.0	23.6	22.8	35.5
SD (1σ)	4.0	7.9	2.6	2.6

SD = standard deviation.

3.3.2. Stray radiation exposure—photon therapy

The RRR value was not sensitive to variations in exposure to stray radiation from photon IMRT. Since leakage radiation during IMRT is proportional to the number of MU required to deliver the treatment, the variation in MU over a sample of prostate cancer patients provided an estimate of the variation in leakage dose from IMRT. In our sample of ten patients, the value of 95% CI for MU was 124, or 17% of the mean MU value. However, the effect of this uncertainty on the RRR calculation was small since exposure to leakage radiation represented only a small fraction of the ERR_p. Thus, the uncertainty in absorbed dose from leakage introduced less than 1% uncertainty into the calculated RRR values.

3.3.3. Stray radiation exposure—proton therapy

As reported in our previous work (Fontenot et al 2008), absorbed dose from stray neutron dose varied by about 50% over the interval of treatment parameters used for proton therapy of the prostate. However, as in the case of photon therapy, the effect of these dose variations on the RRR calculation was small since exposure to stray radiation represented only a small fraction of the ERR_proton. The uncertainty in absorbed dose from stray radiation introduced less than 5% uncertainty into the RRR.

4. Discussion

We conducted a systematic examination of uncertainties in the calculated RRR of developing a SMN following contemporary proton to photon radiotherapies for cancer of the prostate. This revealed that the findings from our previous work—that passively scattered proton therapy could reduce the risk of SMN in early stage prostate cancer patients relative to photon IMRT—were relatively insensitive to the largest contributors to uncertainty in RRR. This insensitivity was mainly attributable to (1) large covariance terms (as was the case for the dose-response model and interpatient variations in absorbed dose) and (2) large relative uncertainties were associated with correspondingly small components of the ERR (as was the case with $\overline{w_R}$). Furthermore, while interpatient variations in absorbed dose had the greatest influence on RRR, uncertainties in patient-specific calculations of RRR were quite small since dose distributions within a given patient are known with good accuracy.

Several recent reports have suggested that uncertainties in the value of $\overline{w_R}$ and possible nonlinearities in the dose-response model may prohibit meaningful comparisons of SMN risk between passively scattered proton therapy and photon IMRT (Hall 2007, 2009). However, our study indicates that relative risk analysis may be a valuable tool in performing such comparisons with acceptable levels of uncertainty. These results are consistent with previous studies from Newhauser et al (2009a), who demonstrated that uncertainties in $\overline{w_R}$ did not influence calculations of second cancer risk for pediatric patients receiving craniospinal irradiation with proton and photon therapies. Kry et al (2007) reported that relative risk analysis could provide meaningful risk assessment when the magnitude of uncertainties precluded absolute risk comparisons. Schneider et al (2008) also utilized relative risk analysis to compare different modalities, and found sensitivities to the shape of the dose-risk model similar to our data.

The uncertainty analysis presented in this work utilized a rigorous propagation of uncertainties in combination with sensitivity analysis. Beginning with highly accurate dosimetric data (Fontenot et al 2008, 2009b), the largest contributors to the uncertainty in calculated risk of SMN were identified and quantified. While it should be noted that the numerical findings of this study are not directly applicable to radiation treatments at other anatomical sites, the methodology is general and therefore is directly applicable to other sites with the appropriate adjustments of dosimetric data and risk models.

This work had several limitations. First, our one-dimensional analysis investigated the sensitivity of calculated RRR values to uncertainties in parameters that were assumed to have a Gaussian distribution. The impact of multi-dimensional analysis (i.e. the interplay of simultaneous variations of several parameters) and non-Gaussian parameter distributions was not investigated. Further discussion of the impact of these assumptions is beyond the scope of this work, and the reader is instead referred to more theoretical texts (Saltelli et al 2008). Second, we used values of w_R from report 92 of the ICRP. The ICRP has subsequently issued report 103 (2007), which provides updated values of w_R. However, due to the comparatively small changes in w_R between reports 92 and 103, the major findings of this work would not be affected by using the most recent values of w_R. Finally, although calculations of RRR provide useful comparative information regarding the risk of SMN, a more complete risk assessment would also include estimation of absolute risk for developing SMN. Although some epidemiological data are available, absolute risk data are highly uncertain and conclusions are controversial (Baxter et al 2005, Brenner et al 2000, Chrouser et al 2005, Kendal et al 2006, Neugut et al 1997, Pickles and Phillips 2002, SEER 2007) and, until the biological uncertainties described in this work are reduced to appropriately low levels, calculations of absolute risks of radiation-induced cancers will remain highly uncertain.

5. Conclusions

A systematic examination of uncertainties revealed that the calculated RRR of developing a SMN following contemporary proton to photon radiotherapies for prostate cancer was insensitive to the largest contributors to the uncertainty. Uncertainties in the radiation weighting factor for neutrons, the shape of the dose-risk model and interpatient variations in therapeutic and stray doses introduced a 95% confidence interval of ±33% around the nominal value.