The Nanocrystal Superlattice Pressure Cell: A Novel Approach To Study Molecular Bundles under Uniaxial Compression

Abstract

Ordered assemblies of inorganic nanocrystals coated with organic linkers present interesting scientific challenges in hard and soft matter physics. We demonstrate that a nanocrystal superlattice under compression serves as a nanoscopic pressure cell to enable studies of molecular linkers under uniaxial compression. We developed a method to uniaxially compress the bifunctional organic linker by attaching both ends of aliphatic chains to neighboring PbS nanocrystals in a superlattice. Pressurizing the nanocrystal superlattice in a diamond anvil cell thus results in compression of the molecular linkers along their chain direction. Small-angle and wide-angle X-ray scattering during the compression provide insights into the structure of the superlattice and nanocrystal cores under compression, respectively. We compare density functional theory calculations of the molecular linkers as basic Hookean springs to the experimental force–distance relationship. We determine the density of linkers on the nanocrystal surfaces. We demonstrate our method to probe the elastic force of single molecule as a function of chain length. The methodology introduced in this paper opens doors to investigate molecular interactions within organic molecules compressed within a nanocrystal superlattice.

Self-assembled superstructures comprised of colloidal nanocrystal (NC) building blocks present many scientifically interesting and technologically important research challenges. Remarkable advances in the ability to create highly ordered NC assemblies have been enabled by access to NCs with precisely tailored size and shape as well as new insights into thermodynamic and kinetic principles governing the self-assembly. Controlling the properties of individual NC building blocks and the structure of the superlattice presents exciting prospects to create novel materials with properties by design.¹ Mechanical properties of superlattices have also been investigated²⁻⁴ and revealed interesting challenges at the confluence of hard and soft matter physics. The concept of using the NC superlattice itself as an experimental platform to probe mechanical properties of organic species confined to the precisely defined interstitial volumes to date has not been demonstrated.

The controlled arrangement of inorganic NC cores and molecular linkers connecting proximate NCs presents new opportunities to probe stresses and strains in elongated molecules. Improved understanding of the mechanical properties of elongated molecules is important to describing their function, for example, studies of DNA’s stretching and twisting properties provide important insights into biological processes like DNA replication and transcription.⁵ Stretching of single molecules can be accomplished by atomic force microscopy,^5,6 optical tweezers,⁷ or microfluidic methods.⁸ Compression along the molecular axis on the other hand has been more elusive in experimental studies. Femtosecond shock compression has been demonstrated to compress monolayers of hydrocarbon chains,⁹ however this approach probes the stresses under nonequilibrium conditions. Here, we report that equilibrium uniaxial compression of aliphatic chains can be achieved in a conventional diamond anvil cell with the aid from PbS NCs.

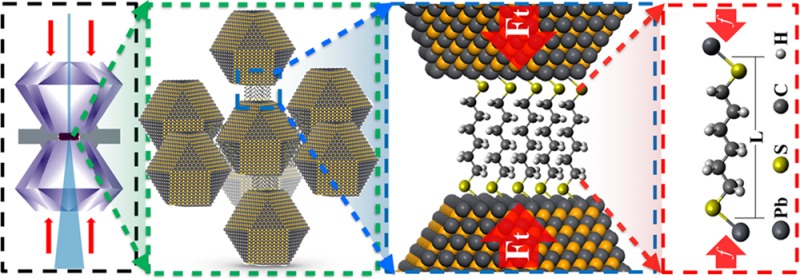
Figure 1 illustrates the concept of the NC superlattice pressure cell to study linker molecules under uniaxial compression. The two ends of alkanedithiol linker molecules are mounted to a pair of neighboring PbS NCs in self-assembled superlattices (SL) by ligand exchange. Loading the NC assemblies into a diamond anvil cell (DAC) and applying mechanical compression leads to uniaxial compression of the molecule chains connecting neighboring NC facets. This method effectively creates a large number (∼10¹⁰) of nanoscopic pressure cells that can be probed in parallel. In situ small-angle (SAXS) and wide-angle X-ray scattering (WAXS) provides real-time information into the structure of the superlattice and NC cores under compression, respectively. We combined the experimental structure analysis with density functional theory (DFT) simulations of compression of a single alkanedithiol molecule to determine the average NC surface linker densities. Furthermore, we derived the elastic force of single molecule as a function of chain length from experimental data and compared with corresponding computational results.

Figure 1.

Illustration of the multiple length scales defining the NC superlattice pressure cell. A millimeter-sized diamond anvil cell (a) defines the applied external pressure that is transmitted to the PbS NC superlattice (b) that in turn compresses the bundle of alkyl chains (c) connecting proximate NC facets. The total force between the NC facets (F_t) can be described by treating the force of individual molecules (f) as a Hookean spring (d).

Results and Discussion

We studied alkanedithiol linkers [HS −(CH₂)_n –SH] of variable length including ethanedithiol (EDT, n = 2), butanedithiol (BDT, n = 4), and hexanedithiol (HDT, n = 6). PbS NC (diameter d₀ = 6.3 ± 0.5 nm) films treated by these linkers are denoted as EDT, BDT, and HDT. Experimental details of the NC synthesis, ligand exchange, and high-pressure X-ray scattering analysis are provided in the Supporting Information. Replacing the native oleic acid ligands with variable length dithiol linkers significantly reduces the interparticle spacing. Figure 2a summarizes the SAXS patterns of the PbS NC films under ambient pressure and confirms the reduction of interparticle spacing (shift to higher q value) consistent with the length of the dithiol linker. Separation between nearest-neighboring NCs, δ_nn in each sample was calculated from SAXS data (Table 1) and shown in the inset of Figure 2a as a function of the number of carbon atoms in a corresponding molecular linker. The results clearly indicate the relationship between δ_nn and the length of the connecting linker chain l₀ (Figure 1d). The interparticle spacing agrees within experimental error (∼0.1 Å) with the separation defined by the molecular linker. SAXS data also show that the structure of the PbS NC films is preserved during alkanedithiol treatment. The NC superlattice maintained a face-centered cubic-like amorphous morphology upon ligand exchange.¹⁰

Figure 2.

(a) Ambient pressure small-angle X-ray scattering patterns of the alkanedithiol treated samples: EDT, BDT, and HDT comparing with an untreated sample OA. Inset shows separation between nearest-neighboring NCs. In situ high-pressure (b) SAXS and (c) WAXS results reflecting the compressibility of superlattices and PbS NC cores, respectively. Bulk moduli were determined by Vinet EOS fitting.

Table 1. Experimental Values of Nearest-Neighbor NC Separation under Ambient Pressure (δ_nn), Bulk Moduli of NC superlattice (B_0,SL) and PbS NC Cores (B_0,NC), “Spring Constants” of the Linker Molecule (k), and Calculated NC Surface Linker Density (σ).

sample	δnn (Å)	B0,SL (GPa)	B0,NC (GPa)	k (nN/nm)	σ (nm–2)
EDT	6.1	17.1	43.8	6.48	1.77
BDT	8.4	17.8	54.3	6.23	1.70
HDT	11.0	18.9	52.0	6.91	1.61

Upon pressurization inside the DAC, the volume of the NC superlattice shrinks due to the compression of both the organic interstitial linkers and, to a lesser extent, the inorganic PbS NC cores. To decouple these two effects, we monitored the compressibility of NC superlattice and NC cores by simultaneous in situ high-pressure SAXS and WAXS (Figure 2b,c).¹¹ We deliberately limited the applied pressure below 6 GPa to avoid the rock salt/orthorhombic atomic phase transition in PbS.^2,4 We fit the experimental pressure–volume trends to the Vinet equation of state (see Supporting Information for details)

1

where B₀= B|_p=0 is the bulk modulus under ambient pressure, B′₀= dB/dp|_p=0 is the initial slope, and v = V/V₀ is the dimensionless unit cell volume of the atomic crystal lattice of PbS NC cores or the superlattice. In this study, B′₀ is fixed at 4.0 and 10.0 for PbS NC cores and superlattice respectively for fair comparison between samples.^2,12

The bulk moduli of the NC superlattice, B_0,SL and the PbS cores, B_0,NC summarized in Table 1 reveal the following three important trends: (1) the stiffness of the superlattice B_0,SL is significantly smaller than that of the PbS NC cores B_0,NC implying that the compression of the superlattice is mainly contributed by the shrinkage of the softer linkers connecting the NCs, (2) B_0,SL increases slightly with increasing linker length mainly due to the increasing stiffness of each linker chain, and (3) B_0,NC of NC linked with EDT is smaller compared to that of BDT or HDT samples. The detailed relationship between NC bulk modulus and surface chemistry is subject to an ongoing study and will be detailed in a future report.

We developed a model to explain the relative compression of the superlattice and the constituent NCs. To a first approximation, the mechanical behavior of the molecular linker connecting the NCs in the superlattice can be treated as a basic nanoscale spring governed by Hooke’s law. For small uniaxial compression, the force–distance relationship of a single linker molecule takes the form

2

where f is the compression force exerted on a single linker (Figure 1d), k is the “spring constant” of a molecule chain, Δl represent compression of the molecular linker with initial length l₀, and ε is the strain. The elastic module of the linear molecule K is determined by DFT simulations of compression of single linker molecules. DFT calculations detailed in the Supporting Information show that the stiffness of EDT, BDT, and HDT molecular linkers are comparable.

The relative contribution of the stiffness of the molecular linker and the compressibility of the NC core to the overall shrinkage of the superlattice volume can be described by the following expression (details of the derivation are provided in the Supporting Information)

3

where σ is the average surface density of alkanedithiol linkers on PbS NC cores. On the basis of the elastic modulus of the molecular spring (from DFT calculations) and bulk moduli of the superlattice and NCs (from X-ray scattering), we determined the linker coverage, σ, to be approximately 1.7 ligands/nm². As summarized in Table 1, the coverage for EDT, BDT, and HDT linkers was approximately the same with a small decrease in coverage with increasing linker length. The basic premise of our model is validated by the fact that the calculated linker coverage agrees well with the ligand coverage on lead salt NCs measured by infrared spectroscopy as described in our previous work¹³ and the results by others.¹⁴

We now describe the force–length, that is, f(l) relationship of molecular linkers within the NC superlattice pressure cell. The pressure applied to the anvil cell and the superlattice can be directly converted to an applied force (see Supporting Information). The distance between NC facets, which confines the length of the linkers, was determined from X-ray scattering data. DFT calculations were performed on linker bundles to simulate the compression. A linker density of 1.6 nm^–2 is simulated in periodic cells by attaching alkanedithiol molecules with their axis perpendicular to a reconstructed slab of PbS(111) surface. To mimic the experimental setup, linker bundles are uniaxially compressed along the axis perpendicular to PbS slab surfaces. Varying compressions are applied with smaller compressions for EDT–PbS configuration due to the small initial ligand length as compared to BDT and HDT ligand lengths. Details of DFT simulation are provided in Supporting Information.

Figure 3 compares the elastic forces computed from DFT with the experimentally determined forces. We find a reasonable agreement between the experiment and DFT, considering that the DFT calculations do not account for several experimental aspects. The experimental measurements used to compute the elastic forces are a result of ensemble averaged properties and include the average effects of trapped solvents, faceting of the NC surfaces, nonuniform ligand coverage, and other local structural variations. Nevertheless, the good order of magnitude agreement shows that the observed forces result predominantly from the compression of the molecular linkers as opposed to much harder crystalline NC core material or much softer liquid phase materials.

Figure 3.

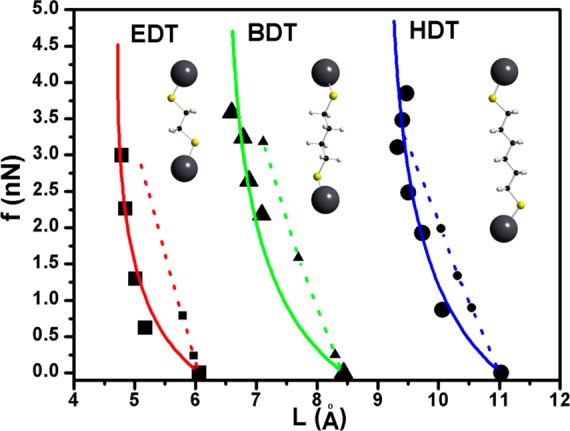
Elastic force of alkanedithiol molecular linkers as functions of their chain length. Comparison of high-pressure X-ray scattering data (black symbols) and the Vinet equation of state fits (solid lines) with the corresponding DFT simulations of the molecular spring.

The discrepancy between the linear force–distance relationship predicted by DFT calculations and the nonlinear trend observed at high pressures is interesting and merits further discussion. We speculate that the nonlinear relationship observed in experiments may arise from a bending of the molecular linkers in addition to the uniaxial compression. Overall, agreement in the DFT and experimental results strengthens the idea of two ends of alkanedithiol linker molecules being mounted to a pair of neighboring PbS NCs in self-assembled SL by ligand exchange.

Conclusions

In summary, we demonstrate the use of nanocrystal superlattice as an experimental platform to probe moleculer bundles under uniaxial compression. We used the assembly itself as a nanoscale pressure cell to probe molecular bundles under uniaxial compression. We combined X-ray scattering experiments with DFT calculations to probe the elastic force of single molecule as a function of chain length. Our research may open new doors to the efforts of manipulating organic molecules and investigating atomic-level interactions within them. Beyond the specific proof-of-concept compression of aliphatic dithiols in a PbS NC superlattice reported here, we see the versatility of this methodology as a unique strength that may also find application in studying more complex molecules (e.g., DNA) under uniaxial compression.

Supporting Information Available

Experimental details of the NC synthesis and high-pressure experiments, PbS lattice expansion, DFT calculations of the molecular spring constant, derivation of the model for superlattice compression, and the force–distance relationship. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States