Electrophoretically induced aqueous flow through single-wall carbon nanotube membranes

Abstract

Electrophoresis, the motion of charged species through liquids and pores under an external electric field, has been principle source of chemical pumping for numerous micro- and nano-fluidic devices platforms. Recent studies of ion current through single or few carbon nanotube channels range from near bulk mobility to 2-7 orders of magnitude of enhancement but cannot directly measure ion flux. Membranes, with large number of nanotube pores, allow independent confirmation of ion current and flux. Here we report that the aqueous electrophoretic mobility of ions within the graphitic cores of carbon nanotube membranes, with a uniform pore size of 0.9 ± 0.2 nm, is enhanced ∼3 times that of bulk mobilities. The induced electroosmotic velocities are 4 orders of magnitude faster than those measured in conventional porous materials. We also show that a nanotube membrane can function as a rectifying diode due to ionic steric effects within tightly controlled nanotube diameter.

Introduction

Micro- and nano-fluidic devices based on electrophoresis¹, have been used for applications such as inorganic ion detection^2-4, organic drug analysis⁵, DNA sequencing and translocation^6-9, peptides and protein separations^{9, 10}, enzyme activity assay¹¹, and nanofluidic transistors and diodes^12-14. Membranes based on carbon nanotubes are attractive for nanofluidic devices and applications^{6, 15-24} for three reasons: the atomically flat graphitic planes allow fast fluid flow; it is possible to covalently functionalize the entrances to the nanotubes with charged groups; and the high electrical conductivity of the nanotubes allows the electric field to be concentrated at the tip of the nanotube. As a result, nanotube membranes can be applied in programmable transdermal drug delivery²⁵, biomolecules separation¹⁰, chemical separation²², DNA translocation⁶, water desalination²³, natural protein channels mimic¹⁹, and gas separation^{26, 27}. Pressure driven flow of gas, liquids, and ions has been investigated using various types of carbon nanotube membranes^{17, 18, 20}. Although a fast fluidic flow rate (m/s-bar) has been confirmed by both experiments and molecular dynamic (MD) simulations, the measurements of ionic electrophoretic mobility in single-walled carbon nanotubes (SWCNTs) has been only measured through single/few channels with the mobility inferred from conductance changes and with wide ranging results^{6, 28}. Reported aqueous electrophoretic mobilities [EM] of K⁺ (8×10⁻⁶m²/V.s) and protons (ranging from 2×10⁻⁵ to 50 m²/V.s) through nanotubes (averaged i.d. = 1.5 nm)are enhanced over bulk mobility (μ_b) by 2-7 orders of magnitude respectively²⁴. Interestingly in that report, Na⁺ had no enhancement (0.96 μ_b) over bulk mobility but K⁺ (105 μ_b) and Li⁺ (205μ_b) had large enhancements, thus making it difficult to understand the origin of the enhancement mechanism. Liu, et al. studied the DNA translocation (in KCl solutions) through a O₂-plasma etched Single Walled nanotube (average i.d.of 1.8 nm) reported 80% of their measured K⁺ electrophoretic mobilities are equal to or less than the bulk K⁺ electrophoretic mobility (7.62×10⁻⁸m²/V.s).⁶.These widely varying studies are based on ionic current fluctuations through single or a handful of nanotubes thus the electrophoretic mobility data are extrapolated or inferred from measured conductivity pulses. With these methods it is difficult to confirm that the measured current is due solely to ion transport through nanotube channels, since the extremely small pore area of single/few nanotube channels makes it impossible to measure ion concentration with conventional chemical analysis techniques such as inductively coupled plasma atomic emission spectroscopy (ICP-AES). Nanotube membranes, with a large number of tubes, possess a much higher pore area²⁵, thereby allowing direct measurement of the electrophoretic mobility by ion concentrations in the permeate using ICP-AES thus confirming the electrical current based measurements. Electroosmosis, where only one charge is allowed to move along an oppositely charged interface and accelerate neutral solvent molecules, is usually an inefficient process. With the nearly ideal slip boundary condition of nanotubes, sustained electroosmotic flow can give energy efficient electroosmotic pumping in multi-, double- and larger single-walled nanotubes (i.d. 7, 1.6, 1.3nm respectively)^{25, 29}. However much of this efficiency may be lost by lack of nanotube diameter control where larger diameter nanotubes allow a large fraction of solvent molecules to not be accelerated by the moving ion in the pore cross-sectional area. Needed for ideal electroosmosis are tightly-controlled sub-nm diameter nanotubes approaching dimensions of ions diameters allowing for efficient electroosmosis.

Results and Discussion

Carbon nanotube membrane synthesis and characterization

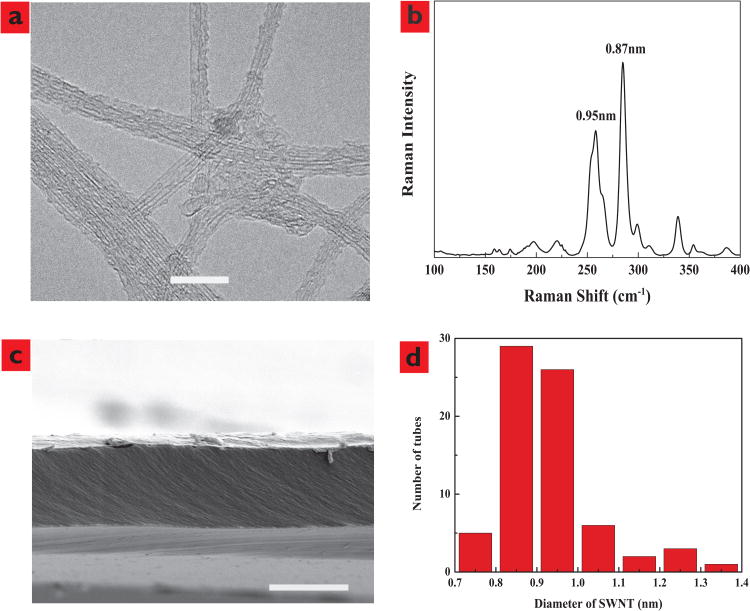
Nanotubes were synthesized using a modification of prior reported chemical vapor deposition (CVD) methods^31-33 but at a reduced growth temperature (750°C) in order to obtain carbon nanotubes with diameters smaller than 1 nm. Figure 1a and 1b show a representative transmission electron microscope (TEM) image of nanotube samples and corresponding Raman spectrum. The average outer diameter of the nanotubes from both TEM and Raman analysis (Figure 1d) shows that the samples are composed of nanotubes with diameter 0.9 ± 0.2 nm. Membranes are formed by microtoming a nanotube/epoxy composite mixture to 5 micron thickness as shown in a representative cross sectional scanning electron microscope (SEM) view (Figure 1c). Bundles of nanotubes are not observed, indicating the uniform dispersion of nanotubes tubes within the epoxy. The pore area of the nanotube membranes was evaluated from the steady-state K⁺ diffusional flux using the following equation:

Figure 1.

Characterization of single wall carbon nanotubes. a, TEM image of SWCNT with a scale bar of 10nm. b, Raman spectra of SWCNT powder sample showing diameters calculated from peak location. c, SEM image of the Cross-sectional view of CNT membrane with a scale bar of 5μm, showing carbon nanotubes are uniformly dispersed in epoxy resin matrix as no bundles of nanotubes can be observed. d, Histogram of SWCNT inner core diameters.

$$A_p=(M\Delta x)/(K_{(\lambda )}D\Delta C)$$ (1)

where A_p (m²) is the pore area, M (mol/s) is the experimental steady-state molar flow rate of K⁺, Δx is the thickness of the membrane measured by scanning electron microscopy (5 μm), ΔC is the concentration difference between the feed and the permeate (100 mol/m³). K_(λ)is the diffusion hindrance factor using the Deen's model³⁴ in equation (2) where λ is relative solute size, which is equal to a/b; a is K⁺ stokes radius, 0.12 nm³⁵; b is pore radius, 0.45 nm.

$$K_{\left(\lambda \right)}=1-2.104\lambda +2.09{\lambda }^3-0.95{\lambda }^5$$ (2)

Permeate concentrations of potassium ions were quantified using inductively coupled plasma–atomic emission spectrometry (Varian Vista-PRO CCD Simultaneous ICP-AES). Potassium standard was purchased from ULTRA Scientific. The pore areas of two nanotube membranes used for this paper are 1.4×10⁻¹¹ and 5.0×10⁻¹² m². As a control experiment Voltage-Current measurements on pure epoxy microtomed films after the same plasma treatment showed only an instrumental open circuit current of +5nA under the same experimental conditions.

The electrophoretic mobilities of K⁺, Na⁺, Li⁺, H⁺ and Ru(bpy)₃²⁺ were calculated using the following equation:

$${\mu }_{\mathit{\text{EM}}}=(M/A_p)\ast ɭ/(C\ast E)$$ (3)

μ_EM is electrophoretic mobility; M is the experimental molar flow rate; ɭ is thickness of membrane; C is solution concentration; E is applied bias. ɭ, C, E are known parameters or constants, and M can be determined from ionic current measurements. The equation used to calculate M is as follows:

$$M=I\ast t^{+}/(e\ast N)$$ (4)

I is measured ionic current (A); t⁺ is transport number of cations; e is elementary charge, and N is Avogadro constant. Bulk transport numbers of K⁺, Na⁺, Li⁺, and H⁺ in 1 mM KCl, NaCl, LiCl and HCl are 0.5, 0.4, 0.3, 0.8 respectively, as reported in the literature. Bulk transport number of Ru(bpy)₃²⁺ is estimated using the following equations:

$$t^{+}={\mu }_{\mathit{\text{RU}}(\mathit{\text{bpy}})3^{2+}}/({\mu }_{{\mathit{\text{cl}}}^{-}}+{\mu }_{\mathit{\text{RU}}(\mathit{\text{bpy}})3^{2+}})$$ (5)

$${\mu }_{\mathit{\text{RU}}(\mathit{\text{bpy}})3^{2+}}=q/(6\eta \pi a)$$ (6)

Where q is charge (2e), η is the dynamic viscosity, a is Stokes radius of Ru(bpy)₃²⁺ (∼4.8 Å). t⁺ of Ru(bpy)₃²⁺ is equal to 0.3 in the case of Ru(bpy)₃Cl₂.

As shown in Table 1, electrophoretic flows of H⁺, K⁺, Na⁺, Li⁺ and Ru(bpy)₃²⁺ within nanotubes have been enhanced by ∼3 times compared to their bulk values. The cation electrophoretic mobility reported herein is consistent with the preliminary reports associated with DNA translocation⁶ and not the dramatic enhancements of 2-7 orders of magnitude²⁴. In the cases of K₃Fe(CN)₆, and Na₇(SO₃)₇CD, electrophoretic mobilities of K⁺ and Na⁺ were calculated under two assumptions. 1) Assuming that bulky anions were not rejected by the anionic carboxylates at the nanotube entrances, the calculated electrophoretic mobilities of cations are only 2 times higher than that in bulk solution. 2) If bulky anions were completely rejected, the obtained cation electrophoretic mobilities are 4.4 times higher than their bulk values.

Table 1.

Electrophoretic mobilities of K⁺, Na⁺, Li⁺, H⁺, and Ru(bpy)₃²⁺ using 2 Ag/AgCl electrodes electrochemical cell system (applied bias, -600 mV); pore area is 1.4×10⁻¹¹ m². Solution concentrations are 1 mM KCl, NaCl, LiCl, HCl, 0.33 mM K₃(Fe(CN)₆), 0.5 mM Ru(bpy)₃Cl₂, and 0.14 mM sulfated cyclodextrin

	K+	Na+	Li+	H+	K+ K3(Fe(CN)6)	Na+ Na7(SO3)7− cyclodextrin	Ru(bpy)32+ Ru(bpy)3Cl2
Conc. (mM)	1	1	1	1	0.33	0.14	0.5
Ionic Current (nA)	80	69	50	200	57	37	58
Measured EM, (m2/s.V)	2.3E-07	1.6E-07	9.6E-08	9.6E-07	1.5E-07 (3.3E-07)*	9.6E-08 (2.2E-07)*	1.1E-07
Bulk EM, (m2/s.V)	7.6E-08	5.2E-08	3.9E-08	3.6E-07	7.6E-08	5.2E-08	3.6E-08
Ratio of Measured EM to bulk EM	3.0	3.1	2.5	2.7	2.0 (4.4)*	1.8 (4.2)*	2.9

^*The electrophoretic mobilities are calculated assuming that Fe(CN)₆³⁻ and CD(SO₃)₇⁷⁻ are completely rejected, and so the transport number of K⁺ and Na⁺ are 1.

Effect of Ionic Strength on K⁺ Electrophoretic Mobility

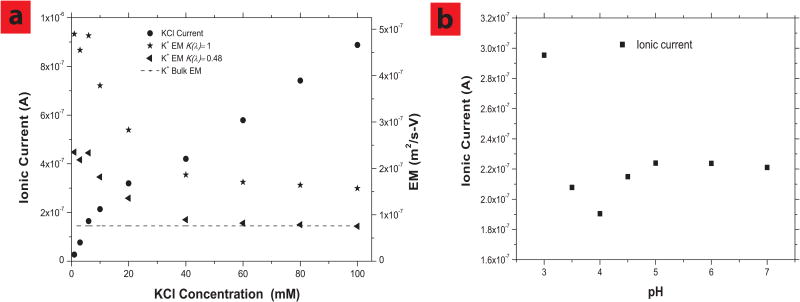
The observed K⁺ electrophoretic mobilities through nanotubes show a KCl concentration dependence (Figure 2a). At lower ionic concentrations ranging from 1 to 6 mM, K⁺ electrophoretic mobility is about 3 times higher than its bulk value and remains almost constant. At higher concentrations, the observed mobility drops to near that of bulk values. One potential explanation of this phenomenon is that the anionic carboxylate groups can reject anions at low solution ionic strength, allowing only cations to flow in the direction of electric field thereby inducing an electroosmotic flow that increases observed electrophoretic mobility as described by:

Figure 2.

Enhanced electrophoretic mobilities in SWCNTs generated by highly efficient electroosmotic flow and effect of charged carboxyl groups on the electrophoretic flow. a, Ionic currents (0.6V) and K⁺ EMs vs. KCl concentrations; Membrane pore area is 5.0×10⁻¹² m². Shown are mobilities calculated with Ap (equation 1) using bulk diffusion (K_(λ)= 1) or hindered diffusion (K_(λ)= 0.48) assumption.b, Ionic current as a function of pH in 10 mM KCl. HCl is used to change pH values, applied bias is 0.6V and Ag/AgCl electrodes are used.

$${\mu }_{\mathit{\text{ob}}}={\upsilon }_{\mathit{\text{eo}}}/E+{\mu }_{\mathit{\text{bulk}}}$$ (7)

where μ_ob is observed electrophoretic mobility, ν_eo is electroosmotic velocity, E electric field and μ_bulk the bulk electrophoretic mobility of the ion. A 3 times enhancement of K⁺ observed mobility would correspond to a high electroosmotic flow of ∼3 cm/s-V in these sub-nm diameter nanotubes. This is significantly faster that electroosmotic velocity observed in larger multi-wall nanotubes and single-wall nanotubes of 0.16-0.18 cm/s-V, presumably due to the smaller diameter forcing a larger percentage of the solvent to be pushed by the accelerated ion. For comparison, more conventional materials such as anionic porous alumina have electroosmotic velocities of 3.7×10⁻⁴ cm/s-V, thus the electroosmotic enhancement within nanotubes is dramatic. However since ionic electrophoretic velocity is typically much faster than electroosmosis, the effect on electrophoretic mobility is relatively modest and within an order of magnitude.

Above 10 mM KCl concentration, the K⁺ electrophoretic mobility enhancement decreases until 40 mM, then the electrophoretic mobility becomes constant and near bulk value. At low concentrations, the Debye screening length is large (∼9.6 nm at 1 mM ≫ single-wall nanotube id, 1 nm) so that anions can be rejected and efficient cationic electroosmosis pumping can enhance the transport of K⁺ through single-wall nanotube giving an enhanced net mobility. At higher ionic concentration the reduced Debye screening length (∼1.5 nm at 40 mM) appears to allow a significant amount of anionic current through the thin layer of anionic charge at nanotube tips, thereby negating the cation driven electroosmotic flow in the opposite direction. As a result, the measured K⁺ electrophoretic mobility values decrease (Figure 2a) to near bulk values at higher concentrations. The concentration at which screening occurs is less than would be predicted by simple Debye screening. This is likely due to charge being only at the pore entrance and not along the entire pore length. A similar phenomenon was seen with desalination studies where ion rejection in slightly larger double-wall nanotubes was screened in the mM concentration range²³.

To study screening effects the pH dependence of ionic current in 10mM KCl solution is shown in Figure 2b. As pH is dropped to the pKa of carboxylate groups near 4, we see a drop in ionic current due to the loss of -electroosmosis (from the opposite direction of unscreened anionic current). At pH values below 4, proton current becomes substantial due to inherently faster mobility of protons relative to K⁺ and overall current increases.

Since pressure flow enhancements for gas and liquid are not definitively established and it is not possible to observe pores by electron microscopy, it is important to test the validity of diffusion measurement to calculate pore area. This was accomplished by showing the ionic diffusion was self-consistent by varying ion size, concentration and changing the charge state of the entrance. When we changed ion size (Li⁺, K⁺, Rb⁺) the resulting calculated pore area varied by ∼25% between K⁺/Rb⁺ and ∼40% between K⁺/Li⁺. This is consistent with our prior report ³⁶ of diffusional transport of ions in larger nanotubes being between bulk and hindered diffusion depending on interaction with entrance. About 40% variation was seen between those extremes. Hindered diffusion for non-interacting spheres in an infinite pore can be calculated by the Deen's model equation (2). When we calculate A_p (and subsequent mobilities) accounting for hindered diffusion, the results are self-consistent with observed mobility in Figure 2a at high concentrations. That is at higher concentrations, when ionic screening prevents electroosmotic flow generation; the observed mobility matches bulk mobility. This self-consistency between mobility and diffusion in the absence of electroosmosis enhancement is important for the validity of the A_p calculation. In the case of assuming bulk diffusivity to calculate pore area, mobility enhancement factors of ∼6 are seen, while using hindered diffusion enhancement factors of ∼3 are seen. Finally the charge at the tips of nanotubes was neutralized by using pH 3 0.1M KCl/HCl solutions to negate potential charge attraction/partitioning at the nanotube tip. Only an 8% increase in calculated pore area was seen at low pH, further supporting the diffusion method to measure A_p.

Confirmation of ionic current by using ICP-AES analysis

Since these single-wall nanotube membranes have higher porosity, we can directly measure the amount of ions transported across nanotube membranes into the permeate solution, directly confirming the electrophoretic mobility values measured by cell current. This would rule out capacitance or membrane electrical conductivity artifacts within the total observed current. ICP-AES^{37, 38} analysis was employed to measure ion concentration in the permeate and evaluate the accuracy of M obtained from ionic currents (equation 3). The experimental conditions are the same as above described, except that the larger feed side of U-shape tube is filled with aqueous salt solution, while the other smaller permeate side is filled with de-ionized (DI) water. After applying -600 mV bias for ∼19 hrs across single-wall nanotube membrane, the concentration of transported metallic ions was measured using ICP-AES. The use of DI permeate allows for the detection of low fluxes and high feed concentration (0.1 M) reduced the experimental time. M (mol/s) can be calculated using the following equation:

$$M=C\ast K/t$$ (8)

C is the metallic ion concentration in the DI water side as determined by ICP-AES; K is volume of permeate solution, t is time. Membrane pore area is 5.0×10⁻¹² m².

Table 2 shows that the M and electrophoretic mobility values obtained by IPC-AES and electrical current are quite close (less than 30% difference), which directly confirms values obtained using ionic current data (Table 1 and Figure 2a). The apparent discrepancy in electrophoretic mobility values can be attributed to the possible increase of K⁺ transport number in nanotubes. The tips of nanotubes are negatively charged due to the presence of carboxyl functional groups, which partially reject Cl⁻ ions, resulting in an increased effective t^K+ in nanotubes and induce electroosmotic flow.

Table 2. Comparison of K⁺ flux (M) and electrophoretic mobility (EM) obtained using ionic current and ICP-AES methods.

	Ionic Current Analysis**	ICP-AES Analysis*
MK+ (moles/hr)	1.6×10−8	2.0×10−8
EMK+ (m2/s-V)	7.7×10−8	9.6×10−8

Note:

^*one side of U-shape tube is composed of 0.1 M KCl solution, and another side is filled with DI water;

^**both sides are filled with 0.1 M KCl solution, assuming transport number of K⁺ is 0.49; applied bias is −0.6V (two electrode system, Ag/AgCl); bulk μ_K+ is equal to 7.6 × 10⁻⁸ m²/s-V; pore area of membrane is 5.0×10⁻¹² m².

Sequential ionic studies

In the reports of proton mobilities being enhanced 4-6 orders of magnitude in nanotubes^{24, 28}, an interesting effect is the reduction of proton current and thus overall current by the addition of KCl. K⁺ presumably blocks a H-bonding coupled mechanism for dramatically enhanced proton transport. The membranes here offer a direct conduction measurement of a large number of nanotubes to examine this effect. When KCl salt is added to pure DI water (pH∼6.5), similar to conditions by Choi et al²⁸, the ionic current increases instead of decreasing, implying that K⁺ ions are not blocking proton transport through the nanotube core. This effect is also seen when proton concentration is increased by using 1 mM HCl solutions on each side of the membrane. Higher HCl concentrations than 1mM were not used since damage to epoxy membrane matrix was seen at lower pHs. When concentrate KCl is added to make 7 mM KCl solutions in the 1mM HCl, the measured ionic current is very close to the sum of ionic currents of 1 mM HCl and 7 mM KCl. This indicates that K⁺ ions don't block a dramatically enhanced proton translocation process through nanotubes. It is important to note that since protons have 7 times the bulk mobility of K⁺, the higher KCl concentration is needed to conclusively show that current increase is well above the proton background.

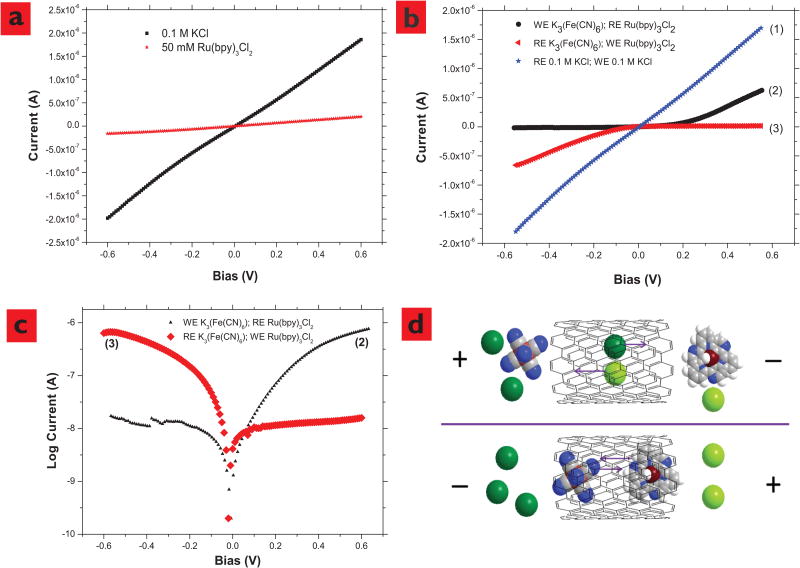
As shown in Figure 3a, there is no apparent threshold voltage to pump potassium ions through nanotube membranes. However, Ru(bpy)₃²⁺ electrophoretic mobility through nanotube membrane was reduced at a higher ionic concentration (50 mM, 0.9×10⁻⁸ m²/s-V), as compared to 1 mM Ru(bpy)₃²⁺ solution (1.1×10⁻⁷ m²/s-V). Ru(bpy)₃²⁺ions are significantly larger than K⁺ ions (∼1 nm dia. compared to 0.4 nm dia)^{20, 23}. At a high ionic concentration, it is likely that the unscreened chloride anions flowing in the opposite direction retard the electrophoretic velocity of Ru(bpy)₃²⁺.

Figure 3.

Effects of ionic concentrations and species on the electrophoretic flow through SWCNTs and SWCNT membrane functioning as a rectifying diode, confirming that the ionic currents are through the SWCNT cores.a, Current vs. Voltage of KCl and Ru(bpy)₃Cl₂ through SWCNT-COO^- membrane. There is no apparent threshold voltage to pump K⁺ through SWCNT and the electrophoretic mobility of Ru(bpy)₃Cl₂ through SWCNT is dramatically reduced at a high ionic strength. b, Ionic currents through SWCNT membranes rectification is seen when one side is filled with 25 mM K₃(Fe(CN)₆), and another side is filled with 50 mM Ru(bpy)₃Cl₂, and the control experiment with KCl. c, current shown on log scale. d, Schematic with space filling molecular models of ionic transport in SWCNT (10, 10) under electric field under opposite bias conditions (Dark green, K⁺; light green Cl⁻ grey, C; blue, N; dark brown, Ru²⁺; light brown, Fe³⁺; white, H). Pore area: 5.0×10⁻¹² m².

Ion steric effects and diode behavior in nanotube membranes

The previous experiment shows that the single-wall nanotube diameters are controlled to be very close to that of large ions and thus sterically affect the observed electrophoretic current. To conclusively prove this size control of nanotubes and the ionic transport through nanotube cores, experiments with large cation/small anion on one side of the membrane and small cation/large anion on the other were performed. Under appropriate bias, one can have transport of only small anions and small cations while the opposite bias will have large cations blocking the large anions within the nanotube. Another important aspect of this experiment is to prove that ion conduction is indeed through nanotube cores. Although ICP-AES studies directly confirm that there is ionic transport across the membrane, it doesn't prove that conductance is through the cores of nanotubes since one would expect near bulk electrophoretic mobility through macroscopic membrane defects. If nanotubes membranes can exclude ionic species whose size is close to the diameter of nanotubes, it can be conclusively proven that ionic conductance is from the nanotubes cores.

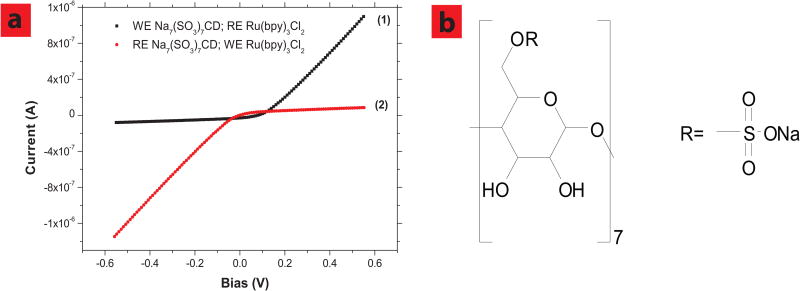
A U-shape tube installed with one reference and one working electrode was used to demonstrate that nanotube membrane can reject ions close to 1 nm in diameter and function as a size based rectifying diode. The working electrode side is filled with 25 mM K₃(Fe(CN)₆) and reference electrode side is filled with 50 mM Ru(bpy)₃Cl₂. It should be pointed out that total ionic strengths at both sides are equal (I_total = Σc_iz_i) and the bias is always applied on working electrode. As shown in Figure 3b-2, the trans-membrane ionic current was shut-off when a negative bias was applied, while high current was seen with applied positive bias. While applying a negative bias, (Fe(CN)₆)³⁻ anions (∼0.6nm in diameter) from the working electrode side and large cationic Ru(bpy)₃²⁺ ions are forced through nanotube from the cationic side. Since the sum of cation and anion diameters (∼1.6 nm) is bigger than the diameter of nanotubes (∼1 nm), it is difficult for them to pass each other within the space-confined nanotube core, resulting in the shut-off of trans-membrane current. In contrast, while applying a positive bias to the working electrode, smaller K⁺ ions and Cl⁻ ions can flow electrophoretically through the nanotube membrane. As a control experiment to rule out any redox current, exchanging the positions of working and reference electrodes to opposite solutions, the rectifying curves can be reversed (Figure 3b-3). If both sides of the U-shape tube are filled with only 0.1 M KCl solutions, no rectifying effect can be observed as shown in Figure 3a and Figure 3b-1. To further demonstrate the rectification phenomenon, we tried another large anion, beta sulfated cyclodextrin CD(SO3)₇⁷⁻ (∼1.2 nm in diameter). As shown in Figure 4a-1 and 4b nanotube membrane rectifying effect was observed again, using Ru(bpy)₃Cl₂ and sulfonated cyclodextrin sodium salt aqueous solutions. Similarly, the I-V curve can be reversed by exchanging the position of working and reference electrodes, because Na⁺ and Cl⁻ ions are pumped though nanotube membrane applying negative bias (Figure 4a-2).

Figure 4.

SWCNT membrane functions as a rectifying diode using other ionic species. a, Ionic currents through SWCNT membranes obtained using 50 mM Ru(bpy)₃Cl₂ and 25 mM Na₇(SO₃)₇CD; after working (WE) and reference electrodes (RE) positions are exchanged, the IV cure was reversed (2). b, molecular structure of Na₇(SO₃)₇CD. Pore area is 5.0×10⁻¹² m².

A rectifying effect has been previously reported in multi-wall nanotube membranes¹⁴, whose underlying mechanism is based on surface charge exclusion, whereas ours is based on size exclusion made possible by strict control of nanotube diameter. The steric effects are more efficient and the present on/off current ratio (∼50) is significantly larger than the literature report (∼3)¹⁴. The unique asymmetric cation/anion experimental design along with smaller nanotube core inner-diameter (1 nm of single-wall nanotube vs. 30-40 of multi-wall nanotube) allows us to observe this type of apparent rectifying effect with a minimum leakage current in the off state. A control experiment of rectification using large 20nm diameter porous alumina membrane did not show rectification and had a linear I-V response. Similarly in a control experiment a large cation/small anion (Ru(bpy)₃Cl₂/KCl) and small cation/small anion pair was examined and no rectification was seen.

In conclusion, the electrophoretic mobility of various ions in single walled carbon nanotube membranes with an average diameter of ∼0.9 nm was measured using ionic currents and confirmed by ICP-AES analysis of the permeate solution. Measured electrophoretic mobilities of K⁺, Li⁺, Na⁺, and H⁺ in SWCNT membrane are enhanced by 2 to 3 times compared to their bulk values. At low ionic strengths (<6 mM), electrophoresis can induce dramatic electro-osmosis and act as an ideal pump for transport of electrically neutral chemical species. Electroosmotic velocities as high as 3 cm/s-V can be inferred from the 3 fold observed electrophoretic mobility enhancements. For comparison, conventional materials such as anionic functionalized porous alumina have electroosmotic velocities of 4×10⁻⁴ cm/s-V^{29, 30}.electrophoretic mobilities of K⁺ ions are reduced at a higher ionic concentration (>6 mM) due to oppositely charged ions moving in the opposite direction, thereby negating the electroosmotic mechanism for the improvements in mobility. Large anion/cation pairs (∼1nm diameter) are shown to have steric blocking and rectification confirming that the ionic conductance is from ionic translocation through the cores of single-walled nanotubes of a monodisperse sub-nm diameter.

Methods

Fabrication and Characterization of SWCNT

CNT materials were synthesized using a modification of prior reported methods^31-33. In order to obtain carbon nanotubes with diameters smaller than 1 nm, the synthesis conditions were modified to obtain < 1nm diameter nanotubes. Specifically, the growth was carried out in a 3 inch Linderberg tube furnace, with the growth temperature set at 750°C and CO as carbon feeding gas at a flow rate of 8 L/min. Catalysts used for the growth is a mixture of Co and Mo supported on MgO support. The average diameter of the nanotubes from both TEM and Raman showed that the samples are made of nanotubes with diameter 0.9 ± 0.2 nm. CNTs were 5-15μm in length and have CNTs 2/3 semiconducting and 1/3 metallic ratios. Bias was applied across the membrane by wire electrodes and thus not directly adding charge to the CNTs.

Fabrication and Characterization of SWCNT Membranes

CNT membranes were fabricated using an approach similar to a prior report and modified for a high CNT loading, 0.5%¹⁵ To describe it briefly, filtered single-walled CNTs were mixed with Epon 862 epoxy resin (Miller Stephenson Chem. Co.), hardener methylhexahydrophthalic anhydride (MHHPA, Broadview Tech. Inc.), catalyst 1-Cyanoethyl-2-ethyl-4-methylimidazole (2E4MZ-CN, Shikoku Chemical, Japan), and 0.1g surfactant Triton-X 100 (Sigma) using a Thinky™ centrifugal shear mixer. As-prepared CNTs-Epoxy composite were cured at 85 °C according to commercial epoxy procedure before being cut into CNT membranes using a microtome equipped with a glass blade. The typical thickness of as-cut CNT membrane is about 5 microns. Finally, each side of as-prepared SWCNT membranes were treated using water plasma oxidation for 1 minute to remove extra polymeric residuals and generate carboxyl functional groups (SWCNTs-COOH) using a Plasma CVD (TEK-VAC Industries, Inc. model PECVD -60-R). The gas inlet was connected to a round bottom flask with water evaporated at low pressure. The mass flow controller set to 20 sccm (N₂) and pressure in the chamber was maintained at 0.6 Torr by throttled exhaust valve. The H₂O plasma enhanced CVD was performed for 1 minute for each side of the membrane at a power of 200 watts while maintaining a substrate temperature of 25°C to 32°C. Ionic current levels through CNT membranes typically increased ∼25% after plasma treatment presumably by the removal of deformed polymer or opening sealed tubes.

Electrophoretic Mobility Measurements using Ionic Currents

A U-shape tube installed with 2 Ag/AgCl electrodes was employed for all the electrophoretic mobility (EM) measurements. Ag/AgCl electrode is purchased from IVM company (part no. E215P). This Ag-AgCl electrode is solid throughout, and made of pure silver-silver chloride without using any fillers or binders. All electrochemical cells were rinsed 5 times and no detection of residue was seen. Constant potential was provided using a Princeton Scientific Model 263A Potentiostat. The distance between reference and working electrodes is about 10 cm, and membrane area is 0.07 cm². Both sides of the U-tube are filled with 1 mM KCl, NaCl, LiCl, HCl, 0.33 mM K₃(Fe(CN)₆), 0.5 mM Ru(bpy)₃Cl₂, or 0.14 mM sulfated cyclodextrin sodium salt (Na₇(SO₃)₇CD, FW 1688) for ionic current measurements. At concentrations below 1 mM KCl, increased solution resistance made EM measurements unreliable due to unknown voltage drops and capacitance. All chemicals were purchased from Sigma Aldrich without further purification.