Recoupling in solid state NMR using γ prepared states and phase matching

Abstract

The paper describes two-dimensional solid state NMR experiments that use powdered dephased anti-phase coherence (γ preparation) to encode chemical shifts in the indirect dimension. Both components of this chemical shift encoded gamma-prepared states can be refocused into inphase coherence by a recoupling element. This helps to achieve sensitivity enhancement in 2D NMR experiments by quadrature detection. The powder dependence of the gamma-prepared states allows for manipulating them by suitable insertion of delays in the recoupling periods. This helps to design experiments that suppress diagonal peaks in 2D spectra, leading to improved resolution. We describe some new phase modulated heteronuclear and homonuclear recoupling pulse sequences that simplify the implementation of the described experiments based on γ prepared states. Recoupling in the heteronuclear spin system is achieved by matching the difference in the amplitude of the sine/cosine modulated phase on the two rf-channels to the spinning frequency while maintaining the same power on the two rf-channels.

1. Introduction

Nuclear magnetic resonance (NMR) spectroscopy opens up the possibility of studying insoluble protein structures such as membrane proteins, fibrils, and extracellular matrix proteins which are difficult to analyze using conventional atomic-resolution structure determination methods, including liquid-state NMR and X-ray crystallography [1–5]. Sensitivity and resolution is a critical issue in all these applications. The most advanced solid-state NMR equipment and techniques still requires hours and days of signal averaging for a simple two-dimensional (2D) spectroscopy of peptides and proteins in a noncrystalline solid form. The resolution of solid state NMR experiments is limited by increased line widths of the powder samples. The present paper describes some new methodology development aimed at making improvements in resolution and sensitivity.

In [6], we addressed a fundamental problem of coherence transfer in solid-state NMR of “powder” samples. We showed how to design experiments that are insensitive to orientations of the crystallite in a powder sample and simultaneously transfer both components of transverse magnetization of spin S to a coupled spin I, in the mixing step of the 2D solid state NMR experiment under magic angle spinning. Simultaneous transfer of both components of the magnetization has been used to develop sensitivity enhanced experiments widely used in liquid-state NMR [7–10]. Pulse sequences for simultaneous transfer of transverse component of magnetization have recently appeared in solid state NMR literature [11]. Transfer schemes presented in [6] are independent of the orientations of the crystallite in a powder sample.

In this paper [13], we show how the powdered dephased coherences (γ prepared states) can be used to develop recoupling experiments with improved resolution and sensitivity. The peaks in the 2D spectrum arising from the chemical shifts encoded on the γ prepared states are shifted in the indirect dimension by the rotor frequency (given that t₁ increments sample the rotor period). The NMR signal arising from these γ prepared states can be manipulated by inserting half rotor period delays in these experiments or suitable phase cycling as described in the paper. In principle, this makes it possible to retain only the peaks arising from the γ prepared states. We describe some methods for achieving this in the paper. These methods could aid in the chemical shift assignment of large molecules, especially for resolving cross-peaks close to the diagonal.

The paper is organized as follows. In Section 2, we describe some homonuclear recoupling experiments that recouple dipolar coupled spins under MAS experiments. These experiments are broadband and robust to rf-inhomogeneity and form the building block for preparation and refocusing of γ prepared states. This work extends recently developed techniques for broadband homonuclear recoupling as reported in the [15–17]. In Section 3, we show how these recoupling blocks can be used to prepare a powder dephased antiphase coherence and refocus both components of the chemical shift encoded γ prepared states (following t₁ evolution) into inphase coherence. In Section 3.1, we show how to design 2D experiments that only retain correlations encoded on the γ prepared states. This then helps to generate 2D spectra, where diagonals are in principle completely suppressed leading to improved resolution. In Section 4, we describe these methods in the context of heteronuclear experiments. In the context of heteronuclear spins, the recoupling is achieved by matching the phase modulations on the two rf-channels (analogous to Hartmann-Hahn matching of the rf-power commonly seen in heteronuclear recoupling experiments). Section 5 describes experimental verification of the proposed techniques. The results are discussed in the conclusion Section 6.

In a standard 2D NMR experiment [18], the initial coherence on spin S evolves under the chemical shift ω_S for time t₁ to S_x → S_xcos(ω_St₁) + S_ysin(ω_St₁). During the mixing step, the x magnetization on spin S is transferred to a coupled spin I, and assuming perfect transfer, S_x → I_x, the spin I precesses under its chemical shift, i.e.,

$$I_{x}cos({\omega }_S{t}_1)\to cos({\omega }_S{t}_1)\{I_{x}cos({\omega }_I{t}_2)+I_{y}sin({\omega }_I{t}_2)\}.$$

The precession is recorded and the experiment is repeated by incrementing t₁, finally leading to a two dimensional signal in t₁ and t₂ that encodes for ω_I and ω_S. Simultaneous transfer of both components of the transverse magnetization during the mixing step, i.e.,

$$S_{x}cos({\omega }_S{t}_1)+S_{y}sin({\omega }_S{t}_1)\to I_{x}cos({\omega }_S{t}_1)+I_{y}sin({\omega }_S{t}_1),$$

is desirable as it enhances the sensitivity of the experiment by a factor of $\sqrt{2}$. Such sensitivity enhanced experiments are performed routinely in liquid-state NMR [7–10]. The simultaneous transfer of both transverse components of the magnetization is usually achieved by synthesizing an isotropic Hamiltonian or a Unitary propagator,

$$U_{\mathit{iso}}=exp(-i\pi \{I_x{S}_x+I_y{S}_y+I_z{S}_z\}).$$

However in solid state NMR experiments under MAS, the dispersion in the coupling strengths arising due to the orientation dependence of the couplings makes the task of synthesizing U_iso for all coupled spin pairs (independent of the orientation) a non-trivial task. This problem can be alleviated by suitably transforming the initial magnetization on spin S, before the t₁ evolution period. This is called γ preparation, as the transformed state depends on angle γ that denotes the rotation of the crystallite around the rotor axis. This transformed state is then made to evolve under the chemical shift of spin S. Because of the initial preparation, it becomes possible to simultaneously transfer both components of the transverse magnetization of spin S after the t₁ precession. The paper proposes many new techniques for creation, manipulation and application of these γ prepared states for design of multidimensional NMR experiments.

Notation

Let S_α(β, γ) denote the rotation of operator S_α around the axis β by angle γ, where α, β ∈ {x, y, z}, i.e., S_α(β, γ) = exp(−iγS_β)S_αexp(iγS_β). For example S_x(z, γ) = S_xcosγ + S_ysinγ. It is straightforward to verify relations of the following kind

$$[-{iS}_x(\beta ,\gamma ),-{iS}_y(\beta ,\gamma )]=-{iS}_z(\beta ,\gamma ).$$

It also follows from definition that for any unitary transformation U,

$${US}_{\alpha }(\beta ,\gamma )U^{\prime }=S_{U\alpha U^{\prime }}(U\beta U^{\prime },\gamma ),$$

where S_UαU′(UβU′, γ), denotes rotation of operator US_αU′ around US_βU′.

Let the unit vectors l, m, n constitute a right handed coordinate system (l × m = n). Then

$${\mathcal{H}}_{ZQ}^l(\gamma )=I_m{S}_m(l,\gamma )+I_n{S}_n(l,\gamma )=S_m{I}_m(l,-\gamma )+S_n{I}_n(l,-\gamma ),$$ (1)

and

$${\mathcal{H}}_{DQ}^l(\gamma )=I_m{S}_m(l,\gamma )-I_n{S}_n(l,\gamma )=S_m{I}_m(l,\gamma )-S_n{I}_n(l,\gamma ),$$ (2)

are used to denote the zero quantum and multiple (double) quantum operators.

2. Phase alternating modulated recoupling

Consider two homonuclear spins I and S under magic angle spinning condition [19]. In a rotating frame, rotating with both the spins at their common Larmor frequency, the Hamiltonian of the spin system takes the form

$$H(t)={\omega }_I(t)I_z+{\omega }_S(t)S_z+{\omega }_{IS}(t)(3I_z{S}_z-I·S)+2\pi A(t)\times (cos\varphi (t)F_x+sin\varphi (t)F_y),$$ (3)

where the operator F_x = I_x + S_x, and ω_I(t) and ω_S(t) represent the chemical shift for the spins I and S respectively and ω_IS(t) represents the time varying couplings between the spins under magic-angle spinning. These interactions may be expressed as a Fourier series

$${\omega }_{\lambda }(t)=\sum _{m=-2}^2{\omega }_{\lambda }^{m}exp(im{\omega }_{r}t),$$ (4)

where ω_r is the spinning frequency (in angular units), while the coefficients ω_λ(λ = I, S, IS) reflect the dependence on the physical parameters like the isotropic chemical shift, anisotropic chemical shift, the dipole-dipole coupling constant and through this the internuclear distance [22].

The term I · S in (3), commutes with the rf-Hamiltonian, and in the absence of the chemical shifts, it averages to zero under MAS. We will, therefore, drop this term in the subsequent treatment, where we truncate the chemical shift Hamiltonian with a strong rf-field.

Consider the rf irradiation on homonuclear spin pair whose amplitude is chosen as $A(t)=\frac{C}{2\pi }$ and the offset Δω(t)

$$\stackrel{.}{\varphi }(t)=-\mathrm{\Delta }\omega (t)={\omega }_{r}cos(Ct+\theta ).$$ (5)

This offset is implemented as a phase modulation

$$\varphi (t,\theta )=\frac{{\omega }_r}{C}\{sin(Ct+\theta )-sin(\theta )\}.$$ (6)

In the modulation frame, which transforms the density matrix from

$$\rho \to exp(i\varphi (t)F_z)\rho exp(-i\varphi (t)F_z),$$

the rf-Hamiltonian takes the form

$$H^{rf}(t)={CF}_x-\stackrel{.}{\varphi }{F}_z={CF}_x-{\omega }_{r}cos(Ct+\theta )F_z,$$ (7)

where C is in the angular frequency units and we choose C ≫ ω_I(t), ω_S(t), ω_IS(t), ω_r. In the interaction frame of the irradiation along x-axis, with the strength C, the chemical shifts of the spins are averaged out. The coupling Hamiltonian of the spin system takes the form

$$H_I^{DD}(t)=\frac{3}{2}{\omega }_{IS}(t)(I_z{S}_z+I_y{S}_y)+\frac{3}{2}{\omega }_{IS}(t)((I_z{S}_z-I_y{S}_y)cos(2Ct)+(I_z{S}_y+I_y{S}_z)sin(2Ct)),$$ (8)

and the rf-Hamiltonian of the spin system transforms to

$$H_I^{rf}(t)=-\frac{{\omega }_r}{2}\{(2F_z{cos}^2(Ct)cos\theta +2F_y{sin}^2(Ct)sin\theta )-sin(2Ct)(F_{y}cos\theta +F_{z}sin\theta )\},$$ (9)

which averages over a period τ_c = 2π/C to

$$H_I^{rf}=-\frac{{\omega }_r}{2}(cos\theta F_z+sin\theta F_y).$$ (10)

We have therefore an effective field along the direction m, where m = −sin θ ŷ − cos θ ẑ. For θ = 0, we have an effective rf-field along the −z direction. For $\theta =\frac{\pi }{2}$, we have an effective field along −y direction.

Now, transforming into the interaction frame of the rf-Hamiltonian $H_I^{rf}$, we only retain terms that give static contribution to the effective Hamiltonian, i.e., terms oscillating with frequency C are dropped and the residual Hamiltonian takes the form (neglecting the terms oscillating at frequency 2ω_r as they are not recoupled)

$$H_{II}(t)={\kappa }_h\{cos({\omega }_{r}t)cos({\omega }_{r}t+\gamma )(I_n{S}_n-I_x{S}_x)+sin({\omega }_{r}t)\times cos({\omega }_{r}t+\gamma )(I_n{S}_x+I_x{S}_n)\},$$ (11)

which averages to

$${\overline{H}}_{II}=\frac{{\kappa }_h}{2}\{cos(\gamma )(I_n{S}_n-I_x{S}_x)-sin(\gamma )(I_n{S}_x+I_x{S}_n)\},$$ (12)

where ${\kappa }_h=\frac{3}{4\sqrt{2}}{b}_{IS}sin(2\beta )$, where $b_{IS}=\frac{{\mu }_0{\gamma }_I{\gamma }^{Sh}}{4\pi r_{IS}^3}$ is the dipole coupling constant and n is the effective direction

$$n=cos\theta \widehat{y}-sin\theta \widehat{z},$$

and m × n = x. From (2), we have prepared an effective Hamiltonian ${\mathcal{H}}_{DQ}^m(-\gamma )$.

This cosine modulated pulse sequence is broadband as a large value of C averages out the chemical shift [15]. The high power cosine modulated pulse sequence is sensitive to rf-inhomogeneity. Let ε denote the inhomogeneity parameter. Then, rewriting H_rf in (7) gives

$$H^{rf}(t)=C(1+\epsilon )F_x-{\omega }_{r}cos(Ct+\theta )F_z.$$ (13)

In the interaction frame of irradiation along x-axis with strength C, the rf-Hamiltonian averages to $\epsilon {CF}_x+\epsilon Co(\frac{{\omega }_r}{C})F_{m^{\prime }}+\frac{{\omega }_r}{2}{F}_m$, where $o(\frac{{\omega }_r}{C})$ denotes a term of order $\frac{{\omega }_r}{C}\ll 1$. For large C, the factor εCF_x significantly reduces the recoupling.

In [17], we presented a method to eliminate this effect of the rf-inhomogeneity by simply phase alternating every ${\tau }_c=\frac{2\pi }{C}$ units of time, by changing

$$\varphi (t,\theta )\to \pi +\varphi (t,-\theta ).$$

We called this a phase alternating pulse sequence.

The effective Hamiltonian produced on the alternate phase is $-\epsilon {CF}_x+\epsilon Co(\frac{{\omega }_r}{C})F_{m^{″}}+\frac{{\omega }_r}{2}{F}_m$.

For $\frac{{\omega }_r}{C}\ll 1$, the resulting Hamiltonian over 2 τ_c is

$$\epsilon Co(\frac{{\omega }_r}{C})F_{n^{\prime }}+\frac{{\omega }_r}{2}{F}_m.$$

The resulting Hamiltonian is linear in the inhomogeneity parameter, ε [20]. However, compared to CMRR, the effect of inhomogeneity is reduced by $o(\frac{{\omega }_r}{C})$ (m′, m″, n′ are vectors in the m-n plane).

In [17], we chose $\theta =-\frac{\pi }{2}$ in (5) and the resulting pulse sequence is called PAMORE (Phase Alternating MOdulated REcoupling). The effective Hamiltonian it produces is ${\mathcal{H}}_{DQ}^y(-\gamma )$.

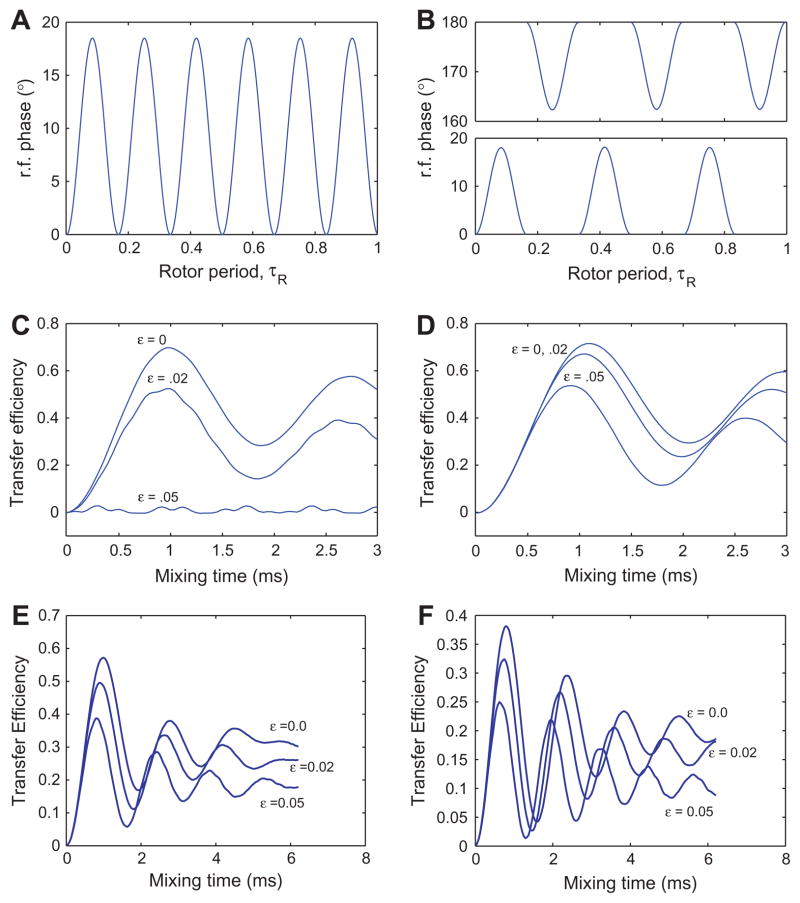
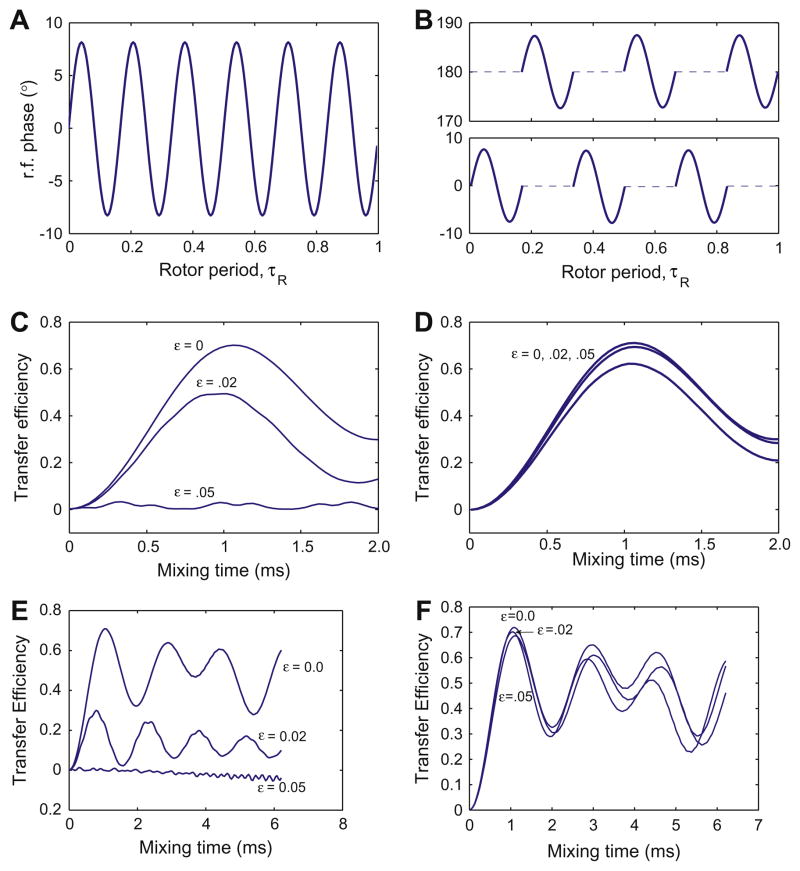
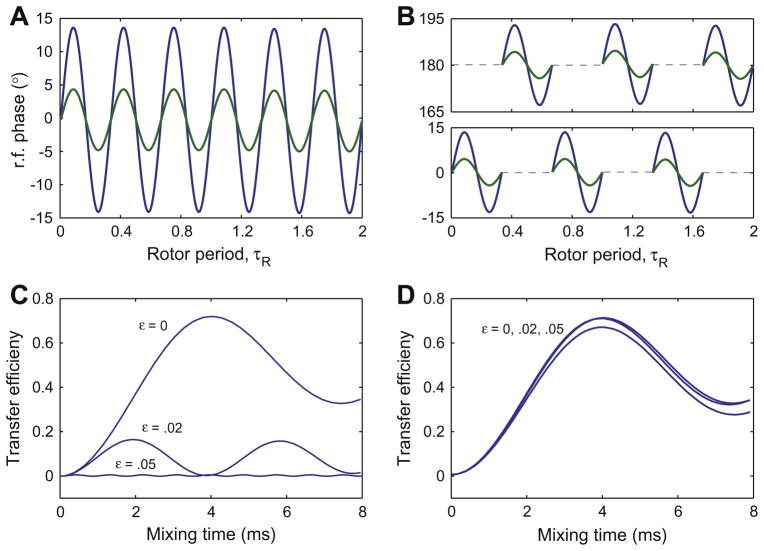
By choosing θ = 0, we obtain the effective Hamiltonian $-{\mathcal{H}}_{DQ}^z(\gamma )$. The resulting experiment is called Z-PAMORE (signifying recoupling with an effective z field). When we choose θ = π, we obtain the effective Hamiltonian $-{\mathcal{H}}_{DQ}^{\overline{z}}(\gamma )$. We call this experiment Z̄-PAMORE. Figs. 1 and 4 show the rf-phase modulations and transfer using the PAMORE and Z-PAMORE recoupling blocks.

Fig. 1.

The top two panels show the phase of the rf irradiation as a function of time (in the units of τ_R) for the CMRR (A) and PAMORE (B) pulse sequences when C = 6ω_r. The bottom two panels show numerical simulations of the transfer efficiency for the ¹³C–¹³C spin-pair, 1.52 Å apart in a powder sample subject to 8 kHz MAS, an external magnetic field corresponding to a 360 MHz (Larmor frequency for ¹H) spectrometer and nominal rf-field strength on the ¹³C channel of 48 kHz, for the CMRR (C) and PAMORE (D) pulse sequences, for three different values of rf-inhomogeneity parameter, ε(0, .02, .05). Simulations use C = 6ω_r, giving τ_c = 125/6 μs and rf-power of ${\omega }_{rf}^C/2\pi =48\text{kHz}$. The efficiency is reduced with increasing ε. In panel C at ε = .05, there is almost no transfer. Simulations were done with SPINEVOLUTION software [14]. In Fig. C and D, we assume spins on resonance with no CSA. In Fig. E and F, we simulate the performance of the PAMORE pulse sequence with phase modulation implemented as constant phases over interval of .2 (as in C and D) and 1.3 μs respectively. The later correspond to experimental realization shown in Figs. 3 and 5. The simulated transfer is for I_y → S_y, where I and S spins are C_α and CO, respectively. Carrier is placed on CO resonance with C_α and CO resonances at 35 and 170 ppm respectively. Chemical shift ansiotropy of 19.3 and 70.2 ppm and asymmetry parameter η = 1.225 and η = 1.05 are used for C_α and CO spins respectively. The Euler angles (α, β, γ) relating the chemical shielding tensors to the principle axis system of the dipolar tensor are ${\mathrm{\Omega }}_{PC}^{{\mathrm{C}}_{\alpha }}=(-33.7,-95.3,48.92)$ and ${\mathrm{\Omega }}_{PC}^{\text{CO}}=(154.32,-2.9250,-106.8120)$ [12].

Fig. 4.

Panel A and B show the phase of the rf irradiation as a function of time (in the units of τ_R) for the Z-PAMORE recoupling element with and without phase alternation, respectively, when C = 6ω_r. In (5), this corresponds to θ = 0. Panel C and D show numerical simulations of the transfer efficiency, $\frac{\langle S_z\rangle }{\langle I_z\rangle }$, for the ¹³C–¹³C spin-pair, 1.52 Å apart in a powder sample subject to 8 kHz MAS, an external magnetic field corresponding to a 360 MHz (Larmor frequency for ¹H) spectrometer and nominal rf-field strength on the ¹³C channel of 48 kHz, for the phase modulations as shown in figure A and B respectively, for three different values of rf-inhomogeneity parameter, ε(0, .02, .05). Simulations use C = 6ω_r, giving τ_c = 125/6 μs and rf-power of ${\omega }_{rf}^C/2\pi =48\text{kHz}$. The efficiency is reduced with increasing ε much more rapidly in the absence of phase alternation. Simulations were done with SPINEVOLUTION software [14] and Fig. C and D, assume an ideal two spin system with no isotropic and anisotropic shifts. In Fig. E and F, we simulate the performance of the ZPAMORE pulse sequence without and with phase alternation with the carrier placed midway between C_α and CO resonances at 35 and 170 ppm respectively. The simulated transfer is for I_z → S_z, where I and S spins are C_α and CO respectively. Chemical shift ansiotropy of 19.3 and 70.2 ppm and asymmetry parameter η = 1.225 and η = 1.05 are used for C_α and CO spins respectively. The Euler angles (α, β, γ), relating the chemical shielding tensors to the principle axis system of the dipolar tensor are ${\mathrm{\Omega }}_{PC}^{{\mathrm{C}}_{\alpha }}=(-33.7,-95.3,48.92)$ and ${\mathrm{\Omega }}_{PC}^{\text{CO}}=(154.32,-2.9250,-106.8)$ [12]. Phase modulation is discretized over intervals of .2 μs.

3. Gamma-preparation

Consider the Hamiltonians,

$${\mathcal{H}}_{DQ}^z(\gamma )=I_x{S}_x(z,\gamma )-I_y{S}_y(z,\gamma )$$ (14)

and

$${\mathcal{H}}_{DQ}^{\overline{z}}(\gamma )=I_y{S}_y(\overline{z},\gamma )-I_x{S}_x(\overline{z},\gamma ),$$ (15)

that can be prepared by the Z-PAMORE and Z̄-PAMORE experiment respectively. Note

$$exp(-i\frac{\pi }{2}{F}_x){\mathcal{H}}_{DQ}^y(-\gamma )exp(i\frac{\pi }{2}{F}_x)={\mathcal{H}}_{DQ}^{\overline{z}}(\gamma ).$$

Therefore these Hamiltonians can also be prepared by the PAMORE experiment by nesting with $\frac{\pi }{2}$ pulses. Now, consider the following experiment,

$$I_x\underset{[I]}{\overset{{\left({\mathcal{H}}_{DQ}^z(\gamma )\right)}_{\pi }}{\to }}2I_z{S}_y(z,\gamma )\underset{[II]}{\overset{{\omega }_s{S}_z}{\to }}2I_z{S}_y(z,\gamma +{\omega }_s{t}_1)\underset{[\mathit{III}]}{\overset{{\left({\mathcal{H}}_{DQ}^z({\gamma }^{\prime })\right)}_{\pi }}{\to }}-I_x(z,{\gamma }^{\prime }-\gamma -{\omega }_s{t}_1),$$ (16)

where, ${\left({\mathcal{H}}_{DQ}^z(\gamma )\right)}_{\pi }$, represents evolution $exp\left(-i\pi {\mathcal{H}}_{DQ}^z(\gamma )\right)$, for a nominal value of β (the angle internuclear vector makes with the spinning axis). Step I constitutes the preparation phase, step II, the evolution of chemical shift and step III refocusing the gamma-prepared state. The terms I_xS_x(z, γ) and I_yS_y(z, γ) in the Hamiltonian commute, so there effect can be analyzed separately. For a right handed unit vector triple l, m, n, we note that

$$I_m(l,\gamma +\theta )=I_m(l,\gamma )cos\theta +I_n(l,\gamma )sin\theta .$$ (17)

This identity is used in analyzing the refocusing stage in Eq. (16).

If the preparation Hamiltonian ${\mathcal{H}}_{DQ}^z(\gamma )$ is applied for an integral number of rotor periods, then

$${\gamma }^{\prime }=\gamma +{\omega }_r{t}_1.$$

The final state following the refocusing is

$$-I_x(z,({\omega }_r-{\omega }_s)t_1)=-I_{x}cos({\omega }_s-{\omega }_r)t_1+I_{y}sin({\omega }_s-{\omega }_r)t_1.$$

The salient feature of the experiment is that both components of the chemical shift encoded gamma-prepared magnetization can be transferred following the evolution in the indirect dimension. The indirect dimension frequency is displaced by the rotor frequency.

When the recoupling is performed using the effective Hamiltonian ${\mathcal{H}}_{DQ}^{\overline{z}}(\gamma )$, then we get

$$I_x\underset{[I]}{\overset{{\left({\mathcal{H}}_{DQ}^{\overline{z}}(\gamma )\right)}_{\pi }}{\to }}-2I_z{S}_y(\overline{z},\gamma )\underset{[II]}{\overset{{\omega }_s{S}_z}{\to }}-2I_z{S}_y(\overline{z},\gamma -{\omega }_s{t}_1)\underset{[\mathit{III}]}{\overset{{\left({\mathcal{H}}_{DQ}^{\overline{z}}({\gamma }^{\prime })\right)}_{\pi }}{\to }}-I_x(z,\gamma -{\gamma }^{\prime }-{\omega }_s{t}_1).$$ (18)

If the preparation Hamiltonian ${\mathcal{H}}_{DQ}^{\overline{z}}(\gamma )$ is applied for an integral number of rotor periods, then

$${\gamma }^{\prime }=\gamma +{\omega }_r{t}_1.$$

The final state following the refocusing is

$$-I_x(z,-({\omega }_r+{\omega }_s)t_1)=-I_{x}cos({\omega }_r+{\omega }_s)t_1+I_{y}sin({\omega }_r+{\omega }_s)t_1.$$

Remark 1

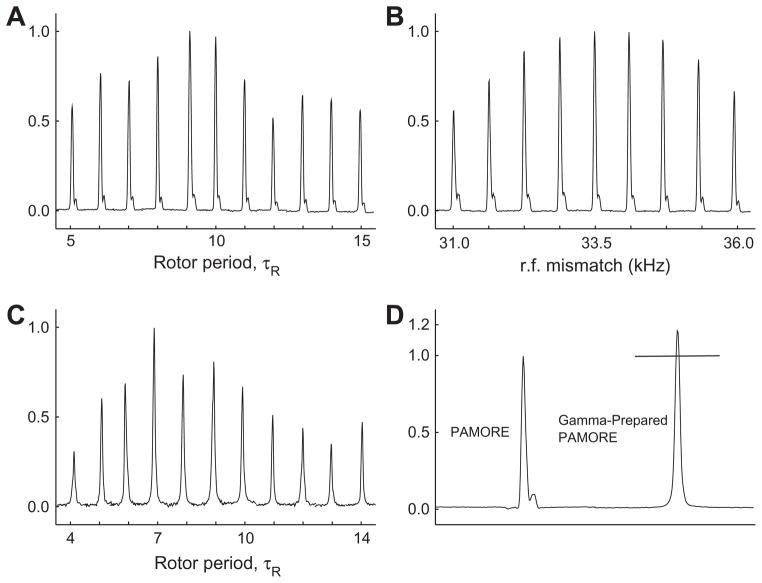
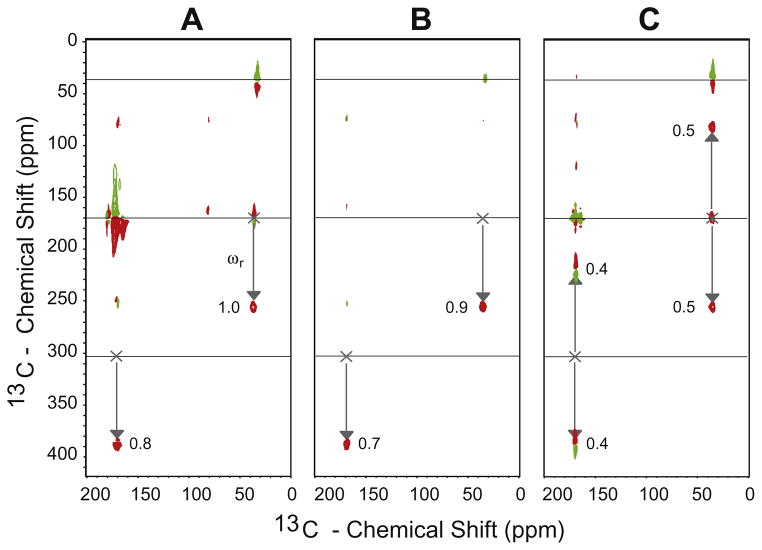
The shift in the rotor frequency is different depending on if the preparation and refocusing is performed with $H_{DQ}^z(\gamma )$, or $H_{DQ}^{\overline{z}}(\gamma )$. We use this feature to cross check Gamma-Prep peaks in the 2D spectra. Fig. 3C shows the build up of the Gamma-Prep PAMORE peak by using processing as shown in Fig. 2C.

Fig. 3.

Panel A shows the build up of cross-peak, indirect evolution on C_α and direct evolution on CO, (obtained from the experiment shown in Panel A for Fig. 2) as a function of the mixing time in units of number of rotor period (rotor period is 125 μs). Panel B shows the transfer efficiency as function of rf-power variation. Panel C shows the build up of Gamma-Prep peak, indirect evolution on CO and direct evolution on C_α, as the function of the mixing time in units of number of rotor periods. Panel D compared the height of cross-peaks for the PAMORE and gamma-prepared PAMORE, where the mixing time is 9 and 7 rotor periods, respectively. The mixing period is chosen from individual build up curves to give the best transfer efficiency. The spectrum for the PAMORE experiment uses the States method to combine the two quadrature components in the indirect dimension. Gamma-Prep PAMORE experiment is processed using echo/anti-echo as shown in Fig. 2C. The PAMORE mixing block was designed for a nominal power of 48 kHz, which is then experimentally optimized to maximize transfer efficiency. The carrier is placed at the CO resonance. Uniformly ¹³C, ¹⁵N-labeled sample of glycine was used in the full volume of standard 4 mm rotor at ambient temperature.

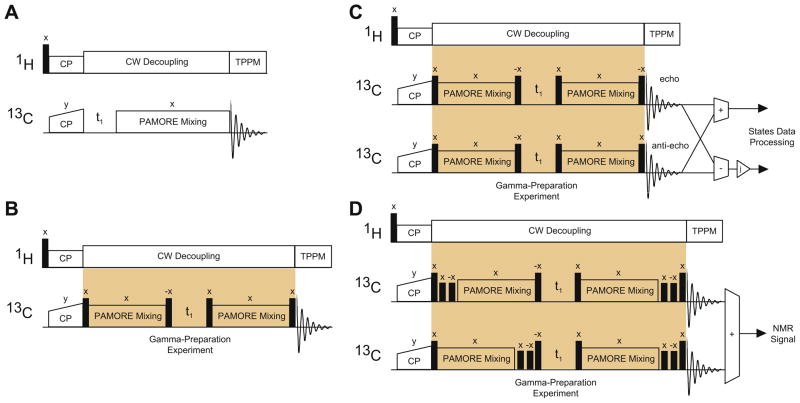
Fig. 2.

Panel A in the figure shows the basic ¹³C–¹³C correlation experiment using the PAMORE pulse element as the building block. The build up of the cross-peaks is used to generate a build up curve for the PAMORE recoupling. In (5), this corresponds to $\theta =-\frac{\pi }{2}$. Panel B shows the pulse sequence for the gamma-preparation experiment. The x phase on the PAMORE recoupling block indicates the initial phase at the start of PAMORE recoupling. Panel C shows the initial processing of the two Gamma-Prep experiments before processing by States to achieve sensitivity enhancement. Multiplication by j, shown in triangle in Fig. C, generates cosine and sine modulated signals for states processing, see Eqs. (31) and (32). Panel D shows combining two Gamma-Prep experiments with suitably placed half rotor period delays to isolate the Gamma-Prep signals and suppress other peaks in the 2D spectra. All hard pulses are $\frac{\pi }{2}$pulses.

3.1. Suppression of diagonals

If the experiment described in (16) or (18) is performed twice with two different values of γ₁, e.g. ${\gamma }_1^{\prime }$ and ${\gamma }_2^{\prime }$, then we will be able to retain the Gamma-Prep peaks by adding the signals from the two experiments when ${\gamma }_2^{\prime }=\pi +{\gamma }_1^{\prime }$ (this is obtained by inserting the half rotor period delay in experiment 2 between the preparation and refocusing step in (16)). The delay is implemented by an xx̄ pulse sequence using large rf-power to significantly eliminate chemical shift and other interactions, and any net rf-rotation due to uncaliberated power or rf-inhomogeneity. To keep the length of the experiment 1 and 2 the same, an identical delay is introduced in experiment 1 before the preparation phase, as depicted in Fig. 2D. The inphase magnetization arising from the gamma-prepared states have opposite signs after the refocusing block, where as the residual part of the magnetization has the same sign. By adding the two experiments and alternating the receiver phase, we only retain the signals giving rise to Gamma-Prep peaks in the spectrum and significantly suppress all other signals including the diagonal peaks.

4. Phase matching and heteronuclear recoupling

Consider two coupled heteronuclear spins I and S under magic angle spinning condition [21]. The spins are irradiated with rf fields at their Larmor frequencies along say the x direction. In a double-rotating Zeeman frame, rotating with both the spins at their Larmor frequency, the Hamiltonian of the system takes the form

$$H(t)={\omega }_I(t)I_z+{\omega }_S(t)S_z+{\omega }_{IS}(t)2I_z{S}_z+H^{rf}(t),$$ (19)

where ω_I(t), ω_S(t), and ω_IS(t) represent time-varying chemical shifts for the two spins I and S and the coupling between them, respectively. These interactions can be expressed as a Fourier series ${\omega }_{\lambda }(t)={\sum }_{m=-2}^2{\omega }_{\lambda }^{m}exp(im{\omega }_{r}t)$, where ω_r is the spinning frequency (in angular units), while the coefficients ω_λ, (λ = I, S) reflect the dependence on the physical parameters like the isotropic chemical shift, anisotropic chemical shift, the dipole-dipole coupling constant and through this the internuclear distance [22,23].

Consider the rf irradiation on heteronuclear spin pair, where amplitude on spin I and S is chosen as $A_{\lambda }(t)=\frac{C_{\lambda }}{2\pi }(\lambda =I,S)$ and the offset Δω_λ(t) = −B_λcos(C_λt). This offset is implemented as a phase modulation

$${\varphi }_{\lambda }(t)=\frac{B_{\lambda }}{C_{\lambda }}sin(C_{\lambda }t).$$ (20)

The rf-Hamiltonian for the irradiation takes the form

$$H_I^{rf}(t)=C_I{I}_x+C_S{S}_x-{\stackrel{.}{\varphi }}_I{I}_z-{\stackrel{.}{\varphi }}_S{S}_z,$$ (21)

which then gives

$$H_I^{rf}(t)=C_I{I}_x+C_S{S}_x-B_{I}cos(C_{I}t)I_z-B_{S}cos(C_{S}t)S_z,$$ (22)

where C_λ is in angular frequency units and we choose C_λ≫ ω_λ(t), B_λ.

We choose C_I = C_S = C. In the interaction frame of the irradiation along x-axis, with the strength C_I and C_S on the two spins, the coupling Hamiltonian is averaged to

$$H_I^{DD}(t)={\omega }_{IS}(t)(I_z{S}_z+I_y{S}_y)+{\omega }_{IS}(t)((I_z{S}_z-I_y{S}_y)cos(2Ct)+(I_z{S}_y+I_y{S}_z)sin(2Ct)),$$ (23)

and the rf-Hamiltonian of the spin system transforms to

$$H_I^{rf}(t)=\frac{B_I}{2}(-2{cos}^2(C_{I}t)I_z+sin(2C_{I}t)I_y)+\frac{B_S}{2}(-2\times {cos}^2(C_{S}t)S_z+sin(2C_{s}t)S_y),$$ (24)

which averages over a period ${\tau }_c=\frac{2\pi }{C}$ to

$$H_I^{rf}=-\frac{B_I}{2}{I}_z-\frac{B_S}{2}{S}_z,$$ (25)

which we rewrite as

$$H_{in}^{rf}=-B^{+}\frac{I_z+S_z}{2}-B^{-}\frac{I_z-S_z}{2},$$ (26)

where $B^{+}=\frac{B_I+B_S}{2}$ and $B^{-}=\frac{B_I-B_S}{2}$.

Now, if we choose B⁻ = ω_r and B⁺, removed from ω_r and 2ω_r (e.g., choose $B_I=\frac{3{\omega }_r}{2}$ and $B_S=\frac{-{\omega }_r}{2}$), then other resonances are avoided and one prepares a static coupling Hamiltonian in (23).

This then takes the form

$${\mathcal{H}}_{ZQ}^z(-\gamma )={\kappa }_d\underset{I_x{S}_x(z,-\gamma )+I_y{S}_y(z,-\gamma )}{\underbrace{\{(I_x{S}_x+I_y{S}_y)cos(\gamma )-(I_x{S}_y-I_y{S}_x)sin(\gamma )\}}}$$ (27)

which will recouple the spins I and S. Note, this recoupling Hamiltonian is a zero quantum Hamiltonian.

Remark 2

If we choose B_I = ω_r and B_S = −ω_r, we also get B⁻ = ω_r and B⁺ = 0. This choice may be avoided as it will also couple the homonuclear spin pair I, if present.

Now observe, we can also prepare a double quantum Hamiltonian by choosing B⁺ = ω_r and B⁻, removed from ω_r and 2 ω_r (e.g., choose $B_I=\frac{3{\omega }_r}{2}$ and $B_S=\frac{{\omega }_r}{2}$). The resulting rf-phase modulation and transfer efficiency is as shown in Fig. 7 where the I − S spin pair is ¹⁵N–¹³C_α.

Fig. 7.

Panel A and Panel B show the phase of the MOM and POEM rf irradiation as a function of time (in the units of τ_R) for the ¹³C (blue) and ¹⁵N (green) channel without (A) and with (B) phase alternating respectively. Panel C and Panel D show numerical simulations of the transfer efficiency as function of mixing time using MOM and POEM for the ¹⁵N–¹³C spin-pair, 1.52 Å apart in a powder sample subject to 8 kHz MAS, an external magnetic field corresponding to a 360 MHz (Larmor frequency for ¹H) spectrometer and nominal rf-field strength on the ¹⁵N and ¹³C channel of 24 kHz, respectively. Simulations used ${\delta }_{\mathit{iso}}^C=0,{\delta }_{an\mathit{iso}}^C=0$ and ${\delta }_{an\mathit{iso}}^N=0$. In Panel C and D, three different values of rf-inhomogeneity parameter, ε(0, .02, .05) are used. Simulations use C = 3ω_r, giving τ_c = 125/3 μs and rf-power of ${\omega }_{rf}^C/2\pi =24\text{kHz}$. The efficiency is reduced with increasing ε. In panel C at ε = .05, there is almost no transfer. Simulations were done with SPINEVOLUTION software [14]. Starting and target operator are I_z and S_z.

Then, one prepares a static coupling Hamiltonian in (23). This takes the form

$$-{\mathcal{H}}_{DQ}^z(\gamma )={\kappa }_d\underset{-(I_x{S}_x(z,\gamma )-I_y{S}_y(z,\gamma ))}{\underbrace{\{(I_y{S}_y-I_x{S}_x)cos(\gamma )-(I_x{S}_y+I_y{S}_x)sin(\gamma )\}}}.$$ (28)

We call the above experiments MOM (MOdulation Matched) recoupling experiments.

We can make these experiments robust to rf-inhomogeneity, by simply phase alternating the phase ϕ(t) to π + ϕ(t), every ${\tau }_c=\frac{2\pi }{C}$ units of time, i.e., (ϕ(t + τ_c) = ϕ(t)). We call this the POEM experiment (Phase alternated MOdulation Matched ExperiMent).

Now, consider the following set of 2D experiments, based on the recoupling block, where γ′ = γ + ω_rt₁.

$$-I_x\underset{[I]}{\overset{{\left({\mathcal{H}}_{ZQ}^z(-\gamma )\right)}_{\pi }}{\to }}2I_z{S}_y(z,-\gamma )\underset{[II]}{\overset{{\omega }_s{Z}_z}{\to }}2I_z{S}_y(z,-\gamma +{\omega }_s{t}_1)\times \underset{[\mathit{III}]}{\overset{{\left({\mathcal{H}}_{ZQ}^z(-{\gamma }^{\prime })\right)}_{\pi }}{\to }}{I}_x(z,({\omega }_s+{\omega }_r)t_1).$$ (29)

Simlarly, we have

$$-I_x\underset{[I]}{\overset{-{\left({\mathcal{H}}_{DQ}^z(\gamma )\right)}_{\pi }}{\to }}2I_z{S}_y(z,\gamma )\underset{[II]}{\overset{{\omega }_s{S}_z}{\to }}2I_z{S}_y(z,\gamma +{\omega }_s{t}_1)\underset{[\mathit{III}]}{\overset{-{\left({\mathcal{H}}_{DQ}^z(\gamma )\right)}_{\pi }}{\to }}{I}_x(z,({\omega }_r-{\omega }_s)t_1).$$ (30)

These experiments transfer both components of the magnetization to the other spin. In above, we have made repeated use of the identity (17) and the fact that operators I_xS_x(z, γ) and I_yS_y(z, γ), in the Hamiltonian commute and hence the effect can be analyzed separately.

Finally, observe that if choose B⁺ = ω_r and B⁻ = −ω_r (by choosing B_I = 0), then we recouple both the zero and multiple quantum terms, resulting in an effective Hamiltonian 2I_yS_y(z, γ). This Hamiltonian can then be used to implement the first step in (29) and (30), in half the time.

5. Experimental Results

All experiments [13] were performed on a 360 MHz spectrometer (¹H Larmor frequency of 360 MHz) equipped with a triple resonance 4 mm probe. Uniformly ¹³C, ¹⁵N-labeled sample of glycine (purchased from Cambridge Isotope Laboratories, Andover, MA) was used in the full volume of standard 4 mm rotor at ambient temperature using $\frac{{\omega }_r}{2\pi }=8\text{kHz}$ sample spinning. The experiments used 3s recycling delay. All 2D experiments use 1024 sampling points in the direct dimension with 25 μs sampling dwell time and 128 points in the indirect dimension with 12.5 μs sampling dwell time. A 100 kHz CW decoupling is used during recoupling and TPPM during acquisition. For the Homonuclear experiments shown in Figs. 3 and 5, The C_α and CO resonances that are 12 kHz apart at 35 and 170 ppm respectively. The carrier is placed at CO resonance.

Fig. 5.

Two-dimensional Gamma-Prep PAMORE ¹³C–¹³C experiment carried out on uniformly ¹³C, ¹⁵N-labeled samples of glycine. Panel A shows the standard Gamma-Prep 2D spectra resulting from pulse sequence and processing as shown in Fig. 2C, where the cross-peaks are phase shifted by the rotor frequency ω_r. Panel B shows the Gamma-Prep 2D spectra where we insert a half rotor period delay between the preparation and refocusing step and alternate the receiver phase to suppress the diagonal peaks. Panel C shows the Gamma-Prep 2D spectra where we invert the sign of the bracketing $\frac{\pi }{2}$ flip pulses around the PAMORE block and alternate the receiver phase to suppress the diagonal peaks. The net effect is two cross-peaks that are each phase shifted by the rotor frequency {ω_r, − ω_r}. All peak heights are normalized to the height of the ¹³C_α–¹³CO–¹³C_α cross-peak in Panel A. The numbers .4, …, .9 denote relative peak heights.

Fig. 3A shows the build up of the cross-peak as function of mixing time, in units of number of rotor periods for the ¹³C_α–¹³CO correlation experiment with PAMORE as the recoupling block as shown in Fig. 2A. The experiment uses an initial ramped CP for ¹H to ¹³C cross polarization. The number of acquisitions for every t₁ increment is 1. The PAMORE recoupling block is designed for a nominal power of 48 kHz. In experiment this power is optimized to give maximum transfer efficiency. Fig. 3B shows the dependence of the cross-peak height as function of rf-power for a mixing time of eight rotor periods when the rf power is varied over a range of 5 kHz. The experiment used CW decoupling on protons of $\frac{{\omega }_{rf}^H}{2\pi }=100\text{kHz}$ during the transfer. Fig. 3C shows the build up of the Gamma-Prep peak as function of the mixing time, in units of number of rotor periods for the ¹³C_α–¹³CO Gamma-Prep correlation experiment with PAMORE as the recoupling block as in Fig. 2C, showing echo/anti-echo processing. Fig. 5A shows a typical spectra where the Gamma-Prep peaks are shifted by −ω_r (the rotor frequency) after it is processed as shown in Fig. 2C. The build up shown in Fig. 3C is for the ¹³C_α–¹³CO–¹³C_α cross-peak (marked A). The PAMORE recoupling block used in the Gamma-Prep experiment is identical to the experiment as shown in Fig. 2A. Fig. 3D compares the peak heights of ¹³C_α → ¹³CO transfer and ¹³C_α–¹³CO–¹³C_α Gamma-Prep peak for a mixing time of 9 and 7 rotor period respectively. The ¹³C_α–¹³CO–¹³C_α Gamma-Prep peak is extracted from a 2D spectra as shown in Fig. 5A.

Fig. 2C shows how two Gamma-Prep experiments are processed. The Gamma-Prep signal from the two experiments has the form s₁(t₁, t₂) = exp(−jω_St₁)exp(−jω_It₂) and s₂(t₁, t₂) = exp(jω_St₁)exp(−jω_It₂).

The processing gives

$$s_A=s_1(t_1,t_2)+s_2(t_1,t_2)=2cos({\omega }_S{t}_1)exp(-j{\omega }_I{t}_2)$$ (31)

$$s_B=-j(s_1(t_1,t_2)-s_2(t_1,t_2))=2sin({\omega }_S{t}_1)exp(-j{\omega }_I{t}_2)$$ (32)

which are used as inputs to States. If equal relaxation is assumed for antipase and inphase states, theoretically, the peak height should double as a result of Gamma-Prep experiment compared to a 2D PAMORE. Fig. 3D shows the obtained enhancement when mixing time for PAMORE and Gamma-Prep PAMORE are optimized.

Fig. 2D combines two Gamma-Prep acquisitions with half rotor period delays inserted suitably. The delay is implemented by an xx̄ pulse sequence using large rf-power to significantly eliminate chemical shift and other interactions and any net rf-rotation due to uncalibrated power or rf-inhomogeneity. The powers are chosen large enough to prevent chemical shift evolution and avoid Hartmann-Hahn and rotary resonance conditions and thereby prevent dipolar recoupling. The exact values are experimentally optimized. The calibrated ¹³C power during half rotor delay is 32.9 (kHz). The receiver phase is inverted to subtract the two acquisitions. The same experiment is repeated (with two acquisitions) with the phase of the last x pulse inverted as shown in Fig. 2D. The resulting spectra obtained from the two experiments are processed as shown in Fig. 2C.

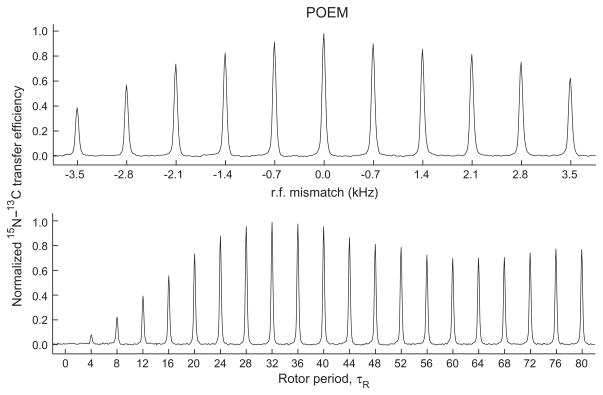
Fig. 8 shows the build up of magnetization on ¹³C_α, extracted from a 2D experiment as shown in Fig. 6, using a POEM recoupling block. Four scans are collected per t₁ increment. The experiment consists of an initial ramped CP transfer from ¹H to ¹⁵N, with proton power calibrated on 50 kHz and ¹⁵N ramped from 42 to 46 kHz. The POEM power on ¹⁵N and ¹³C channels is calibrated to 24 kHz. The ¹⁵N carrier is at 4.5 kHz (125 ppm) and ¹³C carrier at 10 kHz (110 ppm). The ¹⁵N resonance is at 25 ppm. The phase modulation over a rotor period is as shown in Fig. 7B. The bottom panel of Fig. 8 shows the build up of magnetization as a function of the number of rotor periods. The top panel of Fig. 8 shows the transfer efficiency as function of variation in the rf power on the ¹³C channel [13].

Fig. 8.

The bottom panel in the figure shows the transfer efficiency of the ¹⁵N to ¹³C transfer using a POEM transfer block as a function of mixing time in the units of number of rotor periods. The top panel shows the transfer efficiency as function of varying the rf-power on the carbon channel.

Fig. 6.

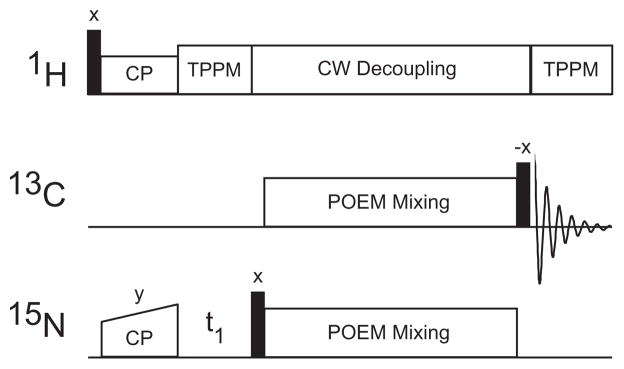
The figure shows the pulse sequence for the heteronuclear transfer using

6. Discussion and conclusion

The build up of the Gamma-Prep peak as a function of the mixing time t (of individual recoupling PAMORE blocks), is of the form ${sin}^2\left(\frac{{\kappa }_h(\beta )}{4}t\right)$, where κ_h is the strength of the dipolar coupled Hamiltonian as in Eq. (11). The cross-peak build up in a regular PAMORE or any γ-encoded recoupling block also has the same form and when averaged over β, the maximum efficiency is .73. Therefore we expect the Gamma-Prep peak to be twice the strength as compared to a normal cross-peak due to transfer of both components. The observed gains in Fig. 3D are less than expected and can be attributed to imperfections in the recoupling block from factors including rf-inhomogeneity, finite duration rf pulses, rotor syncronization of rf pulses, and limitations on how finely, we can discretize the rf-modulation and implement it as discrete phases. On our spectrometer, we were limited to constant phases over 1.3 μs duration for homonuclear experiments and 2.6 μs for the heteronuclear experiments.

In the Gamma-Prep spectra shown in Fig. 5A, the sign of displacement of chemical shift in the indirect dimension by the rotor frequency is different depending on if the preparation and refocusing is performed with $H_{DQ}^z(\gamma )$, or $H_{DQ}^{\overline{z}}(\gamma )$. We can switch between the two Hamiltonians by simply inverting the sign of the bracketing $\frac{\pi }{2}$ pulses around the PAMORE building block. By adding the spectra from two such experiments and inverting the receiver phase, we can also suppress diagonal peaks in the Gamma-Prep experiment. We obtain the two copies of the Gamma-Prep peak as shown in the figure separated by 2ω_r as shown in Fig. 5C. We use this feature to cross-check Gamma-Prep peaks in the 2d spectra. Methods proposed here for suppression of diagonals can help to resolve cross-peaks near the diagonals.

Note given the Hamiltonian ${\mathcal{H}}_{DQ}^I(\gamma )$, we can prepare $-{\mathcal{H}}_{DQ}^I(\gamma )$, by simply using the identity

$$-{\mathcal{H}}_{DQ}^I(\gamma )=exp\left(-i\frac{\pi }{2}{F}_l\right){\mathcal{H}}_{DQ}^l(\gamma )exp\left(i\frac{\pi }{2}{F}_l\right).$$

Now again performing the experiment described in (16) or (17) twice and inverting both the sign of the refocusing Hamiltonian and the receiver phase we can suppress the diagonal peaks. In future work we plan to investigate the merits of different diagonal suppression schemes in the presence of J couplings.

The heteronuclear POEM experiment can be used as a building block to perform gamma-prepared heteronuclear experiments as shown in Fig. 2B where the PAMORE block is replaced by POEM and one of the channels is ¹⁵N.

The modulating recoupling block described in this paper recouples the first Fourier component of time varying dipolar coupling constant. By simply increasing the phase ϕ(t) in the various recoupling blocks to twice its value, we can obtain an effective recoupling field with twice its value and hence collect the second Fourier component. The methods proposed here are expected to be useful for creating multidimensional solid state NMR experiments for improved resolution and sensitivity.

In this paper, we introduced a set of recoupling experiments, which belong to the class of phase modulated recoupling experiment [15–17,24,13]. In particular, we showed how these recoupling blocks can be used to develop two-dimensional NMR experiments which transfer both components of the magnetization [6]. Finally we showed how introducing half rotor period delays between the two recoupling periods, we can substantially suppress all diagonal peaks, leading to significantly resolved 2D spectra.