New spectral-spatial imaging algorithm for full EPR spectra of multiline nitroxides and pH sensitive trityl radicals

Abstract

An algorithm is derived and demonstrated that reconstructs an EPR spectral-spatial image from projections with arbitrarily selected gradients. This approach permits imaging wide spectra without the use of the very large sweep widths and gradients that would be required for spectral-spatial imaging with filtered backprojection reconstruction. Each projection is defined as the sum of contributions at the set of locations in the object. At each location gradients shift the spectra in the magnetic field domain, which is equivalent to a phase change in the Fourier-conjugate frequency domain. This permits solution of the problem in the frequency domain. The method was demonstrated for 2D images of phantoms consisting of (i) two tubes containing ¹⁴N and ¹⁵N nitroxide and (ii) two tubes containing a pH sensitive trityl radical at pH 7.0 and 7.2. In each case spectral slices through the image agree well with the full spectra obtained in the absence of gradient.

1. Introduction

If the environment of an electron spin probe is spatially heterogeneous, the EPR spectrum is the sum of contributions from all locations. Spectral-spatial imaging divides the sample's volume into an array of small spatial segments and calculates the EPR spectrum for each of these segments [1]. This allows mapping of the local environment, such as pO₂ [2-7] or pH [8, 9], by measuring the spatial variation in the EPR spectrum. Magnetic field gradients are used to encode spatial information into EPR spectra, which are called projections. The spectral-spatial image is reconstructed from these projections. The most commonly-used EPR image reconstruction algorithm is Filtered Back Projection (FBP) [10, 11]. This method was initially developed for X-ray tomography, which involves rotation of the sources and detectors around the imaged object, such that projections are collected at small constant angular increments encompassing 180° [12]. The FBP algorithm, which was adapted for EPR spectral-spatial imaging, imposes additional experimental constraints [1]. Because the image has a spectral dimension, it constitutes a mathematical pseudo-object. The equivalent of rotation in the spectral dimension is achieved by changing the gradient amplitude. The maximum angle for a particular set of experimental constraints can be calculated using Eq.(1) [10]:

$${\alpha }_{max}=arctan({\mathit{\text{LG}}}_{max}/\mathrm{\Delta }B)$$ (1)

where L is the spatial length of the image, ΔB is the spectral length of the image, and G_max is the maximum gradient. For spin probes with large ΔB, Eq. (1) shows that either G_max must be extremely large (which may result in poor signal-to-noise), or the length L of the reconstructed image must be artificially increased relative to the sample size; otherwise α_max becomes too small relative to 90°. Missing angle algorithms can partially compensate for small decreases in α_max [13]. The FBP algorithm requires equiangular data collection, so the value of α_max limits the number of projections. If the number of projections is too small, a ‘star-effect’ distortion may be produced in the image [12]. For reconstruction of spectral-spatial images using projections described by Eq. (1), the sweep widths are required to increase proportional to 1/(cos α). For in vivo imaging at 250 MHz, the center field is about 90 G and sweep widths cannot exceed 180 G, which puts an additional constraint on the maximum gradient that can be used.

Nitroxide spin probes are widely used in EPR spectroscopy and imaging. Most nitroxide radicals contain I=1 ¹⁴N, which gives rise to a three-line spectrum with an isotropic hyperfine splitting of about 16 G. The EPR spectrum then spans about 40 G. Substitution of this value of ΔB into Eq.(1), assuming in vivo imaging G_max= 10 G/cm and L= 2 cm, gives α_max ∼ 27° which is too small to be practical. It is common to use only one of the three hyperfine lines for imaging, which decreases ΔB to a few gauss. This approach severely limits spatial resolution because the maximum gradient must not produce overlap of the adjacent hyperfine lines. In addition, only one-third of the electron spins contribute to the EPR signal that is imaged. Isotopic substitution of ¹⁴N by ¹⁵N (I=1/2) (i) decreases the number of hyperfine lines from 3 to 2, which increases signal amplitude by a factor of 1.5 [14], (ii) increases the nitrogen hyperfine splitting to about 23 G which permits about 40% increase in gradient without overlap of hyperfine lines, and (iii) reduces the spectral width by about 30% which increases α_max (Eq. 1). However, the increased cost of ¹⁵N nitroxides make this option expensive.

Alternatives to FBP such as maximum entropy (MEM) [15] and regularized optimization (RO) [16] are not restricted by Eq.(1). These types of iterative algorithms have demonstrated substantial improvement in the quality of the reconstructed images, but are computationally inefficient (compared to FBP) and require large amounts of computer memory. Computational inefficiency is a limiting factor for 3D and 4D spectral-spatial imaging. Another approach has been suggested by adaptation [17, 18] of the single-point pulse EPR imaging algorithm [19] to perform CW spectral-spatial imaging. Limitations of this method include: (i) gradients must be equally spaced, and (ii) the spatial resolution and field of view depend on the timing for the single point. It is not clear how well this method performs if the spectral width is large enough to encompass a full nitroxide spectrum (40-60 G).

If the EPR spectrum is invariant through the sample, the hyperfine splitting can be removed by deconvolution [20, 21], but then there is no spectral dimension in the image. To deal with multi-line nitroxide spectra Kuppusamy and Zweier assumed that all information of interest was contained in a single hyperfine line and used post-acquisition processing to remove artifacts that were observed when high gradient projections caused partial overlap of hyperfine lines [22, 23].

The image reconstruction method described in the current paper does not require equally-spaced projection and the constraints of Eq. (1) do not apply. The numerical algorithm is optimized for parallel computing and produces an image in one iteration. The method has been used to reconstruct full spectrum images of phantoms consisting of (i) a ¹⁴N and ¹⁵N nitroxide or (ii) a pH-sensitive trityl radical at pH = 7.0 and 7.2. Projections were obtained by rapid scan [24-26] which improves signal-to-noise relative to CW [27]. The ability to obtain spectral-spatial images without the constraints of Eq (1) or the need for large sweeps and the improved S/N from rapid scan EPR overcome major hurdles for low frequency EPR imaging.

2. Algorithm description

The first step is to select the spatial resolution, dL, for the image to be reconstructed. As a starting value one can use the estimate:

$$\mathit{\text{dL}}=G_{max}/{\mathit{\text{LW}}}_{min},$$ (2)

where LW_min is the smallest linewidth of a single line in a multiline EPR spectrum. Selection of dL divides the sample volume into K segments (see Fig.1). An unknown spectral function sp_k(B) is assigned to each k^th segment. A set of functions {sp_k (B), k = 1: K} constitutes the spectral-spatial image. The image can be computed from projections obtained with a set of gradients {G_n, n = 1: N}. Although no particular gradient pattern is required, the spectral and spatial information content of the projections must be sufficient for image reconstruction. The numbers of projections at lower and higher gradients may be selected to enhance spectral and spatial resolution, respectively.

Fig. 1.

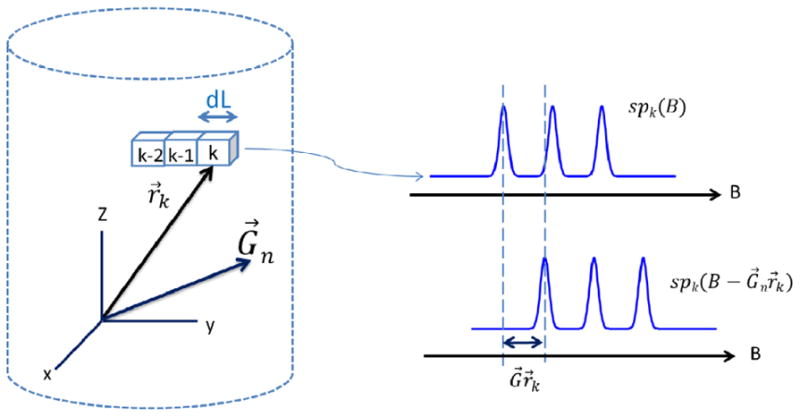
Schematic of the geometry for the imaging experiment and the spectral shift at location k.

In a homogeneous magnetic field, the zero gradient projection is the sum of all spectral functions:

$${\mathit{\text{pr}}}_0(B)=\sum _{k=1}^K{\mathit{\text{sp}}}_k(B),$$ (3)

In a non-zero gradient, G_n modifies Eq.(3) into the form

$${\mathit{\text{pr}}}_n(B)=\sum _{k=1}^K\underset{V_k}{\int }{\mathit{\text{sp}}}_k(B-{\mathbf{G}}_n•\mathbf{r})\mathit{\text{dV}}$$ (4)

that takes into account two factors: (i) the spectral shift of sp_k(B) in the magnetic field domain by the amount of the scalar product G_n•r (see Fig.1) and (ii) the spatial extent of the k^th segment. The latter factor is introduced by integration over the volume V_k in Eq.(4).

Using the fact that the shift in the magnetic field is equivalent to a phase change in the Fourier domain, Eq.(4) can be transformed and simplified to

$${\mathit{\text{PR}}}_n({\omega }_m)=\sum _k{\mathit{\text{SP}}}_k({\omega }_m)\underset{V_k}{\int }\mathit{exp}(-j{\omega }_m{\mathbf{G}}_n•\mathbf{r})\mathit{\text{dV}};n=1,\dots ,N;k=1,\dots ,K;{\alpha }_m=2\pi m/\mathit{\text{SW}};m=-M/2+1,\dots ,M/2,$$ (5)

where M is the number of discrete frequencies. M is selected to be large enough to encompass all frequencies in the signal. SP_k in Eq.(5) is the Discrete Fourier transform of the spectral-spatial image along the spectral dimension and is the final goal of the algorithm; SW denotes the sweep width of the projections in the magnetic field domain. If the sweep width is varied, projections must be zero-filled and interpolated to have the same starting and ending fields and number of points. This results in the same set of frequencies ω_m for all projections (Eq. 5), and allows rearranging the set of N equations (5) with respect to gradients into a set of M equations with respect to ω_m:

$${\mathbf{\text{PR}}}^{(m)}={\widehat{\mathbf{W}}}^{(m)}{\mathbf{\text{SP}}}^{(m)};W_{\mathit{\text{nk}}}^{(m)}=\underset{V_k}{\int }\mathit{exp}(-j{\omega }_m{\mathbf{G}}_n•\mathbf{r})\mathit{\text{dV}},m=-M/2+1,\dots ,M/2$$ (6)

Eq.(6) is written in convenient vector-matrix form, where vector PR^(m) has N elements corresponding to N projections; vector SP^(m) consists of K elements corresponding to K spatial segments, and Ŵ^(m) is an N×K matrix. Since Ŵ^(m)is not a square matrix, solution of Eq.(6) for unknown SP^(m) can be computed either by Moore-Penrose pseudo-inversion of Ŵ^(m):

$${\mathbf{\text{SP}}}^{(m)}={\widehat{\mathbf{W}}}_{\mathit{\text{MP}}}^{{(m)}^{-1}}{\mathbf{\text{PR}}}^{(m)},m=-M/2+1,\dots ,M/2$$ (7)

or by using Tikhonov regularization [28]:

$${\mathbf{\text{SP}}}^{(m)}={({\widehat{\mathbf{W}}}^{{(m)}^T}{\widehat{\mathbf{W}}}^{(m)}+\mathrm{\alpha }{\mathrm{\Gamma }}^{\mathbf{T}}\mathrm{\Gamma })}^{-1}{\widehat{\mathbf{W}}}^{{(m)}^{\mathbf{T}}}{\mathbf{\text{PR}}}^{(m)},m=-M/2+1,\dots ,M/2$$ (8)

where Γis the regularization operator and αis the regularization parameter. Equations for SP^(m) are independent for different indexes m and can be solved in parallel on a graphics processor unit or computer cluster. After SP^(m) have been computed for m=1, …, M, the results are combined into a multi-dimensional array, Inverse Fourier transform of which along the frequency dimension produces the spectral-spatial image.

3. Experiment

3.1 Phantoms

Two phantoms composed of two types of spin probes, nitroxides and triarylmethyl radicals, were used to test the algorithm. The imaging phantoms were constructed of two 6 mm o.d. quartz tubes inside a larger tube with 16 mm o.d. and 14 mm i.d. A foam spacer held the 6 mm tubes 2 mm apart inside the larger tube. The center-to-center distance between the two tubes that contained radicals was 8 mm (Fig 2). For phantom 1 the 6 mm tubes contained deoxygenated aqueous ¹⁴N-PDT (0.2 mM) or ¹⁵N-PDT (0.53 mM) with liquid column heights that are longer than the height of the resonator. ¹⁴N and ¹⁵N perdeuterated Tempone (PDT) were purchased from CDN Isotopes (Quebec Canada). The pH sensitive triarylmethyl radical (aTAM₄) was prepared at Ohio State [29]. For phantom 2 the 6 mm tubes contained aTAM₄. The samples were prepared by dissolving radical in 200 μL absolute ethanol and diluting with 800 μL of 1mM phosphate buffer for a final concentration of 0.5 mM in 80:20 buffer:ethanol. Solutions in the two tubes had pH of 7.2 and 7.0, respectively.

Fig. 2.

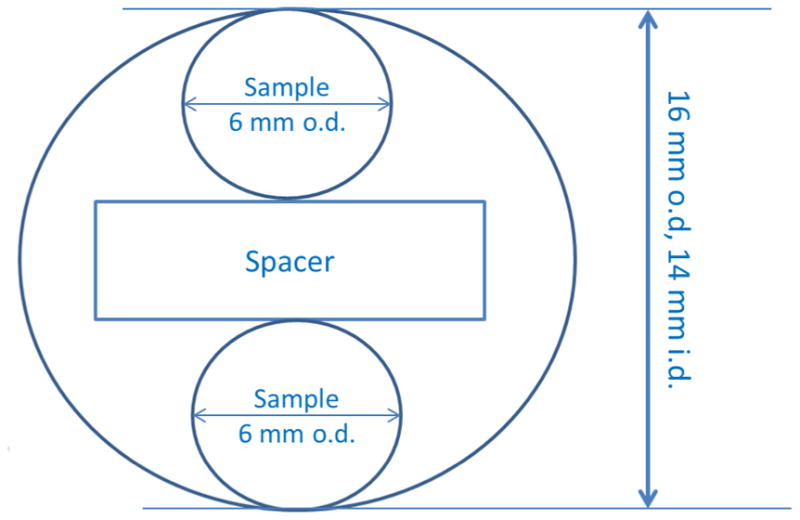
Geometry of the phantom.

3.2 Spectrometer

EPR spectroscopy was performed at the University of Denver. Projections for rapid-scan 2D spectral-spatial images were acquired at 251 MHz with a modified Bruker E540 console, the magnet and gradient coils described previously [30-32], and a 16 mm cross-loop resonator [27] with Litz wire coils to provide wide scans. The maximum z-gradient was 10 G/cm (0.10 T/m). The original rapid-scan bridge [32] provided a maximum RF output of 50 mW. A 7 W amplifier (MiniCircuits model ZHL-03-5WF) was added to provide increased power to the resonator. The sinusoidal rapid scans were generated with a driver similar to the one described in [33], but with an additional option to trigger the digitizer after a specified number of cycles. This modification permits acquiring multiple scans after a single trigger. Combining the data in the multiple scans functions like a comb filter and decreases noise [26, 34-36]. The signal went through a 1 MHz (Krohn-Hite model 3955) low-pass filter and was digitized in quadrature using a Bruker SpecJet II.

3.3 Spectroscopy

The three ¹⁴N nitroxide hyperfine lines (Fig. 3) lines have an asymmetric splitting pattern at 250 MHz due to Breit-Rabi effects [37]. The splitting between low-field and center-field, and center-field to high-field lines was 14.8 and 17.6 G, respectively, for a total spacing of 32.4 G. The splitting of the ¹⁵N low-field to high-field line is 22.6 G. To cover the entire spectrum in the presence of maximum gradients ranging from -10 G/cm to 10 G/cm with 1 G/cm step, rapid sinusoidal scans of 65 G width and 3.5 kHz frequency were used for all projections. The total number of projections was 21. The microwave B₁ of 72 mG, was in the linear response regime. The acquisition time per projection was 44 s.

Fig. 3.

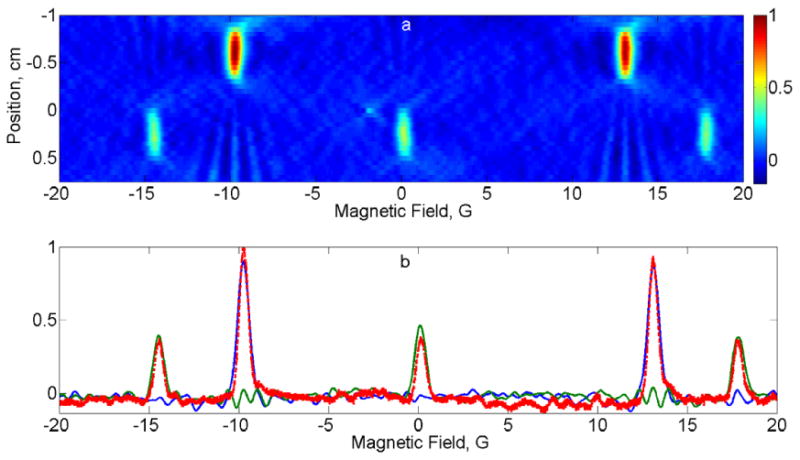
(a) 2D spectral-spatial image of phantom 1 consisting of ¹⁴N and ¹⁵N PDT. (b) Comparison of spectral slices (¹⁴N in green, ¹⁵N in blue) through the image with the zero-gradient spectrum (dashed red).

Zero-gradient spectra of aTAM radicals are significantly narrower than for nitroxides (Fig. 4). For this reason scan widths were varied to cover the entire spectral width of the gradient-broadened spectra. Scan frequency of 3 kHz was used for all projections. The microwave B₁ of 36 mG, was in the linear response regime. Three different gradient patterns were examined: (i) Equidistant gradient stepping from -10 G/cm to 10 G/cm with 1 G/cm step; (ii) FBP equidistant angle stepping with a total of 18 projections, 16 of which are in the range from -3.2 to 3.2 G/cm; (iii) projections were added to the FBP set that fill the gaps between ±3.2 and the maximum value of ±10 G/cm. These projections were in the intervals from ±4 to ±9 G/cm with 1 G/cm step plus the zero-gradient projection. The acquisition time per projection was 60 s.

Fig. 4.

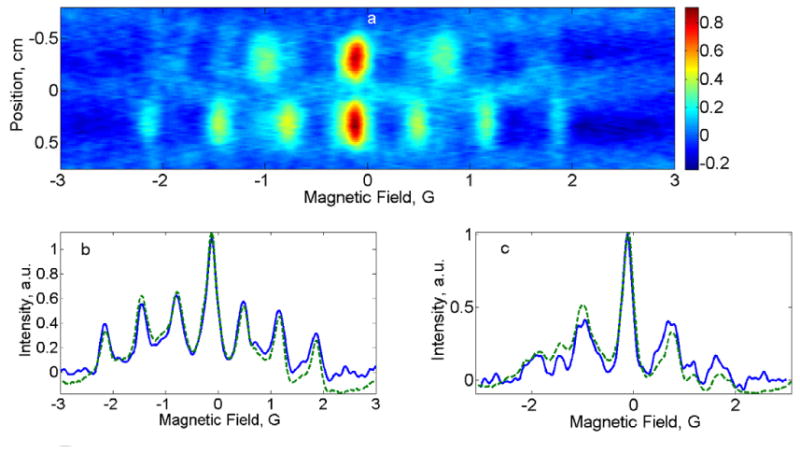
(a) 2D spectral-spatial image of phantom 2 consisting of pH=7.0 and pH=7.2 aTAM₄ radicals. (b) Comparison of the spectral slice for pH=7.2 (blue) with the zero-gradient spectrum (dashed green). (c) Comparison of pH=7.0 slice (blue) with the zero-gradient spectrum (dashed green)

Projections were obtained from the rapid scan signal as described in [24, 25].

3.3 Image Reconstruction

To test the algorithm described above, two-dimensional spectral-spatial images were reconstructed and compared using Moore-Penrose pseudo-inversion (see Eq.(7)) and Tikhonov regularization (see Eq.(8)). For Moore-Penrose pseudo-inversion reconstruction a standard Matlab routine pinv was used. The tolerance level for pinv was selected to produce a stable solution without distorting the image. For Tikhonov regularization two types of regularization operators were tested: identity operator and first derivative operator. The image reconstructed using the identity operator was very similar to the one reconstructed using the pseudo-inversion method. The use of the first derivative operator did not produce a meaningful image. The Tikhonov regularization parameter α was adjusted to give a stable solution without causing distortion. The images produced using Tikhonov regularization and Moore-Penrose pseudo-inversion were very similar. No additional filtering was applied to the images.

Fig.3a and Fig.4a show spectral-spatial images reconstructed using Moore-Penrose pseudo-inversion for the PDT and aTAM₄ phantoms, respectively. Spectral slices at the centers of the radical-containing tubes are compared to the spectra obtained in the absence of the gradient field in Fig.3b, Fig.4b and Fig.4c. Because the hyperfine lines of ¹⁴N-PDT and ¹⁵N-PDT do not overlap, comparison in Fig.3b was done with the spectrum of the entire phantom. To measure the individual aTAM₄ spectra shown in Fig.4b and Fig.4c, the phantom was disassembled and the two 6mm tubes were measured independently. The changes in spectra from pH = 7.0 to 7.2 are consistent with the literature report [29]. Comparison of the images reconstructed from data acquired with the three gradient selection schemes described in the Spectroscopy section, revealed that the third pattern produces the best results. Equidistant gradient sampling in scheme (i) produced artefacts in the baseline regions of the image that extended out from regions of high intensity. Scheme (iii) resulted in an image with a slightly better spatial resolution compared to the FBP scheme (ii). These results confirm a known concept behind the FBP algorithm that low-gradients responsible for spectral information need to be sampled with a higher density compared to high-gradients that predominantly carry spatial information. However, the small number of projections with high gradients that are used in the FBP method may impair spatial content of the reconstructed image. The flexibility of the proposed algorithm with respect to gradient selection allows the user to tailor the selection of gradients to suit the goals of an experiment.

The center-to-center distances between the two tubes in Fig.3a and Fig.4a agree well with the known dimensions in the phantoms.

4. Discussion

Rapid scan imaging provides improved S/N relative to CW [27]. Sinusoidal field scans with resonated coils permit wider sweeps than linear scans [33]. Deconvolution, background subtraction, and filtering of the rapid scan data obtained in the presence of magnetic gradients produce projections [24]. Application of the algorithm in Eq. (5) – (7) produced the image in the Fourier domain. Inverse Fourier transform gives the final images.

The spectral-spatial imaging algorithm described in this paper lifts limitations imposed on data collection to allow full-spectrum imaging of multiline EPR spin probes such as nitroxides and pH sensitive radicals. Since overlap of contributions from adjacent lines in multiline spectra in the presence of magnetic field gradients is not a restriction, larger gradients can be used to increase spatial resolution. Unconstrained choice of gradients allows the experimenter to reduce data acquisition time by selection of fewer projections with the most complementary information content. This can be done additively. Analysis of an intermediate image may guide gradient selection for the next projections [38]. The algorithm allows relaxing homogeneity specifications for external magnet and gradient coils. Assuming that magnetic field is homogeneous and gradients are constant within each spatial segment, the deviations from homogeneity can be measured – for example, with a strong sample with a known constant lineshape – and the correction terms Δ_k can be introduced in Eq.(4)

$${\mathit{\text{pr}}}_n(B)=\sum _{k=1}^K\frac{1}{V_k}\underset{V_k}{\int }{\mathit{\text{sp}}}_k(B-{\mathrm{\Delta }}_k-{\mathbf{G}}_n•\mathbf{r})\mathit{\text{dV}},$$ (9)

$${\mathrm{\Delta }}_k=\mathrm{\Delta }{B}_k+\mathrm{\Delta }{\mathbf{G}}_n({\mathbf{r}}_k){\mathbf{r}}_k$$ (10)

In Eq.(10) the first and second terms are the corrections for the external magnetic field and gradient.

Since the projection is represented as a sum of contributions from a set of spatial regions, the imaging problem of any dimensionality is reduced to a two-dimensional problem (see Eq.(6)). The difference with respect to the image dimensionality is primarily in the increased number of projections K and number of spatial regions N. If the required spatial resolution is 1 mm and the object is 20 mm in each of the three spatial dimensions, the size of the array to be inverted would be about 8000 × 8000 (see Eq.(7-8)), which is still feasible in a PC. However, the algorithm has not yet been tested for 4D imaging. . The size of W^(m) can be reduced by choosing only those spatial regions in the image where the concentration of the spin probes is expected to be above a certain threshold level. In addition, integration over the volume V_k in Eq.(4) allows more sparse gridding of the image, larger dL, than otherwise would be required for the standard imaging method.

Research Highlights.

• Spectral-spatial algorithm reconstructs image from arbitrary set of projections.

• The spectral width is not constrained by the maximum gradient.

• Results are demonstrated for phantoms of nitroxides and pH-sensitive trityls.