Angle Sensing in Magnetotaxis of Magnetospirillum magneticum AMB-1

Abstract

The mechanism of how magnetotactic bacteria navigate along magnetic field has been a puzzle. Two main models disagree on whether the magnetotactic behavior results from passive alignment to the magnetic field or active sensing of the magnetic force. Here, we quantitatively studied the swimming patterns of Magnetospirillum magneticum AMB-1 cells to understand the origin of their magnetotaxis behaviors. Single-cell tracking and swimming pattern analysis showed that the cells follow a mixed run/reverse/tumble pattern. The average run time decreased with the angle between the cell’s moving velocity and the external magnetic field. For mutant cells without the methyl-accepting chemotaxis protein (MCP) Amb0994, such dependence disappeared and bacteria failed to align to magnetic field lines. This dysfunction was recovered by complementary amb0994 on plasmid. At high magnetic field (>5mT), all strains with intact magnetosome chains (including the Δamb0994-0995 strain) showed alignment with the external magnetic field. These results suggested that the mechanism for magnetotaxis is magnetic field dependent. Due to the magnetic dipole moment of the cell, the external magnetic field exerts a torque on the cell. In high magnetic fields, this torque is large enough to overcome the random re-orientation of the cell, and the cells align passively with the external magnetic field, much like a compass. In smaller (and biologically more relevant) external fields, the external force alone is not strong enough to align the cell mechanically. However, magnetotactic behaviors persist due to an active sensing mechanism in which the cell senses the torque by Amb0994 and actively regulate the flagella bias accordingly to align its orientation with the external magnetic field. Our results reconciled the two putative models for magnetotaxis and revealed a key molecular component in the underlying magneto-sensing pathway.

Introduction

Bacteria cells employ taxis pathways to sense extracellular stimuli and regulate their motility accordingly^1,2. For example, Escherichia coli uses its chemotaxis system to compute chemical concentration gradient and adjust flagella bias to migrate towards favorable conditions³; magnetotactic bacteria such as M. magneticum AMB-1 can navigate along magnetic field⁴. While the mechanism of bacterial chemotaxis has been well studied and modeled quantitatively⁵, the mechanism for adjusting swimming direction according to magnetic field is still unclear. Although M. magneticum AMB-1 has an unusual high number of chemotactic receptors⁶, whether these receptors are involved in magnetotaxis is unknown. Indeed, in one popular model for magnetotaxis, a bacterial cell is treated as a swimming compass^7,8. The magnetite crystals inside cell form magnetosomes, which are arranged along cell axis and act as magnetic dipole^4,7. The interaction of the dipole moment and the geomagnetic field was calculated to be strong enough to overcome rotational diffusion of the cell orientation induced by thermal noise in the medium. Based on this argument, it was proposed that an active sensing mechanism is unnecessary^9–12, and magnetotaxis results purely from passive alignment of the cell’s magnetic dipole moment with the external magnetic field. The follow-up experiments have mainly focused on presenting semi-quantitative evidences on the advantage of magneto-aerotaxis^13–15.

In contrast to the passive alignment model, Greenberg et al.¹⁶and Pan et al.¹⁷ proposed that magnetotactic multicellular prokaryotes (MMP) and magnetotactic cocci may use a receptor mechanism for sensing the magnetic field. Recent study has investigated possible connections between magnetosomes and putative chemotaxis proteins¹⁸. Filamentous cytoskeletal protein MamK helps magnetomes arranging in chain along long axis of spirilla^19–22; it may serve as a mechanic sensor to detect the torque generated from the interaction between the magnetosome dipole moment and the external magnetic field¹⁸. In addition, the MamK filaments seem to interact with Amb0994, the only MCP in magnetosome island lacking extracellular domain, and overproduction of amb0994 interferes with the reaction of the AMB-1 cells to the change of magnetic field¹⁸. Based on these observations, it was speculated that active sensing may be involved in magnetotaxis, like in bacterial chemotaxis.

Is active sensing involved in bacterial magnetotaxis? How is the magnetic field sensed by the cell? To address these questions, we developed a well-controlled microfluidic device²³ and quantitatively studied the magnetotactic behavior of M. magneticum AMB-1 at single cell level in a range of magnetic fields. Our experiments showed that active sensing exists in magnetotaxis and Amb0994 functions as a magnetic receptor that senses the angle between the instantaneous velocity of the cell and the external magnetic field (v-B angle). The signal is then transferred to the motors to adjust the flagella bias and the swimming pattern of the cell. This active sensing mechanism enables magnetotaxis under modest magnetic field (<5mT), and the passive alignment mechanism become relevant under higher magnetic fields.

Results

The three-state swimming pattern in AMB-1 and its dependence on magnetic field

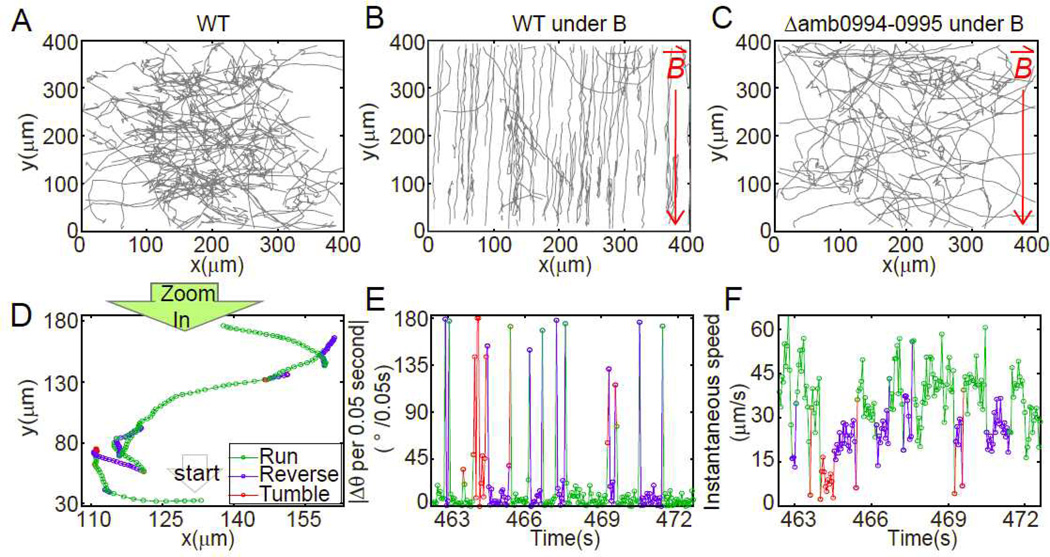
Time-lapse microscopy showed that the amphitrichous flagellated^24,25 AMB-1 can backtrack its forward swimming path before resuming its forward swimming (Fig. 1D, SI movie). The forward and backtrack states are defined as run and reverse respectively. Cells have larger instantaneous speed and longer motion time during runs than those during reverses (Fig. 1F, Fig. 2A–C). The angular shift between two successive states is larger than 90° when swimming pattern changes from run to reverse or verse vice (see SI results for details). Sometimes a short transition period is observed, during which a cell changes its orientation erratically without moving its position (Fig. 1E&F, Fig. 2A&D). We define this transition state as tumble, which is probably caused by the disruption of the flagella bundle. Note that within the 0.05s resolution, there is not always an observable tumble state between a run and reverse states. Also, tumbling does not necessarily lead to reversal of the cell’s motion, i.e., run-tumble-run and reverse-tumble-reverse are possible. During run and reverse states, the cell’s directional angle change per 0.05s is 6.82±7.13° and 15.48±23.29° respectively, much smaller than the angle change during tumble (97.43±55.53°/0.05s). This swimming pattern, in which a cell switches among run, reverse and tumble states, is common in marine bacteria^26,27.

Fig. 1.

The tracks of AMB-1 show the magnetotactic behavior (A–C) and the three-state swimming pattern (D–F). 80 trajectories in 10 minutes were displayed for (A) WT cells at control condition; (B) WT cells under 1.0mT applied magnetic field; (C) Δamb0994-0995 deletion cell under 1.0mT applied magnetic field. Red arrows pointed to the direction of applied magnetic field. (D) Single trajectory can be resolved into three states. Small circles represent the position at an equal time interval of 0.05s. The corresponding sequential angular change per observation time (0.05s) and instantaneous speed are shown in (E) and (F) respectively. Green, blue and red mark the run, reverse and tumble states respectively.

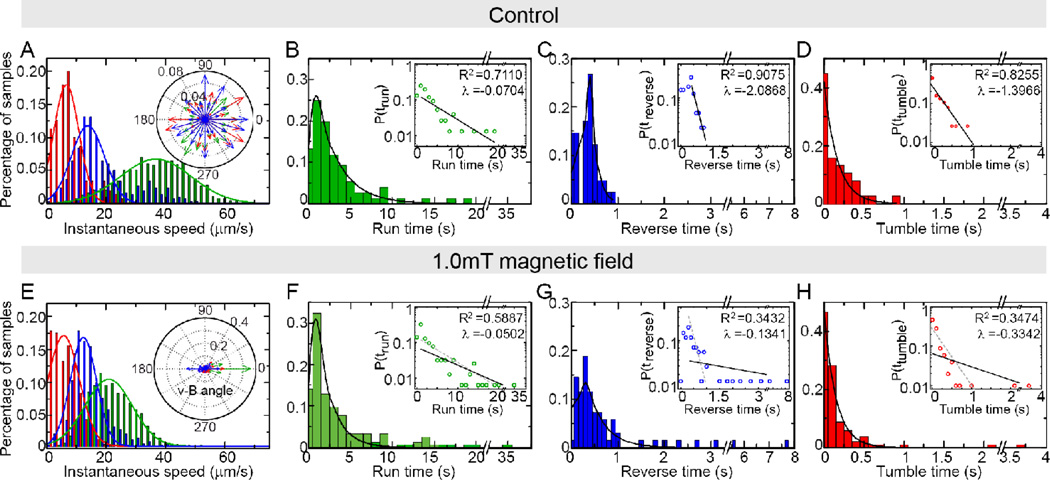
Fig. 2.

Statistical analysis of the WT cells under control condition (A–D) or 1.0mT magnetic field (E–H). (A) and (E) shows the distribution of instantaneous speed of run (green), reverse (blue) and tumble (red) and fitted by Gaussian curves (solid lines); the insets show the distributions of the angle between speed and magnetic field. The probability distribution of duration of run (B, F), reverse (C, G) and tumble (D, H) in the two cases are plotted. The solid lines are exponential fitting of the tail parts of the data. Insets are the same data plotted semi-log and fitted by linear: log₁₀ y = λx + b (solid line), where decay rate λ and coefficient of determination R² are given. The gray dashed lines in the inset of F–H are the exponential fit of B–D inset for comparison.

To elucidate how AMB-1 uses the three-state swimming strategy to navigate along magnetic field, we applied 1.0mT magnetic field on-chip and monitored the cells’ movement patterns. The control experiments were conducted without external magnetic field. The trajectories of individual bacteria are randomly oriented in the control experiment (Fig. 1A and Fig. 2A inset). However, under 1.0mT magnetic field, the distribution of the angle between the cells’ moving directions and the direction of external field is centered at 0° and 180° (Fig. 1B and Fig.2E inset). The duration time in each state and the instantaneous speed of run are also affected by magnetic field (Fig. 2&Table 1). Under the control condition, all duration time distributions follow an exponential form (insets of Fig.2B–D), indicating that the flagella switching events are likely controlled by simple Poisson processes²⁸. In the presence of external magnetic field, these distributions become much more dispersed with much larger standard deviations (Fig. 2F–H&Table 1). Although the data can still be forced to fit to an exponential distribution with a smaller decay rate parameter λ, the fitting is rather poor with much lower R² (Fig.2 F–H inset). In fact, these distributions are better fitted to a power law distribution (Fig. S1). The same fat-tail behaviors were also reported in the counter-clock-wise duration time distribution in E. coli²⁹, which can be explained by the slow and large fluctuations of the response regulator (CheY-P) concentration³⁰. Due to lack of understanding of the internal signaling pathway for magnetotaxis, it remains unclear what may cause the non-exponential distribution for the run time in magnetotaxis and why it only occurs in the presence of a magnetic field. In AMB-1, both the duration times in each state and the ratio between them are modulated by magnetic field (Table 1), suggesting that bacteria flagella bias and the switching kinetics are both affected by magnetic field. This is different from Vibrio alginolyticus chemotaxis where flagella bias remains the same and only kinetics is affected³¹.

Table 1.

Summary of instantaneous speed and motion time.

strain	measurement	control experiments			under 1.0mT magnetic field
		run	reverse	tumble	run	reverse	tumble
WT	Instantaneous speed (µm/s)	36.08±11.59	18.03±10.01	8.17±5.44	21.96±7.87	21.14±9.77	7.73±4.45
	Motion time(s)	3.26±3.66	0.36±0.22	0.20±0.20	3.61±4.84	0.77±1.20	0.20±0.43
	λ*	−0.0704	−2.0868	−1.3966	−0.0502	−0.13411	−0.3342
	R2*	0.7110	0.9075	0.8255	0.5887	0.3432	0.3474
Δamb0994−0995	Instantaneous speed (µm/s)	37.76±11.42	20.08±8.05	7.87±4.81	41.07±12.95	20.52±7.57	7.66±6.75
	Motion time(s)	3.25±3.77	0.53±0.36	0.10±0.09	1.92±2.14	0.40±0.25	0.11±0.12
	λ	−0.0592	−0.5972	−3.4947	−0.1546	−1.0656	−2.2249
	R2	0.3841	0.6592	0.8821	0.8185	0.8232	0.8065
Δamb2196	Instantaneous speed (µm/s)	35.63±10.87	24.38±7.46	8.32±5.99	35.02±10.36	22.52±6.65	4.60±4.00
	Motion time(s)	4.06±3.87	0.54±0.35	0.17±0.16	3.19±3.78	0.69±0.49	0.08±0.06
	λ	−0.0698	−0.5224	−1.8461	−0.0658	−0.2333	−4.7567
	R2	0.7743	0.6532	0.8710	0.5130	0.2690	0.9850
Camb0994−0995	Instantaneous speed (µm/s)	44.02±15.6	24.24±9.59	9.18±6.35	39.14±13.44	35.23±13.51	7.39±6.41
	Motion time(s)	2.91±2.56	0.65±0.84	0.21±0.28	2.74±3.08	0.71±0.69	0.24±0.38
	λ	−0.12607	−0.22865	−0.8315	−0.10087	−0.26635	−0.4572
	R2	0.8778	0.52358	0.62426	0.65645	0.52165	0.42398

^*The tail parts of the distributions (in semilog scale) were fitted linearly: log₁₀y = λx + b where λ is the slope of the linear fit. This equation can be transformed into exponential distribution y=(10^b)·10^λx λ̣ is the parameter characterizing the decay rate in the exponential distributions. Larger absolute value of λ indicates faster decay of the distribution. R² is the coefficient of determination of linear fit for the tail of semilog data³¹.

Amb0994 is essential for magnetic sensing

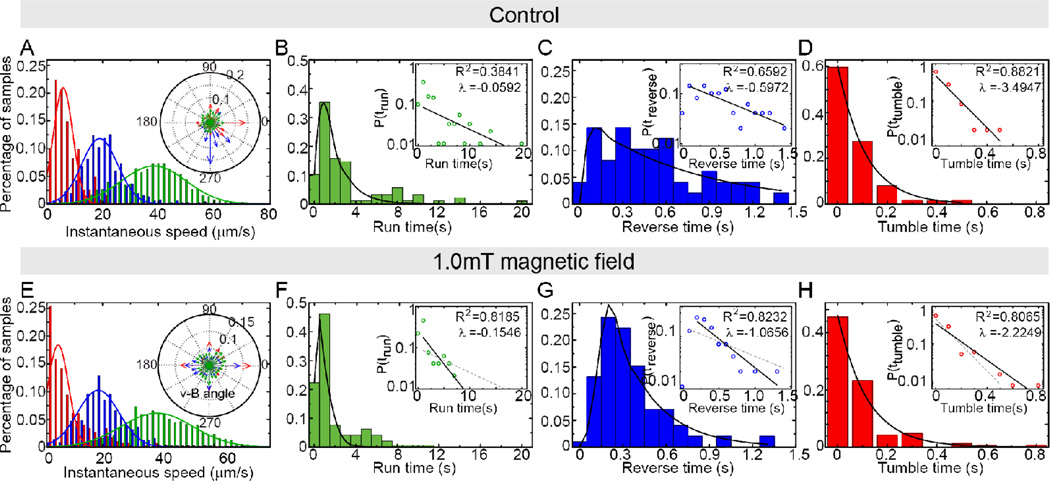
To investigate the molecular basis of the magnetotactic pathway, we knocked out amb0994, which was suggested as the potential magneto-receptor¹⁸. For convenience of genetic manipulation we deleted both amb0994 and amb0995 (Δamb0994-0995), the latter only contains a PAS domain which is a potential oxygen sensor but cannot function as a receptor. The synthesis and alignment of magnetosomes in the mutant cells were not affected (Fig. S2&S3), and the swimming behavior of Δamb0994-0995 was similar to that of WT cells under the control conditions (Fig.3A–D). However, there was no observable magnetotactic behavior in Δamb0994-0995 under 1.0mT magnetic field. Cells failed to align with the magnetic field (Fig. 1C), and the v-B angle remained uniformly distributed (Fig. 3E inset). The distributions of motion time still had exponential tails (Fig.3&Table 1), with the decay parameters λ slightly larger than those at control conditions (Fig. 3. All these experimental observations indicate that the amb0994 knockout strain fails to sense and respond to the 1.0mT external magnetic field, which suggests that Amb0994 possibly acts as the receptor that senses the torque induced by the external magnetic field.

Fig. 3.

Statistical analysis of the Δamb0994-0995 cells under control condition (A–D) or 1.0mT magnetic field (E–H). (A) and (E) shows the distribution of instantaneous speed of run (green), reverse (blue) and tumble (red) and fitted Gaussian (solid lines); insets show the angle distribution between speed and magnetic field angles. The probability distribution of duration of run (B, F), reverse (C, G) and tumble (D, H) in the two cases are plotted. The solid lines are exponential fitting of the tail parts of the data. Insets are the same data plotted semi-log and fitted by linear: log₁₀y = λx + b (solid line), where decay rate λ and coefficient of determination R² are given. The gray dashed lines in the inset of F–H are the exponential fit of B–D inset for comparison.

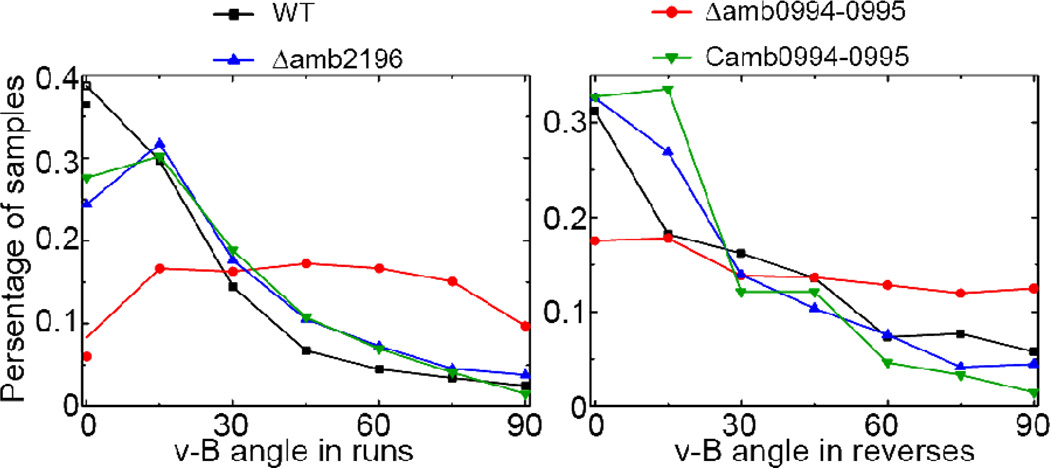
To check whether other MCPs may also function as magnetic receptor similar to Amb0994, we identified another MCP, amb2196, which shares the highest similarity (97%, see Fig. S4) with amb0994 in M. magneticum AMB-1 at protein level. We created a mutant strain Δamb2196 without amb2196 Our experiments showed that the Δamb2196 cells display aligned traces under the 1.0mT magnetic field similar to the WT cells (Fig. 4). In addition, we also showed that the phenotype of amb0994 deletion strain can be rescued by introducing amb0994 expressing cassette on plasmid (Fig. 4, see SI materials and methods for details of the strain). The v-B angle distributions of WT, Δamb2196 and Camb0994-0995 strains all peak near zero with similar decaying shapes, while Δamb0994-0995 strain displays a much broader angular distribution (Fig.4 A&B). These results confirm that Amb0994 plays a unique role in the cell’s magneto-sensing pathway.

Fig. 4.

The angle distribution of instantaneous v-B angle in different strains for (A) run states and (B) reverse states. The magnetic strength here is 1.0mT. The percentage of samples (trajectories) per angle bin (size 15°) is shown.

The active angle sensing in AMB-1

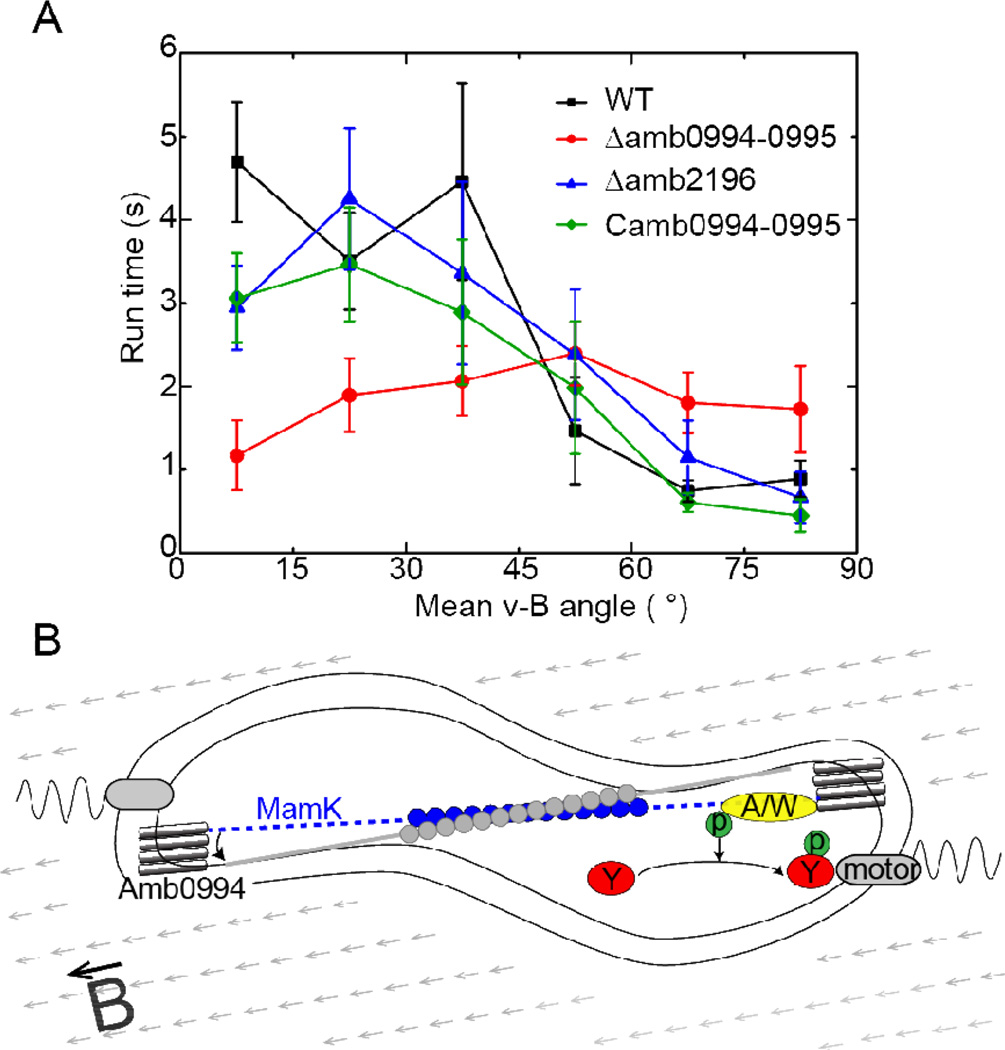
For magnetotaxis, the input of the signaling pathway is the torque, which depends on the angle between the magnetic dipole moment inside the cell (along the cell’s long axis) and the external magnetic field. Thus, to confirm magneto-sensing in bacteria, we have plotted the average run time versus the v-B angle in Fig. 5A (see also Fig. S5). The strong negative correlation between these two variables in wild type (WT) cells shows that bacteria adjust the motion time according to the v-B angle. Specifically, higher torque generated by large v-B angle increases the probability of tumble, and the switching probability is suppressed when the cell is aligned with the magnetic field. This dependence (correlation) detected in the run states suggests that the run/reverse/tumble bias may be controlled by a magnetotaxis pathway like in chemotaxis. Here, the effect of a large (small) v-B angle is analogous to that of a lower (higher) attractant concentration in chemotaxis³². Since the run time is shortened for large v-B angle and lengthened for small v-B angle, the range of possible run times is thus broadened in the presence of a magnetic field. This provides a possible explanation for the more dispersed distribution of motion time under magnetic field (Fig. 2F–H). The correlation between the average motion time and the angle between velocity and magnetic field (v-B angle) is weak for reverse states (Fig. S6). However, the duration of the reverse state is relatively short (Table 1), the correlation between the overall motion and the v-B angle is preserved (Fig. S7). We have also studied the correlation between the run time and the v-B angle for the mutant strains. For the Δamb0994 strain, the run time is found to be roughly independent of the v-B angle (Fig. 5A). However, both Δamb2196 and the in trans complemented amb0994 strain (Camb0994-0995) maintain the negative correlation between the motion time and the v-B angle (Fig. 5A), similar to that of the WT cells.

Fig. 5.

The active angle sensing in magnetotaxis. (A) The average run time for cells moving with a given mean v-B angle (the angle bin size is 15°). The magnetic field intensity is 1.0mT. The dataset has been normalized to [0, 90]° by assuming the cell is axial sensing (i.e, ϕ is equivalent to π–ϕ). The bar indicates the standard error ($(\text{standard deviation}/\sqrt{n})$) of the population, where n is the number of episodes. (B) The illustration of a possible magnetotaxis signaling pathway in AMB-1. The MCP receptor is Amb0994 which senses the magnetic torque or equivalently the v-B angle through its interaction with MamK. The magnetic torque can induce a conformational change in Amb0944 that changes the activity of an attached kinase (A/W), which modulates the phosphorylation level of a response regulator (Y) that controls the motor switching and the cell’s swimming pattern. The A/W and Y components are hypothetical parts of the signaling pathway, motivated by an analogy to the two-component system in bacterial chemotaxis.

All these experimental evidences indicate that magnetotaxis of AMB-1 involves active sensing of the angle between its direction of motion and the magnetic field through Amb0994. Considering the filament protein MamK which is parallel to the cell’s magnetic moment and co-localizes with Amb0994¹⁸, we suggest a hypothetical but possible active magneto-sensing mechanism in the cell as illustrated in Fig. 5B. The signal is the magnetic field induced torque which depends on the angle between the MamK filament and the external magnetic field. This mechanical signal is transduced (through MamK) to Amb0994 and induces a conformational change in Amb0994, which activates a response regulator that eventually controls the flagella motor, similar to other bacterial two component systems^33,34.

The passive alignment model and its shortcomings

Our experiments can also be used to evaluate the effect of the passive alignment mechanism, in which the rotational motion of the rod-shaped AMB-1 cell is driven mechanically by the magnetic torque and the thermal fluctuations, like a compass^7–8. Since all the strains in our experiments have the same C_mag value (coefficient of magnetically induced differential light scattering), the same number of magnetosomes per cell, and the same arrangement of magnetosome chain (Fig.S2&S3), the magnetic components are intact and compass-like behavior should exist in all strains. Thus, if the cells were aligned to the external magnetic field purely according to the passive alignment mechanism, the distribution of cell's direction (relative to the magnetic field) for all the strains should be given by the Boltzmann distribution:

$$p(\varphi )=A{e}^{-E_m/kT}$$ [1]

The magnetic energy is given by E_m = −mB|cosθ|, where m is the cell’s magnetic dipole moment, B the external magnetic field, θ the angle between the cell’s polar direction and B, A the normalization constant. Since the angle v-B angle ϕ is measured in our experiments by projection into the 2-D observation plane, its mean value can be obtained as

$$\langle \varphi \rangle =\frac{{\int }_0^{\pi }d\theta {\int }_0^{2\pi }d\phi e^{\frac{mB\left|\mathit{\text{cos}}\theta \right|}{k_{b}T}}\mathit{\text{sin}}\theta ·\text{arccos}(\frac{\left|\mathit{\text{cos}}\theta \right|}{\sqrt{{\mathit{\text{cos}}}^2\theta +{\mathit{\text{sin}}}^2\theta {\mathit{\text{cos}}}^2\phi }})}{{\int }_0^{\pi }d\theta {\int }_0^{2\pi }d\phi e^{\frac{mB\left|\mathit{\text{cos}}\theta \right|}{k_{b}T}}\mathit{\text{sin}}\theta }$$ [2]

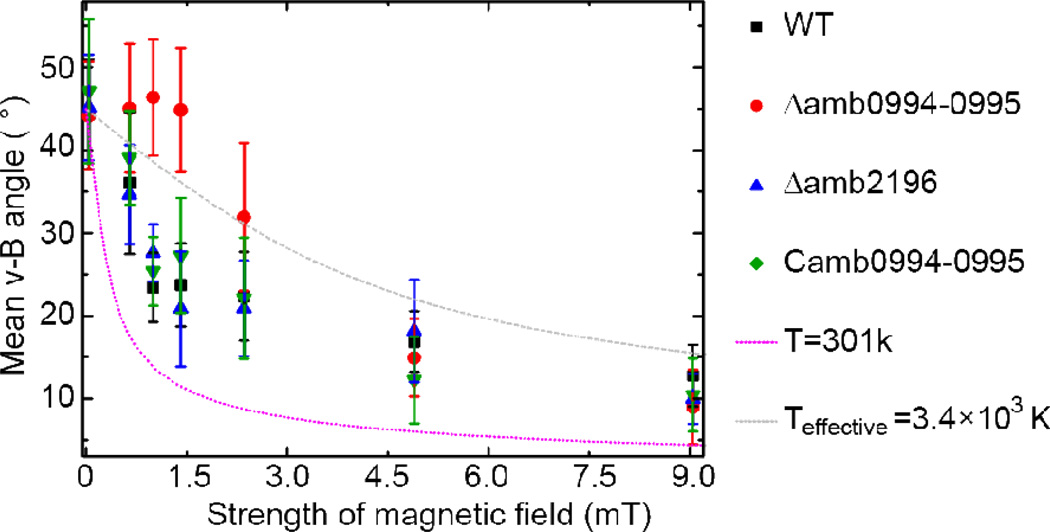
The average magnetic moment for AMB-1 is ~5×10⁻¹⁷Am² from the most recent study³⁵. At the room temperature (301K), the mean of v-B angle given by equation [2] is plotted in Fig. 6 (pink dotted line) along with the experimental measurement of v-B angle as a function of magnetic intensity. We observed that the average v-B angle predicted from the passive alignment model (Eq. [2]) is systematically lower than the experimental results.

Fig. 6.

The mean of v-B angle as a function of magnetic intensity. About 12 bacteria were traced for 12s for each condition. The pink line is the result of the passive alignment model with the room temperature. The gray line is obtained by fitting the passive alignment model with the experimental data, which results to an effective temperature T_effective=3,400K (see text for details). The bar indicates the stand error ($(\text{standard deviation}/\sqrt{n})$) of the population, where n is the number of bacteria.

What causes this large discrepancy? In particular, why did the passive alignment model fail to explain the magnetic responses even for the Δamb0994-0995 strain where active sensing is absent (at least in low to modest magnetic fields)? In the passive alignment model, it was assumed that the cell’s angular motion is driven by the balance between the magnetic energy (mB) driving alignment and the thermal energy (k_bT) favoring random orientation. However, our single cell tracking measurements clearly showed that the cell’s change of orientation, seemingly random, does not follow a passive rotational diffusion process or Brownian motion. Instead, a cell changes its orientation by actively controlling its swimming patterns (run/tumble/reverse) and the durations of each swimming mode (see Fig. 1 and Table 1). This active change of cell’s orientation effectively increases the randomness of the cell motion. The strength of this active randomness may be described by an effective “temperature” T_effective, which can be obtained by fitting experimental data by Eq. [2] with T as a tuning parameter. Specifically, by fitting equation [2] (Fig.6 gray line) to the data from the Δamb0994-0995 strain, which has the same C_mag value and arrangement of magnetosome chain as those of the WT cells (Fig.S2&S3) but lacks the magneto-sensor, we obtained an effective temperature of T_effective=3.4×10³K (with R²=0.833). Although the equilibrium Boltzmann distribution is not suitable to describe all the detailed statistical properties of the intrinsically nonequilibrium run/tumble/reverse cell motility dynamics, the effective temperature gives an estimate of the overall strength of the noise caused by active random switching of a cell’s orientation. The fact that T_effective is much higher than the room temperature means that the active random switching of a motile cell introduces a much larger noise than the thermal fluctuations in the environment. This large active noise source was not considered in the original passive alignment model⁹, which is likely the reason for its failure in explaining our experiments.

Next, we evaluate the relative contributions to magnetotaxis from active sensing versus passive alignment by comparing the magnetotactic behaviors of WT cells and different mutants under different magnetic field intensities (Fig. 6). All the active sensing strains with Amb0994 (WT, Δamb2196 and Camb0994-0995) show very similar alignment behaviors as shown in Fig. 6. However, the alignment of the active sensing deficient Δamb0994-0995 cells to the magnetic field is much worse than the active sensing strains at low magnetic fields. This observation confirms the crucial role of Amb0994 in active sensing. For very high magnetic intensity (i.e., B≥5mT), all the strains regress to roughly the same mean v-B angle and therefore the same magnetic response. This result suggests that the effect of passive alignment under high magnetic field becomes relevant and dominant in comparison with the active sensing mechanism. Taken together, our data suggest that both active sensing and passive sensing exist in bacterial magnetotaxis: the cell uses its active sensing function to navigate at relatively low magnetic intensity, when passive alignment is not strong enough to overcome the active random motion of the cell; under high magnetic field, the passive alignment mechanism becomes relevant.

Discussions and Conclusions

In summary, we studied the magnetotactic behaviors of M. magneticum AMB-1 by measuring the trajectories of individual cells (WT and mutants) with and without external magnetic fields. We found that the cells follow a mixed run/tumble/reverse swimming pattern. The time in different motion states (run, reverse, and tumble) is modulated by the external magnetic field, providing strong evidence in support of the cell’s active sensing of magnetic field. Furthermore, we found that Amb0994 is needed for the cells to sense the angle between the cell’s orientation and the direction of the external field. This information of the cell’s relative orientation (angle) with respect to the magnetic field is then used by the cell to adjust the switching of its motor and consequently the duration time of its run (Fig. 5B). We also tested the passive alignment mechanism by using a mutant strain incapable of active sensing. We found that the measured alignment between cell motion and the external magnetic field is much weaker than that predicted by the passive alignment model used in previous studies, which only considered thermal noise. This discrepancy is most likely caused by the fact that the fluctuation due to the random but active switching motion of the cell (the run-reverse-tumble motion) was not taken into account in previous studies. In WT cells, both the passive alignment mechanism and the active sensing mechanism exist with the latter dominant in modest (physiologically relevant) magnetic fields (<5mT). This mixture of active sensing and passive alignment is common in migrate vertebrates or insects^36,37. The study of magnetotaxis in bacteria shed lights on the investigation of magnetic response in other organisms.

Several unsettled issues require further studies. First, the well-accepted evolutionary benefit for magnetotaxis is to find the suitable oxygen concentration¹¹. In our experiments, we did not observe any disruption in aerotaxis in the Δamb0994-0995 strain (Fig. S8). The responses of aerotaxis and magnetotaxis may be coupled downstream, i.e., by jointly controlling the switching rate of the flagellar motors. Therefore, more experiments are needed to understand the interaction and relation between aerotaxis and magnetotaxis. Second, many questions remain in understanding the switching dynamics of the flagella motors. Since we were not able to stain the flagella successfully, we can only speculate the pattern of motor switch based on the cell’s swimming pattern. It is crucial to directly observe the switching of flagella to understand the origin of the different swimming modes (run, revere, and tumble) and to explain our experimental results such as the decrease of instantaneous velocity in the presence of magnetic field. Third, more experiments are needed to find the key elements in the regulatory network downstream of amb0994, which convey the information from the sensor to the motor. It would also be interesting to find out whether the magnetotaxis system is capable of signal amplification and adaptation, like in chemotaxis. Finally, unlike previous claims^9–12, our study showed that AMB-1 cells are only weakly aligned under the geomagnetic field. We argue that this may be reasonable considering that microaerobic condition may not be the only benefit bacteria seek for. For example, free-living bacteria often encounter only patches of attractants (e.g., nutrients), for which a purely 1D search enforced by a strong alignment with the geomagnetic field would be highly inefficient. Our results suggest that magnetotaxis may only provide a weak guidance to cell’s motion, which is flexible enough to allow the cell to response efficiently to other stimuli. However, the benefit of the weak magnetotaxis effect under geomagnetic field remains an open question. More experiments, such as magnetotaxis in the presence of other stimuli, should be carried out to investigate the possible functions of the amb0944 mediated active magnetotaxis behaviors shown here.

Materials and methods

Cell Strains and Preparation

WT M. magneticum AMB-1 (ATCC700264) were grown in EMSGM medium³⁸ for 24h at 28°C and diluted at 1:10 for another 24h two times. AMB-1 Δamb0994-0995 cells were grown by adding 5µg/ml gentamicin (Beijing Xingjingke Biotechnology). AMB-1 Δamb2196 were grown by adding 5µg/ml tetracycline (Beijing Xingjingke Biotechnology). AMB-1 Δamb0994-0995, complemented amb0994-0995 were grown by adding 5µg/ml kanamycin (Beijing Xingjingke Biotechnology). The motility of bacteria was checked using optical microscope. Details of mutant strain preparation were described in SI materials and methods.

Microfluidic Design and Fabrication

The fabrication method of three layer chip was mentioned before²³. As shown in Fig.S9, the observation window was designed 400µm×400 µm to fit the field of view using 20X objective lens and fabricated to be 25µm in height considering both the depth of field and the swimming of bacteria. The focal plane is set at 6µm below the top surface of the chamber to avoid additional boundary effects.

On-chip oxygen concentration control

Because M. magneticum AMB-1 is microaerobic, gas control is necessary for observation. The gas was controlled by a 3-way solenoid valve²³ and introduced to gas channel (see SI methods for more details). The injection pressure was 0.02MPa. The diffusion constant of gas remained the same even under 10 fold change of pressure³⁹.

Microscopy and data analysis

Because the observation window had large area and only one entrance, the chip was deposited under negative pressure to inhale liquid in. 0.1% BSA was firstly fed to coated chip walls that prevent bacteria from sticking to surfaces⁴⁰. After the chip degassed again, EMSGM medium was introduced to be motility medium. Bacteria suspension was loaded from inlet. Because the direction of suspension flow was perpendicular to the entrance of observation window, only motile bacteria can swim into the observation channel. The magnetic field is achieved by placing two magnetic bars parallel at the boundary of incubator. In experiments that are not specified, the magnetic field is 1.0mT, which is biorelavent¹². All experiments were performed without shielding geomagnetic field.

The motion of bacteria was observed under phase-contrast microscopy (Nikon Ti-E) with 20X phase-contrast objective lens and recorded 20fps by a CCD camera (Andor IXon Ultra 897). We use the MTrackJ plugin of ImageJ (National Institutes of Health) to trace single cell, and MATLAB (The Mathworks, Inc.) to do further analysis. Cells were picked randomly, and total of ~250 traces of ~20 bacteria under each condition was analyzed.