Optoacoustic spectroscopy for real-time monitoring of strongly light-absorbing solutions in applications to analytical chemistry

Abstract

An optoacoustic technique for solutions of strongly light-absorbing analytes at 0.1–0.01 mol l⁻¹ is proposed. The technique is based on the wide-band forward mode detection of temporal profiles of laser-generated ultrasonic pulses (optoacoustic signals). The leading edge of the signal repeats the distribution of the laser fluence in the medium, which makes it possible to determine its optical absorption and investigate its dynamics during a reaction. The range of light-absorption coefficients starts from 1 to 5 and reaches 10⁴ to 10⁵ cm⁻¹. The determination of iron(II) as ferroin shows the possibility of probing 0.1 mol l⁻¹ of iron(II), which was not previously achieved for this reaction by optical spectroscopy. To further prove the concept, kinetic measurements for ferroin decomposition at the level of 0.1 mol l⁻¹ and at high pHs are performed. The results are compared with spectrophotometry at lower concentrations and show good reproducibility and accuracy of kinetic constants.

1. Introduction

Expanding the range of concentrations is one of the primary tasks of analytical chemistry. Reaching for low levels appears clear, and the methodology, sample preparation, and detection techniques for trace and ultra-trace analysis are in active development. In the shadow of this trend, high-precision analysis of high concentrations seems simpler and less relevant. However, this problem is no less multi-factor, complex, and important from the viewpoint of scientific and practical significance. The problem of analysis of highly concentrated solutions is not a single task, but rather a number of various and sometimes-different challenges. First, some applications require not a single analysis but continuous monitoring of the sample itself or some consecutive factors like in technological processes or disperse systems [1] or for in vivo analyses [2]. Another challenge is the determination of low amounts against a highly concentrated matrix (e.g. high purity reagents [3,4] or trace components in biological samples against a highly absorbing matrix like hemoglobin or albumin [5,6]), which should also be characterized in detail, and with minimum pretreatment. As the signal of the main component overwhelms the other, the applicability of electroanalysis or chromatography is sometimes hindered [7,8], and thus require sophisticated separation/isolation techniques. A separate case is the determination of trace absolute amounts in ultra-low volumes or ultra-thin layers [9,10].

Various spectroscopic techniques have been used and most frequent are low-angle fluorescence [11], low-angle static [12] and dynamic [13] light scattering, and attenuated total reflection techniques [11,14,15]. Still, these methods have limitations (i) due to sophisticated methodology; (ii) spectral interfering effects like reabsorption; or (iii) related to the limited number of detectable substances (like luminophores or Mie-scattering entities). Thus, the applications of molecular-absorption spectroscopy would be preferable. However, its common techniques are transmission-based, and their applicability to samples with linear absorptivities above 5 cm⁻¹ is not approaching due to very strong attenuation of the probe beam. Thus, they are not suitable for samples with strongly absorbing analytes usually used in analytical chemistry (molar absorptivities or extinction coefficients above 10³ L mol⁻¹ cm⁻¹) with their bulk concentrations above 10⁻³ to 10⁻² mol l⁻¹.

This can benefit from another molecular-absorption technique, optoacoustic (OA) spectroscopy [16,17]. It is based on the conversion of the absorbed electromagnetic radiation into local nonstationary heating of the sample, which generates pressure pulses, OA signals. When nanosecond laser pulses are used, thermal diffusion from the heated zone can be neglected (so called thermal confinement condition [18]) for most of dielectric media. OA spectroscopy is the unique method for direct measurements of the laser fluence distribution providing the determination the optical properties and optical inhomogeneity of a medium. In such a case, the pressure signal is used as a ‘train’ to extract the optical information from the bulk of the medium. OA spectroscopy has been rapidly developing in physics and in biomedical applications for the last decade [10,19–23], but still has very scarce analytical applications for condensed samples [16,24–26]. The use of lasers resulted in a burst in OA applications, especially strongly light-scattering samples including biological tissues [27–29]. The rectilinear dependence of the generated OA signal on the sample optical absorption has led to the creation of unique techniques like OA tomography and microscopy [18,21,30,31], which provide the information on the light absorption coefficient against 1000-fold higher scattering coefficients. However, to the best of our knowledge, OA spectroscopy was never used for the problems of analytical chemistry of high concentrations, although it is suitable for solving all the above-mentioned problems.

Here, we propose an OA technique, which provides the measurements of linear absorptivities at the level of 1–10⁴ cm⁻¹. The aims of this work are to demonstrate its applicability for (i) determining a model substance in highly concentrated solutions with high precision and for (ii) monitoring the course of a reaction at high concentration levels of reactants. As a model, we used a well-known photometric reaction, iron(II) chelation with 1,10-phenanthroline [32–36].

2. Theory

The proposed OA technique is based on the time-resolved detection of temporal profiles of OA signals excited in the medium under study by forward-propagating acoustic waves (Fig. 1). The rigorous and detailed description of the optoacoustic phenomena can be found in [17,37]. In this section, we demonstrate just a typical temporal profile of the generated OA signal and shortly describe the information that can be extracted from the detected OA signal.

Fig. 1.

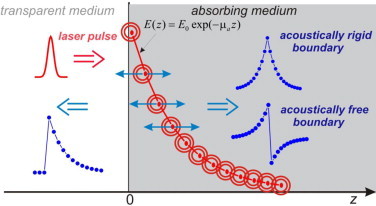
Diagram of the proposed OA technique.

Imagine that an interface of a transparent and an absorbing media is irradiated with nanosecond laser pulses from the side of the transparent medium along the surface normal (positive $\overrightarrow{z}$ direction, z = 0 corresponds to the absorbing medium surface). The wavefront of the optical radiation can be considered as plane when the light penetration depth d_op is much smaller than the laser beam diameter d. The thermal confinement condition is fulfilled very well for most of dielectric media when nanosecond laser pulses are used for OA signal generation [18], i.e.

$$d_{th}=\sqrt{\chi {\tau }_L}\ll d_{op}\text{,}$$ (1)

where d_th is the depth of thermal-wave diffusion within the laser pulse duration τ_L, and χ is the thermal diffusivity.

The measurements are performed also under the stress confinement condition [17]:

$$d_{ac}=c_0{\tau }_L\ll d_{op}={{\mu }_a}^{-1}\text{,}$$ (2)

where c₀ is the speed of sound and μ_a is the light absorption coefficient.

When the stress and thermal confinement conditions are met, the temporal profile I(t) of the laser fluence rate f(t) envelopment can be expressed as

$$I(t)=I_{0}f(t)=I_0{\tau }_L\delta (t)=E_0\delta (t)\text{,}$$ (3)

where I₀ is the incident laser fluence rate, δ(t) is a delta function, and $E_0=I_0{\int }_{-\infty }^{\infty }f(t^{\prime })d{t}^{\prime }$ is the laser fluence in the incident laser pulse; t′ is the integration variable.

The absorption of laser radiation under these conditions can be considered as instantaneous, and the temporal profile of the generated OA signal, which is then detected in the light absorbing medium (the forward detection mode), can be expressed as [17,37]:

$$p_0\left(\tau =t-\frac{z}{c_0}\right)=\left(\frac{{\mu }_a{c}_0^2\beta E_0}{2c_p}\right)\left\{\begin{array}{l}E(-c_0\tau ),\tau <0\hfill \\ \frac{1-N}{1+N}E(c_0\tau ),\tau >0\hfill \end{array}\right)$$ (4)

Here, β is the volume thermal-expansion coefficient, c_p is the specific heat of the medium, N is the ratio of acoustic impedances of the absorbing and transparent media, and τ is the running time. As follows from (4), in the limit of an acoustically free boundary (N ≫ 1), the OA signal represents the rarefaction phase following the compression signal front. In the limit of an acoustically rigid boundary (N ≪ 1), the wave reflected from the medium boundary is also compressive. The most important conclusion from (4) is that the leading edge of the generated OA signal repeats the distribution of heat release in the medium and thereby the distribution of the laser fluence. In the case of a purely absorptive character of the medium under study (a scattering-free medium), the in-depth light penetration along z-axis obeys the Bouguer–Lambert–Beer law

$$E(z)=E_0\text{exp}(-{\mu }_{a}z)\text{,}$$ (5)

and thereby the OA signal front is exponential. Thus, fitting the leading edge of the OA signal profile with an exponential function makes it possible to extract light absorption coefficients with a high precision [27,28,31,37] and independently from the absolute value of the OA signal amplitude.

In the case of a short but finite-duration pulse, it is necessary to take into account a change in the heat-release distribution during the laser-pulse impact:

$$p(t)={\int }_{-\infty }^{\infty }{p}_0(t)f(t-\tau )d\tau \text{,}$$ (6)

As a result, the steep gradient in the OA signal profile around the moment τ = 0 will be pulled within the laser pulse duration. This circumstance limits from above the range of light absorption coefficients which can be measured by this technique. For example, for τ_L = 0 ns, the maximum value is μ_a ≈ 1000 cm⁻¹ at c₀ = 1500 m/s.

Note that OA signals are usually detected at a distance from the generation zone. This leads to the appearance of diffraction transformations of the detected profile related with the spread of low-frequency harmonics away from the z-axis. The characteristic distance at which the OA signal profile starts to change considerably depends on the medium light-absorption coefficient, propagation distance, and the laser beam diameter. As a result, the OA signal amplitude decreases and the falling edge of the OA signal becomes no longer exponential. A more detailed description of this effect can be found in [38]. However, of prime importance is that the leading edge of OA signal does not change and keeps its profile with an exponent proportional to μ_a [17,37].

3. Materials and methods

3.1. Reagents

We used doubly distilled deionized water (specific resistance not less than 18.0 MΩ cm, Millipore, France). The following reagents were used throughout: cp conc. H₂SO₄ (density, 1.87 g ml⁻¹, 98% wt.; Sigma–Aldrich, CAS no. 7664-93-9) and p.a. grade ferrous tris(1,10-phenanthrolinate) sulfate, Fe(C₁₂H₈N₂)₃SO₄ (ferroin, CAS no. 14634-91-4, M = 692.52 g mol⁻¹; Labtekh, Russia), stock solutions of 0.1442 mol l⁻¹ (calibration) and 0.1083 mol l⁻¹ (kinetics). Calibration solutions were made from the stock solution using doubly distilled deionized water giving the range of 1.9–140 μmol l⁻¹.

3.2. Auxiliary measurements

Absorption spectra were measured using a Shimadzu UVmini 1240 spectrophotometer (Japan) in a quartz cells (path lengths, l = 1 cm and l = 0.1 cm) at room temperature in the wavelength range 190–1100 nm. For weighing, a Kern 770 analytical balance (Germany, precision ±0.1 μg) was used. To intensify the dissolution, a GRAD 38-35 ultrasonic bath (Grad Technology, Russia) was used. Samples were taken with Eppendorf Pro automatic pipettes (Germany), (20 ± 1)–(200 ± 1) μl, (100 ± 1)–(1000 ± 1) μl, and (500 ± 1)–(5000 ± 1) μl.

3.3. Procedure

Kinetic measurements using spectrophotometry and OA spectroscopy were made for a ferroin concentration of 3.2 × 10⁻² mol l⁻¹ in 12.9 mol l⁻¹ sulfuric acid. The stock ferroin solution was added to sulfuric acid in a test tube, quickly cooled to room temperature with a water flow, the initial temperature was controlled, and the measurements are started. At the stage of spectrophotometric measurements, the kinetic curve was recorded at 532 nm (to correspond to OA measurements) in a cell with 1 mm path length each 2 s. OA measurements were every 2–4 min (the total of 20 measurements per curve).

3.4. Data treatment

The measurement results are treated presented in accordance with the requirements of ISO/IEC 17025:2005 [39]. The limits of detection (LOD) were calculated from the 3σ-criterion according to the IUPAC 1998 recommendations for the presentation of the results of chemical analysis [40]. All the procedures were characterized by the repeatability relative standard deviation (RSD), and the minimum values of this error curve was used as another metrological parameter. To determine the significance of contributions to the signal of the control experiments, the series were compared by Student's t-tests; variances were compared using the Fisher test.

3.5. Optoacoustic setup

OA measurements were performed using the experimental setup illustrated in Fig. 2a. For the generation of OA signals in the medium under study, the radiation of the second harmonic (λ = 532 nm) of a pulsed Nd:YAG laser (a Solar LQ129, Belarus) was used. The laser pulse duration τ_L = 22 ns at the 1/e level, which was measured with a photodiode. The laser pulse energy could be varied with a number of neutral filters and did not exceed 1 mJ and the corresponding laser fluence did not exceed few mJ cm⁻². The laser radiation propagated through the system of a light scatterer and a convex lens to homogenize light distribution in the beam cross-section and make the beam diameter 12 mm at the surface of the medium under study. The laser pulse repetition rate was 50 Hz, which allowed us to register OA signals in 3 s (at 128 signal averages) and thereby neglect any signal changes related with chemical reactions inside the OA cell.

Fig. 2.

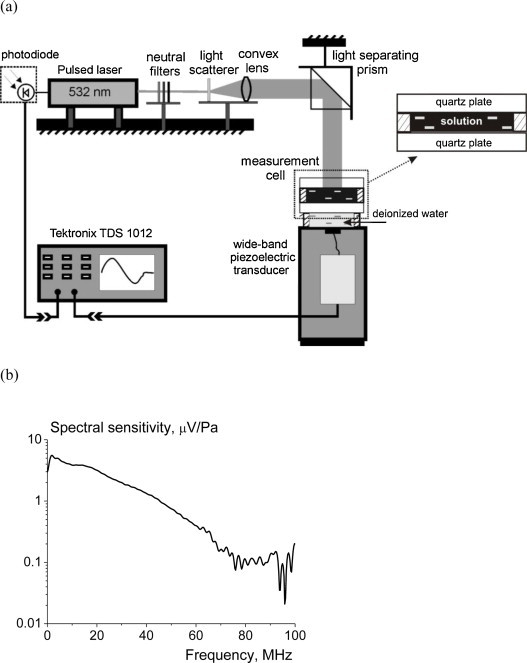
Diagram (a) of the optoacoustic setup and (b) spectral transfer function of the transducer used.

The OA cell is comprised of two polished quartz plates of 6 mm in thickness and 25 mm in diameter and a quartz cylinder of 5 mm in thickness and 20 mm in hole diameter in between the quartz plates. The outer diameter of the cylinder was the same with those for the quartz plates. All the surfaces of the cell components were gently polished and made plane parallel with the thickness variation of about 2 μm to avoid any possible distortions of the OA signal profile due to a non-parallelism of OA source and detector surfaces.

During experiments, the OA cell was filled with the test solution. A 5-mm thick deionized-water layer filling another cylinder of the same thickness and diameter was used as an immersion between the cell and a home-made ultra wide-band piezoelectric detector. The design of the cell provides a very easy and rapid procedure of solution filling. This procedure consists of the set up of the whole cell except the cover quartz plate. Next, the volume of the test solution corresponding to the inner volume of the cell cylinder is added, and the upper quartz plate is put to the cylinder edge and is moved by slipping it in the horizontal plane, this tightly covering the cell and removing the excess sample liquid. The process of filling and covering the cell takes about 2 s, which is very suitable not only for batch measurements (building calibration curves of stable solutions), but for monitoring kinetic measurements in this study.

The detector was made on the base of a 28 μm PVDF film (Precision Acoustics, UK) and operated in the open-circuit regime [41]. A typical pressure of the detected OA signals varied in the range of 10²–10⁵ Pa. The detector was calibrated in the frequency range of 0.1–50 MHz, had a smooth spectral transfer function in the range of 0.1–40 MHz and the low frequency sensitivity of 4.5 μV/Pa (see Fig. 2b). The detected OA signals were amplified and digitized by a Tektronix TDS 1012 digital oscilloscope (USA; analog frequency, 100 MHz; sampling rate, 1 GHz) and finally transferred to a PC for further signal processing.

It is important that the detector makes it possible to acquire pressure signals with the minimum amplitude of few tens of Pa without any changes of the front of OA signals for all the test solutions. Similar detectors were used also in our previous works [29,42] and showed an extremely high efficiency of their application for the wide-band detection.

4. Results

4.1. Detected signals and data processing

Fig. 3a illustrates a typical OA signal detected by the wide-band transducer. It shows that the signal had a quite predictable temporal profile and a very good SNR (∼40 dB) providing precise extraction of the information on the light absorption during chemical reactions occurring in the OA cell. Fig. 3b shows, in the logarithmic scale, the leading edge of the detected signal (points) and its fitting with a linear function (solid line):

$$\text{ln}U=a+b\times t$$ (7)

Fig. 3.

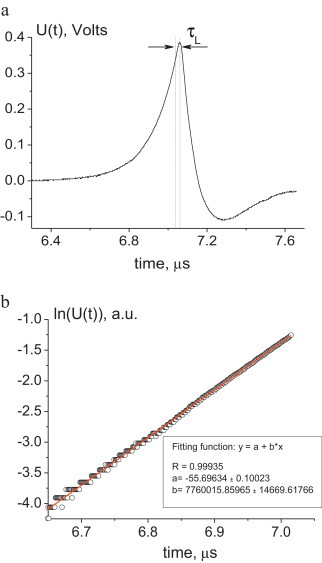
Temporal profile of an OA signal detected in the ferroin solution with the linear light absorption coefficient μ_a = 52.1 cm^–1 (a); leading edge of this signal in the logarithmic scale and its fitting with the linear function (b).

Here, a is a constant. The slope b = μ_ac₀ is then used for the calculation of the linear light absorption coefficient μ_a. Such fitting has usually a very good correlation (r > 0.999) with the detected signal front, which provides high accuracy of the light absorption coefficient determination (RSD ca. 0.1% [27,28,31]). As described above by Eqs. (2) and (6), a part of the signal profile which is closer than τ_L to the signal maximum is not exponential and should not be used in fitting.

The speed of sound c₀ in the solution is also measured experimentally by a signal propagation time indicated in the position of the signal maximum. For the determination of the ultrasound speed in the solution under study, we measured the time delay between the primary detected OA signal and its double propagation within the OA cell. This measurement is totally independent on the position of the OA source. All the quartz components of the OA cell were polished and plane-parallel. It made it possible to have the medium thickness fixed with the precision better than few μm for all the investigated solutions. Note that the value of c₀ could be inconstant in the course of a chemical reaction due to the formation and decomposition of species affecting the thermophysical parameters of the medium. The relative error of the speed of sound measurement was lower than 0.5%.

Thus, time-resolved detection of OA signal profiles provided with the value of light absorption coefficient μ_a [cm⁻¹] for the current experiment, i.e. for a current state of the solution. In case of kinetic measurements, values of μ_a detected at different moments were treated as a kinetic signal depending on the reaction time t_reac after mixing all the reagents (see below), which was fitted as

$$\text{ln}\left(\frac{{\mu }_a}{{\mu }_a^{\max }}\right)=A-k_v{t}_{reac}\text{,}$$ (8)

where ${\mu }_a^{\max }$ is the maximum value of light absorption coefficient in the current reaction and A is an experimental constant. The rate constant k_v was then determined from Eq. (8).

4.2. Calibration and performance parameters comparison for spectrophotometry and OA technique

To select the model for OA measurements at high concentrations, we used the chelation of iron(II) with 1,10-phenanthroline, as (i) it gives the stable product, ferroin and (ii) it shows high sensitivity and reproducibility of photometric measurements and reliable characteristic constants [32–36]. Important also is that very highly concentrated aqueous solutions of this chelate could be readily prepared. This reaction was previously tested using photothermal spectroscopy showing its thermal and photostability under laser excitation as well as good reliability [43].

Spectrophotometric measurements were made for pre-synthesized ferroin and showed the linear calibration curve at the absorption band maximum (510 nm, l = 1 cm) with the slope of (1.0 ± 0.1) l mol⁻¹, which is in concordance with the molar absorptivity of ferroin of ɛ_max = 11,000 l mol⁻¹ cm⁻¹. For the excitation wavelength of the OA technique, 532 nm, ɛ₅₃₂ = 6500 l mol⁻¹ cm⁻¹. From the curve at 510 nm, it is possible to measure up to 2 × 10⁻⁴ mol l⁻¹ (the linear light absorption coefficient of 5.1 cm⁻¹). The maximum determined concentration can be increased 10-fold by using photometric cells with lower path lengths (l = 0.1 cm).

Next, we have tested the linearity of OA measurements for ferroin in the whole range of light absorption coefficients of the setup. For this purpose, we used different concentrations of ferroin as described in Section 3.1. Variations of the speed of sound from the value of 1490 m/s were lower than 0.5% and could be neglected during measurements. The light absorption coefficient μ_a of the solution was determined using the procedure described in the Section 4.1. Fig. 4 demonstrates the dependence of μ_a on c, which can be described with the linear function

$${\mu }_a=Kc=2.303\epsilon c\text{,}$$ (9)

where ɛ is the molar absorptivity. K = (14, 900 ± 300)l mol⁻¹ cm⁻¹, which results in the value for ferroin of ɛ = 6500 l mol⁻¹ cm⁻¹ (at 532 nm), which is in good concordance with the value of molar absorptivity at 532 nm obtained from absorption spectra by spectrophotometry. As seen, the relative error of the dependence slope is about 1.8%. Because the relative error of the OA method itself in the light absorption measurement (see Fig. 3) is about 0.1%, we believe that the primary error is actually determined by an uncertainty of concentration obtained during the preparation of solutions, and this value fits well with the accuracy data on the calibrated glassware and pipettes used.

Fig. 4.

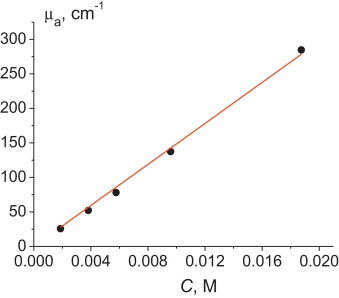
The linear light absorption coefficient at 532 nm as the function of the concentration of ferroin (the calibration curve).

4.3. Monitoring the course of the reaction of decomposition of iron(II) tris(1,10-phenanthrolinate)

The reaction of the decomposition of ferroin was selected as a model reaction for determining the characteristic constants of ferroin as it is a first-order kinetics according to the existing data [32,33],

$${[\text{Fe}{(\text{Phen})}_3]}^{2+}\underset{k_1}{\overset{k_{-1}}{\rightleftarrows }}{[\text{Fe}{(\text{Phen})}_2]}^{2+}+\text{Phen}\stackrel{\text{fast}}{\rightleftarrows }{[\text{Fe}(\text{Phen})]}^{2+}+2\text{Phen}\stackrel{\text{fast}}{\rightleftarrows }{\text{Fe}}^{2+}+3\text{Phen}$$ (10)

and the reaction rate can be easily controlled using the acidity as the 1,10-phenantroline released in the reaction is bound into undissociated 1,10-phenanthrolinium.

$$\text{Phen}+{\text{H}}_3{\text{O}}^{+}\stackrel{\text{fast}}{\rightleftarrows }{\text{PhenH}}^{+}+{\text{H}}_2\text{O}$$ (11)

First, the comparison of OA and spectrophotometric measurements at a high concentration level of iron demanded high concentrations of acid. This was needed to maintain the average reaction rate (a low reaction rate shows a very low slope that can be calculated with high precision; at high reaction rates, equilibrium is attained too fast to record a time-resolved kinetic curve). Moreover, the selection of a strong acid is also rather specific: we cannot use hydrochloric and phosphoric acids as they form rather stable complexes with iron, chloric acid as it forms difficultly soluble ion pairs with ferroin, and nitric acid due to its strong oxidative properties. Thus, the only possible selection is sulfuric acid. We selected 13 mol l⁻¹ sulfuric acid as medium and 0.03 mol l⁻¹ ferroin.

Under these conditions, the reaction takes 2 h, which provided good resolution of kinetic curves. The expected initial linear absorption coefficient is 118 cm⁻¹, and the changes in μ_a in the major part of the kinetic curve are from 20 to 1 cm⁻¹, which can be measured by both spectrophotometry (at the upper boundary of the dynamic range) and the OA setup (at the middle of the dynamic range, see Fig. 4). Spectrophotometric kinetic measurements in 0.1 cm cells led to the equation

$$\text{ln}\left(\frac{{\mu }_a}{{\mu }_a^{\max }}\right)=A^{sp}-k_v^{sp}{t}_{reac}\text{,}$$ (12)

where A^sp = (−2.5 ± 0.5), ${\mu }_a^{\max }=(40\pm 20){\text{\hspace{0.17em}cm}}^{–1}$, $k_v^{sp}=(3.9\pm 0.9)\times {10}^{-4}{\text{\hspace{0.17em}s}}^{-1}$ (n = 18; confidence level, 0.95).

The reaction of ferroin decomposition using the OA technique was studied as described above. The OA cell (see Fig. 2) was filled with the solution under study. OA signals generated in the cell were recorded every 2–4 min during the reaction permitting to calculate the light absorption coefficient at the current stage of the reaction. Calculation of the kinetic curve based on the optoacoustically measured light absorption coefficients were performed according to the same procedure as in the spectrophotometric measurements. Three curves (Fig. 5) are approximated with the equation

$$\text{ln}\left(\frac{{\mu }_a}{{\mu }_a^{\max }}\right)=A^{OA}-k_v^{OA}{t}_{reac}$$ (13)

Fig. 5.

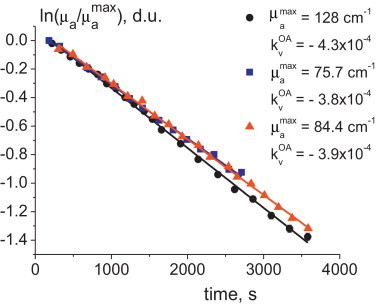
Kinetic curves (in the logarithmic form) for three experiments for ferroin decomposition and the data (in legend) calculated from these OA measurements.

The parameters are given at Fig. 5. The average value of $k_v^{OA}=(4.0\pm 0.2)\times {10}^{-4}{\text{\hspace{0.17em}s}}^{-1}$. The speed of sound in the test solution was increased but not higher than 0.5% from its initial value of 1560 m/s during the reaction. Thus, relative changes of the speed of sound were not substantial but taken into account in the dependence in Fig. 5.

5. Discussion

The comparison of the data obtained in this study with spectrophotometry and the OA technique and the existing data are summed up in Table 1. We would like to emphasize few important issues related with the OA technique in the application to analytical chemistry. First, let us discuss the limitations as an optical technique based on the direct measurement of a laser fluence distribution within the medium under study. Since spectrophotometry is a very robust and conventional technique in analytical chemistry also based on the measurement of light absorption, first of all, we need to compare these methods from the viewpoint of their applicability limits.

Table 1.

Experimental characteristic rate constants found with spectrophotometry and the OA technique and their comparison with existing data (confidence level 0.95).

Conditions (initial iron concentration)		Characteristic rate constant k−1, s−1 ×105	Characteristic rate constant ${\tilde{k}}_{-1}$, corrected for H2SO4 concentration, s−1 ×105
cFe = (1 − 100) × 10−8 mol l–1 pH 0.5, (0.3 mol l−1 H2SO4), 20 °C (thermal lensing) [44]		5.0	6.5
cFe = (1 − 100) × 10−6 mol l–1 1 mol l−1 HCl, 25 °C (spectrophotometry) [34,45]		7.4	–
cFe = (1 − 100) × 10−6 mol l–1 0.5 mol l−1 H2SO4, 25 °C (spectrophotometry) [32,33]		7.5	7.5
cFe = (1 − 100) × 10−6 mol l–1 1 mol l−1 H2SO4, 25 °C (spectrophotometry) [46]		7.33	7.3
cFe = 3.2 × 10−2 mol l−1 pH-1.4 (13.1 mol l−1 H2SO4) 25 °C	This study, spectrophotometry (n = 18)	39 ± 9	7 ± 2
	This study, OA technique (n = 3)	40 ± 2	7.8 ± 0.4

Because spectrophotometry works with the light propagated through the measured volume, there is a range of light absorption coefficients where its application is not useful or even impossible. For example, measurements of solutions with μ_a > 5 cm⁻¹ faces serious difficulties due to necessity of using a submillimeter depth and submilliliter volume which is very difficult for controlling reactions. Thus, the upper boundary of the spectrophotometric linear range is usually μ_a ∼ 5 cm⁻¹.

The OA technique does not require the detection of the light transmitted through the sample and, contrary to spectrophotometry, needs the probe light radiation to be completely absorbed within the measured volume. Thus, the measured values of μ_a are limited from below. In our previous papers, we demonstrated that the minimum value of light absorption that can be readily measured with the OA technique using a tabletop setup and conventional mJ nanosecond lasers is of an order of μ_a ∼ 0.05 [47]. However, the smaller is light absorption, the larger should be the depth ($\sim {\mu }_a^{-1}$) of the sample cell. Therefore, when the medium under study contains light scattering substances, the application of the OA technique is quite reasonable and sometimes is solely possible [27–29,31,47]. On the other hand, if it is known that the medium under study absorbs uniformly and is scattering free, there is a reason to apply conventional spectrophotometry rather than the OA technique.

There is an opposite situation when the light absorption is of the order of hundreds of inversed centimeters. In such a case, the OA technique is advantageous. In this paper, we demonstrate that a very simple OA setup is applicable for online precise monitoring of strongly absorbing solutions. It is important to note that the maximum value of light-absorption coefficients that can be assessed with the OA technique is determined by the laser pulse duration only (see Eq. (2)) and reaches 10⁴–10⁵ cm⁻¹.

The RSD of light absorption measurement with the OA technique does not depend on the measurement volume and is of the order of 0.1%. Such a high accuracy is reached by hundreds of points used at fitting the laser fluence distribution.

Laser pulse energy and laser fluence were measured before measurements but we did not control it during each a laser pulse. The stability of the laser energy was about 3%, which was almost eliminated by averaging over 128 laser shots. We would again emphasize that the proposed method is amplitude-independent and any variances in laser pulse energy do not affect the leading edge of the OA signal at all. This is also a big advantage of the proposed method.

At the stage of kinetic measurements, spectrophotometric measurements showed rather low reproducibility of both the slope of the kinetic curve and the initial absorbance value. Certainly, the primary reason is that mixing low volumes of concentrated solutions of ferroin and sulfuric acid result in an increase in the error of measurements. Also, the irreproducible heating of the mixture in the first seconds of the reaction results in a differing values of absorbance at the beginning of the main linear section of the kinetic curve.

The second factor decreasing reproducibility can be accounted for by the measurement of the initial part of the kinetic curve with high errors (in the vicinity of the upper boundary of the linear dynamic range of the spectrophotometer). This value shows that the characteristic rate constants found in this study are higher than the existing values (Table 1).

This could result from differing conditions for this study (12.59 mol l⁻¹ sulfuric acid) and much lower values of acidity in previous studies. Thus, we need to take into account the formation of mixed-ligand sulfate–1,10-phenathrolinate complexes [48–50]:

$${\left[\text{Fe}{(\text{Phen})}_3\right]}^{2+}+\text{S}{\text{O}}_4^{2-}\stackrel{{\tilde{k}}_{-1}}{\underset{{\tilde{k}}_1}{\rightleftarrows }}{\left[\text{Fe}{(\text{Phen})}_2(\text{S}{\text{O}}_4^{2-})\right]}^{2+}+\text{Phen}$$ (14)

In such a case, the reaction at any given pH can be considered as a reaction of a pseudo-first order toward iron(II) with another rate constant ${\tilde{k}}_{-1}$, which can be measured by correcting the experimental value k₋₁ taking into account the concentration of sulfate. This results in better agreement of the data (Table 1, third column). In this case, the characteristic rate constant is closer to the existing values.

From the viewpoint of kinetic measurements, it is important that the value of constants achieved in OA experiments fit existing data for lower concentrations with much smaller errors (see Table 1). We account it for the fact that the starting parts of spectrophotometric kinetic curves are obtained at the upper limit of the linear dynamic absorbance range of the spectrophotometer (absorbances from 3 to 5), which lead to a high RSD of the measurements, thus, to a lower apparent value of absorption coefficient and, thus, lower slope of the kinetic curve.

Further, this could be extended to rate constants of ferroin formation and thermodynamic constants. One of first applications of this can be the determination of characteristic constants of complexes at high concentration levels, which is important for creating, e.g. new metal-based medicines [50]. These findings could also be extended with systems other than metal complexes and required by applied analysis: dye compositions in complicated samples, dyes, proteins and their complexes in biological solutions or highly absorbing oil samples, as a whole – for the determination of concentrated solutions when the dilution cannot be accomplished as it decomposes the reaction system [1,3,5,6]. Therefore, the OA technique can be the sole means to accomplish these tasks.

6. Conclusions

Thus, the optoacoustic technique was successfully used for studying highly concentrated, strongly light-absorbing solutions and monitoring the course of reactions at this concentration level. The probing of the concentration range of more than an order and at the level of 10⁻¹ mol l⁻¹ of iron(II) was not previously achieved by optical spectroscopy. In this study, in spite of methodological difficulties with concentrated iron(II) and sulfuric-acid solutions, we achieved good reproducibility of both the calibration data and kinetic curves. This allowed us to achieve the reproducible results both with iron(II) determination and the values of rate constants. As a whole, the robustness of the OA method for successfully solving the problem of chemical analysis has been shown. The results to be obtained are of high precision because, contrary to conventional methods, every measured coefficient is calculated by fitting the OA signal profile consisting of hundreds of points. As the signal-generation theory and data gathering algorithms are developed and can be easily automated, and the OA setup has a simple and handy design, which can be implemented as a compact instrument, we believe that this method can be introduced in practice of various specialties of basic and applied analytical problems.

Conflict of interest

The authors declare that there are no conflicts of interest.

Biography

Mikhail Proskurnin is the professor at the Chemistry faculty of M.V. Lomonosov Moscow State University. He received his Ph.D. and D.Sc. degrees from this university, and was a Visiting Scientist in Tokyo University (1999–2000), FZK (Germany, 2002), and UAMS (AK, USA, 2012). He is a member of The Bureau of The Scientific Council on Analytical Chemistry of The Russian Academy of Sciences. He is the author and translator of 9 books, 2 patents, and 130+ papers on photothermal spectroscopy and analytical chemistry. The scientific interests of Prof. Proskurnin lie in the development of photothermal spectroscopy in analytical chemistry and applied biological studies.Dmitry Volkov is a Research Scientist at the Chemistry faculty of M.V. Lomonosov Moscow State University. He has 10 papers in the field of physicochemical studies and analytical investigations and monitoring of carbon nanomaterials.Tatyana Filimonova is a graduate student at the Chemistry faculty of M.V. Lomonosov Moscow State University. Her work is connected with the development of methodological aspects of optoacoustic techniques in applied chemical analysis.Ivan Pelivanov is the Assistant Professor at the Physics faculty of M.V. Lomonosov Moscow State University, Visiting Assistant Professor at the University of Washington (WA, USA). He graduated from the group of Prof. A.A. Karabutov, which is a pioneering and renowned team in various physical and biological applications of optoacoustic spectroscopy, and received his Ph.D. degree in 2000. His recent research focuses on designing sensitive wide-band detectors, application of optoacoustic method in NDT and material evaluation, analytic chemistry, and in medicine. Ivan Pelivanov is one of the most active members in optoacoustic research for more than a decade.