Highly Accelerated Aortic 4D Flow MR Imaging with Variable-Density Random Undersampling

Abstract

Purpose

To investigate an effective time-resolved variable-density random undersampling scheme combined with an efficient parallel image reconstruction method for highly accelerated aortic 4D flow MR imaging with high reconstruction accuracy.

Materials and Methods

Variable-density Poisson-Disk Sampling (vPDS) was applied in both the phase-slice encoding plane and the temporal domain to accelerate the time-resolved 3D Cartesian acquisition of flow imaging. In order to generate an improved initial solution for the iterative self-consistent parallel imaging method (SPIRiT), a sample-selective view sharing reconstruction for TIme-Resolved Random UndersamPling (STIRRUP) was introduced. The performance of different undersampling and image reconstruction schemes were evaluated by retrospectively applying those to fully sampled data sets obtained from three healthy subjects and a flow phantom.

Results

Undersampling pattern based on the combination of time-resolved vPDS, the temporal sharing scheme STIRRUP, and parallel imaging SPIRiT, were able to achieve 6-fold accelerated 4D flow MRI with high accuracy using a small number of coils (N=5). The normalized root mean square error between aorta flow waveforms obtained with the acceleration method and the fully sampled data in three healthy subjects was 0.04 ± 0.02, and the difference in peak-systolic mean velocity was −0.29 ± 2.56 cm/s.

Conclusion

Qualitative and quantitative evaluation of our preliminary results demonstrate that time-resolved variable-density random sampling is efficient for highly accelerating 4D flow imaging while maintaining image reconstruction accuracy.

1. Introduction

4D flow magnetic resonance imaging (MRI) is a powerful tool for comprehensive hemodynamic assessment [1] but is hampered by long scan times. Different acceleration schemes have been proposed to shorten the scan time. Parallel imaging is well accepted as an acceleration method for MRI [2, 3] and has been applied to flow imaging [4]. k-t based parallel imaging techniques have been proposed for further acceleration by exploiting spatial-temporal redundancies [5, 6]. Other k-t based acceleration methods for flow imaging include view sharing [7, 8] and principal component analysis (PCA) [9] methods. Recently compressed sensing (CS) has been suggested as a means to reduce scan time by exploiting image sparsity [10], and has been investigated for accelerating flow imaging [11–13]. CS combined with parallel imaging (PI) has also been used for flow imaging [14–16]. The CS/PI methods mentioned above have been applied using conventional Cartesian acquisition with the requirement of random sampling [10]; non-Cartesian acquisitions using radial [17, 18] and spiral [19, 20] sampling have also been investigated for accelerating flow imaging.

Generally, view sharing introduces temporal compromise and several studies have reported that k-t SENSE and k-t BLAST methods result in temporal blurring and an underestimation of peak velocities during systole [21–24]. However, recent work has reported improved performance with modified k-t methods [9, 25]. In this study, we introduce a new undersampling scheme to accelerate 4D flow imaging while maintaining accurate velocity measurements. We investigated an effective variable-density pseudo-random undersampling scheme [26] for 4D flow MRI, with time-resolved 3D Cartesian acquisition. We proposed Sample-selective view sharing reconstruction for TIme-Resolved Random UndersamPling (STIRRUP) to reduce the effects of undersampling by sharing data from other frames based on the temporal distance to the time frame of interest. This view sharing reconstruction was then utilized to improve the initial solution for the Iterative Self-consistent Parallel Imaging Reconstruction from arbitrary k-space (SPIRiT) [27]. The combination of the proposed effective undersampling scheme, view sharing method (STIRRUP) and parallel imaging reconstruction (SPIRiT) with the improved initial solution was applied to highly accelerate 4D flow MRI. We evaluated the image reconstruction accuracy using STIRRUP, SPIRiT, and the improved initial solution SPIRiT (iiSPIRiT) respectively in imaging of the thoracic aorta, with an acceleration factor of 6 (targeting a 5 minute scan).

2. Materials and methods

2.1. Theory

2.1.1. Undersampling on k_y-k_z plane

To recover images from undersampled data using compressed sensing and specific parallel imaging methods such as SPIRiT [10, 27], incoherent and random undersampling is desired. In practice, pseudo-random undersampling is applied. For 3D Cartesian acquisition, random undersampling can be implemented on the phase-encoding plane (k_y-k_z). Poisson-Disk sampling (PDS) provides a random but even distribution of samples [28, 29]. PDS outperforms the conventional uniform random distribution and is well-suited to CS and PI [27]. Variable-density Poisson-Disk Sampling (vPDS) acquires data more densely at low frequencies and less densely at high frequencies, resulting in improved acceleration efficiency [26]. In this study, vPDS was applied to aortic 4D flow MRI. vPDS was generated independently at each time frame, achieving the same acceleration factor across all the time frames.. A fully sampled k-space center was acquired for coil calibration of the parallel imaging reconstruction. As shown in Figure 1a, random undersampling with an acceleration factor of 6 was achieved along the k_y-k_z plane and the temporal domain.

Figure 1.

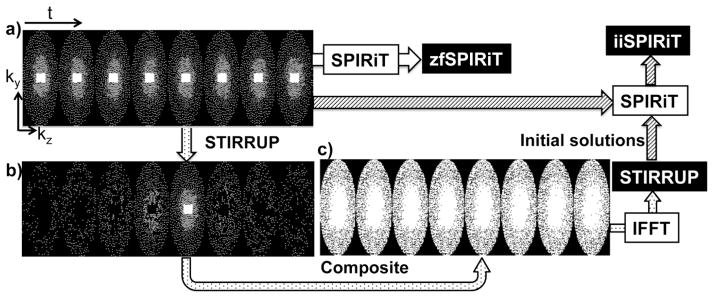
Data sampling strategies. a) Variable-density Poisson-Disk sampling on k_y-k_z plane through time (each block is for one time frame; k-space center is fully sampled), b) the samples at each time frame selected with STIRRUP for generating a composite data at the time frame of interest, c) composite sampling patterns through time. The composite data sets are reconstructed as STIRRUP results, which are used for improving the initial solution for SPIRiT (iiSPIRiT).

2.1.2. View Sharing

The basic concept of view sharing has been widely adopted in time-resolved MRI applications, with a variety of implementations [30–32]. For most applications, the specific sampling pattern used was constrained by the requirements of the sharing scheme used. In this study, we propose STIRRUP, a generalized view sharing method for time-resolved random undersampling, described above. STIRRUP reduces the effects of undersampling by filling the missing sample points with the data from other frames, such that the sample point of the adjacent frames with the closest temporal distance to the time frame of interest is selected to fill k-space. The Cartesian k_y-k_z grid at each time frame is filled to the extent possible from selected adjacent time frames to form composite data sets for image reconstruction. As shown in Figure 1b, for a representative time frame of interest (the middle time frame), certain points are selected from the other time frames using the strategy described above. Consequently, little data is shared between time frames that are located far apart. Figure 1c shows the composite sampling patterns for all the time frames. The STIRRUP algorithm is designed to efficiently minimize the degree of undersampling. However, with high acceleration factors the composite data sets will still have missing points. One way of handling the missing data points is to simply apply zero filling. We refer to this image reconstruction approach as STIRRUP reconstruction. Similar to other view sharing methods, the results obtained with STIRRUP are expected to display a temporal smoothing effect, although this effect is expected to be relatively small because of the efficient sharing algorithm.

2.1.3. Improved SPIRiT

The parallel imaging method SPIRiT iteratively solves the optimization problem subject to data fidelity and based on an initial estimation for the solution [27]. The initial solution has been found to be critical for solving the final solution in terms of computation efficiency and reconstruction accuracy [27]. The simplest approach to an initial solution is to use zero-filling image reconstruction (which we refer to as zfSPIRIT.) However, for high undersampling factors such as R=6 (Figure 1a), the zero-filling image reconstruction may not work well, resulting in either poor reconstruction quality, high SPIRiT computation cost or both. In this study, we propose the STIRRUP reconstruction (Figure 1c), which largely reduces the undersampling, as an improved initial solution for SPIRiT. We refer to the improved initial solution SPIRiT as iiSPIRiT. It is expected to achieve improved reconstruction accuracy and robustness compared to zfSPIRiT.

2.2. Data Acquisition & Image Reconstruction

A prospectively gated Cartesian 3D CINE phase-contrast sequence with interleaved three-directional velocity encoding was applied to acquire fully sampled 4D flow data on a 1.5T Siemens Avanto scanner (Siemens Medical Systems, Erlangen, Germany) with a 5-channel coil in three volunteers (two females, one male, 29 ± 3 years old). Scan settings were VENC = 200 cm/s, FOV = 320 × 240 × 55 mm³, image matrix = 128 × 96 × 22, 2.5 mm isotropic resolution, TR/TE=6.1/3.2 ms, FA=15°, Pixel bandwith = 651 Hz/pixel, 16–19 time frames with a temporal resolution of 35 ms, and scan time of 26.5±8.8 mins with respiratory NAV gating window of 7 mm (efficiency 63.1±11.9%).

Generally, flow features in the aorta are relatively smooth. To further evaluate if highly variable spatial frequency structures are maintained with the acceleration methods, we also applied the methods on a flow phantom with a flow jet. The phantom is a patient specific replica of an internal carotid aneurysm. The aneurysm is about 25 mm long, 14 mm wide and 18 mm high. It was connected to a computer controlled flow pump that was built in-house. The flow model was constructed by printing the geometry in wax, the embedding in silicone (Sylgard 184, Dow Corning). Once the silicone had set, the wax was melted out leaving the lumen of the aneurysm and vessels hollow. Since the model is in a silicone block, the walls are considered rigid. The flow pump consists of a gear pump (Oberdorfer) connected to a servo-motor and controller (Blu-AC-Q, Applied Motion). The computer, servo-motor, gear pump and water reservoir were placed in the control room and flexible Polyvinyl chloride (PVC) tubing was used to run gadolinium-doped water (1:100) to the model. The model itself was placed in the scanner. Flow was measured using 2D Phase Contrast MRI sequence and set to approximate flow rates encountered in vivo. In this study, the peak flow rate was set to be about 100 cm/s. A 5V signal was sent to the external trigger port at the beginning of every pulse (1 Hz) from the DAC Card (USB-6011, National Instruments) in order to allow for a steady triggering signal. Pulsatile flow was generated in the phantom, simulating 17 time frames through the pulsation cycle. Data was collected on a 3.0T Siemens Skyra scanner (Siemens Medical Systems, Erlangen, Germany) with a 16-ch coil. Scan settings were VENC = 150cm/s, FOV = 240 × 120 × 25 mm³, image matrix = 192 × 96 × 20, TR/TE = 6.8/3.4ms, FA=8°, Pixel bandwith = 400 Hz/pixel, and scan time of about 16 mins.

k_y-k_z undersampling was retrospectively applied to the fully sampled data sets using vPDS with an acceleration factor of R = 6 [33]. A 12 × 12 fully sampled k-space center on the k_y-k_z plane was used for coil calibration of the parallel imaging reconstruction. The algorithm was repeated independently for each time frame. The undersampled data sets obtained with time-resolved variable-density random sampling were reconstructed with the three different reconstruction methods: STIRRUP; zfSPIRiT; and iiSPIRiT. Fully sampled data sets were reconstructed as the reference. The effect of the number of time frames included for view sharing (called length of sharing) in the STIRRUP algorithm was assessed by varying the length of sharing step-wise from 1 to 9 (corresponding to n×2+1 frames for generating composite data set). In the SPIRiT reconstruction, the kernel size was chosen as 5×5. The zfSPRiT and iiSPIRiT reconstructions were carried out with 1–20 iterations to evaluate the effect of the number of iterations. All data processing was implemented in Matlab (The MathWorks, Natick, MA).

Image reconstruction in this study was implemented in Matlab and run on a PC with Intel (R) Xeon (R) Processor. Each “eight-dimensional” (three spatial, three velocity, time and coil) data set was separated into 6 parts and the reconstruction was looped over these 6 parts so as to use only 4 GB of memory. This non-optimized approach resulted in reconstruction times of about 8 hours for each data set.

2.3. Data analysis

For each subject, five planes perpendicular to the ascending (AA) and the descending aorta (DA) were defined (refer to the dash line location in Figure 3b). For each plane, intraluminal ROIs were delineated manually. The through-plane per-pixel velocities as well as spatially averaged velocities in ROIs (mean velocities) were evaluated. Flow-vs-time waveforms were generated in for each ROI. Assessment of the accuracy of the different reconstructions was performed using linear regression and Bland-Altman analysis of the per-pixel velocities as well as the mean velocities in the ROIs. Correlation coefficients, linear fittings, mean differences and 95% limits of agreement were calculated. Normalized root-mean-square errors (NRMSE) of the flow velocities measured in the undersampled data sets compared to those obtained with the reference were defined as NRMSE = ||v_ref − v_unds||₂/||v_ref||₂, where v_ref and v_unds are the flow values obtained with fully sampled and undersampled data sets respectively, and ${\Vert \overrightarrow{x}\Vert }_2=\sqrt{{|x(1)|}^2+\cdots +{|x(n)|}^2}$ is the Euclidean norm. Pathline visualization was generated with commercial flow visualization software EnSight (EnSight 9.2 CEI, USA), and the length of the pathlines was measured for each acceleration method.

Figure 3.

4D data sets from the aorta. a) Magnitude and b–d) flow images reconstructed with the fully sampled data set and undersampled data sets with vPDS using STIRRUP, zfSPIRiT and iiSPIRiT reconstructions. Flow velocity profiles across the AA and DA (dashed line) are plotted through time (e).

3. Results

All scenarios were evaluated with a fixed acceleration factor of 6.

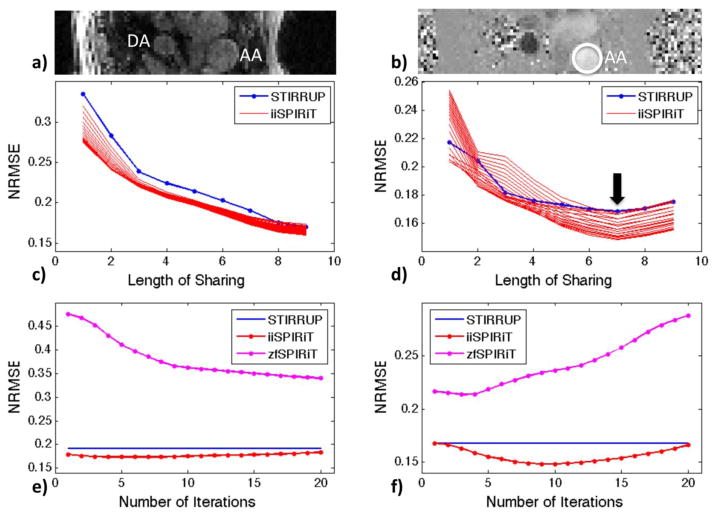
The normalized root-mean-square error for both magnitude and velocity images reconstructed with STIRRUP, zfSPIRiT and iiSPIRiT, were calculated to evaluate the effect of the length of sharing on STIRRUP, and the effect of the number of iterations on SPIRiT (Figure 2). The level of the selected slice corresponds to the dashed line in Figure 3b. For magnitude images, the error gets smaller when more data is shared (Figure 2c), however, the error of the mean velocity measured within the ascending aorta gets higher after a certain length of sharing (Figure 2d). In Figure 2d that length of sharing is seen to be L=7 (15 time frames), which was chosen for evaluating errors with different number of iterations for SPIRiT. For the magnitude image (Figure 2e), zfSPIRiT has a larger error (>34%) and converges slower than the iiSPIRiT method whose error stays relatively flat through the iterations (<18%). For the velocity image (Figure 2f), the errors of the mean velocity measured within the ascending aorta with SPIRiT increase with increasing iterations, due to the sensitivity to noise or error accumulation through the iterations. This suggests using a small number of iterations (N<10) for flow imaging with SPIRiT.

Figure 2.

Cross-sectional view of the Ascending Aorta (AA) and Descending Aorta (DA) for: a) Magnitude image, and b) velocity image. Normalized root-mean square errors (NRMSEs) versus length of sharing for: c) magnitude images; and d) through-plane mean velocities within AA. The group of curves with iiSPIRiT (c&d) corresponds to different numbers of iterations (1 to 20). NRMSEs versus number of SPIRiT iterations for: e) magnitude images; and f) through-plane mean velocities within AA. The identified optimal view sharing length of L=7 (15 time frames) was used in e&f.

Image reconstruction and evaluation were successfully applied to all subjects. Figure 3a–d shows representative magnitude and flow images for one of the subjects, at the time frame with the peak aortic velocity, obtained with the fully sampled data set and with the vPDS data set (R=6) reconstructed with STIRRUP, zfSPIRiT and iiSPIRiT respectively. Since the acceleration factor R=6 exceeds the number of coils (N_c=5), noticeable artifacts are present in the magnitude images obtained with conventional parallel imaging (zfSPIRiT.) In contrast, the STIRRUP and iiSPIRiT results have less noticeable artifacts. The maintenance of temporal information was visually assessed by creating profiles at one location and plotting those through all time frames. It was selected as a cross-section across both the AA and DA (dashed line in Figure 3b). Lines through all the time frames are plotted together to form the profiles shown in Figure 3e. The red pattern (high velocities) refers to AA, and the blue pattern (low velocities) refers to DA. We observed that DA region with zfSPRiT had an obviously deformed shape compared to the other methods.

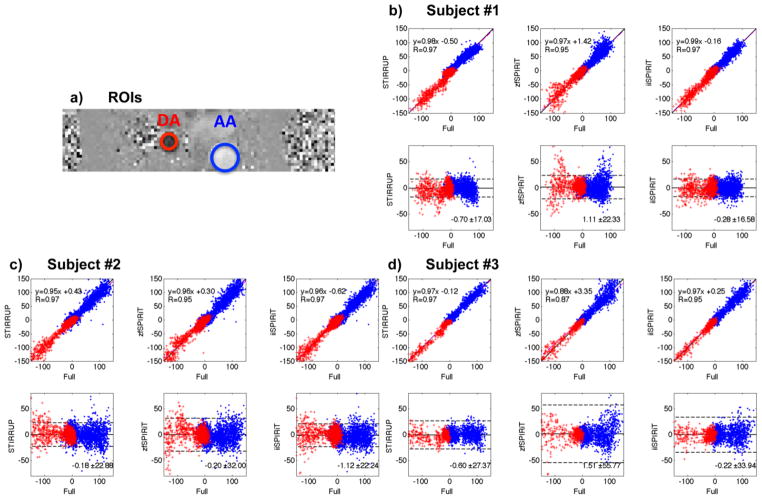
Quantitative comparisons between the different acceleration methods were performed by assessing per-voxel velocities and mean velocities in the five selected planes in the AA and DA (Figure 4a) through all times frames. For the per-pixel velocity assessment, linear regression and Bland-Altman analysis (Figure 4b–d) show that all acceleration methods correlate strongly with the reference (R≥0.95) except the zfSPIRiT method for the third subject (R=0.87). zfSPIRiT consistently has relatively wide limits of agreement, while iiSPIRiT has more narrow limits of agreement.

Figure 4.

Comparisons of per-pixel flow velocities in the AA and DA with different undersampling strategies. (a) ROIs through the AA and DA. (b–d) linear regression and Bland-Altman plots of the undersampled data with the fully sampled data of all subjects.

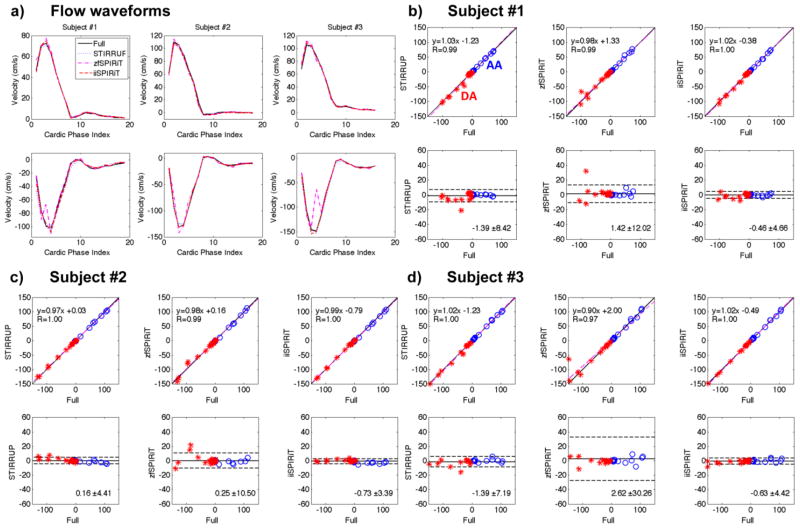
AA and DA flow-waveforms (mean velocity through time) for all subjects are plotted in Figure 5a. Since zfSPIRiT has more artifacts and tends to have more phase-wraps, outlier measurements can occur (lower row of Figure 5a). It should be noted that phase-unwrapping algorithms could be used to reduce the extent of such phase wraps. The errors of the flow-waveforms from all subjects were measured and analyzed (Figure 5b–d). zfSPRIT had the widest limits of agreement for all subjects because of phase degradation caused by the artifacts. The NRMSEs of the flow-waveforms of all subjects (both AA and DA) are plotted in Figure 6. The overall NRMSEs of different acceleration methods are 0.06 ± 0.04 (STIRRUP), 0.14 ± 0.10 (zfSPIRiT) and 0.04 ± 0.02 (iiSPIRiT), plotted at the last block of Figure 6 (standard deviation shown as error bars). Overall iiSPRIT had the smallest error and standard deviation. The AA flow measurement at the time-frame of peak flow was also analyzed; the mean difference and standard deviation compared to the reference was −2.56 ± 0.65 cm/s, 2.94 ± 2.87 cm/s, and −0.29 ± 2.56 cm/s for STIRRUP, zfSPIRiT and iiSPIRiT respectively. For all subjects, with STIRRUP, the peak flow measurements in the AA were all lower than the reference (difference: −1.98, −3.26 and −2.44 cm/s), indicating a slight but consistent temporal blurring effect.

Figure 5.

Comparisons of flow-waveforms in the AA and DA with different undersampling strategies.. a) Flow waveforms from all subjects. b–d) linear regression and Bland-Altman plots of the undersampled data compared to the reference. All acceleration methods have good correlations with the reference, especially the STIRRUP and iiSPIRIT methods. The bias data points were caused by the phase degradation due to artifacts with zfSPIRiT.

Figure 6.

The NRMSEs of the AA and DA flow waveforms obtained from three subjects. The overall errors are 0.06 ± 0.04 (STIRRUP), 0.14 ± 0.10 (zfSPIRiT), 0.04 ± 0.02 (iiSPIRiT).

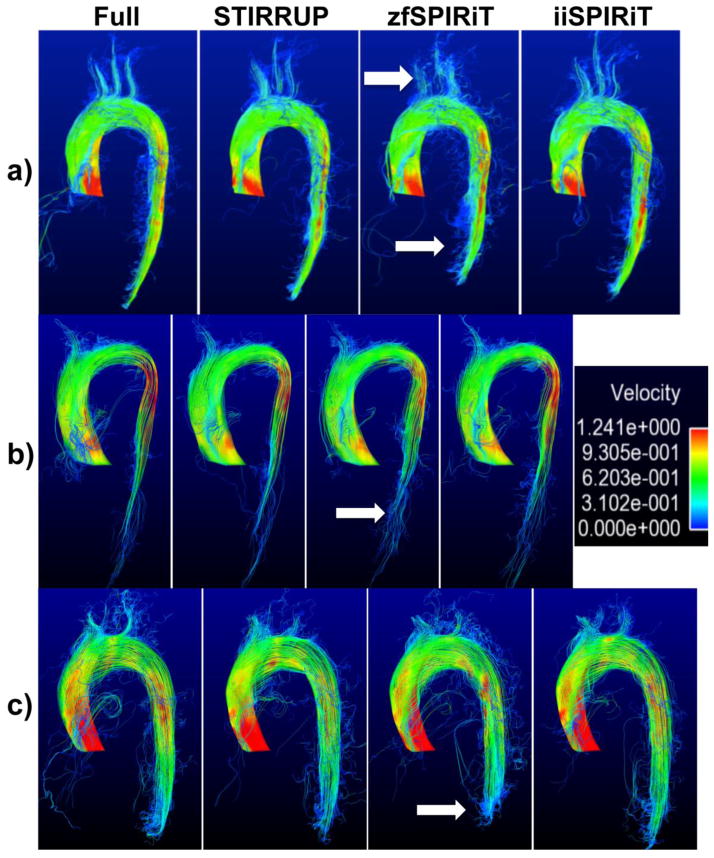
Pathline visualization was generated for all subjects (Figure 7). STIRRUP and iiSPIRIT provide clear pathline visualization, while zfSPIRIT had more errors and shorter pathlines. The relative length of the pathlines compared to that of the reference was measured as 95.6 ± 2.5%, 90.4 ± 2.6% and 96.8 ± 2.2% for STIRRUP, zfSPIRIT and iiSPIRiT methods respectively.

Figure 7.

Pathline visualization of the aorta of three subjects (a–c). zfSPIRIT has more errors and shorter pathlines (arrows).

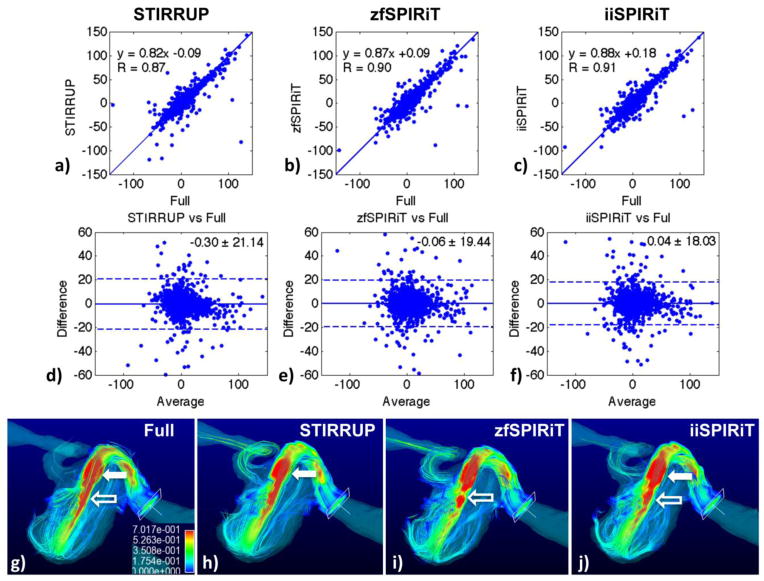
Figure 8 shows the results of the carotid aneurysm model. A cross-section through the phantom in the plane of the flow jet was selected for plotting the linear regressions and Bland-Altman analysis of the velocities within the aneurysm (Figure 8a–f). The high spatial frequency structure (flow jet) is maintained with all acceleration methods, STIRRUP has the lowest correlation (R=0.86), linear fitting (slope 0.82), biggest mean difference (−0.30 cm/s) and limits of agreement (21.14 cm/s) compared to the SPIRiT methods. The peak flow measurements at the jet of the aneurysm were 99.17 ± 22.69, 96.94 ± 36.90, 100.84 ± 25.30 and 99.05 ± 24.93 cm/s for the reference, STIRRUP, zfSPIRiT and iiSPIRiT respectively. The mean differences and standard deviations for the acceleration methods compared to the reference were −2.23 ± 19.37, 1.67 ± 9.87, −0.12 ± 9.05 cm/s for STIRRUP, zfSPIRiT and iiSPIRiT respectively. STIRRUP result showed a larger negative bias (underestimation) than iiSPIRiT (−2.23 vs −0.12 cm/s). Pathline visulizations of the phantom are shown in Figure 8g–j. Compared to the reference (Figure 8g), STIRRUP result (Figure 8h) has a visually smaller region of high velocities (in red, solid arrow) that corresponds to the reduced flow velocities (underestimation), and zfSPIRiT has flow discontinuities (Figure 8i, hollow arrow), while the iiSPIRiT result is closest to the reference.

Figure 8.

Evaluation in a carotid aneurysm model. a–f) Linear regression and Bland-Altman plots of per-pixel flow velocities with different acceleration methods compared to the fully sampled data. g–j) show pathline visualization with the different methods. Compared to the reference (g), STIRRUP (h) has a visually smaller region of high velocities (solid arrow) that corresponds to the reduced flow velocities (underestimation), and zfSPIRiT has flow discontinuities (i, hollow arrow), while the iiSPIRiT result is closest to the reference.

4. Discussion

In this study, we investigated an effective undersampling scheme and an efficient parallel image reconstruction method to achieve highly accelerated 4D flow CMR with high reconstruction accuracy. We have qualitatively and quantitatively demonstrated that with a limited number of coils (smaller than the acceleration factor), image quality and velocity accuracy with the conventional SPIRiT method was unsatisfactory. The view sharing method (STIRRUP) with the proposed undersampling scheme (time-resolved vPDS) appeared capable of generating aortic flow images comparable to that of fully sampled data and of further improving the image reconstruction with SPIRiT by providing an improved initial solution. For healthy subjects, the velocities within the AA and DA are relatively smooth, which is an ideal situation for view sharing methods. The flow phantom study demonstrated that high spatial frequency structures in the velocity images were reasonably maintained with all acceleration methods, although the STIRRUP and zfSPIRiT methods had underestimation or discontinuity errors. Overall, the iiSPIRiT method appears very accurate and reliable. This suggests that iiSPIRiT would work well for patients with aortic aneurysms or stenoses that cause abnormal flow patterns with high spatial frequency structures.

Although alternative ways of improving the initial solution of SPIRiT, such as using the reconstruction of an adjacent time frame [27], are not difficult to implement but may not make optimal use of the data throughout different time frames. For applications where changes over time are rapid in relation to the temporal resolution (intensity change, movements, and so on), the initial solution could cause bias and become ineffective. With random undersampling in the phase-slice encoding plane and temporal domain, the view share scheme STIRRUP is an easy but reliable way to generate a near-optimal estimation of the solution. Notice that the composite data sets obtained with STIRRUP may still have undersampled data. Although zero filling was used in this study, compressed sensing or parallel imaging could be applied to the composite data sets with increased computation cost.

Parallel imaging methods (SENSE or GRAPPA) [2, 3] have been used widely in MRI, however they usually achieve a modest acceleration factor of about 2 (and may go up to 4). As demonstrated by others, improved k-t methods combined with parallel imaging have great potential for achieving higher acceleration (5 to 8) with maintained accuracy [6, 9]. k-t methods also work for a small number of receive coils or even a single coil (without parallel imaging). The aforementioned methods generally require specific undersampling patterns in space and time domains. In this study, we proposed a generalized and flexible random sampling pattern in space and time, which is suitable for CS and SPIRiT (the latter was used in this study). Since we also exploited the k-t information, the achieved acceleration factor could even exceed the number of the receive coils with well maintained accuracy.

As shown in Figure 2c&d, the error with different length of sharing may have different trends for magnitude and phase images. This can be attributed to the fact that there are significant changes over time in the velocity images but not in the magnitude images and suggests that there is that an optimal length of sharing for achieving accurate velocity images. Images reconstructed with zfSPIRiT had more artifacts and tended to have more phase wrapping errors, which may cause outlier measurements (Figure 5). Phase-unwrapping could be applied to remove such phase-wraps (not used in this study).

Others have also recently demonstrated flow imaging with highly accelerated scan time [9, 14, 22]. In [14], a promising 2D acceleration technique achieved 6-fold acceleration with NRMSE of 2.59% for velocity measurements, mean difference and limits of agreement of −0.29 ± 4.96 cm/s for peak flow measurements. Our 4D method achieve the same acceleration with comparable errors: NMRSE of 0.04 and mean difference and standard deviation of −0.29 ± 2.56 cm/s.

The major limitations of this study include the small number of subjects and retrospective undersampling of the 4D flow data. For data analysis, we included all time frames and five different locations for measuring AA and DA of each subject. Future work includes more subject scans for improving statistical power, as well as prospective implementation of the undersampling scheme. In this study, we evaluated the acceleration methods on aortic flow imaging of healthy subjects as well as a carotid model with a flow jet. Notice that the purpose of the flow model experiment was not to generate an absolute match of in vivo aortic flow characteristics, but rather to test if highly variable spatial frequency structures are maintained with the acceleration methods. In this study we focused on a fixed acceleration factor of 6, aiming for 4D flow MRI scan times of 5 minutes or less. This was also based on current literatures on accelerated flow imaging, where a reasonable acceleration factor of 4 to 6 was chosen in different flow imaging studies. Similar to other methods that use fully acquired k-space center for coil calibration, around 10% center region of the k-space data is usually chosen. The larger the full k-space center region is, the better data fidelity is maintained, but the acceleration factor is reduced. In this study, for our image matrix size (k_y-k_z: 96×22), we intended to choose a slightly larger region 12×12 to keep data fidelity. In the future, we will investigate different acceleration factors and k-space center sizes, and also plan to acquire data with a larger number of coil elements. A combination of compressed sensing and k-t methods with parallel imaging will also be investigated. The current reconstruction is relatively slow and not ready for online use. Optimization of the programming would be expected to reduce the reconstruction time significantly. In MR flow imaging, there are a number of sources can results in errors in velocity measurements, including eddy current effects, Maxwell terms and gradient distortions, which need to be taken care of with the prospective implementation of the proposed acceleration method.

5. Conclusions

We employed undersampling patterns based on vPDS, a temporal sharing scheme STIRRUP, and parallel imaging SPIRIT to achieve 6-fold accelerated aortic 4D flow MRI with only five coils. Qualitative and quantitative evaluation of our preliminary results demonstrated that the time-resolved variable-density random sampling vPDS was efficient for highly accelerated 4D flow imaging using either STIRRUP, which while easy to apply might have a slight temporal compromise, or iiSPIRIT which had a higher computation cost but maintained high image reconstruction accuracy.