Pathways for virus assembly around nucleic acids

Abstract

Understanding the pathways by which viral capsid proteins assemble around their genomes could identify key intermediates as potential drug targets. In this work we use computer simulations to characterize assembly over a wide range of capsid protein-protein interaction strengths and solution ionic strengths. We find that assembly pathways can be categorized into two classes, in which intermediates are either predominantly ordered or disordered. Our results suggest that estimating the protein-protein and the protein-genome binding affinities may be sufficient to predict which pathway occurs. Furthermore, the calculated phase diagrams suggest that knowledge of the dominant assembly pathway and its relationship to control parameters could identify optimal strategies to thwart or redirect assembly to block infection. Finally, analysis of simulation trajectories suggests that the two classes of assembly pathways can be distinguished in single molecule fluorescence correlation spectroscopy or bulk time resolved small angle x-ray scattering experiments.

II. INTRODUCTION

In many virus families, the spontaneous assembly of a protein shell (capsid) around the viral nucleic acid (NA) genome is an essential step in the viral life cycle [1]. These families include most viruses with single stranded RNA (ssRNA) genomes, as well as the Hepadnaviridae (e.g. hepatitis B virus, HBV). Understanding the mechanisms which underlie this cooperative assembly process could facilitate efforts to develop anti-viral drugs that block or derail the formation of infectious particles (for reviews see [2, 3]) and promote efforts to reengineer them for biomedical delivery. In this article, we explore how the interactions between the molecular components determine the mechanism of assembly, and how these interactions can be altered by changing solution conditions or mutagenesis to modulate assembly pathways.

The most detailed knowledge of capsid-NA interactions comes from structural analysis of assembled viral particles. Atomic resolution structures of capsids assembled around ssRNA have been obtained by x-ray crystallography and/or cryo-electron microscopy (cryo-EM) (e.g. [4–16]). The packaged nucleic acids are less ordered than their protein containers and thus have been more difficult to characterize. However cryo-EM experiments have identified that the nucleotide densities are nonuniform, with a peak near the inner capsid surface and relatively low densities in the interior[7, 17, 18]. While atomistic detail has not been possible in these experiments, all-atom models have been derived from equilibrium simulations [19–21]. In some cases, striking image reconstructions reveal that the packaged RNA adopts the symmetry of the overlying capsid (e.g. [7, 10, 16, 22, 23]). While it has been proposed that this order arises as a function of the assembly mechanism for several viruses [24–26], computational analysis of polyelectrolyte configurations inside capsids also indicate that capsid-polymer interactions can generically drive spatial organization of the packaged polymer [20, 27–38]. Theoretical works have also characterized the relationship between the NA charge and structure and the length which is optimal for packaging [27, 31, 32, 38–45].

In addition to this structural data on assembled capsids, an extensive combination of mass spectrometry, assembly kinetics experiments, constraints from assembled capsid structures, and mathematical modeling has delineated assembly pathways for several viruses, with a particular focus on the role of interactions between CPs and specific RNA sequences called ‘packaging signals’. Recent single molecule fluorescence correlation spectroscopy (smFCS) experiments indicate that, for these viruses, assembly around the viral genome is more robust and proceeds by a different mechanism as compared to around heterologous RNA [46]. Yet, in other cases capsid proteins show no preference for genomic RNA over heterologous RNA (e.g. HBV [47]), and cowpea chlorotic mottle virus (CCMV) proteins preferentially encapsidate heterologous RNA (from BMV) over the genomic CCMV RNA with equivalent length [48]. Furthermore, experimental model systems in which capsid proteins assemble into icosahedral capsids around synthetic polyelectrolytes or other polyanions [49–61]) demonstrate that specific RNA sequences are not required for capsid formation or cargo packaging. Thus, a complete picture of capsid assembly mechanisms requires understanding how assembly pathways depend on those features which are generic to polyelectrolytes, as well as those which are specific to viral RNAs.

In previous work on assembly around a simple model for a polymer, Elrad and Hagan [37] proposed that mechanisms for assembly around a cargo (i.e. RNA, polymer, or nanoparticle) can be classified on the basis of two extreme limits. In the first (originally proposed by McPherson [62] and then Refs [20, 63]), strong protein-cargo interactions drive proteins to adsorb ‘en masse’ onto the cargo in a disordered manner, meaning there are few protein-protein interactions. Once enough subunits are bound, subunits undergo cooperative rearrangements (potentially including dissociation of excess subunits) to form an ordered capsid. This mechanism has been observed in recent simulations [37, 38, 63–65]. In the second limit, where protein-protein interactions dominate, a small partial capsid nucleates on the cargo, followed by a growth phase in which individual proteins or small oligomers sequentially add to the growing capsid. This class of pathways resembles the nucleation-and-growth mechanism by which empty capsids assemble [66], except that the polymer plays an active role by stabilizing protein-protein interactions and by enhancing the flux of proteins to the assembling capsid [37, 67, 68].

It is difficult to determine assembly mechanisms directly from experiments, due to the small size (≲ 10 of nm) and transience (~ms) of most intermediates. Observations in vitro suggest that both mechanisms may be viable. Kler et al. [69] used time-resolved X-ray scattering (trSAXS) to monitor simian virus 40 (SV40) capsid proteins assembling around ssRNA. The scattering profiles at all time points during assembly could be decomposed into unassembled components (RNA + protein subunits) and complete capsid; the absence of any signal corresponding to a large disordered intermediate suggests this assembly follows the nucleation-and-growth (ordered) assembly mechanism [69]. Other observations suggest that viruses can assemble through the en masse mechanism. Refs. [70, 71] found that in vitro assembly CCMV assembly was most productive when performed in two steps: (1) at low salt (strong protein-RNA interactions) and neutral pH (weak protein-protein interactions) the proteins undergo extensive adsorption onto RNA, then (2) pH is reduced to activate binding of protein-protein binding [70]. Similarly, a recent observation of capsid protein assembly around charge-functionalized nanoparticles found that assembly initially proceeded through nonspecific aggregation of proteins and nanoparticles, followed by the gradual extrusion of nanoparticles within completed capsids [72]. These experiments used viral proteins with relatively weak protein-protein interactions (CCMV and BMV) [73] and moderate salt concentrations (100–150mM). The Kler et al. [69, 74] experiments considered SV40 proteins, which have strong protein-protein interactions [73], and high salt (250mM) Together, these in vitro experiments suggest that productive assembly could proceed by either the en masse or nucleation-and-growth mechanism.

In this work, we use dynamical simulations to investigate the extent to which the assembly mechanism can be controlled by tuning solution ionic strength and protein-protein attractions. We extend a model that was recently used to calculate the thermostability and assembly yields of viral particles as a function of protein charge and nucleic acid (NA) length and structure. Those previous simulations found quantitative agreement between predicted NA lengths that optimize capsid thermostability and viral genome length for seven viruses [38]. Here, we perform extensive new simulations of assembly, in which protein-protein interactions, the sequence of charges in capsid protein-NA binding domains, and the solution ionic strength are varied. We find that, by varying these control parameters, the assembly mechanism can be systematically varied between the two extreme limits described above. Our results suggest that knowledge of protein-protein and protein-NA binding affinities may be sufficient to predict which assembly mechanism will occur, and we estimate relative protein-NA binding interactions for three viruses (based on non-specific electrostatic interactions). These findings suggest that assembly mechanisms can be rationally designed through choice of solution conditions and mutagenesis of capsid protein-protein interfaces and protein-NA binding domains. Finally, by calculating hydrodynamic radii and SAXS profiles associated with assembly intermediates, we show that assembly mechanisms can be distinguished by experimental techniques recently applied to virus assembly, respectively smFCS [46]) and trSAXS [69]. While the NA is represented by a linear polyelectrolyte in most of the simulations, we obtain qualitatively similar results when considering a model for base-paired NAs developed in Ref. [38].

III. RESULTS

To study how capsid assembly around a polyelectrolyte depends on the strength of protein subunit-subunit and subunit-polyelectrolyte interactions, we performed Brownian dynamics simulations with a recently developed model [38] (Figure 1). The capsid is modeled as a dodecahedron composed of 12 pentagonal subunits (each of which represents a rapidly forming and stable homopentamer of the capsid protein, which then more slowly assembles into the complete capsid, as is the case for SV40 in vitro around ssRNA [69, 74, 75]). This model was motivated by the observation [69, 74] that purified SV40 capsid proteins assemble in vitro around ssRNA molecules to form capsids composed of 12 homopentamer subunits. Though SV40 in vivo forms a larger capsid when assembling around its compacted, minichromosomal DNA genome [75], this 12-subunit capsid has provided the most precise experimental characterization of ssRNA-mediated assembly kinetics to date [69, 74], and may provide the opportunity to experimentally test our model predictions (see section 8).

FIG. 1.

(A),(B) Model schematic for (A) a single subunit, and (B) two interacting subunits, showing positions of the attractor (‘A’), Top (‘T’), and Bottom (‘B’) pseudoatoms, which are defined in the Model section and in the Methods. (C) (left) The pentameric SV40 capsid protein subunit, which motivates our model. The globular portions of proteins are shown in blue and the beginning of the NA binding motifs (ARMs) in yellow, though much of the ARMs are not resolved in the crystal structure [117]. Space-filling model of the generic subunit model (middle) and a pentamer from the PC2 model (right). For all simulation snapshots shown in this article, beads are colored as follows: blue=excluders, green=attractors, yellow=positive ARM bead, gray=neutral ARM bead, red=polyelectrolyte.

Model subunits are attracted to each other via attractive pseudoatoms at the vertices (type ‘A’) and driven toward a preferred subunit-subunit angle by repulsive ‘Top’ pseudoatoms (type ‘T’) and ‘Bottom’ pseudoatoms (type ‘B’) (see Fig. 1 and the Methods section). These attractions represent the interactions between capsid protein subunits that arise from hydrophobic, van der Waals, and electrostatic interactions as well as hydrogen bonding [1]). The magnitude of these interactions varies between viral species [73] and can be experimentally tuned by pH and salt concentration [1, 76, 77]. Here, the attraction strength is controlled by the model parameter ε_ss. To relate ε_ss to the free energy of dimerization, we have run a separate series of calculations, where in the absence of cargo, we find that the free energy of subunit of dimerization is g_ss = 5.0 – 1.5 * ε_ss (see SI section 12). Throughout this article energies are given in units of the thermal energy, k_BT.

Capsid assembly around nucleic acids and other polyelectrolytes is primarily driven by electrostatic interactions between negative charges on the encapsulated polyelectrolyte and positive charges on the inner surfaces of capsid proteins [1]. We consider a linear bead-spring polyelectrolyte, with a charge of e per bead and a persistence length comparable to that of ssRNA in the absence of base pairing. Positive charges on capsid proteins are located in flexible polymers affixed to the inner surface of the model subunit, which represent the highly charged, flexible terminal tails known as arginine rich motifs (ARMs) that are typical of positive-sense ssRNA virus capsid proteins (e.g., [16]). We will begin with a simple model capsid in which the ARMs consist of 5 positively charged segments. Below, we consider models that represent specific viruses, with ARMs that can be substantially longer (≲ 50 segments) and include neutral amino acids (and even acidic) amino acids in addition to basic residues.

Electrostatics are modeled using Debye-Hückel (DH) interactions, where the Debye screening length (λ_D) is determined by the ionic strength I as λ_D ≈ 0.3/I^1/2 with λ_D in nm and I in molar units. We consider monovalent salt, for which I is given by the salt concentration C_salt. Perlmutter et al. [38] showed that DH interactions compare well to simulations with explicit counterions for the parameter values under consideration; however, we note that the DH approximation is less accurate at lower salt concentrations. For example, the polyelectrolyte lengths that minimize the free energy of the assembled nucleocapsid (the thermodynamic optimal length) computed using the DH approximation or Coulomb interactions with explicit counterions are compared at several ionic strengths in Fig. S1. Furthermore, analysis of the free energy of uniformly charged spheres found strong agreement between DH and Poisson-Boltzmann electrostatics at moderate salt concentrations (≥ 100mM), but weaker agreement at ≤ 10mM [78]. We note that divalent ions can impact NA structure, and sufficiently large concentrations of multivalent ions modify the osmotic pressure of densely packed dsDNA within bacteriophage capsids [79]. However, inclusion of divalent ions (modeled with Coulomb interactions) at physiological relevant concentrations (5mM) had only a small effect on properties such as the optimal genome length (~ 10%) in our model system [38] (Fig. S1). The effect of base-pairing on the optimal length was also considered in that reference [38].

In [38] we demonstrated that the thermodynamic optimum length corresponds to the length which maximizes the finite-time yield. Therefore, we have calculated the thermodynamic optimal length for each salt concentration (supplementary figure S1) and for each dynamical simulation described here we have used the polyelectrolyte with the optimal length for the simulated salt concentration.

A. Kinetic phase diagram

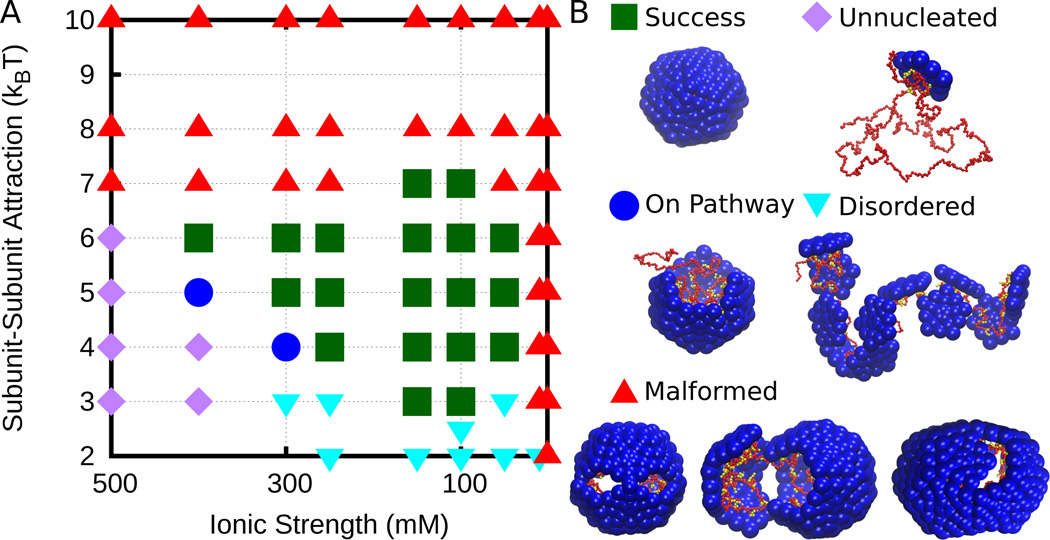
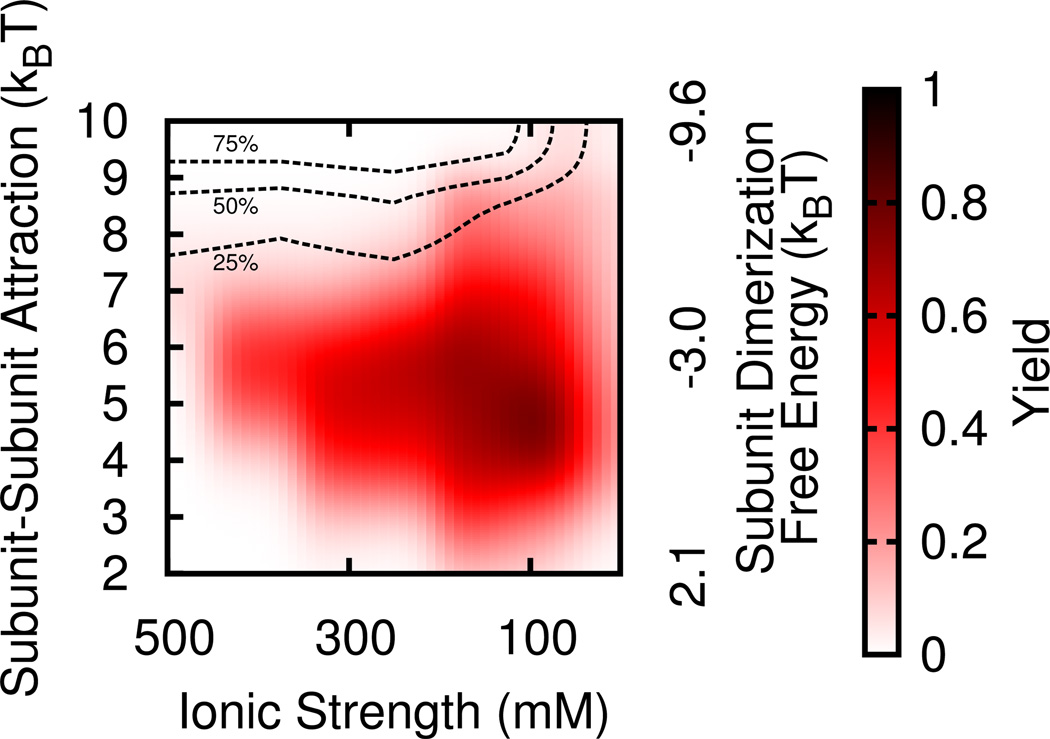
We first consider the predominant assembly products (Fig. 2) and the packaging efficiency (Fig. 3) as a function of Debye length λ_D and subunit-subunit interaction strength ε_ss. The packaging efficiency is defined as the fraction of trajectories in which the polyelectrolyte is completely encapsulated by a well-formed capsid, which contains 12 subunits each of which interact with 5 neighbors. We refer to this as a kinetic phase diagram [1, 80] because we characterize products at a finite observation time of t_f=2 × 10⁸ time steps, which is long enough that assemblages do not vary significantly with time (except for under weak interactions, see below), but is not sufficient to equilibrate kinetic traps if there are large activation barriers [1, 37]. We see that for the range of simulated ionic strengths (1 ≤ C_salt ≤ 500 mM or 10 ≥ λ_D ≥ 0.4 nm) assembly yields are highest for ε_ss=5k_BT and C_salt=100 mM (the parameter values focused on in [38]), and that for moderate subunit-subunit interaction strengths (4 ≤ ε_ss ≤ 6, k_BT) yield to remain high as the ionic strength is increased to about 300 mM (λ_D ≈ 0.6 nm). For higher salt concentrations, yields are depressed by the appearance of long-lived on-pathway intermediates. As will be discussed further below, weakening the electrostatic interaction between the polymer and protein limits the ability of the polymer to promote assembly. Although we expect that these simulations would eventually result in complete capsids, the low yield at our finite measurement time reflects the fact that assembly is less efficient than for lower salt concentrations. At the highest ionic strength considered (C_salt=500 mM), the most prevalent outcome is that no nucleation occurs. At lower salt concentrations (C_salt ≥ 10 mM), rapid adsorption of a super-stroichiometric quantity of subunits results in malformed capsids.

FIG. 2.

(A) Kinetic phase diagram showing the most prevalent final product at the conclusion of assembly simulations (t_f=2 × 10⁸ time steps). (B) Snapshots illustrating categories.

FIG. 3.

Kinetic phase diagram showing fraction of simulations which result in successful assembly of a complete capsid. The black isosurface lines show the fraction of subunits which are not adsorbed to the polymer and show any partial assembly, i.e. above the 75% line, ≥ 75% of the subunits not bound to the polymer are clustered.

At larger-than-optimal protein-protein interaction strengths (ε_ss > 6) assembly yields are lower for two reasons. The first, and more frequent outcome, is long-lived malformed structures with strained interactions. This kinetic trap arises in a wide variety of assembly systems when interactions become strong in comparison to the thermal energy, because strained interactions are unable to anneal before additional subunits lock them in place [1, 81, 82]. In our simulations, we found that these structures frequently result from an incorrect merger between two partial capsid intermediates; even when each individual interaction is too weak to lock-in the non-optimal structure, multiple erroneous interactions formed by two partial capsids are effectively irreversible on our timescale. The tendency for oligomer binding to lead to malformed structures was seen previously in the context of empty capsid assembly [80, 83]. Here, the polymer helps to bring oligomers together, and thus this trap arises when nucleation on the polymer is faster than growth of a nucleus into a complete capsid. This trap resembles Geminivirus particles, which are composed of a union of two nearly complete capsids [84].

The second obstacle to polyelectrolyte encapsulation arises at the highest protein-protein interaction strengths studied (ε_ss ≥ 8k_BT), for which subunits not associated with the polyelectrolyte undergo spontaneous assembly. The resulting off-polyelectrolyte assembly depletes the pool of available monomers and small oligomers available for assembly on the polyelectrolyte, leading to a form of the monomer-starvation kinetic trap previously discussed for empty capsid assembly [1, 66]. Triggering formation of empty capsids and thus preventing nucleic acid encapsidation by strengthening subunit-subunit interactions has been suggested as a mode of action for a putative antiviral drug for hepatitis B virus [85, 86].

At smaller-than-optimal protein-protein interaction strengths (ε_ss < 4) assembly is unsuccessful for two reasons, depending upon the ionic strength. At smaller values (C_salt ≤ 300 mM), electrostatic interactions are relatively strong, and many proteins adsorb onto to the polymer. However, because of the weak protein-protein interaction strength, these proteins do not form stable capsids, predominantly because nucleation is slow in comparison to t_f (the final observation time, t_f=2 × 10⁸ time steps). In a minority of cases, a nucleus will form, but completion is prevented by the excess number of subunits adsorbed to the polyelectrolyte. We refer to the resulting configurations as disordered, due to the lack of ordered binding between protein subunits. At larger ionic strengths (C_salt > 300 mM) electrostatic interactions are relatively weak, and individual subunits rapidly desorb from the polyelectrolyte. In this regime, assembly requires a fluctuation in the number of adsorbed subunits which leads to nucleation of a partial capsid intermediate which has enough subunit-polyelectrolyte interactions to be stable against rapid desorption. The nucleation rate decreases exponentially with subunit-subunit interaction strength [1, 68], and thus most simulations at high salt and weak subunit-subunit interactions never undergo nucleation. (We categorize simulations with fewer than 3 subunits adsorbed to the polyelectrolyte and no subunit-subunit interactions (i.e. no progress towards assembly) as ‘unnucleated’.)

Importantly, we expect that trajectories in this region of parameter space will eventually undergo nucleation. Thus, as the finite assembly time t_f is increased the region of successful assembly will expand to lower values of ε_ss and higher ionic strength, until eventually reaching values below which capsid assembly is thermodynamically unstable (see Fig. 7 in Ref. [80]). To confirm this possibility, we used the Markov state model (MSM) approach described in Ref. [65] to characterize assembly with ε_ss=5, 6 and C_salt=500 mM (see Fig. 4C and SI Fig. S5). In contrast, the malformed capsids encountered under large parameter values typically will not resolve on any relevant timescales, since numerous strong interactions would need to be broken [1]. Thus, the boundaries of successful assembly at large ε_ss values are insensitive to t_f.

FIG. 4.

(A) Snapshots from trajectories corresponding to the en masse and nucleation-and-growth (ordered) assembly mechanisms, at indicated parameter values. (B) The number of subunits adsorbed (n_ad) to the polyelectrolyte and the size of the largest cluster (n) are shown as a function of simulation time steps, averaged over all trajectories at the two sets of parameter values shown in (A). The labels ‘a’ through ‘e’ connect each structure pictured in (A) to its corresponding value of n_ad in (B). (C) Average values of n_ad and n are shown as a function of time step for parameters that lead to the nucleation-and-growth mechanism with a larger nucleation barrier than in (B).

Several additional conclusions can be drawn from the variation of packaging efficiency (Fig. 3). Firstly, the yield of complete virus-like particles is relatively high for moderate subunit-subunit interaction strengths ε_ss ∈ [4, 6] across a range of ionic strengths (C_salt ∈ [100, 300] mM). Even above (C_salt > 300 mM) and below (C_salt=10 mM) this range we observe moderate yields of complete particles. Secondly, as electrostatic interactions are weakened (moving to the left), the subunit-subunit interaction strength which optimizes the yield increases (i.e. from ε_ss = 5k_BT at C_salt = 100 mM to ε_ss = 6k_BT at C_salt : 150 – 400 mM to ε_ss = 7k_BT at C_salt = 500 mM). This result suggests that one interaction type can compensate for the other within a limited range. However, though all successful capsids contain the same subunit geometry, the mechanism by which they form depends on the relative interaction strengths, as discussed next.

B. Assembly mechanisms

As noted previously [1, 37, 63], pathways for assembly around a central core such as a polyelectrolyte can be roughly separated into two classes. In the first class (Fig. 4a), which we refer to as the ‘en masse’ mechanism, subunits first adsorb onto the polyelectrolyte in a disordered manner, followed by cooperative rearrangements to form an ordered capsid. In the second class (Fig. 4b), referred to as the nucleation-and-growth mechanism, a small partial capsid nucleates on the polyelectrolyte followed by the sequential, reversible addition of subunits or small oligomers until assembly completes. In contrast to the earlier models which considered a qualitative subunit-polyelectrolyte interaction, we study here how assembly pathways depend on the ionic strength.

To quantify the degree of order along assembly pathways, we record the total number of subunits adsorbed to the polyelectrolyte n_ad and the number of subunits in the largest cluster n. Trajectories that pass through configurations with a large value of n_free = n_ad – n are disordered, with many adsorbed subunits not participating in ordered assemblies. In Fig. 4, these quantities are shown as a function of time averaged over all simulation trajectories (leading to successful assembly or not), for parameter sets that respectively lead to the en masse mechanism (Fig. 4A) and nucleation-and-growth mechanism (Fig. 4B). In the first case, there are strong subunit-polyelectrolyte interactions (low ionic strength, C_salt=100 mM) and weak subunit-subunit interactions (ε_ss=3k_BT). Subunits therefore initially adsorb nonspecifically and form only transient subunit-subunit interactions, leading to a rapid rise in n_ad with n ≈ 0. Once enough subunits are adsorbed (~ 12 around an optimal-length polyelectrolyte for this model with a 12-subunit capsid), a cooperative fluctuation in subunit configurations eventually leads to a stable nucleus and then rapid completion of the ordered capsid geometry. Since this nucleation process is stochastic, there is a distribution of waiting times and thus a more gradual increase in the average cluster size n (see Fig. S3). We note that more than 12-subunits can adsorb onto the polymer. In some cases, typically under moderate subunit-polyelectrolyte interactions, these excess subunits are shed and well-formed capsids are assembled. Under stronger subunit-polyelectrolyte interactions, adsorption of excess subunits typically leads to ‘disordered’ assemblages (Fig. 2). In the nucleation-and-growth case, on the other hand, the subunit-polyelectrolyte interactions are weak (C_salt=300 mM) and the subunit-subunit interactions are strong (ε_ss=6k_BT). There is limited nonspecific subunit adsorption onto the polyelectrolyte, adsorbed subunits form relatively strong associations, and thus n_ad and n increase nearly in lockstep. Snapshots from typical trajectories for each of these parameter sets are shown in Fig. 4A.

To visualize the degree of order as a function of parameter values, we define a trajectory-averaged order parameter n̄_free, which is n_free averaged over all configurations with 4 ≤ n ≤ 6 and over all trajectories at a given parameter set[87]. Large values of this parameter (n̄_free & 5) indicate the en masse mechanism, while small values (n̄_free ≲ 2) indicate the nucleation-and-growth mechanism. As shown in Fig. 5, the degree of order generally increases with ionic strength and subunit-subunit interaction strength, with the most ordered assembly occurring at C_salt = 500 mM (where on average fewer than one subunit is adsorbed nonspecifically) and ε_ss = 6k_BT. However, notice that for ε_ss = 3 assembly is always disordered; for such weak subunit-subunit interactions the critical nucleus size is large and a high density of adsorbed subunits is required to achieve nucleation. On the other hand, for moderate subunit-subunit interactions we do not observe the extreme limit of the en masse mechanism even for low ionic strength. This observation can be explained by the fact that the en masse mechanism requires significant subunit adsorption to occur before cluster nucleation takes place. Though a low ionic strength drives strong nonspecific subunit adsorption, absorbed subunits collide frequently due to cooperative polymer motions and subunit sliding along the polymer [37, 67]. For ε_ss > 3 adsorbed subunits therefore achieve nucleation before nonspecific absorption has time to saturate at all ionic strengths considered.

FIG. 5.

Dependence of the assembly mechanism on the subunit-subunit attraction strength ε_ss and the ionic strength C_salt. The assembly order parameter n̄_free (the average number of adsorbed subunits not in the largest partial capsid) is shown as a function of parameter values. As described in the text, n̄_free ≲ 2 corresponds to ordered nucleation-and-growth assembly pathways, whereas larger values correspond to disordered pathways. The alternate y-axis shows the subunit-subunit dimerization free energy g_ss corresponding to ε_ss (see section VII B) and the alternate x-axis shows the linear adsorption density of subunits in the absence of assembly (see Fig. 6 below).

The nucleation-and-growth trajectories can be further classified based on the relative timescales of nucleation and growth. When nucleation is slow compared to growth (Figs. 4C and S5), the reaction is effectively two-state — each critical nucleus rapidly proceeds to completion, leading to low concentrations of intermediates which are essentially undetectable in a bulk experiment. When nucleation and growth timescales are comparable, multiple capsids within a spatial region can be assembling simultaneously, and thus potentially could be detected in bulk experiments. Below, we consider whether it is possible to experimentally distinguish between the latter case, ordered assembly with rapid nucleation, and en masse assembly pathways characterized by disordered intermediates.

Biological ARM sequences

The simulations described to this point demonstrate that the assembly mechanism depends on the subunit-polyelectrolyte binding affinity, which we have controlled by varying the solution ionic strength. However, while we have considered a simplified peptide ARM with five positive charges, the actual number and charges of amino acids in the ARM varies between viruses, which should also affect the binding affinity. Indeed, our previous equilibrium simulations demonstrated that the thermodynamic optimal length for encapsidation depends on the ARM amino acid sequence [38]. To place our results in the context of specific viruses, we calculated the polyelectrolyte binding affinity for subunits containing ARMs representing those of three viruses, SV40, Brome mosaic virus (BMV), and Porcine circovirus 2 (PC2). Specifically, the number and charges of beads in the simulated ARM was determined from the ARM amino acid sequence for each virus, with amino acids classified as neutral, cationic, or anionic. Each ARM sequence is shown in Table I, and Fig. 1C compares the ARMs of the simple model and the SV40 model. The binding affinity was estimated by setting the subunit-subunit attraction strength to zero (but keeping repulsive excluded volume interactions) and recording the equilibrium average number of adsorbed subunits at varying C_salt (or Debye length λ_D).

TABLE I.

Amino acid sequence of ARMs investigated in Fig. 6. The secondary lines indicate whether model ARM segments are designated neutral (0), positively charged (+), or negatively charged (−).

Virus	ARM Amino Acid Sequence
SV40	mkmaptkrkgscpgaapkkpke
	0+0000+++00000000++0+-
BMV	mstsgtgkmtraqrraaarrnrwtarvqpviveplaagqgkaik
	0000000+00+00++000++0+000+000000-0000000+00+
PC2	mtyprrryrrrrhrprshlgqilrrrpwlvhprhryrwrrkng
	0000+++0++++++0+0+00000+++0000+0+++0+0+++00

The measured equilibrium linear densities of adsorbed subunits, c_eq, are shown as a function of C_salt in Fig. 6A–C. In all cases the linear density increases monotonically with decreasing C_salt; saturating at a maximum density. The simplified ARM has the largest binding affinity, despite having the lowest net positive charge (+5, 0 neutral segments) of the four species considered. Comparison with SV40 (+6, 14 neutral segments) and BMV (+9, 33 neutral segments) illustrates the expected result that that neutral segments decrease the binding affinity, particularly at high salt. The PC2 subunits, with net charge +22 demonstrate markedly different behavior, with significant subunit absorption at the highest salt concentration simulated (500 mM), but saturating at about 300 mM ionic strength due to subunit-subunit charge repulsions. Variations in adsorption density with subunit concentration are shown in Fig. S2.

FIG. 6.

Average number of subunits adsorbed to polymer (in absence of assembly), depending on Debye Length and ARM sequence. Comparison between simple, +5-ARM and SV40 (A), BMV (B), and PC2 (C). (D) n̄_free values obtained during assembly simulations are plotted for varying values of c_eq and subunit-subunit dimerization free energy for our simple 5-ARM assembly model (circles) and the SV40 model (squares). ARM net charge and total length: SV40 +6/22, BMV +9/44, PC2 +22/43.

Next, we investigated how the ARM sequence and its corresponding polyelectrolyte binding affinity affects assembly dynamics, by performing dynamical assembly simulations (with finite subunit-subunit attraction strength) for subunits with the SV40 ARM. Based on our analysis of the assembly dynamics for the simplified 5-ARM, we anticipated that the polyelectrolyte binding affinity (as measured by the equilibrium adsorption without subunit-subunit attractions) correlates to the assembly order parameter. To test this hypothesis, we plot the assembly order parameter n̄_free as a function of c_eq (controlled by varying C_salt), for several values of the subunit dimerization free energy (determined by ε_ss and C_salt) for the 5-ARM and SV40 models. Plotting against c_eq rather than C_salt (λ_D) allows us to overlay data from these two models while accounting for the differences in affinity due to ARM sequence described above. In support of the proposed link between binding affinity and assembly mechanism, we find rough agreement in the measured assembly order parameters between the two models. The results indicate that ARM sequence can significantly influence the assembly mechanism. For example, if we define n̄_free ≤ 2 as the nucleation-growth mechanism, Fig. 6D indicates that nucleation-growth occurs for $c_{\text{eq}}\le c_{\text{eq}}^{*}$ with the threshold value $c_{\text{eq}}^{*}=0.0375$ for ε_ss ≥ 2.5k_BT. From Fig. 6A–C, we can then identify the threshold values of ionic strength $c_{\text{salt}}^{*}$, above which the nucleation-growth mechanism will occur: $c_{\text{salt}}^{*}\approx 300\text{mM}$ for the 5-ARM and $c_{\text{salt}}^{*}\approx 175\text{mM}$ for the BMV and SV40 models; while PC2 is below the threshold value for all salt concentrations considered. This allows us to predict, for example, that recent experiments on SV40 assembly (at C_salt=250mM and observed strong subunit-subunit attraction) would have a very low n̄_free (~ 1), which is consistent with SAXS observations [69].

C. Experimental Observables

We now seek to provide experimental signatures through which the capsid assembly pathways discussed above can be distinguished. We focus on two experimental techniques which have recently been applied to respectively probe the formation of individual capsids and bulk assembly kinetics.

smFCS measurements on individual capsids can distinguish assembly mechanisms

Borodavka et al. [46] used single molecule fluorescence correlation spectroscopy (smFCS) to monitor the hydrodynamic radii R_H of nucleocapsid complexes during assembly of MS2 and STNV capsid proteins around cognate RNA or non-cognate RNA. Assembly around cognate RNA was characterized by either constant R_H or, in some trajectories, a collapsed complex followed by gradual increase until reaching the size of an assembled capsid. In contrast, assembly around non-cognate RNA led to an increase in R_H before eventually decreasing to the size of the capsid. The difference between these two behaviors can be attributed to sequence-specific ‘packaging signals’ on cognate RNA that interact with the capsid proteins. In this article we do not consider the effect of packaging signals (these will be considered in a subsequent article); instead, we consider whether the pathways described in the previous section can be distinguished by this experimental technique.

We estimated the hydrodynamic radii R_H for polymer-subunit intermediates using the program HYDROPRO, which has been shown to accurately predict R_H for large protein and protein-NA complexes [88]. The resulting R_H are shown during representative en masse and ordered assembly trajectories in Fig. 7E. We see that the complex R_H first increases as subunits adsorb onto the complex and then decreases as subunits assemble (Fig. 7E). However, the en masse mechanism leads to a much larger and longer duration increase in R_H, due to the extensive and long-lived disordered adsorption of unassembled subunits. The difference in R_H between en masse and ordered trajectories is conserved across their respective parameter ranges (see SI Fig. S4 for other trajectories), and also occurs for assembly trajectories around the model nucleic acid with intramolecular base-pairing developed in Ref. [38] (see SI Fig. S4C,F). These results suggest that smFCS can distinguish among the classes of assembly pathways observed in our simulations. They are consistent with an interpretation of the Borodavka et al. [46] results in which assembly around the non-cognate RNA proceeds via the disordered mechanism while packaging signals lead to an ordered mechanism.

FIG. 7.

(A),(B) Average polymer radius of gyration during assembly as a function of varying ε_ss with constant C_salt (A) and varying C_salt with constant ε_ss (B). (C),(D) Average polymer radius of gyration during assembly as a function of number of adsorbed subunits n_ad (C) and size of the largest cluster n (D) for parameters that lead to relatively disordered (squares) and ordered (circles) pathways. (E) Approximate average radius of hydration for representative ordered and disordered trajectories.

To further characterize the differences in polymer conformations between disordered and ordered assembly pathways, we show the polymer radius of gyration, R_g, during assembly trajectories in Fig. 7. In contrast to R_H, contributions of the capsid proteins are not included in R_g. While the results in Fig. 7 are averaged over multiple trajectories, example individual trajectories are shown in SI Fig. S3. In all cases of successful assembly, the polymer is gradually compacted from its free size into its encapsidated size. However, at fixed C_salt=100mM, the average rate of compaction increases with ε_ss, with a dramatic increase in rate for ε_ss > 3k_BT (Fig. 7A). Similarly, decreasing C_salt increases the rate of compaction (Fig. 7B). Notice that the rate of polymer compaction is not determined by the assembly mechanism | increased order correlates with faster compaction in Fig. 7A but with slower compaction in Figure 7B. When the R_g is plotted as a function of number of adsorbed subunits (n_ad), the en masse and ordered pathways clearly split into two groups (Fig. 7C). However, this distinction disappears when R_g is plotted as a function of the number of subunits in the largest cluster (n, Fig. 7D). Taken together, these data demonstrate that polymer compaction is driven by adsorbed subunits forming ordered intermediates, with the rate of compaction consequently mirroring the rate of capsid assembly.

trSAXS measurments of bulk assembly kinetics can distinguish assembly mechanisms

While smFCS can detect individual assembly intermediates, Kler et al. [69, 74] recently used time resolved small angle x-ray scattering (trSAXS) to elucidate structures of assembling capsids in bulk. They found that the SAXS profiles at all time points could be decomposed into scattering contributions from the unassembled and complete components, suggesting that assembly proceeded by an effectively two-state reaction with undetectable levels of intermediates (i.e. the nucleation-and-growth pathway with relatively slow nucleation). While it is evident that profiles from profiles from a two-state reaction can be decomposed in this way, we investigated the extent to which SAXS profiles from the other pathway classes (en masse or nucleatation-and-growth with rapid nucleation) can be distinguished from the two-state case.

First, Fig. 8A,B shows SAXS profiles calculated (using CRYSOL [89]) from simulation snapshots along ensembles of en masse and ordered assembly trajectories. For each parameter set, SAXS profiles are averaged over 6 time windows. In both cases, the first profile is dominated by scattering from free subunits (Fig. 8C) and the final time segment shows clear minima and maxima corresponding to the complete capsid (Fig. 8C). For comparison, Fig. 8C presents the SAXS profiles for ordered subunit clusters ranging in size from a single subunit (black) to a complete capsid (yellow). As the capsid grows distinct minima and maxima appear and become more pronounced. We note that the positions of the minima and maxima in the complete model capsid are similar to those observed experimentally for SV40 [69].

FIG. 8.

SAXS profiles for (A) the nucleation-and-growth (ordered) and (B) the en masse (disordered) assembly mechanisms, at indicated parameter values. Simulations were divided into six segments of equal length to describe time evolution from beginning (1) to completion (6). (C) Scattering of subunit clusters from 1 subunit (black) to a 12 subunit capsid (yellow). (D,E,F) Best fit to SAXS profiles at an intermediate time (line 2 in (A,B)) assuming two-state kinetics (a linear combination of complete capsid and unassembled subunits) for ordered (D), disordered (E), and ordered with rate-limiting nucleation (F).

To test the extent to which these trajectories can be distinguished from the two-state case, we attempted to fit SAXS profiles using a linear combination of the profiles for unassembled polymer and subunits and the complete capsid. The resulting fits for the second fifth of the trajectory (where intermediates are most plentiful) are shown in Figs. 8D–F. At this stage, the ordered systems contain mostly incomplete subunit clusters (6–11 subunits), while the disordered simulations contain mostly adsorbed but unassembled subunits. For the ordered simulations, we find that the fit reproduces all of the features of the intermediates, except at low q. In contrast, the intermediates in the disordered trajectory display a shoulder at q ~ 0.3nm⁻¹ that is not observed in any of the unassembled or assembled components. This shoulder is a distinct feature of the disordered intermediate, and thus could be used to identify this class of pathways. Finally, as expected, SAXS profiles from trajectories at parameter sets (Fig. 4C) which lead to two-state kinetics are very well fit by a linear combination of polymer/subunit and complete capsid (Fig. 8F).

A significant distinction between the SAXS profiles is that the ordered pathways lead to an isosbestic point at q ~ 0.3nm⁻¹ (as seen in SV40 experiments[69]), whereas the disordered pathways do not. The presence of an isosbestic point is frequently assumed to indicate two-state behaviour; however, it occurs in our data for ordered trajectories even when the reaction is far from two-state due to rapid nucleation. In these cases the isosbestic point appears due to due to the similarity in scattering from the ordered intermediates and the complete capsid. This suggests that an isosbestic point may distinguish ordered from disordered assemblies, but is less sensitive to the extent to which the reaction kinetics can be approximated as two-state (i.e., how undetectable the intermediate concentrations are).

IV. DISCUSSION

Our simulations demonstrate that capsid assembly around a NA or other cargo can proceed through two mechanisms, and that which mechanism occurs depends on the relative strengths of protein-protein and protein-cargo interactions. The assembly mechanism can be rationally designed by tuning these interactions through solution conditions or mutagenesis of capsid protein-NA binding domains. However, because productive assembly requires weak interactions, the parameters must be tuned within relatively narrow ranges, and alterations which increase (decrease) the strength of one type of interaction must be compensated by a decrease (increase) in the other. Our results suggest that the subunit-cargo dissociation constant is an important parameter, whose value might be used to map specific viruses onto our phase diagrams (Figs. 2, 3, 5), although experimental tests of this capability are required. Finally, we have shown that the nature of assembly pathways can be inferred from the results of recently developed techniques to monitor the assembly of individual capsids or bulk assembly kinetics.

System-dependence of model predictions

An important consideration is to what extent results from this model can be extrapolated to other systems. First, while we have considered the smallest relevant icosahedral capsid geometry (12 pentameric subunits [69, 74]), viruses can assemble from much larger numbers of subunits. However, previous simulations using more simplified models for assembly around polymers or nanoparticles with 20 or 30 subunits observed similar assembly outcomes and also observed the two classes of assembly mechanisms described here [37, 63]. In fact, the en masse and nucleation-and-growth mechanisms can be more easily distinguished for larger capsids, where there can be more adsorbed-but-unassembled subunits and thus a wider range of n_free values. A second factor is the role of interactions between capsid proteins and specific NA sequences [90]. We have performed additional simulations in which model subunits interact with specific sites (‘packaging signals’) on the polyelectrolyte. We find that, while introducing packaging signals can change which assembly mechanism occurs at a specific set of parameter values (i.e. ionic strength and subunit-subunit interaction strength), over the range of relevant parameter values both mechanisms can be observed in the presence of packaging signals. These results will be described in a subsequent article.

The previous arguments suggest that the qualitative trends predicted from our simulations can apply to a wide range of systems. However, the simulations presented here demonstrate that the assembly mechanism and assembly outcome are determined by a balance between different interactions (subunit-polyelectrolyte, subunit-subunit) and different timescales (adsorption, assembly). Thus, predicting the quantitative location of boundaries between different assembly outcomes and different assembly mechanisms in the phase diagrams (Figs. 2, 3, and 5) will require calculating several biophysical parameters in addition to solution conditions. For example, we have shown here that changing the ARM sequence changes the thermodynamic polyelectrolyte binding affinity and thus alters the ionic strength at which the mechanism changes from en masse to nucleation-and-growth (Fig. 6). Factors which change timescales include subunit diffusion constants, subunit-subunit association rates, allosteric or autosteric subunit conformational changes [2, 91], and the number of subunits in a complete capsid (which controls the adsorption timescale and the timescale for a nucleated capsid to grow to completion).

Relationship between model predictions and experiments or potential future experiments

Our simulations predict that a single viral species can be driven to assemble via different mechanisms in vitro by changing solution conditions. In particular, under a constant subunit-subunit binding energy (ε_ss ~ 5–6k_BT) robust assembly occurs for a range of solvent conditions, with highly ordered or disordered assemblies occurring depending on salt concentration (C_salt ∈ [50, 400] mM). To our knowledge, this prediction has not yet been realized experimentally, although the signatures of the two classes of assembly pathways have been seen in experiments on different viruses and/or different cargoes [46, 69–72].

One recent experimental study sought to test the role of of C_salt and subunit-subunit attractions (controlled by solution pH) on in vitro assembly of CCMV around RNA [70]. In some regards, these experiments mirror our observations, with malformed capsids observed for strong subunit-subunit attractions, disordered products for weak subunit-subunit attractions, and well-formed capsids at intermediate conditions. However, robust assembly was only observed for a two-step process: first C_salt was reduced (from 1M) to drive RNA-subunit interactions, and then secondly pH was reduced to activate subunit-subunit attractions. The resulting assembly pathways resemble the en masse mechanism described here. On the other hand, one-step assembly led to malformed particles even at moderate pH, suggesting an inability to assemble through a nucleation-and-growth mechanism in these experiments. In our simulations, this outcome would only occur at high salt concentrations (e.g. C_salt ∈ 400 – 500mM, see Figs. 2, 3), where the narrow range of ε_ss leading to successful assembly indicates that parameters must be finely tuned. Reproducing such a lack of successful assembly at moderate salt concentrations would require a reduction in the orientation-dependence of the subunit-subunit interaction potential (see Methods), or introduction of additional factors as discussed below. Experiments in which solution conditions are changed for other viruses which do undergo one-step assembly (e.g. SV40 [69, 74]), may elucidate which of these possibilities to pursue and would directly test our prediction that the assembly mechanism can be controlled by solution conditions.

Understanding capsid assembly mechanisms and their location within the assembly phase diagram has important implications for the design of antiviral agents. As one example, we consider the recently developed class of HBV inhibitors based on phenylpropenamides [85, 86], which act by increasing the strength of subunit-subunit interactions, driving subunits to assemble in the absence of their genome and thus increasing the generation of empty, non-infective capsids [85, 86]. Comparing Figs. 3 and 5 shows that a virus that undergoes ordered assembly (e.g. ε_ss ~ 6 – 7, C_salt ≤ 300 mM), sits close to parameters that support empty capsid assembly, which are demarcated by dashed lines in Fig. 3. Thus only a small increase in subunit-subunit interactions is required to trigger unproductive RNA-free assembly. In contrast, a much larger perturbation would be required to achieve empty capsid assembly for a virus that assembles via the en masse mechanism.

Outlook

We have described two classes of assembly pathways and several distinct failure modes (Fig. 2) that arise when assembly is driven by nonspecific electrostatic subunit-cargo interactions. Our phase diagrams can serve as a starting point to understand how virus-specific features, such as packaging signals [90], allosteric NA-induced [9, 74] or ‘autosteric’ protein-induced conformational changes [91], base pairing-induced NA-structure [38, 46, 92], coordination between assembly and RNA replication [93, 94], or subcellular localization [95] can robustly avoid failure modes amidst the crowded intracellular milieu while enabling selective assembly around the viral genome [23, 94, 96]. For example, allosteric or autosteric conformational changes may allow for strong subunit-subunit interactions on the NA while avoiding the off-cargo assembly we observe at large ε_ss. Systematically studying how these additional factors expand (or contract) regions of parameter space that lead to successful assembly will ultimately reveal how viruses have optimized their structures and interactions for robust assembly in vivo and how their assembly in vivo or in vitro can be manipulated for biomedical or materials science applications.

V. METHODS

Model

We have recently a presented a complete description of our model system, which we summarize here briefly [38] and in the SI. Our model subunits are based upon that previous used to simulate assembly of empty capsids [97–99] which we extended previously to model assembly around cargo [38]. The pseudoatoms in the capsid subunit model are illustrated in Fig. 1. Subunit assembly is mediated through an attractive Morse potential between Attractor (‘A’) pseudoatoms located at each subunit vertex. The Top (‘T’) pseudoatoms interact with other ‘T’ psuedoatoms through a potential consisting of the repulsive term of the Lennard-Jones (LJ) potential, the radius of which is chosen to favor a subunit-subunit angle consistent with a dodecahedron (116 degrees). The Bottom (‘B’) pseudoatom has a repulsive LJ interaction with ‘T’ pseudoatoms, intended to prevent ‘upside-down’ assembly. The ‘T’, ‘B’, and ‘A’ pseudoatoms form a rigid body [97–99]. See Refs. [37, 63, 64, 80, 81, 99–111] for related models.

To model electrostatic interaction with a negatively charged NA or polyelectrolyte we extend the model as follows. Firstly, to better represent the capsid shell we add a layer of ‘Excluder’ pseudoatoms which have a repulsive LJ interaction with the polyelectrolyte and the ARMs. Each ARM is modeled as a bead-spring polymer, with one bead per amino acid. The ‘Excluders’ and first ARM segment are part of the subunit rigid body. ARM beads interact through repulsive LJ interactions and, if charged, electrostatic interactions modelled by a Debye-Hückel potential. We note that repulsion between subunits due to the positive charges does affect the magnitude of the subunit-subunit interaction. Previously, we estimated this repulsion contributes 1k_BT to the dimerization free energy [38]. This contribution (and entropic terms) are not included in ε_ss, which is the magnitude of the Morse potential depth. See SI section VII B) for a discussion of binding free energies.

Simulations and units

Simulations were performed with the Brownian Dynamics algorithm of HOOMD, which uses the Langevin equation to evolve positions and rigid body orientations in time [112–114]. Simulations were run using a set of fundamental units. The fundamental energy unit is selected to be E_u ≡ 1k_BT. The unit of length D_u is set to the circumradius of a pentagonal subunit, which is taken to be 1D_u ≡ 5 nm so that the dodecahedron inradius of 1.46D_u = 7.3 nm gives an interior volume consistent with that of the smallest T=1 capsids. To calculate the thermodynamic optimal encapsidation length, we placed a very long polymer in or near a preassembled capsid, with one of the capsid subunits made permeable to the polymer and performed unbiased Brownian dynamics. Once the amount of packaged polymer reached equilibrium, the thermodynamic optimum length $c_{\text{eq}}^{*}\text{mM}$ was measured. We previously [38] found that this strategy closely matched that produced using the Widom insertion method [115] as applied to growing polymer chains [37, 116]. Assembly simulations were run at least 10 times for each set of parameters, each of which were concluded at either completion, persistent malformation, or 2 × 10⁸ time steps. This observation time was chosen based on the time after which assembly yields and outcomes change only logarithmically with time for most parameter values. For all dynamics simulations there were 60 subunits with box size=200 × 200 × 200 nm, resulting in a concentration of 12µM.

SAXS profile and hydrodynamic radius estimations

Small Angle X-ray Scattering (SAXS) analysis was performed using CRYSOL [89]. For this analysis the all-atom structure of an SV40 pentameric subunit [117] was aligned into the position of each coarse-grained subunit and the polymer was replaced with a carbon chain. We note that this entails significant simplification: segments of the protein which were not resolved in the crystal structure were not reconstructed and there is no optimization of structure at the all-atom resolution. We believe this approximation is suitable, given that our analysis is limited to the X-ray scattering profile in the small angle regime, which reflects ~nm scale structural features. Fitting of the scattering profiles was performed using least squares fitting. Hydrodynamic radius analysis was performed using HYDROPRO [88]. This program is capable of calculating the hydrodynamic radius of large protein complexes and protein-NA complexes. Our treatment of the polyelectrolyte chain in this analysis involves two approximations. The first is that we neglect the specific chemistry of their polyelectrolyte, instead treating it as an amino acid chain. Based on our observations, the R_H is dominated by the adsorbed capsid subunits and removing the polymer entirely from the R_H calculation has a minimal effect on R_H (see Fig. S4A). This suggests a more accurate representation of the polyelectrolyte would not qualitatively alter our conclusions. The second approximation is analyzing a flexible polyelectrolyte using an algorithm intended to calculate the hydrodynamics radius of ‘rigid’ molecules (such as globular proteins). However, there is a long precedent for applying the rigid body method to flexible polymers: in these cases an ensemble of conformations is generated, and the hydrodynamic radius is the ensemble average of the ‘instantaneously rigid’ conformations [118]. Note that in Fig. 7E we are presenting the average over many independent assembly simulations. Simulations were visualized using VMD [119].

Research Highlights.

• The spontaneous assembly of viral capsids is an essential step in the lifecycle of many viruses and provides a paradigm for efficient, high fidelity molecular self-assembly.

• Capsid assembly around a negatively charged substrate can proceed through two classes of pathways, depending upon the properties of the capsid proteins and solution conditions.

• We perform computer simulations which predict that these pathways can be distinguished using two different experimental techniques

• Assembly pathways and their sensitivity to control parameters may be an important factor in determining the effectiveness of anti-viral agents and engineered delivery vectors.