Computation of relative numerosity of circular dot textures

Abstract

To find out whether there are separate visual mechanisms for size, density, and numerosity computation in textures, we investigated the ability of human observers both to discriminate differences in numerosity between approximately circular textures and to decide whether the differences were due to a change in circle size or dot density. The standard texture always contained 64 irregularly spaced fuzzy dots of random contrast polarity. Dots were added or subtracted from the test pattern either by changing the dot density with the pattern size constant or the pattern size with density constant. Observers had to decide whether size or density had changed and whether the change was an increase or a decrease (mixed task condition). In a separate condition, they reported differences in numerosity (numerosity condition). Numerosity changes were more accurately reported when they were correlated with changes in size than with changes in density, arguing against a single mechanism for numerosity. Observers showed a bias toward reporting larger patterns as denser and vice versa. The data were consistent with a mechanism in which observers compute numerosity from size and density signals and decide whether size or density had changed by the signal detection theory MAX rule after transforming signals into z-values. Because thresholds were not significantly lower in the numerosity condition than in the mixed task condition, we conclude that the direct numerosity mechanism, if it exists, must be noisier than the mechanisms that respond to changes in size and density.

Introduction

There has been growing interest in the mechanisms for the computation of approximate visual numerosity using sparse textures, such as those illustrated in Figure 1, in adult humans (Burr & Ross, 2008; Dakin, Tibber, Greenwood, Kingdom, & Morgan, 2011; Durgin, 1995, 2008; Ross & Burr, 2010), in infants (Xu & Spelke, 2000), in animals (Brannon, Wusthoff, Gallistel, & Gibbon, 2001; Gallistel, 1989; Leslie, Gelman, & Gallistel, 2008), in functional magnetic resonance imaging studies (Piazza, Pinel, Le Bihan, & Dehaene, 2007), and even in single neurons for small (<10) numbers of objects (Nieder, 2005). Psychophysical experiments show that two regular shapes, such as circles, can be discriminated on the basis of the number of elementary objects they contain and that the threshold Weber fraction for this ability in adult humans of normal ability is in the region of 20% (Ross & Burr, 2010). What is less clear is how this is done. It is usually assumed, because of the speed with which large (<10) numbers can be discriminated and because of the adherence to Weber’s law, that the computation is not done by direct enumeration (Ross & Burr, 2010). But if not by enumeration, how? The way in which large numbers are measured in physics may provide a clue. In physics, numbers are dimensionless and are thereby distinguished from constants, which are measured along dimensions such as length (m) and temperature (K). For example, Avogadro’s number (~6.022 × 10²³) represents the number of elementary entities of a substance in 1 mole of that substance. Clearly, this very large number was not obtained by enumeration. Instead, it was established in the first instance as a ratio of the charge of 1 mole of electrons to the elementary charge. By suitable choice of two measurements having the same dimension, a dimensionless number can always be obtained as a ratio.¹

Figure 1. Examples of stimuli used.

The middle panel is a standard patch containing 64 dots of random contrast polarity randomly scattered within a notional circle of a 3.1° radius (150 pixel). The left-hand panel shows a stimulus with 32% fewer dots in the same area (density-varying trial). The right-hand panel shows more dots with the same density as the standard in a 18% larger area (size-varying trial).

The obvious way to measure the number of dots in a circle is to multiply the dot density (dimension m⁻²) by the area (dimension m²) and thus obtain a dimensionless quantity. It is known that both density (Barlow, 1978; Durgin, 2008) and area (Morgan, 2005; Nachmias, 2011) can be measured by human observers, so this is a plausible way to compute number. The fact that Weber fractions for number discrimination are no lower than for density (Ross & Burr, 2010) might seem to support this argument. However, Ross and Burr contradicted the density explanation with an experiment that compared density discrimination and number discrimination using the same kind of stimuli. The stimuli were dot clusters varying in size and dot density (Figure 1). Conditions of constant area, constant density, and constant number were randomly intermingled so that the observer had no way of knowing on a given trial whether to base a number decision on density or area. They argue that this would have made it hard for the observer to use density as a proxy for number. However, it is still the case that the observer could report a greater number when they see a greater density than the standard or when they see a greater area. Ross and Burr argue that this decision process would introduce greater noise into the computation of number. However, to determine what loss of accuracy this would produce, if any, requires a signal-detection model of the choice process, and that is the main purpose of the present article.

An ideal observer with access to a distinct numerosity mechanism should use it in preference to signals of size and density when the latter are independent, provided that it is not noisier. In the Ross and Burr (2010) experiment, only a single number pedestal was used, so density and size could not be independent. It is not possible with this design to determine whether observers are using a numerosity signal or signals of size and density. We used the same design. However, we also introduced a condition that forced observers to use size and density signals (mixed task condition). Specifically, density-varying and size-varying trials were randomly interleaved, and observers had four buttons to distinguish (a) test denser, (b) test less dense, (c) test larger, and (d) test smaller than standard. This was contrasted with the numerosity condition, in which observers had only to report the number difference between standard and test. If there were a direct numerosity mechanism, and if this mechanism were comparable in sensitivity to size and density mechanisms, observers would be expected to detect differences in numerosity more accurately in the numerosity condition than in the condition in which they had to distinguish changes in size from changes in density. In addition, we measured separately the thresholds for size and density discrimination.

We modeled all the data with an ideal observer that subtracted the signal in each of two independently noisy channels (size and density) from an internal memory reference and based the decision on which is more numerous, denser, or larger on the sign of the difference. The decision on the task “size versus density” was made when required by choosing the larger of the two (unsigned) differences.

Methods

Stimuli and procedure

Examples of stimuli are shown in Figure 1. Stimuli were presented on the LCD display of a MacBook Pro laptop computer with screen dimensions of 33 × 20.7 cm (1440 × 900 pixels) viewed at 0.57 m so that one pixel subtended a visual angle of 1.25 arcmin. The background screen luminance was 50 cd/m². Stimulus presentation was controlled by MATLAB and the PTB3 version of the Psychtoolbox (Brainard, 1997). On each trial, subjects saw consecutively two stimuli, which they were required to compare for number, density, or size. Each stimulus contained a number of fuzzy dots with a diameter of 10 arcmin and a Gaussian decline with a space constant of 2.5 arcmin. The dots were black (0.4 cd/m²) or white (300 cd/m²) with equal probability and were randomly scattered within a notional circle with a standard radius of 3.18 (150 pixels). The standard stimulus, which was always presented first for 0.5 s, contained 64 dots. The variable stimulus, which was presented second for 0.5 s, contained 64 ± 64·W dots, where W is a fraction between 0% and 100% in steps of 5%. The value of W on each trial was chosen by an adaptive procedure (Watt & Andrews, 1981) designed to obtain the 50% point (μ) and the standard deviation (σ) of the psychometric function efficiently by concentrating values of W at μ ± σ. There was a 0.75 s blank period before each stimulus, during which only a fixation point was presented in the center of the screen. The test and reference positions were separately offset from the fixation point to avoid interference by afterimages and to prevent the observer from using landmarks on the screen for size judgments. The offset was randomly selected in both x and y direction from a uniform distribution with a width equal to 60.75 of the circle radius.

On density-varying trials, the radius of the test was the same as the standard, and the density of dots covaried with their number. On size-varying trials, the density of the dots in the test was the same as in the standard, and the radius was adjusted to accommodate the greater or smaller number of dots at that fixed density. In the first conditions, size-varying and density-varying trials were presented as a single staircase in separate blocks, and observers made a binary choice: larger/smaller or denser/less dense. These experimental conditions are subsequently called size task and density task, respectively. In two further conditions, trials of varying density and varying size were randomly interleaved. In the mixed task, observers had four keys (up, down, left, and right arrows) to indicate whether the test was denser, less dense, larger, or smaller. In the numerosity task, the observers had to indicate whether the test had more or less dots than the standard numerosity discrimination. In the density, size, and numerosity task, observers had only two keys (the left and right arrows on the keyboard) as response options. Each observer completed eight sessions of all conditions. In the single stair condition (size task and density task), each session contained 128 trials, whereas in mixed task and numerosity task, two stairs with 128 trials each were interleaved, summing to 256 trials per session.

Subjects

A male high school student with no previous psychophysical experience (Observer 4) supplemented the observations made by experienced authors (Observers 1–3). Subject 2 was an uncorrected myope (−0.75D/−0.75D). The vision of the remaining subjects was normal or corrected to normal.

Data analysis and modeling

Individual psychometric functions for each subject, condition, and stair (density- and size-varying trials) were fit by cumulative Gaussian functions with parameters μ (50% point) and σ (standard deviation) using maximum-likelihood methods (Morgan, 2012). Confidence limits (95%) for the individual points on the psychometric functions and those for the fitted parameters of the psychometric functions were obtained by a bootstrapping procedure. The maximum likelihood values were used to generate 640 new psychometric functions by simulation of the exact experimental procedure. The central 95% of the fitted values were taken to define the confidence limits. The optimal parameters of the psychometric functions for all subjects and conditions are given in Table 1.

Table 1. The table shows for each condition and observer the mean (μ) and standard deviation (σ) of the fitted psychometric functions and the log likelihood of the fits (see black curves in Figure 3).

The fourth row for each observer shows the significance level (*: p < 0.1, **: p < 0.01, ***: p < 0.001) and χ² between the separate fits to size- and density-varying trials and for their combined fit. Single stair: separate density and size judgments in blocked density-varying and size-varying trials. Mixed task: interleaved size- and density-varying trials. Numerosity task: numerosity judgment of interleaved density and size trials.

	Single stair			Mixed task			Numerosity task
Obs	Dens		Size	Dens		Size	Dens		Size
1
μ	3.82		2.13	−0.33		0.18	−1.48		−0.86
σ	15.81		9.35	15.3		7.45	14.03		9.19
log(L)	242.66		182.44	225.77		154.30	302.30		255.28
χ2		11.68***			19.52***			7.33***
2
μ	0.16		2.65	2.96		1.90	2.47		1.49
σ	19.17		10.97	22.16		10.89	35.82		13.23
log(L)	257.65		192.77	277.41		202.06	280.38		239.73
χ 2		13.06***			18.08***			30.86***
3
μ	4.30		−0.81	6.18		2.76	4.93		2.90
σ	14.91		5.93	15.32		6.27	12.43		8.95
log(L)	246.69		160.44	243.58		144.33	205.70		178.59
χ 2		40.92***			33.39***			5.93**
4
μ	−2.41		−4.78	0.34		0.46	−2.34		−2.74
σ	14.19		9.52	14.00		9.45	11.41		15.15
log(L)	421.32		354.45	398.21		313.75	387.55		450.80
χ 2		18.89***			11.79***			6.71**

Signal detection models were fit to the data of a single subject under all experimental conditions. Details are given at the appropriate point in the article and in the Appendix.

Results

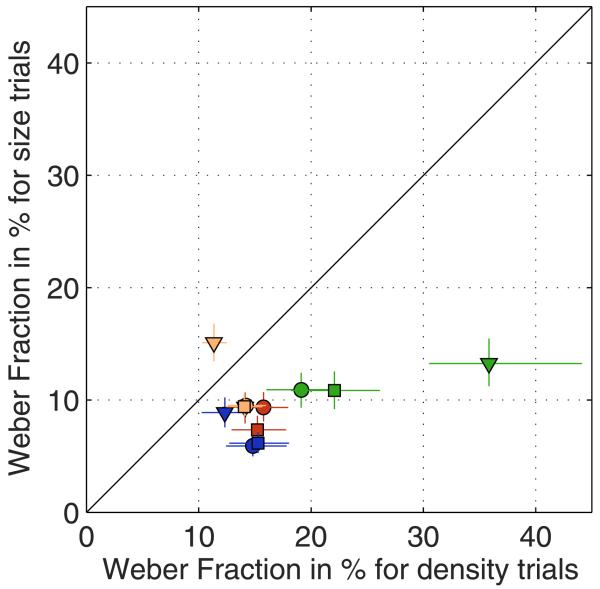
Figure 2 shows the thresholds in terms of Weber fractions from all experimental conditions, with Weber fractions on density-varying trials plotted against those on size-varying trials. Thresholds are expressed as the percentage change in dot number, whether it is accompanied by a size or density change. There is nothing to prevent the subject from using the numerosity cue in all tasks. However, it is immediately apparent from Figure 2 that thresholds on size-varying trials are lower than on density-varying trials, whether they are presented as single stair (density task and size task) or interleaved (mixed task and numerosity task) and whether the subject is explicitly discriminating size, density, or number. We made pairwise comparisons between size-varying and density-varying trials for each of the conditions separately by comparing the likelihood of a single psychometric function to all trials of one condition for a given observer with the sum of the likelihoods of the separate fits to the density- and size-varying trials of each condition and observer. To be sure that any differences were due to changes in accuracy rather than bias, we allowed the psychometric data from density-varying and size-varying trials to have different means but the same standard deviation. Hence, we compared three parameter fits (two μs and one σ) to four-parameter fits (two μs and two σs). In all conditions but one, Weber fractions for density-varying trials were significantly higher than Weber fractions for size-varying trials (df = 1, see Table 1). Only naïve Observer 4 showed, in the number discrimination task, a significantly higher Weber fraction on size-varying trials than on density-varying trials.

Figure 2. The figure plots thresholds on density-varying trials against those on size-varying trials.

Data for Subjects 1 to 4 are indicated by symbol colors red, green, blue, and yellow, respectively. The shape of the symbols indicates the experimental condition. Circles: single stair size- and density-varying trials (size and density task). Squares: size- and density-varying trials are randomly interleaved, and the subject has to indicate not only in which direction the test stimulus is changed but also whether it differs in size or density (mixed task). Triangles: size- and density-varying trials are randomly interleaved, and the subject has to indicate whether the test has more or fewer dots than the standard (numerosity task). The error bars represent 95% confidence limits estimated by bootstrapping.

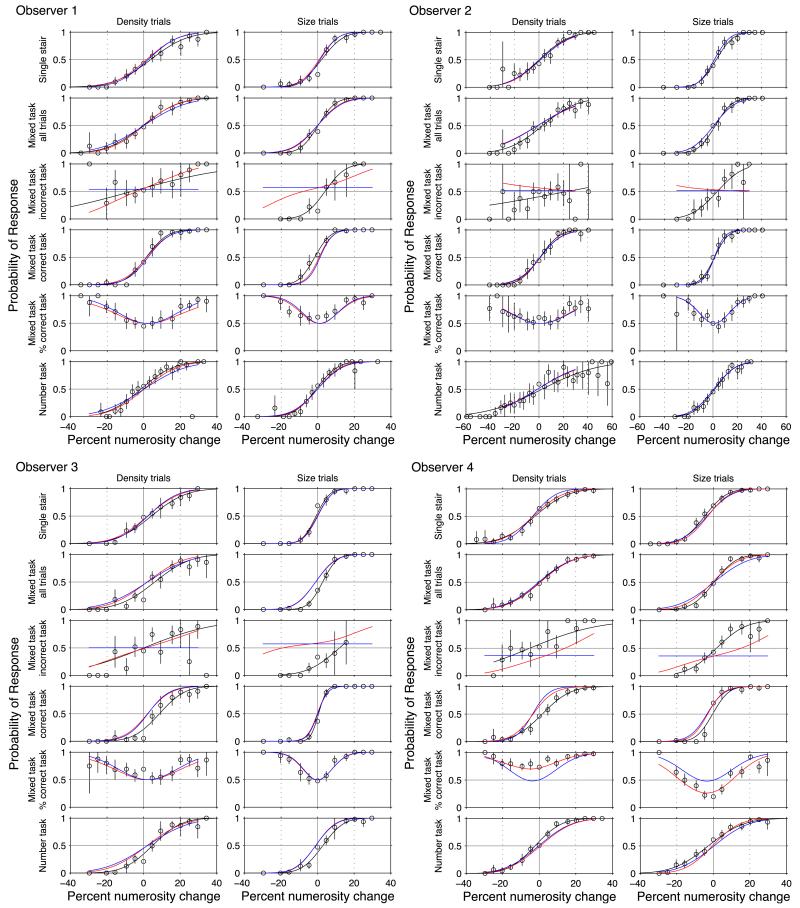
The psychometric functions under all conditions and the fits of various models are shown in Figure 3. To model the observer’s choice behavior we used a version of the signal detection theory MAX rule (Green & Swets, 1966; Morgan & Solomon, 2006; Palmer, Ames, & Lindsey, 1993; Palmer, Verghese, & Pavel, 2000), in which the observer monitors two noisy sources (size and density of the test patch in this case) and chooses the source that deviates most significantly from its reference value. Each source is described with the mean μ and standard deviation σ. Having chosen the source, the observer decides the response (which stimulus was larger/denser/more numerous) on the basis of the sign of the deviation. Details of the calculation are given in the Appendix. The blue curves in Figure 3 show the fits based on the four-parameter MAX model. It should be noted that this model for two channels gives identical results for the described experiment to a model in which the two signals are summed before the response on the direction of the change is made (Morgan & Solomon, 2006).

Figure 3. Each set of 12 panels shows the results from a different observer.

The vertical axis of the first four panel rows within each set show the probability of the response “denser” (left column)/“larger” (right column). The y-axis of the bottom-most panels depicts the probability of response “more.” Within each set, the top two panels show the psychometric functions of density-varying trials in the density task (left) and size-varying trials (right) in the size task. The panels in Rows 2 to 5 show the results on the mixed task when the size- and density-varying trials were randomly interleaved and the observer chose between four responses. Row 2 shows all trials under that condition. Row 3 shows the results when the observer chose the wrong task, for example, responded to density when the patches had a size difference. Row 4 shows results on trials when the observer chose the correct task. Row 5 shows the probability of correctly choosing the density task on density trials (left) and correctly choosing the size task on size trials (right). Row 6 shows the results of the numerosity task, when the density and size trials were randomly interleaved and the observer chose between two responses (“more” vs. “less”). The error bars show 95% confidence levels. The solid black curves depict two-parameter μ, σ fits to the individual psychometric functions (see Table 1). The blue curves show the best fits to all the data of the corresponding subject (including Row 5) of the four-parameter MAX model. The red curves for Observers 1 to 3 show the fit of a five-parameter model, identical to the four-parameter model but with the addition of a parameter accounting for the crossover between the size and density signals. The effect of the crossover parameter is evident in the slopes of the red curves in Row 3. The red curves for Observer 4 are the best fits of a six-parameter model that incorporates an additional sixth parameter accounting for the bias toward selecting the density response over the size response (Table 2).

Close inspection of the fits reveals important failures of this four-parameter MAX model. One is seen in the third row of Figure 3, which plots the psychometric functions for the mixed task for trials when the observer chooses the wrong task (density or size). The model predicts that these should be flat, but in general they are not. There is a trend toward getting the direction of the response (larger/denser or smaller/less dense) right, even when the wrong task has been chosen, that is, responding “denser” when the stimulus was larger, and vice versa. To account for this bias, a fifth parameter (crossover parameter) was added representing a fraction of the density signal crossing over into the size channel, and vice versa. The red curves for Observers 1, 2, and 3 show the fit of this model, which is noticeably different from the four-parameter fit (blue curves) only in trials in which the observer responded incorrectly (Row 3 of Figure 3). The likelihood ratio analysis in Table 2 shows the values of the fitted parameters and the significance of the improvement due to adding the fifth parameter. The improvement in fit was significant for Observers 1, 3, and 4 but not for Observer 2.

Table 2.

The first three tables show best-fitting parameter values for three models described in the text. Columns 1 denote the observer. Model A (first table) shows the parameters μ_Dens, σ_Dens, μ_Size, and the signal ratio of the four-parameter MAX model. Model B is supplemented by a crossover factor between size and density channels. Model C is further supplemented by a bias in the choice between size and density channels. The last columns show the log likelihood of each fit. The last table contains the results of a likelihood ratio comparison between two models indicated in Column 1 (four-parameter MAX model vs. five-parameter MAX model and five-parameter MAX model vs. six-parameter MAX model). For each observer, the values of χ² defined as 2[log(L_A) − Log(L_B)] and the significance levels (*: p < 0.1, **: p < 0.01, ***: p < 0.001) are shown. The modeled Weber thresholds r are represented in the slope of the blue and red psychometric functions in Figure 3. Similarly, μ is represented as the horizontal shift of the modeled psychometric functions in Figure 3. The influence of the crossover parameter is evident in the slope of the red curve in Figure 3, Row 3. The bias parameter accounts well for the vertical shift of Observer 4’s data in Row 5.

Model A
Obs	μ Dens	σ Dens	μ Size	Ratio	log(L)
1	1.39	7.66	1.28	1.70	1973.5
2	0.50	10.00	1.08	2.03	2087.1
3	1.12	6.21	0.07	2.09	1795.9
4	−3.84	10.59	−3.48	0.95	3416.2

Model B
Obs	μ Dens	σ Dens	μ Size	Ratio	Crossover	log(L)
1	0.92	8.05	0.77	1.72	0.20	1958.5
2	0.60	9.89	1.18	1.97	−0.04	2086.6
3	0.98	6.34	−0.14	2.21	0.11	1789.6
4	−3.40	11.69	−3.18	0.92	0.23	3398.8

Model C
Obs	μ Dens	σ Dens	μ Size	Ratio	Crossover	Bias	log(L)
1	0.91	8.03	0.77	1.73	0.20	0.01	1958.6
2	0.59	9.69	1.21	2.08	−0.03	0.09	2084.7
3	0.86	6.12	−0.19	2.43	0.13	0.14	1786.1
4	−2.53	9.62	−3.11	1.33	0.22	0.59	3277.7

Model Comparison
	Obs 1		Obs 2		Obs 3		Obs 4
	χ 2	Sig	χ 2	Sig	χ 2	Sig	χ 2	Sig
A vs. B	29.94	***	0.87	—	12.50	***	34.90	***
B vs. C	−0.17	—	3.91	*	7.00	**	242.20	***

Second, the four-parameter MAX model fails to account for biases in choosing for density changes versus size changes (Row 5 of Figure 3). For zero or small number differences between the standard and the test texture, this bias was strong in Observer 4, weaker in Observers 3 and 2, and virtually absent in Observer 1. To model this effect, we used a sixth parameter to account for the bias in choosing the task. The fit of this model to Observer 4’s data is shown by the red curve in Figure 3. The improvement over the five-parameter fit was significant (p < 0.001) for Observer 4, Observer 3 (p < 0.01), and Observer 2 (p < 0.05), but not for Observer 1 (p > 0.1).

Discussion

The results of the numerosity and density task agree in essentials with those of Ross and Burr (2010). Thresholds when size-varying and density-varying trials are randomly interleaved are generally no higher than when they are presented in single blocks.² Our additional findings are (a) thresholds for explicit size discrimination are lower than those for density, when expressed as changes in numerosity; (b) thresholds for size and density are no higher when observers have to distinguish them explicitly, rather than reporting numerosity; (c) thresholds in the interleaved conditions (mixed task and numerosity task) are similar to those predicted from a MAX model from signal detection theory; and (d) there is a bias toward reporting larger patterns as denser and vice versa.

An economical explanation of these facts is that observers in the mixed task respond to size and density cues independently, even when notionally responding to numerosity. We cannot rule out the existence of a third numerosity mechanism as suggested by Ross and Burr (2010), but if it exists, it cannot be more precise than density discrimination and is not being used on size-varying trials because these have lower thresholds expressed as dot number. Moreover, for three observers, the numerosity thresholds in size-varying trials was significantly lower than the threshold in density-varying trials in the number condition. Because a numerosity mechanism would not be sensitive to whether the numerosity changes are due to changes in size or density, these results conflict with a pure numerosity channel.

Ross and Burr (2010) argue that approximate numerosity is computed directly, neither by enumeration nor by combining other explicit measurements such as size and density. This does not leave a lot of alternatives. Direct matching to internal templates would be a possible mechanism for small number computation by neurons but is less plausible for large (>50) dot numbers. Ross and Burr argue that numerosity thresholds could not be derived from combining size and density because if they were, they would be higher than density alone. However, because it is variances rather than standard deviations that add under convolution, in the case where size and density thresholds are similar, numerosity thresholds would increase by a $\sqrt{2}$ factor relative to the size and density threshold. If density thresholds are double those for size, the increase in threshold for the joint computation would be only 1.118 relative to density threshold, which would require a large amount of data to detect. In any case, the factor by which numerosity thresholds exceed density is still unknown.

We find that observers tend to report larger stimuli as denser, and vice versa, which may be evidence for a numerosity cue that is independent of size and density, because the bias is in the direction of responding to numerosity rather than size and density. However, other interpretations are possible. A correlation between observed size and density has previously been reported by Dakin and colleagues (2011), who note previous reports of the same phenomenon. The correlation takes the form of larger stimuli appearing denser, and denser stimuli appearing larger, the same as the correlation observed in the present data. Dakin et al. (2011) interpret their findings with a model in which density is computed by ratios of energy in different spatial frequency channels. Here we suggest an alternative based on size constancy scaling (Thouless, 1972). Texture density gradients are well-established cues for depth, and higher densities are associated with greater distance. On average, further objects have smaller retinal sizes. There may thus be a negative correlation between size and density in natural images, which the visual system attempts to remove by decorrelation (Barlow & Földiák 1989). Thus, other things being equal, larger objects may be judged as having a higher density, the effect found by Dakin et al. (2011) and in the present experiment.

In conclusion, we propose that discrimination of numerosity can be based on size or density when these cues are correlated with number. For the stimuli used by Ross and Burr (2010), observers can decide which of two patterns has the higher numerosity by determining which one has the higher density and/or size. This could be done either by applying the signal detection theory MAX rule to the independent channels or by summing the two signals, which gives under our conditions an identical mathematical result (Morgan & Solomon, 2006). We cannot rule out the existence of a separate numerosity mechanism, either direct or based on the computation of size × density. The sensitivity of such a mechanism could be measured only with a true 2AFC design with roving number pedestals and independent perturbation of size and density. It remains to be determined what numerosity thresholds would be in such an experiment. However, it is interesting to note that Dakin et al. (2011), although they did not use a roving pedestal, interleaved blocks with nine different combinations of three levels of size. Under these conditions, thresholds for number discrimination were 40%, roughly four times higher than the Weber fractions we observed.

Appendix

MAX rule calculations

We assume initially that there are independent size and density channels and that the observer monitors only the appropriate channel when he or she is informed whether the trials were size varying (size task) or density varying (density task). We model a psychometric function plotting the probability of a large/denser response against the signed physical difference between standard and test. To avoid confusion, note that these are not the same as functions plotting the probabilities of a correct response. For example, the probability of a denser response varies from 0 to 1 as we vary the density difference between standard and test from strongly negative to strongly positive values.

Although observers were presented with a standard and a test stimulus in each trial, we do not use a true 2AFC model because the standard stimulus was always presented first (method of constant stimuli, e.g., Pfaffman, 1938) and could be ignored by the observer in favor of an internal standard (Green & Swets, 1966; Morgan, Watamaniuk, & McKee, 2000). Therefore, the signal m is assumed to be the signed difference between the test and a comparatively noiseless internal standard. The probability of a larger/denser response to a signal m is computed as the integral from −inf to m of a normal distribution with variance σ² and mean (m + μ), where μ is the observer’s bias. There is no late noise in the model.

The mixed task condition and the numerosity condition in which we interleaved two stairs are more complicated. In the mixed task condition, the observer had four buttons: denser, less dense, larger, and smaller. The purpose of the model is to compute the probabilities of all four responses. The proposed model assumes that the observer monitors two noisy sources, A and B, which would be the density and the size of the test stimulus in the described experiments, or vice versa. In our example, it is assumed that the signal is present in source A. The expected value of source B is zero. The observer measures the signed differences of A and B from the internal memory standard, which is assumed to be comparatively noiseless. The two noisy sources A and B contain Gaussian noise with variances σ_A² and σ_B². Any bias in deciding on the direction of change (first or second interval larger/denser/more numerous) is denoted as μ_A and μ_B. The model assumes that the observer decides whether size or density is different from the standard by determining which of the two noisy signals (in A and B) on a given trial has the larger absolute value (the MAX rule). At the same time, the sign of the Max signal is used to determine whether the difference is positive or negative.

To compute the probabilities of the four kinds of responses, we use the Gaussian probability density function

$$g(x;\mu ,\sigma ,m)=1∕\sqrt{2\pi {\sigma }^2}{e}^{\frac{-{(x-\mu -m)}^2}{2{\sigma }^2}}$$ (1)

and the corresponding cumulative density function

$$G(x;\mu ,\sigma ,m)={\int }_{-\infty }^{m}g(x;\mu ,\sigma ,m)$$ (2)

with μ and σ being the midpoint and the standard deviation of the probability density function. The external signal size is given as m, which can take on negative or positive values.

Consider now the two signal sources A and B (in our case, density and size, or vice versa) with noise variances σ_A² and σ_B² and means μ_A and μ_B, the first of which carries a signed signal m_A. Following Green and Swets (1966), we assume that each sensory event can be mapped on to a signed internal variable x. The probability that a sample of the source distribution carrying the signal m_A takes on the internal value x and that this has a larger absolute value than the sample from source B carrying no signal (m_B = 0) is given by

$$p_0(x,m)=g(x;{\mu }_A,{\sigma }_A,m_A)\cdot \left[G\right(x;{\mu }_B,{\sigma }_B,0)-G(-x;{\mu }_B,{\sigma }_B,0\left)\right]$$ (3)

Hence, the probability that any sample of source A has a greater absolute value than one from source B and that x > 0 is found by integrating p₀ over all positive values of x:

$$p_1\left(m\right)={\int }_0^{\infty }{p}_0(x,m)dx$$

For example, if m_A > 0, this would be the probability of deciding that the test is denser than the standard, when this is in fact the case.

The probability that a sample of source A carrying the signal has a larger absolute value x than the sample from the other source, meaning the signal source is correctly identified as A, and that x < 0 (for example, if m_A > 0 deciding that the stimulus is less dense when it is in fact denser) is found by integrating as follows over all negative values of x:

$$p_2\left(m\right)={\int }_{-\infty }^{0}g(x;{\mu }_A,{\sigma }_A,m_A)\cdot \left[G\right(-x;{\mu }_B,{\sigma }_B,0)-G(x;{\mu }_B,{\sigma }_B,0\left)\right]dx$$ (4)

The probability that a sample of source A takes on a smaller absolute value than a sample x from the distribution B and that x > 0 is found by integrating over all positive values of x:

$$p_3\left(m\right)={\int }_0^{\infty }g(x;{\mu }_B,{\sigma }_B,0)\cdot \left[G\right(x;{\mu }_A,{\sigma }_A,m_A)-G(-x;{\mu }_A,{\sigma }_A,m_A\left)\right]dx$$ (5)

Here, the signal m_A of source A is wrongly perceived as coming from source B. For example, p₃ could be the probability that a denser test was perceived as larger than the standard.

Finally, the probability that a sample of source A has a smaller absolute value x than the sample from source B and that x < 0 is found by integrating over all negative values of x as follows:

$$p_4\left(m\right)={\int }_{-\infty }^{0}g(x;{\mu }_B,{\sigma }_B,0)\cdot \left[G\right(-x;-{\mu }_A,{\sigma }_A,m_A)-G(x;-{\mu }_A,{\sigma }_A,m_A\left)\right]dx$$ (6)

Here, p₄ is the probability that the signal m_A is perceived as coming from source B and as being smaller than 0 (e.g., perceived smaller when it was denser).

From these four probabilities, which necessarily sum to unity, other probabilities can be calculated by simple addition. For example, the probability of a denser or larger response on density-varying trials is given by p₁ + p₃, where source A is density. The probability of correctly identifying the change as density in the mixed task condition is given by (p₁ + p₂) on density-varying trials.

In this way, we can calculate the probabilities for all the psychometric functions of Figure 3.

Row 1 of the figure shows the probability of denser/larger response in the density task (blocked density-varying trials, left panel) and size task (blocked size-varying trials, right panel) conditions.

Row 2 of Figure 3 shows the probability of larger/denser response in all trials of the mixed task condition calculated as p₁ + p₃ (with density on the left and size on the right).

Row 3 shows the data of trials in which the observer had chosen the incorrect task in the mixed task condition. Our four-parameter model (blue line) assumes the probability of a larger response when a size selection is made on density-varying trials (left panel) and the probability of a denser response when a density selection is made on size-varying trials (right) to be flat at a value predicted by the biases in the choice of the direction for size and density, respectively.

Row 4 in Figure 3 depicts the trials of the mixed task condition in which the observer had chosen the correct task. The probability of a denser response when a density selection is made on density-varying trials (left) and the probability of a larger response when a size selection is made on size-varying trials (right) is p₁/(p₁ + p₂).

Row 5 shows the probability of choosing the correct task: selecting a density response on density-varying trials (left) and a size response on size-varying trials, which is p₁ + p₂.

The bottom row of Figure 3 shows the data and model for the numerosity condition. Recall that in this condition, density-varying and size-varying trials are randomly interleaved, but the observer has only two buttons, to decide “more” or “less.” Because there is no numerosity channel in our model, we assume that the observer uses exactly the same MAX rule as in the mixed task condition and reports the sign of the Max source. Note that if a numerosity channel were available, it would be inefficient to monitor two noisy channels, unless the noise in the numerosity channel had greater variance than the sum of the variances in the size and density channels.