Variability in high-throughput ion-channel screening data and consequences for cardiac safety assessment

Abstract

Introduction

Unwanted drug interactions with ionic currents in the heart can lead to an increased proarrhythmic risk to patients in the clinic. It is therefore a priority for safety pharmacology teams to detect block of cardiac ion channels, and new technologies have enabled the development of automated and high-throughput screening assays using cell lines. As a result of screening multiple ion-channels there is a need to integrate information, particularly for compounds affecting more than one current, and mathematical electrophysiology in-silico action potential models are beginning to be used for this.

Methods

We quantified the variability associated with concentration-effect curves fitted to recordings from high-throughput Molecular Devices IonWorks® Quattro™ screens when detecting block of I_Kr (hERG), I_Na (NaV1.5), I_CaL (CaV1.2), I_Ks (KCNQ1/minK) and I_to (Kv4.3/KChIP2.2), and the Molecular Devices FLIPR® Tetra fluorescence screen for I_CaL (CaV1.2), for control compounds used at AstraZeneca and GlaxoSmithKline. We examined how screening variability propagates through in-silico action potential models for whole cell electrical behaviour, and how confidence intervals on model predictions can be estimated with repeated simulations.

Results

There are significant levels of variability associated with high-throughput ion channel electrophysiology screens. This variability is of a similar magnitude for different cardiac ion currents and different compounds. Uncertainty in the Hill coefficients of reported concentration-effect curves is particularly high. Depending on a compound’s ion channel blocking profile, the uncertainty introduced into whole-cell predictions can become significant.

Discussion

Our technique allows confidence intervals to be placed on computational model predictions that are based on high-throughput ion channel screens. This allows us to suggest when repeated screens should be performed to reduce uncertainty in a compound’s action to acceptable levels, to allow a meaningful interpretation of the data.

1. Introduction

Unwanted drug interactions with cardiac ion channels can lead to an increased pro-arrhythmic risk in the clinic (Roden, 2008). It is therefore a priority for safety pharmacology teams to detect these interactions as early as possible during drug development. As such, it is now common for pharmaceutical companies to perform high-throughput screening (HTS) on large numbers of novel compounds, early in development, to detect whether they block cardiac ion channels (Pollard et al., 2010). Discovering that a lead compound carries a high cardiac risk at later stages of development is very costly.

At both AstraZeneca (AZ) and GlaxoSmithKline (GSK), results from HTS assays for multiple cardiac ion channels inform mathematical models for a compound’s action on whole-cell electrophysiology (Davies et al., 2012; Mirams et al., 2011). Simulations are run to predict whether significant changes to cellular electrophysiology may occur with a given compound, and at which concentrations. Development of compounds that are flagged as having a significant effect can then be de-prioritised, or they can be referred for further safety testing, which is more accurate, but also more expensive.

In this study we characterised the variability associated with the results of HTS assays for cardiac ion channels, and examined how that variability affects predictions that are made for drug-induced changes to whole-cell electrophysiology.

1.1. High throughput screening

The current ‘gold standard’ of electrophysiological screening for ion-channel block involves manual patch clamping of single cells. This method is resource intensive and technically challenging, consequently it has a throughput that is far too low to be of commercial use during early drug discovery, when a large number of compounds need to be screened. To some extent, this problem has been overcome in recent years with the development of dedicated planar array high-throughput electrophysiology platforms. These platforms allow high precision recordings of ion-current inhibition by compounds, while being amenable to high-throughput screening (HTS).

A number of different planar array electrophysiology platforms have been developed in recent years, namely: Qpatch by Sophion Bioscience (Mathes, Friis, Finley, & Liu, 2009), PatchXpress by Molecular Devices (Ly, Shyy, & Misner, 2007), PatchLiner by Nanion Technologies (Polonchuk, 2012), IonFlux by Fluxion (Golden et al., 2011), CytoPatch by Cytocentrics (Stett, Burkhardt, Weber, Van Stiphout, & Knott, 2003) and IonWorks™ HT/Quattro and Barracuda by Molecular Devices. A recent comparison of hERG IC50 values obtained across these platforms with manual patch clamp experiments can be found in Gillie, Novick, Donovan, Payne, and Townsend (2013, Table 2). The Molecular Devices FLuorometric Imaging Plate Reader (FLIPR® Tetra, Schroeder & Neagle, 1996) assay is also used to measure changes in calcium transients (Sullivan, Tucker, & Dale, 1999).

HTS provides a measurement of the concentration-effect curve of ion-channel current inhibition, and has established a good record in detecting ion-channel blockade for a wide variety of compounds and ion channels.

In this study we consider the Molecular Devices IonWorks® Quattro™ assays for detecting block of I_Kr (hERG), I_Na (NaV1.5), I_CaL (CaV1.2), I_Ks (KCNQ1/minK) and I_to (Kv4.3/KChIP2.2), and the Molecular Devices FLIPR assay for I_CaL (CaV1.2). These assays have been used routinely at AZ and GSK for novel compound screening for a number of years.

1.2. Concentration-effect curves

Ion-channel current inhibition is commonly described by concentration-effect curves, such as those seen in Fig. 1. This curve describes how an ‘effect’ or ‘response’ R depends on a ‘dose’ or compound ‘concentration’ [C]. In this case, the peak ionic current following a voltage step is recorded repeatedly, and the proportion of this that remains after addition of a certain concentration (or dose) of a compound is the recorded effect (or response). Such curves are commonly described by a Hill function (Hill, 1910):

$$R\left(\right[C\left]\right)=\frac{{\left[{\mathbf{IC}}_{50}\right]}^n}{{\left[C\right]}^n+{\left[{\mathbf{IC}}_{50}\right]}^n}$$ (1)

or equivalently

$$R\left(\right[C\left]\right)={\left[1+{\left(\frac{\left[C\right]}{\left[{\mathit{IC}}_{50}\right]}\right)}^n\right]}^{-1}.$$

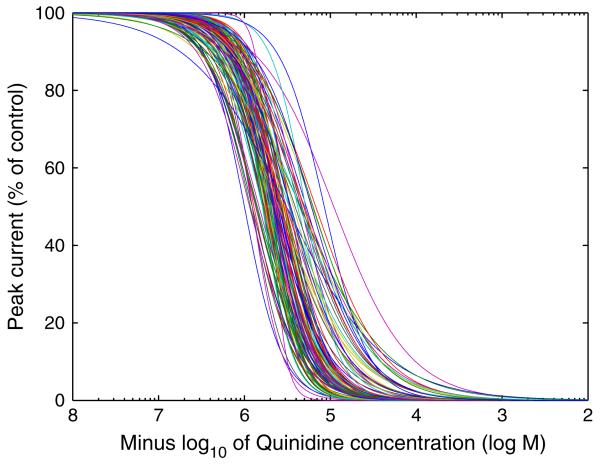
Fig. 1.

Variability in the concentration-effect curves fitted to results of an IonWorks Quattro™ hERG screen using Quinidine. These were recorded as a control at GSK, N = 120 separate assay runs.

This function of concentration [C], has two parameters: [IC₅₀], the half-maximal inhibitory concentration; and the Hill coefficient n.

In Fig. 1 we present concentration-effect curves that have been fitted to the output of a hERG-channel HTS that was performed 120 times (on different screening plates). Only those HTS assays that passed quality-control criteria, i.e. ones in which the positive controls registered an acceptable positive result, are considered in this study. We are therefore considering only the variability in ‘acceptable’ measurements, not across all the measurements that were taken. For discussion of typical quality control criteria used in these assays please see Bridgland-Taylor et al. (2006), Harmer et al. (2008), and Davies et al. (2012). Whilst the concentration-effect curves consistently detect the compound’s blockade of I_Kr, it is immediately evident that there is substantial variability between individual curves shown in Fig. 1. Our use of the term ‘variability’ is intended to represent the variation in IC₅₀ values and Hill coefficients fitted to concentration-effect curves recorded by HTS assays that are carried out on separate occasions. Indeed, HTS is thought to provide more variable results than the ‘gold-standard’ of manual patch clamp, and we seek to characterise this HTS variability in this study.

1.3. Aims

For most novel compounds that are of interest in drug development, repeats of only N = 1 or N = 2 are common. It is therefore difficult to draw any conclusions about the variability associated with screening a particular novel compound. Fortunately, a large number of repeats exist for those compounds used as controls in the assays.

Since AZ and GSK both run positive controls on each IonWorks Quattro or FLIPR Tetra plate, a whole concentration-effect curve is evaluated for a control compound each time any compound is screened. This has led to the accumulation of an unprecedented amount of information on HTS variability, which we have utilised here to determine the statistical distributions of both IC₅₀ values and Hill coefficients that describe the concentration-effect curves.

By using in-silico action potential (AP) simulations, AZ and GSK have begun to integrate quantitative information on concentration-effect curves that is gained from a panel of cardiac ion channel screens (Davies et al., 2012; Mirams et al., 2013). The aim of these simulations is to provide a prediction of how a compound is likely to affect the whole cardiac cell, or even the whole heart, early in compound development (Fletcher et al., 2011; Mirams & Noble, 2011). For example, in related work, we show how HTS data can be used to predict the results of a rabbit left-ventricular wedge assay (Beattie et al., 2013–this issue). It has not yet been considered how variability in HTS results, that are taken as inputs into in-silico models, might affect such simulation outputs.

The aims of this article are therefore two-fold: firstly, to quantify the variability in concentration-effect curves produced by HTS, by examining variability in the IC₅₀ values and Hill coefficients that describe them; and secondly, to provide a method for estimating the subsequent variability in the output of in-silico action potential simulations based upon HTS.

2. Methods

2.1. Ion-channel screening

Here we describe the IonWorks and FLIPR platforms in general terms. For details of the experimental protocols that are used at AZ and GSK, please refer to Supplementary material S1.

The IonWorks™ Quattro platform (first described by Schroeder, Neagle, Trezise, and Worley (2003)) has been the mainstay of ion channel electrophysiology HTS at AZ and GSK in recent years. On this platform, the glass electrodes typical of manual patch clamping rigs have been replaced by planar, 96 or 384 well, “chips” (known as the PatchPlate™). Each of the wells contains one hole to which one cell is clamped. Briefly, the PatchPlate™ is placed on the machine at the interface between two separate fluid compartments. The extracellular compartment (above the holes), is loaded with an external solution. The surface below the PatchPlate™ (the intracellular compartment), is perfused with a second solution. A vacuum is used to attach the cells onto the small holes at the base of each well, creating a high resistance seal (≈100 MΩ) between the cell and the edge of the PatchPlate™.

Unlike other methods, this suction is not used to break the cell membrane. Instead, a cell membrane-perforating agent (Amphotericin-B) is introduced into the intracellular compartment allowing access to the intracellular compartment from the underside while the high-resistance seal is maintained. This method, known as ‘perforated patch’, allows many of the intracellular components required for ion channel modulation to be retained (Wood, Williams, & Waldron, 2004). The cell can then be voltage clamped and currents across the membrane are measured by a 48 channel amplifier. Separate measurements can be taken from each well using this method.

An updated method, known as population patch clamping (PPC) was developed by Dale, Townsend, Hollands, and Trezise (2007). This protocol can be utilised on IonWorks™ Quattro and Barracuda machines and allows for more accurate recordings. In PPC mode, each PatchPlate™ is perforated by many holes allowing one amplifier to take recordings from up to 64 different cells. The recorded current is then the mean current from a number of cells. This dramatically improves consistency in the recordings, by helping to overcome some of the inter-cell variability that has been observed with the single-hole approach (Finkel et al., 2006). All of the data discussed in this study were acquired using the IonWorks Quattro in the PPC mode, as described in Supplementary material S1. In brief, cells were placed into wells at a concentration of between 1 and 5 million cells/ml (depending on the HTS target), cells were incubated in the presence of the test compound for 3–5 min before measurements were taken, and compounds were tested up to the limit of solubility.

We also consider the FLIPR screen that GSK has been using to detect blockade of CaV1.2 channels (Sullivan et al., 1999). This screen uses calcium-sensitive dyes to record changes in fluorescence. Intracellular calcium transients occur upon the addition of a depolarising solution, reductions in these transients relative to control wells are used as a proxy for blockade of the L-type calcium current. Details of the protocols that were used are given in Supplementary material S1.3.

2.2. pIC₅₀ and Hill coefficient distributions

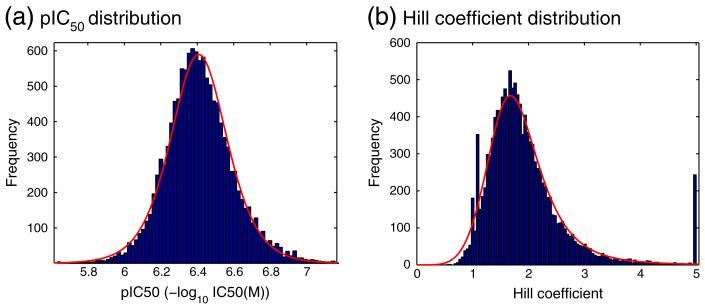
Of particular note, in terms of size, is the IonWorks hERG control at AZ, in which the compound Cisapride is used. At the time of writing there had been N = 12,638 replications of this experiment. We therefore use this example to discuss the fitting of the data to particular probability distributions. A histogram of the pIC₅₀ values that have been recorded is shown in Fig. 1. For ease of presentation and intuition we will work with pIC₅₀ values throughout this article. These are calculated from IC₅₀ values using pIC₅₀ = −log₁₀(IC₅₀) with units of Molar for IC₅₀ and therefore log(Molar) for pIC₅₀. Probability plots revealed that the logistic distribution is a good descriptor of pIC₅₀ variability in this dataset, this was true for all of the different HTS control assays (please see Supplementary material S2 for more detail).

To estimate the parameters of the distribution we used maximum likelihood estimates, provided by the MatLab™ statistics toolbox ‘mle’ function (the datasets and fitting code are available to download from http://www.cs.ox.ac.uk/chaste/download). The logistic distribution is fitted to the Cisapride hERG control data, and is shown overlaid in Fig. 1.

Throughout this investigation we therefore assume that pIC₅₀ follows a logistic distribution (pIC₅₀ ~ Logistic(μ, σ), where μ is the centering parameter and σ is the spread parameter). Note that since the pIC₅₀ is calculated from the IC₅₀ using a logarithm, this implies that IC₅₀ follows a log-logistic distribution (IC₅₀ ~ LogLogistic(α, β)), where the two distributions are related by α = e^μ and β = 1/σ. For the equations of the distributions please see the Supplementary material S2.

We perform a similar characterisation of the variability in Hill coefficients, that were fitted to concentration-effect curves at the same time as pIC₅₀ values. In this case all Hill coefficients appeared to follow a log-logistic distribution, as IC₅₀ values do (Hill ~ LogLogistic(α, β)). In Fig. 1 we present a histogram of the Hill coefficients that correspond to the same assay as the pIC₅₀ values shown in Fig. 1.

The peaks at 1.0 and 1.1 in Fig. 1 may illustrate unconscious ‘rounding’ by human operators, affecting the values that are logged into a database, whereas no such bias exists for pIC₅₀ values. Also of note is the accumulation of Hill coefficients at 5.0, which was the maximum allowed Hill coefficient in the fitting process.

2.3. Inferring underlying distributions from limited repeats

In order to simplify this section we discuss pIC₅₀ values, exactly the same procedure can be followed for Hill coefficients by substituting α for μ and β for σ, in the following discussion.

When an HTS assay is performed on a novel compound, we will typically have only a limited number of concentration-effect curves, and hence very limited knowledge of the distribution of concentration-effect curve parameters (in contrast to the control cases discussed above, where we have a very good approximation to the true distribution).

We must therefore make some assumptions about a distribution for the novel compounds:

1. When an HTS is repeated a large number of times, μ is equal to the ‘true’ pIC₅₀ value. This is a reasonable approximation since μ is equal to the mean, median and mode of the logistic distribution (and for the Hill coefficient case, with the log-logistic distribution, α is equal to the median). Note this is only really the ‘true pIC₅₀’ if the HTS assay has no systematic bias resulting in under- or over-reporting of pIC₅₀ values.

2. The deviation parameter (σ) is the same as that of the relevant control assays; i.e. if we repeated the HTS for the novel compound hundreds of times we would fit a distribution with the same deviation (σ) as the relevant control for that HTS assay, but with a different median (μ). As we will see in Section 3.1, this is a reasonable assumption for most of the assays, as different control compounds tend to share similar deviation parameters, and for a first approximation we might expect a novel compound to do the same.

In Supplementary material S3 we provide details of how these assumptions are used in inference calculations to estimate the underlying distribution of the true pIC₅₀, from individual runs of the assay. Here we discuss an example of the inference procedure, shown in Fig. 3.

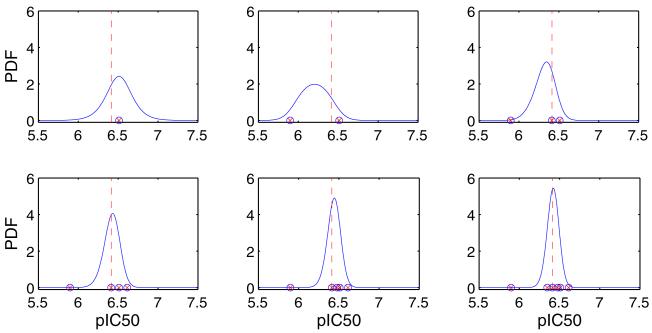
Fig. 3.

An example of how Bayesian inference informs the probability density function (PDF — solid line) for the ‘true pIC₅₀’ (dashed line), based on individual samples from the hERG Cisapride dataset. In the top left we consider the case where we have run one assay, N = 1, observing just one pIC₅₀ (red cross in blue circle). We plot the inferred probability distribution for μ, based on these data. Moving across the top row we have N = 2, then N = 3; and in the second row N = 4, N = 5 and N = 6. The example assay results were sampled at random from the Cisapride dataset shown in Fig. 1, and the Bayesian inference scheme used the spread parameter that was fitted to that distribution (σ = 0.1035).

In Fig. 3 we observe how the incorporation of repeat assay results into our inference procedure influences our confidence in the possibilities for the ‘true’ pIC₅₀. If repeat experiments yield similar values (as will we see, this is suggested by the results in Section 3.1), the effect of including them is to reduce the effective spread of the probability distribution for μ. We therefore tend to obtain more accurate estimates for the ‘true’ pIC₅₀ values when multiple experiments are performed, as demonstrated in Fig. 3.

2.4. In-silico action potential modelling

2.4.1. Model

In-silico action potential models are based on the Nobel Prize winning work of Hodgkin and Huxley (1952). These models describe the evolution through time of voltage across a cell membrane that results from differences in intracellular and extracellular ionic concentrations, caused by transmembrane ion currents, which are themselves voltage and time dependent. The first cardiac action potential models were developed over 50 years ago (Noble, 1962), and models now exist for multiple species and types of cardiac myocyte (Noble, Garny, & Noble, 2012). These cellular models have also been integrated into models of tissue electrophysiology to predict the path of electrical waves up to the whole heart scale (Clayton et al., 2011). We have recently reviewed the use of these biophysical cardiac electrophysiology models in pro-arrhythmic safety testing (Mirams, Davies, Cui, Kohl, & Noble, 2012).

In this study we used the Ten Tusscher and Panfilov (2006) (TT06) human ventricular action potential model (epicardial variant). This model was chosen as it has a relatively low number of equations, making simulations relatively fast, and appears to be robust under multiple-ion-channel drug action (Mirams et al., 2013). We have used a simple conductance-block model for ion channel blockade, so that the maximal conductance of a given channel, g_j, is modified under drug block according to

$$g_j=g_{j\text{control}}R\left(\right[C\left]\right)$$ (2)

where R([C]) is the degree of ion-channel block given by the concentration-effect curve (Eq. (1)), and g_{j control} is the maximal conductance of the channel in control (drug free) conditions.

The TT06 model includes all of the currents that are screened by the HTS assays we are considering, with the exception of an individual fast I_to current. Fast I_to is molecularly distinct from slow I_to (Niwa & Nerbonne, 2010), and so models that have separate components may provide more realistic simulation predictions for use in pharmaceutical safety assessment. However, here we are interested in demonstrating the method, rather than the quantitative accuracy of the predictions, and so we block the whole TT06 I_to current according to the concentration-effect curve from the fast I_to assays.

2.4.2. Sampling from distributions

In the results section we consider data from a screen of a number of marketed reference compounds. This screen was performed once, so to emulate the process of repeat HTS experiments we assume the screened values represent the ‘true’ values. If the experiment was to be repeated we assume that the individual sample pIC₅₀ values and Hills would follow the PDF of those HTS screens, assuming true median values for μ to be those given in Table 2 and spread parameters to be as in Table 1. The Bayesian inference scheme is then applied to 1, 2, 4 or 8 data points, drawn at random from these distributions (if one did possess raw data from multiple repeats the Bayesian inference scheme should be applied directly to these values).

Table 1.

Distribution of concentration-effect curves for control compounds. This table lists the fitted parameters for the pIC₅₀ (logistic) and Hill (log-logistic) distributions for each control compound, for each cardiac ion channel assay.

Ion channel	Control compound	HTS platform	Performed at	Repeats N	pIC50 Logistic		Hill Log-logistic
					μ	σ	α	1/β
NaV1.5	Flecainide	IonWorks	AZ	2307	5.235	0.0760	1.188	0.0835
NaV1.5	Amitryptiline	IonWorks	GSK	362	5.765	0.1388	1.744	0.1983
NaV1.5	Tetracaine	IonWorks	GSK	248	6.060	0.1459	1.530	0.2089
NaV1.5	GSK-A	IonWorks	GSK	121	5.315	0.2044	0.930	0.1529
CaV1.2	Verapamil	IonWorks	AZ	369	5.571	0.1597	0.605	0.1206
CaV1.2	Nicardipine	FLIPR	GSK	395	7.378	0.2216	1.325	0.2386
CaV1.2	Nifedipine	FLIPR	GSK	328	7.248	0.1856	1.179	0.2213
CaV1.2	Diltiazem	FLIPR	GSK	244	5.249	0.1560	0.979	0.2263
hERG	Cisapride	IonWorks	AZ	12638	6.408	0.1034	1.790	0.1784
hERG	Quinidine	IonWorks	GSK	120	5.625	0.1033	1.708	0.1544
hERG	Pimozide	IonWorks	GSK	94	7.321	0.1914	1.586	0.2486
hERG	Haloperidol	IonWorks	GSK	84	6.852	0.1498	1.469	0.2031
hERG	Verapamil	IonWorks	GSK	72	6.169	0.1464	1.429	0.2025
IKs	XE991	IonWorks	AZ	525	6.217	0.1053	1.127	0.1510
IKs	XE991	IonWorks	GSK	79	5.927	0.1342	1.011	0.1837
IKs	GSK-B	IonWorks	GSK	451	7.414	0.1808	1.318	0.1677
Ito	Flecainide	IonWorks	AZ	366	4.860	0.0860	1.063	0.0862

Table 2.

Results of a screen for a number of compounds with varying ion-channel blocking profiles. These screens were performed once for each ion channel at AZ. Where 50% block was not achieved, we have performed a least-squares fit of a concentration-effect curve to the original data, with a minimum allowed pIC₅₀ of 0, a minimum allowed Hill coefficient of 0.5, and a maximum of 5.00.

Compound	hERG		NaV1.5		CaV1.2		KCNQ1/minK		Kv4.3/KChIP2.2
	pIC50	Hill	pIC50	Hill	pIC50	Hill	pIC50	Hill	pIC50	Hill
Alfuzosin	4.66	0.92	3.69	0.71	3.75	1.64	3.95	0.50	3.04	0.50
Dofetilide	6.85	1.88	3.46	0.79	3.77	5.00	3.65	0.50	0.00	1.00
Lacosamide	0.00	1.00	3.34	0.72	4.33	0.44	3.62	0.50	0.00	1.00
Nilotinib	4.20	0.53	2.97	0.71	3.67	0.67	3.39	0.50	2.48	0.72
Tolterodine	6.89	1.58	5.24	1.08	0.00	1.00	4.10	0.60	4.93	1.07

Having inferred a probability density function for μ, as described in Section 2.3, we can then sample an estimate for the ‘true’ pIC₅₀, which is subsequently used to create a sample concentration-effect curve R([C]), using Eq. (1).

Then for any drug concentration of interest, the sample concentration-effect curve is used to calculate a new maximal channel conductance using the conductance block model (Eq. (2)). This process is repeated as required for all channels of interest.

We differentiate between the cases where we allow: only pIC₅₀ to be sampled (and Hill coefficient is assumed to be equal to one) or both pIC₅₀ and Hill (independently, as discussed in Supplementary material S3); and the inclusion of variability on different numbers of the ion currents (just hERG, or hERG/NaV/CaV or hERG/NaV/CaV/I_Ks/I_to).

2.4.3. Simulations

A pIC₅₀ and Hill coefficient are selected, for each channel, using the sampling method described above in Section 2.4.2. These values define a concentration-effect curve for each ion current. We modified the Ten Tusscher and Panfilov (2006) model to allow scaling of the channel conductances in response to drug block, as described in Section 2.4.1 and Eq. (2). We begin with the model in steady state 1 Hz pacing drug-free control conditions. The channel conductance scalings are applied, then regular 1 Hz pacing continues until the model reaches a new steady state (limit cycle). The action potential duration (at 90% repolarization, APD₉₀) is then calculated and recorded. Note that any marker of interest could be processed from the simulated action potentials, for example upstroke velocity, or triangulation. Here we have restricted the analysis to APD₉₀, as this is the most widely used marker in computational cardiac safety assessment at present, and has been linked to human clinical Torsadogenic risk (Mirams et al., 2011). The process is repeated for a range of concentrations for each sample of pIC₅₀ and Hill coefficient. This ‘workflow’ is depicted in schematic form in Fig. 4.

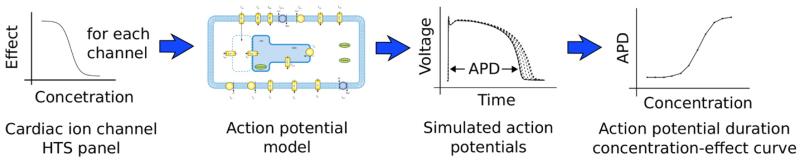
Fig. 4.

A schematic of the simulation and processing workflow. Step 1: concentration-effect curves are fitted to the result of each HTS assay. Step 2: for a given concentration, percentage blocks of the relevant ion channels are calculated from the concentration-effect curves, and applied to the mathematical electrophysiology model. Step 3: the model is paced at 1 Hz until it reaches a steady state, and the resulting action potential is recorded. Step 4: steps 2 & 3 are repeated for a range of concentrations, to build up a concentration-APD curve.

A new pIC₅₀ and Hill coefficient are sampled, and the process shown in Fig. 4 is repeated for the new values. By repeating this process 200 times for each compound, resulting in 200 distinct APD-response curves, we can build up a probability distribution for the outputs. By ignoring the 5 maximum and 5 minimum of the 200 simulated APDs at each concentration, the remaining spread of APDs defines an estimate for the 95% credible interval for the simulated response curve. The simulation takes a few hours on a single processor of a modern desktop PC (the time varies depending on the action-potential model used), but moving the calculations to parallel evaluation on larger computing resources is trivial.

For the interested reader we have made the following resources available: the full control datasets to which distributions were fitted, with the corresponding MatLab script; the Bayesian sampling code; the action potential modelling software; and the scripts for generating the figures presented in this article. These can be downloaded as a ‘bolt-on project’ for the open-source cardiac simulation software Chaste (written to work with v3.1) from http://www.cs.ox.ac.uk/chaste/download.

A brief description of the computational techniques follows. We used a machine readable version of the Ten Tusscher and Panfilov (2006) model, taken from the CellML repository (Lloyd, Lawson, Hunter, & Nielsen, 2008). PyCML was used to convert the CellML format into C++ code, the CellML file being tagged with metadata denoting the conductances of interest (Cooper, Corrias, Gavaghan, & Noble, 2011; Cooper, Mirams, & Niederer, 2011). The equations were solved using the adaptive CVODE solver (Hindmarsh et al., 2005), with relative and absolute tolerances of 10⁻⁶ and 10⁻⁸ respectively, in a custom-made program based on the open-source Chaste library (Mirams et al., 2013; Pitt-Francis et al., 2009).

3. Results

3.1. Screening variability

In this section we present the variability associated with fitting concentration-effect curves to the output of HTS assays. Each of the compounds we consider has been screened a large number of times as a positive control at either AZ or GSK.

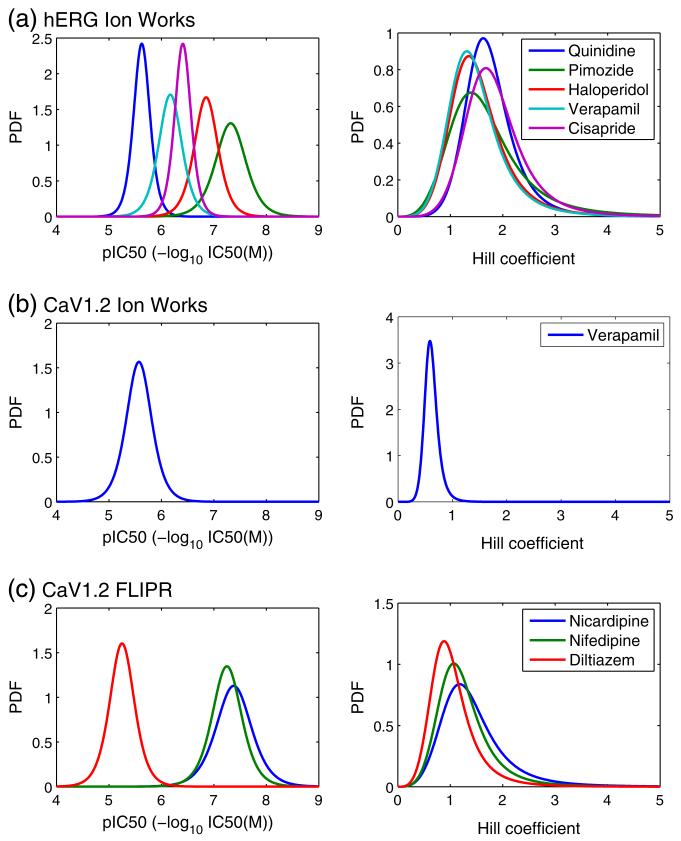
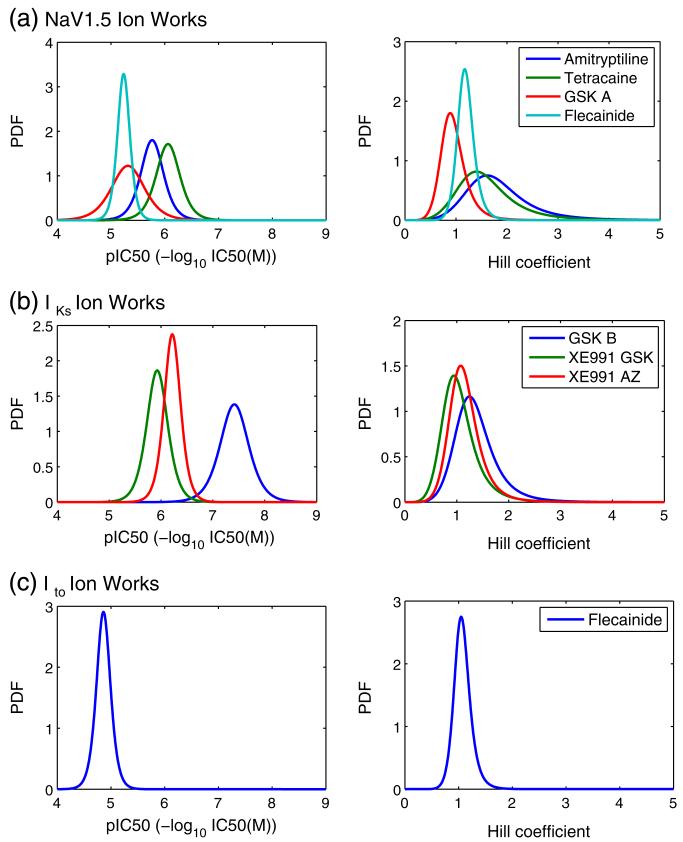
Each assay generates a histogram of reported pIC₅₀ and Hill coefficients, such as those shown in Fig. 2 for Cisapride in the hERG IonWorks screen. Analogous figures are presented in Supplementary material S4 for each control compound. The probability distributions that were fitted to the datasets for each control compound, as discussed in Section 2.2, are shown in one figure for each assay (Figs. 5 & 6). The individual fit parameters are summarised in Table 1.

Fig. 2.

Histograms of (a) pIC₅₀ values and (b) Hill coefficients, from an IonWorks Quattro Cisapride hERG assay. These values were fitted to recordings taken at AZ for N = 12,638 independent assay runs. Solid red lines denote the distributions that have been fitted to these data as described in the text.

Fig. 5.

Probability density functions for: (left) pIC₅₀ values; (right) Hill coefficients, as fitted to the distributions resulting from large numbers of repeat screens with control compounds.

Fig. 6.

Probability density functions for: (left) pIC₅₀ values; (right) Hill coefficients, as fitted to the distributions resulting from large numbers of repeat screens with control compounds.

Of particular interest in Table 1 is the consistency in the values of the ‘spread’ parameters σ and 1/β for each assay, as we would expect μ and α to vary between different compounds. Note that the spread of the Hill (log-logistic) distribution shown in Figs. 5 & 6 naturally increases as the median α increases, even with an unchanged scaling (1/β) parameter (see Supplement Fig. S4). The values in Table 1 may therefore be a better representation of the differences in the variability associated with the Hill coefficients than Figs. 5 & 6.

Those assays with multiple controls, which are hERG (Fig. 4), CaV1.2 FLIPR (Fig. 4), and I_Ks (Fig. 5), demonstrate similar levels of variability in both pIC₅₀ and Hill coefficients for all of the compounds considered. These results provide evidence that the second assumption we made in Section 2.4.2 about consistency in the spread of pIC₅₀ and Hill coefficients is reasonable for these assays. A possible exception to this is the NaV1.5 IonWorks screen, that shows slightly higher variability in the pIC₅₀ spread associated with different compounds. Ideally data would be acquired on additional NaV1.5 control compounds to characterise this assay further. In the absence of any further information, we keep the same assumption for the CaV1.2 IonWorks and I_to screens, for which data were only available for one control compound each.

Figs. 5 & 6 and Table 1 show that the variability associated with Hill coefficients fitted to HTS results is considerable (but the level of variability is consistent between different compounds in a given assay). Such high variability may suggest that there would be less error associated with making the assumption that the Hill coefficient is always equal to one, than there is in taking the Hill coefficient from an HTS assay.

There did not appear to be a correlation between the pIC₅₀ and Hill coefficients recorded in any of the assays (see Supplementary material Fig. S5).

3.2. Simulation variability

In this section we show how the uncertainty in the ‘true’ concentration-effect parameters propagates through an action potential simulation. We performed HTS at AZ for the ion channels of interest for a number of reference compounds, the results are shown in Table 2.

We selected an underlying spread parameter for each assay, shown in Supplementary material Table S1, based on the data shown in Table 1. Where there was a choice to be made between AZ or GSK spread parameters, we chose the AZ ones, as the experiments for this section were performed using those reagents, protocols and machines. We then performed the Bayesian inference method to obtain probability distributions for the ‘true’ pIC₅₀ value and Hill coefficient, as discussed in Section 2.4.2. We sampled from these distributions to explore the range of possible concentration-effect curves that are input into the simulations (as shown in Fig. 4). In practice to apply this method, you should characterise the variability of your own assay as shown above, and use the resulting spread parameters in the inference step.

The results consist of concentration-effect curves for action potential duration (APD₉₀), with 95% confidence limits evaluated from the many trajectories of the individual runs, as shown in Tables 3 & 4 and Tables S2–S9. In the following sections we present the variation we expect to be associated with simulation outputs, based on the level of variability in the HTS ion channel screens, for each of the compounds listed in Table 2.

Table 3.

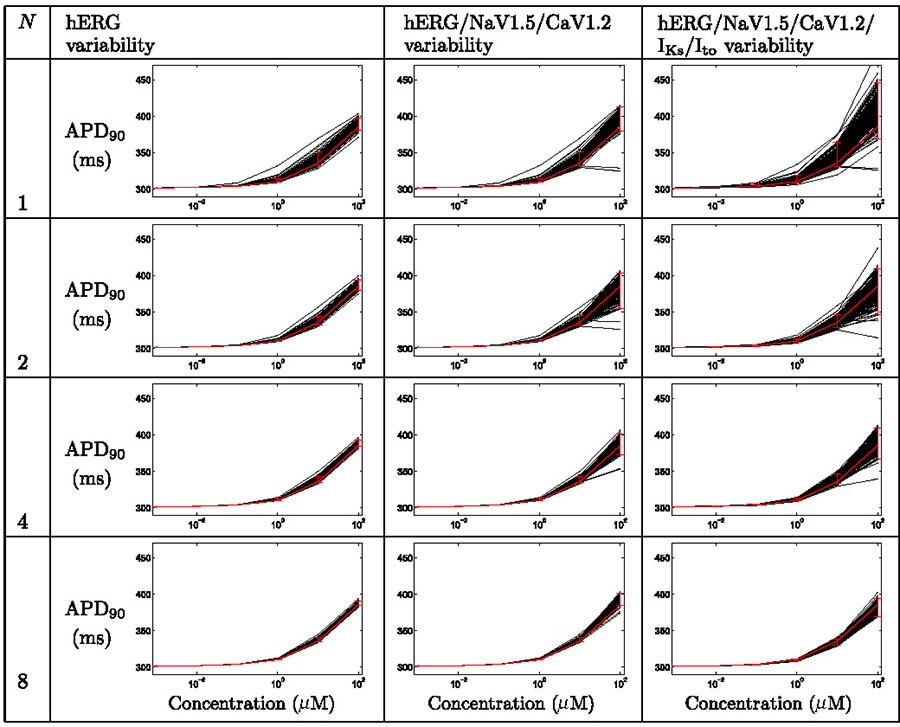
Uncertainty in concentration-effect curves for action potential duration under the action of Alfuzosin, when considering ion-channel assay variability in pIC₅₀ values (not in Hill coefficients), for various numbers of repeats. Each plot displays action potential duration, APD₉₀, as a function of concentration. Black lines represent simulation results for each set of sampled concentration-effect inputs, the red line denotes the result when using the numbers reported by the assay directly, with 95% credibility intervals imposed as described in the text.

Table 4.

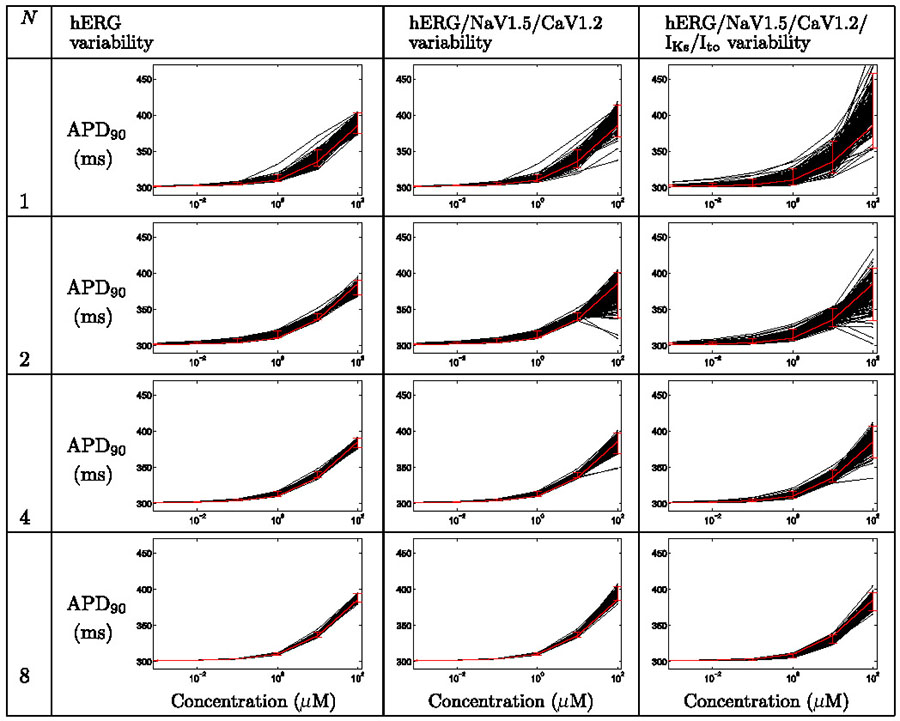
Uncertainty in concentration-effect curves for action potential duration under the action of Alfuzosin, when considering ion-channel assay variability in pIC₅₀ values and Hill coefficients, for various numbers of repeats. Each plot displays action potential duration, APD₉₀, as a function of concentration. Black lines represent simulation results for each set of sampled concentration-effect inputs, the red line denotes the result when using the numbers reported by the assay directly, with 95% credibility intervals imposed as described in the text.

3.2.1. Alfuzosin case study

Table 3 summarises the findings for Alfuzosin when considering the variability associated with pIC₅₀ measurements, but not Hill coefficients. Table 4 summarises the findings when including both sources of variability.

In the Thorough-QT (TQT) study a maximum QTc prolongation of 7.7 ms was observed (Gintant, 2011). In Tables 3 & 4 we see that simulations based on single screens could give misleading results. In some cases small, and in others very large, prolongation is predicted at high concentrations (top right plots in each table), particularly when considering variability associated with Hill coefficient measurements (Table 4).

By repeating the ion channel screens we gain more reliable channel block estimates, and the lower panels exhibit the correct behaviour — mild/moderate prolongation of repolarization.

3.2.2. Dofetilide case study

The remaining simulated concentration-action potential duration (APD₉₀) curves for this section are presented in Supplementary material S5. Tables S2 & S3 summarise the findings for Dofetilide.

Dofetilide is a well known QT-prolonging hERG blocker, we see that prolongation occurs at low concentrations of 0.01–0.1 μM. Since the hERG IC₅₀ is in this range, a large amount of variability is introduced at these concentrations. When considering only hERG block (Tables S2 & S3, left columns) the variability is reduced at high concentrations. This is due to the blockade of hERG being close to 100% at 1 μM and above, regardless of the variation in IC₅₀ reported by the HTS assay. In a similar situation, at 100 μM of Quinidine in Fig. 1, all 120 assay runs reported at least 90% block.

When we consider the results of the other channel assays, variability is introduced at higher concentrations, where those assays’ concentration-effect curves become active (Tables S2 & S3, centre and right columns). In particular, the next IC₅₀ to be encountered is that of CaV1.2 (Table 2); and as we might expect blockade of the L-type calcium current at concentrations close to 100 μM begins to cause significant shortening in some of the runs, and correspondingly large confidence intervals on the simulation output.

3.2.3. Lacosamide case study

Lacosamide is an example of a QT-shortening compound. It has a very low hERG affinity, and a significant CaV1.2 affinity. In the TQT study Lacosamide showed a shortening of around 6.3 ms (Gintant, 2011).

Tables S4 & S5 summarise the simulation results for Lacosamide. As we might expect, including assay variability for hERG has almost no effect, as the concentrations we are considering (up to 100 μM) are never close to any of the possible ‘true’ hERG IC₅₀ values.

The majority of variability is associated with the CaV1.2 IC₅₀ value, and accordingly the additional variability introduced when considering I_Ks and I_to is negligible. This example shows how it is possible, if unlikely, to get very strange behaviour due to HTS variability, in 0.5–1% of cases with just one assay repeat (N = 1), the simulations predict prolongation instead of shortening. In this case we would choose to screen CaV1.2 multiple times, as this has the largest benefit in terms of constraining the confidence intervals.

3.2.4. Nilotinib case study

Tables S6 & S7 summarise the findings for Nilotinib. In our screens Nilotinib is not a strong blocker of any current, and simulations suggest a mild prolongation, or even a possible shortening at high concentrations and low numbers of repeats. By increasing the number of assay repeats, we would consistently predict prolongation.

In the TQT study Nilotinib was a prolonger with 15.8 ms of QTc prolongation being observed (Gintant, 2011). By examining this compound’s FDA pharmacology review,¹ we find that hERG IC₅₀=0.13 μM was reported, substantially lower than our screening result (Table 2).

3.2.5. Tolterodine case study

The assays suggested that Tolterodine is a strong hERG blocker (Table 2) that we might expect to have a similar profile to Dofetilide. Tables S8 & S9 summarise the simulation findings for Tolterodine. The difference in the profiles shown (ever-longer prolongation at higher concentrations for Tolterodine but not Dofetilide) is explained by the fact that there is no CaV1.2 block to stabilise the hERG prolongation at higher concentrations, and instead blockade of I_Ks and I_to can be introduced.

This potentially risky profile would suggest repeating most of the screening panel multiple times in order to minimise uncertainty in prolongation predictions.

4. Discussion

The variability that we have observed in the high-throughput screens (HTS) could be caused by a large number of factors, including (but not limited to):

• Noise in recording or ‘instrument error’.

• Variability in the number and condition of cells in each well.

• Variability in the concentration and differences in the condition/batch of the compound added.

• Variability in the temperature at which the recordings were taken; temperature is not fixed at a physiological 37° in the screens we have considered.

Firstly, we characterised variability in pIC₅₀ values and Hill coefficients resulting from HTS assays by examining controls that have been repeated a large number of times. pIC₅₀ values fitted to data from an IonWorks or FLIPR screen are described by a logistic distribution, and Hill coefficients follow a log-logistic distribution. We observed moderate variability in pIC₅₀ values (Table 1) that is consistent with a ± ½ log₁₀ unit ‘rule of thumb’. There is a larger amount of variability associated with Hill coefficients.

There can be such a high level of variability associated with Hill coefficients that it is not clear that including the Hill coefficient from a HTS adds useful information: there may be less error introduced by assuming that the Hill coefficient associated with each concentration-effect curve (n in Eq. (1)) is equal to one. This is something we are investigating in parallel work (Beattie et al., 2013–this issue).

The use of in-silico action potential models to integrate information from HTS rests on the fact that the average result of a HTS is giving the ‘correct answer’. Careful analysis should be made to ensure that these screens are not consistently over- or under-reporting ion channel blockade, by comparing results with manual patch clamping.

We would like other companies and device manufacturers, that have repeated screens large numbers of times, particularly with other machines and for other ion channels, also to publish their datasets. The variability that is associated with different assays, reagents and protocols could then be characterised, and the most reliable screening methods selected for use.

We also characterised the resulting uncertainty in whole-cell responses via simulating the action potential duration based on the uncertainty in the screening data (that the simulation uses as inputs). This was done by performing a Bayesian inference step: inferring the distribution of likely ‘true’ concentration-effect parameters, from a number of sample assay runs, by assuming that the variability level for a novel compound is similar to that of the relevant control assay compounds. We then sampled possible concentration-effect curves for each channel and performed repeated simulations to build up a probability distribution for the resulting action-potential-duration vs. concentration curves.

The approach we have proposed does not rule out the consideration of other sources of variability, for example due to stochasticity of ion channel gating (Dangerfield, Kay, & Burrage, 2012), or inter-individual variability (Davies et al., 2012), and could be considered in addition to these.

The choice of number of screening repeats to perform initially depends upon the expense of the screen, the level of accuracy that is required, and the time and cost involved in repeating screens to reduce uncertainty at a later date. An organisation could decide to perform each screen once, analyse uncertainty using the proposed method, and perform additional screens as required; whilst another organisation could choose to perform each screen four times, or more, to minimise uncertainty from the outset.

Whatever strategy is adopted, our methodology provides a means to determine whether a particular screen is introducing large amounts of uncertainty, and whether the uncertainty in whole-cell behaviour predictions is at an acceptable level. This is a basic requirement for sensible interpretation of simulation results, and therefore a pre-requisite for the possible future use of simulation in reduction and replacement of animal-based safety tests.

Abbreviations

AP(D)

Action Potential (Duration)

AZ

AstraZeneca

FLIPR

FLuorometric Imaging Plate Reader

GSK

GlaxoSmithKline

HTS

High Throughput Screening [assays]

IC₅₀

Concentration for 50% Inhibition

I_CaL

L-type calcium current

I_Kr

rapid delayed rectifier potassium current

I_Ks

slow delayed rectifier potassium current

I_Na

fast sodium current

I_to

[fast] transient outward potassium current

PDF

Probability Density Function

pIC₅₀

minus log₁₀ of IC₅₀

PPC

Population Patch Clamping

QT(c)

QT interval of the electrocardiogram (corrected for heart rate)

TQT

Thorough QT, human clinical QT prolongation trial

TT06

Ten Tusscher and Panfilov (2006) human ventricular cell model