Abstract
Aging-related declines occur in many different domains of cognitive function during later adulthood. However, whether a global dimension underlies individual differences in changes in different domains of cognition, and whether global genetic influences on cognitive changes exist, is less clear. We addressed these issues by applying multivariate growth curve models to longitudinal data from 857 individuals from the Swedish Adoption/Twin Study of Aging, who had been measured on 11 cognitive variables representative of verbal, spatial, memory, and processing speed abilities up to 5 times over up to 16 years between ages 50 and 96 years. Between ages 50 and 65 years scores on different tests changed relatively independently of one another, and there was little evidence for strong underlying dimensions of change. In contrast, over the period between 65 and 96 years of age, there were strong interrelations among rates of change both within and across domains. During this age period, variability in rates of change were, on average, 52% domain-general, 8% domain-specific, and 39% test specific. Quantitative genetic decomposition indicated that 29% of individual differences in a global domain-general dimension of cognitive changes from 65 to 96 years were attributable to genetic influences, but some domain-specific genetic influences were also evident, even after accounting for domain-general contributions. These findings are consistent with a balanced global and domain-specific account of the genetics of cognitive aging.
Keywords: Cognitive Aging, Common Cause Hypothesis, Generalist Genes Hypothesis, Behavioral Genetics
Shared and Unique Genetic and Environmental Influences on Aging-Related Changes in Multiple Cognitive Abilities
Aging-related cognitive declines occur for healthy adults on a broad variety of cognitive variables representative of many different aspects of cognitive function (e.g. memory, processing speed, and reasoning). One recurring question within the field of cognitive aging concerns the extent to which each of these manifold changes are best conceptualized as a unique change process, or rather as alternative manifestations of a few more basic general processes (Rabbitt; 1993; Salthouse, 1994; Salthouse & Czaja, 2000; Tucker-Drob, 2009; Tucker-Drob, 2011a). Moreover, some researchers have recently elaborated on this question to ask whether the genetic contributions to changes in many different cognitive variables are unique or overlapping (Deater-Deckard & Mayr, 2005; Harris & Deary, 2011). These are particularly important issues, because if global dimensions underlie large proportions of variance in cognitive changes, researchers who investigate aging-related deficits on specific tasks or cognitive domains will need to incorporate the operation of general mechanisms along with more specific mechanisms in to their explanatory accounts. Similarly, if there is evidence for large proportions of domain-specific changes, the aggregation of data across multiple domains may serve to obscure important phenomena occurring at more specific levels. Moreover, if genetic influences on cognitive changes predominantly act at domain-general levels, research on the genetic mechanisms of cognitive aging may be most productive when data are aggregated across multiple cognitive variables, whereas if genetic influences on cognitive changes predominantly act at domain-specific levels, such research would do well to examine different outcomes individually.
One reason why the answer to this seemingly basic question remains largely unanswered is that the vast majority of past research on the topic has been based on cross-sectional data (Salthouse, 2004; Salthouse & Ferrer-Caja, 2003; Salthouse, 2009; Petrill, 1997). Cross-sectional comparisons of different individuals tested at different ages are quite informative about the dimensions on which population-level patterns of average age-related effects on cognitive variables operate, but they are not directly informative about the question of whether different domains of cognitive function decline in tandem for specific individuals. As Baltes and Nesselroade (1979, p. 25), wrote some time ago, “only longitudinal research, involving repeated observation of multiple behaviors, can provide a direct data base for… interrelationships in changes among behaviors. In principle, static (cross-sectional) observations do not contain direct evidence on interrelationships in behavioral change. Multivariate observations obtained in cross-sectional design formats provide structural information on static patterns of interindividual differences but not on changes in such patterns.”
A small number of investigations have recently begun to apply multivariate statistical methods to longitudinal data to examine whether aging-related changes in different cognitive variables correlate positively with one another (Anstey et al., 2003; Ferrer et al., 2005; Lemke & Zimprich, 2005; Reynolds et al., 2002; Sliwinski & Buschke, 2004; Hall, 2003; Tucker-Drob, Johnson, & Jones, 2009; Tucker-Drob, 2011b; Zelinski & Stewart, 1998; Zimprich & Martin, 2002). On the whole, findings have been consistent with at least some domain-general aspect of cognitive aging, as correlations between changes in measures representative of different domains of functioning have been moderate to large in size. An even smaller number of studies have, in fact, fit factor models to rates of cognitive change. These studies have indicated that a general factor of change accounts for approximately 50% of the variance in age-related rates of cognitive change in variables representative of multiple domains of cognitive function. Hertzog, Dixon, Hultsch, and MacDonald (2003) used confirmatory factor analysis to extract a single general factor accounting for approximately 41% of the variation in 6-year changes in multiple domains of cognition, including speed, working memory, and episodic memory in data from the Victoria Longitudinal Study. Lindenberger and Ghisletta (2009) used exploratory factor analyses to extract a cognitive change factor accounting for approximately 60% of the variation in 13-year changes in multiple domains of cognition in data from the Berlin Aging Study. Wilson and colleagues (2002) extracted a single principal component accounting for approximately 62% of the variation in 6 year changes in multiple cognitive variables from the Religious Orders Study. Using a subset of the variables and datapoints that were used in the current project, Reynolds, Gatz, and Pedersen (2002) used exploratory factor analysis to extract a general change factor and a digit span change factor from 10 year changes in multiple cognitive variables from the Swedish Adoption/Twin Study of Aging. The general change factor accounted for approximately 34% of the variance in change. Using data on 8 year changes in three cognitive variables along with a measure of grip strength and self-reported sensory disability, Christensen et al. (2004) found that 47% of individual differences in change were accounted for by a common slope factor. Ghisletta, Rabbitt, Lunn, & Lindenberger (2012) Using performed exploratory factor analysis to levels and slopes of 20 year longitudinal data on 20 cognitive tasks. They found that a slope factor accounted for approximately 66% of individual differences in aging-related changes in fluid intelligence, crystallized intelligence, perceptual speed, and memory. Only Tucker-Drob (2011a), however, has comprehensively examined whether a global and domain-specific hierarchical structure underlies longitudinal changes in a broad variety of cognitive variables. Using 7-year multivariate longitudinal data from a community sample of young, middle aged, and older adults measured on 12 tests representing four distinct cognitive domains, Tucker-Drob (2011a) found that approximately 40% of aging related cognitive changes were global, 30% were domain-specific (processing speed, episodic memory, fluid reasoning, and spatial visualization), and 30% were tasks specific. The Tucker-Drob (2011a) findings are consistent with a balanced global and domain specific view of cognitive aging.
It is important, however, that the robustness of these new findings be tested by way of replication and extension. In particular, the Tucker-Drob (2011a) study was only based on a time lag of 1 to 7 years (3 years on average), and only contained 2 observations per participant. Tucker-Drob (2011a) capitalized on the fact that retest intervals varied across individuals in order to apply growth curve models to the data. Moreover, while the Tucker-Drob (2011a) study analyzed the dimensionality of changes in a variety of measures of effortful processing, he did not analyze changes in measures of verbal ability.
Behavioral genetic studies have been limited in similar respects: Multivariate behavioral genetic studies of cognition have been cross-sectional, whereas longitudinal behavioral genetic studies of cognition have been either univariate or bivariate. Nevertheless, the established patterns of results from these two lines of behavioral genetic research are of relevance. First, multivariate quantitative genetic analyses have now strongly established that genetic influences on individual differences in different forms of cognition act largely through domain-general mechanisms (Petrill, 1997; Plomin & Spinath, 2002; Finkel, Pedersen, McGue, & McClearn, 1995). This pattern is consistent with what Kovas and Plomin (2006) have termed the “generalist genes” hypothesis. Second, univariate longitudinal quantitative genetic studies have reported moderate heritabilities of aging-related changes in general cognitive ability indices (McGue & Christensen, 2002; Reynolds, Finkel, McArdle, Berg, & Pedersen, 2005; McArdle, Prescott, Hamagami, & Horn, 1998), and bivariate longitudinal quantitative genetic studies have reported overlapping genetic effects on pairwise combinations of variables representing different domains of cognition (Finkel, Reynolds, McArdle, & Pedersen, 2005; Finkel, Reynolds, McArdle, Hamagami, & Pedersen, 2009). However, we are not aware of any previous study that has simultaneously estimated the extent of global and domain-specific genetic influences for longitudinal changes in more than two cognitive variables. Using single-time point data, it not possible to strongly test whether domain-general genetic variation observed in later life reflects domain-general genetic mechanisms occurring in earlier life, or actually reflects domain-general contributions to aging-related processes. Using bivariate (but not multivariate) longitudinal data, it is not possible to strongly test whether genetic influences on cognitive changes occur at a truly domain general level, or are instead only shared between specific pairs of domains. In summary, although previous studies have used multivariate models to examine the genetics of individual differences at a single point in time, and bivariate models to examine the genetics of aging-related cognitive change, no study has combined more than two variables to examine whether a domain-general set of genes underlies global patterns of aging-associated cognitive changes.
To overcome previous shortcomings, the current project makes use of multivariate cognitive ability data from a study with a longitudinal time lag of up to 16 years and 5 occasions of measurement. We examine the factor structure underlying rates of linear change in 11 cognitive variables representative of four basic domains of cognitive function: verbal, spatial, memory, and processing speed. We test a single factor model of change against two-factor and four-factor models of change. We also submit our change intercorrelation matrices to exploratory factor analysis to ensure that an alternative factor structure isn’t missed. After establishing the structure of changes at the phenotypic level, we go on to apply multivariate longitudinal quantitative genetic models to the data. We examine the extents to which genetic and environmental influences on changes in the different cognitive domains occur at domain-general and domain-specific levels.
Method
Participants
The current project made use of data from the Swedish Adoption/Twin Study of Aging (SATSA), which includes both monozygotic and dizygotic twin pairs, some of whom had been reared together, and some of whom had been separated before 11 years of age and reared apart. Participants were measured during 4-hour in-person testing sessions for up to five times over 16 years. The first, second, and third waves of in-person testing occurred at 3-year intervals, the fourth wave occurred 7 years after the third wave, and the fifth wave occurred 3 years after the fourth wave. Ages ranged from 50 years to 96 years. Data came from 857 individuals, 515 of whom contributed one or more datapoint between ages 50 and 65, and 671 of whom contributed one or more datapoint between ages 65 and 96 (329 individuals contributed datapoints both before and after age 65).1 A total of 2,744 assessments were made, yielding an average of 3.2 assessments per individual. The sample included 192 monozygotic twins reared together (MZT), 128 monozygotic twins reared apart (MZA), 239 dizygotic twins reared together (DZT), 291 dizygotic twins reared apart (DZA), and 7 twins of unknown zygosity (UZ), from a total of 447 twin pairs. Sample sizes at waves 1 through 5 were 618 (143 MZT, 95 MZA, 166 DZT, 207 DZA, 7 UZ), 576 (118 MZT, 92 MZA, 163 DZT, 198 DZA, 5 UZ), 567 (121 MZT, 85 MZA, 165 DZT, 191 DZA, 5 UZ), 541 (114 MZT, 74 MZA, 159 DZT, 191 DZA, 3 UZ), and 442 (91 MZT, 56 MZA, 138 DZT 155 DZA, 2 UZ) respectively. Sixty percent of participants were female. Educational attainment was reported on a 4 point scale (1=elementary school; 2=O-level or vocational school or folk high school; 3=gymnasium (A-level); 4=university or higher), and averaged 1.60 (SD = 0.881).
Measures
The cognitive measures employed in SATSA have been described previously (Pedersen, Plomin, Nesselroade, & McClearn, 1992). In short, four cognitive domains were measured. Verbal knowledge was measured with Analogies, Synonyms, and the Information subtest. Spatial ability was measured with Block Design, Figure Logic, and Card Rotations. Memory was measured with Digit Span, Names and Faces, and Picture Memory. Processing speed was measured with Symbol Digit and Figure Identification. Reliabilities range from .82 to .96 (Pedersen et al., 1992). To keep scores on similar metrics for the purposes of facilitating model convergence, each raw score was standardized to a Z metric based on its distribution at the first wave. The absolute values of the skewness and kurtosis indices for these distributions were less than 1 for all variable except for Names and Faces for which Skewness = 1.16 and Kurtosis = 1.20. Inspection of the histogram for this variable indicated a possible floor effect that could not be ameliorated via transformation. Models that excluded the Names and Faces variable from analyses produced very similar parameter estimates to those reported here.
Dementia was diagnosed at each wave according to a detailed case ascertainment method described in depth in Gatz, Pedersen, Berg, Johansson, Johansson, Mortimer, Posner, Viitanen, WInblad, and Ahlbom (1997). In the current study, we used all available cognitive data and controlled for whether the cognitive data were collected subsequent to a dementia diagnosis. There were 48 individuals with a diagnosis of dementia during the course of the SATSA study and who had non-missing cognitive scores.
Accounting for Nonlinearity: Testing for Different Patterns Before and After Age 65
Previous applications of univariate linear growth curves to cognitive data from SATSA have indicated that a single linear age-based slope cannot fully account for the patterns of cognitive changes occur from middle to late adulthood. Two approaches have proven useful in accounting for the nonlinear patterns by which cognitive declines accelerate in later adulthood. One approach has been to model age-based changes in cognition in the entire SATSA sample using growth curves with both linear and quadratic change components (Reynolds et al., 2005). The linear components have been interpreted to represent the steady pattern of decline that occurs from middle age through late adulthood, and the quadratic components have been interpreted to represent the accelerated rate of cognitive decline that occurs in later adulthood. A second approach has been to model age-based changes using two linear slopes: one slope representing changes occurring before age 65 years and a second slope representing changes occurring after age 65 years (Finkel, Reynolds, McArdle, Gatz, & Pedersen, 2003). Consistent with analyses making use of quadratic growth models, analyses making use of such bi-linear growth models, have generally indicated steeper rates of change after 65 years than before 65 years. Reynolds et al. (2005) have reported that both approaches produce the same substantive patterns of phenotypic and biometric results (p. 5). Based on this previous work, it was important to examine whether the results of the current analyses are consistent across both middle adulthood (prior to age 65), where age-related cognitive changes are more moderate, or later adulthood, (after age 65), where age-related cognitive changes are more pronounced. We therefore provide results of linear growth curve models applied to the entire age range of the sample (50–96 years), as well as for middle adulthood (50–65 years), and older adulthood (65–96 years) separately. Because the analyses of the entire age range only include a single linear slope for each variable (it was not computationally feasible to fit multivariate spline models or multivariate quadratic models in these data), the results from the separate analyses of data from middle adulthood and older adulthood are likely to be more accurate representations of the data. We highlight similarities and differences between results obtained from each age range.
Phenotypic Analyses
The analyses for the current project made use of a multivariate growth curve modeling approach. This approach simultaneously estimates individual growth curves for each of the 11 cognitive tests, and factor structures for the levels and the slopes. Although the growth curve and factor portions of the models are written separately below, they were simultaneously estimated in one step. The growth curve model portion of this model is written as
| 1 |
where Y[t] is score of a given person on variable v at age t, i (i.e. intercept) is the inferred level of performance for a given person at a single point in time, s (i.e. slope) is the longitudinal rate of change for a given person, and e[t] is a unique factor score (disturbance) of a given person at age t. The parameters d and w are used to estimate the effects of time-varying covariates, dementia (coded 0 for pre-dementia time points, and 1 for post-dementia time points) and wave (coded 0 for wave 1, 1 for wave 2, 2 for wave 3, 3 for wave 4, and 4 for wave 5) respectively. Therefore, the parameter d can be interpreted to reflect the average cognitive deficit associated with a dementia diagnosis and the parameter w can be interpreted to reflect both practice effect and history effect confounds. The model is able to statistically identify the effects of aging separate from those of history and maturation by estimating aging as a function of participant age and history/maturation as a function of wave of measurement (McArdle & Woodcock, 1997). Because participants entered into the study at many different ages, age and wave are not perfectly confounded, as they would be in a panel study of an age-homogenous group of individuals (Tucker-Drob et al., 2009). Note that results were very similar when cognitive assessments following a dementia diagnosis were set to missing and the r and d parameters were not estimated.
Because growth curves are simultaneously fit to multiple outcomes, the subscript v is used to indicate that a term is allowed to differ across variables. The levels (with the subscript i) and the slopes (with the subscript s) of the different outcomes are each allowed to have random effects. Relations among random effects may be modeled via covariances and/or factor models. If a factor model is chosen, it can be generally written as:
| 2a |
| 2b |
where the υ's represent level and slope means, and the λ’s represent loadings on intercept factor(s) Fi and slope factor(s) Fs. Individual differences in performance levels (intercepts) are equivalent to cross-sectional differences. Therefore, for all models the factor structure of the performance levels was specified to that which is well-established in the literature for cognitive abilities in general (Carroll, 1993) and these variables in particular (Pedersen et al., 1992). Performance levels for each test were specified to load on either a verbal knowledge, a spatial ability, a memory, or a processing speed factor, and each of these factors are specified to, in turn, load on a higher order general factor. However, as discussed in the introduction to this paper, very little work has been done to examine the factor structure of changes. Arriving at a parsimonious factor-analytic representation of changes was a primary focus of the current analyses. Note that equation 1, 2a, and 2b represent different portions of a comprehensive model in which all parameters can be simultaneously estimated.
Phenotypic Results
All phenotypic models were fit as two-level models in Mplus (Muthén & Muthén, 1998–2010) using maximum likelihood estimation with standard errors that are corrected for non-independence of observations (from twins within the same pair), and robust to departures from normality. Maximum likelihood estimation avoids parameter estimation bias due to participant drop-out under the assumption that any patterns of drop-out that systematically relate to the study outcomes can be accounted for by the patterns of relations for which data are present (see Dominicus, Palmgren, & Pedersen, 2006, for an in-depth examination of this issue both in simulated data, and in data from SATSA). To facilitate model convergence, age was centered at 65 and divided by 10.
Table 1 presents unstandardized parameter estimates (with 95% confidence intervals) from the growth curve portions of a multivariate linear growth curve model of the 11 cognitive variables in which all slopes were allowed to freely intercorrelate, for the entire age range (ages 50 to 96 years), as well as for middle adulthood (ages 50–65 years) and older adulthood (ages 65–96 years) separately. A number of observations are of note. First, for both the entire age range, and specifically in older adulthood, dementia coefficients (d) were all negative, and the vast majority were significantly different from 0, indicating an overall pattern of cognitive deficits associated with an assessment occurring after a dementia diagnosis. Given that a primary factor in diagnosing dementia is cognitive impairment, this pattern was to be expected. We do not report dementia coefficients for the middle age group, because only one person in this age range was diagnosed with dementia and it is therefore unknown whether the dementia coefficients in this age group are at all generalizable. Second, it can be seen that in the entire age range, as well as in middle and older adulthood, the wave coefficients (w) were nearly all positive, and many were significantly different from zero, indicating that assessments made at later waves were associated with a boost in performance, possibly due to practice effects (c.f. Salthouse & Tucker-Drob, 2008). Third, the mean rates of change, scaled in decades (recall that age was centered at 65 and divided by 10) were negative, moderate to large, and all significantly different from zero. In younger adulthood, the mean rates of change were not significantly different from zero for the verbal tests, but were significantly negative for the speed tests, the memory tests, and two out of three of the spatial tests. Finally, there was statistically significant evidence for heterogeneity in rates of change, as indicated by the significant standard deviations in the slopes in all but one case (change in block design performance in middle adulthood).
Table 1.
Unstandardized estimates and associated 95% confidence intervals for key parameters of growth curve models.
| Variable | Dementia Coefficient (d) |
Wave Coefficient (w) |
Mean of Age Slope |
SD of Age Slope | Time-Specific Variance |
|---|---|---|---|---|---|
| ENTIRE AGE RANGE (50–96 years) | |||||
| Analogies | −.493+/−.353 | .051+/−.110 | −.417+/−.265 | .298+/−.069 | .168+/−.047 |
| Synonyms | −.199+/−.249 | .060+/−.063 | −.235+/−.159 | .242+/−.051 | .116+/−.035 |
| Information | −.854+/−.349 | .125+/−.069 | −.381+/−.174 | .393+/−.053 | .203+/−.049 |
| Block Design | −.619+/−.241 | .059+/−.080 | −.507+/−.190 | .298+/−.047 | .092+/−.031 |
| Figure Logic | −.228+/−.367 | .290+/−.123 | −.980+/−.294 | .369+/−.086 | .116+/−.041 |
| Card R otations | −.526+/−.349 | .163+/−.100 | −.857+/−.239 | .316+/−.053 | .350+/−.059 |
| Digit Span | −.414+/−.333 | .161+/−.114 | −.611+/−.269 | .244+/−.069 | .379+/−.071 |
| Names and Faces | −.412+/−.345 | .185+/−.122 | −.738+/−.288 | .306+/−.071 | .229+/−.061 |
| Picture Memory | −.925+/−.425 | .126+/−.112 | −.525+/−.263 | .328+/−.065 | .248+/−.065 |
| Symbol Digit | −.439+/−.282 | .145+/−.082 | −.940+/−.194 | .311+/−.047 | .019+/−.031 |
| Figure ID | −.827+/−.343 | .290+/−.096 | −1.195+/−.231 | .397+/−.061 | .207+/−.039 |
| MIDDLE ADULTHOOD (50–65 years) | |||||
| Analogies | - | .009+/−.184 | −.114+/−.461 | .388+/−.169 | .276+/−.041 |
| Synonyms | - | −.030+/−.104 | .109+/−.257 | .223+/−.123 | .095+/−.012 |
| Information | - | .067+/−.092 | .072+/−.220 | .245+/−.186 | .101+/−.018 |
| Block Design | - | .050+/−.112 | −.224+/−.267 | .152+/−.174 | .138+/−.022 |
| Figure Logic | - | .214+/−.176 | −.617+/−.414 | .287+/−.237 | .365+/−.049 |
| Card Rotations | - | .056+/−.169 | −.458+/−.410 | .540+/−.202 | .278+/−.043 |
| Digit Span | - | .193+/−.196 | −.581+/−.498 | .356+/−.204 | .349+/−.053 |
| Names and Faces | - | .276+/−.186 | −.807+/−.461 | .307+/−.384 | .341+/−.053 |
| Picture Memory | - | .194+/−.165 | −.446+/−.398 | .398+/−.182 | .242+/−.039 |
| Symbol Digit | - | .125+/−.153 | −.627+/−.361 | .280+/−.214 | .181+/−.051 |
| Figure ID | - | .443+/−.172 | −1.234+/−.431 | .525+/−.184 | .247+/−.039 |
| OLDER ADULTHOOD (65–96 years) | |||||
| Analogies | −.453+/−.357 | .005+/−.145 | −.358+/−.343 | .330+/−.102 | .345+/−.037 |
| Synonyms | −.185+/−.284 | .081+/−.086 | −.356+/−.216 | .339+/−.080 | .123+/−.014 |
| Information | −.889+/−.372 | .129+/−.090 | −.576+/−.233 | .448+/−.074 | .131+/−.018 |
| Block Design | −.583+/−.278 | −.014+/−.114 | −.454+/−.270 | .344+/−.069 | .174+/−.037 |
| Figure Logic | −.156+/−.384 | .256+/−.171 | −1.012+/−.400 | .437+/−.139 | .551+/−.067 |
| Card Rotations | −.498+/−.386 | .166+/−.125 | −.977+/−.310 | .375+/−.088 | .246+/−.031 |
| Digit Span | −.391+/−.378 | .129+/−.149 | −.604+/−.345 | .345+/−.104 | .375+/−.043 |
| Names and Faces | −.506+/−.341 | .133+/−.163 | −.620+/−.394 | .390+/−.096 | .439+/−.047 |
| Picture Memory | −.950+/−.423 | .038+/−.153 | −.454+/−.361 | .421+/−.112 | .356+/−.043 |
| Symbol Digit | −.447+/−.294 | .043+/−.098 | −.831+/−.227 | .332+/−.053 | .167+/−.018 |
| Figure ID | −.786+/−.341 | .239+/−.112 | −1.177+/−.267 | .425+/−.073 | .230+/−.027 |
Note: Parameters in bold are significant in p<.01. Parameters in bold italics are significant at p<.05. Confidence intervals were calculated by multiplying the standard error of each estimate by 1.96. For middle adulthood, dementia was controlled for. However, given that they were derived from a single individual, they should not be considered generalizable and are therefore not reported.
As a first step towards examining the dimensionality of the longitudinal slopes, three confirmatory models of linear change were fit: a model that specified a single common factor of change; a model that specified a verbal change factor and a nonverbal change factor; and a four factor model that specified changes to occur along verbal, spatial, memory, and processing speed dimensions. As mentioned earlier, all models specified the same hierarchical factor structure of the levels (intercepts) as described above. This structure was composed of four first-order factors (verbal, spatial, memory, and processing speed) and one second-order general factor. Independent latent variables (latent variables with no loadings on any other variables, e.g. the higher order general factor in the hierarchical factor structure) in all models were allowed to intercorrelate. Moreover, for all models, residual correlations were allowed for the level-slope pairing from each individual task (e.g. block design level with block design slope), and for both the four-factor and the higher-order factor models (residuals of) level and slope factors that corresponded with one anther were allowed to correlate (verbal level with verbal change spatial level with spatial change, memory level with memory change, and speed level with speed change).
Table 2 provides parameter estimates for hierarchical structure of the levels, for the entire age range (ages 50 to 96 years), as well as for middle adulthood (ages 50–65 years) and older adulthood (ages 65–96 years) separately. It can be seen that the individual tests load at moderate to high levels on the first order factors, with the memory tests loading somewhat lower on their respective factor than the tests representing the verbal, spatial, and processing speed domains. It can further be seen that the factors representing effortful processing (spatial, memory, and processing speed) load substantially higher on the higher order factor than does the factor representing verbal knowledge. The similarity of factor solutions can be index by the congruence coefficient, which is on the same scale as the correlation coefficient (i.e. −1 to +1), and takes into account both the actual magnitudes of the factor loadings and their relative magnitudes compared to one another (see Jensen, 1998). Congruence coefficients of .90 are considered very high. The congruence coefficients for the pairwise combinations of the three solutions in table 2 were all greater than .99, indicating virtually perfect correspondence.
Table 2.
Standardized parameter estimates (with unstandardized parameter estimates and associated 95% confidence intervals in parentheses) from hierarchical factor model of levels of performance
| Variable | Verbal | Spatial | Memory | Speed | g |
|---|---|---|---|---|---|
| ENTIRE AGE RANGE (50–96 YEARS) | |||||
| Analogies Slope | .847 (.430+/−.049) | ||||
| Synonyms Slope | .933 (.516+/−.059) | ||||
| Information Slope | .851 (.447+/−.057) | ||||
| Block Design Slope | .930 (.313+/−.057) | ||||
| Figure Logic Slope | .877 (.265+/−.049) | ||||
| Card Rotations Slope | .719 (.255+/−.055) | ||||
| Digit Span Slope | .603 (.194+/−.059) | ||||
| Names and Faces Slope | .750 (.220+/−.090) | ||||
| Picture Memory Slope | .784 (.254+/−.098) | ||||
| Symbol Digit Slope | .992 (.274+/−.067) | ||||
| Figure ID Slope | .828 (.244+/−.055) | ||||
| GC | .787 (1.277+/−.221) | ||||
| GV | .910 (2.192+/−.492) | ||||
| GM | .912 (2.228+/−.906) | ||||
| GS | .933 (2.592+/−.696) | ||||
| MIDDLE ADULTHOOD (50–65 YEARS) | |||||
| Analogies Slope | .902 (.563+/−.080) | ||||
| Synonyms Slope | .942 (.574+/−.080) | ||||
| Information Slope | .886 (.482+/−.073) | ||||
| Block Design Slope | .864 (.262+/−.102) | ||||
| Figure Logic Slope | .848 (.234+/−.088) | ||||
| Card Rotations Slope | .639 (.239+/−.098) | ||||
| Digit Span Slope | .528 (.186+/−.182) | ||||
| Names and Faces Slope | .585 (.172+/−.208) | ||||
| Picture Memory Slope | .641 (.205+/−.243) | ||||
| Symbol Digit Slope | 1.012 (.331+/−.098) | ||||
| Figure ID Slope | .862 (.324+/−.088) | ||||
| GC | .723 (1.047+/−.227) | ||||
| GV | .940 (2.752+/−1.192) | ||||
| GM | .934 (2.619+/−3.044) | ||||
| GS | .902 (2.087+/−.694) | ||||
| OLDER ADULTHOOD (65–96 YEARS) | |||||
| Analogies Slope | .842 (.428+/−.067) | ||||
| Synonyms Slope | .940 (.552+/−.082) | ||||
| Information Slope | .856 (.491+/−.080) | ||||
| Block Design Slope | .935 (.343+/−.080) | ||||
| Figure Logic Slope | .954 (.291+/−.071) | ||||
| Card Rotations Slope | .716 (.268+/−.071) | ||||
| Digit Span Slope | .610 (.195+/−.092) | ||||
| Names and Faces Slope | .721 (.232+/−.123) | ||||
| Picture Memory Slope | .775 (.275+/−.137) | ||||
| Symbol Digit Slope | .912 (.205+/−.174) | ||||
| Figure ID Slope | .701 (.187+/−.153) | ||||
| GC | .784 (1.262+/−.261) | ||||
| GV | .903 (2.096+/−.570) | ||||
| GM | .916 (2.286+/−1.229) | ||||
| GS | .966 (3.756+/−3.271) | ||||
Note: Parameters in bold are significant in p<.01. Parameters in bold italics are significant at p<.05. Confidence intervals were calculated by multiplying the standard error of each estimate by 1.96.
Table 3 presents parameter estimates from each of the alternative confirmatory models of linear change for the entire age range (ages 50 to 96 years), as well as for middle adulthood (ages 50–65 years) and older adulthood (ages 65–96 years) separately. Table 4 contains AIC values for each of the three models, in addition to Χ2 values from nested model comparisons. Focusing first on the model comparisons, it can be seen that for both age ranges, as well as for the entire age range, both the AIC fit index and the nested model comparisons indicated that the four correlated factors model was the best representation of the data. That the more complex, four factor model fit better than the simpler one and two factor models, suggests that the process of cognitive aging cannot be simply described one or two common dimensions. Turning toward the parameter estimates, it can be seen that for the entire age range, and specifically for older adulthood, the loadings and factor intercorrelations from each of the three models were positive, all loadings and factor intercorrelations but one (the loading involving change in digit span) were large in magnitude, and all loadings and factor intercorrelations were statistically significant. This indicates that, at least after age 65 years, individual differences in longitudinal changes in different cognitive variables strongly which is generally supportive of the hypothesis that there are global aspects of cognitive aging that occur across different domains of functioning (cf. Reynolds et al., 2002). Results differed, however, when middle adulthood was considered on its own. For the models fit to data from this age range (50 to 65 years), factor loadings were not uniformly high in magnitude, but were instead quite variable, many of them being very close to zero. Moreover, only a small proportion of the factor loadings were statistically different from zero, and there was little evidence in either the two-factor solution or the four-factor solution that the factors of change were interrelated. To further illustrate the differences in results across the two age groups, we calculated median first order factor loadings for the four factor solution. For the entire age range, the median first order loading was .91, and for older adults this statistic was .82. In contrast, the median first order loading for middle adulthood was .27. This indicates that while the change factors were highly cohesive in older adulthood, there was very little cohesion amongst change factors in middle adulthood. In other words, while there appear to be strong dimensions of aging-related cognitive changes in older adulthood, there does not appear to be nearly as robust a structure of aging-related cognitive changes in middle adulthood.
Table 3.
Standardized parameter estimates (with unstandardized parameter estimates and associated 95% confidence intervals in parentheses) from alternative factor models of longitudinal changes.
| ONE FACTOR MODEL |
TWO FACTOR MODEL | FOUR FACTOR MODEL | HIERARCHICAL MODEL |
|||||
|---|---|---|---|---|---|---|---|---|
| Variable | General Change Factor |
F1 (Nonverbal change) |
F2 (Verbal change) |
F1 (Verbal change) |
F2 (Spatial change) |
F3 (Memory change) |
F4 (Speed change) |
Higher Order Factor of change |
| ENTIRE AGE RANGE (50–96 YEARS) | ||||||||
| Analogies Slope |
.445 (.216+/−.061) |
.722 (.215+/−.067) |
.797 (.247+/−.065) |
|||||
| Synonyms Slope |
.472 (.174+/−.057) |
.880 (.208+/−.055) |
.907 (.217+/−.055) |
|||||
| Information Slope |
.559 (.298+/−.067) |
.920 (.355+/−.067) |
.878 (.339+/−.071) |
|||||
| Block Design Slope |
.673 (.280+/−.049) |
.954 (.279+/−.051) |
.954 (.277+/−.051) |
|||||
| Figure Logic Slope |
.670 (.316+/−.074) |
.859 (.311+/−.074) |
.857 (.311+/−.074) |
|||||
| Card Rotations Slope |
.378 (.244+/−.061) |
.930 (.254+/−.055) |
.913 (.255+/−.055) |
|||||
| Digit Span Slope |
.144 (.091+/−.051) |
.393 (.092+/−.051) |
.376 (.088+/−.053) |
|||||
| Names and Faces Slope |
.519 (.288+/−.057) |
.961 (.285+/−.059) |
.962 (.283+/−.057) |
|||||
| Picture Memory Slope |
.522 (.302+/−.069) |
.964 (.297+/−.071) |
.974 (.306+/−.071) |
|||||
| Symbol Digit Slope |
.922 (.285+/−.043) |
.985 (.292+/−.043) |
1.000 (.310+/−.045) |
|||||
| Figure ID Slope |
.575 (.320+/−.061) |
.930 (.335+/−.061) |
.974 (.375+/−.063) |
|||||
| F1 |
.815 (.194+/−.065) |
|||||||
| F2 |
.798 (.798+/− .137) |
.809 (.809+/−.143) |
1.000 (.286+/−.049) |
|||||
| F3 |
.924 (.924+/−.145) |
.971 (.971+/−.139) |
1.000 (.303+/−.069) |
|||||
| F4 |
.623 (.623+/−.172) |
.917 (.917+/−.122) |
.839 (.839+/−.131) |
.873 (.269+/−.043) |
||||
| MIDDLE ADULTHOOD (50–65 YEARS) | ||||||||
| Analogies Slope |
−.245 (−.085+/−.188) |
.114 (.037+/−.263) |
.626 (.350+/−.745) |
|||||
| Synonyms Slope |
−.597 (−.070+/−.149) |
1.000 (.185+/−.094) |
.470 (.178+/−.282) |
|||||
| Information Slope |
−.246 (−.049+/−.133) |
.755 (.159+/−.122) |
.272 (.116+/−.400) |
|||||
| Block Design Slope |
.801 (.095+/−.112) |
.822 (.101+/−.100) |
.175 (.064+/−.098) |
|||||
| Figure Logic Slope |
.560 (.079+/−.172) |
.566 (.081+/−.155) |
.191 (.069+/−.196) |
|||||
| Card Rotations Slope |
.830 (.397+/−.218) |
.838 (.402+/−.210) |
.598 (.519+/−.165) |
|||||
| Digit Span Slope |
.173 (.041+/−.200) |
.135 (.032+/−.208) |
−.112 (−.084+/−.270) |
|||||
| Names and Faces Slope |
.464 (.088+/−.186) |
.505 (.096+/−.169) |
.222 (.127+/−.216) |
|||||
| Picture Memory Slope |
.025 (.008+/−.169) |
.057 (.018+/−.159) |
.071 (.042+/−.214) |
|||||
| Symbol Digit Slope |
.920 (.239+/−.129) |
.920 (.233+/−.120) |
1.000 (.292+/−.139) |
|||||
| Figure ID Slope |
.988 (.524+/−.149) |
.983 (.515+/−.149) |
.713 (.527+/−.165) |
|||||
| F1 | −.444 (−.155+/−.116) |
|||||||
| F2 | −.321 (−.321+/−.582 ) |
−.096 (−.096+/−.951) |
.783 (.044+/−.084) |
|||||
| F3 | .186 (.186+/−2.279) |
.174 (.174+/−1.599) |
.418 (−.017+/−.063) |
|||||
| F4 | −.482 (−.482+/−.553) |
.808 (.808+/−.323) |
.440 (.440+/−1.617) |
1.000 (.298+/−.110) |
||||
| OLDER ADULTHOOD (65–96 YEARS) | ||||||||
| Analogies Slope |
.745 (.238+/−.067) |
.736 (.239+/−.067) |
.825 (.289+/−.076) |
|||||
| Synonyms Slope |
.620 (.191+/−.080) |
.659 (.205+/−.086) |
.771 (.253+/−.098) |
|||||
| Information Slope |
.667 (.294+/−.092) |
.727 (.321+/−.100) |
.771 (.347+/−.108) |
|||||
| Block Design Slope |
.924 (.304+/−.055) |
.929 (.306+/−.055) |
.914 (.305+/−.059) |
|||||
| Figure Logic Slope |
.814 (.335+/−.092) |
.818 (.336+/−.092) |
.814 (.339+/−.098) |
|||||
| Card Rotations Slope |
.799 (.251+/−.078) |
.812 (.255+/−.076) |
.831 (.266+/−.076) |
|||||
| Digit Span Slope |
.382 (.119+/−.061) |
.392 (.122+/−.061) |
.409 (.129+/−.065) |
|||||
| Names and Faces Slope |
.811 (.298+/−.074) |
.813 (.297+/−.076) |
.819 (.296+/−.078) |
|||||
| Picture Memory Slope |
.843 (.338+/−.090) |
.836 (.335+/−.090) |
.876 (.349+/−.114) |
|||||
| Symbol Digit Slope |
.964 (.312+/−.051) |
.967 (.314+/−.051) |
.967 (.316+/−.059) |
|||||
| Figure ID Slope |
.854 (.328+/−.071) |
.862 (.330+/−.071) |
.889 (.349+/−.073) |
|||||
| F1 |
.827 (.228+/−.076) |
|||||||
| F2 |
.915 (.915+/−.165) |
.710 (.710+/−.239) |
1.000 (.313+/−.053) |
|||||
| F3 |
.889 (.889+/−.231) |
.964 (.964+/−.276) |
1.000 (.340+/−.088) |
|||||
| F4 |
.676 (.676+/−.212) |
.978 (.978+/−.202) |
.863 (.863+/−.286) |
.924 (.297+/−.053) |
||||
Note: Parameters in bold are significant in p<.01. Parameters in bold italics are significant at p<.05. Confidence intervals were calculated by multiplying the standard error of each estimate by 1.96.
Table 4.
Model Fit Indices for Single Factor, Two Factor, and Four Factor Models of Longitudinal Slopes.
| Model | LL | AIC | Χ2 Comparison With Single Factor Model (df) |
Χ2 Comparison With Two Factor Model (df) |
|---|---|---|---|---|
| ENTIRE AGE RANGE (50–96 YEARS) | ||||
| Single Factor Model | −29886.1 | 60002.18 | ||
| Two Factor Model | −29875.8 | 59985.7 | 16.175 (2) | |
| Four Factor Model | −29841.3 | 59938.53 | 65.483 (13) | 81.692 (11) |
| MIDDLE ADULTHOOD (50–65 YEARS) | ||||
| Single Factor Model | −11579.2 | 23388.4 | ||
| Two Factor Model | −11572.7 | 23379.4 | 10.821 (2) | |
| Four Factor Model | −11558.1 | 23372.27 | 17.112 (13) | 26.064 (11) |
| OLDER ADULTHOOD (65–96 YEARS) | ||||
| Single Factor Model | −18378.2 | 36986.42 | ||
| Two Factor Model | −18371.8 | 36977.68 | 7.050 (2) | |
| Four Factor Model | −18360.8 | 36977.63 | 27.951 (13) | 34.190 (11) |
Note: The best fitting models are highlighted in bold. All Χ2 comparisons are significant at p<.05. Chi squared values were calculated by applying model-specific scaling coefficients in conjunction with the differences in −2×logliklihood values of the models in question. The degrees of freedom of the model comparisons take into account differences in the numbers of estimated factor loadings in addition to differences in the numbers of estimated covariances.
To distinguish the extent to which domain-general versus domain-specific influences were operating on the changes, we went on to fit a hierarchical factor model that specified a higher order factor to underlie the relations among verbal, spatial, memory, and processing speed dimensions. Loadings on the higher-order global change factor are presented in the rightmost column of Table 3. It can be seen that for the entire age range and for older adulthood in specific, the loadings of the first order spatial and memory change factors on the higher order global factor is unity, the loading of the speed change factor on the global factor is approximately .9, and the loading of the verbal change factor on the global factor is approximately .8. In comparison, when middle adulthood is considered on its own, the loadings on the higher order factor are inconsistent, with only two out of four being statistically significant (on positive and one negative in magnitude). Moreover, while the correlations from the four correlated factors model were well approximated by the higher order factor for the entire age range and older adulthood (root mean square difference = .06 and .08 respectively), this was not the case for middle adulthood (room mean square difference = .19). These results are consistent with a strong domain-general dimension underlying aging related cognitive changes in older adulthood, but not in middle adulthood.
Focusing on the entire age range and older adulthood in specific, we went on to use the hierarchical solution to compute the average proportions of individual differences in changes in the 11 cognitive variables that were explained by the general factor, domain-specific factors, and that were unique the individual tests. We found that these proportions were 68%, 11%, and 21% respectively for the entire age range, and 52%, 8%, and 39% for older adulthood. These proportions are consistent with a strong domain-general dimension of variation in cognitive changes in older adulthood, but also indicate nontrivial domain-specific and test specific contributions to aging-related cognitive changes.
Finally, we performed exploratory factor analysis (EFA). This was done in two steps. First, we estimated a model in which the 11 growth curve slopes were all free to intercorrelate. We then submitted the estimated slope intercorrelation matrix to an exploratory factor analysis with oblique rotation. The eigen values for the entire age range (ages 50 to, 96, years), were, 7.394, 1.301, 0.909, 0.562, 0.321, , 0.201, 0.119, 0.065, 0.060, 0.038, and 0.030. The eigen values for middle adulthood (ages 50–65 years) were 3.334, 2.685, 1.489, 1.113, 0.866, 0.812, 0.302, 0.161, 0.121, 0.066, and 0.049. The eigen values for older adulthood (ages 65–96 years) were 6.220, 1.234, 0.936, 0.620, 0.526, 0.409, 0.359, 0.258, 0.204, 0.147, and 0.086. That the first eigen value for both the entire age range and for older adulthood were 7.394 and 6.220 indicates that a single dimensions captures a substantial amount of variation on aging-related cognitive changes (67% and 57% respectively. In contrast the first eigen value of 3.334 for middle adulthood indicates a much more modest amount of variance accounted for by a single dimension (30%). We went on to inspect parameter estimates from the two and four factor solutions for each age range. All three 2 factor solutions did differentiate somewhat along the verbal vs. nonverbal tests. However, the two factors were correlated at approximately .5 for the complete age range and for older adulthood, where the two factors were uncorrelated (r=.009) for middle adulthood. The four factor solutions were not readily interpretable, although there was a much more consistent pattern of positive factor correlations for the entire age range and for older adulthood than for middle adulthood. These EFA solutions are provided in the online supplement to this article.
Biometric Analyses
For phenotypic analyses of both the entire age range and of older adulthood in particular, results indicated a strong global dimension underlying variation in aging-related across the four cognitive domains. The purposes of our subsequent biometric analyses was to use similarity within monozygotic (MZ) and dizygotic (DZ) twins to estimate the extent to which this global dimension of change was attributable to a common set of genes for cognitive aging, and the extent to which there were genetic influences on these domain-specific dimensions of change. To reduce the complexity of our biometric models, we first created unit-weighted composite scores for each of the four cognitive domains, by summing the z transformed scores on the individual tests based on the mean and standard deviation of the corresponding test at the first wave. We then fit a biometric model that simultaneously fit growth curves with time varying dementia and occasion covariates to each of the four composite scores for each twin from each pair, partitioned level and change information into domain-general and domain-specific components, and decomposed each of these components, in turn, into genetic and environmental components. In order to allow for the estimation of general and specific dimensions of levels and change, our model specified the intercepts to load on a single common intercept factor, Fi, and the slopes to load on a single common slope factor, Fs, as in equation 1, 2a, and 2b presented earlier. Between-person differences in the common factors were decomposed into genetic and environmental variance components (Neale & Cardon, 1992):
| 3a |
| 3b |
where A is a latent factor representing additive genetic variation, E is a factor representing nonshared environmental variation, and a and e are model estimated parameters representing the respective degrees of influence of A and E. Based on quantitative genetic theory, the A factors were assumed to be correlated at 1.0 for MZ twins (who share all of their genes) and were assumed to be correlated at .50 for DZ twins (who on average share 50% of the genes that vary among humans).
Finally, between-person differences in the unique factors of each composite variable, v, (representing verbal, spatial, memory, and speed domains) were also decomposed into genetic and environmental variance components.
| 4a |
| 4b |
Corresponding A components and corresponding E components of levels and slopes from corresponding levels of analysis were allowed to correlate (e.g., the unique A factor for Speed level was allowed to correlate with the unique A factor for Speed slope, and the unique E factor for Speed level was allowed to correlate with the unique E factor for Speed slope). Note that the models described above did not estimate a factor representing the shared environment, as previous work with SATSA (e.g. Finkel et al., 2005), has indicated very little evidence for significant shared environmental variation in cognitive performance and cognitive change. Finally, it is important to note that although the growth curve, factor, and biometric portions of the models were written separately above, they were simultaneously estimated in one step.
Biometric Results
Biometric models were fit as two-level models in Mplus (Muthén & Muthén, 1998–2010) using a maximum likelihood estimation method that was robust to departures from normality. To facilitate model convergence, age was centered at 65 and divided by 10. Because our phenotypic analyses indicated that there was not strong evidence for a robust general dimension of aging-related cognitive changes when data from middle adulthood (ages 50–65 years) were analyzed separately, our biometric analyses were performed on data from the entire age range, and on data specifically from older adulthood (ages 65–90 years).
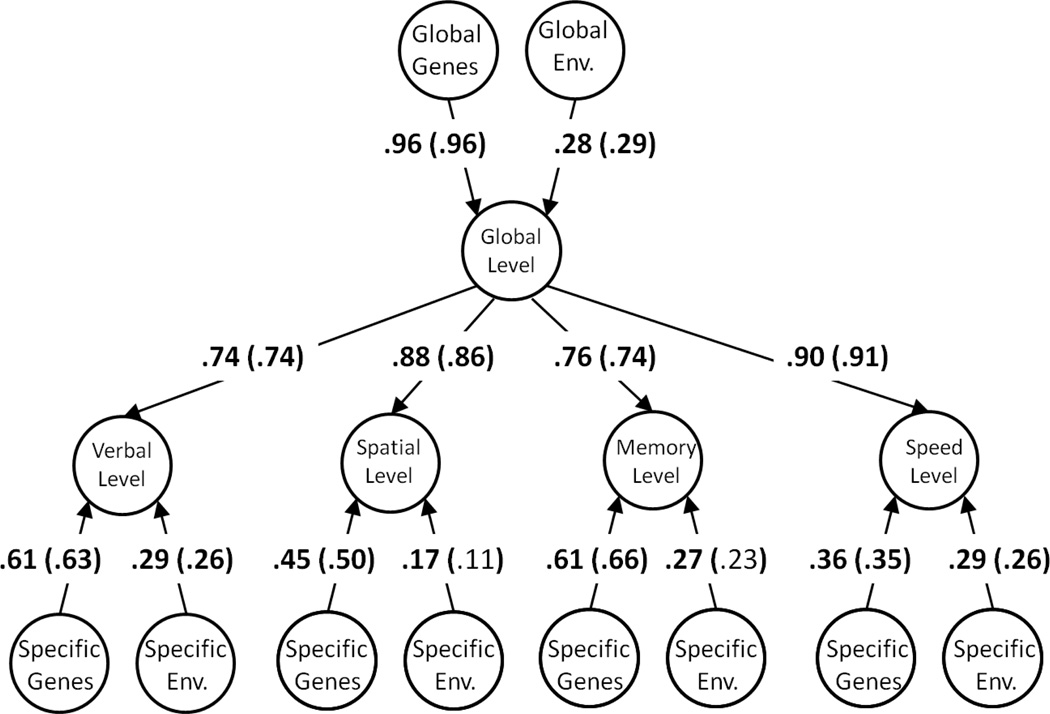
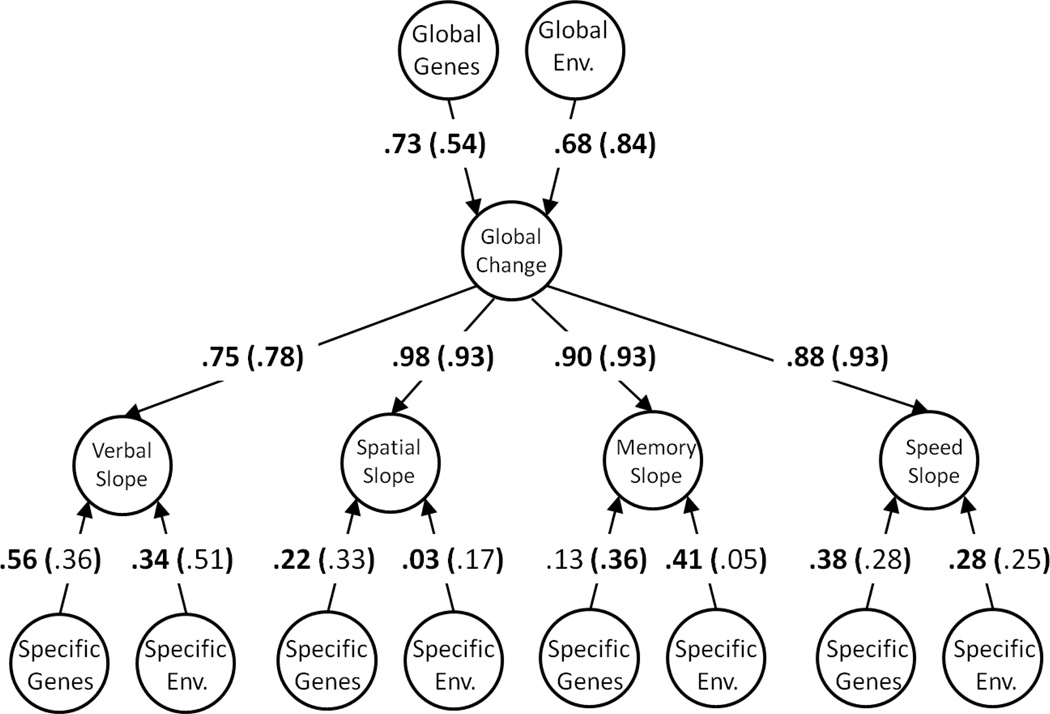
Both standardized and unstandardized parameter estimates from the multivariate biometric decomposition of the common and specific level and slope factors are presented in Table 5, both for the entire age range and for older adulthood. To more clearly illustrate these results, standardized parameter estimates are superimposed the corresponding paths in the path diagram representing the multivariate biometric decompositions of the levels in Figure 1, and the slopes in Figure 2. Beginning with the levels, it can be seen that there are strong genetic influences on the common factor, and moderate genetic influences unique to the domains. For both the entire age range and specifically in older adulthood genes account for 92% of the variation in the common factor of the levels, whereas the environment accounts for only 8%. This result is consistent with well-established findings (e.g. Petrill, 1997) of strong genetic influences on individual differences on the general factor of intelligence, and with other well-replicated findings that genetic influences on cognition are most pronounced in mid-to-late adulthood (McGue, Bouchard, Iacono, & Lykken, 1993). In comparison, the common factor of the slopes was influenced to a much larger degree by the environment. In the analysis of the entire age range, genes only accounted for 53% of the variation in the common slope in the global change factor, and in the analysis of older adulthood in particular, this proportion was 29%. Residual genetic influences were also apparent on the individual domains. These domain-specific genetic effects were statistically significant in three out of four of the domains in the analysis of the entire age range, but only statistically significant in one out of four of the domains in the analysis of older adulthood. Because the magnitudes of the parameters reflecting domain-specific genetic effects do not appear to be appreciably smaller from the analysis of older adulthood compared to the analysis of the entire age range, this difference in number of significant parameters is likely to be attributable to the lower power associated with analyzing only a subset of the data.
Table 5.
Parameter estimates for multivariate behavioral genetic growth curve models of levels and changes in cognitive abilities.
| Levels | Slopes | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Outcome | Loading on General A |
Loading on General E |
Loading on General Factor |
Loading on Specific A |
Loading on Specific E |
Loading on General A |
Loading on General E |
Loading on General Factor |
Loading on Specific A |
Loading on Specific E |
| ENTIRE AGE RANGE (50–96 YEARS) | ||||||||||
| Verbal |
.736 (1.156+/−.133) |
.610 (.494+/−.051) |
.294 (.238+/−.049) |
.750 (.899+/−.237) |
.564 (.131+/−.067) |
.344 (.080+/−.096) |
||||
| Spatial |
.877 (1.231+/−.131) |
.447 (.323+/−.045) |
.174 (.126+/−.061) |
.975 (1.368+/−.310) |
.221 (.060+/−.039) |
.033 (.009+/−.061) |
||||
| Memory |
.758 (©1) |
.608 (.413+/−.045) |
.234 (.159+/−.059) |
.903 (©1) |
.130 (.028+/−.039) |
.410 (.088+/−.055) |
||||
| Speed |
.895 (1.287+/−.135) |
.360 (.267+/−.067) |
.265 (.196+/−.065) |
.882 (1.398+/−.357) |
.381 (.117+/−.090) |
.277 (.085+/−.123) |
||||
| General Factor |
.961 (.495+/−.053) |
.276 (.142+/−.035) |
.732 (.142+/−.049) |
.681 (.132+/−.041) |
||||||
| OLDER ADULTHOOD (65–96 YEARS) | ||||||||||
| Verbal |
.736 (1.182+/−.155) |
.625 (.509+/−.074) |
.258 (.210+/−.112) |
.782 (.959+/−.282) |
.361 (.090+/−.186) |
.509 (.127+/−.139) |
||||
| Spatial |
.861 (1.254+/−.149) |
.496 (.366+/−.069) |
.112 (.083+/−.110) |
.928 (1.369+/−.361) |
.333 (.100+/−.063) |
.167 (.050+/−.094) |
||||
| Memory |
.741 (©1) |
.664 (.454+/−.067) |
.101 (.069+/−.200) |
.931 (©1) |
.362 (.079+/−.061) |
.050 (.011+/−.182) |
||||
| Speed |
.908 (1.397+/−.159) |
.349 (.272+/−.110) |
.232 (.181+/−.133) |
.928 (1.406+/−.386) |
.276 (.085+/−.106) |
.250 (.077+/−.216) |
||||
| General Factor |
.958 (.486+/−.065) |
.286 (.145+/−.065) |
.541 (.110+/−.108) |
.841 (.171+/−.073) |
||||||
Note: @1 indicates that a loading was fixed to 1 to identify the metric of the factor. Parameters in bold are significant in p<.01. Parameters in bold italics are significant at p<.05. Confidence intervals were calculated by multiplying the standard error of each estimate by 1.96.
Figure 1.
Standardized parameter estimates for behavioral genetic model of levels. Parameters outside of the parentheses are for a model applied to data from all ages (50–96 years). Parameters in parentheses are for a model applied to data from older adulthood (65–96 years). Parameters in bold are significant at p<.05. See Table 5 for unstandardized parameter estimates and confidence intervals.
Figure 2.
Standardized parameter estimates for behavioral genetic model of slopes. Parameters outside of the parentheses are for a model applied to data from all ages (50–96 years). Parameters in parentheses are for a model applied to data from older adulthood (65–96 years). Parameters in bold are significant at p<.05. See Table 5 for unstandardized parameter estimates and confidence intervals.
A complementary way of interpreting the results is to calculate the proportions of variance attributable to genes (A) and environments (E) occurring through the general level and change factors, and uniquely occurring on the individual domains. These proportions are presented in Table 6. It can be seen that genetic influences occur on both the general factor of levels and the general factor of slopes, although a much larger amount of genetic variance occurs through the global factor than occurs uniquely on the domains.
Table 6.
Proportions of variance attributable to genes (A) and environments (E) occurring through the general level and change factors, and uniquely occurring on the individual domains.
| Levels | Slopes | |||||||
|---|---|---|---|---|---|---|---|---|
| Domain | A via General |
E via General |
A Unique |
E Unique |
A via General |
E via General |
A Unique |
E Unique |
| ENTIRE AGE RANGE (50–96 YEARS) | ||||||||
| Verbal | 49.99% | 4.11% | 37.25% | 8.65% | 30.21% | 26.11% | 31.82% | 11.87% |
| Spatial | 71.12% | 5.85% | 19.98% | 3.04% | 50.98% | 44.05% | 4.86% | 0.11% |
| Memory | 53.15% | 4.37% | 37.00% | 5.48% | 43.72% | 37.78% | 1.70% | 16.79% |
| Speed | 73.93% | 6.08% | 12.99% | 7.00% | 41.76% | 36.08% | 14.50% | 7.66% |
| OLDER ADULTHOOD (65–96 YEARS) | ||||||||
| Verbal | 49.81% | 4.43% | 39.10% | 6.66% | 17.88% | 43.20% | 13.01% | 25.91% |
| Spatial | 68.11% | 6.06% | 24.56% | 1.26% | 25.20% | 60.91% | 11.11% | 2.78% |
| Memory | 50.46% | 4.49% | 44.03% | 1.02% | 25.37% | 61.30% | 13.08% | 0.25% |
| Speed | 75.72% | 6.74% | 12.15% | 5.38% | 25.21% | 60.93% | 7.62% | 6.25% |
Note: Proportions were calculated from multiple parameters from the multivariate behavioral genetic growth curve models. See Table 5 for individual parameter estimates and their associated confidence intervals.
Discussion
A classic and recurring issue within the area of cognitive aging has concerned extent to which the aging-related deficits observed in multiple aspects of cognitive function each represent a unique and independent phenomenon, a few more basic phenomena, or a single general phenomenon (Balinski, 1941; Rabbit, 1993; Salthouse & Czaja, 2000; Tucke-Drob, 2009; Tucker-Drob & Salthouse, 2011). For example, Salthouse & Czaja (2000, p. 33) asked “in accounting for the age-related influences on a variety of different cognitive variables, do researchers need… narrow and specific explanations, … broad and general explanations, or some mixture of the two?” Speculating that cognitive aging may represent a largely global phenomenon, Rabbitt (1993) asked “Does it all go together when it goes?” Most attempts to answer these questions have been unsatisfactory, as they have been based on cross-sectional data and are thus informative about the similarity of population-average trends in the aging of different cognitive abilities, but not about whether different abilities change together for specific individuals. Moreover, multivariate quantitative genetic models applied to data from a single time point, even if that time point is measured during later adulthood, are informative about the contributions of domain-general and domain-specific influences of genes and environments to overall levels of cognitive performance, but are not directly informative about the contributions of domain-general and domain-specific influences of genes and environments to aging-related cognitive changes. To move beyond these limitations, Deater-Deckard & Mayr (2005, p. 25) wrote:
“It will be critical to combine longitudinal studies that allow uncovering the dimensionality of change across a wide range of cognitive abilities, on the one hand, with quantitative genetic analyses, on the other. Such work will be essential to answering questions regarding to what extent—and, ultimately, in what ways—genetic and environmental influences cause change in the one or more cognitive aging factors.”
The current project took such an approach. Because of evidence that cognitive changes in middle adulthood may qualitatively differ from those occurring in later adulthood, we analyzed our data separately over two age ranges: ages 50 to 65, and ages 65 to 96. Indeed we found differing patterns of results across the two age ranges. Our multivariate longitudinal growth models indicated little evidence for cohesive dimensions underlying variability in aging-related changes in middle adulthood: test-specific rates of change tended to load at very low levels on more general factors, and these factors in turn tended not to be appreciably related. In contrast, there was strong evidence for cohesive dimensions of changes in late adulthood: test-specific changes loaded strongly on factors representative of changes in verbal ability, spatial ability, memory, and processing speed, and these domain-specific factors were in turn highly intercorrelated. When a higher order factor of change was superimposed on this structure, it accounted for substantial proportions of variation in the individual domains. As a subsequent step, we went on to combine our multivariate longitudinal growth curve approach with a quantitative genetic approach to estimate the extent to which genetic influences on cognitive changes occurring after age 65 years operated at domain-general and domain-specific levels. We found significant contributions of genes to cognitive change at both levels. In older adulthood, approximately one third of the variance in domain-general linear cognitive change was estimated to be influenced by genetic factors, and the remaining two thirds by environmental factors. Moreover, although the majority of genetic influences on cognitive changes were statistically mediated by the general change factor, there was also evidence for domain-specific genetic influences on cognitive changes. In sum, our results indicate that genetic influences on cognitive aging are neither entirely domain-specific nor entirely domain-general.
Explaining Differences Observed Before and After Age 65 Years
Because previous work (e.g. Finkel et al., 2003; Reynolds et al., 2005) has indicated distinct patterns of longitudinal cognitive changes before leading up to age 65, and following age 65, in may not be surprising that the multivariate structure of aging-related cognitive changes was also found to differ across these two age ranges. Our findings that a robust low-dimensional factor structure of aging-related cognitive changes does not emerge until later adulthood, is consistent with hypotheses that broadly-affecting constraints on cognitive function emerge and strengthen with age. This hypothesis finds it roots in the closely related age-dedifferentiation hypothesis that a common factor should account for increasing variability in cognitive abilities with advancing adult age (Balinsky, 1941, see, Tucker-Drob, 2009 and Tucker-Drob & Salthouse, 2008 for overviews of recent research on this hypothesis). More recently, Baltes and Lindenberger (1997, p. 17) have stated: “According to our common cause hypothesis, mechanisms related to brain aging function as a general and increasingly severe ‘common’ constraint for many different functional systems.” De Frias et al. (2007, p. 381) used a similar rationale to predict that “how individuals change in one cognitive ability is increasingly related to the ways they change in other cognitive abilities with advancing age.” Nevertheless, this finding is quite novel and in need of future replication. We are aware of only two other studies that have examined whether the extent to which a common factor underlies aging-related changes differs between middle and older adulthood. De Frias, Lovden, Lindenberger, & Nilsson (2007) sought to examine whether correlations among rates of change in recall, knowledge, fluency, and visuospatial ability increased from middle to late adulthood, but were unable to carry out this analysis because they did not detect individual differences in change prior to old age. However, their finding that variability in change increased with age was taken as consistent with the perspective that global sources of decline strengthen with age. Tucker-Drob (2011), fit a common factor to changes in abstract reasoning, spatial visualization, episodic memory, and processing speed, and found that the proportions of variance accounted for by that factor were 39%, 55%, and 53% in 18–49 years, 50–69 years, and 70–95 years age groups respectively. The differences across age groups, however, were not statistically significant. Future work on age differences in the multivariate structure of aging-related cognitive changes will be necessary before a definitive conclusion can be drawn regarding the emergence or strengthening of a common factor of longitudinal changes with age.
Limitations
While the current study represents a considerable improvement upon the few previous studies on the dimensionality of aging-related cognitive changes, it is still limited in a number of ways. First, as with any longitudinal project, not all participants remained in the study for its entirety. We therefore had to make use of modern missing data methods to deal with the possibility that attrition was nonrandom. The maximum likelihood estimation that we used assumed that any systematic patterns of missingness that related to the dependent variables could be accounted for via the patterns of relations that were observed in the nonmissing data. This is generally considered an acceptable assumption in longitudinal studies of cognitive aging, but it is nevertheless an untestable assumption. Second, while SATSA contains a diverse set of cognitive variables, it does not contain all variables that may be of interest to contemporary researchers. In particular, there were no direct measures of executive functions, such as switching, updating, or inhibition. Previous studies (e.g. Salthouse, 2005; Salthouse, Atkinson, & Berish, 2003) have found executive functions to be strongly related to spatial and memory abilities of the sort that were measured in SATSA. However, whether executive functions and other cognitive abilities change together in adulthood remains an unanswered question. Third, while longitudinal growth curve models represent a tremendous advantage over simple cross-sectional approaches, very large sample sizes and/or very long time intervals are often necessary to detect more nuanced effects. The multivariate biometric linear growth models fit for the current project were highly complex, and it is unlikely that even more complex models would have had sufficient power to parse nuanced effects such as small magnitude effects of shared or otherwise correlated childhood rearing environments, into common and domain-specific components. Fourth, factor models of psychological traits (or, as was the case for the current investigation, changes in psychological traits) are not informative about the dimensionality of the causes of the traits under investigation- they are only informative about the dimensionality individual differences in the traits themselves, and for testing the extent to which patterns of associations between the traits under investigation and other variables (such as associations with latent genetic and environmental variables) occur via the general or specific dimensions of the traits. An in-depth discussion of this issue is provided in Tucker-Drob (2011). Finally, the current project was limited in only providing a descriptive account of the aging process. We did not test whether specific genes, neurobiological substrates, or environmental experiences had general vs. specific effects on cognitive change, nor did we examine whether genes and environments interacted to predict different aspects of cognitive change. It will be important for future work to test hypotheses that concern specific causal factors.
Implications for Research and Theory
It is important to consider how the current findings should be interpreted, and what they do and do not imply about the genetics of cognitive aging. First, our factor analyses of longitudinal cognitive changes were informative about the number of behavioral dimensions (within the set of variables examined) on which the causes of cognitive change are manifest, but, as stated above, were not informative about the number of distinct causes of cognitive changes that were operating. In other words, our finding that a global dimension can account for large proportions of variation in aging-related cognitive changes in older adulthood indicates that late-life cognitive aging is manifest in a largely global pattern of change across multiple variables, but does not indicate that a single cause is responsible for global changes. It is very possible, if not likely, that many thousands of genetic and environmental causes of cognitive aging exist. What the current findings indicate is that, in late adulthood, these many causes tend to operate at very broad levels to affect many forms of cognition.
Building on this point, it is important to keep in mind that our application of quantitative genetic modeling does not assume the existence of a single or small number of genes for cognitive aging, each with large effects. In fact, quantitative genetic models assume quite the opposite: latent variables are modeled as normally distributed continuous variables, an approach that relies on the assumption of strong polygenicity (many genes affecting the trait). Indeed, the concept of polygenicity has recently aided in progress towards resolving what has come to be termed the “missing heritability” paradox- the finding that the proportion of variance in complex traits that can be accounted for in total by robust associations with specific genetic variants is miniscule in comparison to the proportion of variance that quantitative genetic studies of twins and adoptees indicates is accounted for by genes in total (see Turkheimer, 2011, for a sophisticated discussion of this issue). Studies that make use of measurements of hundreds of thousands of molecular genetic markers have established that complex behavioral traits, such as intelligence are “highly heritable and polygenic” (Davies et al., 2011). In other words, recent molecular genetic research indicates that a core assumption of the quantitative genetic approach is correct: complex traits are affected by a large number of genes, each with very small effects (Yang et al., 2010). Our finding that in older adulthood, genetic influences on changes in multiple cognitive functions occur largely via a global factor of change indicates that a large proportion of the many small genetic effects that are likely to occur for cognitive aging in older adulthood are effects that are shared across multiple cognitive variables.
Finally, it is important to emphasize that our findings of genetic influences on global cognitive change do not indicate that genetic influences on cognitive aging are deterministic or that cognitive aging is impervious to intervention. First, our estimates of genetic and environmental variance components represent the amount of variance in cognitive changes that naturally occurred in the social and historical contexts in which the SATSA participants lived during the course of the study. Social, educational, medical, and economic policy and intervention can not only affect the amount of variance attributable to environmental factors, but also have the potential to affect the amount of variance attributable to genetic factors, for instance, via environmental experiences that suppress or amplify gene expression. Second, our estimates of genetic variance do not necessarily all reflect direct biological pathways between gene-to-protein-to-neurobiology-to-cognition, but may also reflect environmentally-mediated pathways. For instance, genes can influence proteins that influence neurotransmitters that influence personality factors that in turn influence health and exercise decisions which in turn affect cognitive aging trajectories. Developmental processes that give way to such patterns of gene-environment correlation are discussed in detail by Scarr & McCartney (1983) and Deater-Deckard and Mayr (2005). Turkheimer (2000) has emphasized likelihood that the pathway from genotype to phenotype is likely to be highly complex, interactive, and even bidirectional.
Conclusion
In conclusion, we found that a four factor model best described individual differences in aging-related longitudinal changes in multiple measures of verbal, spatial, memory, and processing speed abilities, particularly in older adulthood. In middle adulthood, loadings on the four factors were weak, and the four factors were not robustly correlated, indicating that cognitive changes occur largely independently of one another with during this age period. In contrast, in older adulthood, the individual rates of change had strong loadings on the four factors, indicating robust common dimensions of aging-related cognitive decline. Moreover, in older adulthood, the four factors were highly intercorrelated and when specified to load on a higher order global change factor, had very strong loadings on this factor, indicating that a global domain-general dimension substantially underlies variability in aging-related changes in late adulthood. When multivariate longitudinal behavior genetic models were fit to the data from older adulthood, 29% of the variance of this global dimension of change was found to be accounted for by genes. However, genes also contributed moderately to residual variation in the specific domains. While the results are quite valuable in describing the general patterns by which cognitive functions change in adulthood, future research will be necessary to identify the specific explanatory mechanisms that underlie these patterns.
Supplementary Material
Acknowledgements
The Swedish Adoption/Twin Study of Aging is supported by the National Institute on Aging (Grants AG04563 and AG10175), the MacArthur Foundation Research Network on Successful Aging, and the Swedish Research Council (Grant 97:0147:1B, 2009-0795). The Population Research Center at the University of Texas at Austin is supported by a center grant from the National Institute of Child Health and Human Development (R24 HD042849).
Footnotes
The availability of 16 year longitudinal data allowed us to compare distinct periods of development, rather than merely compare distinct groups of individuals We therefore grouped datapoints, rather than individuals, into middle and late adulthood periods, with some individuals contributing datapoints during both middle adulthood and older adulthood.
References
- Anstey KJ, Hofer SM, Luszcz MA. A latent growth curve analysis of late-life sensory and cognitive function over 8 years: Evidence for specific and common factors underlying change. Psychology and Aging. 2003;18:714–726. doi: 10.1037/0882-7974.18.4.714. [DOI] [PubMed] [Google Scholar]
- Balinsky B. An analysis of the mental factors of various age groups from nine to sixty. Genetic Psychology Monographs. 1941;23:191–234. [Google Scholar]
- Baltes PB, Lindenberger U. Emergence of a powerful connection between sensory and cognitive functions across the adult life span: A new window to the study of cognitive aging? Psychology and Aging. 1997;12:12–21. doi: 10.1037//0882-7974.12.1.12. [DOI] [PubMed] [Google Scholar]
- Baltes PB, Nesselroade JR. History and rationale of longitudinal research. In: Nesselroade JR, Baltes PB, editors. Longitudinal Research in the Study of Behavior and Development. New York: Academic Press; 1979. pp. 1–39. [Google Scholar]
- Christensen H, Mackinnon A, Jorm AF, Korten A, Jacomb P, Hofer SM, Henderson S. The Canberra Longitudinal Study: Design, Aims, Methodology, Outcomes, and Recent Empirical Investigations. Aging Neuropsychology and Cognition. 2004;11:169–195. [Google Scholar]
- Davies G, Tenesa A, Payton A, Yang J, Harris SE, Liewald D, Deary IJ. Genome-wide association studies establish that human intelligence is highly heritable and polygenic. Molecular Psychiatry. 2011;16:996–1005. doi: 10.1038/mp.2011.85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deater-Deckard K, Mayr U. Cognitive change in aging: Identifying gene- environment correlation and nonshared environmental mechanisms. Journals of Gerontology, Series B: Social Sciences. 2005;60:24–31. doi: 10.1093/geronb/60.special_issue_1.24. [DOI] [PubMed] [Google Scholar]
- Ferrer E, Salthouse TA, McArdle JJ, Stewart WF, Schwartz BS. Multivariate modeling of age and retest in longitudinal studies of cognitive abilities. Psychology and Aging. 2005;20:412–422. doi: 10.1037/0882-7974.20.3.412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finkel D, Pedersen NL, McGue, McClearn GE. Heritability of cognitive abilities in adult twins: Comparison of Minnesota and Swedish data. Behavior Genetics. 1995;25:421–431. doi: 10.1007/BF02253371. [DOI] [PubMed] [Google Scholar]
- Finkel D, Reynolds CA, McArdle JJ, Gatz M, Pedersen NL. Latent growth curve analyses of accelerating decline in cognitive abilities in late adulthood. Developmentla Psychology. 2003;39:535–550. doi: 10.1037/0012-1649.39.3.535. [DOI] [PubMed] [Google Scholar]
- Finkel D, Reynolds CA, McArdle JJ, Pedersen NL. The longitudinal relationship between processing speed and cognitive ability: Genetic and environmental influences. Behavior Genetics. 2005;35:535–549. doi: 10.1007/s10519-005-3281-5. [DOI] [PubMed] [Google Scholar]
- Finkel D, Reynolds CA, McArdle JJ, Hamagami F, Pedersen NL. Genetic variance in processing speed drives variation in aging of spatial and memory abilities. Developmental Psychology. 2009;45:820–834. doi: 10.1037/a0015332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Frias CM, Lövdén M, Lindenberger U, Nilsson L-G. Revisiting the dedifferentiation hypothesis with longitudinal multi-cohort data. Intelligence. 2007;35:381–392. [Google Scholar]
- Gatz M, Pedersen NL, Berg S, Johansson B, Johansson K, Mortimer JA, et al. Heritability for Alzheimer’s disease: The study of dementia in Swedish twins. Journals of Gerontology: Series A: Biological Sciences and Medical Sciences. 1997;52:M117–M125. doi: 10.1093/gerona/52a.2.m117. [DOI] [PubMed] [Google Scholar]
- Ghisletta P, Rabbitt P, Lunn M, Lindenberger U. Two thirds of the age-based changes in fluid and crystallized intelligence, perceptual speed, and memory in adulthood are shared. Intelligence. 2012;40:260–268. [Google Scholar]
- Harris SE, Deary IJ. The genetics of cognitive ability and cognitive ageing in healthy older people. Trends in Cognitive Sciences. 2011;15:388–394. doi: 10.1016/j.tics.2011.07.004. [DOI] [PubMed] [Google Scholar]
- Hertzog C, Dixon RA, Hultsch DF, MacDonald SWS. Latent change models of adult cognition: Are changes in processing speed and working memory associated with changes in episodic memory? Psychology and Aging. 2003;18:755–769. doi: 10.1037/0882-7974.18.4.755. [DOI] [PubMed] [Google Scholar]
- Jensen AR. The G factor: The science of mental ability. Westport, CT: Praeger; 1998. [Google Scholar]
- Kovas Y, Plomin R. Generalist genes: Implications for the cognitive sciences. Trends in Cognitive Sciences. 2006;10:198–203. doi: 10.1016/j.tics.2006.03.001. [DOI] [PubMed] [Google Scholar]
- Lemke U, Zimprich D. Longitudinal changes in memory performance and processing speed in old age. Aging, Neuropsychology, and Cognition. 2005;12:57–77. [Google Scholar]
- Lindenberger U, Ghisletta P. Cognitive and sensory declines in old age: Gauging the evidence for a common cause. Psychology and Aging. 2009;24:1–16. doi: 10.1037/a0014986. [DOI] [PubMed] [Google Scholar]
- McArdle JJ, Prescott CA, Hamagami F, Horn JL. A contemporary method for developmental-genetic analyses of age changes in intellectual abilities. Developmental Neuropsychology. 1998;14:69–114. [Google Scholar]
- McArdle JJ, Woodcock RW. Expanding test–retest designs to include developmental time-lag components. Psychological Methods. 1997;2:403. [Google Scholar]
- McGue M, Bouchard TJJ, Iacono WG, Lykken DT. Behavior genetics of cognitive ability: A life-span perspective. In: Plomin R, McClearn GE, editors. Nature, nurture, and psychology. Washington, DC: American Psychological Association; 1993. pp. 59–76. [Google Scholar]
- McGue M, Christensen K. The heritability of level and rate-of-change in cognitive functioning in Danish twins aged 70 years and older. Experimental Aging Research. 2002;28:435–451. doi: 10.1080/03610730290080416. [DOI] [PubMed] [Google Scholar]
- Muthén BO, Muthén L. MPlus user’s guide. Sixth Edition. Los Angeles, CA: Muthén and Muthén; 1998–2010. [Google Scholar]
- Neale MC, Cardon LR. Methodology for genetic studies of twins and families. Dordrecht: Kluwer; 1992. [Google Scholar]
- Pedersen NL, Plomin R, Nesselroade JR, McClearn GE. A quantitative genetic analysis of cognitive abilities during the second half of the life span. Psychological Science. 1992;3:346–353. [Google Scholar]
- Petrill SA. Molarity versus modularity of cognitive functioning? A behavioral genetic perspective. Current Directions in Psychological Science. 1997;6:96–99. [Google Scholar]
- Plomin R, Spinath FM. Genetics and general cognitive ability (g) Trends in Cognitive Sciences. 2002;6:169–176. doi: 10.1016/s1364-6613(00)01853-2. [DOI] [PubMed] [Google Scholar]
- Rabbitt P. Does it all go together when it goes? The Nineteenth Bartlett Memorial Lecture. The Quarterly Journal of Experimental Psychology. 1993;46:385–434. doi: 10.1080/14640749308401055. [DOI] [PubMed] [Google Scholar]
- Reynolds CA, Gatz M, Pedersen NL. Individual variation for cognitive decline: Quantitative patterns for describing patterns of change. Psychology and Aging. 2002;17:271–287. [PubMed] [Google Scholar]
- Reynolds CA, Finkel D, McArdle JJ, Gatz M, Berg S, Pedersen NL. Quantitative Genetic Analysis of Latent Growth Curve Models of Cognitive Abilities in Adulthood. Developmental Psychology. 2005;41:3–16. doi: 10.1037/0012-1649.41.1.3. [DOI] [PubMed] [Google Scholar]
- Reynolds CA, Gatz M, Prince JA, Berg S, Pedersen NL. Serum lipid levels and cognitive change in late life. Journal of the American Geriatrics Society. 2010;58:501–509. doi: 10.1111/j.1532-5415.2010.02739.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salthouse TA. How many causes are there of aging-related decrements in cognitive functioning? Developmental Review. 1994;14:413–437. [Google Scholar]
- Salthouse TA. Localizing age-related individual differences in a hierarchical structure. Intelligence. 2004;32:541–561. doi: 10.1016/j.intell.2004.07.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salthouse TA, Atkinson TM, Berish DE. Executive functioning as a potential mediator of age-related cognitive decline in normal adults. Journal of Experimental Psychology: General. 2003;132:566–594. doi: 10.1037/0096-3445.132.4.566. [DOI] [PubMed] [Google Scholar]
- Salthouse TA. Relations between cognitive abilities and measures of executive functioning. Neuropsychology. 2005;19:532–545. doi: 10.1037/0894-4105.19.4.532. [DOI] [PubMed] [Google Scholar]
- Salthouse TA. Decomposition age correlations on neuropsychological and cognitive variables. Journal of the International Neuropsychological Society. 2009;15:650–661. doi: 10.1017/S1355617709990385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salthouse TA, Czaja S. Structural constraints on process explanations in cognitive aging. Psychology and Aging. 2000;15:44–55. doi: 10.1037//0882-7974.15.1.44. [DOI] [PubMed] [Google Scholar]
- Salthouse TA, Ferrer-Caja E. What needs to be explained to account for age-related effects on multiple cognitive variables? Psychology and Aging. 2003;18:91–110. doi: 10.1037/0882-7974.18.1.91. [DOI] [PubMed] [Google Scholar]
- Salthouse TA, Tucker-Drob EM. Implications of short-term retest effects for the interpretation of longitudinal change. Neuropsychology. 2008;22:800–811. doi: 10.1037/a0013091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scarr S, McCartney K. How people make their own environments: A theory of genotype→environment effects. Child Development. 1983;54:424–435. doi: 10.1111/j.1467-8624.1983.tb03884.x. [DOI] [PubMed] [Google Scholar]
- Tucker-Drob EM. Differentiation of cognitive abilities across the life span. Developmental Psychology. 2009;45:1097–1118. doi: 10.1037/a0015864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tucker-Drob EM, Johnson KE, Jones RN. The cognitive reserve hypothesis: A longitudinal examination of age-associated declines in reasoning and processing speed. Developmental Psychology. 2009;45:431–446. doi: 10.1037/a0014012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tucker-Drob EM. Global and domain-specific changes in cognition throughout adulthood. Developmental Psychology. 2011a;47:331–343. doi: 10.1037/a0021361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tucker-Drob EM. Neurocognitive functions and everyday functions change together in old age. Neuropsychology. 2011b;25:368–377. doi: 10.1037/a0022348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tucker-Drob EM, Salthouse TA. Adult age trends in the relations among cognitive abilities. Psychology and Aging. 2008;23:453–460. doi: 10.1037/0882-7974.23.2.453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tucker-Drob EM, Salthouse TA. Individual differences in cognitive aging. In: Chamorro-Premuzic T, von Stumm S, Furnham A, editors. The Wiley-Blackwell Handbook of Individual Differences. First Edition 2011. [Google Scholar]
- Turkheimer E. Three laws of behavior genetics and what they mean. Current Directions in Psychological Science. 2000;9:160–164. [Google Scholar]
- Turkheimer E. Still missing. Research in Human Development. 2011;8:227–241. [Google Scholar]
- Wilson RS, Beckett LA, Barnes LL, Schneider JA, Bach J, Evans DA, Bennett DA. Individual differences in rates of change in cognitive abilities of older persons. Psychology and Aging. 2002;17:179–193. [PubMed] [Google Scholar]
- Yang J, Benyamin B, McEvoy BP, Gordon S, Henders AK, Nyholt DR, Madden PA, Heath AC, Martin NG, Montgomery GW, Goddard ME, Visscher PM. Common SNPs explain a large proportion of the heritability for human height. Nature Genetics. 2010;42:565–569. doi: 10.1038/ng.608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zelinski EM, Stewart ST. Individual differences in 16-year memory changes. Psychology and Aging. 1998;13:622–630. doi: 10.1037//0882-7974.13.4.622. [DOI] [PubMed] [Google Scholar]
- Zimprich D, Martin M. Can longitudinal changes in processing speed explain longitudinal age changes in fluid intelligence? Psychology and Aging. 2002;17:690–695. doi: 10.1037/0882-7974.17.4.690. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.