A SVM-based Quantitative fMRI Method For Resting State Functional Network Detection

Abstract

Resting state functional magnetic resonance imaging (fMRI) aims to measure baseline neuronal connectivity independent of specific functional tasks and to capture changes in the connectivity due to neurological diseases. Most existing network detection methods rely on a fixed threshold to identify functionally connected voxels under the resting state. Due to fMRI non-stationarity, the threshold cannot adapt to variation of data characteristics across sessions and subjects, and generates unreliable mapping results. In this study, a new method is presented for resting state fMRI data analysis. Specifically, the resting state network mapping is formulated as an outlier detection process that is implemented using one-class support vector machine (SVM). The results are refined by using a spatial-feature domain prototype selection method and two-class SVM reclassification. The final decision on each voxel is made by comparing its probabilities of functionally connected and unconnected instead of a threshold. Multiple features for resting state analysis were extracted and examined using a SVM-based feature selection method, and the most representative features were identified. The proposed method was evaluated using synthetic and experimental fMRI data. A comparison study was also performed with independent component analysis (ICA) and correlation analysis. The experimental results show that the proposed method can provide comparable or better network detection performance than ICA and correlation analysis. The method is potentially applicable to various resting state quantitative fMRI studies.

1. Introduction

The human brain is organized into multiple functional connectivity networks. With advances of functional magnetic resonance imaging (fMRI) technology, it is feasible to characterize brain functional network in vivo using resting state fMRI [1,2]. Recent studies have demonstrated a great potential of resting state fMRI for various neuroscience and clinical applications, such as characterization of Alzheimer’s disease, schizophrenia, attention-deficit hyperactivity disorder, autism, and neurosurgical planning [2–8]. However, reliable mapping of resting state functional networks remains a challenge because BOLD signals usually have a low signal-to-noise ratio under resting state.

The most commonly used methods for detecting a resting state network are parametric model-based hypothesis driven approaches where the network is detected by comparing the temporal profile of each voxel with that of a seed via regression or correlation analyses. Test statistics extracted using these methods are quantified by statistical parametric models. If a voxel’s test statistic is above a predefined threshold with respect to a parametric model, then the voxel is considered as functionally connected to the seed. The hypothesis driven approaches are originated from task-related fMRI studies where the role of a seed is replaced by a task stimulation paradigm. In task-related fMRI studies, the choices of model and threshold usually depend on experiential knowledge, and no single modeling or thresholding approach has been approved to be optimal [9]. In addition, the spatial extent of activated brain regions identified using a statistical threshold depends on “the quality and quantity of signal acquired” instead of the real boundaries of brain function [10,11]. These statements can be extended to the resting state fMRI studies because the methodology of using parametric model and threshold is the same for both types of studies.

Due to fMRI non-stationarity [12,13], fMRI signal and noise characteristics change across sessions and subjects even under identical imaging conditions [14–17]. In order to obtain correct inference, the underlining assumption of probability distribution and/or significance threshold should be changed accordingly. This issue was discussed in task-related fMRI studies [11,18]. A similar issue was also oticed in a graph-based test-retest evaluation of resting state fMRI [19]. However, it is difficult to know how the model and threshold should be adjusted. Consequently, ambiguities could be generated from the analysis results. For example, in a single-subject multi-session experiment, an increase of functionally connected brain area was observed compared to the previous sessions. It is not clear if this increase is due to the change of brain function, or improper setting of the threshold. Therefore, quantitative analysis methods that 1) can automatically adapt to signal and noise variation, and 2) are not affected by arbitrarily or experientially chosen thresholds are desired for the resting state fMRI research.

Nonparametric data driven methods, such as clustering [20–23], principal component analysis (PCA) [24,25], and independent component analysis (ICA) [26–28], have been paid increased attention in recent years for resting state fMRI. These methods do not superimpose parametric models to test statistics, and may adapt to the variation of data characteristics. However, specific issues have to be considered when these methods are used for resting state fMRI. Clustering techniques, such as K-means [23,29,30], implicitly assume that clusters are hyper-spherical or hyper-ellipsoidal and separable in a feature space, which are not always true. Any brain voxel, no matter being part of a network or not, will always be assigned to a class by the clustering process. If a brain region is part of more than one network, then the clustering could split the region into multiple sub-regions, each of which is considered a network, leading to incorrect mapping results [22]. Additionally, the determination of cluster number is an unsolved challenge although there are various theoretical criteria. PCA only considers the second order statistics that are not sufficient to characterize fMRI data structure [31]. Since resting state functional signal is at similar or lower intensity levels than confounding noise and artifacts, noise patterns that are not orthogonal to the signal could be characterized by principal components that also contain signal information [32], leading to unreliable network detections. ICA considers high-order dependencies among multiple voxels and performs better than PCA in several task-related comparison studies [33,34]. ICA has also been shown an efficient tool for resting state fMRI [8,35]. When ICA methods are used, it should be aware that the assumptions of linear combinations of spatial (or temporal) independent sources, unknown number of signal and noise sources, suboptimal initialization of un-mixing matrix, and suboptimal solution of ICA could lead to improper decomposition of signal and noise [33,36]. Similar to clustering, ICA results are usually not corresponding to a unique network because there exists multiple networks and each slice may contain regions belong to different networks. Therefore, ICA results need to be either visually inspected or compared to spatial templates to obtain expected networks [1,27,37].

In this work, we study another data driven technique, support vector machine (SVM), for its application in resting state fMRI study. SVM is a supervised classification tool that can automatically learn a classification hyperplane in a feature space by optimizing margin-based criteria [38]. Nonlinearity can be introduced into the SVM learning using the kernel methods [39]. SVM has been used to classify brain cognitive states under task stimulation [40–42]. More recently, it was applied to resting state fMRI for the classification of major depressive disorder [43], schizophrenia [44], Asperger disorder [45], drug induction [46,47], and adolescent brains from normal adult brains [48–50]. In these studies, SVM was used to classify specific brain states in a supervised way. Due to inter- and intra-subject variability, an SVM trained using a data set from a subject at certain time may not perform well across sessions and subjects. Therefore, these methods are not suitable for the general detection of resting state functional networks. In our previous work [51], a SVM-based method was developed for the general brain activation detection under various task stimulus. It has been successfully applied to a quantitative fMRI study where a comparison of brain activation across multiple animal subjects over a learning process was required [52]. This method is not directly applicable to resting state fMRI because it cannot distinguish functional signal and noise under resting state. In this work we propose a SVM-based method to detect resting state functional network. The method differs from existing approaches from two major aspects: first, it can adapt to the inter-session and inter-subject variation in fMRI data, and does not need a significance threshold for the final detection. Second, compared to existing SVM-based methods, it is a network detection method, not a classification method.

2. Material and Methods

2.1 Problem Formulation

A recent study on more than 8000 subjects shows that the functionally connected voxels in a specific network constitute less than 50% of all brain voxels [53]. This forms the basic assumption of the proposed method. With this assumption, the mapping of a functional network can be considered as an outlier detection procedure. One-class SVM (OCSVM) is an efficient tool for outlier detection, where the voxels within a network are treated as the “outliers”, and the other voxels are considered as the “majority”. The OCSVM parameter v determines an upper bound of number of voxels that are detected as “outliers”. This parameter is network-specific and cannot be accurately set due to inter-session and inter-subject variation. Consequently, OCSVM can only provide an initial mapping, and we need to develop a method that is not affected by inaccurate setting of v.

2.2 Proposed Method

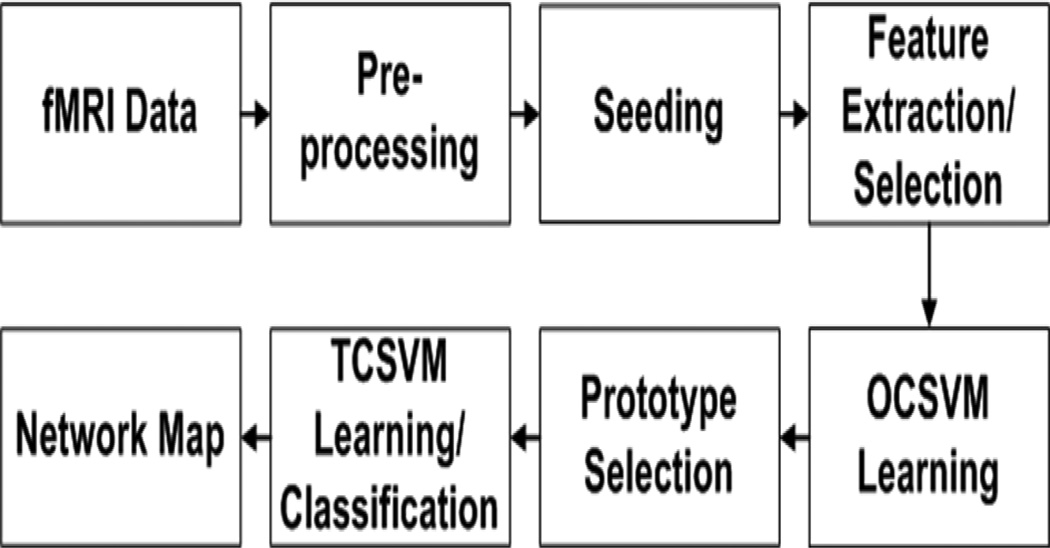
Figure 1 is the block diagram of the proposed method. The input fMRI data are first preprocessed to remove subject movement artifacts, and filtered spatially and temporally. Then a seed is selected from a brain region that is part of a specific functional network, based upon which multiple features are extracted from each voxel. An offline feature selection was performed to select most representative features to represent each voxel. Based on the selected features, an OCSVM is used to provide an initial mapping of the network. The prototype selection aims to identify voxels that are correctly classified as part of the network by OCSVM. The identified voxels are used to train a two-class SVM (TCSVM) to reclassify all voxels to obtain the final network mapping. The details of these steps are described in the following subsections.

Figure 1.

The block diagram of the proposed method. The OCSVM learning provides an initial mapping of a functional network based on a seed. Training prototypes are selected via the prototype selection, and the selected prototypes are used to train a TCSVM to re-classify the original fMRI data to obtain a refined network map.

2.2.1 Preprocessing and Seeding

Small subject movement artifacts in fMRI data are first attenuated using a 2D rigid body registration method [54], which is embedded in the FSL package [55]. Then the data are spatially smoothed using a wavelet domain Bayesian noise removal method [56], and low-pass filtered at a cut-off frequency of 0.1 Hz to extract low frequency fluctuations of interest in resting state. All fMRI data were normalized to zero mean and unit variance. A seed region that belongs to a network of interest is manually identified from the preprocessed fMRI data.

2.2.2 Feature Extraction and Selection

The average time course (TC) of the selected seed is first calculated. For each voxel, eleven candidate features are extracted to represent this voxel [29,51]. These features can be categorized into temporal and spatiotemporal features. Temporal features capture temporal characteristics of the voxel, including the Pearson’s correlation coefficient (cc) between the seed and voxel, the maximum intensity of the voxel’s TC, the signed extreme value of the cross correlation function (ccf) between the seed and voxel, and p value of Student’s t test. The spatiotemporal features are computed using the 3×3 neighborhood of the voxel, including the average, maximum and minimum cc values between the seed and voxels within the neighborhood, the average signed extreme value of the ccfs between the seed and voxels in the neighborhood, and the average, maximum and minimum cc values between the voxel and other voxels within its neighborhood. All features are normalized between 0 and 1 as required by the SVM learning. Other features that could facilitate the network detection can also be added to the analysis.

Not all features can contribute to the SVM-based network detection. An offline feature selection is necessary to identify most representative features. In this work, a SVM-based feature selection method was used to quantify the contribution of each candidate feature to the construction of SVM classification hyperplane [57]. Given the d^th candidate feature, its contribution I^d is estimated by the integration of the first derivative of the SVM decision function f_c with respect to the feature $x_i^d$ around the hyperplane, and is approximated by [57]:

$$I^d\approx \sum _{i=1}^{N_{SV}}|\frac{\partial f_c}{\partial x_i^d}|=\sum _{i=1}^{N_{SV}}|\sum _{j=1}^{N_{SV}}{\alpha }_j{y}_j{K}^d({\mathbf{x}}_j,{\mathbf{x}}_i)|,$$ (1)

where N_SV is the number of total support vectors, x_i is the i^th support vector, and $x_i^d$ is the d^th feature of x_i, y_j ∈ {−1, 1} is the class label of x_j, and α_j is the Lagrange multiplier defined in SVM formulation [38]. K(x_j,x _i) is a kernel defining a dot product between projections of x_i and x_j in a feature space [39], and K^d(x _j,x_i) is the first derivative of the kernel regarding the d^th dimension evaluated at x_i. An I^d value from a stand-alone feature does not provide any useful information. Only when comparing I^d values from multiple features, a larger I^d value indicates a greater contribution to the SVM learning.

Since the p -value from Student’s t test follows a uniform distribution between 0 and 1, from a pattern recognition aspect, it is the least discriminative feature compared to the others. If a feature is more discriminative than the p-value, it should receive a greater I^d value. All candidate features were examined and the results are described in section 3.1. After the feature selection, the top r features with the highest I^d value are used to represent brain voxels for the OCSVM and TCSVM learning.

2.2.3 Initial Detection Using OCSVM

OCSVM learns a linear classification hyperplane in a feature space to separate a pre-specified fraction of data with the maximum distance to the origin. The detailed technical review of OCSVM can be found in its original article [58]. Kernel methods are often used to extend the linear OCSVM to a nonlinear one [39]. A kernel function can project the original features into a higher dimensional feature space where a linear classification hyperplane learned by OCSVM is equivalent to a nonlinear classification in the input space. In this work, the radial basis function (RBF) kernel was used to implement nonlinear OCSVM classification. The RBF kernel is widely used in various complex pattern classification tasks. It is defined as: k(x,x_i) = e^−γ||x–x_i^||2, where γ is the kernel width parameter. A large γ value corresponds to a small kernel width that introduces more nonlinearity to the analysis than a large kernel width. The kernel width may significantly affect the classification performance. In practice, γ is usually experientially determined or estimated by cross validation.

The OCSVM implements an unsupervised learning on the selected features to provide an initial detection of a network of interest. As described in section 2.1, it is almost impossible to accurately set the OCSVM parameter v that controls the number of voxels detected as part of the network. The following strategy is used to set v [51]: (1) If v is entirely unknown, we may set v to be relatively large but no greater than 0.5 to guarantee a sufficient detection sensitivity. (2) If v is approximately known a priori from previous experiments, we may define a range with possible v values, and any value within this range can be used for OCSVM.

2.2.4 Prototype Selection

A prototype consists of a feature vector representing a voxel and its class label (functionally connected or unconnected). OCSVM results usually contain a significant number of mis-detections due to improper setting of v. Prototype selection is used to select prototypes that are correctly classified by OCSVM for the TCSVM training. Since functionally connected voxels are spatially grouped together at multiple anatomic sites, we may use graph-based spatial domain editing methods to remove spatially isolated mis-detections [59,60]. However, if there are significant mis-detections that could also be spatially grouped together, spatial domain operations are not sufficient to remove mis-detections. In such cases, we need to further consider the feature space distribution of the prototypes and use both spatial and feature space information to select training prototypes for TCSVM. In this work, we proposed a combined spatial and feature domain prototype selection method.

A voxel’s relationship to neighboring voxels can be described by Gabriel graph [59]. Given n points Z = {z₁,…,z_n}in a q-dimensional feature space R^q, a Gabriel graph G(V,E) is a proximity graph with a set of vertices V=Z and edges E, such that (z_i ,z_j) ∈ E if and only if the following triangle inequality is satisfied:

$$d(z_i,z_j)\le \sqrt{d^2(z_i,z_k)+d^2(z_j,z_k)},$$ (2)

where z_k ∈ Z, and d is the Euclidean distance in R^q. When Z is the spatial coordinates of all brain voxels, q=2. Given the 3×3 neighborhood of z_i, if z_i ‘s label is not dominant in the neighborhood, zi will be removed from the training data based upon the Gabriel graph’s 1st-order graph neighborhood editing technique with voting strategy [60].

After this operation, all voxels remaining in the training data are examined in the feature space. If s_i represents the distance between the i^th prototype x_i and the OCSVM classification hyperplane in the feature space, when s_i<0, x_i is classified as “outlier” (connected), and when s_i>0, it is identified as “majority” (unconnected). s_outlier < 0 is the maximal distance of the outlier to the hyperplane, and s_majority > 0 is the maximal distance of the majority to the hyperplane. Since both “outlier” and ‘majority” classes contain mis-detections, the following feature space prototype selection procedure is proposed to identify correctly classified prototypes. If x_i is classified as “outlier” and

$$s_i\le (1.0-e^{-\eta \nu })s_{\mathit{\text{outlier}}},$$ (3)

or x_i is classified as “majority” and

$$s_i\ge (1.0-e^{-\lambda \nu })s_{\mathit{\text{majority}}},$$ (4)

where η and λ are parameters controlling the fraction of prototypes that are close to the hyperplane and should be removed, and v is the OCSVM parameter, then x_i is considered as correctly classified by OCSVM and selected for the TCSVM training. The values of η and λ can be experimentally determined.

2.2.5 TCSVM Learning and Classification

The selected prototypes are used to train a TCSVM and reclassify all voxels to obtain a refined network map. TCSVM is a supervised learning and classification tool that aims to estimate a linear classification hyperplane in a feature space so that two classes can be maximally separated [38]. In this work, the two classes are “connected” and “unconnected”, corresponding to the “outlier” and “majority” classes in the OCSVM learning. The TCSVM learning usually allows training errors where a parameter C is used to control a tradeoff between the hyperplane complexity and the training error. The RBF kernel is also used to implement nonlinear TCSVM.

It is possible that some functionally connected voxels cannot be detected by OCSVM (false negative), or detected but removed by the prototype selection. It is also possible that a few unconnected voxels are selected as the training prototypes for the connected voxels (false positives). In order to re-detect false negatives and/or attenuate the effects from the remaining false positives, the TCSVM training should have a sufficient generalization performance so that the trained classifier is not sensitive to the minor false positives/negatives in the training data. To favor a high generalization performance, the TCSVM parameters are carefully set with large RBF kernel width and small C values. The outputs of TCSVM are transferred into probability values using a method proposed by Wu et al. [61]. If $p_i^o$ and $p_i^m$ indicate the probability of x_i to be “outlier (or connected)” and “majority (or unconnected)”, then the final decision is a “soft” decision: If $p_i^o>p_i^m$, x_i is classified as “connected”, and if $p_i^m>p_i^o$, then x_i is classified as “unconnected”.

The TCSVM training and reclassification can be repeated one or more times to further refine the mapping results. If this is performed, we may start with a probability threshold higher than 0.5 for $p_i^o$ and $p_i^m$ after the first round of TCSVM classification. For instance, if $p_i^o(\text{or}{p}_i^m)>p^{\mathit{\text{th}}}$, p^th > 0.5 , then x_i will be selected as a training prototype for the “outlier” (or “majority”) class in the next round of TCSVM training. In the final round of TCSVM classification, the decision is made by a direct comparison between $p_i^o$ and $p_i^m$ as described in the previous paragraph. Due to the high generalization performance of TCSVM, the final results are not sensitive to a moderate change of p^th .

2.3 Evaluation Methods

The proposed method was evaluated using both synthetic and experimental fMRI data acquired from human subjects as described in sections 2.4 and 2.5. The method was also compared with the conventional correlation analysis and independent component analysis (ICA) methods. OCSVM and TCSVM were implemented by using the LIBSVM tool [62]. Correlation analysis was performed with a false discovery rate (FDR) control [18]. ICA was conducted using the tool in FSL. For the synthetic data, the sensitivity of the proposed method to the OCSVM parameter v was first examined. The proposed method was then compared with the correlation analysis and ICA in terms of accuracy, precision, and recall rates, which were calculated from the networks in the synthetic data detected by these methods under a same level of false positive rate, and defined as follows:

$$\mathit{\text{Accuracy}}=\frac{\mathit{\text{No. of truly connected and truly unconnected voxels}}}{\mathit{\text{No. of all voxels}}},\mathit{\text{Precision}}=\frac{\mathit{\text{No. of truly connected voxels that are detected}}}{\mathit{\text{No. of connected voxels that are detected}}},\mathit{\text{Recall}}=\frac{\mathit{\text{No. of truly connected voxels that are detected}}}{\mathit{\text{No. of truly connected voxels}}}.$$ (5)

Accuracy is the percentage of voxels that are correctly classified as “connected” and “unconnected”. Precision indicates the percentage of detected voxels that are truly in the network. Recall is the percentage of truly connected voxels that can be detected. For the experimental fMRI data, the dependence of the proposed method on v was examined based on part of the default mode network (DMN) and sensorimotor network (SMN) identified by the proposed method. Since there is no ground truth available for the location of these networks in the experimental data, the comparison study with the correlation analysis and ICA was performed in terms of regional homogeneity under a comparable level of detection sensitivity, which is determined with the following two steps: (a) An ROI is first defined from a targeted brain region that is part of a network of interest. (b) The thresholds for ICA and correlation methods are adjusted in a way to detect an equal number of contiguously clustered voxels in the ROI to that identified by the proposed method. Under the same detection sensitivity in the ROI, there may exist mis-detections in other brain regions that are not part of the network and/or under-detections in the network. The mis-detections and under-detections can be partially reflected via the regional homogeneity of the detected networks. Kendall’s coefficient of concordance (KCC) was calculated among connected voxels to measure the regional homogeneity of detected functional networks [63]. All algorithms were implemented in Matlab on a Dell Precision T5500 workstation with two Intel Xeon quad-core 2.13G Hz CPU and 6 GB Memory.

2.4 Resting State fMRI Experiments

Three resting state fMRI experiments were performed using a 3 Tesla GE system with an 8-channel coil. In the first experiment, four sets of fMRI data were acquired from a healthy adult volunteers on a same day using T2*-weighted parallel echo planar imaging (EPI) with an acceleration factor of 2, while the subject was instructed to look at a crosshair. The scan time for each run was 4 minutes. EPI parameters included a repetition time (TR) of 2 sec, an echo time (TE) of 30 msec, and a flip angle of 90^°. 30 axial-slices were collected for each volume with 4 mm slice thickness and 1 mm gap, FOV was 24 cm × 24 cm, and image matrix size was 120 × 120 after the sensitivity encoding reconstruction, corresponding to an in-plane resolution of 2 × 2 mm². Inversion-recovery (IR) prepared spin-echo EPI was also acquired to provide an anatomic reference with identical voxel geometry and geometric distortions as in fMRI. IR-EPI scan parameters included TR = 5 sec, TE = 24 msec, IR time = 1 sec, flip angle = 90^°, slice thickness = 4 mm (with 1 mm gap), FOV = 24 cm × 24 cm, in-plane matrix size = 120 × 120 (with 2 segments), and 30 axial slices. In the second experiment, two data sets were collected from two subjects using a T2*-weighted EPI sequence (TR=2 sec, TE= 25 msec) with SENSE acceleration factor of 2 while the subjects were instructed to look at a crosshair. The scan time for each run was 5 min. 35 axial-slices were collected in each volume with 3 mm slice thickness. FOV was 24 cm × 24 cm, and the image matrix size was 64 × 64. In the third experiment, six sets of fMRI data were collected from six healthy adults on different days. During each scan, the subject was instructed to look at a crosshair. The imaging parameters were TR = 4 sec, TE = 35 msec. flip angle =90°, FOV = 24 cm × 24 cm, and the image matrix size was 140 × 140. 56 axial slices were acquired in each volume with a 3 mm slice thickness, and 74 volumes were collected in each data set.

2.5 Synthetic Resting State fMRI Data

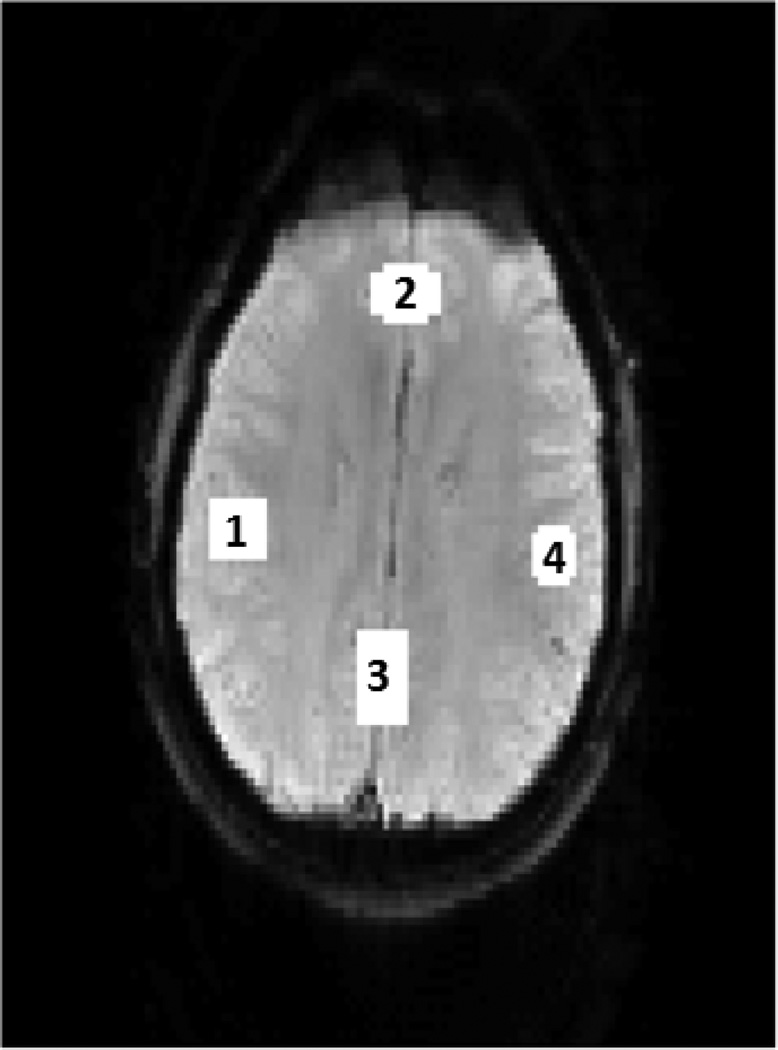
A synthetic single-slice resting state fMRI time series of 100 images was generated from a single-slice EPI image with artificially added functional connections in four regions as shown in Figure 2. Region 1 represents 1.54% of the brain area. A sinusoid wave was added to this region at a frequency of 0.08 Hz and the amplitude is 1.07 times of the baseline average. Region 2 represents 1.69% of the brain area. The amplitude of sinusoid signal added to this region is 1.02 times of the baseline average, and the frequency is 0.03 Hz. Region 3 represents 2.15% of the brain region. The amplitude of sinusoid wave in this region is 1.03 times of the baseline average, and the frequency is the same as that of Region 2 with a phase shift of 0.78 radians. Region 4 represents 1.1% of the brain area. The sinusoid signal added to this region has an amplitude of 1.04 times of the baseline average, and the frequency is the same as that of Region 1 with a phase shift of −0.52 radians. Since the sinusoid signals in Regions 1 and 4 have the same frequency, the two regions are functionally connected, and the corresponding network is called network A in the following sections. Similarly, Regions 2 and 3 are connected and the corresponding network is called network B. The non-additive Rician noise was added to the synthetic data using the method proposed by Wink and Roerdink [64]. After subtracting the image sequence from its mean, the SNR is −23.76dB.

Figure 2.

One slice of the synthetic resting state fMRI data with two artificially generated functional networks. Region 1 represents 1.54% of the brain area. A sinusoid wave was added to this region at a frequency of 0.08 Hz with the amplitude 1.07 times of the baseline average. Region 2 represents 1.69% of the brain area. The amplitude of sinusoid signal added to this region is 1.02 times of the baseline average, and the frequency is 0.03Hz. Region 3 represents 2.15% of the brain. The amplitude of sinusoid wave in this region is 1.03 times of the baseline average. The frequency is the same as that of region 2 with a phase shift of 0.78 radians. Region 4 represents 1.1% of the brain area, and a sinusoid signal was added with the amplitude 1.04 times of the baseline average. The frequency of the signal is the same as that of region 1 with a phase shift of −0.52 radians. Regions 1 and 4 are connected and the network is called network A. Regions 2 and 3 are connected and the network is called network B.

3 Results

3.1 Feature Selection

The experimental fMRI data were used to extract candidate features based on a 2 voxels × 2 voxels seed in DMN manually identified in the medial prefrontal cortex (mPFC) region. Table 1 lists the average I^d values of the eleven candidate features normalized against the largest one, and the rank of them. Although the features’ contributions to the SVM learning may be slightly different when different fMRI data were tested, it was found that three features always ranked in the top in all tests: the maximum and average cc values between a voxel’s 3×3 neighborhood and a seed, and the cc value between a voxel and a seed. Their average I^d values confirmed this finding. In addition, the average signed extreme value of the ccfs between a seed and a voxel’s 3×3 neighborhood also shows a significant contribution. Except for the cc value between the seed and a voxel, the other three features contain both spatial and temporal information. It was also found that the p -value of Student’s t test has the least I^d values, and other candidate features have greater I^d values than the p -value, which are consistent to our expectation. Some features’ I^d values are slightly higher than that of the p -value, such as the maximum intensity of a voxel, implying no significant contribution to the SVM learning, and were excluded from the feature representation of each voxel. In this work, the four features with the highest average I^d values were chosen to represent voxels for SVM learning.

Table 1.

Feature selection results

Candidate feature	Id value	Rank
Corr_ seed	0.74	3
Max_ cross_ seed	0.23	8
T_ test_p	0.15	11
Avg_corr_seed	0.93	2
Avg_ corr_ neighbor	0.43	6
Max_ corr_ seed	1.00	1
Min_ corr_ seed	0.47	5
Max_ corr_ neighbor	0.22	9
Min_ corr_ neighbor	0.42	7
Avg_ xcorr_ seed	0.58	4
Max_ tc	0.17	10

All I^d values were normalized against the largest one. (Corr_seed: correlation between a voxel and a seed; T_test_p: p value of t test; Avg/Max/Min_corr_seed: average, maximum, minimum correlation between neighboring voxels of a voxel and a seed; Avg/Max/Min_corr_neighbor: average, maximum, and minimum correlation between a voxel and its neighboring voxels; Max_xcross_seed: the signed extreme value of the cross correlation function between a voxel and a seed;. Avg_xcorr_seed: the average signed extreme value of the cross correlation functions between neighboring voxels of a voxel and a seed; Max_tc: maximum intensity of a voxel’s time course.)

3.2 Synthetic Data

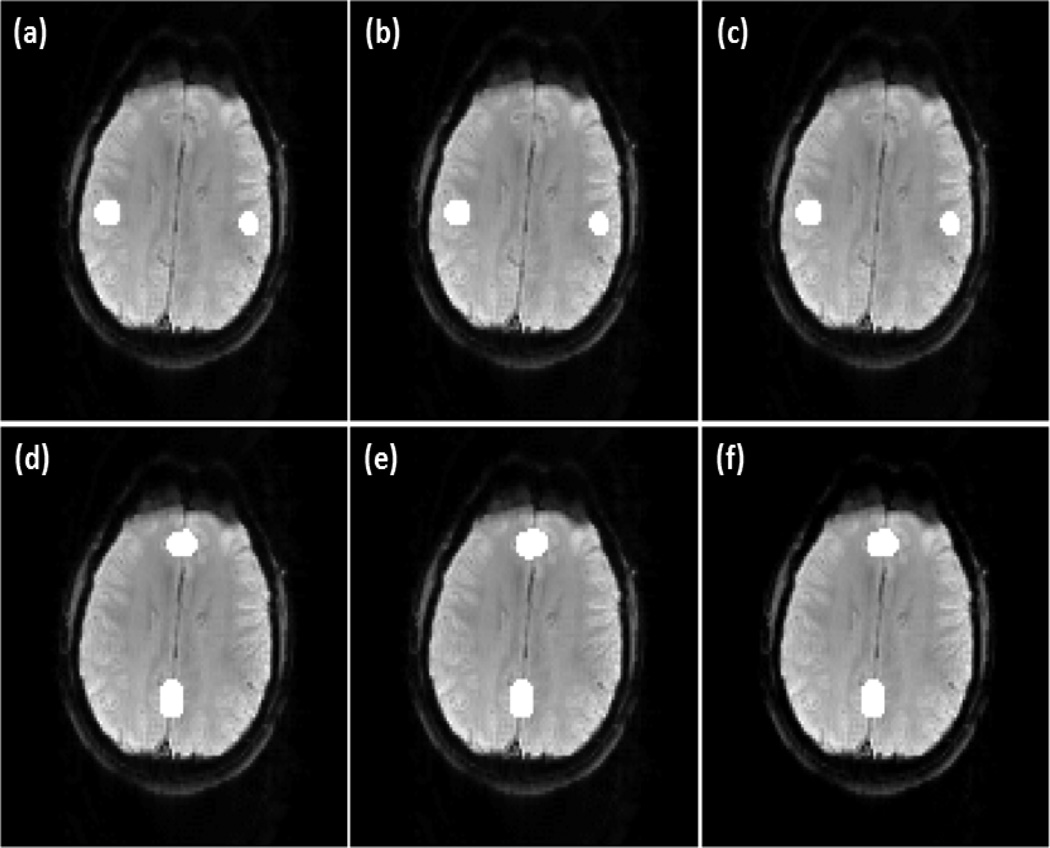
The synthetic data was first used to evaluate the proposed method. For OCSVM, the RBF kernel parameter γ was set to be the reciprocal of feature dimension, which is the default setting of LIBSVM. For TCSVM, γ is 0.25 times of that of OCSVM, resulting in an increased kernel width, and the C value is 10. This setting favors a high generalization performance in TCSVM reclassification, reducing possible effects from OCSVM mis-classifications that cannot be removed by the prototype selection. For prototype selection, different combination of η and λ were tested, and η=5.0, λ=1.0 leads to the highest detection accuracy. It was also found that a moderate variation of η and λ will not significantly affect the detection performance. Two rounds of TCSVM training and reclassification were performed. Different p^th values between 0.55 and 0.75 were examined after the first round of TCSVM reclassification, and no apparent changes were observed in final mapping results after the second round of TCSVM reclassification. p^th =0.6 was finally used in the experiment. Two one-voxel seeds were selected in Regions 1 and 2. Figure 3 (a)-(c) show the maps of network A detected by the proposed method with the seed in Region 1. Three different v values, v=0.25, 0.29, and 0.33, were used to initialize OCSVM. Little difference is observed from these results. Figure 3 (d)-(f) are the maps of network B detected by the proposed method with the seed in Region 2. The same three v values in (a)-(c) were used for OCSVM.

Figure 3.

The networks in the synthetic fMRI data detected using the proposed method, (a)-(c) Network A obtained by using v=0.25, 0.29. and 0.33, respectively, (d)-(f) Network B detected using the same set of v values as in (a)-(c). Little change can be observed when different v values were used to initialize the proposed method.

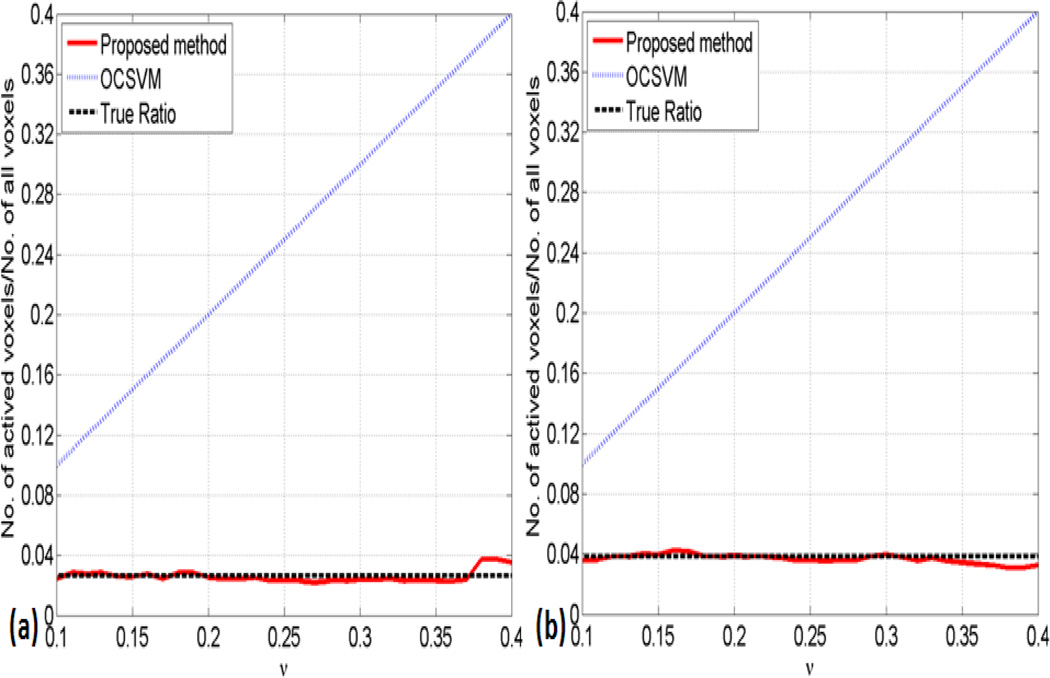
The sensitivity of the proposed method to v was further examined over a wide range of v values from 0.1 to 0.4 (step size 0.01). Figure 4 (a) and (b) show the ratios of functionally connected voxels in (a) network A and (b) network B to all brain voxels as a function of v for the synthetic data using OCSVM (dot blue lines), and the proposed method (solid red lines). The latter are much closer to the true ratio of 2.64% in network A (a) and 3.84% in network B (b) (dash dark lines) with negligible dependence on v over this range, as compared to OCSVM. For network A, the proposed method is 23.1 times less dependent on v (measured by the slope) than OCSVM. For network B, the proposed method is 26.1 times less dependent on v than OCSVM.

Figure 4.

The ratio of detected voxels to all brain voxels shown as a function of v for the synthetic data using OCSVM (dot blue line), and the proposed method (solid red line). The latter is much closer to the true ratio (dash dark line) with negligible dependence on v over this range, as compared to OCSVM. (a) Network A with a true ratio of 2.64%; (b) Network B with a true ratio of 3.84%.

When v is from 0.25 to 0.33, the false positive rate obtained from the proposed method is almost a constant around 0.2% for networks A and B. It was found that ICA and the correlation analysis can achieve the same false positive rate by changing their thresholds. Table 2 shows a comparison of the numerical performance between the proposed method, ICA, and correlation analysis with the FDR control, at the false positive rate of 0.2%. Three numerical criteria were used, including accuracy, precision, and recall. It can be seen from Table 2 that the proposed method can provide the highest accuracy and precision rates for network A, and the highest accuracy, precision and recall rates for network B at the false positive rate of 0.2%.

Table 2.

A comparison of the accuracy, precision, and recall rates calculated from the networks A and B in the synthetic data detected by the proposed method, ICA, and the correlation analysis with the FDR control under a false positive rate of 0.2%.

	Network A			Network B
	Accuracy	Precision	Recall	Accuracy	Precision	Recall
Proposed Method	99.8%	99.0%	94.4%	99.7%	95.5%	95.5%
ICA	98.1%	89.8%	56.1%	98.9%	87.1%	68.5%
Correlation	99.7%	92.0%	96.2%	97.6%	89.5%	43.3%

3.3 Experimental Resting State fMRI Data

Two resting state functional networks, the default mode network (DMN) and the sensori-motor network (SMN), were examined in this study. When implementing the proposed method, the RBF kernel parameter for OCSVM and TCSVM, C parameter for TCSVM, and p^th after the first round of TCSVM reclassification are the same as those used for the synthetic data. For prototype selection, detection accuracy cannot be computed to identify appropriate η and λ values because there is no ground truth of voxels’ class labels in the experimental data. Different η and λ values were experimentally evaluated and those lead to a high detection sensitivity in regions of interest in DMN and minimum mis-detections in other regions were selected. η=0.5 and λ=2.0 were finally chosen and fixed for the detection of DMN and SMN in experimental data from the multiple subjects. A 2×2 voxels seed was manually identified in the mPFC region for the detection of DMN, and a 2×2 voxels seed was selected in the primary motor cortex (MI) region for the identification of SMN.

Figure 5 (a)-(c) show part of DMN in an individual slice detected by the proposed method using three different v values: v=0.31, 0.37, and 0.41. There are 3558 voxels involved to the processing, and the increase of v from 0.31 to 0.41 implies approximately 356 (10%) more voxels would be identified as part of DMN if OCSVM was used. As shown in Figure 5 (c), however, only 31 (1.2%) more voxels were identified as the part of DMN, 8.3 times less sensitive to v compared to the OCSVM results. Figure 5 (d)-(f) are the SMN in another slice detected by the proposed method with three v values: v=0.25, 0.31, and 0.35. There are totally 2148 voxels in the brain area of this slice, and the increase of v from 0.25 to 0.35 indicates about 215 (10%) more voxels will be detected as part of SMN by OCSVM. As shown in Figure 5 (f), however, only 28 (1.3%) more voxels were detected as part of SMN in this slice, 7.7 times less sensitive to v than OCSVM.

Figure 5.

Network maps detected by the proposed method using the fMRI data from the first experiment, (a)-(c) Part of DMN detected with (a) v=0.31 (b) v=0.37, and (c) v=0.41. (d)-(f) Part of SMN detected with (d) v=0.25. (e) v=0.31. and (f) v=0.35. These results indicate that the proposed method can provide a consistent detection of the functional networks over a range of v values.

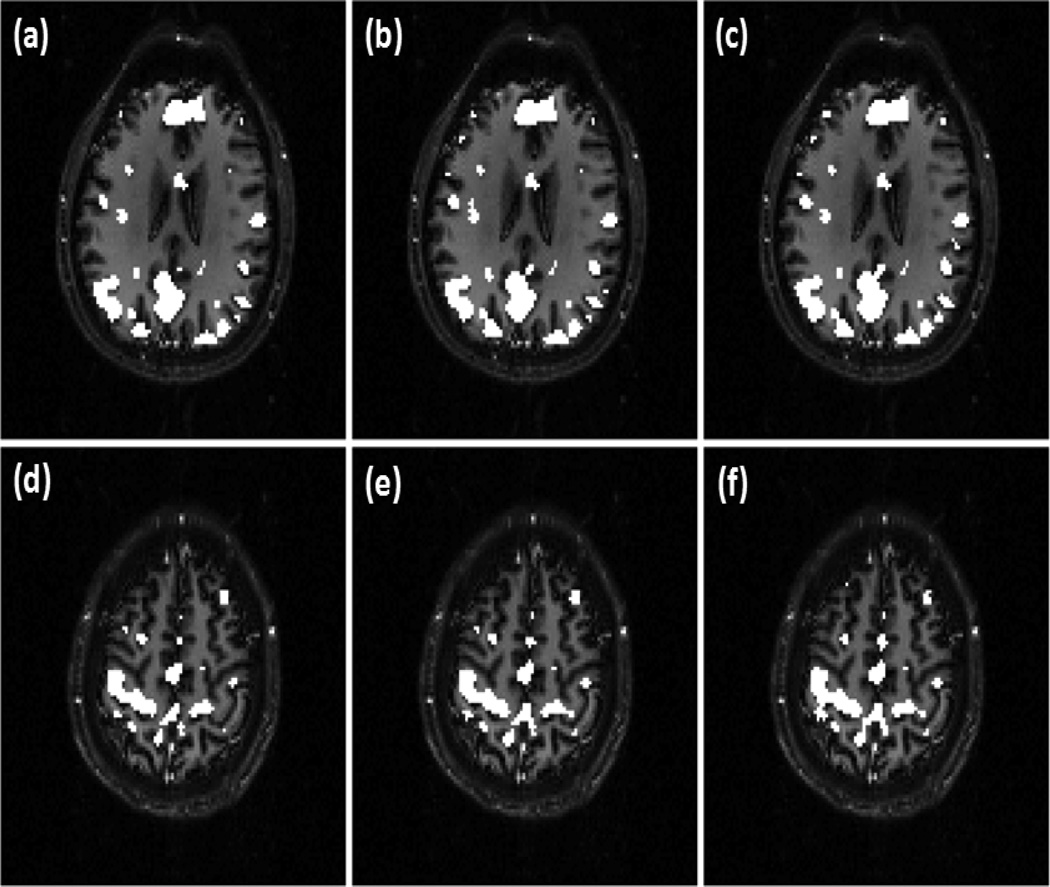
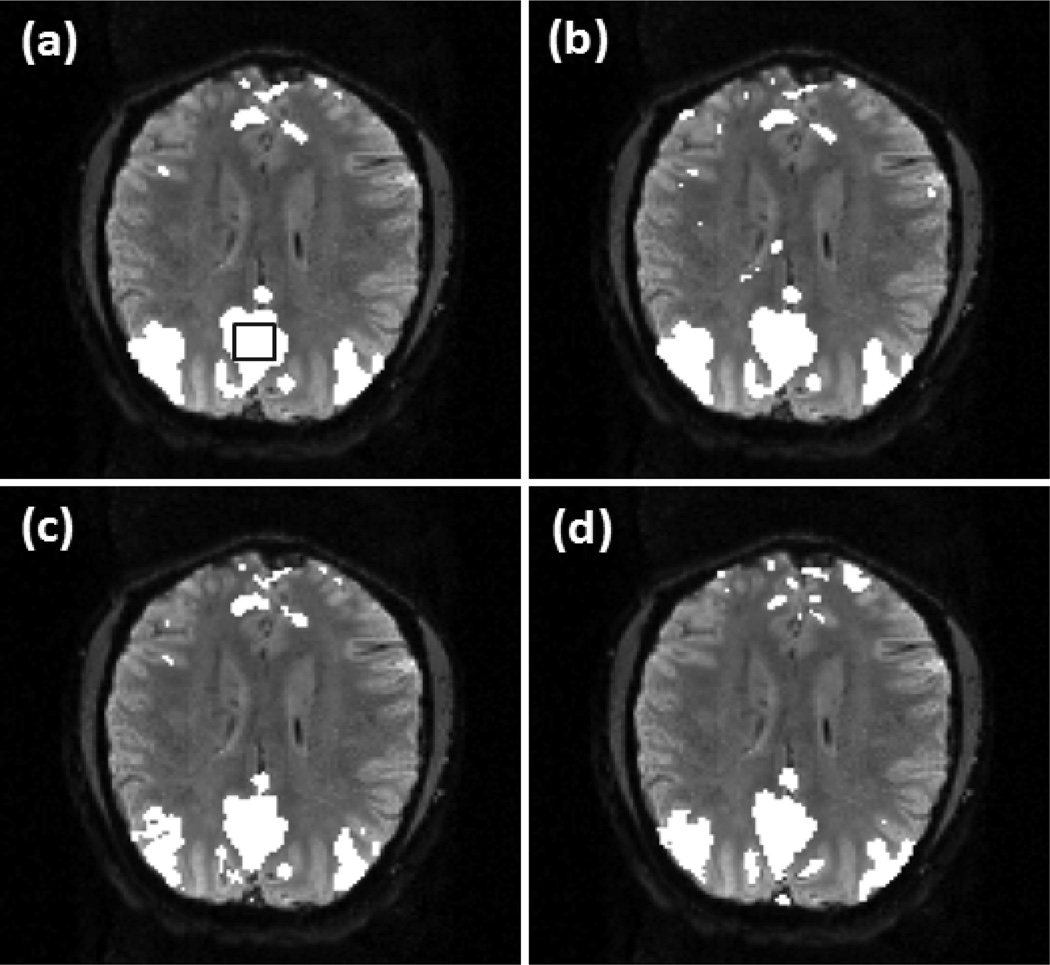
Figure 6 shows a comparison of the detected DMN and SMN in two individual slices using the proposed method, correlation analysis, and ICA. The relative performance of these methods was evaluated under a comparable level of detection sensitivity. For the comparison, the thresholds for correlation analysis and ICA were set to detect an equal number of contiguously clustered voxels in a preselected region within DMN or SMN to those identified by the proposed method. Figure 6 (a) shows part of the DMN in the individual slice detected using the proposed method with v =0.39. The encircled rectangular region in this slice indicates a 6 voxels × 6 voxels area in the posterior cingulate cortex (PCC) region, and was selected for the comparison study. Figure 6 (b) is the network detected by the correlation analysis using the FDR control with a q value of 1× 10⁻⁴. Figure 6 (c) is the ICA result. Sixteen independent components (IC) were used in the analysis. Since ICA split the connected brain regions in DMN into several components, we visually examined the obtained ICs and identified four DMN-related ICs that were combined to form the network map in Figure 6 (c). Figure 6 (d) is part of SMN detected using the proposed method with v =0.35, and the encircled 3 voxels × 4 voxels rectangular region in MI was selected for the comparison study. Figure 6 (e) and (f) are the network maps identified by the correlation analysis and ICA. In the correlation analysis, a q value of 4×10⁻⁴ was used to detect all connected voxels in the encircled region in MI. In the ICA analysis, fourteen components were used and one SMN-related IC was identified. It was observed from Figure 6 (c) that the regions around mPFC and ventral anterior cingulate cortex (VACC) are significantly under-detected after thresholding the ICs of this data set. KCC values were calculated to evaluate the regional homogeneity of identified network regions and are listed in Table 3.

Figure 6.

Comparison between the proposed method, correlation analysis, and ICA under a comparable level of detection sensitivity in specified regions, (a)-(c) Part of DMN generated by (a) the proposed method with v=0.39. (b) correlation analysis with the FDR control, and (c) ICA. (d)-(f) Part of SMN identified by (d) the proposed method with v=0.35, (e) correlation analysis with the FDR control, and (f) ICA. The encircled rectangular region in (a) indicates a 6 voxels × 6 voxels area in PCC, and the encircled region in (d) indicates a 3 voxels × 4 voxels region in MI. The thresholds of correlation analysis and ICA methods were adjusted to detect all voxels in these two regions for the comparison purpose.

Table 3.

A comparison of the KCC values calculated from part of DMN and SMN detected by the proposed method, ICA, and the correlation analysis with the FDR control, as shown in Figure 6.

	DMN	SMN
Proposed Method	0.18	0.26
ICA	0.14	0.25
Correlation	0.20	0.23

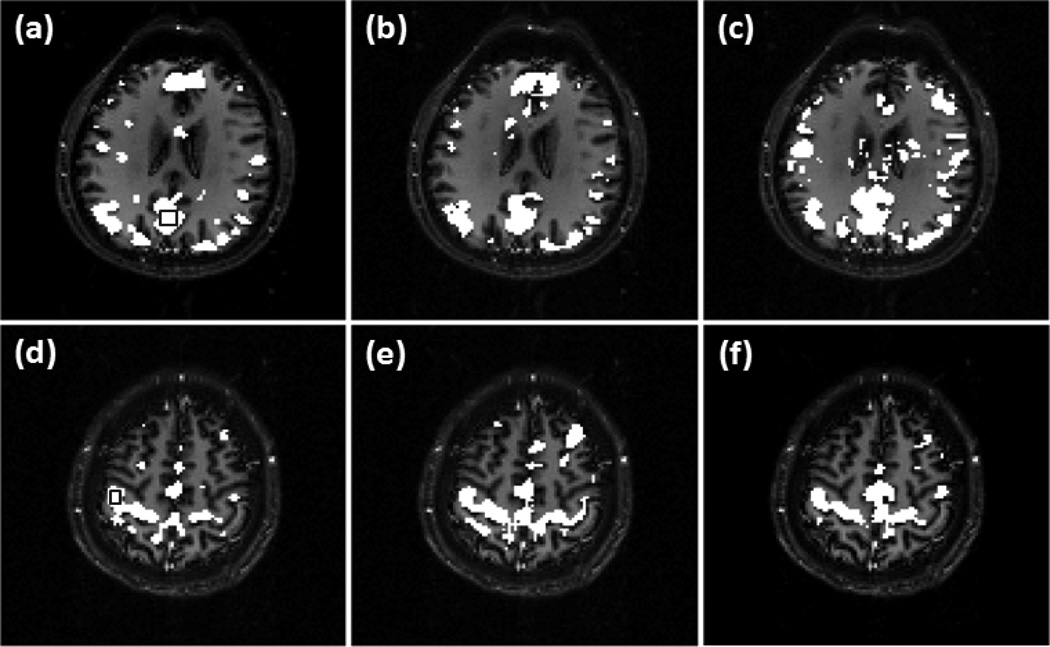
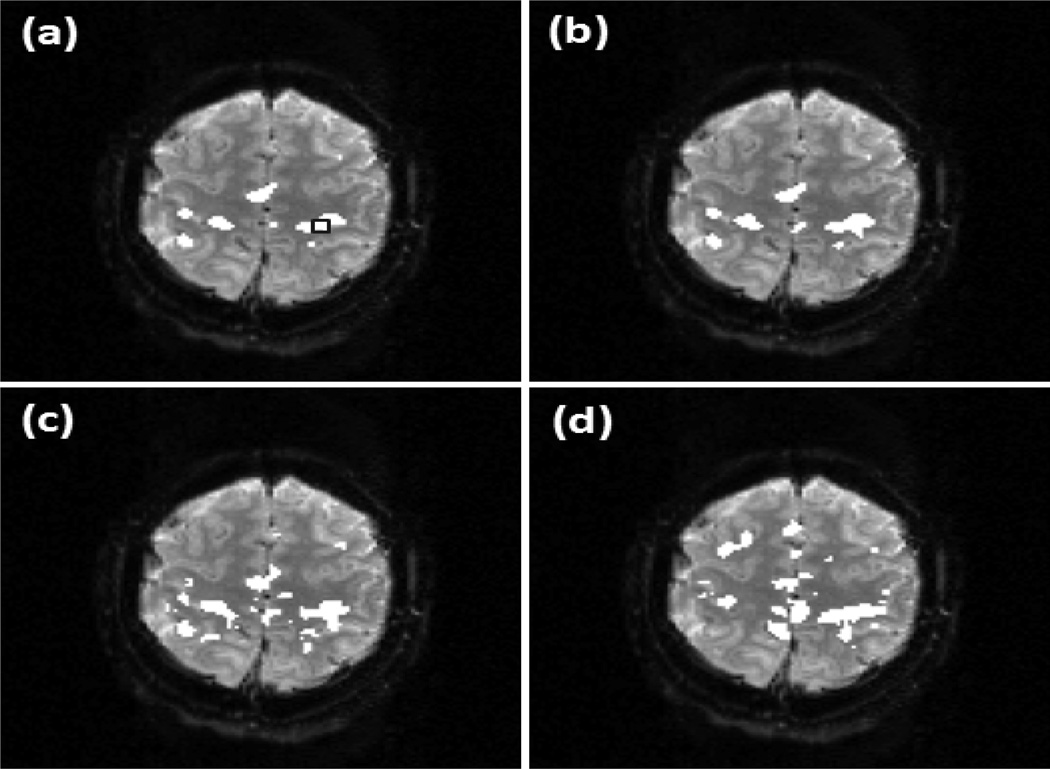
Figure 7 shows the results from another set of fMRI data acquired from the second resting state experiment. It is from a different subject with different spatial resolution and scan duration. Figure 7 (a)-(d) are the identified DMN maps overlaid on an individual slice using the proposed method with v =0.31, 0.37, 0.39, and 0.41, respectively. 2031 voxels were used in the processing, and only 10 more voxels (0.49%) are identified as part of DMN when v increases from 0.31 to 0.41, indicating approximately 20 times less dependence on the change of v than OCSVM. The encircled rectangular region in (c) indicates a 10 voxels × 6 voxels area in VACC. For comparison, the thresholds of correlation analysis and ICA methods were adjusted to detect the same number of voxels in this region. and Figure 7 (e) and (f) are part of DMN identified by using the correlation analysis and ICA. For correlation analysis, a q value of 1×10⁻⁴ was used. In ICA analysis, 21 ICs were obtained and three ICs was visually identified as DMN-related and combined to form the network map.

Figure 7.

Part of DMN detected from a subject in the second experiment by using the proposed method with v = (a) 0.31, (b) v =0.37, (c) v =0.39, (d) v =0.41, and by using (e) the correlation analysis with the FDR control and (f) ICA. The encircled rectangular region in (c) indicates a 10 voxels × 6 voxels area in VACC. The thresholds of correlation analysis and ICA methods were adjusted to detect all voxels in this region.

Figure 8 shows part of SMN detected from the same data set in a different slice as that shown in Figure 7. Figure 8 (a)-(d) are the network maps identified by the proposed method using v =0.25, 0.29, 0.31, and 0.35, respectively. There are 1356 voxels in this slice involved to the analysis. Only 12 more voxels (0.88%) were detected as part of SMN when v increases from 0.25 to 0.35 (10%), indicating about 11.36 times less dependence on the change of v than OCSVM. The encircled rectangular region in (c) indicates a 4 voxels × 4 voxels area in MI. The thresholds of correlation analysis and ICA methods were changed to identify the same number of voxels in this region. Figure 8 (e) and (f) are the SMN maps detected using the correlation analysis and ICA. In the correlation analysis, a q value of 3× 10⁻⁵ was used to identify the same number of connected voxels in the encircled region in MI as detected by the proposed method. For ICA, 19 ICs were computed and one of them was identified to be SMN-related. KCC values of the identified DMN and SMN maps in Figures 7 and 8 are listed in Table 4.

Figure 8.

Part of SMN detected from the same subject as in Figure 7 by using the proposed method with (a) v = 0.25, (b) v =0.29, (c) v =0.31, (d) v =0.35, and by using (e) the correlation analysis with the FDR control and (f) ICA. The encircled rectangular region in (c) indicates a 4 voxels × 4 voxels region in MI. The thresholds of correlation analysis and ICA methods were adjusted to detect all voxels in this region.

Table 4.

A comparison of the KCC values calculated from part of DMN and SMN detected by the proposed method, ICA, and the correlation analysis with the FDR control, as shown in Figures 7 and 8.

	DMN	SMN
Proposed Method	0.13	0.11
ICA	0.11	0.11
Correlation	0.14	0.13

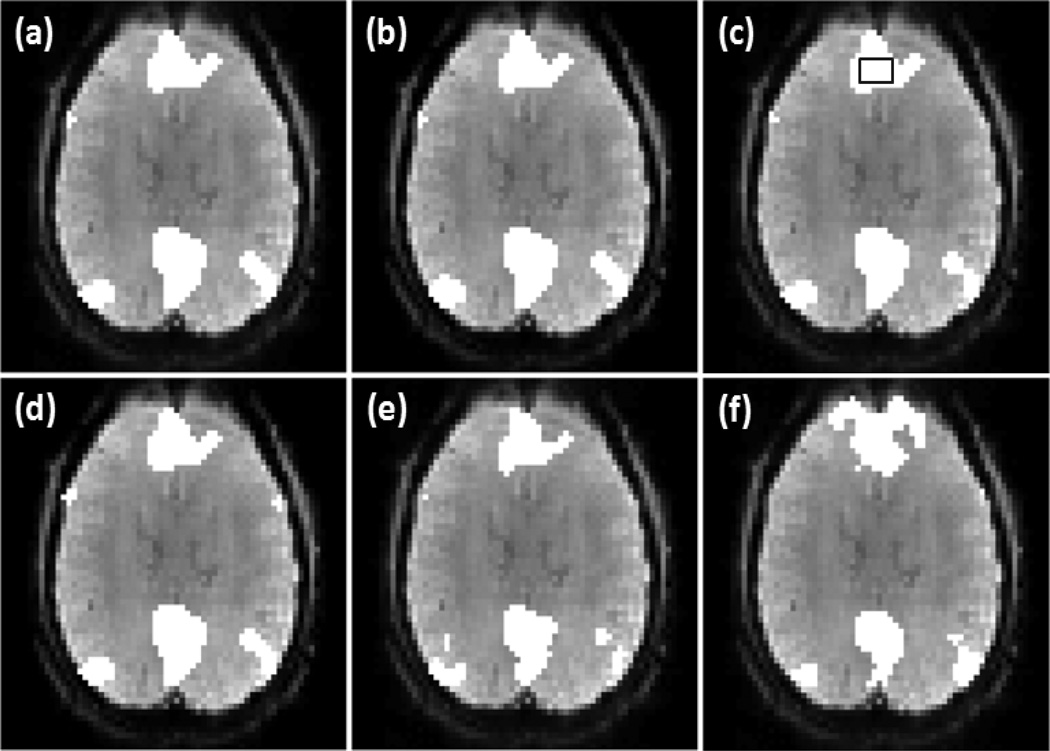
Figure 9 shows part of DMN overlaid on an individual slice detected from a data set acquired in the third experiment using the proposed method, correlation analysis, and ICA. Figure 9 (a) and (b) were obtained using the proposed method with v =0.31 and 0.41, respectively. There are 6915 voxels in this slice involved to the analysis, and only 86 more voxels (1.2%) were detected as part of DMN when v increases from 0.31 to 0.41, showing 8.33 times less dependence on the change of v than OCSVM. The encircled region in Figure 9 (a) is a 10 voxels × 10 voxels area in PCC. For comparison, the thresholds of correlation analysis and ICA methods were adjusted to identify the same number of voxels in this area. Figure 9 (c) is part of DMN identify by the correlation analysis using the FDR control with a q value of 4×10³. In ICA analysis, six ICs were estimated and one DMN-related IC was identified and thresholded, as shown in Figure 9 (d).

Figure 9.

Part of DMN detected from a subject in the third experiment by using the proposed method with (a) v = 0.31, (b) v =0.41, and by using (c) the correlation analysis with the FDR control and (d) ICA. The encircled region in (a) indicates a 10 voxels × 10 voxels region in PCC. The thresholds of correlation analysis and ICA methods were adjusted to detect all voxels in this region.

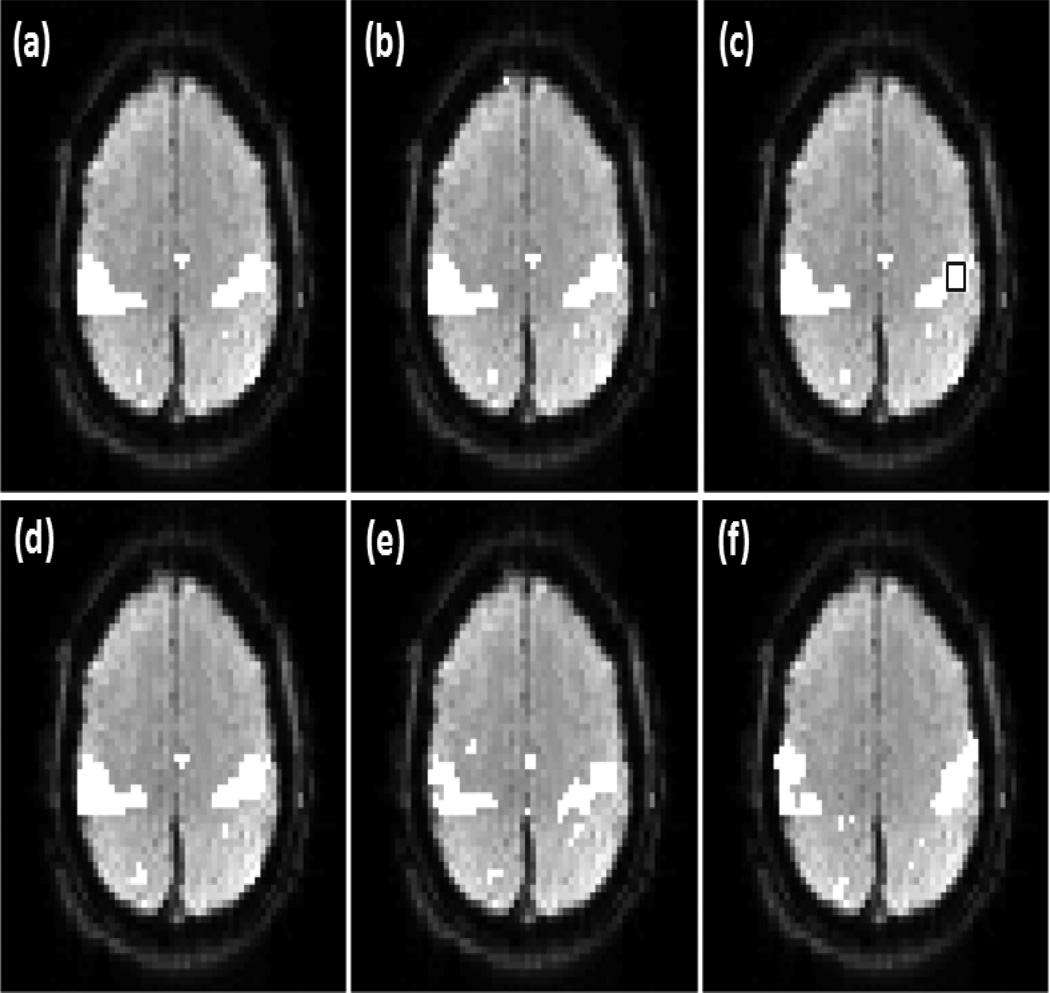
Figure 10 illustrates part of SMN identified from a slice of the same data set used to detect DMN shown in Figure 9. Figure 10 (a) and (b) were obtained using the proposed method with v =0.25 and 0.35, respectively. 3116 voxels from this slice were used in the analysis, and 46 more voxels (1.4%) were detected as part of SMN when v varies from 0.25 to 0.35, indicating 7.14 times less dependence on the change of v than OCSVM. The encircled region in Figure 10 (a) is a 4 voxels × 4 voxels area in MI., and again the thresholds of correlation analysis and ICA were modified to identify the same number of connected voxels in this area. A q value of 2.3×10⁻² was used in the correlation analysis with the FDR control, and the detected network is shown in Figure 10 (c). Eleven ICs were generated by ICA and one SMN-related IC was visually identified and thresholded as shown in Figure 10 (d). KCC values of the detected DMN and SMN regions in Figure 9 and 10 are listed in Table 5.

Figure 10.

Part of SMN detected from the same subject as in Figure 9 by using the proposed method with (a) v = 0.25, (b) v =0.35, and using (c) the correlation analysis with the FDR control and (d) ICA. The encircled rectangular region in (a) indicates a 4 voxels × 4 voxels area in MI. The thresholds of correlation analysis and ICA methods were adjusted to detect all voxels in this region.

Table 5.

A comparison of the KCC values calculated from part of DMN and SMN detected by the proposed method, ICA, and the correlation analysis with the FDR control, as shown in Figures 9 and 10.

	DMN	SMN
Proposed Method	0.65	0.23
ICA	0.59	0.19
Correlation	0.64	0.23

4. Discussion

Although the proposed method and correlation analysis use seed and cc value to identify functional networks, they are fundamentally different approaches. Correlation analysis is a univariate approach where each voxel is analyzed against the seed separately from other voxels, and a significance threshold is used to make a final decision. In addition, only temporal information of the voxel is involved to the analysis. The proposed method is a multivariate approach where both spatial and temporal information from a voxel are used for the network detection. It essentially explores a true boundary between functionally connected and unconnected voxels in a feature space, and the final decision is made by comparing each voxel’s probabilities of “connected” and “unconnected”. Statistically this is more reliable than using a threshold that might not fit the true boundary between connected and unconnected voxels in the feature space.

There are two interesting findings from the feature selection results. First, the most representative features identified by the SVM-based feature selection method are all related to a seed. This is reasonable because the seed provides prior information based upon which a network of interest can be identified. Second, most of the selected features contain both spatial and temporal information. Functionally connected voxels not only show temporal correlation with each other, but also spatially cluster together in specific brain regions. Considering both spatial and temporal information will facilitate the network detection. There are also other findings that are consistent with our experience. For example, the signal intensity does not contribute too much to the resting state network detection. If there exists a co-variation between different groups of voxels in a network with small time delays, the peak delay of ccf could be another useful feature only if the temporal sampling rate is sufficiently high. This is not the case in most multislice fMRI experiments, including those in this study, and consequently not considered in this work.

In the prototype selection, the feature space operation is more conservative than the spatial domain operation. The two parameters η and λ in formulas (3) and (4) control the portion of removed training prototypes that are close to the OCSVM classification hyperplane. It was found that a moderate adjustment of η and λ does not significantly change the final detection results. This is reasonable because the TCSVM reclassification with a high generalization performance can minimize the effects from possible remaining mis-detections or the removal of correctly classified prototypes around the hyperplane.

SVM learning assumes that training data are independently drawn from an unknown probability distribution. However, fMRI data show strong local spatial correlations and ignoring such correlation may affect the detection performance. In general, there are four possible ways to apply spatial constraint to the analysis. The first is to use spatial smoothing in the preprocessing. The second is to use features containing information of fMRI spatial correlation [29,51]. The third is to use spatial constraint based prototype selection [51], and the forth is to integrate spatial constraints into classifier learning [65,66]. The first, second and third approaches are considered in this study.

The results of the synthetic data shown in Figure 3 indicate that the proposed method can provide a consistent detection of functional networks. The dependence of the proposed method on v was evaluated for both networks shown in Figure 2 with a large range of v values from 0.1 to 0.4, which are greater than the true ratios of functionally connected voxels. The mapping results show little dependence on v values. The outlier ratios obtained from the OCSVM results are represented by the dot blue lines in Figure 4, and are almost consistent to the original v values because v is an upper bound of the outlier ratio when only OCSVM is used for the detection. The solid red lines in Figure 4 (a) and (b), which represent the ratios of connected voxels detected by the proposed method as a function of v, are quite close to the true ratios represented by the dash dark lines.

When the proposed method, ICA, and correlation analysis were compared at the same false positive rate of 0.2%, as shown in Table 2, the proposed method can achieve the highest accuracy and precision rates than the other two methods for network A, while the correlation analysis can provide the highest recall rate for this network. When the methods were used to detect network B at the same false positive rate, the proposed method outperforms the others with the highest accuracy, precision, and recall rates. The recall rate calculated from the correlation analysis results is lower than 50%. This is expected because the phase shift between the sinusoid signals in regions 2 and 3 leads to a significant decrease of correlation between the regions. The proposed method is a multivariate approach that incorporates both spatial and temporal information into the analysis and the final results are not affected by the phase shift.

If the accuracy is a constant, any classification system that performs better than a random decision exhibits a tradeoff between precision and recall [67]. This indicates that if the accuracy cannot be further increased, we may only improve precision by sacrificing recall, and vice versa. A simultaneous increase of precision and recall cannot be achieved unless accuracy can be increased. Increasing accuracy is usually difficult and costly, and typically a consistent tradeoff between precision and recall is expected when the possible highest accuracy level is reached. The precision and recall rates would change significantly when different thresholds are used for ICA and correlation analysis, while the proposed method can provide a consistent tradeoff between precision and recall.

The dependence of the proposed method on v was further examined using the experimental fMRI data as shown in Figure 5. All three v values used to detect DMN in this individual slice are greater than the true ratio of voxels in the network because the smallest v is 0.31, almost 1/3 of the brain area. Functionally connected voxels were identified in the mPFC, inferior parietal cortex (IPC), and PCC regions, as shown in Figure 5 (a)-(c). The results using the three v values are similar and are consistent with the anatomically defined cortical representation of DMN. When the proposed method was used to detect SMN, the smallest v is also greater than the true ratio of SMN in this individual slice. Similarly, consistent detections were obtained although v values increase 10% from 0.25 to 0.35.

The comparison of the three methods using the experimental data was based on a same detection sensitivity in a pre-specified brain region that is part of a network of interest. From Figure 6 (a)-(c), it was observed that the maps of DMN detected by the proposed method and correlation analysis are similar to each other, while the map from ICA shows a under-detection in mPFC and VACC. This under-detection is not due to the missing of DMN-related ICs, but is because of the thresholding of ICs that led to the same detection sensitivity in PCC among the three methods. The KCC values of the detected regions are listed in the second column of Table 3, which indicates that the network regions detected by the proposed method and correlation analysis have a higher regional homogeneity than those identified by ICA. In addition, the correlation analysis method provides a slightly higher regional homogeneity than the proposed method. The third column of Table 3 lists the KCC values computed from part of SMN identified by these methods using the same data but from a different slice. The corresponding network maps are shown in Figure 6 (d)-(f). The network detected by the proposed method has a higher regional homogeneity than those detected by ICA and correlation analysis. The network detected by the correlation analysis exhibits the lowest regional homogeneity. This is because of a significant number of mis-detections around the right side of middle frontal gyrus (MFG). The seed used in the proposed method is the same one used by the correlation analysis, and the cc value with the seed is one of features used by the proposed approach. Due to the contribution from the other features, the mis-detections in MFG generated by the proposed method is not so significant compared to those detected by the correlation analysis. The image slices shown in Figures 7, 8, 9, and 10 are from another data sets acquired from different subjects in the second and third resting state experiments. The data sets have different spatial resolutions and temporal durations to the data shown in Figures 5 and 6. Figure 7 (a)-(d), Figure 8 (a)-(d), Figure 9 (a), (b), and Figure 10 (a), (b) verify that the method can provide a consistent mapping of DMN and SMN although v values vary significantly. The KCC values in Tables 4 and 5 indicate that the regional homogeneities of networks detected by the proposed approach are close to those identified by the ICA and correlation analysis methods. It is worth of mentioning that KCC is used to provide accessory evaluation of the detected networks. KCC alone cannot provide a complete evaluation. For example, in the second column of Table 4, the KCC value calculated from the correlation analysis is slightly higher than that from the proposed method. It was observed in Figure 7 (e) that less voxels in the right IPC region were identified as part of DMN by the correlation analysis than the proposed method, leading to a higher KCC value. Therefore, a high KCC could be associated with a low detection sensitivity, and an inspection of the corresponding network map is necessary. The comparison studies using the synthetic and experimental data show that the proposed method can provide a similar or better mapping performance of resting state networks to the widely used ICA and correlation analysis methods. Since the proposed method does not require a threshold to make the final decision and can provide a consistent mapping of different resting state networks, it would be an efficient tool for resting state quantitative fMRI study.

Conclusion

We proposed a SVM-based method for resting state quantitative fMRI data analysis and compared it with the commonly used ICA and correlation analysis methods using both synthetic and experimental data. The innovation of the method is to formulate the mapping of a resting state network as an outlier detection process that can be performed by OCSVM. In the proposed method, OCSVM is used to generate an initial detection, and the OCSVM results are analyzed by a spatial and feature domain prototype selection method to identify reliable training samples for a TCSVM-based reclassification. The proposed method has several advantages. First, it is data-driven requiring no threshold to make the final decision. Second, it performs well for a range of v, and the final results are not sensitive to v. Third, it is computationally efficient. The experiment results data show that the proposed method can provide comparable or better results than the correlation analysis and ICA methods. It allows for accurate measurements of functionally connected brain area from fMRI data. This capability is important for quantitative fMRI studies where a change in size of functionally connected regions may be linked to variation of activated neurons during a aging, learning, memorizing, or medical treatment process.