See corresponding articles on pages 787 and 806
Typical instruments for assessing energy intake in humans rely primarily on self-report and are now recognized to be quantitatively inaccurate and imprecise (1, 2). This limitation poses a major challenge for human obesity research because energy intake is believed to be an important driver in the pathogenesis of obesity and is a key target of obesity treatment at both the individual and population levels. Fortunately, the principle of energy conservation can be used to calculate average energy intake over a given time period by using an approach that has come to be known as the “intake-balance method” (3).
Full implementation of the intake-balance method requires repeated measurements of body composition to assess changes in body energy stores and repeated measurements of energy expenditure. Because these measurements are expensive and require sophisticated equipment and highly trained personnel, the intake-balance method is not currently practical for widespread use in large research studies or for clinical use in counseling individual patients.
Several years ago, my research group proposed that mathematical models of human metabolism and body weight dynamics might be used as an adjunct to the intake-balance method by replacing some of the expensive measurements with model predictions (4–7). Investigators could then inexpensively estimate energy intake changes over time by using repeated body weight measurements as model inputs. This concept has since been implemented in a variety of applications (8–11). In this issue of the Journal, 2 new studies have used mathematical modeling approaches to estimate human energy intake. Gilmore et al (12) investigated experimental overfeeding, and Thomas et al (13) investigated the body weight plateau experienced by many dieters at ∼6 mo into a weight-loss intervention.
In the study by Gilmore et al (12), the investigators used baseline measurements of energy requirements and proposed a mathematical model of how energy expenditure changes during experimental overfeeding. The modeled energy expenditure included the thermic effect of overfeeding and the energy cost to deposit fat and fat-free tissues. The model predictions were used as part of the intake-balance method to dispense with subsequent energy expenditure measurements. Gilmore et al found that the estimated average energy intake during overfeeding reasonably matched the actual energy intake and the uncertainty of the method amounted to a few hundred kilocalories per day. These results are far superior to self-report methods and provide further support for the intake-balance method during periods of overfeeding and weight gain.
Interestingly, the energy expenditure model used by Gilmore et al did not account for the increased maintenance energy expenditure associated with weight gain, the so-called maintenance energy gap (6). The magnitude of this energy expenditure component for weight gained over short time periods is relatively small (∼20–30 kcal/d per kg of weight gained), but the maintenance energy gap has important implications when investigating energy intake changes underlying long-term weight gain (5, 6). Gilmore et al also acknowledge that their energy expenditure model did not consider changes in physical activity during overfeeding. In particular, they did not model nonexercise activity thermogenesis (NEAT), which has previously been implicated as the primary, but highly variable, determinant of individual weight gain during overfeeding (14). Perhaps this omission may help explain some of the individual variability in the estimated energy intake measurements compared with actual intake.
Apart from these omissions, there are also some important limitations of the energy expenditure model proposed by Gilmore et al. For example, the energy cost for tissue deposition was lumped together within the calculated changes in body energy stores in their Equation 2. Unfortunately, the parameter values defining the tissue deposition efficiencies were derived by using a method that has recently been criticized as prone to nonphysiologic results because the efficiency coefficients are derived from an ill-posed statistical procedure whose results cannot be justifiably transferred from one study to another (15).
Perhaps the most serious limitation in extending the analyses of Gilmore et al to other studies is that their model of the thermic effect of overfeeding used the actual energy intake as a model input. Of course, this is the very quantity that the intake-balance method was intended to estimate, and the fact that it was used as a model input can be seen by expanding Equations 1 and 3 of Gilmore et al as follows:
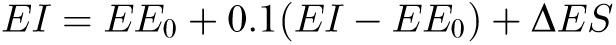 |
where EE0 is the baseline energy requirement, ΔES is the rate of change in body energy stores, and the quantity to be estimated, EI (energy intake), is clearly on the right side of the equation that was used in its own estimation. Although the current study had access to the actual EI, which thereby provides the most accurate way to estimate the thermic effect of overfeeding, other studies would not have access to this quantity. Fortunately, the following simple rearrangement of this equation could be used in cases in which actual EI is unknown:
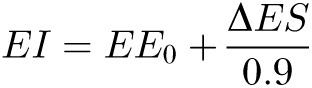 |
It would be interesting to reanalyze the data of Gilmore et al with the use of different energy expenditure models to investigate the impact of the various model assumptions on the accuracy and precision of the derived energy intake estimates.
The study of Thomas et al (13) used a mathematical model of energy balance dynamics to address the reason for the body weight plateau that typically occurs at ∼6 mo after initiating a weight-loss intervention (16). At the weight plateau, the rate of weight change is zero and a state of energy balance is achieved with energy intake equaling expenditure. Thomas et al addressed whether the timing of the weight plateau primarily results from suppressed energy expenditure or a loss of diet adherence. Previous mathematical models addressing this question concluded that loss of diet adherence was the primary driver of the typical weight plateau, with the level of energy restriction at the beginning of the intervention having waned considerably by the time of the plateau (4, 6).
To investigate the role of variable amounts of metabolic adaptation, Thomas et al adjusted a model parameter that controlled the suppression of energy expenditure during weight loss. They found that variations of this parameter only affected the magnitude of weight change but did not affect the timing of the weight plateau. Specifically, a step reduction in energy intake resulted in model-simulated weight-loss trajectories that were approximately exponential with half-times of ∼20 wk and independent of the energy expenditure parameter (the authors’ Figure 2). Therefore, a weight plateau at 6 mo could not be explained by the modified energy expenditure model and loss of diet adherence was concluded to be the primary driver of the weight plateau, in agreement with previous models (4, 6).
Thomas et al also included a stochastic element within their model by allowing random fluctuations in energy intake to simulate intermittent loss of diet adherence. Previous mathematical models have shown that large, random, uncorrelated variations in energy intake over time result in relatively small weight fluctuations, and the overall weight trajectory is primarily determined by the long-term average energy intake (17–19), including the ubiquitous weight plateau (17). However, when energy intake fluctuations have a substantial autocorrelation over many days, fluctuations in body weight become more prominent and can exhibit extended periods of increasing or decreasing body weight (17). Thomas et al suggest that such weight oscillations may be indicative of intermittent periods of diet nonadherence lasting many days and that detection of these periods may be clinically useful. This is an important idea that could be implemented by using personalized mathematical models of metabolism in concert with repeated body weight and physical activity measurements to provide quantitative feedback to patients and weight-management professionals to help guide individual weight-loss programs (17).
Acknowledgments
The author reported a US patent application assigned to the NIH related to the use of mathematical models of human metabolism for body weight management.
REFERENCES
- 1.Freedman LS, Commins JM, Moler JE, Arab L, Baer DJ, Kipnis V, Midthune D, Moshfegh AJ, Neuhouser ML, Prentice RL, et al. Pooled results from 5 validation studies of dietary self-report instruments using recovery biomarkers for energy and protein intake. Am J Epidemiol 2014;180:172–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Schoeller DA, Thomas D, Archer E, Heymsfield SB, Blair SN, Goran MI, Hill JO, Atkinson RL, Corkey BE, Foreyt J, et al. Self-report-based estimates of energy intake offer an inadequate basis for scientific conclusions. Am J Clin Nutr 2013;97:1413–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Racette SB, Das SK, Bhapkar M, Hadley EC, Roberts SB, Ravussin E, Pieper C, DeLany JP, Kraus WE, Rochon J, et al. Approaches for quantifying energy intake and %calorie restriction during calorie restriction interventions in humans: the multicenter CALERIE study. Am J Physiol Endocrinol Metab 2012;302:E441–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hall KD. Predicting metabolic adaptation, body weight change, and energy intake in humans. Am J Physiol Endocrinol Metab 2010;298:E449–66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hall KD, Guo J, Dore M, Chow CC. The progressive increase of food waste in America and its environmental impact. PLoS ONE 2009;4:e7940. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hall KD, Sacks G, Chandramohan D, Chow CC, Wang YC, Gortmaker SL, Swinburn BA. Quantification of the effect of energy imbalance on bodyweight. Lancet 2011;378:826–37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Jordan PN, Hall KD. Dynamic coordination of macronutrient balance during infant growth: insights from a mathematical model. Am J Clin Nutr 2008;87:692–703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Göbel B, Sanghvi A, Hall KD. Quantifying energy intake changes during obesity pharmacotherapy. Obesity (in press). [DOI] [PMC free article] [PubMed]
- 9.Hall KD. Diet versus exercise in “the biggest loser” weight loss competition. Obesity (Silver Spring) 2013;21:957–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hall KD, Chow CC. Estimating changes in free-living energy intake and its confidence interval. Am J Clin Nutr 2011;94:66–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Thomas DM, Schoeller DA, Redman LA, Martin CK, Levine JA, Heymsfield SB. A computational model to determine energy intake during weight loss. Am J Clin Nutr 2010;92:1326–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Gilmore LA, Ravussin E, Bray GA, Han H, Redman LM. An objective estimate of energy intake during weight gain using the intake-balance method. Am J Clin Nutr 2014;100:806–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Thomas DM, Martin CK, Redman LM, Heymsfield SB, Lettieri S, Levine JA, Bouchard C, Schoeller DA. Effect of dietary adherence on the body weight plateau: a mathematical model incorporating intermittent compliance with energy intake prescription. Am J Clin Nutr 2014;100:787–95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Levine JA, Eberhardt NL, Jensen MD. Role of nonexercise activity thermogenesis in resistance to fat gain in humans. Science 1999;283:212–4. [DOI] [PubMed] [Google Scholar]
- 15.Hall KD. Mathematical modelling of energy expenditure during tissue deposition. Br J Nutr 2010;104:4–7. [DOI] [PubMed] [Google Scholar]
- 16.Franz MJ, VanWormer JJ, Crain AL, Boucher JL, Histon T, Caplan W, Bowman JD, Pronk NP. Weight-loss outcomes: a systematic review and meta-analysis of weight-loss clinical trials with a minimum 1-year follow-up. J Am Diet Assoc 2007;107:1755–67. [DOI] [PubMed] [Google Scholar]
- 17.Chow CC, Hall KD. Short and long-term energy intake patterns and their implications for human body weight regulation. Physiol Behav (in press). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Horgan GW. The behaviour of a neutral model of weight regulated only by body mass. J Theor Biol 2011;270:1–6. [DOI] [PubMed] [Google Scholar]
- 19.Payne PR, Dugdale AE. Mechanisms for the control of body-weight. Lancet 1977;1:583–6. [DOI] [PubMed] [Google Scholar]


